Open Access Article
Open Access ArticlePhysico-chemical and biological properties of C60-L-hydroxyproline water solutions†
Konstantin N. Semenov *a,
Anatolii A. Meshcheriakova,
Nikolay A. Charykovb,
Maria E. Dmitrenkoa,
Viktor A. Keskinovb,
Igor V. Murina,
Gayane G. Panovac,
Vladimir V. Sharoykoa,
Elena V. Kanashc and
Yuriy V. Khomyakovc
*a,
Anatolii A. Meshcheriakova,
Nikolay A. Charykovb,
Maria E. Dmitrenkoa,
Viktor A. Keskinovb,
Igor V. Murina,
Gayane G. Panovac,
Vladimir V. Sharoykoa,
Elena V. Kanashc and
Yuriy V. Khomyakovc
aSaint-Petersburg State University, Universitetskii pr. 26, St. Petersburg, 198504, Russia. E-mail: semenov1986@yandex.ru; Fax: +7 812 2349859; Tel: +7 812 3476435
bSaint-Petersburg State Technological Institute (Technical University), Moskovskii pr., 26, St. Petersburg, 190013, Russia
cAgrophysical Research Institute, Grazhdansky pr. 14, St. Petersburg, 195220, Russia
First published on 7th March 2017
Abstract
This paper presents experimental data on a physico-chemical and biological study of C60-L-hydroxyproline derivative water solutions. The data on the temperature dependence of solubility in water, concentration dependences of density, specific conductivity, molar conductivity, and dissociation constants as well as experimental data on dynamic light scattering and biological effects on in vitro proliferation of cultured human epithelial kidney cells and in situ – on state of plants are presented and discussed.
1. Introduction
The relevance of studying derivatives of fullerenes with amino acids is mainly associated with their potential applications in biology and medicine.1–3 We will briefly discuss the main results obtained in this area. Kotelnikova et al. studied the influence of water-soluble derivatives of C60 with DL-alanine and DL-alanyl-DL-alanine on the structure and permeability of the lipid bilayer of liposomes based on phosphatidylcholine.4 Hu et al. synthesized and characterized amphiphilic derivatives of C60 with alanine, cysteine and arginine. It was revealed that these compounds can penetrate into the cell membrane and reduce the accumulation of reactive oxygen species (ROS) and cell injury caused by hydrogen peroxide in the pheochromocytoma cells (PC12).5 Kumar et al. synthesized a conjugate of C60 with lysine and studied the biological properties of the obtained compound.6 It was shown that a C60 – lysine derivative demonstrates a high effectiveness against cleavage of DNA upon irradiation with visible light in the presence of a reduced form of nicotinamide adenine dinucleotide (NADH). Jiang et al. synthesized a derivative of C60 with glycine.7 It was shown that the C60 – glycine derivative leads to the death of cancer cells, and the effectiveness of the synthesized compound increases in a dose-dependent manner.7 Authors of ref. 8 and 9 have explored the neuroprotective properties of hybrid structures based on C60 and derivatives of proline. Kotelnikova et al. studied the antioxidant properties of water-soluble derivatives of C60 with sodium salts of aminobutyric and aminocaproicacid.10 The authors revealed that amino acid derivatives are potential suppressors of cytomegalovirial infection.Jennepalli et al. carried out the synthesis of mono and bis[60]fullerene-based dicationic peptoids.11 The resulting hydrophobic, scaffolded di- and tetra-cationic derivatives were tested against Staphylococcus aureus NCTC 6571 and Escherichia coli NCTC 10418. Zhang et al. synthesized N-substituted, 3,4-fullero pyrrolidine according to the 1,3-dipolar cycloaddition of azomethineylide and concluded that synthetized compounds would have unique properties and potential uses in medicine and biology.12
Additional groups of scientific articles are devoted to the theoretical study of fullerene derivatives with amino acids: (i) the ability of C60 fullerene to interact with amino acids (the calculation was performed using DFT-B3LYP/3-21G);13 (ii) calculation of the molecular structure of hybrid derivatives based on C60 and amino acids using quantum-chemical methods;14 and (iii) calculation of dissociation constants (pKa) of fullerene derivatives with amino acids.15 A series of experimental papers devoted to the (i) investigation of pH, ionic strength and nature of the substituent influence on the C60 – amino acids, peptides derivatives degree of association,16–21 (ii) measuring of heat capacities of the amino acids and peptides derivatives aqueous solutions,22 (iii) studying of temperature dependence of solubility in water, concentration dependences of density, specific conductivity, molar conductivity, dissociation constant, activity coefficients as well as size distribution in water solutions should also be mentioned.23–25
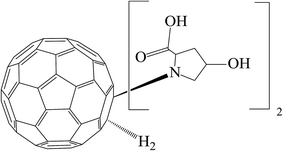
The present paper is devoted to a physico-chemical and biological investigation of water solutions of the C60-L-hydroxyproline derivative (C60-Hyp) (Fig. 1) — C60(C5H9NO3)2 (isothermal and temperature dependences of the densities, concentration dependence of the refractive index, specific and molar conductivities, size distribution in water as well as the solubility of the C60-Hyp–water binary system and in vitro cytotoxic effect of C60-Hyp on human epithelial kidney cells (HEK293) and in situ – influence of the C60-Hyp on state of some plants are presented and discussed).
2. Experimental section
The amino acid derivative of C60 fullerene with L-hydroxyprolin (C60-Hyp) – C60(C5H9NO3)2 of a mass fraction purity of 99.8% was used for the physico-chemical investigation of the water solutions. The reagent was produced in Ltd ZAO “ILIP” (St. Petersburg). Additionally, we have carried out the identification of the purchased C60-Hyp using complex physico-chemical methods (IR and UV spectroscopy, mass-spectrometry, elemental analysis).The measurements of the concentration dependence of the density of the C60-Hyp aqueous solutions was performed using a pycnometer method. We used a quartz pycnometer, and the volume calibration was performed with distilled water. The accuracy of the temperature control during the density measurements was ΔT = ±0.1 ÷ 0.2 K degrees, and the accuracy of the density determinations was equal to Δρ = ±0.001 g cm−3. The series of the C60-Hyp water solutions were prepared by dilution of the stock solution at 298.15 ± 0.05 K.
The concentration dependence of the refractive index of the C60-Hyp derivative water solutions (nD20) was measured by refractometry using an Abbe refractometer IRF-454B2M (measurement limits in transmission light nD25 = 1.3–1.7, ΔnD20 = ±0.0001, the accuracy of temperature control ΔT = ±0.2 K).
The temperature dependence of the C60-Hyp derivative solubility in water in the temperature range 293.15–353.15 K was carried by the method of isothermal saturation in ampoules. The saturation time was equal to 8 h; the temperature was maintained with an accuracy equal to ±0.05 K. For the C60-Hyp water solution saturation, the LAUDA ET 20 thermostatic shaker was used at a shaking frequency ω ≈80 c−1, and quantitative determination of the C60-Hyp concentrations in water was performed using a spectrophotometric technique at 330 nm (after the dilution and cooling of the saturated solutions). The relative uncertainty of the solubility determination was equal to ±5%. Relative air humidity was 40–50%.
For the thermal investigation of the C60-Hyp derivative, we used a NetzschSTA 449 F1 Jupiter and Netzsch QMS 403CAeolos apparatus, and the temperature range was 303.15–1300.15 K in the air. The heating rate was 5 K min−1.
For determination of the specific conductivity of the C60-Hyp water solutions, the Cyber Scan PC-300 measuring device was used. The relative uncertainty of the specific conductivity determination was equal to ±1%. The solutions used were saturated by atmospheric air.
The measurements of the C60-Hyp nanoparticle size distribution in aqueous solutions of different concentrations and the electrokinetic potential measurements were carried out by dynamic light scattering on the Malvern Zetasizer (Great Britain) device. The relative uncertainty of the zeta-potential determination was equal to 5% (Δς = ±5 arb.%).
For the cytotoxicity assay of the C60-Hyp, the human embryonic kidney cells (HEK 293) were cultured in a CO2-incubator at 310.15 K in a humidified atmosphere containing air and 5% CO2. HEK 293 cells were obtained from BioloT (Saint Petersburg, Russian Federation) and were grown in Dulbeccos Modified Eagle's Medium (BioloT) containing 10% (v/v) heat-inactivated fetal bovine serum (FBS, HyClone Laboratories, UT, USA), 1% L-glutamine, 50 U ml−1 penicillin, and 50 μg ml−1 streptomycin (BioloT).
The toxicity of the C60-Hyp was assessed using a standard colorimetric assay of functionality of mitochondrial dehydrogenases with tetrazolium dye – 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT-assay). HEK293 cells were plated at a density of 10 × 103 cells per 200 μl per well in 96-well microtiter tissue culture plates (Falcon, USA) and were given time to adhere to the plate. After overnight culture, fresh Dulbeccos Modified Eagle's Medium containing different concentrations of the C60-Hyp (0–100 μM) was added into the wells, and the HEK293 cells were incubated for 48 h. After that, 100 μl per well of Dulbeccos modified Eagle's medium and 20 μl of a 2.5 mg ml−1 MTT solution were added, and the cells were incubated for 1 h at 310.15 K. After careful removal of the supernatants, the MTT-formazan crystals formed by the metabolically viable cells were dissolved in dimethyl sulfoxide (100 μl per well), and the absorbance was measured at 540 nm and 690 nm in a multimodal plate reader (Varioskan™ LUX, Thermo Fishes Scientific). Statistical analysis of the MTT data was done utilizing the Student t-test. Differences between the mean values were considered significant when p <0.05.
Estimation of the biological activity of the C60-Hyp derivative included determination of the concentration ranges with positive, neutral and inhibiting effects on germination of the “Ajur” variety cress (Lepidium sativum L.) seeds as well as on roots and sprout growth within 7 days after the seed soaking. The control samples were grown in pure water. After 3 days, we determined the seeds germinating energy, and after 7 days, we calculated the germinative ability of the seeds and measured the root and sprout lengths. The investigation was carried out according to the International seed testing association rules (ISTA) and generally accepted methods.26–29 All experiments were repeated in triplicate.
The C60-Hyp plant growth stimulating ability, influence on the photosynthetic apparatus function in leaves as well as the antioxidant properties of the plants were determined in two vegetation experiments carried out in a controlled environment with spring barley (Hordeum vulgare L.). The plant growth was performed using aeration tanks with hydroponic solutions and artificial illumination.30 The C60-Hyp concentration in the hydroponic solution containing micro and macro-elements was equal to 1 mg l−1.31
The plants grown using the nutrient solution without C60-Hyp in the pH range 6.2–6.9 were used as a control. Aerating of the solutions was performed continuously using compressors and air-conducting elements. Changing the solutions as well as pH monitoring were performed every three days. Experiments were carried out under the following conditions: duration of light period was equal to 14 hours, the temperature was maintained within 25 ± 2 °C, and the relative humidity was equal to 65 ± 5%.
For estimation of the physiological state of the plants, we used a spectroscopic method based on the radiation reflection from the leaves' surfaces. The reflective spectra were registered in situ using the fiber-optic spectroradiometric system Ocean Optics (USA) with an optical resolution of 0.065 nm. For spectroscopic investigations, we used well-formed and established leaves. All spectra we recorded for no fewer than 10 plants and repeated in duplicates. According to the obtained data, we calculated the reflective indexes32,33 and the chlorophyll (ChlRI) and anthocyanin (ARI) indexes (eqn (1) and (2)):
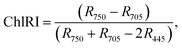 | (1) |
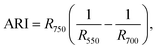 | (2) |
Both of the indexes (ChlRI and ARI) are in a correlation with the net productivity of plants, which allowed an estimation of the physiological state of plants.32,33
The assimilated surface area of the leaves was calculated according to eqn (3):
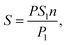 | (3) |
Evaluating the C60-Hyp ability to influence the antioxidant properties of plants was performed according to generally accepted methods.36–39 For the antioxidant properties investigation, we determined several parameters: (i) intensity of lipid peroxidation, (ii) total content of ROS, and (iii) superoxide dismutase (SOD) activity.
The intensity of the lipid peroxidation in barley leaves was determined by measuring the malondialdehyde–thiobarbituric acid adducts.36,37
ROS content was evaluated according to the method based on transformation of adrenalin to adrenochrome with a further spectrophotometric analysis of the adrenochrome concentration at 480 nm. The rate of superoxide radical formation was calculated according to eqn (4):
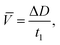 | (4) |
SOD activity was measured using a method based on the ability of SOD to compete with nitroblue tetrazolium dye for superoxide radicals.39
After finishing the vegetation experiments, the plant growth biometrics were measured: the length of the roots and aboveground parts of the plant, number of culms and leaves, total mass of the plants as well as the masses of the plant organs: culms, leaves and roots. The root length values corresponded to the length of the longest root and the length of the aboveground parts corresponding to the highest plant shoots. The Wilcoxon rank test was used for statistical analysis. Differences between the mean values were considered significant when p <0.05. All calculations were performed in the Statistica 8 program.
3. Results and discussion
3.1 Isothermal solution densities
Experimental data on the isothermal water solutions densities of the C60-Hyp derivative are presented in Fig. 2. The concentration dependence of the average molar volume (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) of the solution components was calculated, according to the classical thermodynamic equation (eqn (5)):
) of the solution components was calculated, according to the classical thermodynamic equation (eqn (5)):
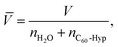 | (5) |
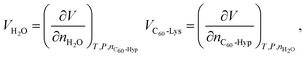 | (6) |
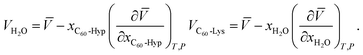 | (7) |
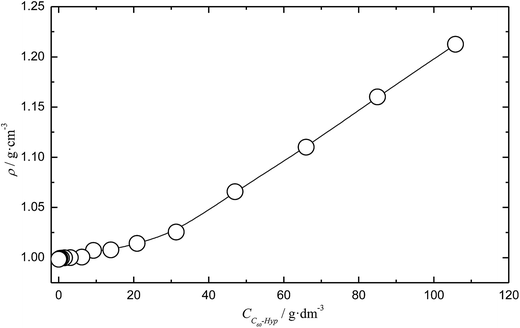 | ||
| Fig. 2 Concentration dependence of the C60-Hyp water solution density (ρ) at 298.15 K. CC60-Hyp is a volume concentration of the C60-Hyp derivative. | ||
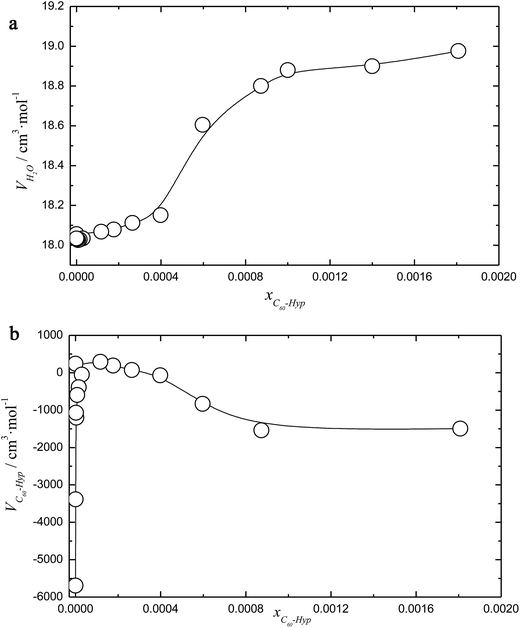
The concentration dependence of the average molar volume (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) and partial molar volumes of the water solution components (VH2O and VC60-Hyp) are represented in Fig. 3 and 4. An analysis of Fig. 3 and 4 shows that the VC60-Hyp(xC60-Hyp) – function is convex–concave, thus, the
) and partial molar volumes of the water solution components (VH2O and VC60-Hyp) are represented in Fig. 3 and 4. An analysis of Fig. 3 and 4 shows that the VC60-Hyp(xC60-Hyp) – function is convex–concave, thus, the 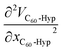 derivative changes to negative in the area of infinitely diluted solutions to positive in the area of more concentrated solutions. The opposite situation takes place with the concentration dependence of VH2O. The latest function is concave–convex, and the
derivative changes to negative in the area of infinitely diluted solutions to positive in the area of more concentrated solutions. The opposite situation takes place with the concentration dependence of VH2O. The latest function is concave–convex, and the 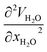 function changes from positive in the area of infinitely diluted solutions to negative in more concentrated solutions.
function changes from positive in the area of infinitely diluted solutions to negative in more concentrated solutions.
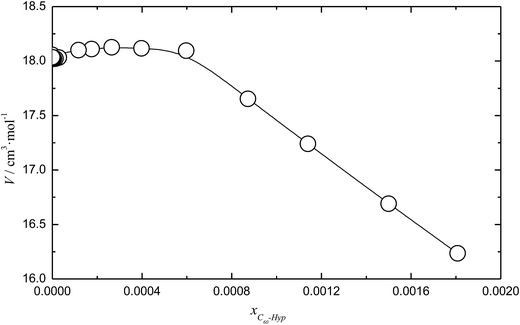 | ||
| Fig. 3 Mole fraction (xC60-Hyp) dependence of the average molar volume (V) of the C60-Hyp water solution at 298.15 K. | ||
 | ||
| Fig. 4 Mole fraction dependence of the partial volumes (VH2O and VC60-Hyp) of the solution components (a and b) at 298.15 K. | ||
One can see that in the area of diluted solutions, the concentration dependence of the C60-Hyp partial molar volume is rather complex. Fig. 4b shows the fast increasing of the VC60-Lys(xC60-Hyp) function in the area of low concentrations, xC60-Hyp <3 × 10−5. The high absolute values of the C60-Hyp partial molar volumes in the concentration range xC60-Hyp <3 × 10−5 reveal that the addition of even small portions of the C60-Hyp derivative result in extreme compactness and structures the solution. This fact demonstrates that the C60-Hyp molecules are naturally embedded in the structure of the solution and occupy the volume corresponding to the electronic structure. Moreover, the VC60-Lys values in the area of the infinitely diluted solutions exceed (in modulus) the value of the average molar volume of the solid C60-Hyp more than 20 times. The same dependences were previously demonstrated for binary system carboxylated fullerenes (C60[C(COOH)2]3, C70[C(COOH)2]3)–water,43,44 fullerenols (C60(OH)22–24, C70(OH)12)–water,45,46 C60-Arg–water.25
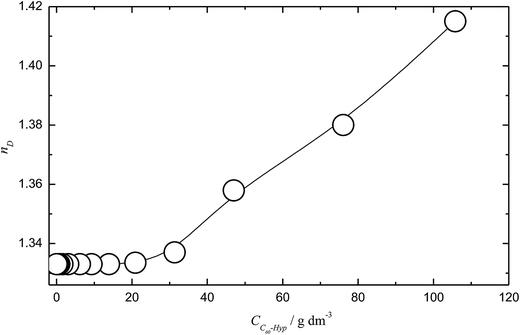
3.2 Refraction of water solutions
The concentration dependence of the C60-Hyp water solutions' refraction index (nD25) is presented in Fig. 5. The concentration dependences of specific and molar refractions of the C60-Hyp aqueous solutions at 298 K were calculated using (eqn (8) and (9)).47
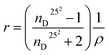 | (8) |
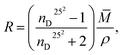 | (9) |
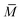 is the average molecular weight of the solution:
is the average molecular weight of the solution: ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = xH2O·MH2O + xC60-Hyp·MC60-Hyp (g mol−1). Concentration dependencies of molar and specific refractions are presented in the ESI† (Fig. 1 and 2). According to the rule of additivity of the solution refractions, we can obtain (eqn (10) and (11)):47
= xH2O·MH2O + xC60-Hyp·MC60-Hyp (g mol−1). Concentration dependencies of molar and specific refractions are presented in the ESI† (Fig. 1 and 2). According to the rule of additivity of the solution refractions, we can obtain (eqn (10) and (11)):47
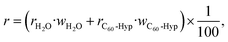 | (10) |
| R = RH2O·xH2O + RC60-Hyp·xC60-Hyp | (11) |
We can also calculate the C60-Hyp molar refraction according to the Eisenlohr additivity rule35 using the atomic refractions – Ri(j) of the i-th atom in the j-th functional group:
Radd ≈ 70Rc + 4RO(–OH) + 2RO(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CO) + 2RN(–NH2) + 18RH + 2R CO) + 2RN(–NH2) + 18RH + 2R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ≈ 208 ± 10 cm3 mol−1, ≈ 208 ± 10 cm3 mol−1,
| (12) |
The discrepancy in the molar refraction calculation is connected to the choice of the spectral lines (Hα[λ = 658.3 (nm)] and Hγ[λ = 436.1 (nm)]).
The specific refraction of the C60-Hyp derivative can be calculated using (eqn (13)):
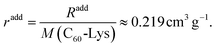 | (13) |
The values of the specific and molar refractions calculated according to the Eisenlohr additivity rule well agreed with the date calculated from the solution refraction indexes. Moreover, the value of the C60-Hyp specific refraction is very close to the specific refraction of water – (radd(HOH) ≈ 0.207 ± 0.003 cm3 g−1).
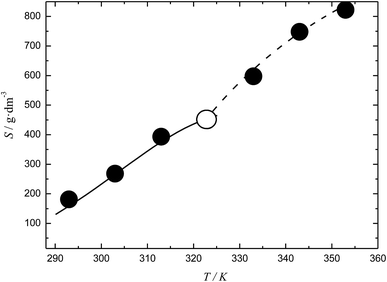
3.3 Temperature dependence of the C60-Hyp solubility in water and water solution densities
The temperature dependences of the C60-Hyp solubility and density in water are presented in Fig. 6. One can see the following: (i) the C60-Hyp derivative is rather soluble in water (hundreds g dm−3), and such values correspond to the solubility of soluble phases such as fullerenol-d45 or, for example, halite—NaCl;48 (ii) the diagram of the solubility consists of two branches corresponding to the solubility of the crystallohydrate C60(C5H9NO3)2·2H2O (low-temperature branch) and non-hydrated fullerene derivative C60(C5H9NO3)2 (high-temperature branch). Such dependences are not surprising, for example, the same dependences take place in the C60–nonane, C60(C70)–butanoic acid binary systems.49,50 In addition, the branch of the C60(C5H9NO3)2·2H2O crystallization produced in the metastable region is situated almost on the same line as the branch of crystallization for the non-hydrated fullerene derivative; (iii) the solubility diagram consists of one nonvariant point (point O in Fig. 6) corresponding to simultaneous saturation by both solid phases (C60(C5H9NO3)2·2H2O and C60(C5H9NO3)2); (iv) the solubility of the crystallohydrate C60(C5H9NO3)2·2H2O and C60(C5H9NO3)2 significantly increases with the increasing temperature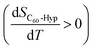 .
.
The same singularity in the phase transition in the solid phase was observed for the temperature dependence of the density (ρ(T)) for the C60-Hyp–water system (Fig. 5 of ESI†). The complex density dependence of the solubility can be caused by several factors: decreasing the solvent and solution densities; symbate changing of the solution densities and concentrations of the C60-Hyp solutions.
3.4 Conductivity of water solutions of C60-Hyp
The concentration dependence of the specific electric conductivity of the C60-Hyp water solutions at 298.15 K was investigated by carrying out measurements of the specific resistance of the solutions ρ (ohm cm):51
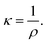 | (14) |
The specific electric conductivity corresponds to the conductivity of the unit volume of solution located between two parallel planar electrodes (at the distance of 1 cm) with the surface equal to 1 cm2. One can see (Table 1) that the dependence κ(CM) (CM is molarity of the C60-Hyp water solution) increases with the increasing concentration.
| C/g dm−3 | M/mol dm−3 | α | κ/S cm−1 | λ/S cm2 mol−1 | pKD |
|---|---|---|---|---|---|
| 0 | 0 | 1.00 (extrapolation) | 0.00 | 1455 (extrapolation) | 4.2 (extrapolation) |
| 0.109 | 1.126 × 10−4 | 0.77 | 1.255 × 10−4 | 1115 | 4.2 |
| 0.219 | 2.262 × 10−4 | 0.68 | 2.240 × 10−4 | 990 | 4.3 |
| 0.437 | 4.514 × 10−4 | 0.64 | 4.223 × 10−4 | 935 | 4.4 |
| 0.875 | 9.039 × 10−4 | 0.62 | 8.115 × 10−4 | 897 | 4.4 |
| 1.750 | 1.81 × 10−3 | 0.59 | 1.55 × 10−3 | 855 | 4.4 |
| 2.500 | 2.58 × 10−3 | 0.56 | 2.09 × 10−3 | 809 | 4.4 |
| 5.000 | 5.17 × 10−3 | 0.53 | 4.00 × 10−3 | 774 | 4.2 |
Molar electric conductivity (λ – S cm2 mol−1), i.e., conductivity of the electrolyte volume containing 1 mole of the solute, was calculated using (eqn (15)):51
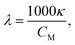 | (15) |
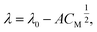 | (16) |
The apparent degree of dissociation α was calculated, according to eqn (17):51
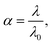 | (17) |
The calculated values of the apparent degree of dissociation are presented in Table 1 (λ0 ≈ 1.5 × 103 S cm2 mol−1). The analysis of Table 1 shows that in the whole concentration range, the C60-Hyp is a middle-strength and strong electrolyte. We propose the protonic mechanism of the C60-Hyp derivative dissociation according to the following scheme eqn (18):
| C60(C4H6NOCOOH)2H2 ↔ C60(C4H6NOCOOH)H2C4H6NOCOO− + H+ | (18) |
The concentration dependence of the concentration dissociation constant – KD (see Table 1) was calculated according to the “Ostwald dilution law” (neglecting the activity coefficients of the ions and non-dissociated molecules – γi = γ± = 1):51
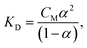 | (19) |
The thermodynamic dissociation constant – KthermD was calculated by extrapolation of KD(CM) dependence into the region of an infinitely diluted solution:
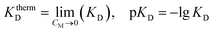 | (20) |
According to our calculation, pKthermD = 3.7.
It should be noted that the calculation of the concentration dependence of pKD is conventional because the C60-Hyp particles exist in solution in the form of large colloid species. Thus, the amino acid moieties may be hidden from water, and the real number of the ionizing groups is lower than the formal molar concentration presented in eqn (19) and (20).
3.5 Size distribution of the C60-Hyp associates in water solutions
The experimental data on the concentration dependence of the size distribution of the C60-Hyp associates in water solutions at 298.15 K are represented in Fig. 7 and Table 2. From the experimental and calculated data presented in Table 2, we can conclude the following: (i) no monomer molecules (with linear dimension-diameter ≈2 nm) were detected in all the investigated solutions (even in diluted solution);43–46 (ii) we observed the formation of three types of associates in the C60-Hyp–water binary system in the concentration range up to 5 g dm−3: a first order associate with linear dimensions of 40 nm, a second order associate with linear dimensions of 200 nm and a third order associate with linear dimensions of 5000 nm; (iii) for the description of such experimental facts in the association process, the model of consequent hierarchical association can be used.45–48 We consider that the monomer spherical molecules form the first type spherical associates, and the first type spherical associates form the second type spherical associates. After that, the second type spherical associates form the third type spherical associates (the last one corresponds to the colloid heterogeneous system).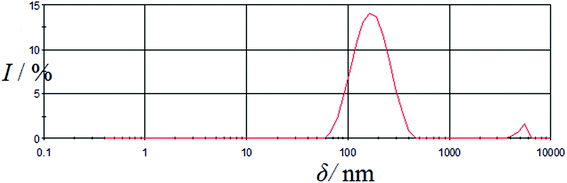 | ||
| Fig. 7 Size distribution of the C60-Hyp nanoparticles in aqueous solutions (1 g dm−3). I – intensity (%), δ – size of the associates (nm). | ||
| C/g l−1 | δ0/nm | δI/nm | δII/nm | δIII/nm | N0→1 | N0→2 | N0→3 | N1→2 | N1→3 | N2→3 | ξ/mV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | — | — | — | 1 | — | — | — | — | — | |
| 0.01 | — | 40 | 200 | — | 8 × 103 | 3 × 105 | — | 300 | — | — | −35 |
| 0.1 | — | 40 | 200 | — | 8 × 103 | 3 × 105 | — | 300 | — | — | −40 |
| 1.0 | — | — | 200 | 5000 | — | 3 × 105 | 2 × 109 | — | 5 × 105 | 8 × 103 | −40 |
| 2.5 | — | — | 200 | 5000 | — | 3 × 105 | 2 × 109 | — | 5 × 105 | 8 × 103 | −40 |
| 5 | — | — | 200 | 5000 | — | 3 × 105 | 2 × 109 | — | 5 × 105 | 8 × 103 | −50 |
The number of i-th type associates packed into the (i + 1)-th type associates – Ni→i+1 was estimated by the following equation:43–46
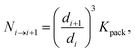 | (21) |
Additionally, the concentration dependence of the ξ-potential was measured for the C60-Hyp water solutions at 298 K. The experimental data on the ξ-potential determination are presented in Table 2 and Fig. 8. Analysis of the presented data reveals that the ξ-potential values of the investigated C60-Hyp water solutions are negative (in the concentration range 0.01–5 g l−1), and the ξ-potential values decrease from −35 mV (C = 0.01 g l−1) to −50 mV (C = 5 g l−1) with the increasing C60-Hyp concentration. We can conclude that the C60-Hyp colloid solutions are stable, and the stability of the colloid systems increases with the increasing solution concentration.
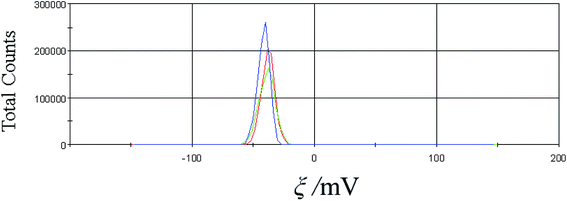 | ||
| Fig. 8 Zeta potential of the C60-Hyp water solution (C = 2.5 g dm−3). The measurements were repeated three times (red, blue and green curves). | ||
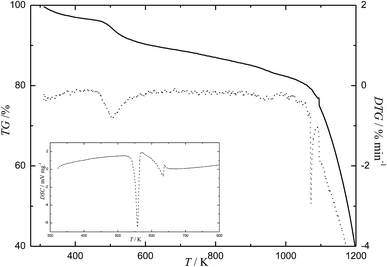
3.6 Complex thermal analysis of the C60-Hyp derivative
The results of the complex thermal analysis of the C60-Hyp derivative are presented in Fig. 9 and Table 3. Analysis of Fig. 9 reveals the following: (i) the C60-Hyp derivative is rather thermally sensitive under the conditions of the experiment. The C60-Hyp decomposition starts at 493 K, and the temperature of the complete decomposition is equal to 1103 K; (ii) Fig. 9 and Table 3 shows that in the temperature range of 303–473 K, the dehydration of the C60-Hyp crystallohydrate takes place and, at 493 K, the process of oxidative thermal degradation of the amino acid substituting group. The latest process is followed by dehydration (–H2O), denitrogenation (–N2), decarboxylation (–CO2). The above mentioned processes come to end at 1103 K. Thus, the fullerene core significantly stabilizes the amino acid substituting groups; (iii) the oxidation of the fullerene core (C60) starts at 1123 K.| No. | Tm/°C (Tb − Te)/K | Δmi/mcalc0 (%) | Δmi/mexp0 (%) | Process |
|---|---|---|---|---|
| 1 | 428.15, 303.15–473.15 | 3.5 | 3.7 | C60(C5H9NO3)2·2H2O → C60(C5H9NO3)2 + 2H2O |
| 2 | 623.15, 493.15–733.15 | 8.4 | 8.8 | C60(C5H9NO3)2 → C60(C4H9NO)2 + 2CO2 |
| 3 | 893.15, 773.15–1103.15 | 14.2 | 14.4 | C60(C4H9NO)2 + 11.5O2 → C60 + N2 + 8CO2 + 9H2O |
| 4 | 1173.15, 1123.15–1253.15 | >60 | >60 | Particular oxidation of C60 |
3.7 Biological activity of C60-Hyp
The results of the biological investigation performed using the cress (Lepidium sativum L.) and spring barley (Hordeum vulgare L.) revealed that the C60-Hyp derivative has significant biological activity. The treatment of the seeds by the water solutions of C60-Hyp leads to the following effects:(i) In the concentration range 0.1–25 mg l−1, we have determined the positive influence of the C60-Hyp derivative on plant growth during the early stages of ontogeny; (ii) in the concentration range up to 0.1 mg l−1, we did not detect any noticeable effects of C60-Hyp on plant growth; (iii) treatment of plants by C60-Hyp solutions in the concentration region from 50 to 100 mg l−1 leads to decreasing germinating ability. Further increasing the C60-Hyp concentration up to 500 mg l−1 results in decreasing germinating ability and the lengths of the roots or sprouts (Table 4).
| C60-Hyp concentration, mg l−1 | Germination energy | Germination capacity | Shoot length | Root length | ||||
|---|---|---|---|---|---|---|---|---|
| % | % to control | % | % to control | cm | % to control | cm | % to control | |
| a Significant difference from control at p <0.05. | ||||||||
| 0 (water) | 61 | 100 | 70 | 100 | 3.9 ± 0.3 | 100 | 5.5 ± 0.5 | 100 |
| 0.001 | 63 | 103 | 72 | 103 | 4.2 ± 0.5 | 108 | 5.7 ± 0.5 | 104 |
| 0.01 | 57 | 93 | 70 | 100 | 4.2 ± 0.3 | 108 | 5.6 ± 0.7 | 102 |
| 0.1 | 51a | 84a | 68 | 97 | 4.5 ± 0.3a | 115a | 5.8 ± 0.8 | 106 |
| 1 | 43a | 71a | 65 | 93 | 4.7 ± 0.3a | 121a | 6.0 ± 0.7 | 109 |
| 10 | 30a | 49a | 64 | 91 | 4.7 ± 0.3a | 121a | 6.4 ± 0.6 | 116 |
| 25 | 32a | 53a | 67 | 96 | 4.4 ± 0.3 | 113 | 6.2 ± 0.7 | 113 |
| 50 | 25a | 41a | 56a | 80a | 4.3 ± 0.3 | 110 | 5.7 ± 0.6 | 104 |
| 100 | 20a | 33a | 50a | 71a | 4.1 ± 0.3 | 105 | 5.3 ± 0.5 | 96 |
| 500 | 16a | 26a | 44a | 63a | 3.1 ± 0.3a | 79a | 4.2 ± 0.5a | 76a |
The values of the germination energy determined after 3 days of seed steeping in water solutions of C60-Hyp showed the retarding of seed germination in the concentration range 0.1–500 mg l−1. Additionally, in the concentration range 0.1–25 mg l−1, the effect of seed germination retarding was temporary, and after six days, the germinating ability characteristics were the same as the control experiments.
For carrying out the vegetation experiment, the concentration of C60-Hyp was equal to 1 mg l−1 for introducing the plant root zone.
Addition of 1 mg l−1 of the C60-Hyp derivative to the aerating rooting medium under the hydroponic method of barley growing leads to an increase in the leaf surface area and the chlorophyll content (Table 5).
| Experimental conditions | Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Index of pigment content, relative units | Area of assimilating leaf surface, cm2 | Dry mass, g | |||||
| ChlRI | ARI | Roots | Stalks | Leaves | Total | ||
| a * Significant difference from control at p <0.05. ** The average parameters are presented. | |||||||
| Control, absolute values | 0.41–0.45 | 0.55–0.72 | 168–374 | 0.10–0.19 | 0.24–0.25 | 0.35–0.41 | 0.69–0.85 |
| C60-Hyp, absolute values | 0.45–0.51* | 0.43*–0.58* | 192*–348 | 0.23*–0.34* | 0.38*–0.41* | 0.48*–0.53* | 1.12*–1.24* |
| C60-Hyp, deviation to control, % | +10 to +13* | −22* to −19* | −7 to +14* | +79* to +130* | +58* to +64* | +29* to +37* | +46* to +62* |
| Hydroxyprolin, absolute values | 0.44–0.49 | 0.54–0.61* | 222*–292* | 0.24*–0.33* | 0.30*–0.36* | 0.48*–0.54* | 1.03*–1.22* |
| Hydroxyprolin, deviation to control, % | +7 to +9 | −15* to −2 | −22* to +32* | +74* to +140* | +25* to +44* | +32* to +37* | +44* to +49* |
The obtained data revealed that the addition of C60-Hyp leads to the formation of a photosynthetic apparatus with a higher potential for photosynthesis and accumulation of dry matter in the plant. Moreover, the decreasing anthocyanin index and increasing plant growth parameters were observed in the presence of the C60-Hyp water solution in barley rooting medium. The latest fact indirectly confirms the improvement of the physiological state of plants (Table 5).
Addition of C60-Hyp to the nutrient solution leads to an increase of the total plant biomass of 46–62%, in particular increasing the leaves, stems and root mass. The statistical analysis of the obtained data based on a nonparametric statistics method as well as the Wilcoxon test revealed the fidelity of the experimental results.
Moreover, it was determined that in comparison with pure L-hydroxyproline, the C60-Hyp derivative has a stronger influence on the physiological state of barley plants and their stem growth and an equal influence on the leaves and root growth. The latest fact shows the formation of plants with higher values of biomass under the influence of C60-Hyp (see Table 5).
Additionally, we have determined that the presence of C60-Hyp in the nutrient solutions influence the antioxidant properties of plants. In particular, the level of lipid peroxidation in barley leaves decreased by 18% and the superoxide dismutase activation in roots by 18% with a concomitant increase in the ROS generation in the leaves and roots (see Table 6).
| Parameters | Leaves | Roots | ||||
|---|---|---|---|---|---|---|
| Control, absolute values | C60-Hyp | Control, absolute values | C60-Hyp | |||
| Absolute values | Deviation to control, % | Absolute values | Deviation to control, % | |||
| a Significant difference from control at p <0.05. | ||||||
| Lipid peroxidation, mM g−1 | 0.0065 | 0.0053a | −18a | 0.0069 | 0.0069 | 0 |
| SOD, relative units | 1.0680 | 0.9513 | −11 | 1.0770 | 1.2669a | +18a |
| ROS, relative units | 3.3300 | 3.8700a | +16a | 0.3300 | 0.63a | +91a |
The ambiguity of the obtained experimental data can be explained by the ROS participating in the plant metabolism as well as the immunomodulatory effect of the C60-Hyp derivative. The action of C60-Hyp can be compared to a vaccine starting the immune response to a hazardous factor before its affection and significantly increasing the plant resistance.
3.8 Cytotoxicity of the C60-Hyp derivative
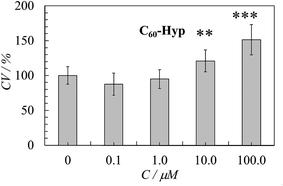
The MTT-assay for the HEK29 cells revealed that a 48 h incubation with the C60-Hyp derivative did not change the cell viability in the concentration range from 0.1 and 1.0 μM or significantly increased in the concentration range from 10.0 and 100.0 μM (Fig. 10). These results indicated that the C60-Hyp in the concentration range of 1–100 μM is nontoxic for human embryonic kidney cells and increases cell proliferation.4. Conclusions
The complex novel physico-chemical properties of C60-Hyp water solutions were investigated. The concentration dependence of the density was investigated by the pycnometer method; the average molar and partial volumes of the solution components were calculated at 298.15 K. By the isothermal saturation method, the temperature dependence of the solubility of the C60-Hyp–water binary system was studied. The specific and molar conductivities, dissociation constant and apparent degree of dissociation were calculated for the C60-Hyp water solutions. By the dynamic light scattering method, the average size of the C60-Hyp associates was determined.The biological study of C60-Hyp revealed the plant growth stimulating ability at certain concentrations caused by the positive influence of the C60-Hyp derivative on the photosynthesis apparatus work and antioxidant properties.
The C60-Hyp used for the in vitro study of HEK293 cells was non-toxic. The moderate stimulatory effect of the C60-Hyp on cell proliferation (about 1.5 times) was shown on cultured HEK293 cells. Therefore, the C60-Hyp might be a very attractive agent with potential utility in medicine and cosmetology to treat, for example, injury and wounds, such as muscle or tendon recovery, burns, after surgery, and to promote collagen production. The biological effect of the C60-Hyp and molecular mechanisms of its action require further detailed studies. The urgency of such investigations are closely connected with possibilities for application of the obtained results for the development and optimization of the water-soluble amino acid derivatives of fullerene application in biology and medicine.
Acknowledgements
This work was supported by the Russian Fund of Fundamental Investigations – RFFI (Projects No. 16-08-01206, 15-08-08438, 15-29-05837), by the Grant of the President of Russian Federation for supporting young scientists MK-4657.2015.3 and the Grant from St. Petersburg State University (No. 12.42.1003.2016). Research was performed using the equipment of the Resource Centers ‘GeoModel’, Center for Chemical Analysis and Materials Research, Center on Development of Molecular and Cell Technologies as well as Center for Thermogravimetric and Calorimetric Research of Research park of St. Petersburg State University.References
- L. N. Sidorov and M. A. Yurovskaya, Fullerenes, Ekzamen, Moscow, 2005 Search PubMed.
- F. Cataldo and T. Da Ros, Carbon materials: Chemistry and Physics: Medical Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotube, Springer, Berlin, 2008 Search PubMed.
- L. B. Piotrovskii and O. I. Kiselev, Fullerenes in biology, Rostok, Saint-Petersburg, 2006 Search PubMed.
- R. A. Kotelnikova, A. I. Kotelnikov, G. N. Bogdanov, V. S. Romanova, E. F. Kuleshova, Z. N. Parnes and M. E. Volpin, FEBS Lett., 1996, 389, 111–114 CrossRef CAS PubMed.
- Z. Hu, W. Guan, W. Wang, L. Huang, X. Tang, H. Xu, Z. Zhu, X. Xie and H. Xing, Carbon, 2008, 46, 99–109 CrossRef CAS.
- A. Kumar, M. V. Rao and S. K. Menon, Tetrahedron Lett., 2009, 50, 6526–6530 CrossRef CAS.
- G. Jiang, F. Yin, J. Duan and G. Li, J. Mater. Sci.: Mater. Med., 2015, 26, 1–7 CAS.
- V. V. Grigoriev, L. N. Petrova, T. A. Ivanova, R. A. Kotelnikova, G. N. Bogdanov, D. A. Poletayeva, I. I. Faingold, D. V. Mishchenko, V. S. Romanova, A. I. Kotel'nikov and S. O. Bachurin, Biol. Bull., 2011, 38, 125–131 CrossRef CAS.
- L. V. Tatyanenko, O. V. Dobrokhotova, R. A. Kotelnikova, D. A. Poletayeva, D. V. Mishchenko, I. Y. Pikhteleva, G. N. Bogdanov, V. S. Romanova and A. I. Kotelnikov, Pharm. Chem. J., 2011, 45, 329–332 CrossRef CAS.
- R. A. Kotelnikova, I. I. Faingold, D. A. Poletaeva, D. V. Mishchenko, V. S. Romanova, V. N. Shtolko, G. N. Bogdanov, A. Y. Rybkin, E. S. Frog, A. V. Smolina, A. A. Kushch, N. E. Fedorova and A. I. Kotelnikov, Russ. Chem. Bull., 2011, 6, 1172–1176 CrossRef.
- S. Jennepalli, K. A. Hammer, T. V. Riley, S. G. Pyne and P. A. Keller, Eur. J. Org. Chem., 2015, 1, 195–201 CrossRef.
- J. Zhang, L. Yuan and Y. D. Zhang, Adv. Mater. Res., 2012, 463–464, 538–542 CAS.
- A. Leon, A. F. Jalbout and V. A. Basiuk, Chem. Phys. Lett., 2008, 452, 306–314 CrossRef.
- T. Y. Dolinina and V. B. Luzhkov, Russ. Chem. Bull., 2012, 61, 1631–1634 CrossRef CAS.
- V. B. Luzhkov, V. S. Romanova and A. I. Kotelnikov, Russ. Chem. Bull., 2014, 63, 567–571 CrossRef CAS.
- G. I. Timofeeva, A. A. Tepanov, V. A. Lopanov and V. S. Romanova, Russ. Chem. Bull., 2012, 61, 1635–1637 CrossRef CAS.
- G. I. Timofeeva and V. S. Romanova, Russ. Chem. Bull., 2010, 59, 284–287 CrossRef CAS.
- G. I. Timofeeva and V. S. Romanova, Russ. Chem. Bull., 2007, 56, 2389–2393 CrossRef CAS.
- G. I. Timofeeva, E. F. Kuleshova and V. S. Romanova, Mendeleev Commun., 1997, 7, 37–38 CrossRef.
- G. I. Timofeeva, E. F. Kuleshova and V. S. Romanova, Russ. Chem. Bull., 1997, 46, 472–475 CrossRef CAS.
- G. I. Timofeeva, V. S. Romanova and L. A. Lopanova, Russ. Chem. Bull., 1996, 45, 834–837 CrossRef.
- A. N. Danilenko, V. S. Romanova, E. F. Kuleshova, Z. N. Parnes and E. E. Braudo, Russ. Chem. Bull., 1998, 47, 2134–2136 CrossRef CAS.
- M. Y. Matuzenko, D. P. Tyurin, O. S. Manyakina, K. N. Semenov, N. A. Charykov, K. V. Ivanova and V. A. Keskinov, Nanosyst.: Phys., Chem., Math., 2015, 6, 704–714 CrossRef.
- M. Y. Matuzenko, A. A. Shestopalova, K. N. Semenov, N. A. Charykov and V. A. Keskinov, Nanosyst.: Phys., Chem., Math., 2015, 6, 715–725 CrossRef.
- A. A. Shestopalova, K. N. Semenov, N. A. Charykov, V. N. Postnov, N. M. Ivanova, V. V. Sharoyko, V. A. Keskinov, D. G. Letenko, V. A. Nikitin, V. V. Klepikov and I. V. Murin, J. Mol. Liq., 2015, 211, 301–307 CrossRef CAS.
- GOST 12038-84, Agricultural seeds. Methods for determining the germination, Moscow, 1985, p. 58 Search PubMed.
- H. T. Hartmann, D. E. Kester, F. T. Davies and R. L. Geneve, Plant propagation: Principles and Practices, Prentice-Hall, Englewood Cliffs NJ, 6th edn, 1997 Search PubMed.
- Methodical recommendations 2.1.7.2297-07, N. V. Rusakov and others, Justification hazard class of waste production and consumption according of phytotoxicity: Methodical recommendations, Moscow, 2007, pp. 7–9.
- ISTA, International Rules for Seed Testing, 2016, DOI:10.15258/istarules.2016.
- G. G. Panova, I. N. Chernousov, O. R. Udalova, A. V. Alexandrov, I. V. Karmanov, L. M. Anikina, V. L. Sudakov and V. P. Yakushev, Russ. Agric. Sci, 2015, 41, 17–21 Search PubMed.
- G. G. Panova, I. N. Ktitirova, O. V. Skobeleva, N. G. Sinjavina, N. A. Charykov and K. N. Semenov, Plant Growth Regul., 2016, 79, 309–317 CrossRef CAS.
- E. V. Kanash and J. A. Osipov, presented in part at the 7th European conference on precision agriculture, Wageningen, 2009 Search PubMed.
- V. P. Yakushev, E. V. Kanash, Y. A. Osipov, V. V. Yakushev, P. V. Lekomtsev and V. V. Voropaev, Agric. Biol., 2010, 3, 94–101 Search PubMed.
- D. A. Sims and J. A. Gamon, Remote Sens. Environ., 2002, 81, 337–354 CrossRef.
- M. N. Merzlyak, A. A. Gitelson, O. B. Chivkunova, A. E. Solovchenko and S. I. Pogosyan, Plant Physiol., 2003, 50, 785–792 Search PubMed.
- A. S. Lukatkin, Plant Physiol., 2002, 49, 697–702 Search PubMed.
- D. Mark Hodges, J. M. DeLong, C. F. Forney and R. K. Prange, Planta, 1999, 207, 604–611 CrossRef.
- A. C. Purvid, R. L. Shewfeld and J. W. Gegogeine, Physiol. Plant., 1995, 94, 743–749 CrossRef.
- G. F. Nekrasova and I. S. Kiseleva, Guide to Laboratory and Practical Exercises Environmental Plant Physiology, Ural State University AM Gorky, Ekaterinburg, 2008 Search PubMed.
- A. V. Storonkin, Thermodynamics of Heterogeneous Systems, LGU, Leningrad, 1967 Search PubMed.
- A. Muenster, Chemical Thermodynamics, Mir, Moscow, 1971 Search PubMed.
- A. G. Stromberg, Physical Chemistry, VisshajaShkola, Moscow, 1973 Search PubMed.
- O. S. Manyakina, K. N. Semenov, N. A. Charykov, N. M. Ivanova, V. A. Keskinov, V. V. Sharoyko, D. G. Letenko, V. A. Nikitin, V. V. Klepikov and I. V. Murin, J. Mol. Liq., 2015, 211, 487–493 CrossRef CAS.
- K. N. Semenov, N. A. Charykov, I. V. Murin and Y. V. Pukharenko, J. Mol. Liq., 2015, 201, 50–58 CrossRef CAS.
- K. N. Semenov, N. A. Charykov and V. N. Keskinov, J. Chem. Eng. Data, 2011, 56, 230–239 CrossRef CAS.
- K. N. Semenov, N. A. Charykov, I. V. Murin and Y. V. Pukharenko, J. Mol. Liq., 2015, 201, 1–8 CrossRef.
- B. V. Ioffe, Refractometric Methods, Khimia, Leningrad, 1983 Search PubMed.
- A. N. Kirginzev, L. N. Trushnikova and V. G. Lavrent'eva, Solubility of Inorganic Substances in Water, Khimia, Leningrad, 1972 Search PubMed.
- K. N. Semenov, N. A. Charykov, V. N. Postnov, V. V. Sharoyko and I. V. Murin, Russ. Chem. Rev., 2016, 85, 38–59 CrossRef CAS.
- K. N. Semenov, N. A. Charykov, V. N. Keskinov, A. K. Piartman, A. A. Blokhin and A. A. Kopyrin, J. Chem. Eng. Data, 2010, 55, 13–36 CrossRef CAS.
- B. B. Damaskin and O. A. Petrii, Introduction to electrochemical kinetics, Khimia, Moscow, 1983 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26621e |
| This journal is © The Royal Society of Chemistry 2017 |