Geometrical and electronic structures of small Co–Mo nanoclusters

Abstract

The geometries, energetics and electronic structures of Co₁₃, Mo₁₃, Co₁₂Mo and Mo₁₂Co clusters are systematically investigated by using the first principles method combined with a genetic algorithm. A new candidate is found for the ground-state geometry of Mo₁₃. Compared to the ground-state geometry of Co₁₃ possessing high stability, there are many isomers energetically closer to the ground-state of Mo₁₃. The relatively high stability of the pure Co₁₃ can be reduced by doping, but the isomerization near the ground-state of the pure Mo₁₃ can be suppressed by doping. With respect to that of the central doping Mo atom in the high symmetric close-packed geometry, there are significantly more d electrons near the Fermi energy of the Mo atom in the ground-state Co₁₂Mo cluster and as a result the d–d hybridization between the doped atom and the matrix is significantly enhanced. In contrast, compared to the excited structure with a relatively higher energy, the d–d hybridization near the Fermi energy between the doped atom and the matrix of the ground-state Mo₁₂Co cluster is significantly decreased, which implies that the d–d hybridization near the Fermi energy between the doped atom and the matrix is strongly influenced by the component ratio and geometry of the cluster, and the competition between them can have a crucial impact on the catalytic property of the mixed cluster. An explanation is proposed for the excellent catalytic abilities of the Co–Mo alloy nanoclusters with approaching component ratios in the catalytic growth of carbon nanotubes.

---

1 Introduction

In the past few decades, people have paid much attention to the study of small metal clusters (especially the transition-metal (TM) clusters). The unique physical and chemical properties of clusters are strongly dependent on their sizes and geometries.^1–3 Study on clusters has important scientific significance and potential applications in many fields such as optics, adsorption, catalysis, nano electronic devices and so on. The pure (mono-component) transition metal catalysts (i.e., Fe, Co and Ni) are often used in the catalytic chemical vapor deposition (CVD) synthesis of carbon nanotubes (CNTs),⁴ and extensive research has been performed to understand the role of the catalytic particles. The experimental investigations have revealed that some alloy (multi-component) transition metal particles (i.e., Co–Mo,^5–8 Fe–Mo^9,10 and Fe–Co¹¹) often lead to improved CNT growth as compared to the pure transition metal catalysts. For example, as comparing with the pure Co or Mo catalyst, the mixed Co–Mo nanoparticles show significant advancement towards the controlled production of single-walled carbon nanotubes (SWCNTs), and the capability of the Co–Mo catalysts depends on the Co : Mo component ratio, and the Co–Mo nanoparticles have the best catalytic abilities for producing the SWCNTs when the proportions of the two components are closer (Co : Mo = 2 : 1, 1 : 1 or 1 : 2).⁵ Considering that the physical and chemical properties (such as the catalytic property) of a cluster are strongly correlated with its geometry (especially the ground-state geometry), determination of the ground-state geometry of the mixed Co–Mo cluster has becoming the primary research content.

Among the numerous small sized clusters, the 13-atom clusters are especially concerned. Previous studies have pointed out that the ground states of 13-atom transition metal clusters tend to form high symmetric close-packed structures, but the recent first principles calculations show that for the 13-atom transition metal clusters most of their ground state structures are not inclined to form high symmetric close-packed structures. For example, for the 4d transition metal clusters, through strict theoretical calculations, some non close-packed structures such as the simple cubic structures¹² and the buckled biplanar (BBP) structures¹³ are found to be much more favorable in energy than the close-packed icosahedral structures.

The electronic structures and magnetic properties of 13-atom Co clusters with the high symmetric close-packed geometries (like the octahedron and icosahedron) are extensively investigated previously.^14–20 Through considering abundant initial configurations, the rigorous theoretical calculations have indicated that the ground-state geometry of Co₁₃ is a hexagonal bilayer (HBL) structure.^21–25 Dong et al.²¹ investigated the atomic and electronic structures of Co_N clusters (13 ≤ N ≤ 23) by density functional theory (DFT) calculations with the generalized gradient approximation (GGA) formulated by Perdew and Wang (PW91) and they found that the layer-like structures with hcp or fcc stacking are favorable in energy than the icosahedral structures (a energy difference of 1.63 eV is obtained for Co₁₃). Based on the spin-polarized DFT calculations within the GGA formulated by Perdew, Burke, and Ernzerhof (PBE), Piotrowski et al.²³ studied the geometrical, energetic and magnetic properties of 13-atom 3d, 4d and 5d transition metal clusters, and the HBL structure of Co₁₃ is found to be lower in energy (∼1.14 eV) than the icosahedron. Through adopting the all-electron DFT calculations within the BPW91-GGA exchange correlation functional, Gutsev et al.²⁵ studied the geometrical and electronic properties of the neutral and singly charged M₁₂ and M₁₃ (M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn) clusters and the HBL structure is confirmed as the lowest energy one of the neutral Co₁₃ cluster.

Compared to the large amount of studies on Co₁₃ clusters, researches on Mo₁₃ clusters are quite rare. Earlier the magnetic properties of 13-atom M clusters (M = Y, Zr, Nb, Mo, and Tc) with three possible high symmetry geometries have been studied by Deng et al.²⁶ using the discrete-variational local-spin-density-functional method, and the cuboctahedral structures are found to be more energetically stable than the icosahedral ones for Mo₁₃ and Tc₁₃ clusters. Using the first-principles calculations based on DFT and the plane-wave basis and Vanderbilt-type ultrasoft pseudopotentials, Chang et al.¹³ investigated the atomic geometries, electronic structures, and magnetic moments of 4d transition-metal clusters with 13 atoms, and they found that the ground-state geometry of Mo₁₃ is a strongly distorted icosahedral-like structure (which is about 1.83 eV lower in energy than the perfect icosahedron). After that, Zhang et al.²⁷ studied the Mo_N (N = 2–55) clusters within the framework of the DFT with a plane-wave basis set and the PW91-GGA exchange–correlation functional, and the ground-state Mo₁₃ is confirmed to be a distorted icosahedral-like structure. Recently Sun et al.²⁸ performed global optimization and property calculations by DFT with the PBE-GGA functional for a series of 4d transition-metal clusters M₁₃ (M = Y–Pd), and they found that the ground-state geometry of Mo₁₃ is a relatively loose structure without a central atom, and this lowest-energy structure is about 0.20 eV lower in energy than the distorted icosahedral-like structure. Subsequently, a DFT investigation of 3d, 4d, and 5d 13-atom metal clusters by Piotrowski et al.²³ also confirmed that a relatively loose structure of Mo₁₃ is the most favorable one in energy.

Considering that the physical and chemical properties of the pure metal clusters can be changed or improved by doping (such as to improve the catalytic activities or to enhance the magnetic moments), much attention have been paid to study the structures and properties of the mixed metal clusters in recent years. Several experimental^29–31 and theoretical^32–35 research works have been performed to study the Co-based or Mo-based mixed metal clusters, which mainly focus on the relationship between cluster magnetism and doping. For example, Yin et al.²⁹ investigated the magnetism of Co_NMn_M and Co_NV_M (N ≤ 60, M ≤ N/3) clusters experimentally and they found that, with increasing the doping amount (the ratio of the number of the doping atoms to the total number of atoms in a cluster), the average magnetic moment per atom increases (decreases) for Co_NMn_M (Co_NV_M). Theoretically based on the DFT calculations with the PBE-GGA functional, Aguilera-Granja et al.³⁴ studied the structures, binding energies and magnetic moments of the clusters Mo_N (N = 2–13) and Mo₁₂X (X = Fe, Co and Ni), and they found that the impurities exhibit weak magnetic moments parallel coupled to the total magnetic moments of the Mo atoms in Mo₁₂Co and Mo₁₂Ni, whereas in Mo₁₂Fe the impurity shows a high moment with antiparallel coupling. For the Co–Mo mixed clusters, very recently Liebing et al.³⁶ investigated the geometries, electronic structures and magnetism of the mixed clusters Co_nMo_m (n + m = x, 2 ≤ x ≤ 6) by all electron DFT study with the PBE-GGA functional.

In this paper, the geometrical and electronic properties of 13-atom clusters Co₁₃, Mo₁₃, Co₁₂Mo and Mo₁₂Co are investigated systematically by using the density-functional calculations combined with a genetic algorithm, and we focus on the geometrical characteristics (e.g., the ground-state geometry and its closer isomers) and the electronic peculiarities (e.g., the d–d hybridization between the doped atom and the matrix atoms near the Fermi energy) of the mixed Co₁₂Mo and Mo₁₂Co clusters. The intrinsic connection between the catalysis and the structural and electronic characteristics of the mixed Co–Mo clusters is emphasized.

2 Computational details

Selection of initial structures is very important in order to search the low energy structures of a cluster effectively. For the pure Co₁₃ (Mo₁₃) clusters the initial structures are constructed from the following three aspects: (1) a large number of candidate structures are provided by the genetic algorithm^37,38 based on the interatomic semi-empirical Gupta potential; (2) the ground-state and low-lying structures of Co₁₃ and Mo₁₃ that can be found in the literatures published; (3) four conventional 13-atom high-symmetry (I_h, O_h, D_3h, D_5h) close-packed structures. The initial structures are optimized by the first-principles calculations based on the density functional theory, and thus the ground-state structures as well as the low-lying isomers of the pure Co₁₃ and Mo₁₃ clusters can be obtained. For the mixed (doping) clusters Co₁₂Mo and Mo₁₂Co, the initial structures are constructed from the one-atom replacement of each of the inequivalent positions of the relevant structures (the ground-state and low-lying structures as well as the four high-symmetric structures) of the pure Co₁₃ and Mo₁₃ clusters, and in further the first-principles calculations are performed to optimize these initial structures so as to obtain the low-energy geometries of the mixed clusters.

In this paper, the first-principles calculations are performed in the framework of the density-functional theory (DFT) within the generalized gradient approximation (GGA) formulated by Perdew and Wang (PW91) to the exchange–correlation functional^39,40 as implemented in the VASP code (Vienna ab-initio simulation package).^41,42 The plane-wave pseudopotential method is used. Structural optimizations are performed within a cubic box with the side length of 17–18 Å that the interaction between adjacent clusters can be negligible. The convergences of total energy and atomic forces in structural relaxation of a cluster are set to be 0.0001 eV and 0.01 eV Å⁻¹, respectively.

3 Results and discussion

3.1 Geometric structure and energy

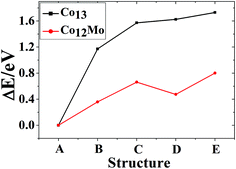
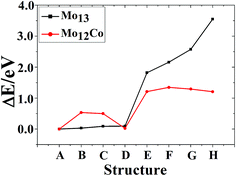
The total binding energies and symmetries of the ground-state geometries, the low-lying isomers and the four high-symmetric configurations of Co₁₃ and Mo₁₃ are listed in Fig. 1 and 2, respectively. For comparison, all structures shown in Fig. 1 and 2 are sorted in increasing order of energy, and the energy of each structure is marked as the energy difference with respect to the ground-state structure (that is, the energy of the ground-state structure is labeled as zero).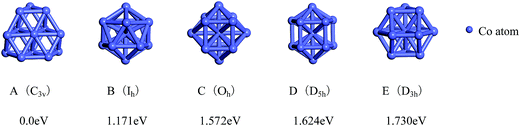

Fig. 1 The referenced total binding energies (see text for details) and symmetries of the ground-state geometry and the four high-symmetric configurations of Co₁₃.

Fig. 2 The referenced total binding energies (see text for details) and symmetries of the ground-state geometry, the low-lying isomers and the four high-symmetric configurations of Mo₁₃.

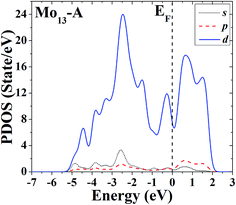
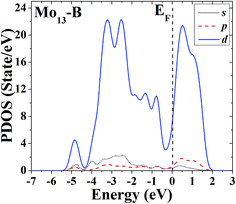
As shown in Fig. 1, the ground-state geometry of Co₁₃ is a hexagonal bilayer-like (HBL-like) structure with the C_3v symmetry which is obtained from the genetic algorithm, and this is completely consistent with the rigorous theoretical prediction of the ground-state structure of Co₁₃ in recent years.^21–25 The four conventional high-symmetric (I_h, O_h, D_5h, D_3h) close-packed geometries do not have any energetic competition of the pure Co₁₃ cluster. There exists many low-lying (nearly degenerate) isomers of Mo₁₃ except its ground-state structure, as can be found in Fig. 2, the two nearly degenerate geometries (Fig. 2B and C) are all comparatively loose structures without central atoms, which have the same low symmetry (C_s) as that of the ground-state structure, and the last low-lying structure (Fig. 2D) can be viewed as a strongly distorted icosahedral-like geometry, which is also very closer in energy to the ground-state structure (with the energy difference less than 0.1 eV). The four structures (Fig. 2A–D) are all obtained by the genetic algorithm, where the structure B is only 0.032 eV high in energy than the structure A and can be regarded as the biggest competitor to the ground-state structure. The structure B shown in Fig. 2 is consistent with the lowest-energy geometry obtained be by Sun et al.²⁸ and Piotrowski et al.^23,24 recently, which implies that, a new candidate of the ground-state of Mo₁₃ is found through the combination of the first-principles method with the genetic algorithm. Similarly to the case of Co₁₃, for Mo₁₃, the four ideal high-symmetric (I_h, O_h, D_5h, D_3h) close-packed structures (Fig. 2E–H) also have not any competitive advantages in energy.

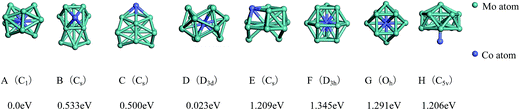
The lowest-energy geometries of the mixed Co₁₂Mo and Mo₁₂Co can be obtained from the single-atom replacement of each of the inequivalent positions of the ground-state, the low-lying and the four high-symmetric configurations of the pure Co₁₃ and Mo₁₃ clusters as listed in Fig. 1 and 2. Through DFT reoptimization of those initial geometries originated from the inequivalent single-atom replacements of the five and eight configurations listed in Fig. 1 and 2, the total binding energies and symmetries of the lowest-energy geometries of the corresponding five and eight configurations are given in Fig. 3 and 4, respectively, and the total binding energies are labeled as the energy differences to the ground-state (i.e., the ground-state energy is labeled as zero). As shown in Fig. 3, the ground-state geometry of Co₁₂Mo comes from the inequivalent single-atom replacements of the ground-state geometry of Co₁₃ (the central atom of the hexagonal of the ground-state HBL-like structure of Co₁₃ is replaced, and the symmetry of the cluster remains unchanged). For each of the four high-symmetric (I_h, O_h, D_5h, D_3h) configurations of Co₁₃ (Fig. 1B–E), the energy of the central-atom replaced configuration is always lower than these of the surface-atom replaced configurations.

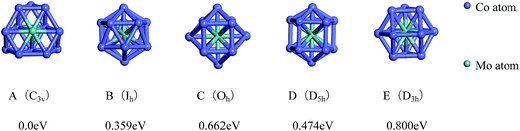Fig. 3 The referenced total binding energies (see text for details) and symmetries of the ground-state geometry and the four high-symmetric configurations of Co₁₂Mo.

Fig. 4 The referenced total binding energies (see text for details) and symmetries of the ground-state geometry, the low-lying isomers and the four high-symmetric configurations of Mo₁₂Co.

As shown in Fig. 4, the ground-state geometry of Mo₁₂Co comes also from the inequivalent single-atom replacements of the ground-state geometry of Mo₁₃. But with respect to the ground-state geometry of Mo₁₃ (Fig. 2A), the ground-state structure of Mo₁₂Co has a significant structural distortion, and the symmetry is also reduced from C_s to C₁. Through the inequivalent single-atom replacements of the nearly degenerate isomer to the ground-state of Mo₁₃ (Fig. 2B), the obtained lowest-energy configuration (Fig. 4B) is not competitive in energy compared to the ground-state of Mo₁₂Co, the energy difference between the two configurations is about 0.533 eV (∼0.04 eV per atom), and the two configurations are no longer the energetically degenerate isomers. Similarly, through the inequivalent single-atom replacements of the nearly degenerate isomer to the ground-state of Mo₁₃ (Fig. 2C), the obtained lowest-energy configuration (Fig. 4C) is also not favorable in energy compared to the ground-state of Mo₁₂Co, and the energy difference between the two configurations is 0.50 eV. But through the inequivalent single-atom replacements of the last nearly degenerate isomer to the ground-state of Mo₁₃ (Fig. 2D), the obtained lowest-energy configuration (Fig. 4D) is competitive in energy compared to the ground-state of Mo₁₂Co (Fig. 4A), the energy difference between the two configurations is only about 0.023 eV (∼0.002 eV per atom), and the two configurations can be regarded as the energetically degenerate isomers.

For the four high-symmetric structures of Mo₁₃ (Fig. 2E–H), the lowest-energy configurations of the corresponding doped clusters Mo₁₂Co (Fig. 4E–H) are all unfavorable energetically (the energy differences to the ground-state are all larger than 1 eV). From the comparison of Fig. 2 and 4 one can find that: there are many nearly degenerate isomers of the pure Mo₁₃, but the degenerate isomers significantly reduced of the mixed Mo₁₂Co, which also highlight the energetically competitive advantage of the ground-state structure of Mo₁₂Co (Fig. 4A).

The referenced total binding energies of different configurations of Co₁₃, Co₁₂Mo, Mo₁₃, and Mo₁₂Co are given in Fig. 5 and 6, respectively. It can be seen that, there is no energetically degenerate isomers of the pure Co₁₃, and the ground-state Co₁₃ has an absolutely higher stability than its isomers. For Co₁₂Mo, the energetically advantage of the ground-state to the isomers is far from that in Co₁₃. For Mo₁₃, similar to that of Co₁₃, variations of the total binding energies of different configurations after doping all decrease obviously. But as comparing that there are many energetically nearly degenerate isomers of Mo₁₃, the isomerization to the ground-state is suppressed after doping.

Fig. 5 The referenced total binding energies of different configurations of Co₁₃ and Co₁₂Mo.

Fig. 6 The referenced total binding energies of different configurations of Mo₁₃ and Mo₁₂Co.

3.2 Density of states

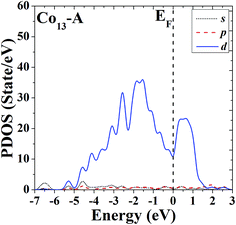
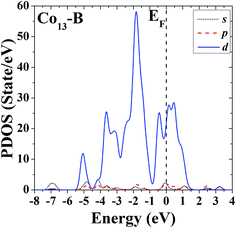
In order to further study the electronic properties and the correlation between different configurations, the s, p and d partial density of states (PDOS) of the ground-state HBL-like geometry and the high-symmetric close-packed icosahedron of Co₁₃ are given in Fig. 7 and 8, respectively. For comparison, the Fermi energy is shifted to zero.

Fig. 7 Partial density of states (PDOS) of the ground-state HBL-like geometry of Co₁₃.

Fig. 8 Partial density of states (PDOS) of the high-symmetric close-packed icosahedron of Co₁₃.

The PDOS of the two configurations of Co₁₃ are all dominated by d electrons, and at the Fermi level the d electrons all have comparatively large values. The difference is, the distribution of PDOS of the icosahedron (structure B) of Co₁₃ is more sharp and discrete, but the distribution of PDOS of the ground-state HBL-like one (structure A) is more uniform, and such a difference can be due to their different symmetries (a high symmetry corresponds to a high degree of degeneracy, which leads to a more sharp and discrete distribution).

The s, p and d PDOS of the ground-state geometry (Fig. 2A) and its nearly degenerate structure (Fig. 2B) of Mo₁₃ are given in Fig. 9 and 10, respectively. Each of the two configurations of Mo₁₃ shows a relatively smooth d electrons dominated distribution of PDOS, and the difference is that the distribution of d electrons in the occupied states near the Fermi level is obviously different: the ground-state has a significant larger distribution than its nearly degenerate isomer. Taking into account that for a cluster the occupied distribution of d electrons near the Fermi level is strongly correlated with its chemical adsorption and catalytic properties (more d electrons may lead to a better catalytic performance), therefore, for the two low energy configurations of Mo₁₃, although their energies are nearly the same, they have completely different catalytic properties. As a result, when interacting with small molecules, the two configurations of Mo₁₃ may have completely different reaction processes (with completely different reaction mechanisms).

Fig. 9 Partial density of states (PDOS) of the ground-state geometry of Mo₁₃.

Fig. 10 Partial density of states (PDOS) of the excited-state geometry of Mo₁₃.

The s, p and d PDOS of the ground-state geometry (Fig. 3A) and the icosahedron with the central doping atom (Fig. 3B) of Co₁₂Mo are given in the left part of Fig. 11 and 12, respectively. Meanwhile the s, p and d PDOS of the twelve matrix atoms and the single doping atom in each of the two configurations are given in the right part of Fig. 11 and 12, respectively.

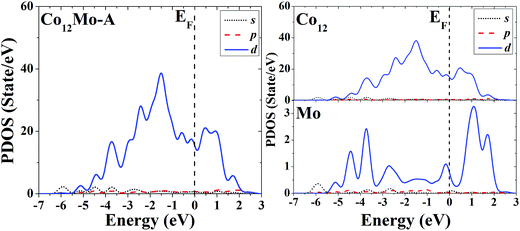Fig. 11 Partial density of states (PDOS) of the whole (left) and components (right) of the ground-state geometry of Co₁₂Mo.

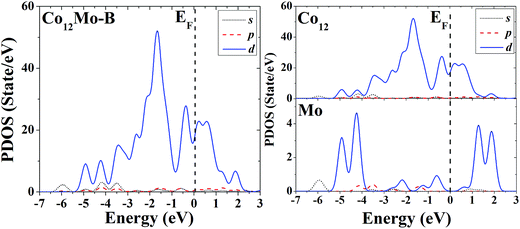Fig. 12 Partial density of states (PDOS) of the whole (left) and components (right) of the high-symmetric close-packed icosahedron of Co₁₂Mo.

Through analyzing the whole PDOS of the two configurations (the relatively low-symmetric ground-state structure (Fig. 3A) and the high-symmetric excited-state structure (Fig. 3B)) of Co₁₂Mo (as shown in left sides of Fig. 11 and 12), one can find the similarities to the whole PDOS of the two corresponding configurations (Fig. 1A and B) of Co₁₃: all reflect the close correlation between cluster symmetry and electron distribution, and all have large distributions of d electrons at the Fermi level. However, as can be seen from the right parts of Fig. 11 and 12, for the PDOS of different components in the two different configurations, the distributions of d electrons near the Fermi energy of the doping atoms in the two configurations are significantly different: for the ground-state structure of Co₁₂Mo (Fig. 3A), the distribution of d electrons near the Fermi energy (around the occupied states) of the doping atom is obviously not negligible, which results in a relatively strong hybridization near the Fermi energy between d electrons of the matrix atoms and that of the doping atom; while for the doping atom in the excited-state structure of Co₁₂Mo (Fig. 3B), its d-electron distribution near the Fermi energy is very weak, and as comparing to that of the ground-state, the hybridization near the Fermi energy between d electrons of the matrix atoms and that of the doping atom of the excited-state structure can be negligible. It seems to show that for the Co₁₂Mo cluster, the lower energy structure may correspond to a stronger d–d electron hybridization near the Fermi energy between the matrix atoms and the doping atom.

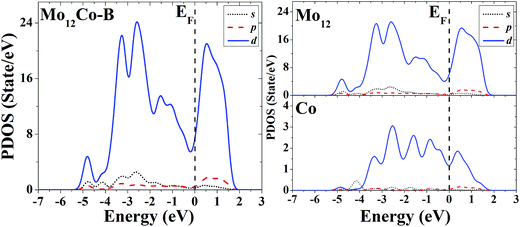
The s, p and d PDOS of the ground-state geometry (Fig. 4A) and the excited-state structure (Fig. 4B) of Mo₁₂Co are given in the left part of Fig. 13 and 14, respectively. Meanwhile the s, p and d PDOS of the twelve matrix atoms and the single doping atom in each of the two configurations are given in the right part of Fig. 13 and 14, respectively.

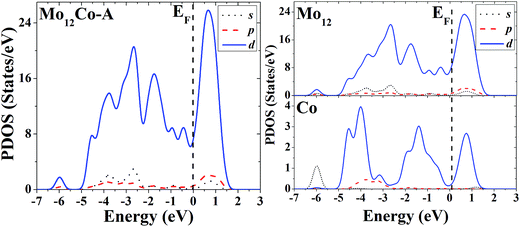Fig. 13 Partial density of states (PDOS) of the whole (left) and components (right) of the ground-state geometry of Mo₁₂Co.

Fig. 14 Partial density of states (PDOS) of the whole (left) and components (right) of the excited-state geometry of Mo₁₂Co.

For the overall distribution of density of states, similar to the case of Co₁₂Mo, the electron distributions of the two configurations of Mo₁₂Co are similar: all have significant distributions of d electrons at the Fermi energy. But for the Mo₁₂Co cluster, the comparative relationship of strengths of d–d hybridizations between the matrix atoms and the doping atom neat the Fermi energy of its two configurations (the ground-state and the excited-state) is completely different with that of the Co₁₂Mo cluster: for the ground-state geometry of Mo₁₂Co (Fig. 4A), the distribution of d electrons near the Fermi energy of the doping atom is very weak, which results in a relatively weak hybridization near the Fermi energy (around the occupied states) between d electrons of the matrix atoms and that of the doping atom; while for the doping atom in the excited-state structure of Mo₁₂Co (Fig. 4B), its d-electron distribution near the Fermi energy is obviously not negligible, which results in a relatively strong hybridization near the Fermi energy (around the occupied states) between d electrons of the matrix atoms and that of the doping atom; so, as comparing to that of the excited-state of Mo₁₂Co, the hybridization near the Fermi energy between d electrons of the matrix atoms and that of the doping atom of the ground-state Mo₁₂Co is obviously reduced, which is just the opposite with the case in Co₁₂Mo. This seems to indicate that for Mo₁₂Co, the lower energy structure does not correspond to a stronger d–d electron hybridization near the Fermi energy between the matrix atoms and the doping atom.

As mentioned in the Introduction, recent experimental studies have shown that, as relative to the pure Co or Mo catalytic clusters, the mixed Co–Mo clusters (with a certain proportion of two components) have better catalytic performance in the catalytic growth of carbon nanotubes.^5–8 Taking into account that the catalytic performance of a transition metal cluster is strongly correlated with its distribution of d electrons around the Fermi energy, if the mixed transition metal clusters (e.g., the Co–Mo clusters) have better catalytic properties than their pure counterparts, there should exist obviously (not negligible) distributions of d electrons around the Fermi energy of both the two components, as the result, there should be a relatively strong d–d hybridization near the Fermi energy between the two components. According to the above discussions, it can be assumed that: for the 13-atom Co–Mo mixed clusters, the ground-state geometry of Co₁₂Mo has better (hybrid or synergistic) catalytic ability than its excited state, but the synergistic catalytic ability of the ground-state structure of Mo₁₂Co is reduced as comparing with that of its excited-state. That means the synergistic catalytic abilities of the Co–Mo mixed clusters are strongly correlated with the structures and component ratios of the mixed clusters. From the two special cases of the 13-atom Co_mMo_n (m : n = 12 : 1 or 1 : 12) mixed clusters mentioned above, one may suppose that, for a given-sized Co–Mo clusters, as comparing to the cases that the differences of the component ratios are quite large, when the proportion of the two components is closer the synergistic catalytic abilities of the mixed clusters can be enhanced. The experimental study on the catalytic growth of single-walled carbon nanotubes by Co–Mo nanoparticles showed that the nanoparticles have the best catalytic abilities when the proportions of the two components are closer (2 : 1, 1 : 1 or 1 : 2),⁵ and we speculate that this may be closely related to the strong d–d electron hybridization near the Fermi energy (around the occupied sates) between the two different components, and this may be one of the main reasons for the high catalytic activity of the Co–Mo mixed clusters in the process of catalytic growth of carbon nanotubes.

4 Conclusion

In this paper, the geometries, energies and electronic properties of Co₁₃, Mo₁₃, Co₁₂Mo and Mo₁₂Co clusters are systematically investigated by using the first principles calculations combined with the genetic algorithm. The main conclusions are as follows:

(1) For the pure Co₁₃ cluster, there are no energetically closer isomers near its ground-state structure. The ground-state HBL-like geometry of Co₁₃ has absolute advantage in energy as comparing the conventional high-symmetric close-packed structures. For the pure Mo₁₃ clusters, a new candidate of the ground-state is found, and there are many energetically closer isomers to the ground-state.

(2) The relatively high stability of the pure Co₁₃ cluster can be decreased by doping (with replacing a Mo atom), but for the pure Mo₁₃ cluster, the isomerization near the ground-state can be suppressed by doping (with replacing a Co atom).

(3) The d–d hybridization near the Fermi energy between the matrix atoms and the doping atom in the ground-state geometry of Co₁₂Mo is enhanced as compared with those in the high-symmetric close-packed excited-state structures of Co₁₂Mo; in the contrary, the d–d hybridization near the Fermi energy between the matrix atoms and the doping atom in the ground-state geometry of Mo₁₂Co is reduced as compared with those in the relatively high excited-state structures of Co₁₂Mo; which indicates that the d–d hybridization near the Fermi energy between the matrix atoms and the doping atom of a mixed Co–Mo cluster is strongly influenced by the geometry and the component ratio of the mixed cluster, and the competition between the two factors may have a crucial impact on the catalytic property of the mixed cluster. We speculate that, for the Co–Mo clusters with a given size, as the component ratio is approaching, the mixed clusters should have better hybrid catalytic abilities, which originates from the enhanced d–d hybridization near the Fermi energy (around the occupied states) between the two different components.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11164029, 11664038).

References

1. X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. Lett., 2005, 95, 237209–237212.
2. M. B. Knickelbein, J. Chem. Phys., 2006, 125, 233–235.
3. S. Sahoo, M. E. Gruner, A. Hucht, G. Rollmann and P. Entel, in Nanoparticles from the Gas phase, ed. A. Lorke, et al., Springer-Verlag, Berlin, Heidelberg, 2012, vol. 3, pp. 77–98.
4. A. Moisala, A. G. Nasibulin and E. I. Kauppinen, J. Phys.: Condens. Matter, 2003, 15, S3011–S3035.
5. B. Kitiyanan, W. E. Alvarez, J. H. Harwell and D. E. Resasco, Chem. Phys. Lett., 2000, 317, 497–503.
6. E. V. Lobiak, E. V. Shlyakhova, L. G. Bulusheva, P. E. Plyusnin, Yu. V. Shubin and A. V. Okotrub, J. Alloys Compd., 2015, 621, 351–356.
7. S. Roy, R. Bajpai, N. Soin, S. S. Roy, J. A. McLaughlin and D. S. Misra, Appl. Surf. Sci., 2014, 321, 70–79.
8. H. Wang, Y. Yuan, L. Wei, K. Goh, D. Yu and Y. Chen, Carbon, 2015, 81, 1–19.
9. A. R. Harutyunyan, B. K. Pradhan, U. J. Kim, G. Chen and P. C. Eklund, Nano Lett., 2002, 2, 525–530.
10. S. K. Youn and H. G. Park, J. Phys. Chem. C, 2013, 117, 18657–18665.
11. E. Flahaut, A. Govindaraj, A. Peigney, C. Laurent, A. Rousset and C. N. R. Rao, Chem. Phys. Lett., 1999, 300, 236–242.
12. Y. C. Bae, V. Kumar, H. Osanai and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125427–125432.
13. C. M. Chang and M. Y. Chou, Phys. Rev. Lett., 2004, 93, 133401–133404.
14. Z. Q. Li and B. L. Gu, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13611–13614.
15. K. Miura, H. Kimura and S. Imanaga, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10335–10338.
16. H. M. Duan and Q. Q. Zheng, Phys. Lett. A, 2001, 280, 333–339.
17. J. L. Rodríguez-López, F. Aguilera-Granja, K. Michaelian and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174413–174421.
18. Q. M. Ma, Z. Xie, J. Wang, Y. Liu and Y. C. Li, Phys. Lett. A, 2006, 358, 289–296.
19. Q. M. Ma, Y. Liu, Z. Xie and J. Wang, J. Phys.: Conf. Ser., 2006, 29, 163–166.
20. S. Rives, A. Catherinot, F. Dumas-Bouchiat, C. Champeaux, A. Videcoq and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085407–085414.
21. C. D. Dong and X. G. Gong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 020409–020412.
22. F. Aguilera-Granja, A. García-Fuente and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134425–134433.
23. M. J. Piotrowski, P. Piquini and J. L. F. Da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155446–155459.
24. M. J. Piotrowski, P. Piquini, L. Cândido and J. L. F. Da Silva, Phys. Chem. Chem. Phys., 2011, 13, 17242–17248.
25. G. L. Gutsev, C. W. Weatherford, K. G. Belay, B. R. Ramachandran and P. Jena, J. Chem. Phys., 2013, 138, 164303–164315.
26. D. Kaiming, Y. Jinlong, X. Chuanyun and W. Kelin, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11907–11910.
27. W. Zhang, X. Ran, H. Zhao and L. Wang, J. Chem. Phys., 2004, 121, 7717–7724.
28. Y. Sun, R. Fournier and M. Zhang, Phys. Rev. A, 2009, 79, 043202–043210.
29. S. Yin, R. Moro, X. S. Xu and W. A. de Heer, Phys. Rev. Lett., 2007, 98, 113401–113404.
30. G. Mpourmpakis, G. E. Froudakis, A. N. Andriotis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104417–104423.
31. A. N. Andriotis, G. Mpourmpakis, G. E. Froudakis and M. Menon, J. Chem. Phys., 2004, 120, 11901–11904.
32. T. Hihara, S. Pokrant and J. A. Becker, Chem. Phys. Lett., 1998, 294, 357–362.
33. M. B. Knickelbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 014401–014406.
34. F. Aguilera-Granja, A. Vega and L. J. Gallego, Nanotechnology, 2008, 19, 1–9.
35. A. Garcia-Fuente, A. Vega, F. Aguilera-Granja and L. J. Gallego, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 184403–184409.
36. S. Liebing, C. Martin, K. Trepte and J. Kortus, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155421–155430.
37. D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291.
38. Y. Zeiri, Comput. Phys. Commun., 1997, 103, 28–42.
39. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
40. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6678.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
42. J. Hafner and G. Kresse, in Properties of Complex Inorganic Solids, ed. A. Gonis, et al., Plenum Press, New York, 1997, pp. 69–82.

---