Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
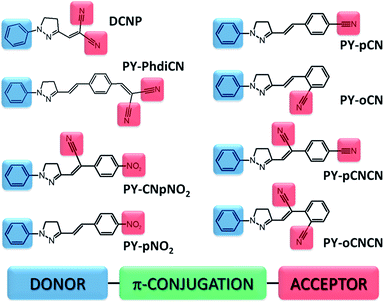
Chemical structure versus second-order nonlinear optical response of the push–pull type pyrazoline-based chromophores
A. Szukalski *a,
B. Sahraouib,
B. Kulykb,
C. A. Lazarc,
A. M. Maneac and
J. Mysliwieca
*a,
B. Sahraouib,
B. Kulykb,
C. A. Lazarc,
A. M. Maneac and
J. Mysliwieca
aFaculty of Chemistry, Advanced Materials Engineering and Modelling Group, Wroclaw University of Science and Technology, Wyb. Wyspianskiego 27, 50-320 Wroclaw, Poland. E-mail: adam.szukalski@pwr.edu.pl
bLUNAM University, MOLTECH-Anjou Laboratory, University of Angers, UMR CNRS 62002, Boulevard Lavoisier, 49045 Angers, France
cFaculty of Applied Chemistry and Materials Science, University Politehnica of Bucharest, Polizu Street No 1, 011061, Bucharest, Romania
First published on 3rd February 2017
Abstract
In this study, we present experimental results of the second-order nonlinear optical response of a series of pyrazoline derivatives. The main aim of this study was to determine the correlation between the chemical structure of the pyrazoline derivatives family and their nonlinear optical properties. The investigated group of materials consists of pairs or triplets of derivatives and structural isomers, which are characterized by the same electron-donor unit, whereas differ in their electron-accepting part. Moreover, some of them possess different moieties, which can change the electron cloud distribution in the molecule. Their efficient nonlinear optical responses and possibility of tuning in this group of materials promote them for various optoelectronic applications where optical nonlinearity plays a crucial role. Since material engineering enables the control of molecular structure, the nonlinear optical features of the created systems can be consequently optimized.
Introduction
One of the main topics in modern materials science and in the field of organic photonics is the search for materials that exhibit multiple useful properties, including large nonlinear optical (NLO) effects, making them suitable for applications in numerous multidisciplinary areas such as frequency conversion, lasing, multiphoton fluorescence, and microscopy or light switching.1–5 To expand these utilities, designing molecules with significant second-order nonlinear optical properties plays a vital role. The push–pull type molecular systems have attracted significant attention in the past few years mainly because of the high optical nonlinearities that they can exhibit, due to the significant delocalization of their electronic clouds.6,7 One of the popular push–pull type molecular systems that is expected to have a high NLO performance is compounds based on the pyrazoline ring. It was shown and proven that pyrazoline derivatives can be used as efficient systems for optical switching or light amplification by stimulated emission, lasing or random lasing action.8–12 Furthermore, because of their high dipole moments and quantum yield, they also exhibit efficient two photon absorption (TPA) and third harmonic generation (THG).13–17The main goal of this study was to determine the correlation between the chemical structure of the pyrazoline derivatives family and their optical nonlinearity by altering the molecular structure of these push–pull organic materials. The strategy of this property modification during molecular design and synthesis is based on the surrounding electron-donor and acceptor group position manipulation and their capability for effective intramolecular charge transfer. The studied group of materials consists of pairs of derivatives and structural isomers, which present the same electron-donor unit, whereas differ in their electron-accepting part. Moreover, some of them possess different moieties, which can change the electron cloud distribution. Due to this variation and efficient nonlinear optical response of this group of materials, their importance for optoelectronic applications is promoted, especially, where optical nonlinearity plays a crucial role.
Materials
The investigated compounds were synthesized according to the Knoevenagel and Fischer method.13,18 Basically, all the systems present the typical push–pull type molecular structure divided in donor (D) and acceptor (A) regions connected by a π-conjugated linkage (Fig. 1). All of them comprise the same simple electron-donor aromatic ring unit; moreover, the pyrazoline ring and π-conjugated system (double bonds and/or another aromatic ring) sustain internal electron transfer in the molecule. The compounds differ in electron-acceptor moieties, which are mainly nitrile (–CN) and nitro (–NO2) groups located in various positions and configurations giving pairs or triplets of derivatives and structural isomers. For instance, the compound (E)-2-(4-(2-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)vinyl)benzylidene)malononitrile (abbreviation: PY-PhdiCN) is an extended version of the well-known DCNP (3-(1,1-dicyanoethenyl)-1-phenyl-4,5-dihydro-1H-pyrazole) molecule,10,19–21 which in this study serves as the reference material among the newly introduced pyrazoline derivatives. PY-PhdiCN has two terminal nitrile groups in the acceptor region, whereas in comparison with DCNP, it also has an additional aromatic ring and ethenyl bond between the D–A parts. Moreover, to determine the synergistic effect arising from the combination of two different electron-acceptor units, we investigated the compound with the abbreviated name PY-CNpNO2 ((Z)-2-(4-nitrophenyl)-3-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)acrylonitrile), which possesses both nitro and nitrile units. Four other molecules can be separated in two different pairs of structural isomers. First, (E)-2-(4-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)vinyl)benzonitrile (PY-pCN) and (E)-2-(2-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)vinyl)benzonitrile (PY-oCN), which possess only one moiety in the electron-acceptor region at the para and ortho positions connected to the aromatic ring, respectively. The second pair of isomers consists of (Z)-2-(1-cyano-4-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)vinyl)benzonitrile (PY-pCNCN) and (Z)-2-(1-cyano-2-(1-phenyl-4,5-dihydro-1H-pyrazol-3-yl)vinyl)benzonitrile (PY-oCNCN). These two molecules possess the same electron acceptor group positioned similarly in the two previous cases, but also again the nitrile group is located in the middle part of each compound. Additionally, (E)-3-(4-nitrostyryl)-1-phenyl-4,5-dihydro-1H-pyrazole (PY-pNO2) was investigated. In this case, only one nitro group located at the end of the chemical structure serves as the electron-acceptor moiety (at the para position). All the designed and synthesized molecules were characterized by different charge distributions, dipole moment values, and directions as well as crystal configurations and nonlinear optical parameters.Experimental
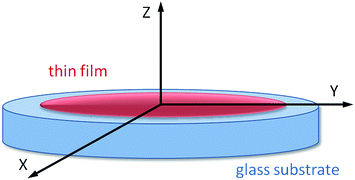
Second harmonic generation (SHG) from thin polymeric films doped with the pyrazoline derivatives was investigated using the Maker fringes technique22 using the experimental set-up employing the fundamental wavelength of 1064 nm of a Nd:YVO4 laser with a 30 ps pulse duration and repetition rate of 10 Hz (Fig. 2). A polarizer and half-wave plate were used to align and adjust the incident laser beam polarization, which was then focused by a 250 mm lens. The samples were positioned on a rotational stage, which enabled to obtain Maker fringes with a step of 0.5 degrees. A KG3 filter allowed the 1064 nm laser beam to be cut out, whereas with an additional interference filter at 532 nm, the SHG signal was preserved and after all was detected by a photomultiplier. The measured signal was modified by appropriate neutral density filters, which were positioned before the photomultiplier to exclude its saturation. Each sample was measured a few times in the close-located places, and then finally these areas were marked and checked under an optical microscope and profilometer. A y-cut single crystal quartz slab (d = 0.5 mm) was used as the reference material during the experiments because it has a well-known nonlinear optical response, χ(2)q = 1.0 × 10−12 m V−1.23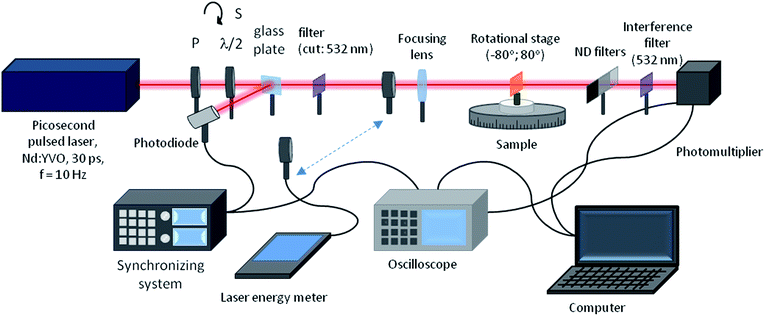 | ||
| Fig. 2 Experimental set-up for the second harmonic generation (SHG) measurements based on the Maker fringes technique. | ||
Poled polymers exhibit the ∞ mm point symmetry, in which from 3 nonzero components of susceptibility tensor only two are relevant: the diagonal χ(2)zzz and the off-diagonal χ(2)xxz. For an unstressed24 thin film and within the free gas model, their ratio is defined by
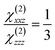 | (1) |
In eqn (1), z is the poling electric field direction and x lies in the poled film plane (Fig. 3).
To determine both the tensor components, the SHG experiments were performed in different fundamental generated harmonic beams polarization configurations: s–p and p–p. As was shown by Kuzyk and co-workers24 (see also: Kajzar,25 Rau and Kajzar26), for these configurations, the generated harmonic intensity at frequency 2ω, created by a fundamental beam with frequency ω, is given by27
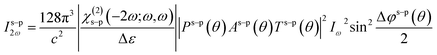 | (2) |
| Δε = ε2ω − εω | (3) |
Ps–p(θ) in eqn (2) is the projection factor for the s–p configuration, which is given by
Ps–p(θ) = sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsω θsω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs2ω θs2ω
| (4) |
Pp–p(θ) = sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpω θpω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp2ω + a θp2ω + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpω(cos θpω(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpω + 2 θpω + 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpω θpω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp2ω) θp2ω)
| (5) |
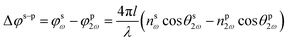 | (6) |
The nonzero quadratic susceptibilities of the studied films were calibrated with the independent SHG measurements on a y-cut α-quartz single crystal plate, performed under the same conditions. Calibration was carried out by fitting eqn (2) to the experimental data and comparing the scale factors. Herein, we first determined the susceptibilities for the s–p configuration, in which the projection factor depends only on χ(2)s–p susceptibility, thus allowing its determination.
For the p–p polarization configuration, the projection factor depends on both χ(2)s–p and χ(2)p–p susceptibilities. Thus, the determination of the diagonal component of the χ(2)(−2ω;ω,ω) tensor can be carried out in two ways:
(i) determining χ(2)s–p from the s–p measurements (eqn (4)), and then injecting it into eqn (5) to obtain the χ(2)p–p value and
(ii) proceeding in the same way for the s–p configuration, whereas assuming the theoretical value for the ratio 1/3 (eqn (1)).
We chose the second approach to avoid the uncertainty in the value of χ(2)p–p susceptibility introduced by the error in s–p measurements. This approach makes the comparison of the χ(2)p–p susceptibilities of the studied compounds more reliable.
Results and discussion
For the requirements of spectroscopic experiments, the series of thin polymeric films for each of the investigated compounds was prepared as follows. We used commercially available poly(methyl methacrylate) (Mw = 966 kDa, Sigma Aldrich®) in powder form and family of the pyrazoline derivatives described above. First, solutions of PMMA/THF and PRD/THF in proper ratios were prepared. After mixing and heating for few days, when the polymer completely dissolved, we mixed the abovementioned solutions to obtain the final mixture (3% dry weight proportion between the pyrazoline derivative and polymer) of a simple guest-host system, where the active material is stabilized by a branched, well-defined, transparent, and oxygen/laser light resistant polymer matrix. After stirring and heating, the final solution (PRD/PMMA/THF) was deposited on a clean silica glass plate using the drop casting technique. The layers were dried in a solvent atmosphere until the evaporation process was finished. The thicknesses of the films are presented in Table 1, which were measured using a profilometer (Tencor, ALFA-Step).| χ(2)(s)a,b [pm V−1] | ds–p [pm V−1] | χ(2)(p)a,b [pm V−1] | dp–p [pm V−1] | α0 [103 cm−1] | L [μm] | |
|---|---|---|---|---|---|---|
| a Calculated according to the used model (considering the linear absorption coefficient at 532 nm).b Maker fringes set-up employing the fundamental exit (1064 nm) of a 30 ps Nd:YVO4 laser with a repetition rate of 10 Hz; the energy per pulse was 40 μJ. | ||||||
| DCNP | 11.0 | 5.50 | 24.4 | 12.2 | 0.207 | 14.9 |
| PY-pCN | 2.40 | 1.20 | 6.04 | 3.02 | 0.002 | 15.2 |
| PY-pCNCN | 5.02 | 2.26 | 7.20 | 3.60 | 0.576 | 7.66 |
| PY-oCNCN | 1.22 | 0.61 | 3.38 | 1.69 | 0.065 | 6.56 |
| PY-oCN | 0.06 | 0.03 | 0.18 | 0.09 | 0.004 | 9.25 |
| PY-CNpNO2 | 10.1 | 5.05 | 9.40 | 4.70 | 0.702 | 54.1 |
| PY-PhdiCN | 9.06 | 4.53 | 10.0 | 5.00 | 2.200 | 17.5 |
| PY-pNO2 | 6.86 | 3.43 | 9.10 | 4.55 | 1.040 | 18.9 |
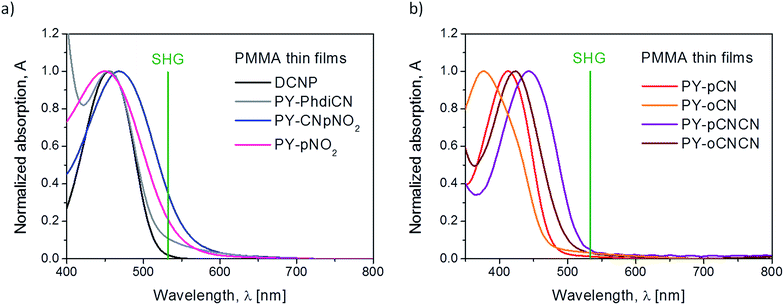
Fig. 4(a) presents the group of four derivatives of pyrazoline, where the absorption maxima are located mainly at around 455 nm. Note that by putting different moieties on the compound or extension of its molecular structure, it does not cause any shift in its absorption maximum, except in the case where the molecule possesses two different moieties (nitrile and nitro groups), the absorption band is red shifted (λmax = 468.8 nm). All these compounds are characterized by a quite significant absorption in the range of the second harmonic generated wavelength at 532 nm (which is also marked in green in the spectrum) except DCNP. According to this fact, for all the samples, we also considered the linear absorption contribution during the 2nd order nonlinear optical susceptibility calculations. Fig. 4(b) shows the absorption spectra of the two pairs of structural isomers. In this case, the maxima of the absorption are positioned at various wavelengths, which is strictly due to the location and number of nitrile substituents linked to the structure. For the isomers having only one electron-acceptor unit (PY-pCN and PY-oCN), their maxima are mostly located in the UV range (412.0 and 377.2 nm, respectively). The absorption maxima for the molecules possessing two –CN units (PY-pCNCN and PY-oCNCN) are red-shifted and are positioned at 442.7 and 423.5 nm, respectively. In the case when the substituent is located at the end of the structure (para position), there is a red shift, which is possible to observe in both the cases (Fig. 4(b)). The different locations of the units and therefore different charge distributions are responsible for this behavior. Moreover, it is clearly visible that herein the linear absorption influence is less significant for the obtained and measured signal of SHG. However, to sustain the calculation method as a comparable method for the all the compounds, we also used the same methodology.
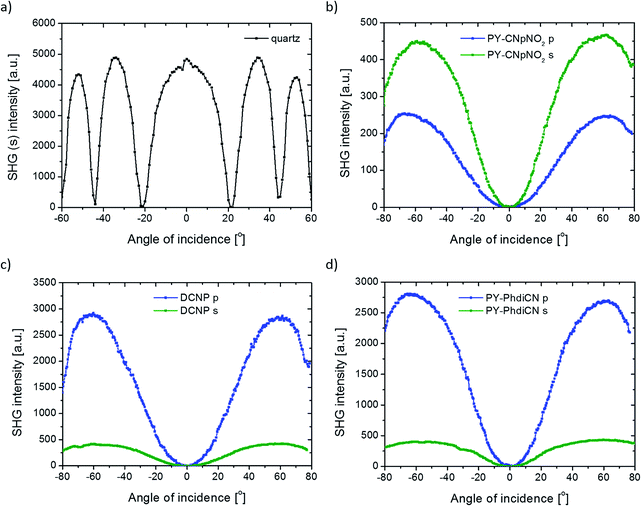
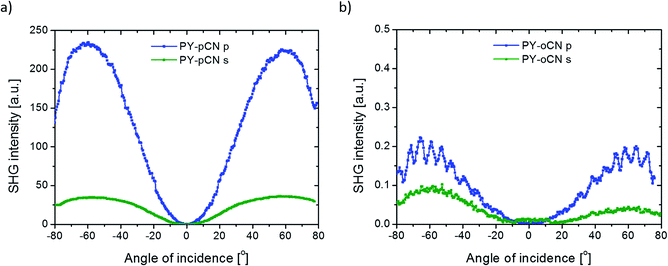
Concerning the 2nd order nonlinear optical effects, it was necessary to use the corona poling (CP) technique for the thin films to break the symmetry inside the layers. Since the parameters for the molecules poling procedure are in thin polymeric layers, we used a high voltage (U = 5 kV) when the substrate reached the high temperature of T = 83 °C (but still below the glass point of PMMA). The poling process took 15 minutes. After this time, the samples were left for thermal relaxation (3 hours for the films to reach room temperature), but still with the applied high voltage. We also tried to measure the second harmonic generation signal from the same systems before the CP treatment; however, no SHG was observed. We measured the Maker fringes due to the NLO response coming from the films as a function of irradiation angle of the incident beam. The typical SHG signal coming from the reference material is shown in Fig. 5(a).
The results presented in Fig. 5(b–d) are comparatively relative. Indeed, after considering the values of the linear absorption coefficient, layer thickness, and using the theoretical model introduced earlier in this study (see also Fig. 6), the final results of the NLO parameters can be compared with respect to the reference (cf. Table 1).
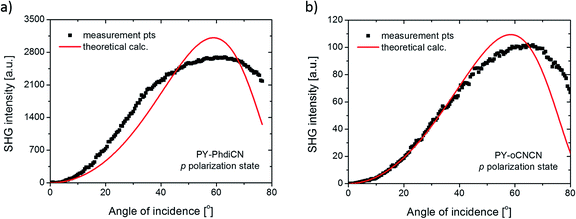 | ||
| Fig. 6 SHG intensity measured points (dots) and calculated theoretical values (red line) for the (a) PY-PhdiCN and (b) PY-oCNCN molecular systems in the p polarization state configuration. | ||
DCNP possesses the highest values of the 2nd order nonlinear optical susceptibility in both experimental polarization configurations (s and p). Note that we succeeded in obtaining almost the same results obtained from other pyrazolines: (i) the molecule with an extended structure (PY-PhdiCN) with respect to DCNP, (ii) by putting two different electron-acceptor units (PY-CNpNO2) or (iii) using only one functional group (PY-pNO2). Furthermore, the presented results concern both the polarization state configurations, and it should be highlighted, refer to these polymeric systems doped by dyes, which are significantly sensitive for the generated harmonic wave due to the possible reabsorption process.
As abovementioned, the molecular system containing PY-CNpNO2 molecule represents one of the highest 2nd order NLO signal among the investigated samples. This behavior is related to the charge distribution coming from two different electron-acceptor moieties, which cause some sort of disorder during molecular poling. Then, the direction of the generated SHG signal could extenuate each other by simple interference, especially since in this case, the linear absorption in this range (532 nm) is significant. Therefore, it proves the high efficiency of this system. Furthermore, in this case, we observed unusual behavior according to the different polarizations of incident beam used. In general, the p-polarized laser light should cause a higher NLO effect than the s light for the same compound (cf. Fig. 5b).
In the case of the PY-PhdiCN molecular system (cf. Fig. 5d), it is clearly visible that with the extension of the π-conjugated linkage and the structure's lability, there is no significant correlation of SHG signal for both polarization conditions (s and p), which were used to compare the influence of the 2nd order NLO effect. Both molecules, PY-PhdiCN (which is the extended version of DCNP) and DCNP (much shorter and stiffer structure), were characterized with almost the same value of the generated signal and the same behavior for the different polarization configurations.
Another compound that is equipped with two (but the same) electron-acceptor units, in the best possible spatial configuration (with respect to the lowest molecular energy and steric hindrance), is also significantly efficient for the SHG phenomenon (PY-pCNCN). According to the structural isomer of this compound (PY-oCNCN), it is worth mentioning that the position of the terminal electron-acceptor unit plays a crucial role in the 2nd order nonlinear optical effect magnification. In this particular case, it is related to the dipole moment value and possibility to obtain a molecular system with broken symmetry as a result of the corona poling treatment. The ortho isomer (PY-oCNCN) has a lower dipole moment value than the para isomer (PY-pCNCN) and also according to the spatial arrangement of the terminal electron-acceptor unit, the shape of the molecule is different, and as a consequence of this, the efficiency of the molecular ordering by the corona poling technique is less effective.
Furthermore, Fig. 7 (for another pair of isomers) and Table 1 (for the all molecules) present the significant correlations between the chemical structure and observed NLO effect with respect to the received values of the 2nd order nonlinear optical susceptibilities for each structure. By only changing the position of the electron-acceptor unit from the para position to the ortho position, it was possible to increase/decrease the SHG signal by one order of magnitude. Using different isomers of the compound, it was even possible to switch on and off the nonlinear translation of the fundamental beam because the value of the SHG signal coming from the ortho isomer is only on the background level and in the same moment, two times lower than that from the para position. In the case of the cis isomer of the PY-oCN compound, it was possible to achieve hydrogen bonding between the hydrogen atom (from the aromatic ring placed in the electron-donor part) and the nitrogen atom from the nitrile group, which undoubtedly stabilizes this bended form and directly hinders the molecular alignment (breaking symmetry efficiency) during the corona poling procedure.9
Another important parameter that should be considered, especially for the PY-pCN, PY-oCN, and PY-pNO2 compounds, is the type of electron-acceptor unit (changing from –CN to –NO2 in our case). We have shown that proper selection of the abovementioned groups allows to enhance the SHG signal roughly by a factor of 3 (for s polarization) and almost two times (for the p polarization configuration) with respect to defined χ(2) susceptibility.
Conclusions
In summary, we derived the second-order optical nonlinearity characterization for the selected group of pyrazoline derivatives, which have been investigated as thin dye-doped PMMA films. Different types of electron-acceptor units have been introduced into the molecular structure. The results confirm a strong correlation between the various investigated molecular systems, giving high values of χ(2), which differ by three order of magnitude (i.e. DCNP and PY-oCN). It has been shown that there is a significant difference in the harmonic light generation magnitude when the substituent (electron-acceptor unit) is connected to the ortho or para position. Moreover, two types of polarizations of incident beam (s and p) have been employed, which, in general, result in the SHG signal enhancement. Finally, according to the obtained experimental results, a clear dependence between the optical nonlinearity and the position as well as number and type of the electron-acceptor groups attached to the structure has been found. This suggests and proves that molecular engineering is an efficient solution to design and/or manipulate the optical nonlinearities of these push–pull type of molecular systems.Acknowledgements
A. S. would like to thank for the financial support received for dissertation preparation under ETIUDA II program, which is financed by the Polish National Science Centre (doctoral scholarship no. Dec-2014/12/T/ST4/00233). The work of C. A. Lazar was funded by the Sectoral Operational Programme Human Resources Development 2007–2013 of the Ministry of European Funds through the Financial Agreement POSDRU/159/1.5/S/132397. B. K. acknowledges the Pays de la Loire region for the financial support of research works in the framework of the “Molecular Systems for Nonlinear Optical Application” (MOSNOA) LUMOMAT project.References
- L. L. Dalton, P. Günter, M. Jazbinsek, O.-P. Kwon and P. A. Sullivan, Organic Electro-Optics and Photonics - Molecules, Polymers and Crystals, Cambridge University Press, Cambridge, 2015 Search PubMed.
- J. Clark and G. Lanzani, Nat. Photonics, 2010, 4, 438 CrossRef CAS.
- T. Yoshimura, Thin-Film Organic Photonics - Molecular Layer Deposition and Applications, CRC Press, NY, 2011 Search PubMed.
- A. D. Boardman, L. Pavlov and S. Tanev, Advanced Photonics with Second-Order Optically Nonlinear Processes, Springer Science and Business Media, B.V., Sozopol, 1997 Search PubMed.
- A. Camposeo, P. Del Carro, L. Persano, K. Cyprych, A. Szukalski, L. Sznitko, J. Mysliwiec and D. Pisignano, ACS Nano, 2014, 8(10), 10893 CrossRef PubMed.
- A. Migalska-Zalas, Z. Sofiani, B. Sahraoui, I. V. Kityk, S. Tkaczyk, V. Yuvshenko, J.-L. Fillaut, J. Perruchon and T. J. J. Muller, J. Phys. Chem. B, 2004, 108(39), 14942 CrossRef CAS.
- H. El Ouazzani, K. Iliopoulos, M. Pranaitis, O. Krupka, V. Smokal, A. Kolendo and B. Sahraoui, J. Phys. Chem. B, 2011, 115(9), 1944 CrossRef CAS PubMed.
- A. Szukalski, K. Haupa, A. Miniewicz and J. Mysliwiec, J. Phys. Chem. C, 2015, 119(18), 10007 CAS.
- A. Szukalski, A. Miniewicz, K. Haupa, B. Przybyl, J. Janczak, A. L. Sobolewski and J. Mysliwiec, J. Phys. Chem. C, 2016, 120(27), 14813 CAS.
- A. Szukalski, L. Sznitko, K. Cyprych, A. Miniewicz and J. Mysliwiec, J. Phys. Chem. C, 2014, 118(15), 8102 CAS.
- K. Parafiniuk, L. Sznitko and J. Mysliwiec, Opt. Lett., 2015, 40(7), 1552 CrossRef CAS PubMed.
- F. Bures, RSC Adv., 2014, 4, 58826 RSC.
- J. Mysliwiec, A. Szukalski, L. Sznitko, A. Miniewicz, K. Haupa, K. Zygadlo, K. Matczyszyn, J. Olesiak-Banska and M. Samoc, Dyes Pigm., 2014, 102, 63 CrossRef CAS.
- I. Papagiannouli, A. Szukalski, K. Iliopoulos, J. Mysliwiec, S. Couris and B. Sahraoui, RSC Adv., 2015, 5, 48363 RSC.
- B. Varghese, S. N. Al-Busafi, F. O. Suliman and S. M. Z. Al-Kindy, Anal. Methods, 2016, 8, 2729 RSC.
- B. Varghese, S. N. Al-Busafi, F. O. Suliman and S. M. Z. Al-Kindy, J. Lumin., 2015, 159, 9 CrossRef CAS.
- B. Varghese, S. N. Al-Busafi, F. O. Suliman and S. M. Z. Al-Kindy, Spectrochim. Acta, Part A, 2017, 173, 383 CrossRef CAS PubMed.
- E. Fischer and E. Knoevenagel, Justus Liebigs Ann. Chem., 1887, 239, 194 CrossRef.
- S. Allen, T. D. McLean, P. F. Gordon, B. D. Bothwell, M. B. Hursthouse and S. A. Karaulov, J. Appl. Phys., 1988, 64, 2583 CrossRef.
- J. M. Cole, C. C. Wilson, J. A. K. Howard and F. R. Cruickshank, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 1085 CrossRef.
- J. M. Cole, C. C. Wilson and J. A. K. Howard, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. B, 2000, 25(1–4), 265 CAS.
- P. D. Maker, R. W. Terhune, M. Nisenhoff and C. M. Savage, Phys. Rev. Lett., 1962, 8, 2 CrossRef.
- F. Kajzar, Y. Okada-Shudo, C. Meritt and Z. Kafafi, Synth. Met., 2001, 117, 189 CrossRef CAS.
- M. G. Kuzyk, K. D. Singer, H. E. Zahn and L. A. King, J. Opt. Soc. Am. B, 1989, 6(4), 742 CrossRef CAS.
- J. Swalen and F. Kajzar, Introduction, in Organic Thin Films for Waveguiding Nonlinear Optics, Gordon & Breach Sc. Publ., Amsterdam, 1996 Search PubMed.
- I. Rau and F. Kajzar, Nonlinear Opt., Quantum Opt., 2008, 38, 99 CAS.
- L. Favaretto, G. Barbarella, I. Rau, F. Kajzar, S. Caria, M. Murgia and R. Zamboni, Opt. Express, 2009, 17(4), 2557 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |