Density functional theory studies on the skeletal isomerization of 1-butene catalyzed by HZSM-23 and HZSM-48 zeolites

Abstract

The reaction mechanism of the skeletal isomerization of 1-butene to isobutene on 10-membered ring zeolites HZSM-23 and HZSM-48 was investigated using the ONIOM(B3LYP/6-31G(d,p):UFF) method. It is demonstrated that the skeletal isomerization follows a monomolecular process, which involves the formation of two important intermediates: 2-butoxide and butoxide. The active centers on both zeolites are identified to involve two Brønsted acid sites and three exposed vertex O atoms of the aluminum–oxygen tetrahedron on the pore surface. We further find that the pore size exhibits a significant confinement effect that affects the energetics of each intermediate's formation on both zeolites. Considering the free energy pathways at 700 K, the rate-determining steps are found to be the transformation of 2-butoxide to butoxide on HZSM-23 and the formation of 2-butoxide on HZSM-48, respectively. Our work provides mechanistic insights on the elementary processes of skeletal isomerization on zeolites.

---

Introduction

Isobutene, an isomer of butene, is a hydrocarbon of industrial significance. It has been used as an important intermediate to produce a variety of chemical products such as methyl tert-butyl ether (MTBE),¹ ethyl tert-butyl ether (ETBE),² neohexene,³ methacrolein^4,5 and pivalic acid.⁶ Therefore, the skeletal isomerization of 1-butene, a catalytic process to produce isobutene, has attracted extensive industrial and scientific attention. Many experimental studies^7–9 have reported that ferrierite (FER) zeolite is the most efficient catalyst for this isomerization and its high selectivity is attributed to the confinement effect of the unique pore structure, which contains intersecting 10-membered ring (4.2 × 5.4 Å) and 8-membered ring (3.5 × 4.8 Å) channels. Three possible mechanisms have been proposed for the skeletal isomerization of 1-butene: monomolecular,^10–12 bimolecular^13–15 and pseudo-monomolecular mechanisms.^16,17 In monomolecular mechanism, a single butene molecule is transformed to isobutene via the transition of carbenium ions and butoxide intermediates.^18,19 In bimolecular mechanism, isobutene and byproducts were produced by the processes of butene dimerization, isomerization and cracking.^20,21 In pseudo-monomolecular mechanism, an active carbonaceous species in coke deposit were considered to be the catalyst for the n-butene isomerization to isobutene.^17,22 Among these three mechanisms, the monomolecular mechanism was generally considered to the predominantly mechanism for the isomerization, whereas the bimolecular route was mainly responsible for the formation of byproducts.^23,24 Recently HZSM-23 and HZSM-48 zeolites, which have 10-membered ring and one-dimensional channel systems, were also reported to exhibit high reactivity for the isomerization process.^7,25–28 Though HZSM-23, HZSM-48 and FER have a similar 10-membered rings, the differences in channel systems such as pore size and shape is believed to have an influence on the reactivity of isomerization.^27,29,30 Nevertheless, the mechanism of 1-butene isomerization on HZSM-23 and HZSM-48 and the effect of the channel systems on the stability of reactive intermediates were rarely mentioned in the literature. For instance, the skeleton isomerization of 1-butene over HZSM-23 has also been believed to follow the monomolecular mechanism by experiment study.²⁵ It was reported that isobutene was formed from n-butene via a methyl cyclopropane carbenium intermediate, but whether the tertiary butyl cation is an intermediate or not is still unclear. Moreover, some experimental studies have indicated that the steric interaction between intermediate and the pore wall can strongly affect the types of products.²⁵ However, the origin of this steric interaction is not clear to explain the influence of channel systems of zeolites on reactions.

In the present study, the reaction mechanism of the skeletal isomerization of 1-butene to isobutene on HZSM-23 and HZSM-48 zeolites were investigated using a quantum chemical ONIOM (B3LYP/6-31G(d,p):UFF) method. Considering the unique shape selectivity of zeolites in the overall reactivity, a complete 10-membered ring channel was contained in all calculation models. In order to investigate the monomolecular mechanism of skeletal isomerization of 1-butene in the presence of environment effects of the zeolite framework, 80T and 96T cluster models for HZSM-23 and HZSM-48 were applied, respectively. The structures of active centre for skeletal isomerization of 1-butene on HZSM-23 and HZSM-48 were proposed and the effects of different channel systems (pore size and shape) on the activation energies required in the intermediates and the reaction elementary steps were discussed.

Models and methods

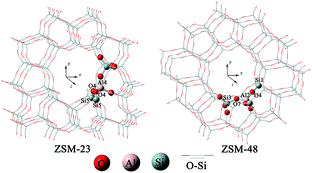
The one-dimensional 10-membered ring channel topologies of the zeolites and the basic structural properties are shown in Fig. 1. The structures of the HZSM-23 and HZSM-48 zeolites were obtained from X-ray diffraction data in IZA structural database.³¹ Based on previous studies on the stability of Brønsted acid sites,^32,33 the most stable sites Al4–O4–Si5 on HZSM-23, and Al2–O4–Si1 and Al2–O7–Si3 on HZSM-48 were chosen as the active centre for isobutene formation (see Fig. 1). According to the previous study by Boronat et al.,³⁴ the long range effect of the zeolite lattice is necessary to accurately describe the local isomerization of 1-butene in the channel of zeolite. To ensure the reliability of our model, specific channels consisting of the complete rings were cut from the crystalline structures of the HZSM-23 and HZSM-48 zeolites as 80T and 96T clusters for calculation, respectively. Since the computational model is rather large, we do not perform high level quantum calculations on the entire region of the model. As an alternative, the ONIOM scheme,³⁵ which typically utilized DFT in combination with classic mechanics using force fields to improve the computational efficiency, has been chose to investigate the isomerization processes under the confinement of zeolite pore networks in the present work.^36–39 This method has been proved to achieve reliable predictions of catalytic processes occurring on large systems.^40–45 Therefore, two-layer ONIOM methodologies^10,11,46 combined with QM/MM calculations were applied in this study.^10,36,47

Fig. 1 The cluster models used in this study. The portions depicted in balls and sticks are the high layers treated with the B3LYP/6-31G(d,p) level, and the portions depicted in wire frame are the low layers treated with the UFF potential.

According to the ONIOM scheme, a minimum of two layers are defined: the “high” level is treated by quantum mechanical methods whereas the “low” level is described either by classical mechanics or a less rigorous quantum mechanical level. In this study, B3LYP/6-31G(d,p) method was employed on the high-level atoms, including 4T cluster model (depicted in balls and sticks). The similar size of the cluster model has also been chosen to be the quantum region in previous studies.^44,45,48 For the low-level atoms (depicted in wires), the universal force field (UFF) method,⁴⁹ was employed to account for the dispersion effects as well as the confinement effects of the zeolites.^50,51 The combined B3LYP:UFF method has been widely used to explore the transition state structure and reaction mechanism over zeolites.^44,48

For all the cluster models, the dangling silicon atoms were terminated by hydrogen atoms along the bond direction of the next lattice oxygen atoms with a distance of 1.47 Å. The atoms of the reactant and the three inner most coordination spheres were relaxed during the optimization procedure, including three Si atoms, four O atoms, one Al atom and an acidic proton. The remaining structures of the zeolites were fixed in their crystallographic positions to retain the zeolite structures. All of the calculations were performed using the GAUSSIAN 09 software package.⁵² The optimization of transition states (TS) was calculated using the synchronous quasi-Newtonian method, QST3.⁵³ Frequency analyses were performed to make sure the TS has only one imaginary frequency.

Results and discussions

Adsorption of 1-butene and isobutene

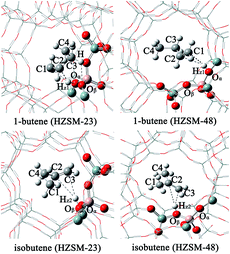
Prior to investigating the catalytic process, we first consider the adsorption of the reactant and production Brønsted acids. It is found that the acidic proton can exhibit a weak π-interaction with the C–C double bond. The optimized structures and the selected bond distances are listed in Fig. 2 and Table 1. After interacting with the acidic proton, the C=C bond 1.34 Å for both 1-butene and isobutene. Meanwhile, the length of O_α–H_z1 slightly elongates from 0.96 to 0.98–0.99 Å. The O_α–Al–O_β angle decreases by ∼3.0° and the Si–O_α–Al angle only increases by ∼1.0°. These results suggest that the adsorption process doesn't significantly change the structures of both adsorbents and zeolites, compared to the isolated structures.⁵⁴ Due to the less steric hindrance for the terminal C atom, the length of C1–H_z1 (2.52 Å for HZSM-23 and 2.45 Å for HZSM-48) is much closer than that of C2–H_z1 (2.59 Å for HZSM-23 and 2.46 Å for HZSM-48). Moreover, the hydrogen is further away from the C=C bond of isobutene than the C=C bond of 1-butene.

Fig. 2 Adsorption complexes of 1-butene and isobutene on the HZSM-23 and HZSM-48 zeolites.

Table 1 Selected bond distances of the adsorption complexes for 1-butene and isobutene on the HZSM-23 and HZSM-48 zeolites (Å)

		HZSM-23	HZSM-48
1-Butene	C1–Hz1	2.52	2.45
	C2–Hz1	2.59	2.46
	Oα–Hz1	0.99	0.98
	C1=C2	1.34	1.34
Isobutene	C2–Hz2	3.06	3.00
	C3–Hz2	2.59	2.24
	Oβ–Hz2	0.98	0.98
	C2=C3	1.34	1.34

---

To further consider the interaction of C–C double bond with Brønsted acids, we calculate the adsorption energies, listed in Table 2. For 1-butene, the adsorption energies show little difference between HZSM-23 and HZSM-48. This is probably attributed that the pore size in both zeolites is larger enough and has little effect on the linear 1-butene molecule. However, for the isobutene molecule, it has a branched-chain structure, leading to a larger steric repulsion with the walls of HZSM-48 than with the walls of HZSM-23. As a result, it exhibits significantly less adsorption energy on HZSM-48 than on HZSM-23. Interestingly, the adsorption energy values of 1-butene is less than that of isobutene on HZSM-23, the trend of adsorption energies is dissimilar to the trend of the intermolecular distances. This result implies that the drop-shaped pore framework in HZSM-23 has an important effect on the adsorption of isobutene. The branched isobutene locates at the place where the hindrance is the smallest due to the widest aperture. Moreover, the hydroxyl group offsets toward the carbon end of isobutene, leading to the formation of two hydrogen bonds, which significantly stabilize isobutene on the Brønsted acid site. These results indicate that the drop-shaped pore framework of HZSM-23 enhance the adsorption of isobutene compared to other zeolites. In addition, our results also reveal that the adsorption energy of isobutene decreases as the pore size increases due to the lower steric hindrances from the pore wall.

Table 2 The adsorption energies (E_ad) of 1-butene and isobutene on the HZSM-23 and HZSM-48 zeolites (kcal mol⁻¹). Zero point energy is included

	HZSM-23	HZSM-48
1-Butene	−19.0	−19.8
Isobutene	−23.6	−17.4

---

Monomolecular mechanism of the skeletal isomerization

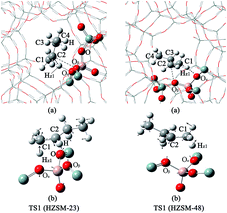
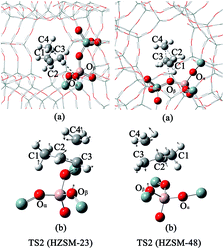
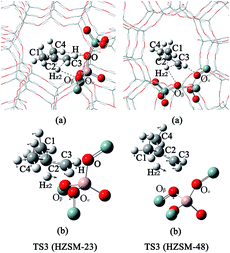
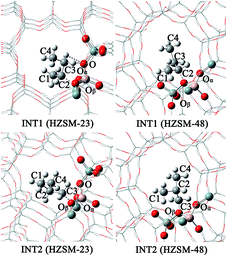
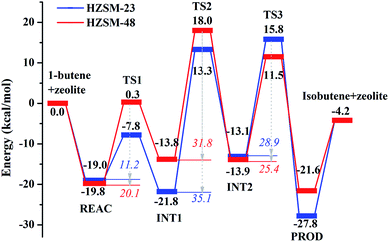
The monomolecular mechanism of the skeletal isomerization is decomposed into three elementary steps, as is shown in Fig. 3. First, the adsorbed 1-butene (REAC) is protonated to form a 2-butoxide intermediate (INT1). In this step, the C1 is protonated by the proton from O_α–H_z1 and C2 is further bonded to the lattice O_β. Second, the 2-butoxide intermediate is transformed into an isobutoxide intermediate (INT2) via a triangular protonated cyclopropyl cation. In this process, the methyl group (C4) shifts from C3 to C2 and C3 is further bonded to the lattice O_β. Finally, the isobutoxide intermediate is converted into isobutene. During this step, the C3–O_β bond is broken and H_z2 is transferred to the lattice O_β, recovering the Brønsted acid site. Fig. 4(a), 5(a), 6(a) and 7 show the optimized structures of elementary steps on the HZSM-23 and HZSM-48 zeolites. The activation energies and the geometrical parameters of the transition states and intermediates involved the isomerization of 1-butene on HZSM-23 and HZSM-48 zeolites are listed in Tables 3 and 4. The imaginary frequency for transition states on zeolites are showed in Table 5. Based on the proposed reaction mechanism, the active center for skeletal isomerization of 1-butene to isobutene is identified to exhibit a special Al–O–Si structure where the three vertex O atoms of the aluminium–oxygen tetrahedron are exposed on the surface of the pores.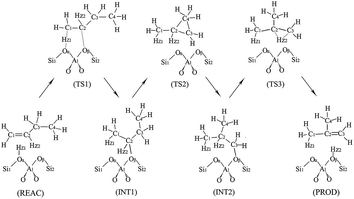

Fig. 3 The monomolecular mechanism of isomerization of 1-butene to isobutene on the HZSM-23 and HZSM-48 zeolites.

Fig. 4 The structures of TS1 on the HZSM-23 and HZSM-48 zeolites. (a) The complete pore of zeolite. (b) The pore of the relaxed part of the zeolite and the corresponding vibrations of the imaginary frequencies of TS1.

Fig. 5 The structures of TS2 on the HZSM-23 and HZSM-48 zeolites. (a) The complete pore of zeolite. (b) The pore of the relaxed part of the zeolite and the corresponding vibrations of the imaginary frequencies of TS2.

Fig. 6 The structures of TS3 on the HZSM-23 and HZSM-48 zeolites. (a) The complete pore of zeolite. (b) The pore of the relaxed part of the zeolite and the corresponding vibrations of the imaginary frequencies of TS3.

Fig. 7 The structures of INT1 and INT2 on the HZSM-23 and HZSM-48 zeolites.

Table 3 Energetics of the transition states and intermediates for the isomerization of 1-butene to isobutene on the HZSM-23 and HZSM-48 zeolites (kcal mol⁻¹). Zero point energy is included

	HZSM-23	HZSM-48
Ea1(TS1-REAC)	11.2	20.1
ΔE1(INT1-REAC)	−2.8	6.0
Ea2(TS2-INT1)	35.1	31.8
ΔE2(INT2-REAC)	8.7	−0.1
Ea3(TS3-INT2)	28.9	25.4
ΔE3(PROD-REAC)	−14.7	−7.7

---

Table 4 Structure parameters of transition states and intermediates during 1-butene isomerization on HZSM-23 and HZSM-48 zeolites (Å)

		HZSM-23	HZSM-48
TS1	C1–Hz1	1.21	1.14
	C2–Hz1	2.05	2.04
	Oα–Hz1	1.51	1.77
	C1=C2	1.41	1.44
	C2–Oβ	2.64	2.47
INT1	C1=C2	1.52	1.53
	C2–Oβ	1.53	1.55
TS2	C2–C4	1.86	1.84
	C3–C4	1.83	1.84
	C2–C3	1.39	1.39
	C3–Oβ	2.46	2.50
INT2	C2–C4	1.55	1.54
	C2–C3	1.53	1.53
	C3–Oβ	1.52	1.52
TS3	C2–C3	1.41	1.40
	C2–Hz2	1.18	1.23
	C3–Hz2	1.59	1.53
	Oβ–Hz2	2.31	2.38

---

Table 5 Imaginary frequencies for the transition states on HZSM-23 and HZSM-48 zeolites (cm⁻¹)

	TS1	TS2	TS3
HZSM-23	−98	−429	−560
HZSM-48	−114	−435	−440

---

The mechanism of the isomerization of 1-butene on HZSM-23. In the first step, the carbon end (C1) of the adsorbed 1-butene (REAC) is protonated by the acid proton of the zeolite via a transition of a secondary carbenium (TS1). The primary carbenium is hard to be formed, due to the steric hindrance that make the proton inaccessible to the C2 atom of 1-butene. The calculated imaginary frequency is 98i cm⁻¹, corresponding to the movement of the H_z1 atom from the O_α to C1 atom (see Fig. 4(b)). The activation energy (E_a1) for this step is calculated to be 11.2 kcal mol⁻¹. During this step, the O_α–H_z1 bond distance is increased from 0.99 Å to 1.51 Å and the C1–H_z1 bond is formed with a bond length of 1.21 Å. Simultaneously, the C2–O_β distance is shorten to 1.53 Å, indicating that there is a strong covalent bond between C2 and O_β, forming a 2-butoxide intermediate (INT1). In the second step, the methyl group (C4) is transferred from C3 to C2 via a transition of a triangular protonated cyclopropyl cation. At the transition state, the distance of C3–C4 bond and C2–C4 bond are 1.83 Å and 1.86 Å, respectively. After the transition, C4 is bound to C2 with a bond length of 1.55 Å and the C4–C3 bond is broken. Simultaneously, C3 becomes bound to the lattice O_β with a bond length of 1.52 Å, forming an isobutoxide intermediate (INT2). This process need to overcome a high activation barrier of 35.1 kcal mol⁻¹. Finally, the isobutoxide intermediate is converted into isobutene by transferring the proton H_z2 to the lattice O_β. The energy barrier for this step is 28.9 kcal mol⁻¹. The transition state of this step is a primary isobutyl carbenium (TS3), which is similar to the previous experimental and theoretical observation over the theta-1 zeolite.^33,55 While Wattanakit¹¹ reported that the last step still need to experience a tert-butyl carbenium intermediate that would be rapidly deprotonated to form isobutene. However, based on our vibrational analysis for the transition state (TS3), the vibrational mode of the imaginary frequency (560i cm⁻¹) demonstrates that H_z2 is inclining to bind with the lattice O_β when it moves towards C3. Therefore, we inferred that isobutene could be formed directly via a primary isobutyl carbenium.

The mechanism of the isomerization of 1-butene on HZSM-48. The isomerization mechanism on HZSM-48 is similar to that on HZSM-23. The adsorbed 1-butene (REAC) is first protonated by the acid proton of the zeolite. The 2-butoxide is formed via the transition of a secondary carbenium. During this step, H_z1 is transferred from the lattice O_α to the C1 atom and C2 becomes bound to O_β atom. The calculated activation energy of this transition state is 20.1 kcal mol⁻¹. Then, the 2-butoxide is converted into the isobutoxide intermediate (INT2) via a triangular cyclopropyl cation transition (TS2). The terminal methyl group (C4) shifts from C3 to C2. This process requires slightly higher activation energy of 31.8 kcal mol⁻¹. In the last step, the isobutoxide intermediate is converted into isobutene via a primary isobutyl carbenium. The relative large pore size of HZSM-48 has a less steric hindrance for the primary isobutyl carbenium, resulting in a lower energy barrier of 25.4 kcal mol⁻¹, compared to HZSM-23.

Mechanistic comparison between HZSM-23 and HZSM-48. To compare the isomerization mechanisms on HZSM-23 and ZSM-48, the whole reaction paths were shown in Fig. 8. First, the formation of 2-butoxide intermediate on HZSM-48 requires a higher activation energy than that on HZSM-23 zeolite (20.1 kcal mol⁻¹ vs. 11.2 kcal mol⁻¹), indicating that the cleavage of the C1=C2 bond is easier to proceed on HZSM-23. The imaginary vibrational frequencies of TS1 on HZSM-23 (Fig. 4(b)) displays a strong interaction between the carbenium and the three O atoms that connects to the Al on the pore surface (i.e., O_α⋯H_z1⋯C1, O_β⋯C2, and O⋯H⋯C3), while the carbenium intermediate only interacts with two O atoms in HZSM-48 zeolites (i.e., C1⋯H_z1⋯O_α and O_β⋯C2). Therefore we speculate that it is the strong coupling between the carbenium with the surface O that leads to the high reactivity of 2-butoxide formation in HZSM-23 zeolite. Second, HZSM-23 exhibits less reactivity for the following steps (both isobutoxide formation and isobutene formation) than the HZSM-48. As shown in Fig. 3, the formation of isobutoxide intermediate need the cleavage of C2–O_β bond in INT1. By comparing the location of the INT1 on HZSM-23 and HZSM-48, it is found that the C1⋯C2⋯C3 plane of INT1 is along the z axis on HZSM-48 or the y axis on HZSM-23 (see Fig. 7). This location relationship of INT1 and zeolites leads to the stronger interaction between C2 atom and O_β atom on HZSM-23 than that on HZSM-48. For the process of isobutene formation the C3–O_β distances in INT2 on HZSM-23 and HZSM-48 are similar. But HZSM-23 exhibits more steric hindrance with a branched structure at the active centre (Al4–O_β–Si5), which is located at the bottom of the drop-shaped channel, making H atom of C2 transform to O_β difficult. Therefore, the special channel shape and pore size of HZSM-23 were found to reduce the reactivity for both isobutoxide formation and isobutene formation.

Fig. 8 Reaction energy profiles of the skeletal isomerization of 1-butene over HZSM-23 and HZSM-48 zeolites. The energies in italic are activation energies (E_an, n = 1, 2, 3), whereas the energies in bold are energy barriers.

Since the confinement effect of zeolite is reported to not only affect the reaction enthalpy but also exhibit a significant role in the reaction entropy,^56,57 we further consider the free energetics along the reaction path by including the harmonic entropy contribution. Note that anharmonic entropy contribution is not considered in this work, though it is found important in recent studies.⁵⁸ For gas molecules, rotational, translational and vibrational entropies were all considered in the free energy estimation while for zeolites and adsorbed intermediates only the vibrational entropy was included.⁵⁹ The temperature used for the entropy estimation is chosen to be 700 K, consistent with the reaction temperature of 1-butene isomerization in recent experimental reports.^60,61

The whole free energy reaction paths on both HZSM-23 and HZSM-48 are shown in Fig. S1† and the comparison of energy barriers with or without entropy contribution are listed in Table 6. The entropy effect does not change the relative comparison for each elementary step between both zeolites. For example, the barrier of 2-butoxide formation (E_a1 or ΔG_a1) on HZSM-23 is always lower than that on HZSM-48 regardless of whether entropy is included; so do isobutoxide formation (E_a2 or ΔG_a2) and isobutene formation (E_a3 or ΔG_a3). However, it is found that the entropy effect strongly affects the energetics for the formation of each intermediate. For the formation of 2-butoxide, it increase the energy barrier by ∼9 kcal mol⁻¹ on both zeolites; for isobutoxide formation and isobutene formation, it, conversely, decreases the energy barriers by ∼3 kcal mol⁻¹ on HZSM-23 and by ∼6 kcal mol⁻¹ on HZSM-48. This leads to the significant shrink of the difference between ΔG_a1 and ΔG_a2. Specially, the rate-determine step on HZSM-48 is changed from isobutoxide formation to 2-butoxide formation when the entropy contribution is included. Finally, the free energy barrier of the rate-determine step on HZSM-23 is 32.3 kcal mol⁻¹, slightly higher than that on HZSM-48 (i.e. 27.5 kcal mol⁻¹). This suggests that HZSM-23 is a little less reactive for butene isomerization than HZSM-48.

Table 6 Comparison of calculated energy barriers with or without harmonic entropy correction (kcal mol⁻¹)

	Without entropy			With entropy
	HZSM-23	HZSM-48		HZSM-23	HZSM-48
Ea1	11.2	20.1	ΔGa1	18.0	27.5
Ea2	35.1	31.8	ΔGa2	32.3	26.1
Ea3	28.9	25.4	ΔGa3	28.9	22.5

---

Conclusions

The reaction mechanisms of skeletal isomerization of 1-butene to isobutene was investigated over one-dimensional 10-membered ring zeolites: HZSM-23 (MTT) and HZSM-48 (MRE) using the ONIOM (B3LYP/6-31G(d,p):UFF) method. The 80T and 96T cluster models were employed to represent the confinement effect from the HZSM-23 and HZSM-48 zeolites, respectively. A monomolecular mechanism for the skeletal isomerisation was proposed, including the following three steps: (1) protonation of 1-butene to form a 2-butoxide intermediate, (2) transformation of 2-butoxide intermediate into an isobutoxide and (3) decomposition of the isobutoxide intermediate into the isobutene. The active center for skeletal isomerization is identified to have a special Al–O–Si structure, where three vertex O atoms of the aluminium–oxygen tetrahedron need to be exposed on the surface of the pores. It was further found that the pore size exhibits distinct confinement effect on the reaction energetic along the reaction path on both zeolites. Considering the entropy effect at 700 K, the rate-determining steps are found to be the transformation of 2-butoxide to the isobutoxide on HZSM-23 and the formation of 2-butoxide on HZSM-48, respectively. Our work implies a significant role of the conferment effect in the chemistry of zeolites.

Acknowledgements

The authors are grateful for the financial support of the National Natural Science Foundation of China (Projects 21206008).

Notes and references

1. F. Collignon, M. Mariani, S. Moreno, M. Remy and G. Poncelet, J. Catal., 1997, 166, 53–66.
2. F. Collignon and G. Poncelet, J. Catal., 2001, 202, 68–77.
3. D. L. Crain and R. E. Reusser, US, US3658927, 1972.
4. L. Moens, P. Ruiz, B. Delmon and M. Devillers, Appl. Catal., A, 1999, 180, 299–315.
5. A. Di Capua, J. L. Dubois and M. Fournier, J. Mol. Catal. A: Chem., 2007, 263, 62–69.
6. D. W. F. Brilman, W. P. M. V. Swaaij and G. F. Versteeg, Chem. Eng. Sci., 1999, 54, 4801–4809.
7. C. L. Oyoung, R. J. Pellet, D. G. Casey, J. R. Ugolini and R. A. Sawicki, J. Catal., 1995, 151, 467–469.
8. J. Houžvička, S. Hansildaar and V. Ponec, J. Catal., 1997, 167, 273–278.
9. P. Mériaudeau, A. V. Tuan, N. H. Le and G. Szabo, Catal. Lett., 1997, 47, 71–72.
10. D. Gleeson, J. Phys. Chem. A, 2011, 115, 14629–14636.
11. C. Wattanakit, S. Nokbin, B. Boekfa, P. Pantu and J. Limtrakul, J. Phys. Chem. C, 2012, 116, 5654–5663.
12. M. Kangas, N. Kumar, E. Harlin, T. Salmi and D. Y. Murzin, Ind. Eng. Chem. Res., 2008, 47, 5402–5412.
13. D. Gleeson, J. Mol. Catal. A: Chem., 2013, 368–369, 107–111.
14. B. D. Ménorval, P. Ayrault, N. S. Gnep and M. Guisnet, Appl. Catal., A, 2006, 304, 1–13.
15. B. D. Ménorval, P. Ayrault, N. S. Gnep and M. Guisnet, J. Catal., 2005, 230, 38–51.
16. A. D. Klerk, Ind. Eng. Chem. Res., 2004, 43, 6325–6330.
17. L. A. M. Petkovic and G. Larsen, J. Catal., 2000, 191, 1–11.
18. W. Q. Xu, Y. G. Yin, S. L. Suib, J. C. Edwards and C. L. Oyoung, J. Phys. Chem., 1995, 99, 9443–9451.
19. P. Mériaudeau, V. A. Tuan, N. H. Le and G. Szabo, J. Catal., 1997, 169, 397–399.
20. Z. X. Cheng and V. Ponec, J. Catal., 1994, 148, 607–616.
21. H. H. Mooiweer, K. P. D Jong, B. Kraushaar-Czarnetzki, W. H. J. Stork and B. C. H. Krutzen, Stud. Surf. Sci. Catal., 1994, 84(4), 2327–2334.
22. M. Guisnet, P. Andy, N. S. Gnep, C. Travers and E. Benazzi, Chem. Commun., 1995, 16, 1685–1686.
23. M. Kangas, T. Salmi and D. Y. Murzin, Ind. Eng. Chem. Res., 2008, 47, 5413–5426.
24. L. Domokos, L. Lefferts, K. Seshan and J. A. Lercher, J. Catal., 2001, 197, 68–80.
25. W. Q. Xu, Y. G. Yin, S. L. Suib and C. L. Oyoung, J. Catal., 1994, 150, 34–45.
26. P. Meriaudeau, V. A. Tuan, L. N. Hung, V. T. Nghiem and C. Naccache, J. Chem. Soc., Faraday Trans., 1998, 94, 467–471.
27. P. Mériaudeau, V. A. Tuan, V. T. Nghiem, G. Sapaly and C. Naccache, J. Catal., 1999, 185(2), 435–444.
28. G. Zhao, J. Teng, Y. Zhang, Z. Xie, Y. Yue, Q. Chen and T. Yi, Appl. Catal., A, 2006, 299, 167–174.
29. S. Teketel, W. Skistad, S. Benard, U. Olsbye, K. P. Lillerud, P. Beato and S. Svelle, ACS Catal., 2012, 2, 26–37.
30. S. German, C. Antonio and C. Avelino, J. Catal., 2000, 195(2), 227–236.
31. http://iza-structure.org/databases/.
32. R. Liu, J. Zhang, X. L. Sun and B. H. Chen, J. Theor. Comput. Chem., 2014, 13, 1450059.
33. R. Liu, J. Zhang, X. L. Sun and B. H. Chen, J. Theor. Comput. Chem., 2014, 13, 1450019.
34. M. Boronat, P. Viruela and A. Corma, Phys. Chem. Chem. Phys., 2001, 3, 3235–3239.
35. S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 461–462(6), 1–21.
36. F. Ferrante, T. Rubino and D. Duca, J. Phys. Chem. C, 2011, 115, 14862–14868.
37. Y. V. Joshi and K. T. Thomson, J. Phys. Chem. C, 2008, 112(33), 12825–12833.
38. A. Zheng, S. B. Liu and F. Deng, Microporous Mesoporous Mater., 2009, 121(1–3), 158–165.
39. A. Zheng, F. Deng and S. B. Liu, Catal. Today, 2011, 164(1), 40–45.
40. B. Jansang, T. Nanok and J. Limtrakul, J. Mol. Catal. A: Chem., 2007, 264(1), 33–39.
41. G. Barone, G. Casella, A. S. Giuffrida and D. Duca, J. Phys. Chem. C, 2007, 111(35), 13033–13043.
42. P. Pantu, B. Boekfa and J. Limtrakul, J. Mol. Catal. A: Chem., 2007, 277(1–2), 171–179.
43. B. Jansang, T. Nanok and J. Limtrakul, J. Phys. Chem. B, 2006, 110(25), 12626–12631.
44. T. Maihom, S. Namuangruk, T. Nanok and J. Limtrakul, J. Phys. Chem. C, 2008, 112(33), 12914–12920.
45. C. Wattanakit, S. Nokbin, B. Boekfa, P. Pantu and J. Limtrakul, J. Phys. Chem. C, 2012, 116(9), 5654–5663.
46. H. Fang, A. Zheng, J. Xu, S. Li, Y. Chu, L. Chen and F. Deng, J. Phys. Chem. C, 2011, 115, 7429–7439.
47. M. Boronat, C. Martínezsánchez, D. Law and A. Corma, J. Am. Chem. Soc., 2008, 130, 16316–16323.
48. Y. H. Guo, M. Pu, B. H. Chen and F. Cao, Appl. Catal., A, 2013, 455(2), 65–70.
49. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddardlll and W. M. Skiff, J. Am. Chem. Soc., 1992, 114(25), 10024–10035.
50. E. G. Derouane, J. Mol. Catal. A: Chem., 1998, 134(1), 29–45.
51. S. Namuangruk, P. Pantu and J. Limtrakul, ChemPhysChem, 2005, 6, 1333–1339.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
53. C. Peng and H. B. Schlegel, Isr. J. Chem., 1993, 33(4), 449–454.
54. H. Y. Li, M. Pu, K. H. Liu, B. F. Zhang and B. H. Chen, Chem. Phys. Lett., 2005, 404, 384–388.
55. R. Byggningsbacka, N. Kumar and L. E. Lindfors, J. Catal., 1998, 178, 611–620.
56. A. Bhan and E. Iglesia, Acc. Chem. Res., 2008, 41, 559–567.
57. R. Gounder and E. Iglesia, Acc. Chem. Res., 2012, 45, 229–238.
58. G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487.
59. G. Psofogiannakis, A. Stamant and M. Ternan, J. Phys. Chem. B, 2006, 110(48), 24593–24605.
60. Y. P. Khitev, I. I. Ivanova, Y. G. Kolyagin and O. A. Ponomareva, Appl. Catal., A, 2012, 441–442(17), 124–135.
61. M. Kangas, N. Kumar, E. Harlin, T. Salmi and D. Y. Murzin, Ind. Eng. Chem. Res., 2008, 47(15), 5402–5412.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26894c

---