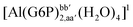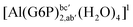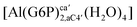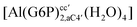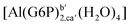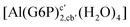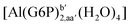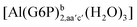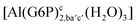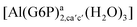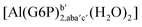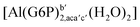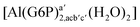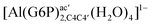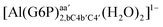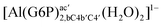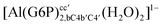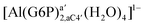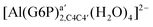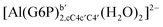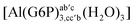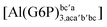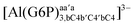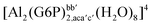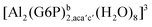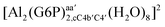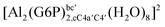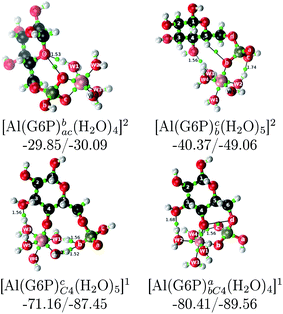Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational study on interaction of aluminum with D-glucose 6-phosphate for various stoichiometries†
Elena Formoso *a and
Xabier Lopez
*a and
Xabier Lopez ab
ab
aDonostia International Physics Center (DIPC), Manuel Lardizabal Iribidea 4, 20018 Donostia, Spain. E-mail: elena.formoso@ehu.eus
bKimika Fakultatea, Euskal Herriko Unibertsitatea (UPV/EHU), P.K. 1072, 20080 Donostia, Spain
First published on 18th January 2017
Abstract
The interaction of aluminum with glucose 6-phosphate (Al-G6P) is thought to disrupt key processes of the glucide metabolism in cells. In this article, a Density Functional Theory study on the interaction of aluminum with D-glucose 6-phoshate is presented, combined with polarizable continuum models to account for bulk solvent effects. 143 aluminum–G6P complexes with different binding modes and various total charges are characterized comprising mononuclear (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (with citrate)) and dinuclear (2
1 (with citrate)) and dinuclear (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) species. This large Al-G6P interaction dataset, the largest theoretical characterization of an aluminum–biophosphate interaction, gives insight into the diversity and complex picture of the interaction of aluminum with phosphate metabolites. We have found that charge and binding mode are driving factors in the binding affinity of glucose 6-phosphate. In addition, our calculations points to a tendency to form dicoordinated binding motifs, in which aluminum is bound to two functional groups of glucose 6-phosphate ligand. This tendency gives rise to a capacity of aluminum to act as a bridging agent in the coordination of several metabolites, a behavior that can be linked to the suspected tendency of aluminum to form aggregates that could induce various toxic effects in biological systems.
2) species. This large Al-G6P interaction dataset, the largest theoretical characterization of an aluminum–biophosphate interaction, gives insight into the diversity and complex picture of the interaction of aluminum with phosphate metabolites. We have found that charge and binding mode are driving factors in the binding affinity of glucose 6-phosphate. In addition, our calculations points to a tendency to form dicoordinated binding motifs, in which aluminum is bound to two functional groups of glucose 6-phosphate ligand. This tendency gives rise to a capacity of aluminum to act as a bridging agent in the coordination of several metabolites, a behavior that can be linked to the suspected tendency of aluminum to form aggregates that could induce various toxic effects in biological systems.
Introduction
Aluminum, the third most abundant metal in the earth’s crust, has largely been excluded from biochemical evolution because of its efficient cycling within the lithosphere.1,2 However, over the last century human intervention (soil acidification, food additives, pharmaceuticals, Al-containers, water treatment, etc.) has increased the availability of biologically reactive aluminum,2 and its presence in our bodies has been linked to various human diseases.3–5 Unfortunately, the molecular basis for aluminum toxicity is still poorly understood. Scientists with very diverse backgrounds are attempting to shed light on this regard. A first step to understand the biochemistry of aluminum is to determine the coordination chemistry of aluminum with those biomolecules that are more prone to interact with it.6–8 However, this is a difficult issue due to the complexity and variety of species that aluminum can form in solution, its low solubility and the difficulty to attain thermodynamic equilibrium due to the slow ligand exchange rate.Aluminum, as a strong Lewis acid, shows a strong preference for binding negatively-charged oxygen atoms. In fact, citrate (Citr), which contains three carboxylates and one alcoholic group (Fig. 1), is recognized as the main aluminum low molecular mass chelator in blood serum.9 On the other hand, molecules containing phosphate groups are also a likely target for interacting with the cation.8,10–14 Due to the variety of cellular processes in which molecules containing phosphate groups are present (ATP, phosphorylated proteins, sugar phosphates, DNA, etc.), this high affinity to form Al(III)–phosphate compounds could disrupt key processes of the cell metabolism. In fact, aluminum is able to cross the blood brain barrier and reach the nucleus4,15 of neurons binding to nuclear chromatin and so disrupt the transcription of genetic information.11,16 Besides, the ability of aluminum to enhance neurofibrilary tangle formation17 through the stabilization of phosphorylated tau protein is well known.18 In this vein, aluminum has been recognized as a neurotoxic compound.
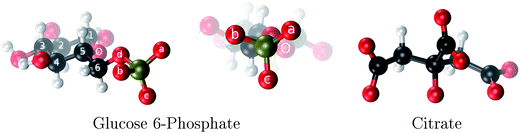 | ||
| Fig. 1 The two aluminum ligands employed in this study: glucose 6-phosphate and citrate. The phosphate oxygens of G6P are denoted as a, b and c. | ||
Among these phosphate containing molecules, sugar phosphates, such as glucose 6-phosphate (Fig. 1), are of great importance. Glucose 6-phosphate (G6P) is the meeting point for glucide metabolism in higher organisms.19 Glucose must be inevitably transformed into G6P to be utilized or stored as glycogen. In fact, there is a low concentration of glucose in cells, most of it actually occurring as G6P. The brain presents a high glucose requirement; it consumes 120 g per day of glucose, while the total body consumes ∼190 g per day. The phosphate group of G6P is not very reactive but it provides a handle which helps enzymes to recognize and to hold onto this glucose derivative. Therefore, if G6P interacts with aluminum this process may be disrupted. In fact, there have been experimental attempts20 to determine the type of complexes that aluminum can form with G6P at different pH using multinuclear NMR and potentiometric studies. However, the inherent difficulties in interpreting these experiments due to the formation of many complexes in various isomeric forms and various possibilities of ligand arrangements, led to an ambiguous peak assignations in NMR spectra. Therefore, computational studies could give very relevant complementary information to unveil aluminum coordination to this important biomolecule.
In the present paper, we have confirmed the high affinity of aluminum to G6P, and the rich biochemistry of this metal by showing the great variety of complexes that can be formed depending on concentration conditions. We provide DFT estimations of the aluminum binding affinity in the context of polarizable continuum models to consider bulk solvent effects for 143 Al–G6P compounds. This dataset comprises mononuclear (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and dinuclear (2
1) and dinuclear (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) complexes with different binding modes and various total charges (see Fig. 2). To the best of our knowledge, this is the largest dataset for an Al–phosphate interaction for a given type of molecule characterized so far, and therefore, the present paper can give insight into the diversity and complex picture of aluminum–phosphate interactions in general. We have found that charge and binding mode are driving factors in the binding affinity of G6P. Our calculations points towards a favored dicoordinated binding mode, in which aluminum is bound to two functional groups of the G6P moiety, and a tendency of aluminum to act as a bridging agent in the coordination of several G6P units.
2) complexes with different binding modes and various total charges (see Fig. 2). To the best of our knowledge, this is the largest dataset for an Al–phosphate interaction for a given type of molecule characterized so far, and therefore, the present paper can give insight into the diversity and complex picture of aluminum–phosphate interactions in general. We have found that charge and binding mode are driving factors in the binding affinity of G6P. Our calculations points towards a favored dicoordinated binding mode, in which aluminum is bound to two functional groups of the G6P moiety, and a tendency of aluminum to act as a bridging agent in the coordination of several G6P units.
Methods
All geometrical optimizations were carried out in solution with an Integral Equation Formalism Polarizable Continuum Model (IEFPCM)21 as implemented in Gaussian09,22 B3LYP functional23–26 with D3 version of Grimme’s dispersion corrections with Becke–Johnson damping27 and 6-31++G(d,p) basis set. To confirm that the optimized structures were real minima on the potential energy surfaces, frequency calculations were carried out at the same level of theory. The frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and the thermal (T = 298 K) vibrational corrections to the enthalpies and Gibbs free energies within the harmonic oscillator approximation. To calculate the entropy, the different contributions to the partition function were evaluated using the standard statistical mechanics expressions in the canonical ensemble and the harmonic oscillator and rigid rotor approximation. The electronic energies were refined by single-point energy calculations at the B3LYP/6-311++G(3df,2p) level of theory. The adequacy of this methodology has been proven to show good performance in the trends in binding affinity.8,28 Nevertheless, to further confirm the adequacy of the methodology, we re-evaluated the affinity energies of the most representative complexes by single-point calculations with four different functionals: PBE0-D3BJ, TPSS-D3BJ, B97D3 and M06-2X. The trends in binding affinity are equally well described by the different functionals. The results can be found in the ESI.†Binding free energies in solution
We studied six different types of complexes: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2
3, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 aluminum–G6P structures, and 1
2 aluminum–G6P structures, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ternary complexes of Al(III), G6P and citrate. The 1
1 ternary complexes of Al(III), G6P and citrate. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex formation stability was studied following the ligand substitution reaction shown in eqn (1):
1 complex formation stability was studied following the ligand substitution reaction shown in eqn (1):| [Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− → [Al(H2O)(6−m)L](aq,1 M)3−q + mH2O | (1) |
ΔHcomplaq = Haq(Al(H2O)(6−m)L) + mHaq(H2O) − Haq(Al(H2O)6) − Haq(L) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) ln(24.46)
| (2) |
Since the enthalpies are determined using an ideal gas at 1 atm as the standard state, the last term in eqn (2) corresponds to the volume change due to the transformation from 1 atm to 1 M in solution, where Δn refers to the change in the number of species in the reaction.29 In a similar way, the free energy of the complexes is determined as:
ΔGcomplaq = Gaq(Al(H2O)(6−m)L) + mGaq(H2O) − Gaq(Al(H2O)6) − Gaq(L) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) + mRT ln(24.46) + mRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.34) ln(55.34)
| (3) |
In the case of the second substitution for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or ternary complexes and third substitution for 1
2 or ternary complexes and third substitution for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes, the considered equations are shown in (4) and (5), whereas the considered equations for dinuclear 2
3 complexes, the considered equations are shown in (4) and (5), whereas the considered equations for dinuclear 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes are shown in (6) and (7), respectively.
2 complexes are shown in (6) and (7), respectively.
| [Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− + T(aq,1 M)r− → [Al(H2O)(6−m)LT](aq,1 M)3−q−r + mH2O | (4) |
| [Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− + T(aq,1 M)r− + X(aq,1 M)s− → [Al(H2O)(6−m)LTX](aq,1 M)3−q−r−s + mH2O | (5) |
| 2[Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− → [2(Al(H2O)(6−m))L](aq,1 M)6−q + 2mH2O | (6) |
| 2[Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− + T(aq,1 M)r− → [Al(H2O)(6−m)Al(H2O)(6−p)LT](aq,1 M)6−q−r + (m + p)H2O | (7) |
The enthalpy and free energy in solution corresponding to the binding of the ligand in these last cases are coherent with eqn (2) and (3) with the corresponding changes.
The pKa values for G6P are ∼1.0 and 6.0 for the phosphate group and 12.28 for the anomeric OH group,20 and the values for citric acid are 3.09, 4.75 and 14.4.30,31 The pKa values of all titratable groups of citrate were computed previously,32 and the value of the alcohol group drops from 14.4 in solution to 5.4 when interacting with Al(III), because the acidity of the ligand changes upon its coordination to Al(III). Thus, the OH group of the citrate is considered protonated in solution under physiological conditions, but deprotonated when coordinated to Al(III). In eqn (2) and (3) the same protonation state was considered for citrate in solution and coordinated to Al(III), therefore a correction must be introduced for those complexes where citrate is involved:
| ΔGdeprot = 2.303RT(pKa − pH) | (8) |
| Molecule | Group | pKa | ΔGdeprot | ΔGprot |
|---|---|---|---|---|
| Citrate47 | OH | 14.4 | 9.5 | |
| G6P | PO42− | 6.01 | 1.9 | |
| OH | 12.28 | 6.66 |
In the case of G6P, we consider some of the complexes with the phosphate group protonated and/or one of the glucose alcoholic OH groups deprotonated. In such cases the two pKa values stated above (6.01 and 12.28) were considered to evaluate the deprotonation energy as in eqn (8) and the protonation energy as:
| ΔGprot = 2.303RT(pH − pKa) | (9) |
The final free energy at physiological pH values (ΔGPhysaq) for all compounds is therefore evaluated as:
| ΔGPhysaq = ΔGcomplaq + ΔGdeprot + ΔGprot | (10) |
Quantum theory of atoms in molecules
Quantum Theory of “Atoms in Molecules” (QTAIM)33 was applied to previously geometrically optimized structures. QTAIM calculations were carried out with the use of AIMAll v13.05.06 program.34 The characteristics of the bond critical points (BCPs) were analyzed.The analysis of BCP provides information on the nature of interatomic interaction. For shared interactions like covalent and polarized bonds the laplacian of electron density (∇2ρBCP) is negative since there is a concentration of electron density in the atom–atom region. For the interactions between closed-shell systems such as van der Waals interactions, ionic ones and hydrogen bonds, there is a depletion of electron charge within the atom–atom region which results in low ρBCP and positive value of the laplacian.
However it was pointed out that for some interactions which may be classified as covalent bonds, the laplacian is positive and the negative value of the total electron energy density at BCP (HBCP) is a sufficient criterion of covalency. Such a situation is often observed for strong A–H⋯B hydrogen bonds classified as partly covalent in nature (HBCP negative at H⋯B BCP), even for very strong hydrogen bonds the laplacian of the electron density at BCP is negative (like for FHF− anion where ∇2ρBCP for both H⋯F contacts is negative). However usually, as for the other closed-shell interactions, for A–H⋯B hydrogen bonds both values, ∇2ρBCP and HBCP, are positive.
The figures were rendered using the VMD software35 while the graphs were generated using grace v5.1.23.
Results
The phosphate group can be twice deprotonated with pKa values of ∼1.0 and ∼6.0. There is a third deprotonation step of the anomeric alcoholic-OH group of glucose with pKa value of ∼12.28.20 Although, the deprotonation of the hydroxylic groups would occur in principle only in highly alkaline pH range, >12.3, it is well-known that the acidity of the ligand can change upon its coordination to Al(III), so it can not be neglected in this instance.36 Moreover, G6P has two possible anomeric forms, α and β. Therefore, a variety of binding modes and protonation states for Al–G6P complexes is possible. A total of 143 compounds were considered here (see ESI†). The aluminum affinity energies can be found in Tables 2, 4 and 5 and Fig. 2. This dataset comprises Al–G6P mononuclear and dinuclear complexes with different binding modes and various total charges (−6, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5). We can classify these complexes in six different groups: (i) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P complexes, (ii) 1
1 Al–G6P complexes, (ii) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(G6P)2 bis-complexes, (iii) 1
2 Al–(G6P)2 bis-complexes, (iii) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Al–(G6P)3 tris-complexes, (iv) 1
3 Al–(G6P)3 tris-complexes, (iv) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P–Citr ternary complexes, (v) 2
1 Al–G6P–Citr ternary complexes, (v) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al2–G6P dinuclear complexes and (vi) 2
1 Al2–G6P dinuclear complexes and (vi) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al2–(G6P)2 dinuclear bis-complexes.
2 Al2–(G6P)2 dinuclear bis-complexes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aluminum G6P complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to the phosphate group during the optimization
1 aluminum G6P complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to the phosphate group during the optimization
| Structure | ΔHcomplaq | ΔGcomplaq | ΔGPhysaq |
|---|---|---|---|
| [Al(G6P)ba(H2O)5]2 | −50.47 | −42.87 | −40.97 |
| [Al(G6P)ca(H2O)5]2 | −46.40 | −40.46 | −38.56 |
| [Al(G6P)ab(H2O)5]2 | −48.17 | −41.06 | −39.16 |
| [Al(G6P)cb(H2O)5]2 | −49.06 | −42.26 | −40.37 |
| [Al(G6P)ac(H2O)5]2 | −44.27 | −40.71 | −38.81 |
| [Al(G6P)bc(H2O)5]2 | −38.59 | −31.52 | −29.62 |
| [Al(G6P)cab(H2O)4]2 | −23.12 | −27.69 | −25.79 |
| [Al(G6P)bac(H2O)4]2 | −32.61 | −33.92 | −32.02 |
| [Al(G6P)abc(H2O)4]2 | −28.60 | −30.17 | −28.27 |
| [Al(G6P)aC1(H2O)5]1 | −66.16 | −60.37 | −51.82 |
| [Al(G6P)cC4(H2O)5]1 | −87.45 | −79.72 | −71.16 |
| [Al(G6P)caC1(H2O)4]1 | −79.28 | −78.45 | −69.89 |
| [Al(G6P)bcC1(H2O)4]1 | −83.72 | −82.51 | −73.96 |
| [Al(G6P)abC4(H2O)4]1 | −89.56 | −88.96 | −80.41 |
| [Al(G6P)cbC4(H2O)4]1 | −82.46 | −83.04 | −74.49 |
| [Al(G6P)a(H2O)5]1 | −68.62 | −63.82 | −63.82 |
| [Al(G6P)b(H2O)5]1 (†) | −84.84 | −77.49 | −77.49 |
| [Al(G6P)c(H2O)5]1 (†) | −84.98 | −76.13 | −76.13 |
| [Al(G6P)ab(H2O)4]1 | −61.63 | −65.64 | −65.64 |
| [Al(G6P)ac(H2O)4]1 | −65.53 | −67.55 | −67.55 |
| [Al(G6P)bc(H2O)4]1 | −60.56 | −63.80 | −63.80 |
| [Al(G6P)C1(H2O)5] | −69.86 | −64.21 | −57.56 |
| [Al(G6P)C4(H2O)5] (†) | −109.45 | −102.19 | −102.19 |
| [Al(G6P)aC1(H2O)4] (†) | −110.46 | −111.26 | −104.24 |
| [Al(G6P)bC4(H2O)4] (†) | −116.55 | −117.23 | −110.57 |
| [Al(Citr)(H2O)3]− | −124.51 | −117.37 | −107.82 |
| Binding mode | Structure | Distance | DI | ρBCP | ∇2ρBCP | HBCP | |
|---|---|---|---|---|---|---|---|
| Bidentate | [Al(G6P)bac(H2O)4]2 | Al–Oa | 1.898 | 0.178 | 0.0685 | 0.3952 | −0.0045 |
| Al–Oc | 1.920 | 0.168 | 0.0648 | 0.3675 | −0.0039 | ||
| Al–W1 | 1.904 | 0.157 | 0.0628 | 0.3852 | 0.0003 | ||
| Al–W2 | 1.915 | 0.148 | 0.0594 | 0.3695 | 0.0014 | ||
| Al–W3 | 1.916 | 0.146 | 0.0590 | 0.3678 | 0.0017 | ||
| Al–W4 | 1.955 | 0.134 | 0.0536 | 0.3221 | 0.0016 | ||
| Oa–O | 3.221 | 0.028 | 0.0063 | 0.0243 | 0.0009 | ||
| HW1–O | 1.531 | 0.138 | 0.0675 | 0.1421 | −0.0159 | ||
| Monodentate | [Al(G6P)cb(H2O)5]2 | Al–Ob | 1.801 | 0.198 | 0.0804 | 0.5475 | −0.0014 |
| Al–W1 | 1.934 | 0.136 | 0.0564 | 0.3472 | 0.0016 | ||
| Al–W2 | 1.955 | 0.150 | 0.0608 | 0.3765 | 0.0011 | ||
| Al–W3 | 1.908 | 0.156 | 0.0626 | 0.3803 | 0.0001 | ||
| Al–W4 | 1.923 | 0.140 | 0.0577 | 0.3605 | 0.0020 | ||
| Al–W5 | 1.955 | 0.134 | 0.0544 | 0.3227 | 0.0010 | ||
| HW3–Oc | 1.736 | 0.092 | 0.0398 | 0.1213 | −0.0022 | ||
| HW4–OC4 | 1.564 | 0.131 | 0.0605 | 0.1411 | −0.0116 | ||
| HC5–Ob | 2.619 | 0.034 | 0.0102 | 0.0344 | 0.0010 | ||
| Monodentate | [Al(G6P)cC4(H2O)5]1 | Al–OC4 | 1.769 | 0.234 | 0.0921 | 0.6141 | −0.0071 |
| Al–W1 | 1.929 | 0.151 | 0.0591 | 0.3534 | 0.0004 | ||
| Al–W2 | 1.928 | 0.153 | 0.0607 | 0.3551 | −0.0007 | ||
| Al–W3 | 1.924 | 0.151 | 0.0597 | 0.3600 | 0.0004 | ||
| Al–W4 | 1.999 | 0.122 | 0.0491 | 0.2783 | 0.0007 | ||
| Al–W5 | 1.975 | 0.126 | 0.0511 | 0.3016 | 0.0015 | ||
| HW1–Ob | 1.557 | 0.138 | 0.0626 | 0.1444 | −0.0129 | ||
| HW2–Ob | 1.516 | 0.161 | 0.0723 | 0.1363 | −0.0196 | ||
| HW3–OC3 | 1.560 | 0.133 | 0.0620 | 0.1415 | −0.0124 | ||
| Dicoordinate | [Al(G6P)abC4(H2O)4]1 | Al–OC4 | 1.770 | 0.225 | 0.0911 | 0.6154 | −0.0061 |
| Al–Ob | 1.868 | 0.176 | 0.0698 | 0.4329 | −0.0017 | ||
| Al–W1 | 1.971 | 0.129 | 0.0520 | 0.3070 | 0.0014 | ||
| Al–W2 | 1.969 | 0.136 | 0.0537 | 0.3077 | 0.0001 | ||
| Al–W3 | 1.975 | 0.129 | 0.0519 | 0.3024 | 0.0090 | ||
| Al–W4 | 1.948 | 0.142 | 0.0558 | 0.3300 | 0.0008 | ||
| OC4–Od | 2.907 | 0.051 | 0.0119 | 0.0429 | 0.0007 | ||
| HW2–OC3 | 1.679 | 0.113 | 0.0464 | 0.1191 | −0.0054 | ||
| HW4–Oc | 1.587 | 0.139 | 0.0602 | 0.1339 | −0.0123 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 aluminum–G6P complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to a phosphate group during the optimization
3 aluminum–G6P complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to a phosphate group during the optimization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (with Citr) and for dinuclear aluminum complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, Al(III) is coordinated by the OH group of that carbon; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition
1) (with Citr) and for dinuclear aluminum complex formation with corrections that account for the physiological pH and de/protonation of the corresponding titratable groups. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, Al(III) is coordinated by the OH group of that carbon; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition
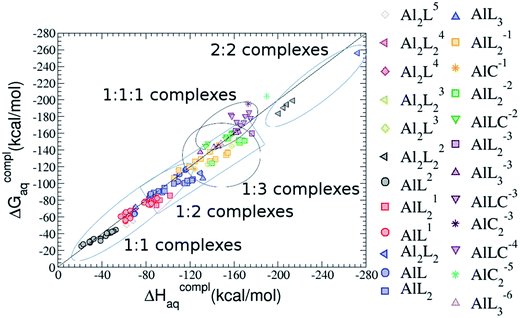
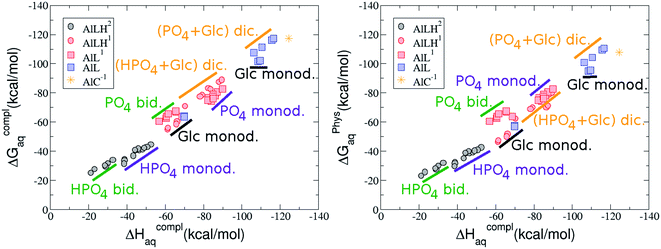
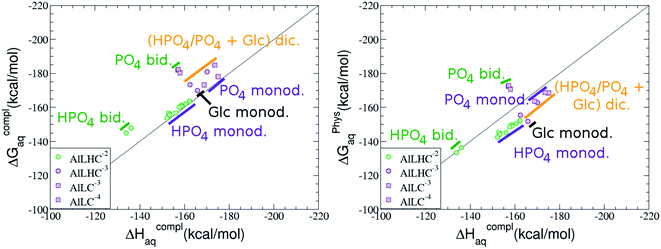
As one can see in Fig. 2, taking into account separately the complexes formed by one aluminum or by two aluminum centres, the charge is a driving factor for the binding affinity in each group, with largest complexation free energies obtained for the highest negatively charge complexes. Moreover, the complexation free energies of monoaluminum structures can be clustered in four different zones with decreasing affinity free energies in the following order: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P–Citr ternary complexes > 1
1 Al–G6P–Citr ternary complexes > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Al–(G6P)3 tris-complexes ≥ 1
3 Al–(G6P)3 tris-complexes ≥ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(G6P)2 bis-complexes > 1
2 Al–(G6P)2 bis-complexes > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P complexes. Thus, the inclusion of the citrate to form ternary complexes stabilizes the interaction of G6P with aluminum. It is also remarkable that within each of the four zones, the binding mode is a factor for the binding affinities, with largest complexation free energies being obtained for dicoordinated complexes in 1
1 Al–G6P complexes. Thus, the inclusion of the citrate to form ternary complexes stabilizes the interaction of G6P with aluminum. It is also remarkable that within each of the four zones, the binding mode is a factor for the binding affinities, with largest complexation free energies being obtained for dicoordinated complexes in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 species, for monodentate complexes in 1
2 species, for monodentate complexes in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 compounds and for bidentate complexes in 1
3 compounds and for bidentate complexes in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compounds. Interestingly, in 1
1 compounds. Interestingly, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes the dicoordinated binding mode of G6P is able to compete with citrate for binding aluminum. From now on, we will denote monodentate complexes as the compounds where the phosphate is binding the aluminum monodentately, bidentate complexes to the systems where the phosphate is binding the aluminum bidentately, and dicoordinate complexes to the species where aluminum is coordinated monodentately by an alcoholic-OH group of the sugar and monodentately by the phosphate group.
1 complexes the dicoordinated binding mode of G6P is able to compete with citrate for binding aluminum. From now on, we will denote monodentate complexes as the compounds where the phosphate is binding the aluminum monodentately, bidentate complexes to the systems where the phosphate is binding the aluminum bidentately, and dicoordinate complexes to the species where aluminum is coordinated monodentately by an alcoholic-OH group of the sugar and monodentately by the phosphate group.
We start by analyzing the results of complexes formed by one aluminum and finish with the bimetallic complexes.
Mononuclear metal 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 3 complexes
3 complexes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 Al–G6P complexes. Taking into account the two anomeric forms and the different pKa values of G6P we analyzed 63 Al–G6P complexes with various total charges, +2, +1 and 0 (see ESI†). The first 15 structures in Table 2 have a monoanionic phosphate group, while the last 10 have a dianionic one.
1 Al–G6P complexes. Taking into account the two anomeric forms and the different pKa values of G6P we analyzed 63 Al–G6P complexes with various total charges, +2, +1 and 0 (see ESI†). The first 15 structures in Table 2 have a monoanionic phosphate group, while the last 10 have a dianionic one.We show the complexation free energies of nine complexes with a total charge of +2, see Table 2. The aluminum is bound by the phosphate monodentately in the first six structures and bidentately in the next three, see Fig. 3a and b. The nine complexes differ between each other in which is the oxygen atom coordinated to aluminum cation and in the protonated phosphate group oxygen.
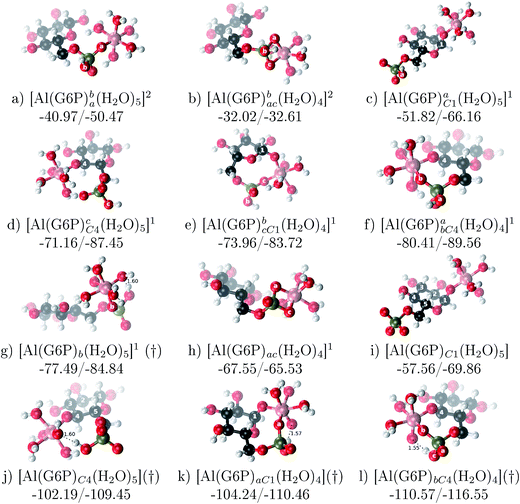 | ||
Fig. 3 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P complexes with complexation free energies for physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). Only one structure is depicted for each family of complexes. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to the phosphate group during the optimization. 1 Al–G6P complexes with complexation free energies for physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). Only one structure is depicted for each family of complexes. The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) indicates a spontaneous proton transfer from a water molecule to the phosphate group during the optimization. | ||
The total charge of the next 12 structures in Table 2 is +1. The phosphate group is in its monoanionic protonation state in the first six structures. Additionally, the first two compounds present a monodentate binding mode of aluminum by G6P’s alcoholic-OH groups, anomeric OH or C4 OH (Fig. 3c and d). The binding mode is dicoordinated in the next four complexes, G6P’s alcoholic-OH group and phosphate group coordinate each of them aluminum monodentately forming an 8- or 9-membered ring (Fig. 3e and f). The last six structures of charge +1 complexes have the aluminum cation coordinated by a totally deprotonated phosphate group. Three of them present a monodentate binding mode, whereas the last three have a bidentate one, see Fig. 3g and h. In two monodentate structures, we observe a spontaneous proton transfer from a water molecule to the phosphate group during the optimization. However, a partial estimation of the energy associated with this proton transfer revealed that its presence does not alter the main qualitative trends in binding affinities outlined in this article.
Finally, four compounds with a dianionic phosphate group and a total charge of 0 are presented. A monodentate binding mode of G6P’s alcoholic-OH groups is observed in the first two complexes (Fig. 3i and j), whereas a dicoordinate binding mode is found in the last two (Fig. 3k and l). Again, in the dicoordinate structures we observe a spontaneous proton transfer from a water molecule to the phosphate group during the optimization. Interestingly, these dicoordinate compounds and the aluminum–citrate complex present a similar physiological complexation free energy (−110.57 kcal mol−1 and −107.82 kcal mol−1, respectively), see Table 2. Therefore, dicoordinate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes can compete with the generation of the Al–Citr complex.
1 complexes can compete with the generation of the Al–Citr complex.
On the other hand, we find that charge (2, 1 and 0) is the driving factor for the binding affinity in this stoichiometry group (spheres in Fig. 2). The largest complexation free energies are obtained for the less positively charge complexes (the more negative ligand). It is also remarkable that within each same charge systems, the monodentate binding mode of the phosphate group is favored against the bidentate binding mode (see Fig. 4). Moreover, the dicoordinate binding mode (G6P’s alcoholic-OH and phosphate) can compete with the phosphate monodentate binding mode, while the monodentate binding mode of G6P’s hydroxyl group can compete with the bidentate binding mode of the phosphate group. Besides, the complexation free energy of the complexes coordinated by C4 hydroxyl group are more favored than the complexes coordinated by anomeric (C1) alcoholic-OH group, see Table 2.
The phosphate monodentate binding mode is favored against the bidentate binding mode by around 7–12/12–22 kcal mol−1 and 9–14/19–24 kcal mol−1 of complexation free/enthalpy energy in [Al–G6P]2 and [Al–G6P]1 complexes, respectively (Table 2 and Fig. 4). The monodentate binding mode of the phosphate group was also suggested by Champmartin et al. for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes.20 However, although they suggest that no direct participation of alcoholic-OH groups of the sugar in aluminum binding can be concluded, we observed that the dicoordinate binding mode of the C4 alcoholic-OH and the dianionic phosphate groups present a complexation free energy able to compete with the aluminum binding of the citrate.
1 complexes.20 However, although they suggest that no direct participation of alcoholic-OH groups of the sugar in aluminum binding can be concluded, we observed that the dicoordinate binding mode of the C4 alcoholic-OH and the dianionic phosphate groups present a complexation free energy able to compete with the aluminum binding of the citrate.
On the other hand, β and α anomers present similar complexation free energies, being a bit more negative for the β conformer, see ESI.†
The Quantum Theory of “Atoms in Molecules” (QTAIM)33 can be applied to representative structures of each coordination mode, see Table 3 and Fig. 5. As expected, a strong interaction between the aluminum and its coordination sphere is observed. It is well demonstrated in various studies that a strong interaction is connected with a high ρBCP value.37 In addition, one can observe that G6P ligand’s coordination with aluminum presents a positive laplacian of electron density at Al⋯OG6P BCP, ∇2ρBCP, an indicator of an electrostatic interaction. However, the electron energy density at Al⋯OG6P BCP, HBCP, presents a small but negative value, which may be treated as a degree of covalency of Al⋯OG6P interaction. Interestingly, aluminum interaction with the alcoholic-OH group shows a higher covalency (HBCP is more negative) than with the phosphate group. This is in good agreement with the obtained delocalization indexes (DI), with the aluminum–alcoholic-OH DI being the highest (see Table 3). Moreover, the covalency character of Al⋯OG6P interactions can be sorted in the decreasing covalency order: Al⋯OC4 in monodentate binding > Al⋯OC4 in dicoordinate binding > Al⋯Oa/b/c in bidentate binding > Al⋯Oa/b/c in monodentate binding ∼ Al⋯Oa/b/c in dicoordinate binding mode. Further, aluminum first solvation water molecules have a tendency to make strong hydrogen bonds with other oxygen atoms, see Fig. 5. They present high values of ρBCP (in the range of 0.0398–0.0723 au) in comparison with typical hydrogen bonds, see Table 3. For example for the water dimer the ρBCP at H⋯O BCP is equal to ∼0.02 au, while for the complexes considered here this value is often greater than 0.04 au. Moreover, some of these hydrogen bonds, H⋯O, show a negative HBCP, which can be treated as a degree of covalency in the H⋯O electrostatic interaction. One can see that the covalent character increases for shorter hydrogen bond distances.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
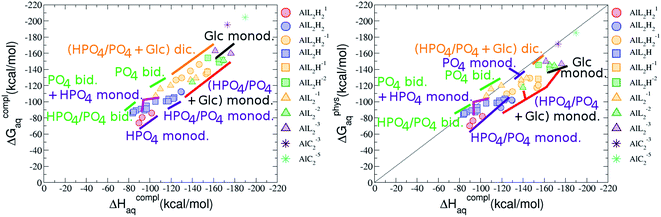
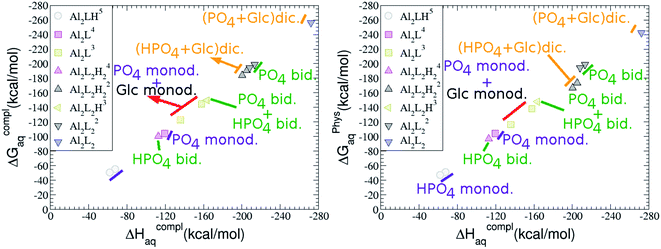
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 2 Al–(G6P)2 bis-complexes. In this section, we analyze the energetics corresponding to the complexation of two G6P ligands by aluminum (see Fig. 6 and Table 4). We have considered 39 different compounds that differ in coordination mode and protonation state of G6P (see Fig. 7 and ESI†). The resultant charges of the bis-complexes are 1, 0, −1, −2 and −3. We find that there is an increase in binding affinity with increasing negative charge of the bis-complex (squares in Fig. 2). The largest complexation free energies are found for the −3 systems, and the lowest for +1 compounds. The monodentate binding mode of the phosphate is preferred against the bidentate mode by around 12–20/26–39 kcal mol−1 of ΔGcomplaq/ΔHcomplaq, within neutral bis-complexes (see Fig. 6c and e). The combination of monodentate and bidentate binding mode of the phosphate groups was also studied for these kinds of complexes (Fig. 6d), giving raise to a complexation free energy between those of monodentate and bidentate binding mode bis-complexes (see Fig. 7 and Table 4). Moreover, the combination of phosphate monodentate binding mode and sugar C4 hydroxyl group coordination was also studied (Fig. 6b, h and m). This binding mode presents a complexation free energy higher than the monodentate binding mode of phosphates by around 7 kcal mol−1 (−112.54 vs. −105.24 kcal mol−1 within neutral complexes, and −136.77 vs. −129.04 kcal mol−1 within −1 systems), see Table 4 and Fig. 7. However, if the deprotonation penalty of the alcoholic group and the protonation of the phosphate groups corrections are taken into account, the physiological complexation free energies are similar, ∼1 kcal mol−1 difference, with a slight preference for phosphate monodentate binding mode (neutral systems ΔGPhysaq = −102.09 kcal mol−1 vs. ΔGPhysaq = −103.34 kcal mol−1, and −1 bis-complexes ΔGPhysaq = −128.22 kcal mol−1 vs. ΔGPhysaq = −129.04 kcal mol−1).
2 Al–(G6P)2 bis-complexes. In this section, we analyze the energetics corresponding to the complexation of two G6P ligands by aluminum (see Fig. 6 and Table 4). We have considered 39 different compounds that differ in coordination mode and protonation state of G6P (see Fig. 7 and ESI†). The resultant charges of the bis-complexes are 1, 0, −1, −2 and −3. We find that there is an increase in binding affinity with increasing negative charge of the bis-complex (squares in Fig. 2). The largest complexation free energies are found for the −3 systems, and the lowest for +1 compounds. The monodentate binding mode of the phosphate is preferred against the bidentate mode by around 12–20/26–39 kcal mol−1 of ΔGcomplaq/ΔHcomplaq, within neutral bis-complexes (see Fig. 6c and e). The combination of monodentate and bidentate binding mode of the phosphate groups was also studied for these kinds of complexes (Fig. 6d), giving raise to a complexation free energy between those of monodentate and bidentate binding mode bis-complexes (see Fig. 7 and Table 4). Moreover, the combination of phosphate monodentate binding mode and sugar C4 hydroxyl group coordination was also studied (Fig. 6b, h and m). This binding mode presents a complexation free energy higher than the monodentate binding mode of phosphates by around 7 kcal mol−1 (−112.54 vs. −105.24 kcal mol−1 within neutral complexes, and −136.77 vs. −129.04 kcal mol−1 within −1 systems), see Table 4 and Fig. 7. However, if the deprotonation penalty of the alcoholic group and the protonation of the phosphate groups corrections are taken into account, the physiological complexation free energies are similar, ∼1 kcal mol−1 difference, with a slight preference for phosphate monodentate binding mode (neutral systems ΔGPhysaq = −102.09 kcal mol−1 vs. ΔGPhysaq = −103.34 kcal mol−1, and −1 bis-complexes ΔGPhysaq = −128.22 kcal mol−1 vs. ΔGPhysaq = −129.04 kcal mol−1).
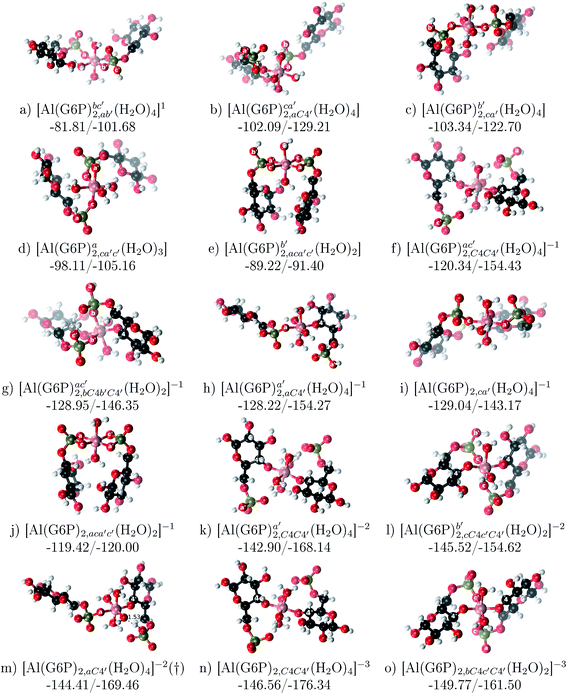 | ||
Fig. 6 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(G6P)2 bis-complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) sign indicates a spontaneous proton transfer from a water molecule to a phosphate group during the optimization. 2 Al–(G6P)2 bis-complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C1 or C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. (†) sign indicates a spontaneous proton transfer from a water molecule to a phosphate group during the optimization. | ||
The complexation free energy of neutral bis-complexes with monodentate binding mode of alcohol and phosphate groups is similar for the coordination in adjacent or opposite sites of the octahedral coordination sphere (see ESI†). Besides, in the bidentate bis-complexes, the two non-coordinating atoms of the phosphates can be in different relative positions (see ESI†), however, the obtained complexation free energies differ by less than 2 kcal mol−1. In addition, the adjacent position of the water molecules which complete the octahedral coordination sphere of the dicoordinated bis-complexes is around 15 kcal mol−1 preferred against the opposite site position (see ESI†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 3 Al–(G6P)3 tris-complexes and charge saturation. The energetics corresponding to the complexation of three G6P ligands by one aluminum is analyzed in this section (see Fig. 9 and Table 4). Taking as reference the studied 1
3 Al–(G6P)3 tris-complexes and charge saturation. The energetics corresponding to the complexation of three G6P ligands by one aluminum is analyzed in this section (see Fig. 9 and Table 4). Taking as reference the studied 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry complexes a total of 11 different compounds that differ in coordination mode and protonation state of G6P ligands are considered (see Fig. 8 and ESI†). The resultant total charge of the complexes is −6, −3 and 0. The 1
2 stoichiometry complexes a total of 11 different compounds that differ in coordination mode and protonation state of G6P ligands are considered (see Fig. 8 and ESI†). The resultant total charge of the complexes is −6, −3 and 0. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Al–(G6P)3 compounds complexation free energy region lies inside the 1
3 Al–(G6P)3 compounds complexation free energy region lies inside the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 bis-complexes region (see Fig. 2). The addition of a third G6P ligand to 1
2 bis-complexes region (see Fig. 2). The addition of a third G6P ligand to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(G6P)2 bis-complexes only produces a small “increase” in the complexation free energies. Surprisingly, the largest complexation free energies are not found for the most negative charge complexes, −6, instead −3 charge compounds present the largest complexation free energies and 0 charge complexes the lowest ones (see Fig. 8). This behavior is indicative that we are reaching the saturation limit of negative charge coordination to the metal positive center.
2 Al–(G6P)2 bis-complexes only produces a small “increase” in the complexation free energies. Surprisingly, the largest complexation free energies are not found for the most negative charge complexes, −6, instead −3 charge compounds present the largest complexation free energies and 0 charge complexes the lowest ones (see Fig. 8). This behavior is indicative that we are reaching the saturation limit of negative charge coordination to the metal positive center.
Regarding the coordination mode, the monodentate binding mode of the phosphate is favored against the bidentate and the dicoordinate ones at physiological pH (see Fig. 8 and 9).
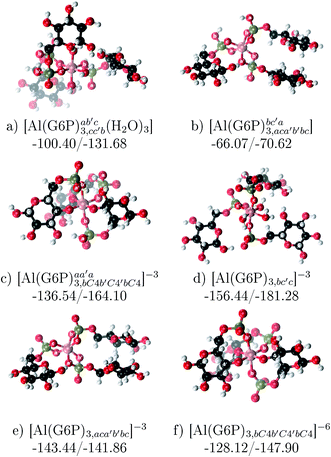 | ||
Fig. 9 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Al–(G6P)3 tris-complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each, C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. 3 Al–(G6P)3 tris-complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each, C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. | ||
Ternary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 Al–G6P–Citr complexes
1 Al–G6P–Citr complexes
The possibility of ternary complex formation in the presence of citrate is analyzed in this section. Taking as reference the studied 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry complexes 20 structures that differ in coordination mode and protonation state of G6P are considered (see Fig. 10 and ESI†). Therefore, complexes of total charge −4, −3 and −2 are studied here, see Fig. 11. Once again, the most negatively charge complexes, −4, present the highest complexation free energy (see Fig. 10). The bidentate binding mode of G6P’s phosphate group shows a smaller complexation free energy than monodentate one in −2 charge complexes, 6–17 kcal mol−1 (see Table 5 and Fig. 11a and b). However, the trend is changed in −3 charge compounds and the phosphate’s bidentate binding mode shows a moderately higher complexation free energy than phosphate’s monodentate one, 2–9 kcal mol−1 (see Table 5 and Fig. 11e and f). The monodentate binding mode of the alcoholic group (Fig. 11c) and the dicoordinate binding mode of OH and phosphate groups (Fig. 11d) is been also studied. These binding modes present smaller complexation free energies at physiological pH than the compounds coordinated only by the phosphate group of G6P, 1–21 kcal mol−1, see Table 5 and Fig. 10.
1 stoichiometry complexes 20 structures that differ in coordination mode and protonation state of G6P are considered (see Fig. 10 and ESI†). Therefore, complexes of total charge −4, −3 and −2 are studied here, see Fig. 11. Once again, the most negatively charge complexes, −4, present the highest complexation free energy (see Fig. 10). The bidentate binding mode of G6P’s phosphate group shows a smaller complexation free energy than monodentate one in −2 charge complexes, 6–17 kcal mol−1 (see Table 5 and Fig. 11a and b). However, the trend is changed in −3 charge compounds and the phosphate’s bidentate binding mode shows a moderately higher complexation free energy than phosphate’s monodentate one, 2–9 kcal mol−1 (see Table 5 and Fig. 11e and f). The monodentate binding mode of the alcoholic group (Fig. 11c) and the dicoordinate binding mode of OH and phosphate groups (Fig. 11d) is been also studied. These binding modes present smaller complexation free energies at physiological pH than the compounds coordinated only by the phosphate group of G6P, 1–21 kcal mol−1, see Table 5 and Fig. 10.
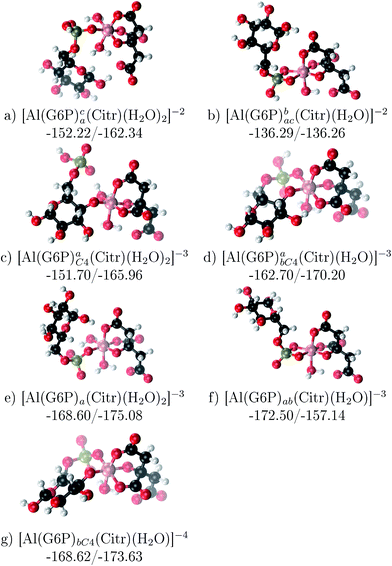 | ||
Fig. 11 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–G6P–Citr complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bind to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C4, Al(III) is coordinated by the OH group of that carbon, see Fig. 1 for oxygen definition. 1 Al–G6P–Citr complexes with complexation free energies at physiological pH (ΔGPhysaq) and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate group: a or b, the Al(III) or the proton is bind to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C4, Al(III) is coordinated by the OH group of that carbon, see Fig. 1 for oxygen definition. | ||
It is remarkable that almost all of the ternary complexes show higher complexation free energies at physiological pH (ΔGPhysaq between −133.36 and −172.50 kcal mol−1) than those of Al–(G6P)2 species (ΔGPhysaq between −70.02 and −149.77 kcal mol−1). However, all of them are smaller than that of Al–(Citr)2, ΔGPhysaq −185.41 kcal mol−1. This points to the formation of ternary compounds when both citrate and G6P are present in solution. Notice that the existence of ternary compounds has been established in the context of citrate and phosphate interactions with aluminum.38,39 Our prediction is that G6P will also be prone to form such complexes.
Dinuclear metal complexes: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 Al2–G6P and 2
1 Al2–G6P and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 Al2–(G6P)2 compounds
2 Al2–(G6P)2 compounds
Dinuclear species formed by two aluminum cations and one or two G6P ligands are studied here (see Fig. 12 and Table 5). Regarding the energetics of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the addition of a second Al(III) (see Fig. 2) leads to complexation free energies only between 4 and 22 kcal mol−1 higher than 1
1 complexes, the addition of a second Al(III) (see Fig. 2) leads to complexation free energies only between 4 and 22 kcal mol−1 higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monodentately bound monoanionic phosphate complexes. This free energy difference is increased to 22–41 kcal mol−1, for the dianionic phosphate complexes with the above mentioned binding mode. Besides, the double metal incorporation to form complexes where one aluminum is coordinated monodentately by an alcoholic group and the other aluminum is coordinated monodentately by the dianionic phosphate group shows an increase of ∼36, ∼60 and ∼53–75 kcal mol−1 in complexation free energy at physiological pH compared to monodentate binding mode of C1 and C4 alcoholic groups and phosphate group, respectively, in 1
1 monodentately bound monoanionic phosphate complexes. This free energy difference is increased to 22–41 kcal mol−1, for the dianionic phosphate complexes with the above mentioned binding mode. Besides, the double metal incorporation to form complexes where one aluminum is coordinated monodentately by an alcoholic group and the other aluminum is coordinated monodentately by the dianionic phosphate group shows an increase of ∼36, ∼60 and ∼53–75 kcal mol−1 in complexation free energy at physiological pH compared to monodentate binding mode of C1 and C4 alcoholic groups and phosphate group, respectively, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dianionic phosphate complexes. Therefore, dinuclear 2
1 dianionic phosphate complexes. Therefore, dinuclear 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes probably can not compete with the generation of two 1
1 complexes probably can not compete with the generation of two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes in the presence of excess of ligand. The formation of two 1
1 complexes in the presence of excess of ligand. The formation of two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes is energetically more favorable than the formation of one 2
1 complexes is energetically more favorable than the formation of one 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex.
1 complex.
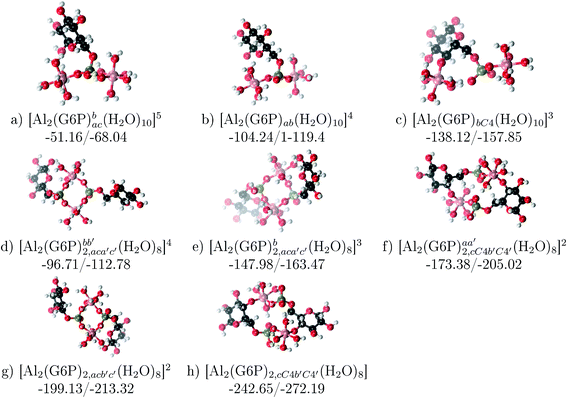 | ||
Fig. 12 Dinuclear 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2 1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes with complexation free energies at physiological pH and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. 2 complexes with complexation free energies at physiological pH and ΔHcomplaq shown in kcal mol−1 (ΔGPhysaq/ΔHcomplaq). The subscripts indicate the coordination mode of G6P to Al(III) and the superscripts refer to the protonation state of the phosphate groups: a or b, the Al(III) or the proton is bound to that oxygen; ab, the Al(III) is binding a and b oxygens, or a and b have one proton each; C4, the Al(III) is coordinated by the OH group of that carbon atom, see Fig. 1 for oxygen definition. | ||
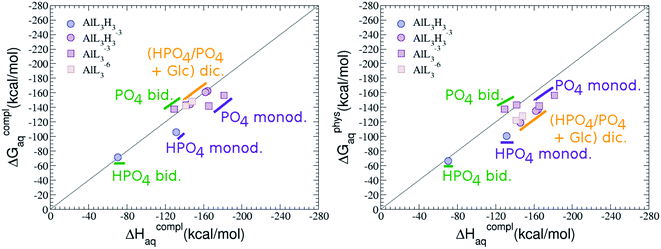
Regarding the charge of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, there is an increase in binding affinity with the charge of the system, finding the largest complexation free energy for +3 complexes and the lowest for +5 compounds, see Fig. 13.
1 complexes, there is an increase in binding affinity with the charge of the system, finding the largest complexation free energy for +3 complexes and the lowest for +5 compounds, see Fig. 13.
On the other hand, the situation is very different for dinuclear species formed by two Al(III) and two G6P ligands. Thus, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dinuclear bis-complexes are more stabilized than two 1
2 dinuclear bis-complexes are more stabilized than two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes of analogous charge (see Fig. 2 and Table 5). The most negative ΔGPhysaq value in +2 charge 2
1 complexes of analogous charge (see Fig. 2 and Table 5). The most negative ΔGPhysaq value in +2 charge 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 compounds is −199.13 kcal mol−1, nearly five times as much as the 1
2 compounds is −199.13 kcal mol−1, nearly five times as much as the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species’ value (−40.97 kcal mol−1). Therefore, there is a high propensity to form 2
1 species’ value (−40.97 kcal mol−1). Therefore, there is a high propensity to form 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dinuclear species at equal concentrations of metal and ligand. In fact, the presence of dinuclear 2
2 dinuclear species at equal concentrations of metal and ligand. In fact, the presence of dinuclear 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 bis-complexes at a wide range of pH (2–7) was observed in the pH-potentiometry and multinuclear NMR experiments of Champmartin et al.20 at equimolar concentrations of aluminum and G6P. Two types of binding motifs are found for these complexes: (i) dicoordinated complexes in which each aluminum forms two monodentate interactions with each of the phosphate group (see Fig. 12g). Thus, both phosphates would be bridging the two aluminum atoms forming a characteristic 8-membered ring, and (ii) dicoordinated complexes in which each aluminum forms a monodentate interaction with each G6P ligand through an alcoholic-OH group of one ligand and the phosphate group of the other ligand forming a 16-membered ring (see Fig. 12h). This last type of binding mode presents the highest complexation free energy (ΔGPhysaq = −242.65 kcal mol−1) of the studied systems. However, it should be noted that for the same charge complexes, +2, the complexation free energies of the two types of binding motifs are competitive (see Table 5 and Fig. 13), with a preference for the formation of the 8-membered ring, where the phosphates act as bridging ligands (see Fig. 12f and g). Besides, the experimental work of Champmartin et al.20 rise a doubt about the participation of the sugar alcoholic-OH groups in the coordination of aluminum. Surprisingly, they could not conclude that aluminum induced deprotonation and subsequent coordination of alcoholic-OH groups in Al–G6P complexes, as have been observed for other similar compounds such as lactic acid,40 malic acid,40 citric acid,32,38 tartaric acid,41 saccharic acid42 or mucic acid.42 They suggested that the formation of the 16-membered ring is hindered because of non-suitable steric arrangements. However, we do not observe any steric hindrance (see Fig. 12h). Moreover, both 8-membered and 16-membered ring complexes are stabilized by the presence of six strong hydrogen bonds between the water molecules, which complete the octahedral coordination spheres of aluminums, and the alcoholic OH groups and non-coordinating atoms of the phosphates (see Fig. 12).
2 bis-complexes at a wide range of pH (2–7) was observed in the pH-potentiometry and multinuclear NMR experiments of Champmartin et al.20 at equimolar concentrations of aluminum and G6P. Two types of binding motifs are found for these complexes: (i) dicoordinated complexes in which each aluminum forms two monodentate interactions with each of the phosphate group (see Fig. 12g). Thus, both phosphates would be bridging the two aluminum atoms forming a characteristic 8-membered ring, and (ii) dicoordinated complexes in which each aluminum forms a monodentate interaction with each G6P ligand through an alcoholic-OH group of one ligand and the phosphate group of the other ligand forming a 16-membered ring (see Fig. 12h). This last type of binding mode presents the highest complexation free energy (ΔGPhysaq = −242.65 kcal mol−1) of the studied systems. However, it should be noted that for the same charge complexes, +2, the complexation free energies of the two types of binding motifs are competitive (see Table 5 and Fig. 13), with a preference for the formation of the 8-membered ring, where the phosphates act as bridging ligands (see Fig. 12f and g). Besides, the experimental work of Champmartin et al.20 rise a doubt about the participation of the sugar alcoholic-OH groups in the coordination of aluminum. Surprisingly, they could not conclude that aluminum induced deprotonation and subsequent coordination of alcoholic-OH groups in Al–G6P complexes, as have been observed for other similar compounds such as lactic acid,40 malic acid,40 citric acid,32,38 tartaric acid,41 saccharic acid42 or mucic acid.42 They suggested that the formation of the 16-membered ring is hindered because of non-suitable steric arrangements. However, we do not observe any steric hindrance (see Fig. 12h). Moreover, both 8-membered and 16-membered ring complexes are stabilized by the presence of six strong hydrogen bonds between the water molecules, which complete the octahedral coordination spheres of aluminums, and the alcoholic OH groups and non-coordinating atoms of the phosphates (see Fig. 12).
The Quantum Theory of “Atoms in Molecules” (QTAIM)33 is being applied to study the presence of strong hydrogen bonds in these type of complexes (see Table 6). It is documented that the high value of ρBCP is connected with the presence of a strong interaction.37 The values of ρBCP found in these 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dicoordinated bis-complexes for the first solvation water molecules are higher (in the range of 0.0315–0.1007 au) than typical hydrogen bonds (∼0.02 au). In addition, in spite of the positive values of the laplacian of electron density at these H⋯O hydrogen bonds (∇2ρBCP), indicative of an electrostatic interaction, their values of energy density (HBCP) show a negative small value, indicative of a strong hydrogen bond interaction (see Table 6).
2 dicoordinated bis-complexes for the first solvation water molecules are higher (in the range of 0.0315–0.1007 au) than typical hydrogen bonds (∼0.02 au). In addition, in spite of the positive values of the laplacian of electron density at these H⋯O hydrogen bonds (∇2ρBCP), indicative of an electrostatic interaction, their values of energy density (HBCP) show a negative small value, indicative of a strong hydrogen bond interaction (see Table 6).
The +2 charge 8-membered ring bis-complex presents six strong hydrogen bonds between water molecules and G6P ligands (see Table 6). Each aluminum first solvation water molecules layer makes three strong hydrogen bonds stabilizing the 8-membered ring bis-complex, where the three hydrogen bonds between water molecules and phosphate groups are the strongest ones. They show the highest ρBCP (0.0576–0.0725 au) and DI (0.134–0.167) values, the most negative values of HBCP (−0.0110 to −0.0202 au) and the shortest H⋯O distances (1.516 to 1.604 Å). The next two strongest hydrogen bonds correspond to the interaction between water molecules and alcoholic-OH groups of the sugar (ρBCP ∼ 0.04 au). There is another strong but weaker, hydrogen bond between a water molecule and the oxygen of one of the sugars. These six hydrogen bonds show a small but negative value of electron energy density, HBCP, which may be treated as a certain degree of covalency of these mainly electrostatic interactions. The complex presents a last hydrogen bond between a C5 H atom of one of the sugars and a water molecule, however, this cannot be considered as a strong interaction, ρBCP = 0.0077. Therefore, the strength of hydrogen bond interactions can be sorted in the next decreasing order: HW⋯Oa/c/b > HW⋯OC4/C1 > HW⋯O > HC⋯OW.
On the other hand, 16-membered ring bis-complexes follow a similar trend (see Table 6). Moreover, each aluminum first solvation layer makes three strong hydrogen bonds stabilizing the 16-membered ring bis-complex. The strongest hydrogen bonds are found for the interactions between water molecules and phosphate atoms. The +2 charge bis-complex presents four strong hydrogen bonds with a small degree of covalency. Two occur between water molecules and phosphate atoms (ρBCP 0.0732 and 0.0792 au, HBCP −0.0194 and −0.0244 au) and another two occur between water molecules and C3 alcoholic-OH groups (ρBCP 0.0485 and 0.0571 au, HBCP −0.0067 and −0.0099 au). Besides, the neutral 16-membered ring bis-complex shows three very strong hydrogen bonds between water molecules and phosphate atoms (ρBCP 0.0930–0.1007 au), and another four strong hydrogen bonds between water molecules and C3 hydroxyl groups or one phosphate oxygen atom. Probably, these last interactions between waters and one of the phosphate oxygens is less strong than the previous mentioned ones, because this oxygen atom is hydrogen bonded by two different water molecules (see ESI†). The seven hydrogen bonds are mainly electrostatic interactions although they present some degree of covalency, being higher for the phosphate atoms (see Table 6). In addition, both 16-membered ring bis-complexes present more hydrogen bond interactions which stabilize the system.
Discussion
Sugar phosphates, like glucose 6-phosphate (Fig. 1), are of great importance for the normal function of the cell biochemistry. Glucose 6-phosphate (G6P) is the meeting point of the glucide metabolism for higher organisms,19 and if G6P interacts with aluminum this process may be disrupted, and induce a malfunctioning of the cell. Indeed, indirect evidences exist that aluminum could alter glucose metabolism:15 it inhibits utilization of glucose in the brain, hexokinase and G6PD,43–45 and it reduces glucose uptake by cortical synaptosomes.46 In the present paper, we have confirmed a high affinity of aluminum to G6P, with a very large number of possible compounds that could be formed depending on concentration conditions. We have seen the high affinity of forming mononuclear 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species, some of them competitive with the formation of aluminum–citrate, one of the main low molecular mass chelators of aluminum in blood serum. We have also established the possibility of the formation of mononuclear 1
1 species, some of them competitive with the formation of aluminum–citrate, one of the main low molecular mass chelators of aluminum in blood serum. We have also established the possibility of the formation of mononuclear 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(G6P)2 species, albeit less competitive with respect to 1
2 Al–(G6P)2 species, albeit less competitive with respect to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–citrate complexes, while the formation of 1
2 Al–citrate complexes, while the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 tris-complexes seems to be close to the charge saturation limit, and therefore less likely when competing with other possible ligands. On the other hand, our calculations also point to the possibility of formation of ternary species with citrate. This is of importance since citrate is the main low molecular mass chelator of aluminum in blood serum, and our calculations show that its presence could enhance the possibility of interaction with G6P. The formation of ternary species is characteristic of aluminum–phosphate interactions38,39 and in this sense, it is not surprising to see such a possibility for G6P as well.
3 tris-complexes seems to be close to the charge saturation limit, and therefore less likely when competing with other possible ligands. On the other hand, our calculations also point to the possibility of formation of ternary species with citrate. This is of importance since citrate is the main low molecular mass chelator of aluminum in blood serum, and our calculations show that its presence could enhance the possibility of interaction with G6P. The formation of ternary species is characteristic of aluminum–phosphate interactions38,39 and in this sense, it is not surprising to see such a possibility for G6P as well.
We have also observed the possibility of forming bigger aggregates through the formation of dinuclear 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 bis-complexes with different possibilities: (i) the two phosphates bridge the two aluminum atoms forming a 8-membered ring or (ii) each aluminum binds to one phosphate and the glucose unit of the other G6P, forming a 16-membered ring. Notice that the presence of 2
2 bis-complexes with different possibilities: (i) the two phosphates bridge the two aluminum atoms forming a 8-membered ring or (ii) each aluminum binds to one phosphate and the glucose unit of the other G6P, forming a 16-membered ring. Notice that the presence of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 aggregates were suggested at different pH values by Champmartin et al.20 Therefore, our calculations, in agreement with experiments, reinforce the capacity of aluminum to act as a bridging agent, forming dinuclear compounds in which each aluminum can bridge two G6P units. Our calculations show that these structures are stabilized by a set of intramolecular hydrogen bonds mediated by the strongly polarized water molecules of the first shell of aluminum.
2 aggregates were suggested at different pH values by Champmartin et al.20 Therefore, our calculations, in agreement with experiments, reinforce the capacity of aluminum to act as a bridging agent, forming dinuclear compounds in which each aluminum can bridge two G6P units. Our calculations show that these structures are stabilized by a set of intramolecular hydrogen bonds mediated by the strongly polarized water molecules of the first shell of aluminum.
In general, for all the type of compounds investigated, we find that the possibilities of ligand arrangements are numerous. This behavior is known to be prototypical of aluminum biocoordination, and in fact, this is one of the factors that introduce inherent difficulties to interpret experimental data. However some basic binding features can be outlined from our calculations. In this sense, we have observed a tendency of aluminum to interact monodentately with phosphates, a behavior highlighted previously in theoretical and experimental studies. Another important structural feature is the possibility of the interaction with alcohol groups of the glucose, in particular the alcohol group at C4 position. This is observed for all types of compounds studied in this work, mono- and dinuclear in different stoichiometries, but it is specially favorable for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. It is also noted that the same coordination motifs are found for well-known aluminum chelators such as lactic acid, malic acid, citric acid, tartaric acid, saccharic acid and mucic acid. However, in the NMR studies of Champmartin et al. no direct participation of the alcoholic–OH groups of the sugar moiety in Al(III) binding could be concluded. A possible explanation highlighted in their paper was the possibility of steric hindering for a direct interaction with aluminum with alcohol groups in the sugar ring. However, our studies do not detect any steric hindrance for the interaction with the alcohol group in any of the type of compounds studied: mononuclear 1
1 complexes. It is also noted that the same coordination motifs are found for well-known aluminum chelators such as lactic acid, malic acid, citric acid, tartaric acid, saccharic acid and mucic acid. However, in the NMR studies of Champmartin et al. no direct participation of the alcoholic–OH groups of the sugar moiety in Al(III) binding could be concluded. A possible explanation highlighted in their paper was the possibility of steric hindering for a direct interaction with aluminum with alcohol groups in the sugar ring. However, our studies do not detect any steric hindrance for the interaction with the alcohol group in any of the type of compounds studied: mononuclear 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, ternary compounds and dinuclear complexes.
2, ternary compounds and dinuclear complexes.
We have completed the aluminum shell by water molecules at our initial geometries, following previous protocols developed in the group. This is a situation realistic for low pH regimes. As the pH is neutralized, deprotonation of waters are expected, and therefore, hydroxide ions would be bound to aluminum. The presence of these hydroxides could alter some of the trends outlined in the present paper. However, our experience in similar systems reveal that the presence of hydroxide ions tend to give similar trends to the ones in which all waters are considered, although they tend to smooth out the difference in energies among the different binding modes. However, we should highlight that in some of our calculations, we have observed deprotonation of one of the water molecules directly coordinating to aluminum. Thus, in the geometry optimization process, one proton was transferred from one of the oxygens of a water molecule to one of the phosphate oxygens that is not directly coordinating to aluminum. This could be either be an artifact of our reduced solvation models or a real possibility. Notice that the pKa of a water molecule bound to an aluminum is 5.3, whereas the second pKa of a phosphate is ∼6, therefore, it is not unreasonable that this type of structures are formed in solution at pH higher than 6. In fact, Champmartin et al.20 pointed out to the presence of one hydroxide ion around aluminum based in NMR studies of these type of compounds. Notice that in any case, upon the presence of an hydroxide around aluminum the octahedral coordination is maintained in our calculations, a type of coordination also suggested by the experiments of Champmartin et al.20 In order to further explore the possibility of the presence of hydroxide ions and how they would alter the observed trends, we have taken some selected structures and substitute one or two water molecules with hydroxides. Our results points that the qualitative trends in binding energies are maintained, although the actual difference in binding energies would be damped, as it corresponds to a lower positive charge of the aluminum cluster (data not shown).
Conclusions
In this paper, we have provided a complete and extensive study of the binding modes of aluminum with glucose 6-phosphate, an important metabolite thought to be particularly sensitive to the presence of aluminum. Our results help in rationalizing previous experimental characterization of this type of compounds. We have observed a rich variety of possible structures, revealing various available isomeric forms which give rise to a complex and rich aluminum chelation chemistry. Some general remarks on the interaction are as follows: (i) there is a large variety of compounds that aluminum could form in the presence of G6P (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mononuclear complexes, 1
3 mononuclear complexes, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ternary complexes with citrate and dinuclear species), with the charge factor being the driving force in binding affinity. (ii) For mononuclear and dinuclear complexes, dicoordinated compounds are favored. In the case of dinuclear species each aluminum would bind to two phosphates, leading to 8-membered rings or to a phosphate and an alcoholic OH group forming a 16-membered ring. (iii) We also observe that the complexes are highly stabilized by the interaction with deprotonated alcohol groups of the glucose, as similarly found for other well known aluminum chelators. (iv) For equimolar concentration of aluminum and G6P the formation of dinuclear complexes would be favored, through the formation of 2
1 ternary complexes with citrate and dinuclear species), with the charge factor being the driving force in binding affinity. (ii) For mononuclear and dinuclear complexes, dicoordinated compounds are favored. In the case of dinuclear species each aluminum would bind to two phosphates, leading to 8-membered rings or to a phosphate and an alcoholic OH group forming a 16-membered ring. (iii) We also observe that the complexes are highly stabilized by the interaction with deprotonated alcohol groups of the glucose, as similarly found for other well known aluminum chelators. (iv) For equimolar concentration of aluminum and G6P the formation of dinuclear complexes would be favored, through the formation of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, rather than 2
2 complexes, rather than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. (v) The formation of ternary compounds with citrate seems to be likely as well, as it is the case for other phosphates (2,3-DPG)28 and other known Al–chelators (ketoglutarate, etc).47 And finally, (vi) aluminum shows a remarkable ability to act as bridging agent to interlink G6P units (2
1 complexes. (v) The formation of ternary compounds with citrate seems to be likely as well, as it is the case for other phosphates (2,3-DPG)28 and other known Al–chelators (ketoglutarate, etc).47 And finally, (vi) aluminum shows a remarkable ability to act as bridging agent to interlink G6P units (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes) with structures stabilized by strong intramolecular hydrogen bonds.
2 complexes) with structures stabilized by strong intramolecular hydrogen bonds.
Abbreviations
| BCP | Bond critical point |
| Bid | Bidentate |
| Citr | Citrate |
| DI | Electron delocalization index |
| Dic | Dicoordinate |
| G6P | D-Glucose 6-phosphate |
| Glc | Glucose |
| DFT | Density functional theory |
| Monod | Monodentate |
| QTAIM | Quantum theory of “Atoms in Molecules” |
Acknowledgements
The authors would like to thank the technical and human support provided by the IZO-SGI SGIker of UPV/EHU and European funding (ERDF and ESF). Financial support comes from UPV/EHU (PES14/35), Eusko Jaurlaritza (IT588-13) and the Spanish Ministerio de Ciencia e Innovacin (CTQ2015-67608-P).References
- C. Exley, J. Inorg. Biochem., 2003, 97, 1–7 CrossRef CAS PubMed , Aluminium in Life: From Acid Rain to Alzheimer’s Disease. Fifth Keele Meeting on Aluminium.
- C. Exley, Trends Biochem. Sci., 2009, 34, 589–593 CrossRef CAS PubMed.
- T. MacDonald and R. Martin, Trends Biochem. Sci., 1988, 13, 15–19 CrossRef CAS PubMed.
- Bharathi, P. Vasudevaraju, M. Govindaraju, A. Palanisamy, K. Sambamurti and K. Rao, Indian J. Med. Res., 2008, 128, 545–556 CAS.
- C. Shaw and L. Tomljenovic, Immunol. Res., 2013, 56, 304–316 CrossRef CAS PubMed.
- T. Kiss, J. Inorg. Biochem., 2013, 128, 156–163 CrossRef CAS PubMed.
- J. Mujika, E. Rezabal, J. Mercero, F. Ruipérez, D. Costa, J. Ugalde and X. Lopez, Comput. Struct. Biotechnol. J., 2014, 9, 1–13 CrossRef PubMed.
- N. Luque, J. Mujika, E. Rezabal, J. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2014, 16, 20107–20119 RSC.
- M. Hémadi, G. Miquel, P. Kahn and J. Chahine, Biochemistry, 2003, 42, 3120–3130 CrossRef PubMed , PMID: 12627980.
- K. Atkári, T. Kiss, R. Bertani and R. Martin, Inorg. Chem., 1996, 35, 7089–7094 CrossRef , PMID: 11666891.
- T. Kiss, P. Zatta and B. Corain, Coord. Chem. Rev., 1996, 149, 329–346 CAS.
- D. Mazzuca, N. Russo, M. Toscano and A. Grand, J. Phys. Chem. B, 2006, 110, 8815–8824 CrossRef CAS PubMed , PMID: 16640440.
- E. Formoso, J. Mujika, S. Grabowski and X. Lopez, J. Inorg. Biochem., 2015, 152, 139–146 CrossRef CAS PubMed.
- R. Grande-Aztatzi, E. Formoso, J. Mujika, J. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2016, 18, 7197–7207 RSC.
- L. J. Tomljenovic, Alzheimer Dis., 2011, 23, 567–598 CAS.
- V. Gupta, S. Anitha, M. Hegde, L. Zecca, R. Garruto, R. Ravid, S. Shankar, R. Stein, P. Shanmugavelu and K. Jagannatha Rao, Cell. Mol. Life Sci., 2005, 62, 143–158 CrossRef CAS PubMed.
- C. Exley, Coord. Chem. Rev., 2012, 256, 2142–2146 CrossRef CAS , Metal Ions in Neurodegenerative Diseases.
- M. Abdel-Ghany, A. El-Sebae and D. Shalloway, J. Biol. Chem., 1993, 268, 11976–11981 CAS.
- S. Liu, Bioprocess Engineering: Kinetics, in Biosystems, Sustainability, and Reactor Design, Elsevier, Amsterdam, 2013, ch. 10 – Cell Metabolism, pp. 473–548 Search PubMed.
- D. Champmartin, P. Rubini, A. Lakatos and T. Kiss, J. Inorg. Biochem., 2001, 84, 13–21 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed , PMID: 16092826.
- M. Frisch, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- S. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- N. Luque, J. Mujika, E. Formoso and X. Lopez, RSC Adv., 2015, 5, 63874–63881 RSC.
- J. Ali-Torres, L. Rodriguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13, 7852–7861 RSC.
- R. Dawson, D. Elliott, W. Elliott and K. Jones, Data for Biochemical Research, Oxford, Clarendon Press, 1986 Search PubMed.
- A. Silva, X. Kong and R. Hider, Biol. Met., 2009, 22, 771–778 CAS.
- J. Mujika, J. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2012, 14, 12465–12475 RSC.
- C. Matta and R. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, 2007 Search PubMed.
- A. Todd and T. Keith, Gristmill Software, Overland Park KS, USA, 2011, aim.tkgristmill.com Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Mujika, J. Ugalde and X. Lopez, Theor. Chem. Acc., 2011, 128, 477–484 CrossRef CAS.
- S. Grabowski, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS PubMed , PMID: 21322583.
- A. Lakatos, F. Evanics, G. Dombi, R. Bertani and T. Kiss, Eur. J. Inorg. Chem., 2001, 3079–3086 CrossRef CAS.
- X. Ma, L. Li, C. Xu, H. Wei, X. Wang and X. Yang, Molecules, 2012, 17, 9379–9396 CrossRef CAS PubMed.
- T. Kiss, I. Sóvágó, R. Martin and J. Pursiainen, J. Inorg. Biochem., 1994, 55, 53–65 CrossRef CAS.
- E. Marklund and L.-O. Ohman, J. Chem. Soc., Dalton Trans., 1990, 755–760 RSC.
- A. Lakatos, R. Bertani, T. Kiss, A. Venzo, M. Casarin, F. Benetollo, P. Ganis and D. Favretto, Chem.–Eur. J., 2004, 10, 1281–1290 CrossRef CAS PubMed.
- J. Joshi, M. Dhar, M. Clauberg and V. Chauthaiwale, Environ. Health Perspect., 1994, 102, 207–213 CrossRef CAS PubMed.
- J. Joshi, Comp. Biochem. Physiol., Part C: Pharmacol., Toxicol. Endocrinol., 1991, 100, 103–105 CrossRef CAS.
- C. Exley, J. Birchall and N. Price, J. Inorg. Biochem., 1994, 54, 297–304 CrossRef CAS PubMed.
- J. Lipman, S. Colowick, P. Lawrence and N. Abumrad, Life Sci., 1988, 42, 863–875 CrossRef CAS PubMed.
- J. Mujika, J. Ugalde and X. Lopez, J. Phys. Chem. B, 2014, 118, 6680–6686 CrossRef CAS PubMed , PMID: 24874214.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27037a |
| This journal is © The Royal Society of Chemistry 2017 |