A first-principles investigation of a new hard multi-layered MnB₂ structure

Abstract

ReB₂-type MnB₂ has always been considered to be the ground-state structure of MnB₂. However, subsequent theoretical study has revealed that this structure is easy to decompose into elemental Mn and B under ambient conditions, which motivated us to look for a stable MnB₂ structure at high pressures. Using structure prediction algorithm USPEX and density functional theory calculations, we found a stable multi-layered MnB₂ structure with space group Immm at high pressure. The calculated hardness of Immm-MnB₂ is 22.5 GPa, which makes it a potential hard multifunctional material along with its conductive and magnetic properties. The hexagonal graphene-like boron networks of Immm-MnB₂ contribute to its hardness and stability.

---

1 Introduction

The research of transition-metal diborides (TMB₂s) never stops due to their outstanding physical and chemical properties, such as superconductivity, magnetism and superhardness, as well as being ultrahigh-temperature ceramics.^1–4 The design philosophy for hard transition-metal diborides makes them very resistant to shear deformation by introducing covalent bonds into highly incompressible metals.^5,6 Boron is a small and highly-bonded element,⁷ which provides a covalent bond network in transition metal borides.⁸ Recently, several transition-metal diborides, such as ReB₂,⁹ OsB₂,¹⁰ and TaB₂,¹¹ with a bulk modulus above 350 GPa, have been synthesized and greatly encouraged studies on transition metal diborides. Particularly, 3d magnetic metal manganese, with abundant valence electrons and “electron-deficient” boron, can form boron-based solids with the specific features of excellent multifunctional materials, such as high melting points, and magnetostructural and electronic behaviour.^12–14 Numerous studies, theoretical and experimental, have been conducted on MnB₂.^15–25 Originally, Binder and Post synthesized AlB₂–MnB₂ (SG P6/mmm) by heating mixtures of metal Mn and B at 1400–1500 °C.¹⁹ Subsequently, in 2009, Aydin and Simsek predicted a superhard phase of MnB₂ with ReB₂-type structure (SG P6₃/mmc), which was regarded as the ground state of MnB₂ at ambient conditions.¹⁶ In the same year, Jing Fan et al.¹⁵ held the view that ReB₂-type MnB₂ could be synthesized only below 1020 K at ambient pressure. Unfortunately, after a prolonged endeavor, ReB₂-type MnB₂ was never successfully synthesized to date. More recently, Haiyang Niu, et al.²⁵ found ReB₂-type MnB₂ to be a metastable phase by variable-composition evolutionary algorithm calculations and first-principles calculations. Now that it is known that no stable MnB₂ phase exists at ambient pressure, it should be investigated whether there are novel phases of MnB₂ with new properties at high pressures. Thus, we investigated the structure, phase stability, electronic properties, and hardness of manganese diborides based on known transition-metal crystal structures and structure predictions. Through our calculations, a new high-pressure phase, Immm-MnB₂, was found. It is mechanically stable and can be quenched at ambient pressure. The electronic structure results indicate that Immm-MnB₂ is a metal and exhibits magnetic properties at ambient pressure, which could provide a new hard multifunctional material with a hardness of 22.5 GPa. Its hardness is mainly due to the strong covalent B–B bonds in the hexagonal graphene-like boron network.

2 Computational details

We performed evolutionary variable-cell simulations on Mn–B systems (at Mn : B ratios of 2 : 1, 1 : 1, 1 : 2, 1 : 3 and 1 : 4) with one to four formula units (FU) at moderate pressures of 0–60 GPa and zero temperature with the USPEX code.^26–28 We mostly applied spin-polarized first-principles calculations with the pseudo-potential plane-wave method using the Vienna ab initio simulation program (VASP) code.²⁹ The exchange and correlation effects were described by the generalized gradient approximation (GGA).³⁰ The valence electron configurations of manganese and boron are 3p⁶4s²3d⁵ and 2s²2p¹, respectively. The bond lengths, cell parameters and atomic positions of any selected structure were fully optimized at different pressures with a plane-wave cut-off energy of 500 eV and dense Monkhorst–Pack k-point meshes with a reciprocal space resolution of 2π × 0.03 Å⁻¹.³¹ These settings enabled excellent convergence of the energy differences, stress tensors, and structural parameters. The elastic constants were calculated using the strain–stress method. The bulk modulus B, shear modulus G, B/G ratio and Poisson's ratio (ν) were estimated using the Voigt–Reuss–Hill (VRH) approximation.³² In addition, we further derived phonon dispersions of the structures proposed by the USPEX with PHONOPY code.³³ The theoretical Vickers hardness was estimated using the Chen's model.³⁴

3 Results and discussion

3.1 Thermodynamic stability and structural characteristics

In addition to the well-known hexagonal phase, ReB₂–MnB₂, we found a new high-pressure orthogonal phase, MnB₂, with space group Immm at about 50 GPa, which is clearly observed in the convex hull diagram. According to the latest Mn–B phase diagram,^18,24,25 the convex hull at different pressures including spin-polarization effects is shown in Fig. 1, connecting α-Mn,³⁵ α-B (0–19 GPa), and γ-B (19–89 GPa)³⁶ at T = 0 K. The formation enthalpy of Mn_xB_y is defined as follows: ΔH = H(Mn_xB_y) − xH(Mn) − yH(B). Our calculations indicate that the experimental AlB₂–MnB₂ and the pre-existing theoretical ReB₂–MnB₂ phase are metastable at ambient pressure (see Fig. 1a). Notably, when further increasing the pressure, the Immm-MnB₂ phase (proposed for the first time) can be synthesized at 50 GPa because its negative formation enthalpy lies in the convex hull^37,38 (Fig. 1b). Consequently, we can also obtain a phase transition of MnB₂ from ReB₂-type structure to Immm phase in the convex hulls.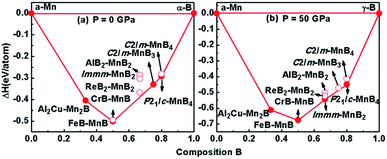

Fig. 1 Convex hull diagram of the Mn–B systems at pressures of 0 GPa (a) and 50 GPa (b). Solid circles represent stable phases, while hollow circles denote metastable phases.

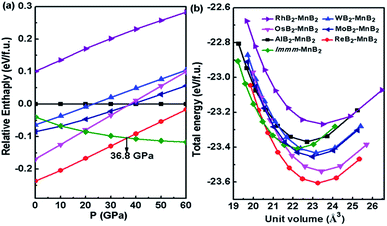
As shown in Fig. 2a, we compared the enthalpies of typical transition-metal diborides (MoB₂-type MnB₂,³⁹ SG R3̄m, WB₂-type MnB₂,¹ SG P6₃/mmc, OsB₂-type MnB₂,⁴⁰ SG Pmmn, RhB₂-type MnB₂,⁴¹ SG P2₁/m), ReB₂–MnB₂ and Immm-MnB₂ as a function of pressure with respect to AlB₂-type MnB₂. As expected, the most thermodynamically stable structure is ReB₂-type MnB₂ at ambient pressure, which is in good agreement with previous first-principles calculations.^15,24 ReB₂-type MnB₂ is stable in the pressure range of 0–36.8 GPa. Above 36.8 GPa, the Immm-MnB₂ is the most energetically favorable up to 60 GPa. The results also show that Immm-MnB₂ can be obtained from Al₂Cu–Mn₂B + γ-B, FeB–MnB + γ-B, Al₂Cu–Mn₂B + P2₁/c-MnB₄ and FeB–MnB + P2₁/c-MnB₄ in the convex hulls. The energy–volume curves of the known MnB₂, illustrated in Fig. 2b, demonstrate a structural transition from ReB₂-type MnB₂ to Immm-MnB₂ within the pressure range considered.

Fig. 2 (a) Computed relative enthalpy diagram of all the considered MnB₂ structures relative to AlB₂-type MnB₂ as a function of pressure. (b) Total energy per formula unit as a function of volume for the MnB₂ structures.

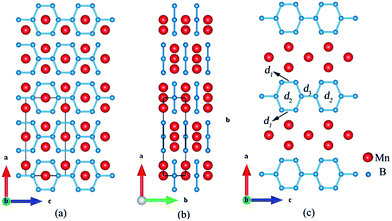
The equilibrium lattice parameters of Immm-MnB₂ are a = 9.717 Å, b = 2.768 Å, c = 4.940 Å at ambient pressure. The orthogonal Immm structure contains six FUs per one unit cell with Mn atoms occupying the Wyckoff positions 2c (0.5, 0.5, 0) and 4e (0.6317, 0.5, 0.5) and B atoms occupying the 4j (0.5, 0, 0.6799) and 8m (0.6778, 0, 0.8205). From Fig. 3a and b, it can be clearly seen that Immm-MnB₂ is a multi-layered structure. However, unlike the common layered structure of graphene-like boron layers that sandwich metal layers along c-axis in transitional diborides, e.g. ReB₂, TaB₂, our predicted Immm-MnB₂ structure consists of hexagonal graphene-like boron networks formed by sp² hybridized B–B bonds and manganese layers in each layer along the b- and c-axis. Two of the B–B bonds in the hexagonal graphene-like boron networks of Immm-MnB₂, have a length of d₁ = 1.773 Å and four of them have a length of d₂ = 1.862 Å. The B–B bond between two adjacent six-membered boron rings has a distance of d₃ = 1.778 Å (see Fig. 3c). The shortest B–B bond length, of 1.773 Å, is shorter than that of superhard ReB₂ (1.820 Å),⁹ indicating a strong covalent bonding in Immm-MnB₂ at 0 GPa. In addition, the structural characteristics of Immm-MnB₂ are very similar to those of high-boron compounds, such as Immm-Mn₃B₄, suggesting that Immm-MnB₂ may have a strong stability and good mechanical properties.

Fig. 3 Crystal structures of Immm-MnB₂: (a) along the b-axis, (b) along the c-axis. (c) View of a one-layer structure of Immm-MnB₂. The large red and small blue spheres represent Mn and B atoms, respectively.

3.2 Dynamical stability, mechanical stability and hardness

Evaluating the dynamical stability is necessary for assessing whether the proposed structure is stable or not. Thus, the phonon dispersion curves of Immm-MnB₂ at different pressures are displayed in Fig. 4. All the phonon modes of Immm-MnB₂ are positive in the entire Brillouin zone, which confirms its dynamic stability. Immm-MnB₂ was determined to be stable at 0–50 GPa, indicating that it can be obtained under ambient conditions.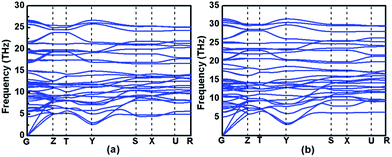

Fig. 4 Phonon dispersion curves of Immm-MnB₂ at (a) 0 GPa, and (b) 50 GPa along the high-symmetry directions of the Brillouin zone.

Evaluating the mechanical properties of Immm-MnB₂ is necessary for determining its mechanical stability and industrial applications. The elastic constants (C_ij) for Immm-MnB₂ were calculated by the strain–stress method, and the results are presented in Table 1. For comparison with the predicted Immm-MnB₂ structure, we also calculated the elastic properties of some common transition-metal diborides such as TMB₂ (TM = Ta, W, Re), using the same approach, as summarized in Table S1 (ESI†). The corresponding elastic modulus (B, G, Y), B/G ratio, Poisson's ratio ν and hardness H_v of all the abovementioned diborides are summarized in Table 1.

Table 1 Calculated bulk modulus B (GPa), shear modulus G (GPa), Young's modulus Y (GPa), B/G ratio, Poisson's ratio ν and hardness H_v (GPa) for Immm-MnB₂ and some common transition-metal diborides TMB₂ (TM = Ta, W, Re) at P = 0 and 50 GPa

Structure	P	B	G	Y	B/G	ν	Hv
a Ref. 42.b Ref. 43.c Ref. 44.d Ref. 16.
Immm-MnB2	0	308	195	483	1.58	0.24	22.5
	50	449	274	684	1.64	0.25	27.0
TaB2	0	312	210	514	1.49	0.23	25.6
	0	308^a	219^a	531^a	1.41^a	0.21^a	26.7^a
WB2	0	329	202	503	1.63	0.25	22.2
	0	320^b	208^b	512^b		0.23^b
ReB2	0	343	268	638	1.28	0.19	36.4
	0	344^c	304^c	642^c	1.14^c	0.21^c
	0	348^d	295^d	691^d	1.18^d	0.17^d	35.9^d

---

From Table S1,† all the studied compounds are mechanically stable because the entire set of elastic constants C_ij satisfies the Born–Huang criterion.⁴⁵ Hence, the predicted Immm-MnB₂ could be mechanically stable at 0 and 50 GPa. By comparing the elastic constants of Immm-MnB₂, we can learn that the C₁₁ (653 GPa) and C₃₃ (643 GPa) are much larger than the C₂₂ (442 GPa), implying that Immm-MnB₂ is relatively strong against compression along the a- and c-axis due to the hexagonal graphene-like boron networks. The computational results for TaB₂, WB₂ and ReB₂ are in good agreement with those of previous studies,^16,42–44 which proves the reliability of our calculations. As it is known, C₄₄ is an important parameter that indirectly controls the hardness of materials. The Immm-MnB₂ phase has a C₄₄ value of 273 GPa, which is comparable with that of ReB₂, indicating a relatively strong shear strength.⁴⁶ The calculated bulk modulus of Immm-MnB₂ is comparable to those of TaB₂,⁴² WB₂ (ref. 43) and ReB₂,⁴⁴ suggesting that Immm-MnB₂ has a strong ability to prevent volume decrease (see Table 1). Moreover, Immm-MnB₂ has a shear modulus of 195 GPa, and hence it is reasonable to think that it could be a hard material, considering that its shear modulus is similar to that of conventional hard materials, such as TaB₂ and WB₂. In addition, the Poisson's ratio ν is indicative of the degree of directionality of the covalent bonding and greatly determines the hardness of materials. The Poisson's ratio of Immm-MnB₂ is 0.24, which is similar to that of TaB₂ and WB₂. This value lies between the covalently-bound materials' value of 0.1 and the value of 0.33 for materials with typically delocalized metal–metal bonds,⁴⁷ indicating a high degree of covalent and metallic bonding in the Immm-MnB₂ structure. The B/G ratio of a material represents its ductility or brittleness, with 1.75 being the critical value.⁴⁷ For Immm-MnB₂, the calculated B/G ratio is less than 1.75, implying that its brittle nature.

We calculated the hardness of Immm-MnB₂ using Chen's model: H_v = 2(k²G)^0.585 − 3.³⁴ The estimated hardness H_v of Immm-MnB₂ is 22.5 GPa at ambient pressure and 27.0 GPa at P = 50 GPa. Indeed, high pressure can enhance the mechanical properties of materials by increasing the elastic constants and elastic moduli. Compared to Immm-Mn₃B₄, with a hardness of 8.5 GPa,²⁵ our predicted structure is a relatively good hard material among common layered transition-metal diborides.

3.3 Electronic structure and magnetic properties

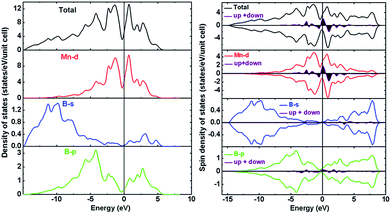
In order to explore the cause of the stability, hardness and magnetic properties of Immm-MnB₂, both the non-polarized and the spin-polarized electronic density of states (DOS) of Immm-MnB₂ at ambient pressure were calculated, and results are depicted in Fig. 5. As seen in Fig. 5, the calculated total density of states (TDOS) is dominated by Mn-d electrons due to their metallic character. This is the most evident feature of TM–B compounds at the Fermi level, and hence Immm-MnB₂ may be a good conductor. The energy range from −15 eV to −7.5 eV is primarily composed of B-s and B-p states, which indicates a strong interaction between B atoms. The overlapping at about −4.3 eV indicates covalency between the Mn-d and B-p states. The Immm-MnB₂ has a sharp peak at the Fermi level in non-polarized-DOS, which is a sign of magnetic instability (i.e., the compounds will be more stable in a magnetic state).⁴⁸ According to the Stoner model, spontaneous magnetization occurs when the condition N_TM(E_F) × I_TM > 1 is satisfied, where N_TM(E_F) is the non-polarized partial density of states of transition metal atoms at the Fermi level and I_TM is the exchange-correlation integral. The value of I_TM for Mn is 0.41 eV,⁴⁹ and hence the obtained result is 13.1 and larger than 1, indicating stable ferromagnetism. We also calculated the total energy versus volume for Immm-MnB_2, with and without spin-polarization, and we present the results in Fig. S1 (ESI†). The magnetic stability is confirmed once again by comparing the non-magnetic and magnetic total energy values calculated at the theoretical equilibrium volume.

Fig. 5 Calculated total and partial DOS for Immm-MnB₂: (left panel) without spin-polarization, and (right panel) with spin-polarization. The vertical line at zero is the Fermi energy level. The area under the curves is the sum of spin-up and spin-down density of states.

The calculated spin-polarized total DOS of Immm-MnB₂ and partial DOS of Mn-d, B-s and B-p states are shown on the right panel in Fig. 5. According to our calculations, the results of the sum of the total spin-up and spin-down density of states (DOS) to the Fermi level reveal that Immm-MnB₂ is a magnetic material in which the local spin moment of Mn is 0.185 μ_B per atom, which is the same as the early experimental result on AlB₂–MnB₂ obtained by Andersson et al. (0.19 μ_B per atom).⁵⁰ The main ferromagnetic moment comes from the spin-polarized Mn-3d electrons. The magnetic moment in Immm-MnB₂ linearly decreases with increasing pressure, as shown in Fig. S2 (ESI†), indicating that the magnetic moment is affected by pressure modulation. In summary, the observation of strong B–B interactions in the hexagonal graphene-like boron network and the relatively strong Mn–B interactions are the main cause for the stability and hardness of Immm-MnB₂. Moreover, the presence of electrical conductivity and magnetic properties makes this multi-layered Immm-MnB₂ structure a potential multifunctional material.

3.4 Chemical bonding

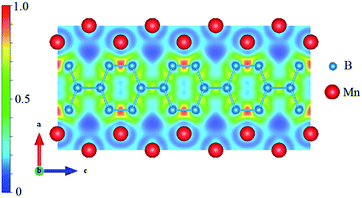
In most studies on transition-metal borides, the strong covalent B–B bonds and the TM–B bonds are always the key factor for structural stability and hardness. Therefore, we calculated the electron localization function (ELF) and Bader charge to understand the nature of the B–B and Mn–B bonding. The spin-polarized ELF for Immm-MnB₂ at zero pressure is shown in Fig. 6. ELF = 1 corresponds to perfect electron-localization of covalent bonds, ELF = 0.5 corresponds to electron-gas-like pair probability, and ELF = 0 corresponds to perfect delocalization. As seen in Fig. 6, based on the ELF value, we can confirm the existence of strong covalent B–B bonding, particularly for the shortest B–B bond in the hexagonal graphene-like boron network, with a bond length of 1.773 Å, because of the high ELF value between this two boron atoms. C atoms have an electron configuration of 2s²2p². Due to short bond lengths, the 2p orbitals can form π bonds, leading to the formation of graphene-like sheets.⁵¹ Through Bader charge analysis (ESI†), it was found that there is much charge transfer from Mn to B. This promotes B⁻ ions to be isoelectronic to C, thus leading to the existence of hexagonal graphene-like boron networks. Meanwhile, the valence electrons of Mn are mostly transferred to B, which helps the 2p orbitals of B atoms to form π bonds. For Immm-MnB₂, the ELF is negligible at the Mn sites and attains maximum values between Mn and B atoms, very close to the B atoms, indicating partially covalent and metallic bonding features of the Mn–B bonds, i.e., weak interactions between the Mn and B atoms. The B–B interactions are much stronger than the Mn–B interactions. From this, combined with the abovementioned analysis of density of states, we can conclude that strong B–B bonds and relatively strong Mn–B bonds are the main cause of the hardness and stability of Immm-MnB₂.

Fig. 6 Electron density map for Immm-MnB₂ in the (0 1 0) plane at 0 GPa.

4 Conclusion

In summary, we found a new multi-layered phase Immm-MnB₂, with a theoretical hardness of 22.5 GPa, by structure search based on the first-principles calculations. This phase is mechanically and dynamically stable at ambient pressure. By analyzing the elastic characteristics and electronic structure, we discovered that Immm-MnB₂ is a metal with magnetic properties, and has a magnetic moment of 0.185 μ_B/Mn, which makes it a promising hard multifunctional material.

The chemical bonding analysis of Immm-MnB₂ showed that the strong covalent B–B bonds in the hexagonal graphene-like boron network and the weak Mn–B interactions contribute to its hardness and stability. These results are important for understanding the structure and properties of magnetic transition-metal borides under high pressures and offer promise for the synthesis of magnetic transition-metal borides in the future.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (No. 51632002, 51572108, 11634004, 11104103), the Program for Changjiang Scholars and the Innovative Research Team in University (No. IRT_15R23), the National Fund for Fostering Talents of Basic Science (No. J1103202),Some of the calculations were performed in the High Performance Computing Center (HPCC) of the Jilin University.

References

1. Q. Li, D. Zhou, W. T. Zheng, Y. M. Ma and C. F. Chen, Phys. Rev. Lett., 2015, 115, 185502.
2. J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63–64.
3. M. C. Cadeville, J. Phys. Chem. Solids, 1966, 27, 667–670.
4. P. Rogl, J. Less-Common Met., 1985, 110, 283–294.
5. J. J. Gilman, R. W. Cumberland and R. B. Kaner, Int. J. Refract. Hard Met., 2006, 24, 1–5.
6. R. B. Kaner, J. J. Gilman and S. H. Tolbert, Science, 2005, 308, 1268–1269.
7. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
8. T. P. Fehlner, J. Solid State Chem., 2000, 154, 110–113.
9. H. Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436–439.
10. R. W. Cumberland, M. B. Weinberger, J. J. Gilman, S. M. Clark, S. H. Tolbert and R. B. Kaner, J. Am. Chem. Soc., 2005, 127, 7264–7265.
11. X. H. Zang, G. E. Hilmas and W. G. Fahrenholtz, Mater. Lett., 2008, 62, 4251–4253.
12. H. Y. Gou, A. A. Tsirlin, E. Bykova, A. M. Abakumov, G. V. Tendeloo, A. Richter, S. V. Ovsyannikov, A. V. Kurnosov, D. M. Trots, Z. Konôpková, H.-P. Liermann, L. Dubrovinsky and N. Dubrovinskaia, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064108.
13. Y. C. Liang, X. Yuan, Y. F. Gao, W. Q. Zhang and P. H. Zhang, Phys. Rev. Lett., 2014, 113, 176401.
14. R. O. Zaitsev and N. V. Terekhina, J. Exp. Theor. Phys., 2002, 94, 367–376.
15. J. Fan, K. Bao, X. L. Jin, X. X. Meng, D. F. Duan, B. B. Liu and T. Cui, J. Mater. Chem., 2012, 22, 17630–17635.
16. S. Aydin and M. Simsek, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134107.
17. S. Khmelevskyi and P. Mohn, Solid State Commun., 2000, 113, 509–512.
18. H. Okamoto, J. Phase Equilib., 1993, 14, 121–122.
19. I. Binder and B. Post, Acta Crystallogr., 1960, 13, 356.
20. X. X. Meng, K. Bao, P. W. Zhu, Z. He, Q. Tao, J. J. Li, Z. P. Mao and T. Cui, J. Appl. Phys., 2012, 111, 112616.
21. G. Y. Gou, G. S. Neumann, E. Bykova, Y. Nakajima, N. Miyajima, Y. Li, S. V. Ovsyannikov, L. S. Dubrovinsky and N. Dubrovinskaia, Appl. Phys. Lett., 2013, 102, 061906.
22. R. Kiessling, Acta Chem. Scand., 1950, 41, 46–159.
23. P. Vajeeston, P. Ravindran, C. Ravi and R. Asokamani, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 045115.
24. B. Wang, X. Li, Y. X. Wang and Y. F. Tu, J. Phys. Chem. C, 2011, 115, 21429–21435.
25. H. Y. Niu, X. Q. Chen, W. J. Ren, Q. Zhu, A. R. Oganov, D. Z. Li and Y. Y. Li, Phys. Chem. Chem. Phys., 2014, 16, 15866–15873.
26. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182.
27. A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237.
28. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
32. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354.
33. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
34. X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275–1281.
35. A. C. Lawson, A. C. Larson, M. C. Aronson, S. Johnson, Z. Fisk, P. C. Canfield, J. D. Thompson and R. B. Von Dreele, J. Appl. Phys., 1994, 76, 7049–7051.
36. A. R. Oganov, J. H. Chen, C. Gatti, Y. Z. Ma, Y. M. Ma, C. W. Glass, Z. X. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867.
37. G. Ghosh, A. van de Walle and M. Asta, Acta Mater., 2008, 56, 3202–3221.
38. X. W. Zhang, G. Trimarchi and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 092102.
39. S. Okada, T. Atoda, I. Higashi and Y. Takahashi, J. Mater. Sci., 1987, 22, 2993–2999.
40. B. Aronsson, E. Stenberg and J. Åselius, Nature, 1962, 195, 377–378.
41. B. H. Chu, D. Li, F. B. Tian, D. F. Duan, X. J. Sha, Y. Z. Lv, H. D. Zhang, B. B. Liu and T. Cui, Sci. Rep., 2015, 5, 10500.
42. W. J. Zhao and Y. X. Wang, J. Solid State Chem., 2009, 182, 2880–2886.
43. X. F. Hao, Y. H. Xu, Z. J. Wu, D. F. Zhou, X. J. Liu, X. Q. Cao and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224112.
44. Y. X. Wang, Appl. Phys. Lett., 2007, 91, 101904.
45. Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
46. M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao, L. P. Ding and X. F. Huang, J. Phys. Chem. C, 2013, 117, 10643–10652.
47. S. F. Pugh, Philos. Mag., 1954, 45, 823–843.
48. S. Kervan, J. Supercond. Novel Magn., 2011, 24, 815–818.
49. J. F. Janak, Phys. Rev. B: Solid State, 1977, 16, 255.
50. L. Andersson, B. Dellby and H. P. Myers, Solid State Commun., 1966, 4, 77–78.
51. M. J. Rice, A. R. Bishop and D. K. Campbell, Phys. Rev. Lett., 1983, 51, 2136.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27148k

---