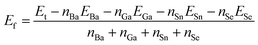Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Centrosymmetric to noncentrosymmetric structural transformation of new quaternary selenides induced by isolated dimeric [Sn2Se4] units: from Ba8Ga2Sn7Se18 to Ba10Ga2Sn9Se22†
Yan-Yan Lia,
Jin-Qiu Wangac,
Peng-Fei Liu ac,
Hua Lina,
Ling Chen
ac,
Hua Lina,
Ling Chen ab and
Li-Ming Wu
ab and
Li-Ming Wu *ab
*ab
aKey Laboratory of Optoelectronic Materials Chemistry and Physics, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, People's Republic of China. E-mail: liming_wu@fjirsm.ac.cn; Fax: +86 10 6220 9119; Tel: +86 10 6220 9980
bKey Laboratory of Theoretical and Computational Photochemistry of Ministry of Education, Department of Chemistry, Beijing Normal University, Xin-wai-da-jie No.19, Beijing, 100875, People's Republic of China
cUniversity of Chinese Academy of Sciences, Beijing 100039, People's Republic of China
First published on 23rd January 2017
Abstract
A noncentrosymmetric structure is a prerequisite of many important properties, such as ferroelectric, piezoelectric and nonlinear optical properties. The design synthesis of a noncentrosymmetric compound is highly desired but it is a great challenge. Herein, two new quaternary selenides, Ba8Ga2Sn7Se18, 1 and Ba10Ga2Sn9Se22, 2, have been discovered by solid-state reactions. Compound 1 crystallizes in the centrosymmetric space group Pnma (no. 62) with a = 12.466 (9) Å, b = 9.358 (6) Å, c = 18.14 (2) Å, V = 2116 (3) Å3, Z = 2; and 2 crystallizes in the noncentrosymmetric space group Cmc21 (no. 36) with a = 9.384 (2) Å, b = 44.834 (6) Å, c = 12.416 (2) Å, V = 5224 (2) Å3, Z = 4. The major motif of both 1 and 2 is the [Ga2Sn7Se18]∞16− ladder chain built by alternately jointed GaSe4 tetrahedra and SnSe4 tetragonal pyramids, and to each of these polyhedra, an accessory (SnSe3 pyramid or Sn2Se4 dimer) is attached. Interestingly, the noncentrosymmetric structure of 2 is the combination of centrosymmetric 1 and the imbedded isolated dimeric [Sn2Se4] with a C2v polar symmetry that separates every two such ladder chains. 1 and 2 directly illustrate that a simple combination reaction can drive the centrosymmetric to noncentrosymmetric structural transformation.
Introduction
Chalcogenides play important roles in many fields owing to their fascinating structural complexity and remarkable properties, such as infrared nonlinear optical (NLO), thermoelectric, and magnetic properties.1–7 Among them, noncentrosymmetric chalcogenides are of special interest, because the noncentrosymmetric structure is a prerequisite for ferroelectric, piezoelectric and NLO properties.8–17 We realize that a slight component variation of a centrosymmetric chalcogenide, via element substitution or stoichiometry tuning, may lead to a structural transformation into a noncentrosymmetric one, as observed in particular in some low-dimensional chalcogenides. For example, adding a secondary building unit SbS3 pyramid (SbS3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GaS4 = 1
GaS4 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) into the centrosymmetric Ba5Ga2S8, which helped to disconnect the isolated GaS4 tetrahedron array in breaking the symmetry of the inversion center, led to an 0D noncentrosymmetric compound Ba23Ga8Sb2S38. And this compound exhibited very large second harmonic generation of 22 × AgGaS2 at 2.05 μm.15 The 0D compounds Ba3(BS3)1.5(SbS3)0.5 and Ba3(BS3)(SbS3) merely differing in the ratio of BS3/SbS3 show an interesting centrosymmetric-to-noncentrosymmetric structural relationship.16 Geng et al. utilized gallium or indium and obtained a centrosymmetric Ba2BiGaS5, and a noncentrosymmetric Ba2BiInS5 (ref. 17) with different alignment of BiS5 tetragonal pyramids and neighboring MS4 (M = Ga, In) tetrahedra. Besides, different Ln cations lead to different crystal symmetries, like: controsymmetric Ba2LnGaTe5 (Ln = Sm or Gd) and noncentrosymmetric Ba2LnGaTe5 (Ln = Dy, Er, Y).18
4) into the centrosymmetric Ba5Ga2S8, which helped to disconnect the isolated GaS4 tetrahedron array in breaking the symmetry of the inversion center, led to an 0D noncentrosymmetric compound Ba23Ga8Sb2S38. And this compound exhibited very large second harmonic generation of 22 × AgGaS2 at 2.05 μm.15 The 0D compounds Ba3(BS3)1.5(SbS3)0.5 and Ba3(BS3)(SbS3) merely differing in the ratio of BS3/SbS3 show an interesting centrosymmetric-to-noncentrosymmetric structural relationship.16 Geng et al. utilized gallium or indium and obtained a centrosymmetric Ba2BiGaS5, and a noncentrosymmetric Ba2BiInS5 (ref. 17) with different alignment of BiS5 tetragonal pyramids and neighboring MS4 (M = Ga, In) tetrahedra. Besides, different Ln cations lead to different crystal symmetries, like: controsymmetric Ba2LnGaTe5 (Ln = Sm or Gd) and noncentrosymmetric Ba2LnGaTe5 (Ln = Dy, Er, Y).18
The family A/Ga/Sn/Q (A = alkaline-earth metal; Q = S, Se, Te) attracts our attention. One reason is that the asymmetric GaQn units are able to build many noncentrosymmetric compounds, such as BaGa4Q7 (Q = S, Se),19 BaGa2GeQ6 (Q = S, Se),20 Ba23Ga8Sb2S38,15 Li2Ga2GeS6,21 ACd4Ga5S12 (A = K, Rb, Cs),22 Ba2Ga8MS16 (M = Si, Ge),23 and Ln4GaSbS9 (Ln = Pr, Nd, Sm, Gd–Ho).24 Another reason is that Sn2+ possessing active lone pair electrons tends to adopt polar local coordinations, e.g., Sn2+Q4 tetragonal pyramid in SnGa4Q7 (Q = S, Se),25 Sn2+S3 pyramid in Ba8Sn4S15,26 and (Sn2+)2S3 trigonal bipyramid in Ba7Sn5S15.27 In these compounds, Sn2+ plays the leading role in the SHG. However, up to now, only three compounds containing Sn4+ in the A/Ga/Sn/Q family are known: noncentrosymmetric Ba4Ga4SnSe12 and BaGa2SnSe6, and centrosymmetric Ba6Ga2SnSe11.28,29 Members containing low oxidation state Sn2+ or mixed oxidation states (Sn2+ and Sn4+) are still rare.
Herein, two new selenides, centrosymmetric Ba8Ga2Sn7Se18, 1 and noncentrosymmetric Ba10Ga2Sn9Se22, 2, are discovered. For the first time, 1 and 2 illustrate an interesting and direct structure transformation from centrosymmetric to noncentrosymmetric. The structure of 2 can be regarded as a composition of structure of 1 with an asymmetric matrix of the isolated dimeric [Sn2Se4]. Syntheses, crystal structures, electronic structures and DFT studies are also reported.
Experimental section
Synthesis
The reagents were used as obtained: Ba rod (Alfa Aesar China (Tianjin) Co., Ltd., 99.9%), Ga shot, Sn grain, and Se powder (Sinopharm Chemical Reagent Co., Ltd., 99.999%). And one single piece of the barium rod was used as the starting reactant. The binary compounds BaSe and SnSe were synthesized at 850 °C by elemental mixture in sealed silica tubes under vacuum of 10−2 Pa. And the binary Ga2Se3 was synthesized at 680 °C by a boron-chalcogen method.30–34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 molar ratio with a total weight of 400 mg. The reactants were loaded into a graphite crucible, and sealed in an evacuated silica tube under 10−2 Pa atmosphere, and then heated to 980 °C within 50 h and kept there for 48 h, then cooled to 400 °C at a rate of 5 °C h−1.
14 molar ratio with a total weight of 400 mg. The reactants were loaded into a graphite crucible, and sealed in an evacuated silica tube under 10−2 Pa atmosphere, and then heated to 980 °C within 50 h and kept there for 48 h, then cooled to 400 °C at a rate of 5 °C h−1.Many efforts revealed that such stoichiometric reactions could not produce pure phase. Instead, black crystals of 1, and Ba6Sn6Se13 (ref. 35) as a secondary phase together with few red crystals of Ba5Ga2Se8 (ref. 36) were produced. We considered the reason might be the insufficient contact/mixing between Ga and the other reactants. Therefore, binary BaSe, Ga2Se3 and SnSe were used instead. The mixture of BaSe, Ga2Se3 and SnSe in a molar ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 with a total weight of about 500 mg was ground carefully and pressed into a pellet. Then the pellet was put into a graphite crucible in an evacuated silica jacket, and subsequently heated to 750 °C in 34 h, kept for 80 h, and then cooled to 300 °C within 100 h before the furnace was turned off. The homogenous 1 was produced according to the XRD pattern as shown in ESI Fig. S1a.†
7 with a total weight of about 500 mg was ground carefully and pressed into a pellet. Then the pellet was put into a graphite crucible in an evacuated silica jacket, and subsequently heated to 750 °C in 34 h, kept for 80 h, and then cooled to 300 °C within 100 h before the furnace was turned off. The homogenous 1 was produced according to the XRD pattern as shown in ESI Fig. S1a.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 ratio with a total weight of 300 mg. And pure phase 2 was obtained by the reaction of cold-pressed pellet of the well ground mixture of binary BaSe, Ga2Se3 and SnSe in a 10
26 ratio with a total weight of 300 mg. And pure phase 2 was obtained by the reaction of cold-pressed pellet of the well ground mixture of binary BaSe, Ga2Se3 and SnSe in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio with a total weight of about 500 mg. The heating profile was heating to 750 °C in 50 h, dwelling for 80 h, then cooling to 300 °C at a rate of 4 °C h−1. The XRD pattern showed the homogeneity of the product (ESI Fig. S1b†). The crystals of 2 were relatively moisture sensitive.
9 ratio with a total weight of about 500 mg. The heating profile was heating to 750 °C in 50 h, dwelling for 80 h, then cooling to 300 °C at a rate of 4 °C h−1. The XRD pattern showed the homogeneity of the product (ESI Fig. S1b†). The crystals of 2 were relatively moisture sensitive.Single-crystal X-ray crystallography
The single crystal diffraction data were collected on a Mercury CCD equipped with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) at 293 K. The data were corrected for Lorentz and polarization factors. And the structures were solved by the direct methods and refined by the full-matrix least-squares fitting on F2 using the SHELX-97.37The single-crystal X-ray diffraction data revealed two sets of new unit cell parameters of a = 12.5 Å, b = 9.4 Å, c = 18.1 Å, α = β = γ = 90° for 1; and a = 9.4 Å, b = 44.8 Å, c = 12.4 Å, α = β = γ = 90° for 2 indicating the orthorhombic crystal system. Subsequently, the structure of 1 was solved in the suggested space group of Pnma (62) and refined with R1 = 9.49% and wR2 = 31.10%. However, an abnormal large atom displacement parameter of Sn(1) (Ueq. = 0.093) was seen, such a value was about 3–4 times as those of other Sn sites (Sn(2): 0.031, Sn(3): 0.021, Sn(4): 0.027). Therefore, the occupancy of Sn(1) was allowed to refine freely. The refinement resulted in a reasonable temperature factor of 0.024 and an occupancy of 45.297% for Sn(1), and better R values (R1 = 0.0408 and wR2 = 0.0928). The PLATON38 checking found no missing or higher symmetry elements exiting in 1. The partial occupancies of Sn were also found in compound BaAu2SnS4.39 To keep the charge balance, the occupancy of Sn(1) was fixed to 0.5. Consequently, the final R values were converged to R1 = 0.0415 and wR2 = 0.920 (Table 1, ESI Table S1a†). The final charge-balanced formula was established as (Ba2+)8(Ga3+)2(Sn2+)7(Se2−)18. Meanwhile, all the subgroups of Pnma were checking. For instance, similar refinement of 1 in Pna21 generated higher R values of R1 = 0.0429 and wR2 = 0.1275. And the subsequent checking with PLATON suggested the space group Pnma. Other subgroups of Pnma, such as Pmn21, Pmc21, and P212121, gave similar results, and none of them generated reasonable bond lengths and atomic displacement parameters. Therefore, the structure solved in Pnma (62) space group was sound.
| a R1 = ∑||Fo| − |Fc||/∑|Fo| for Fo2 > 2σ(Fo2); wR2 = ∑[w(Fo2 − Fc2)]/∑[w(Fo2)2]1/2. | ||
|---|---|---|
| Formula | Ba8Ga2Sn7Se18 | Ba10Ga2Sn9Se22 |
| fw | 3490.27 | 4318.17 |
| Crystal system | Orthorhombic | Orthorhombic |
| Crystal colour | Black | Black |
| Space group | Pnma | Cmc21 |
| a (Å) | 12.466 (9) | 9.384 (2) |
| b (Å) | 9.358 (6) | 44.834 (6) |
| c (Å) | 18.14 (2) | 12.416 (2) |
| V (Å3) | 2116 (3) | 5224 (2) |
| Z | 2 | 4 |
| Dc (g cm−3) | 5.5 | 5.1 |
| μ (mm−1) | 28.1 | 24.1 |
| GOOF on F2 | 1.137 | 0.981 |
| R1, wR2 (I > 2σ(I))a | 0.0415, 0.0920 | 0.0418, 0.0873 |
| R1, wR2 (all data) | 0.0490, 0.0959 | 0.0480, 0.0897 |
| Flack parameter | N/A | 0.00 (3) |
| Largest diff. peak and hole (e Å−3) | 2.19/−1.77 | 1.99/−2.13 |
In case of 2, the space group of Cmc21 was first adopted to solve the structure, which generated good R values (R1 = 0.0663 and wR2 = 0.1791) but relatively large isotropic temperature factors for Sn(1) and Sn(5) (Ueq. = 0.090 and 0.1). Thus, the occupancies of Sn(1) and Sn(5) were allowed to refine freely, which generated comparative temperature factors (0.019 and 0.019), better R values (R1 = 0.0417 and wR2 = 0.0888) and occupancies of 48.64% Sn(1) and 48.64% Sn(5), respectively. Then the occupancies of Sn(1) and Sn(5) were fixed to 0.5, and the final refinement converged to R values of R1 = 0.0418 and wR2 = 0.0873 and a charge-balanced formula of (Ba2+)10(Ga3+)2(Sn2+)9(Se2−)22 (Table 1, ESI Table S1b†). The PLATON checking found no missing or higher symmetry elements exiting in 2. Selected bond distances and angles are listed in ESI Tables S2 and S3.†
Elemental analyses
The semiquantitative energy dispersive X-ray spectra (EDX, Oxford INCA) were measured on a field emission scanning electron microscope (FESEM, JSM6700F). The quantitative inductively coupled plasma (ICP) emission spectra were recorded with the aid of an Ultima-2 inductively coupled plasma emission spectrometer (ICP-OES). The EDX results confirmed the presence of Ba, Ga, Sn, and Se. And the results of EDX and ICP indicated the ratios of Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga
Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn
Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Se in the approximate molar ratio of 8
Se in the approximate molar ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 for 1 and 10
18 for 1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 for 2 (ESI Fig. S2, Tables S4, and S5†), which were in accordance with the single crystal diffraction refinements.
22 for 2 (ESI Fig. S2, Tables S4, and S5†), which were in accordance with the single crystal diffraction refinements.
Powder X-ray diffraction
The XRD patterns were collected on a Rigaku MiniFlex II diffractometer by using Cu Kα radiation. The scanning range was 10–70° in 2θ with a step size of 0.02°. As shown in ESI Fig. S1,† the experimental XRD patterns of 1 and 2 were in good agreement with the simulated ones based on the single crystal data.Thermal analyses
Thermogravimetric (TG) analyses of compound 1 and 2 were measured on a NETZSCH STA 449F3 simultaneous analyzer under a constant flow of N2. The samples were enclosed in an Al2O3 crucible, heated from room temperature to 1200 °C at a rate of 20 °C min−1.Infrared and UV-Vis-near-IR diffuse reflectance spectra
The UV-Vis-near-IR diffuse reflectance spectra were measured at room temperature using a Perkin-Elmer Lambda 950 UV-Vis spectrophotometer equipped with an integrating sphere attachment and BaSO4 as a reference. The absorption spectra were calculated from the reflection spectra according to the Kubelka–Munk function: α/S = (1 − R)2/2R, where α was the absorption coefficient, S was the scattering coefficient, and R was the reflectance.40 The IR data were measured by a Nicolet Magana 750 FT-IR spectrophotometer in the range of 2.5–25 μm for 2. Powder sample of 2 was ground with KBr and pressed into a transparent pellet for the measurement.Powder second harmonic generation (SHG) measurements
The SHG response of compound 2 was performed on a modified Kurtz-NLO system using 1064 nm and 2050 nm laser radiation.41 The particle size of the sieved sample was 30–46 μm. Single crystal of AgGaS2 (2 cm × 2 cm × 2 cm single crystals from Anhui Institute of Optics and Fine Mechanics Chinese Academy of Sciences) was crushed and then sieved into similar particle size, and this was used as a reference.Computational section
Utilizing density functional theory (DFT) implemented in the Vienna ab initio simulation package code,42 the electronic structures were investigated. Projector augmented wave (PAW) method43 were used for the ionic cores and the generalized gradient approximation (GGA) were used for the exchange–correlation potential, in which the Perdew–Burke–Ernzerhof (PBE) type44 exchange–correlation was adopted. Ba 5s25p66s2, Ga 4s24p1, Sn 5s25p2, and Se 4s24p4 were treated as valence electrons. The reciprocal space was sampled with 0.05 Å−1 spacing in the Monkhorst–Pack scheme for the structure optimization, and denser k-point grids less than 0.02 Å−1 spacing were adopted for the property calculation. A mesh cutoff energy of 500 eV was used to determine the self-consistent charge density. All geometries were relaxed until the Hellmann–Feynman force on atoms was less than 0.01 eV Å−1 and the total energy change was less than 1.0 × 10−5 eV. The calculation models of 1 and 2 were shown in ESI Fig. S3 and S4.† The structure of the isostructural BaSnS2 (ref. 45) was adopted to simulate the BaSnSe2 structure in the energy calculation of the combination reaction (Ba8Ga2Sn7Se18 (1) + 2BaSnSe2 = Ba10Ga2Sn9Se22 (2)).Results and discussion
Crystal structure
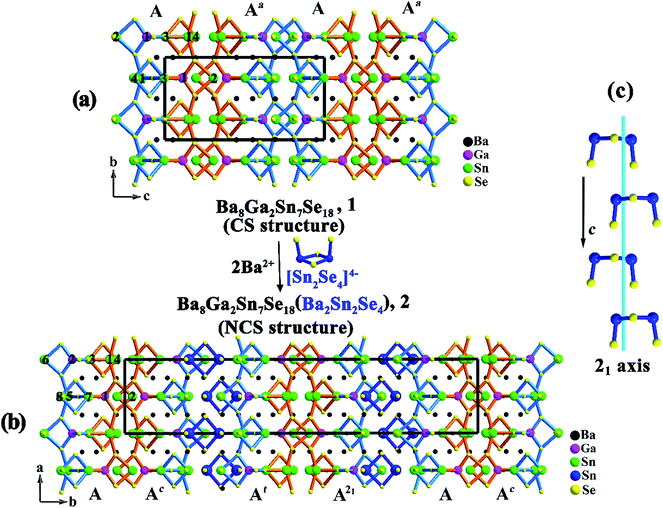
As illustrated in Fig. 1a and 2a, the major structure motif of 1 is the infinite 1D [Ga2Sn7Se18]∞16− ladder chain that is built by alternatively jointed GaSe4 tetrahedron and SnSe4 tetragonal pyramid. To each of such polyhedra, an accessorial SnSe3 (Sn = Sn(2)) pyramid or Sn2Se4 (Sn = Sn(3), Sn(4)) dimer is attached via a common edge or an apex, respectively. Also such a ladder chain can be viewed as the combination of two single chains jointed by common Se atoms, denoted as Chain 1 and Chain 2 (Fig. 2a). As shown, Chain 1 is operated into Chain 2 through the center of symmetry. The ladder chain is packed by a sequence of …AAa… along the c direction (Fig. 1a). Note that the a-glide plane at (x, y, 1/4) operates A into Aa.
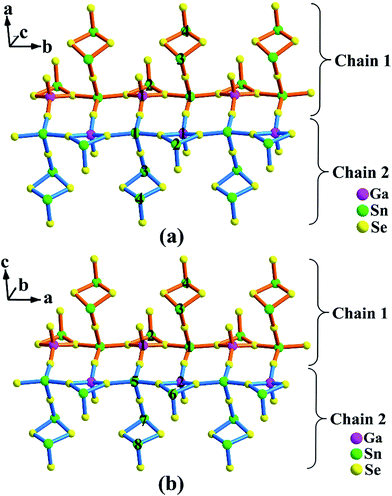 | ||
| Fig. 2 A single ladder chain in Ba8Ga2Sn7Se18, 1 (a); and Ba10Ga2Sn9Se22, 2 (b). The Ga, Sn atoms are marked with atom numbers. | ||
Selected bond distances are listed in ESI Table S2a.† The Ba atom is 7-fold coordinated in a monocapped trigonal prism with Ba–Se bond lengths ranging from 3.282 (2) to 3.576 (2) Å (ESI Fig. S5†). These lengths are comparable to 3.218 (1)–3.859 (2) Å in Ba2MLnSe5 (M = Ga, In; Ln = Y, Nd, Sm, Gd, Dy, Er).46 The Ga–Se distances range from 2.384 (2) to 2.421 (2) Å, which are comparable to those of 2.364–2.499 Å in Ba5Ga2Se8.36 The 3-fold coordinated Sn atoms (Sn(2), Sn(3), Sn(4)) have Sn–Se bond lengths falling in the normal range of 2.584 (2) to 2.891 (2) Å. The calculated bond valence sums (BVS)47 for these Sn–Se bonds are 1.903, 1.771, and 2.374, respectively. The BVS values are close to the reported values of Sn2+ with 3-fold coordination, e.g., from 2.208 to 2.147 in Ba6Sn6Se13.35 Differently, the 4-fold coordinated Sn(1) atom has a site occupancy of 50%, and shows 3 short Sn(1)–Se bonds (2.766 (3), 2.831 (2), and 2.831 (2) Å) and 1 long bond (2.966 (3) Å) (ESI Fig. S6†). The calculated BVS of Sn(1) is 2.025. Hence, the valence state of Sn(1) should be 2+. Similar situations are found in K2Sn4Se8,48 SrSn2Se4,49 and SnGa4Se7,25 in which the Sn–Se bond lengths are ranging from 2.578 to 3.132 Å. Consequently, in Ba8Ga2Sn7Se18, 1, the oxidation states of Ba, Ga, Sn and Se atoms are assigned to be 2+, 3+, 2+ and 2−.
Compound 2 is also a ladder chain structure, surprisingly, the ladder chains in 2 are nearly identical to those in 1. For example, the M–Se bond length and the Se–M–Se bond angle (M = Ga(1), Ga(2); Sn(2)–(4), Sn(6)–(8)) deviate less than 0.4 and 3%, with respect to those in 1 (ESI Tables S2 and S3†). The two short unit cell axes of 1 and 2 are nearly the same, only the long axis is expanded owing to the embedding of [Sn2Se4] dimers (Sn = Sn(9), Sn(10)). As shown in Fig. 1b, every two ladder chains are separated at the light blue moiety by the isolated [Sn2Se4] dimers. The ladder chain in 2 is also built by alternatively jointed GaSe4 tetrahedra (Ga = Ga(1) and Ga(2)) and SnSe4 tetragonal pyramids (Sn = Sn(1) and Sn(5)). To each of such polyhedra, an accessorial SnSe3 (Sn = Sn(2) or Sn(6)) pyramid or Sn2Se4 (Sn = Sn(3), Sn(4) or Sn(7), Sn(8)) dimer is attached (Fig. 2b). Through the operations of the c-glide plane at (x, 0, z), t at (1/2, 1/2, 0), and 2-fold screw axis at (1/4, 1/4, z) (Fig. 1c), such a ladder chain is thus packed in a sequence of …AAcAtA21… along the b direction (Fig. 1b). In short, the major structure difference between 1 and 2 lies in that the latter contains a matrix of isolated dimeric [Sn(9)Sn(10)Se4] units (ESI Fig. S7†).
All the Ba atoms are 7-fold coordinated in monocapped trigonal prism geometries with normal Ba–Se bonds ranging from 3.257 (2) to 3.677 (2) Å (ESI Fig. S8†). The Ga–Se distances are normal, varying from 2.382 (3) to 2.424 (2) Å. The 3-fold coordinated Sn atoms (Sn = Sn(2)–(4), (6)–(10)) have regular Sn–Se bond lengths ranging from 2.581 (3) to 2.920 (2) Å. Similar as in 1, Sn(1) and Sn(5) atoms (with 50% occupancies) are 4-fold coordinated with 3 short Sn–Se bond lengths about 2.83 Å and 1 long bond about 2.95 Å (ESI Fig. S9†). The calculated BVS of Sn(1) and Sn(5) are 1.916 and 1.894, respectively, which demonstrates that the oxidation state of Sn(1) and Sn(5) should be 2+. Selected bond distances are listed in ESI Table S2b.†
Structure relationship
The two short unit cell parameters in Ba8Ga2Sn7Se18, 1 and Ba10Ga2Sn9Se22, 2, are almost the same (a = 12.466 (9) Å, b = 9.358 (6) Å for 1 vs. a = 9.384 (2) Å, c = 12.416 (2) Å for 2) (Table 1), because the motifs of the ladder chains in both 1 and 2 are nearly identical. Only the packing of the ladder chains is different, that is in 2, every two of the ladder chains are separated by the isolated dimeric [Sn2Se4] units, which leads to the expansion of the long axis. This also generates a chemical formula relationship of Ba8Ga2Sn7Se18 (1) + Ba2Sn2Se4 = Ba10Ga2Sn9Se22 (2). The theoretical formation energy calculations below reveal that the energies at the left- and right-hand sides of such an equation are comparable, suggesting a feasible transformation from 1 to 2. The isolated dimeric [Sn2Se4] units in 2 exhibit the point group C2v symmetry. Thus, the involvement of such an asymmetric unit lowers the point group D2h symmetry of 1 via the absence of the symmetry elements of n (1/4, y, z), 21 (1/4, 0, z), 21 (0, y, 0), and center of symmetry. As shown in Fig. 1b, the insertion of isolated [Sn2Se4] units between the light blue Chain 2 leads to the symmetry breaking. As a result, each Chain 2 undergoes a slight distortion. For instance, Se(17)–Sn(8)–Se(4) = 94.8° in 2 vs. Se(1)–Sn(4)–Se(4) = 97.8° in 1, and the average bonds of Sn(3)–Se = 2.79 Å, Sn(4)–Se = 2.68 Å in 1 vary within 0.4% in comparison with the corresponding Sn(7)–Se = 2.78 Å, Sn(8)–Se = 2.72 Å in 2. (ESI Tables S2 and S3†).As detailed above, the packing sequence of 2 (…AAcAtA21…along the b direction) differs from that of 1 (…AAa… along the c direction), giving rise to enlargement about two times of b = 44.834 (6) Å in 2 with respect to c = 18.14 (2) Å in 1, because that the embedding of the [Sn2Se4] dimers separate every two ladder chains. These two structures directly describe that a centrosymmetric structure (1) is transformed to a noncentrosymmetric structure (2) by the introduction of the second building unit. These substantially support the commonly applied strategy of “diversity of the asymmetric unit would enhance the difficulty of spontaneously producing a mirror plane or inversion center during the packing process, an approach involving two or more types of asymmetric building units in a structure would have a high possibility to form a noncentrosymmetric structure”.15 Many other systems are worth exploring to see if the similar phenomenon exists.
Thermal analyses
The thermogravimetric (TG) curves of compounds 1 and 2 are shown in ESI Fig. S10a and b.† The data results indicate that both of the compounds are stable up to 800 °C under a N2 atmosphere. In order to further check the thermal stability of the two compounds, pure 1 and 2 were sealed in silica tubes under vacuum and annealed for 3 h at 850 °C respectively. After such a treatment, the X-ray powder diffraction patterns of two compounds showed obvious impurities, which indicated the decomposition of two occurred at around 800 °C (Fig. S10c and d in the ESI†).UV-Vis-near-IR and IR spectra
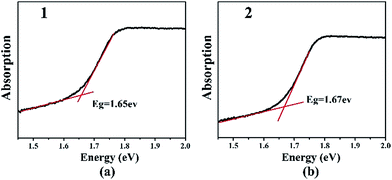
The optical band gaps of 1 and 2 are approximately 1.65 and 1.67 eV, respectively, which are in agreement with their black color (Fig. 3). These values are similar to that of Ba6Sn6Se13 (1.52 eV),35 in which Sn cations have the mixed oxidation states of 2+ and 4+, but smaller than those of Ba4Ga4SnSe12 (2.16 eV),28 Ba6Ga2SnSe11 (1.99 eV),28 and BaGa2SnSe6 (1.95 eV),29 in which the oxidation state of Sn is 4+. Thus, in Ba/Ga/Sn/Se system, compounds containing Sn2+ or mixed valences (Sn2+ and Sn4+) have smaller band gaps than those merely containing Sn4+. The IR spectra and UV-Vis-near-IR spectra of 2 show the transparent range roughly from 0.80 to 25 μm, which is comparable with that of the benchmark AgGaS2 (0.15–23 μm, ESI Fig. S11 and S12†).Second harmonic generation (SHG) property
The SHG of 2 was measured with the 1064 nm and 2050 nm laser radiation as the fundamental wavelength. Unfortunately, no obvious SHG signal was observed. The possible reason might be related to the poor crystallinity of this compound, longer fundamental wavelength should be tried, however, wavelength longer than 2050 nm is not available at present.Electronic structures
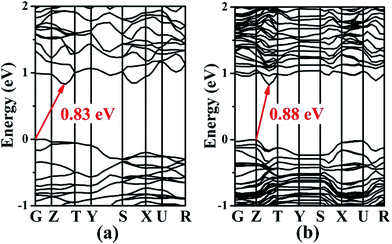
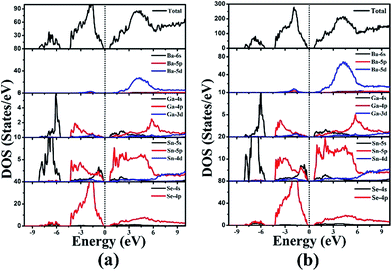
The electronic band structures of 1 and 2 (Fig. 4) reveal the indirect band gaps of 0.83 and 0.88 eV, respectively. Those are smaller than the experimental values (1.65 and 1.67 eV) because of the inaccurate description of the eigenvalues of the electronic states for GGA. The total and partial densities of states (DOS and PDOS) of 1 and 2 are given in Fig. 5. Take 1 as an example, the valence band (VB) between −9 and −5 eV contains Ga-4s and Sn-5s states with minor Se-4p and Se-4s states. The VB from −5 to −2 eV is mainly composed of Ga-4p, Sn-5p, and Se-4p states. The VB top predominantly originates from Se-4p, and minor Ga-4p, Sn-5s, and Sn-5p states. Above the Fermi level, the bottom of the conduction band (CB) is dominated by Sn-5p, and Se-4p states mixed with a small amount of Ga-4s, Ga-4p, and Sn-5s states. The CB ranging from 2 to 5 eV is composed of Ba-5d, Ga-4p, Sn-5p, and Se-4p states. Thus, the band gap absorption is mainly ascribed to the charge transitions from Se-4p to Sn-5p states. By comparing the PDOS of Sn2+ (for 1 and 2) and Sn4+ (for Ba4Ga4SnSe12,28 Ba6Ga2SnSe11,28 and BaGa2SnSe6 (ref. 29)) near the Fermi surface, we find that the Sn-5s state of Sn4+ has no obvious peak at the VB top, while for Sn2+, an obvious contribution of Sn-5s state appears at the VB top, which narrows the band gap. As a result, compounds containing Sn2+ or mixed valences (Sn2+ and Sn4+) have smaller band gaps than those containing Sn4+. This is in good accordance with the experimental results (1.65 and 1.67 eV for 1 and 2; 2.16, 1.99, and 1.95 eV for Ba4Ga4SnSe12,28 Ba6Ga2SnSe11,28 and BaGa2SnSe6,29 respectively).Energies calculation
The formation energies with respect to the isolated atoms of compounds 1, 2 and BaSnSe2 were calculated by the following equation:where Ef is the formation energy and Et is the total energy of a compound.
Compounds 1 and 2 have the following chemical formula relationship:
| Ba8Ga2Sn7Se18 (1) + 2BaSnSe2 = Ba10Ga2Sn9Se22 (2) |
And the energy of the combination reaction can be defined as
| E = Ef(Ba10Ga2Sn9Se22) − Ef(Ba8Ga2Sn7Se18) − Ef(Ba2Sn2Se4) |
The calculated energy of the combination reaction is −1.28 eV indicating that the noncentrosymmetric Ba10Ga2Sn9Se22 is slightly energetically favorable. Hence, the transformation from centrosymmetric 1 to noncentrosymmetric 2 is feasible.
Conclusion
In summary, two new selenides with their own structure types, centrosymmetric Ba8Ga2Sn7Se18, 1 and noncentrosymmetric Ba10Ga2Sn9Se22, 2, have been discovered by solid-state reactions. Both structures feature 1D ladder chain built by alternatively jointed GaSe4 tetrahedron and SnSe4 tetragonal pyramid. To each of these polyhedra, an accessory, SnSe3 pyramid or Sn2Se4 dimer, is attached. Interestingly, the structure of 2 is the combination of that of 1 and the isolated [Sn2Se4] dimer with a C2v symmetry. The embedding of the asymmetric dimeric [Sn2Se4] in 2 vanishes the operations of n, 21, and the center of symmetry that exist in 1. Significantly, 1 and 2 directly describe for the first time that a centrosymmetric-to-noncentrosymmetric structure transformation is caused by a simple combination reaction. This work supports the commonly applied strategy of “involving two or more types of asymmetric building units in a structure would have a high possibility to form a noncentrosymmetric structure”.15 This insight will shed useful light on the future exploration of new NCS materials.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Projects 21233009, 21225104, 91422303, 21301175, 21571020 and 21671023.Notes and references
- (a) X. T. Wu and L. Chen, Structure−Property Relationships in Non-Linear Optical Crystals. I. The UV-Vis Region, Springer, Berlin, 2012, p. 144 Search PubMed; (b) X. T. Wu and L. Chen, Structure−Property Relationships in Non-Linear Optical Crystals. II. The IR Region, Springer, Berlin, 2012, p. 145 Search PubMed.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2014, 26, 849–869 CrossRef CAS.
- (a) H. Lin, L. Chen, L. J. Zhou and L. M. Wu, J. Am. Chem. Soc., 2013, 135, 12914–12921 CrossRef CAS PubMed; (b) Y. Y. Li, P. F. Liu, L. Hu, L. Chen, H. Lin, L. J. Zhou and L. M. Wu, Adv. Opt. Mater., 2015, 3, 957–966 CrossRef CAS; (c) Y. Y. Li, P. F. Liu, H. Lin, M. T. Wang and L. Chen, Inorg. Chem. Front., 2016, 3, 952–958 RSC.
- (a) P. Yu, L. M. Wu and L. Chen, Inorg. Chem., 2013, 52, 724–728 CrossRef CAS PubMed; (b) A. H. Fang, F. Q. Huang, X. M. Xie and M. H. Jiang, J. Am. Chem. Soc., 2010, 132, 3260–3261 CrossRef CAS PubMed.
- P. F. P. Poudeu, N. Takas, C. Anglin, J. Eastwood and A. Rivera, J. Am. Chem. Soc., 2010, 132, 5751–5760 CrossRef CAS PubMed.
- D. Y. Chung, T. Hogan, P. Brazis, M. Rocci-Lane, C. Kannewurf, M. Bastea, C. Uher and M. G. Kanatzidis, Science, 2000, 287, 1024–1027 CrossRef CAS PubMed.
- Z. S. Lin, L. Chen, L. M. Wang, J. T. Zhao and L. M. Wu, Adv. Mater., 2013, 25, 4800–4806 CrossRef CAS PubMed.
- Y. Hotta, E. Rokuta, J.-H. Jhoi, H. Tabata, H. Kobayashi and T. Kawai, Appl. Phys. Lett., 2002, 80, 3180–3182 CrossRef CAS.
- L. Benguigui, R. Weil, E. Muranevich, A. Chack, E. Fredj and A. Zunger, J. Appl. Phys., 1993, 74, 513–520 CrossRef CAS.
- B. Scott, M. Pressprich, R. D. Willet and D. A. Cleary, J. Solid State Chem., 1992, 96, 294–300 CrossRef CAS.
- I. V. Kityk, N. AlZayed, P. Rakus, A. A. AlOtaibe, A. M. El-Naggar and O. V. Parasyuk, Phys. B, 2013, 423, 60–63 CrossRef CAS.
- W. Kuznik, P. Rakus, K. Ozga, O. V. Parasyuk, A. O. Fedorchuk, L. V. Piskach, A. Krymus and I. V. Kityk, Eur. Phys. J.: Appl. Phys., 2015, 70, 30501 CrossRef.
- B. Lagoun, T. Bentria and B. Bentria, Comput. Mater. Sci., 2013, 68, 379–383 CrossRef CAS.
- L. Iordanidis, D. Bilc, S. D. Mahanti and M. G. Kanatzidis, J. Am. Chem. Soc., 2003, 125, 13741–13752 CrossRef CAS PubMed.
- M. C. Chen, L. M. Wu, H. Lin, L. J. Zhou and L. Chen, J. Am. Chem. Soc., 2012, 134, 6058–6060 CrossRef CAS PubMed.
- Y. Y. Li, B. X. Li, G. Zhang, L. J. Zhou, H. Lin, J. N. Shen, C. Y. Zhang, L. Chen and L. M. Wu, Inorg. Chem., 2015, 54, 4761–4767 CrossRef CAS PubMed.
- L. Geng, W. D. Cheng, C. S. Lin, W. L. Zhang, H. Zhang and Z. Z. He, Inorg. Chem., 2011, 50, 5679–5686 CrossRef CAS PubMed.
- W. L. Yin, W. D. Wang, L. Bai, K. Feng, Y. G. Shi, W. Y. Hao, J. Y. Yao and Y. C. Wu, Inorg. Chem., 2012, 51, 11736–11744 CrossRef CAS PubMed.
- (a) X. S. Lin, G. Zhang and N. Ye, Cryst. Growth Des., 2009, 9, 1186–1189 CrossRef CAS; (b) J. Y. Yao, D. J. Mei, L. Bai, Z. S. Lin, W. L. Yin, P. Z. Fu and Y. C. Wu, Inorg. Chem., 2010, 49, 9212–9216 CrossRef CAS PubMed.
- X. S. Lin, Y. F. Guo and N. Ye, J. Solid State Chem., 2012, 195, 172–177 CrossRef CAS.
- Y. Kim, I. S. Seo, S. W. Martin, J. Baek, P. S. Halasyamani, N. Arumugam and H. Steinfink, Chem. Mater., 2008, 20, 6048–6052 CrossRef CAS.
- H. Lin, L. J. Zhou and L. Chen, Chem. Mater., 2012, 24, 3406–3414 CrossRef CAS.
- B. W. Liu, H. Y. Zeng, M. J. Zhang, Y. H. Fan, G. C. Guo, J. S. Huang and Z. C. Dong, Inorg. Chem., 2015, 54, 976–981 CrossRef CAS PubMed.
- M. C. Chen, L. H. Li, Y. B. Chen and L. Chen, J. Am. Chem. Soc., 2011, 133, 4617–4624 CrossRef CAS PubMed.
- Z. Z. Luo, C. S. Lin, H. H. Cui, W. L. Zhang, H. Zhang, Z. Z. He and W. D. Cheng, Chem. Mater., 2014, 26, 2743–2749 CrossRef CAS.
- Z. Z. Luo, C. S. Lin, W. L. Zhang, H. Zhang, Z. Z. He and W. D. Cheng, Chem. Mater., 2014, 26, 1093–1099 CrossRef CAS.
- Z. Z. Luo, C. S. Lin, W. D. Cheng, H. Zhang, W. L. Zhang and Z. Z. He, Inorg. Chem., 2013, 52, 273–279 CrossRef CAS PubMed.
- W. L. Yin, Z. H. Lin, L. Kang, B. Kang, J. G. Deng, Z. S. Lin, J. Y. Yao and Y. C. Wu, Dalton Trans., 2015, 44, 2259–2266 RSC.
- X. S. Li, C. Li, P. F. Gong, Z. S. Lin, J. Y. Yao and Y. C. Wu, J. Mater. Chem. C, 2015, 3, 10998–11004 RSC.
- L. M. Wu, R. Sharma and D. K. Seo, Inorg. Chem., 2003, 42, 5798–5800 CrossRef CAS PubMed.
- L. M. Wu and D. K. Seo, J. Am. Chem. Soc., 2004, 126, 4676–4681 CrossRef CAS PubMed.
- Y. Z. Huang, L. Chen and L. M. Wu, Cryst. Growth Des., 2008, 8, 739–743 CAS.
- Y. Z. Huang, L. Chen and L. M. Wu, Inorg. Chem., 2008, 47, 10723–10728 CrossRef CAS PubMed.
- Y. Z. Huang, L. M. Wu, S. W. Du and L. Chen, Inorg. Chem., 2009, 48, 3901–3903 CrossRef CAS PubMed.
- K. Feng, X. X. Jiang, L. Kang, W. L. Yin, W. Y. Hao, Z. S. Lin, J. Y. Yao, Y. C. Wu and C. T. Chen, Dalton Trans., 2013, 42, 13635–13641 RSC.
- D. J. Mei, W. L. Yin, Z. S. Lin, R. He, J. Y. Yao, P. Z. Fu and Y. C. Wu, J. Alloys Compd., 2011, 509, 2981–2985 CrossRef CAS.
- G. M. Sheldrick, SHELXTL, version 5.1. Bruker-AXS: Madison, WI, 1998 Search PubMed.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- C. L. Teske, Z. Anorg. Allg. Chem., 1978, 445, 196–201 CrossRef.
- G. Kortüm, Reflectance Spectroscopy; Springer-Verlag: 1969 Search PubMed.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. E. Iglesias and H. Steinfink, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1480–1483 CrossRef CAS.
- W. L. Yin, K. Feng, W. D. Wang, Y. G. Shi, W. Y. Hao, J. Y. Yao and Y. C. Wu, Inorg. Chem., 2012, 51, 6860–6867 CrossRef CAS PubMed.
- I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247 CrossRef.
- K. O. Klepp and F. Z. Fabian, Naturforscher, 1992, 47, 406–410 CAS.
- A. Assoud, N. Soheilnia and H. Kleinke, Chem. Mater., 2004, 16, 2215–2221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1475011 and 1475012. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra27253c |
| This journal is © The Royal Society of Chemistry 2017 |