Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The solvothermal synthesis of γ-AlOOH nanoflakes and their compression behaviors under high pressures
Xudong Zhoua,
Jian Zhang†
 *a,
Yanmei Ma†*b,
Hui Tiana,
Yue Wanga,
Yingai Lia,
Lina Jianga and
Qiliang Cuia
*a,
Yanmei Ma†*b,
Hui Tiana,
Yue Wanga,
Yingai Lia,
Lina Jianga and
Qiliang Cuia
aState Key Laboratory of Superhard Materials, Jilin University, Changchun 130012, China. E-mail: zhang_jian@jlu.edu.cn; ymma@jlu.edu.cn
bCollege of Physics, Jilin University, Changchun 130012, China
First published on 17th January 2017
Abstract
Boehmite, γ-AlOOH, has attracted increasing research enthusiasm due to its scientific and technological importance. The compression behaviors of γ-AlOOH are of vital relevance to the insight into geophysical and geochemical processes in Earth's mantle. In this work, free-standing γ-AlOOH nanoflakes with high purity and crystallinity have been synthesized via a template-free, one-step solvothermal alcoholysis strategy. The nanoflakes have high aspect ratio, with the lateral size ranging from 100 to 300 nm, and the thickness ranging from 20 to 45 nm. The band gap of the obtained γ-AlOOH nanoflakes is estimated to be 3.35 eV through UV-vis absorption spectra recorded at room temperature. A broad PL emission band can be observed in the 400 to 700 nm spectrum range, with the maximum at 480 nm. The compression behaviors of γ-AlOOH nanoflakes have been investigated by in situ high pressure synchrotron radiation angle dispersive X-ray diffraction up to 54.9 GPa and Raman scattering spectroscopy up to 22.4 GPa at room temperature. The compression is nearly linear and anisotropic, with b axis more compressible than a and c axes. The zero-pressure bulk modulus of γ-AlOOH nanoflakes is estimated to be 135.2 GPa, higher than the theoretical value of its bulk counterpart. The frequencies of the observed Al–O related Raman modes increase monotonously in a linear manner with increasing pressure. The mode Grüneisen coefficients are estimated, which may provide important information about the anharmonicity in the bonding nature of γ-AlOOH.
1. Introduction
Nanoscale materials with tailored morphologies may exhibit novel physical and chemical properties dependent on their dimensions, sizes, shapes, and exposed facets.1,2 The subsequent utilization of nanocrystals with tailored geometries as building blocks for the fabrication of nanodevices offers the opportunity to control and manipulate the properties and applications of materials as desired. Hence, materials prepared via ‘nanoshape engineering’ have become one of the most promising and challenging issues of nowadays science and technology. Among these materials are nanoscale γ-AlOOH, boehmite, which have attracted increasing research enthusiasm on the synthetic methodology and potential applications recently. Various γ-AlOOH nanostructures with controllable geometries, such as 0D nanoparticles, 1D nanorods and nanowires, 2D nanosheets and nanoflakes, have been prepared and showed versatile potential applications in the fields of biomedicine, environmental chemistry, catalyst, sorbent, ceramic, and optical nanodevices. For instance, a library of γ-AlOOH nanoparticles including nanorods, nanoplates and nano-polyhedra with defined shape, crystallinity, and hydroxyl content, have been designed and synthesized, and these physicochemical properties have been demonstrated to play a key role in the ability of γ-AlOOH to activate superior immune responses.3 Novel 2D γ-AlOOH porous nanosheets have been prepared solvothermally, which may be converted to Al2O3 nanosheets by thermal decomposition.4 The obtained sheet-like Al2O3 may be used as a nanocatalyst support. The flowerlike γ-AlOOH nanoarchitectures, with three hierarchies of self organization, i.e., single-crystalline nanorods, nanostrips, and bundles, have been sequentially synthesized, which exhibited high BET area and excellent porous properties.5 Typically, hydrothermal and/or solvothermal procedures are involved in the synthetic strategies of these γ-AlOOH nanomaterials. Through delicate control of the reaction parameters, such as the pH value, the temperature, the time of processing, and the selection of precursors, solvents, and surfactants, etc., tuning of the dimension, size and shape of the target γ-AlOOH nanomaterials as desired may be achieved.6–16In addition to its technological importance, γ-AlOOH is also of considerable relevance in high pressure studies. As a mineral with intrastructural hydroxyl groups, the structure and stability of boehmite under high pressures is not only relevant for the investigation of geophysical and geochemical processes in the Earth's crust and the upper mantle, but also for the preparation of new materials with specific properties via high pressure/high temperature techniques. γ-AlOOH crystallizes in the orthorhombic dipyramidal structure, which may be described in space group Cmcm, or Cmc21 and P21/c.17–20 The difference among them lies in the position of H atoms only, with the Al–O frame being essentially the same. The unit cell is constituted by distorted AlO3(OH)3 octahedra. The AlO3(OH)3 octahedra contain two types of oxygen atoms: OI has four Al neighbors, OII has but two Al neighbors and forms covalent bond with the H atom. The AlO3(OH)3 octahedra interconnect to form 2D layers perpendicular to the b axis. Each layer possesses hydroxyl OII–H groups on both sides and a zigzag chain of hydrogen bonds of the OII–H⋯OII type is formed between the layers. The plane of the hydrogen bond chain is parallel to the b–c crystallographic plane. γ-AlOOH is polymorphous with α-AlOOH (diaspore) and δ-AlOOH (a metastable AlOOH phase synthesized under high pressures and high temperatures and quenched to ambient conditions).21–23 α-AlOOH is considered as a pertinent model system for high pressure studies of hydrogen bonds. The high pressure behaviors of α-AlOOH have been the matter of intensive experimental and theoretical studies.24–30 It has been found that α-AlOOH remains stable up to at least 15 GPa and 1123 K. The compression of the crystal structure of α-AlOOH proceeds mainly by bond shortening, and particularly by compression of the hydrogen bond. The hydrogen bond in α-AlOOH becomes significantly more symmetric with increasing pressure, but a complete symmetrization has not been reached in the investigated pressure range and does not seem likely to occur even at higher pressures. Initial researches on δ-AlOOH indicated its phase stability under a wide temperature range of less than 2300 K and pressure range from 18 to 134 GPa.21–23,31 However, recent investigations implied that an order–disorder phase transition would occur in δ-AlOOH between 6.1 and 8.2 GPa, concerning the situation of H distribution.32,33 The structural, mechanical and spectroscopic properties of γ-AlOOH under high pressures have been investigated by means of first-principle density functional theory (DFT).34 Isostatic structural compression via the DFT method gives the bulk modulus of 97 GPa in the athermal limit, for which mainly a strong shortening mechanism of interlayer hydrogen bonds is responsible. In contrast to the continuous research enthusiasm on the α- and δ-polymorphs of AlOOH, there are scarcely detailed experimental data for γ-AlOOH under high pressure conditions.
In this work, the compression behaviors of γ-AlOOH under high pressure conditions are reported. The samples under study are high purity, free-standing γ-AlOOH nanoflakes synthesized via a facile, template-free, one-step solvothermal alcoholysis method. The structural stabilities and mechanical properties have been investigated by in situ synchrotron radiation angle-dispersive X-ray diffraction (ADXRD) and Raman scattering techniques. These experimental results will help to further investigate the undisclosed intrinsic physical properties of γ-AlOOH nanomaterials. We expect that this study will not only provide valuable high pressure experimental information of γ-AlOOH, but also offer the opportunity for a better understanding of the hydrogen bond related compression behaviors of other layered compounds with intrastructural hydrogen bond, especially at the nanoscale.
2. Experimental section
2.1. Synthesis of γ-AlOOH nanoflakes
All chemicals were analytical grade reagents and were used without further purification. For the synthesis of γ-AlOOH nanoflakes, powders of 0.2 g anhydrous aluminum chloride (AlCl3, AR, Sinopharm Chemical Reagent Co., Ltd, China) were added into 15 mL methanol. The mixture was agitated vigorously by a magnetic stirrer for 20 minutes and a clear solution was formed. The resulting solution was transferred to a Teflon lined stainless steel autoclave, which was tightly sealed and heated at a rate of 2 °C min−1 in an electric oven to 350 °C and maintained for 3 hours. When the autoclave was cooled naturally to ambient temperature, the products were collected and washed with acetone several times to remove the residual reagents, and then dried at 60 °C for 12 hours. During the whole synthesizing process, there was no need for any shape-directing additives or regulating the pH value of the reaction environment.2.2. Characterization
Structural analysis of the products was carried out by powder X-ray diffractometry on a Shimadzu XRD-6000 diffractometer working with Cu Kα radiation (λ = 0.154178 nm). The SEM images of the samples were taken on a HITACHI S4800 microscope working at 25.0 kV, which is equipped with an energy dispersive spectrometer (EDS). The TEM micrographs of the samples, as well as the selected area electron diffraction (SAED) patterns, were obtained via a JEM-2200FS transmission electron microscope using an accelerating voltage of 200 kV. The ultraviolet-visible (UV-vis) absorption spectra of the synthesized product were taken on a Shimadzu UV-3150 spectrometer, and the photoluminescence (PL) measurement was conducted under 250 nm UV fluorescent light excitation by a Shimadzu RF-5301 PC spectrophotometer at room temperature.2.3. High pressure studies
High pressure experiments were conducted by using a symmetric diamond anvil cell (DAC) furnished with 400 μm culet diamonds. The T301 stainless steel gasket was pre-indented by the diamonds to an initial thickness of about 50 μm and then a center hole of 90 μm in diameter was drilled as the sample chamber. The samples with the liquid quasi-hydrostatic pressure-transmitting medium (silicone oil) were loaded into the sample chamber along with a tiny ruby chip for pressure measurements. The pressure within the sample chamber is increased in a stepwise manner, with intervals of 1–2 GPa. The pressure was determined from the frequency shift of the ruby R1 fluorescence line. The R1 and R2 lines of the ruby fluorescence signal remained well separated throughout the experiments, indicating that a good quasi-hydrostatic condition was maintained even when the pressure medium was solidified. The angle-dispersive XRD experiments were carried out with a wavelength of 0.6199 Å at the 4W2 High-Pressure Station of Beijing Synchrotron Radiation Facility (BSRF). The synchrotron X-ray beam was focused to a spot of about 29 × 15 μm2 in size. The average acquisition time was 300 s. The sample-detector distance and geometric parameters were calibrated using a CeO2 standard from NIST. The Bragg diffraction rings were recorded by using a Mar345 CCD detector and the one dimensional diffraction profiles of intensity as a function of 2θ were obtained by integration of the observed two dimensional patterns with the Fit2D software.35 Lattice parameters of the samples were obtained with Rietveld refinements of the powder XRD patterns performed using GSAS program packages.36 In situ high pressure Raman scattering spectra were collected at room temperature by using an Acton SpectraPro 500i spectrometer with 1800 g mm−1 holographic grating and a liquid nitrogen cooled CCD detector (Princeton Instruments, 1340 × 100). A solid-state diode-pumped Nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vanadate laser (Coherent Inc.) with the output wavelength of 532 nm was employed as the excitation source. Pressure-induced shifts of Raman scattering bands were analyzed by fitting the spectra to Lorentzian functions to determine the line–shape parameters.
vanadate laser (Coherent Inc.) with the output wavelength of 532 nm was employed as the excitation source. Pressure-induced shifts of Raman scattering bands were analyzed by fitting the spectra to Lorentzian functions to determine the line–shape parameters.
3. Results and discussion
The typical XRD patterns of the prepared samples are shown in Fig. 1(a). All the detectable peaks can be unambiguously assigned by their peak positions to γ-AlOOH, as compared with the standard diffraction patterns (PDF no. 21-1307). No additional peaks belonging to other AlOOH phases or impurities can be observed, indicating the high purity of the obtained samples. The sharp peaks also indicate that the prepared samples have perfect crystallinity. The lattice parameters of the synthesized γ-AlOOH samples are determined by Rietveld refinements of the powder XRD patterns. The results indicate that the obtained γ-AlOOH samples can be indexed to an orthorhombic cell with lattice parameters a = 0.369 nm, b = 1.225 nm, c = 0.286 nm.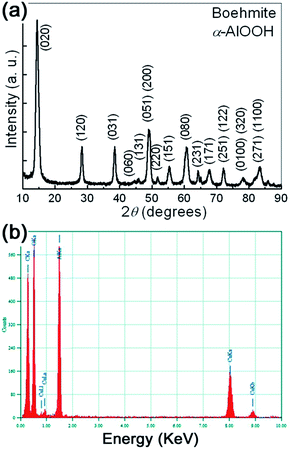 | ||
| Fig. 1 (a) The typical XRD pattern of the prepared samples. (b) The typical EDS spectra of the prepared samples. | ||
In addition to XRD results, the chemical composition of the prepared samples was further checked by energy dispersive X-ray analysis (EDS). The typical EDS spectra is shown in Fig. 1(b). It can be seen that the prepared γ-AlOOH sample contains mainly O and Al elements. C and Cu elements coming from the supporting mesh are also detected. In a wide spectrum range, no signals for other elements can be observed. Therefore, both XRD and EDS analyses show that pure orthorhombic phase γ-AlOOH with high crystallinity is successfully synthesized by the present one-step synthetic strategy.
To provide further insight into the structures of the prepared γ-AlOOH samples, the morphology of the prepared γ-AlOOH samples are observed by SEM and TEM techniques. The typical panoramic SEM image of the sample, as shown in Fig. 2(a), reveals that the sample consists of large quantities of small, thin flakes. The flakes have a quasi-hexagonal shape. From the SEM image of the sparsely dispersed samples (Fig. 2(b)) it can be seen that the nanoflakes have high aspect ratio. The lateral size of them ranges from 100 to 300 nm, and the thickness ranges from 20 to 45 nm. Most of the nanoflakes have well-defined outlines, as shown in the inset of Fig. 2(b). Fig. 2(c) shows the overall TEM image at low magnification of the prepared γ-AlOOH samples. It confirms that the sample comprises large numbers of nanometer scaled flakes. From the high magnification TEM image shown in Fig. 2(d), it can be validated that the quasi-hexagonal nanoflakes are fairly thin, as the overlapping of them can be easily evidenced. In Fig. 2(e) are shown several isolated nanoflakes with different orientations. The one with an orientation perpendicular to others shows clearly its thickness of about 25 nm. The HRTEM image and the corresponding selected area electron diffraction (SAED) pattern of an individual nanoflake, shown in Fig. 2(f), reveal that the nanoflakes are highly single crystalline in nature. The distance between fringes is measured to be about 0.37 nm, very close to the (100) interplanar d-spacing of the orthorhombic γ-AlOOH phase, which is in good accordance with the XRD studies.
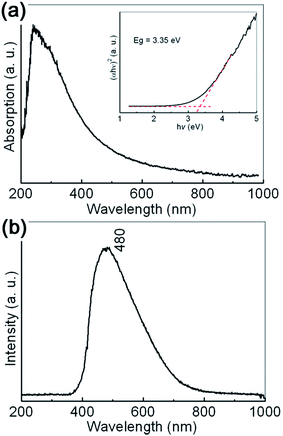
The typical UV-vis absorption spectrum of the prepared sample is shown in Fig. 3(a). An absorption edge can be observed in the 250–500 nm range, which may be reasonably ascribed to O2−→Al3+ charge transfer transitions.37 The broadening of the absorption edge is indicated to be related with the dispersed particle sizes. In order to determine the optical bandgap of the sample, the well known Kubelka–Munk transformation is used as follows:
| (αhν)2 = A(hν − Eg), |
The typical room temperature PL spectrum of the synthesized γ-AlOOH nanoflakes is shown in Fig. 3(b). A broad, asymmetric PL emission band can be clearly observed in the 400 to 700 nm range, with the maximum at about 480 nm (2.58 eV). Generally speaking, the optical properties of γ-AlOOH nanomaterials are not fully understood. However, it is believed that they are strongly dependent on the morphological features, such as size and shape. For example, the center position of the main peak observed for the ultrathin γ-AlOOH nanobelts with an average width of 10 nm, 298 nm (4.16 eV), exhibits an obvious blue shift to that observed for the γ-AlOOH nanowhiskers with an average width of 25 nm, 360 nm (3.44 eV). At the same time, structural defects, such as impurities and color centers (F and F+), may play an important role in the charge transfer and luminescent transitions.37–39
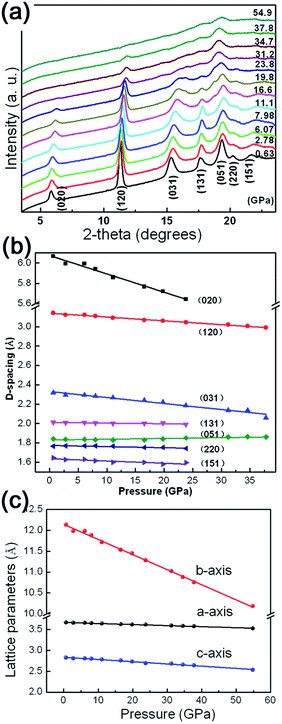
It is well-accepted that applying high pressure is an effective approach to study the structural stability and elastic properties of bulk/nanomaterials. The as-prepared γ-AlOOH nanoflakes are investigated by using in situ high pressure angle dispersive synchrotron radiation X-ray diffraction (ADXRD) techniques. Representative XRD patterns under high pressures up to 54.9 GPa are shown in Fig. 4(a) and the pressure dependent d-spacings of the lattice planes, as well as the unit-cell parameters, are shown in Fig. 4(b) and (c). The diffraction peaks are denoted with Miller indices and can be indexed to the orthorhombic cell of γ-AlOOH. During the entire compression processes, all diffraction peaks shift to higher angles with increasing pressure and no extra peaks appear in the XRD patterns. The corresponding d-spacings decrease approximately in a linear manner with increasing pressure. A similar variation of the unit-cell parameters is also observed. However, by taking a closer look at the lattice parameters, a strong anisotropy of the linear compressibilities of γ-AlOOH is obvious, with the b axis being much more compressible than the a and c axes. It is reasonable, since in boehmite, the Al–O framework forms two-dimensional layers connected via hydrogen bonds. Therefore, its structure is strongly anisotropic and the most compressible along the direction of the hydrogen bonds perpendicular to the a–c plane. Taking the high-pressure XRD results into account, it is suggested that there are no phase transitions in the pressure ranges we achieved in this study. To our knowledge, this is the first time that the effects of pressure on γ-AlOOH have been studied experimentally. Our results are in accordance with the theoretical studies that γ-AlOOH is stable under high pressures.34
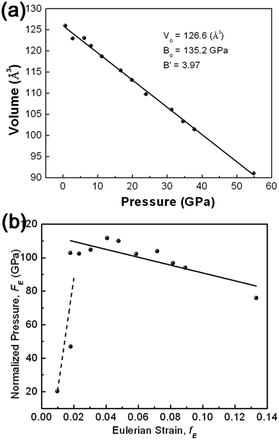
The information on the mechanical properties of γ-AlOOH can be obtained through investigation of the dependence of the structure upon compression. Variation of unit-cell volume with pressure is plotted in Fig. 5(a). It can be seen that the unit-cell volume of γ-AlOOH decrease linearly, at least as a first order approximation, with increasing pressure. Fitting the pressure–volume data to the third-order Birch–Murnaghan (BM) equation of state (EOS) yields the bulk modulus of B0 = 135.2 GPa with B′0 = 3.9. Owing to the lack of other experimental data for γ-AlOOH in the literature, no direct comparison can be performed. However, theoretical values are available. The structural, mechanical and spectroscopic properties of γ-AlOOH have been investigated by means of first-principle density functional theory (DFT) and semiempirical density functional based tight binding (DFTB) methods.34 Isostatic structural compression was performed and the bulk modulus spreading in the range of 82–97 GPa was obtained, exhibiting an enhanced compressibility compared with our experimental results.
In order to obtain a direct indication of the compression behavior and of the quality of the EOS fitting, the compression curve shown as plot of unit cell volume against pressure (P–V plot) is transformed into plot of finite strain fE against normalized stress FE (FE–fE plot), as illustrated in Fig. 5(b). The FE–fE plot is useful to visualize slight anomalies of equation of state that is difficult to be found in the P–V plot. For Birch–Murnaghan equation of state, fE and FE are defined as follows:
| fE = [(V0/V)2/3 − 1]/2 |
| FE = P/[3fE(1 + 2fE)5/2] |
In the FE–fE plot, the slope is equal to 3B0(B′0 − 4)/2, and the intercept on the vertical FE axis is the value of B0. It can be seen from Fig. 5(b) that all the data points except the first two (at low pressures) reside roughly in a line with a slope slightly lower than 0. A linear fitting of the FE–fE data yields B0 = 114.4 GPa and B′0 = 2.6, consistent qualitatively with the fitting of the P–V data to the third-order BM-EOS.
Concerning the experimental studies on the mechanical properties of materials under high pressures, several factors should be taken into accounts, such as hydrostaticity of pressure and the effects of size and shape, which would affect the compressibility. Systematical studies on the compressibility of nanocrystalline materials showed that the bulk modulus is significantly enhanced when measured under nonhydrostatic conditions.40,41 In this study, hydrostatic stress is achieved by immersing the sample in a pressurized fluid medium (silicone oil). This type of medium is able to maintain a hydrostatic/quasihydrostatic state up to 15 GPa.42 Thus the effect of the pressure-induced non-hydrostaticity in the sample chamber could be a possible reason for the enhanced bulk modulus. Pressure profoundly alters matters and materials, especially when they are at the nanoscale. The morphological features of nanomaterials, such as size and shape, play a very important role on their compression and structural behaviors under pressure. Generally speaking, the decrease in the grain size of nanocrystalline materials brings in turn an increase in the bulk modulus, as compared with their bulk counterparts.43,44 This phenomena might be related with the higher surface energy contribution, more grain boundaries and fewer dislocations, of nanocrystalline materials. In our case, the thickness of the γ-AlOOH nanoflakes under study ranges from 20 to 45 nm, implying that they can exhibit an enhanced strength against compression, i.e., reduced compressibility.
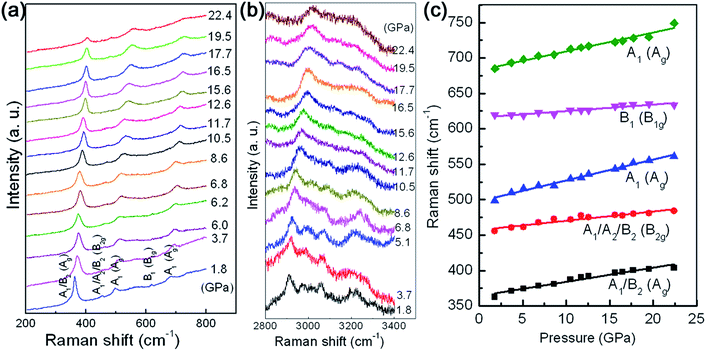
In order to obtain more detailed insight into the question of the high anisotropy of the compressibility, the dependences of the intralayer Al–O and interlayer hydrogen bonds on the volume compression have been studied by using Raman scattering spectroscopy. From the viewpoint of group theory, based on the decomposition of the reducible representation built on the basis of the Cartesian coordinates of the unit cell atoms, the symmetry of the normal modes at the Brillouin zone center (Γ point) of γ-AlOOH, in the space group of either Cmcm or Cmc21, may be assigned as the following:
| ΓCmcm = 4B1u + 4B2u + 4B3u + 4B1g + 4B2g + 4Ag |
| ΓCmc21 = 8A1 + 4A2 + 8B1 + 4B2 |
For the space group Cmcm, the Raman active modes are 4B1g + 4B2g + 4Ag. For the space group Cmc21, the Raman active modes are 7A1 + 4A2 + 7B1 + 3B2. The selected Raman scattering patterns of γ-AlOOH nanoflakes at various pressures are shown in Fig. 6(a) for the modes related with the Al–O bonds (200–800 cm−1), and in Fig. 6(b) for the modes related with the hydrogen bonds (2800–3400 cm−1). In the low frequency region, five features may be distinguished with their Raman shifts at about 363, 456, 499, 620, and 685 cm−1, at 1.8 GPa. These result are in good agreement with the reported theoretical and experimental values in the literature.20,45,46 Therefore, these Raman scattering features may be assigned according to the reports, as shown in Fig. 6 and Table 1. The evolution of these Raman mode frequencies against pressure is shown in Fig. 6(c). All the observed Raman mode frequencies increase monotonously in a linear manner with increasing pressure. The anharmonicity in bonding may have intense influence on the compression behaviors of materials under high pressures. The mode Grüneisen parameter (γ) is a powerful tool to describe the changes in the harmonicity of bonding and can be directly measured from a single high pressure experiment. Generally, the values of mode Grüneisen parameters may be estimated using the following equation:
γ = −(dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω)/(dln ω)/(dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V) = (B/ω)(dω/dP) V) = (B/ω)(dω/dP) |
| Raman shift ω (cm−1) | Assignment | dω/dP (cm−1 GPa−1) | Grüneisen coefficient γ | |
|---|---|---|---|---|
| Cmc21 | Cmcm | |||
| 364 | A1/B2 | Ag | 1.98 | 0.74 |
| 457 | A1/A2/B2 | B2g | 1.31 | 0.39 |
| 498 | A1 | Ag | 2.94 | 0.80 |
| 616 | B1 | B1g | 0.92 | 0.20 |
| 683 | A1 | Ag | 2.67 | 0.53 |
4. Conclusions
In summary, we synthesized γ-AlOOH nanocrystals by using a one-step, template-free solvothermal method via an alcoholysis reaction. The structural and compositional characterizations through XRD and EDS analyses showed that the prepared sample consisted of pure orthorhombic γ-AlOOH with high crystallinity. The morphological studies via SEM and TEM techniques revealed that the prepared sample was comprised of nanometer-scaled single crystalline thin flakes with well-defined shape and high aspect ratio. The optical properties of the obtained γ-AlOOH nanoflakes are characteristic of an average optical bandgap of 3.35 eV, with a broad, asymmetric PL emission band at about 480 nm. In situ high pressure synchrotron radiation ADXRD studies indicated a strong anisotropy of the linear compressibilities of γ-AlOOH nanoflakes, with the b axis being much more compressible than the a and c axes. Fitting the pressure-volume data to the third-order Birch–Murnaghan equation of state yielded the bulk modulus of B0 = 135.2 GPa, higher than the theoretical value of bulk γ-AlOOH. Such reduced compressibility was suggested to be related with the unique intrinsic geometry in the nanoflakes. By following the evolution of the Raman shifts against pressure, the Grüneisen parameters of the observed Raman modes related with the intralayer Al–O bonds were estimated, which may have important implications on the mechanism of the anisotropic linear compression behaviors of γ-AlOOH nanoflakes.Acknowledgements
This work is supported partially by the National Natural Science Foundation of China (Grant no. 11304114). High pressure experiments were carried out at 4W2 beamline, Beijing Synchrotron Radiation Facility (BSRF).Notes and references
- Y. Jun, J. Choi and J. Cheon, Angew. Chem., Int. Ed., 2006, 45, 3414–3439 CrossRef CAS PubMed.
- M. Huang and P. Lin, Adv. Funct. Mater., 2012, 22, 14–24 CrossRef CAS.
- B. Sun, Z. Ji, Y. Liao, M. Wang, X. Wang, J. Dong, C. Chang, R. Li, H. Zhang, A. Nel and T. Xia, ACS Nano, 2013, 7, 10832–10849 Search PubMed.
- S. Liu, C. Chen, Q. Liu, Y. Zhuo, D. Yuan, Z. Dai and J. Bao, RSC Adv., 2015, 5, 71728 RSC.
- J. Zhang, S. Liu, J. Lin, H. Song, J. Luo, E. Elssfah, E. Ammar, Y. Huang, X. Ding, J. Gao, S. Qi and C. Tang, J. Phys. Chem. B, 2006, 110, 14249–14252 CrossRef CAS PubMed.
- P. Pardo, N. Montoya and J. Alarcón, CrystEngComm, 2015, 17, 2091 RSC.
- J. Wen, M. Liu and C. Mou, CrystEngComm, 2015, 17, 1959 RSC.
- X. Song, P. Yang, C. Jia, L. Chen and K. Matras-Postolek, RSC Adv., 2015, 5, 33155 RSC.
- X. Liu, C. Niu, X. Zhen, J. Wang and X. Su, J. Colloid Interface Sci., 2015, 452, 116–125 CrossRef CAS PubMed.
- G. Liu, H. Ye, Y. Dai, L. Yu, H. Jiang, Y. Zhou and K. Han, J. Alloys Compd., 2015, 647, 18–23 CrossRef CAS.
- G. Ji, M. Li, G. Li, G. Gao, H. Zou, S. Gan and X. Xu, Powder Technol., 2012, 215–216, 54–58 CrossRef CAS.
- Y. Zhang, Y. Jia, Z. Jin, X. Yu, W. Xu, T. Luo, B. Zhu, J. Liu and X. Huang, CrystEngComm, 2012, 14, 3005–3007 RSC.
- X. Duan, T. Kim, D. Li, J. Ma and W. Zheng, Chem.–Eur. J., 2013, 19, 5924–5937 CrossRef CAS PubMed.
- Z. Tang, J. Liang, X. Li, J. Li, H. Guo, Y. Liu and C. Liu, J. Solid State Chem., 2013, 20, 305–314 CrossRef.
- Y. Xia, X. Jiao, Y. Liu, D. Chen, L. Zhang and Z. Qin, J. Phys. Chem. C, 2013, 117, 15279–15286 CAS.
- Z. Xu, J. Yu, J. Low and M. Jaroniec, ACS Appl. Mater. Interfaces, 2014, 6, 2111–2117 CAS.
- C. Corbató, R. Tettenhorst and G. Christoph, Clays Clay Miner., 1985, 33, 71–75 Search PubMed.
- X. Bokhimi, J. Toledo-Antonio, M. Guzmán-Castillo and F. Hernández-Beltrán, J. Solid State Chem., 2001, 159, 32–40 CrossRef CAS.
- D. Chiche, M. Digne, R. Revel, C. Chanéac and J. P. Jolivet, J. Phys. Chem. C, 2008, 112, 8524–8533 CAS.
- Y. Noel, R. Demichelis, F. Pascale, P. Ugliengo, R. Orlando and R. Dovesi, Phys. Chem. Miner., 2009, 36, 47–59 CrossRef CAS.
- A. Suzuki, E. Ohtani and T. Kamada, Phys. Chem. Miner., 2000, 27, 689–693 CrossRef CAS.
- E. Ohtani, K. Litasov, A. Suzuki and T. Kondo, Geophys. Res. Lett., 2001, 28, 3991–3993 CrossRef CAS.
- A. Sano, E. Ohtani, T. Kubo and K. Funakoshi, J. Phys. Chem. Solids, 2004, 65, 1547–1554 CrossRef CAS.
- H. Mao, J. Shu, J. Hu and R. Hemley, Solid State Commun., 1994, 90, 497–500 CrossRef CAS.
- J. Xu, J. Hu, L. Ming, E. Huang and H. Xie, Geophys. Res. Lett., 1994, 21, 161–164 CrossRef CAS.
- M. Schmidt, Am. Mineral., 1995, 80, 1286–1292 CAS.
- K. Grevel, M. Burchard, D. Fasshauer and T. Peun, J. Geophys. Res.: Solid Earth, 2000, 105, 27877–27887 CrossRef CAS.
- B. Winkler, M. Hytha, C. Pickard, V. Milman, M. Warren and M. Segall, Eur. J. Mineral., 2001, 13, 343–349 CrossRef CAS.
- A. Friedrich, D. Wilson, E. Haussühl, B. Winkler, W. Morgenroth, K. Refson and V. Milman, Phys. Chem. Miner., 2007, 34, 145–157 CrossRef CAS.
- A. Friedrich, E. Haussühl, R. Boehler, W. Morgenroth, E. Juarez-Arellano and B. Winkler, Am. Mineral., 2007, 92, 1640–1644 CrossRef CAS.
- A. Sano, E. Ohtani, T. Kondo, N. Hirao, T. Sakai, N. Sata, Y. Ohishi and T. Kikegawa, Geophys. Res. Lett., 2008, 35, L03303 CrossRef.
- A. Sano-Furukawa, H. Kagi, T. Nagai, S. Nakano, S. Fukura, D. Ushijima, R. Iizuka, E. Ohtani and T. Yagi, Am. Mineral., 2009, 94, 1255–1261 CrossRef CAS.
- T. Kuribayashi, A. Sano-Furukawa and T. Nagase, Phys. Chem. Miner., 2014, 41, 303–312 CrossRef CAS.
- D. Tunega, H. Pašalić, M. Gerzabek and H. Lischka, J. Phys.: Condens. Matter, 2011, 23, 404201 CrossRef CAS PubMed.
- A. Hammersley, S. Svensson, M. Hanfland, A. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248 CrossRef.
- B. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- A. Alemi, Z. Hosseinpour, M. Dolatyari and A. Bakhtiari, Phys. Status Solidi B, 2012, 249, 1264–1270 CrossRef CAS.
- Z. Yu, C. Wang, X. Gu and C. Li, J. Lumin., 2004, 106, 153–157 CrossRef CAS.
- P. Gao, Y. Xie, Y. Chen, L. Ye and Q. Guo, J. Cryst. Growth, 2005, 285, 555–560 CrossRef CAS.
- B. Chen, D. Penwell and M. B. Kruger, Solid State Commun., 2000, 115, 191–194 CrossRef CAS.
- C. Grant, J. Crowhurst, T. Arsenlis, E. Bringa, Y. Wang, J. Hawreliak, P. Pauzauskie and S. Clark, J. Appl. Phys., 2009, 105, 084311 CrossRef.
- D. Ragan, D. Clarke and D. Schiferl, Rev. Sci. Instrum., 1996, 67, 494 CrossRef CAS.
- Z. Wang, S. Saxena, V. Pischedda, H. Liermann and C. Zha, Phys. Rev. B: Condens. Matter, 2001, 64, 012102 CrossRef.
- Z. Wang, Y. Zhao, D. Schiferl, J. Qian, R. Downs, H. Mao and T. Sekine, J. Phys. Chem. B, 2003, 107, 14151 CrossRef CAS.
- A. Kiss, G. Keresztury and L. Farkas, Spectrochim. Acta, Part A, 1980, 36, 653–658 CrossRef.
- H. Ruan, R. Frost and J. Kloprogge, J. Raman Spectrosc., 2001, 32, 745–750 CrossRef CAS.
Footnote |
| † Jian Zhang and Yanmei Ma contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |