Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational prediction and experimental confirmation of rhombohedral structures in Bi1.5CdM1.5O7 (M = Nb, Ta) pyrochlores†
G. Perenlei ab,
P. C. Talbotab,
W. N. Martens
ab,
P. C. Talbotab,
W. N. Martens a,
J. Richesc and
J. A. Alarco
a,
J. Richesc and
J. A. Alarco *ab
*ab
aSchool of Chemistry, Physics and Mechanical Engineering, Australia. E-mail: jose.alarco@qut.edu.au
bInstitute for Future Environments, Australia
cEarth, Environmental and Biological Sciences Bioscience, Science and Engineering Faculty, Queensland University of Technology, Brisbane, QLD 4000, Australia
First published on 9th March 2017
Abstract
In this study, computationally predicted band gaps and structures using density functional theory (DFT) in Bi1.5CdM1.5O7 (M = Nb, Ta) pyrochlores are confirmed by experimental data on synthesized samples. Ordered Cd substitutions in the B-site of the pyrochlore structures are required to achieve electronic band gaps in the calculated energy band structures, when using full plane waves for DFT calculations, which are supported by a significantly lower total enthalpy. The computationally predicted band gap values are closely matched to experimental band gaps estimated from optical absorption spectra in the UV-Vis. In addition to the prediction of electronic structures, the models also indicate that the large ionic radius of the Cd-cation leads to symmetry modification from the archetypal cubic pyrochlore structure in Bi1.5CdM1.5O7 (M = Nb, Ta). A rhombohedral structure and localized superlattice order are confirmed using X-ray diffraction (XRD) and transmission electron microscopy (TEM) analysis. Energy dispersive X-ray spectroscopy profiles across the superlattice domain interfaces, which are constant within experimental uncertainty, indicate that domain formation is not compositionally driven but likely a mechanism to alleviate strain build up. Raman and FTIR spectroscopy analyses on these two compounds display strong similarities suggesting that peaks and activities belong to the same structure type.
1. Introduction
Pyrochlores, along with perovskites, are ideally cubic structures that allow for significant compositional flexibility, without major changes in crystal symmetries and lattice parameters.1–4 Their extensive compositional ranges display electronic, ferroelectric, ionic, optical and magnetic properties, which make them useful (and potentially tunable) for a remarkably wide variety of technological applications, including microwave capacitors,5–7 dielectric materials,8,9 catalysts,10–13 gas sensors,14 solid electrolytes15 and thermal barrier coatings.16,17Ideal pyrochlores have general formula A2B2O7 (sometimes written as A2B2O6O′, where O and O′ represent oxygen). They can accommodate several combinations of valences of the cation species A and B, including A23+B24+O7 and A22+B25+O7, and have been discussed in detail in the literature.18,19 Oxide pyrochlore structures are composed of two different types of cation coordination polyhedra; the A-site positions are 8-fold coordinated and located within oxygen (O) scalenohedra (at the 16c (0, 0, 0) site in Wyckoff's notation) and the B-site positions are 6-fold coordinated to O and located within trigonal antiprisms (at the 16d (1/2, 1/2, 1/2) site).18 The A-site is usually occupied by larger alkali, alkaline earth or rare-earth metal cations, whereas smaller 3d, 4d or 5d-transition metal cations favour the B-site. Oxygen anions are coordinated to metals at both the A sites (with O′ on the 48f (x, 1/8, 1/8) sites) and at the B sites (with O on the 8b (3/8, 3/8, 3/8) site).18
Many possible cation substitutions at the A and B sites also expand the availability of mixed-valence materials with specific properties of interest.20 The compositional window and unit cell symmetry of substituted compounds, however, can become more sensitive to the nature of the substituting cations.20 Structural disorder in pyrochlores is common and it can be promoted by a large ionic size ratio of the A and B cations. The A2B2O7 pyrochlore structure remains cubic when the cation size ratio, rA/rB, is between 1.46 and 1.78.18,19 If the ratio exceeds this range, the cubic symmetry is distorted and oxygen vacancies are introduced on the anion sublattice or into the A2O′ network.
Existing families of Bi-based pyrochlores, such as bismuth zinc niobate (α-BZN) and bismuth zinc tantalate (α-BZT) with compositions Bi1.5ZnNb1.5O7 and Bi1.5ZnTa1.5O7, respectively, have been extensively investigated in recent times.21–25 Both α-BZN and α-BZT have been reported as cubic structures with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227).26 The crystal structures of BZN and BZT consist mainly of Bi and Nb (Ta) cations at the A and B sites, respectively. Zn cations are found to be equally divided between these two sites, with up to 25% of the Bi and Nb (Ta) cations each being randomly substituted by Zn (in a 1
m (No. 227).26 The crystal structures of BZN and BZT consist mainly of Bi and Nb (Ta) cations at the A and B sites, respectively. Zn cations are found to be equally divided between these two sites, with up to 25% of the Bi and Nb (Ta) cations each being randomly substituted by Zn (in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio) according to the Crystal Information Files (CIF) from the Inorganic Crystal Structure Database (ICSD).26 Thus, the stoichiometric formula of BZN and BZT can be written as (Bi1.5Zn0.5)(Zn0.5Nb1.5O7) and (Bi1.5Zn0.5)(Zn0.5Ta1.5O7), respectively. However, local order of the A-site cations in BZN and subsequent structural relaxation have been determined using neutron and electron diffraction, and Monte Carlo simulations.27
3 ratio) according to the Crystal Information Files (CIF) from the Inorganic Crystal Structure Database (ICSD).26 Thus, the stoichiometric formula of BZN and BZT can be written as (Bi1.5Zn0.5)(Zn0.5Nb1.5O7) and (Bi1.5Zn0.5)(Zn0.5Ta1.5O7), respectively. However, local order of the A-site cations in BZN and subsequent structural relaxation have been determined using neutron and electron diffraction, and Monte Carlo simulations.27
Our recent investigations on the electronic band structures of cubic-BZN and cubic-BZT have shown that the use of the (widely accepted) CIFs as inputs for Density Functional Theory (DFT) calculations, result in complete absence of electronic band gaps when using the Full Plane Wave Functions of the Cambridge Serial Total Energy Package (CASTEP) of Materials Studio.28,29 These results contradict the reported experimental observations of optical band gaps of 3.0–3.2 eV.30,31 A band gap is obtained for fractional occupancy of cations in BZT using the Linear Muffin Tin Potential.32 However, the calculated band gap is much lower than experiment and our calculated results for BZT.29 According to the CIF for BZN and BZT used in these studies, both A and B sites are randomly occupied by Bi/Zn and Nb/Zn (or Ta/Zn) fractional mixtures, respectively.28,29 In contrast, when the substitutions are considered completely or partially ordered (that is assuming all or part of the substitutions at preferential sites), a remarkable match of calculated electronic band gaps to experimental measurements can be obtained.28,29
The DFT calculations on BZN and BZT also predict small modifications from the cubic structure, when complete substitution order is assumed, which appears favoured as attested by the significantly more negative enthalpy of formation.28,29 However, such favourably calculated modified structures could not be clearly detected by standard X-ray diffraction (XRD) or transmission electron microscopy (TEM) characterizations. An overall cubic structure, predicted by the DFT calculation, could be reconciled by assuming partial order, with order just on the B-sites, while the A-sites remained randomly substituted.28,29 This final combination also retained a good match between experimentally determined and DFT calculated electronic band gaps.
This current paper investigates the homologous Bi-based pyrochlores using Cd instead of Zn, that is, bismuth cadmium niobate (BCN) and bismuth cadmium tantalate (BCT), and compares the results to those for BZN and BZT. Cd2+ has ionic radii of 1.10 Å and 0.95 Å for VIII and VI coordination, respectively, which are significantly larger than the corresponding ionic radii of Zn2+ in VIII (0.90 Å) and VI (0.74 Å) coordination, respectively. However, the cation size ratios, rA/rB, are 1.60 and 1.65 for both BCN/T and both BZN/T, respectively, when calculated considering the percentage of mixed cations in the both A and B sites (rA/rB = (0.75rBi + 0.25rM)/(0.75rM′ + 0.25rM) using (Bi1.5M0.5)(M0.5M′1.5O7) M = Zn, Cd; M = Nb, Ta composition). These calculated ratios of BCN and BCT are within the cubic symmetry ranges as mentioned above. Therefore, this work explores whether Cd substitution in BCN and BCT display more clearly detectable trends with respect to ordering and modification of the cubic pyrochlore structure.
2. Methodology
2.1. Experimental synthesis and characterization
Raman spectra and attenuated total reflectance (ATR) FTIR measurements have been recorded in the range of 100–1000 cm−1 using a Renishaw Raman microscope and a Nicolet iS50 ATR-FTIR spectrophotometer, respectively. All measurements have been performed at room temperature, using a He–Ne laser operating at 633 nm with attenuation set to 6. FTIR data have been collected over an accumulation of 4000 scans at a speed of 0.02 min per scan, energy step 0.428 cm−1 and resolution of 4 cm−1, to reduce the noise at low frequencies (<200 cm−1).
Optical absorption spectra in the UV-Vis, wavelength regions of 200–800 nm, have been recorded using a UV-Vis-NIR Cary 5000 Stheno spectrometer. The display of the optical absorption spectra have generally been converted from absorbance vs. wavelength to absorbance vs. photon energy.
Additional microstructural characterization has been performed on powder samples dispersed on Lacey formvar/carbon films (300 mesh Cu) using TEM combined with energy-dispersive X-ray spectrometry (EDS). Bright field and high resolution TEM imaging and selected area electron diffraction (SAED) have been obtained using a JEOL JEM-2100 microscope at an accelerating voltage of 200 kV. TEM-EDS analysis has been carried out using an FEI Tecnai TF20 TEM at 200 kV in the scanning transmission electron microscopy (STEM) mode using a low background double-tilt specimen holder. These techniques have been focused on the identification of potential modifications from cubic symmetry, lattice distortions and defects, and analysis of their crystallography and composition. Image processing of TEM micrographs has been carried out using Gatan's Digital Micrograph software.
2.2. Assumptions for DFT calculations
For both BZN and BZT, the CIFs contain 88 atoms in a cubic unit cell and Zn cations are randomly distributed in both the A(Bi) and B(Nb or Ta)-sites. One of the main differences between the CIF for BZN and that for BZT is that the A-site of BZN contains a slightly higher ratio of Bi in the mixed cations when compared to that for BZT. The cubic structures contain fractionally occupied cations in the ratio Bi/Zn = 78.125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21.875 and Nb/Zn = 75
21.875 and Nb/Zn = 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 for BZN, and the ratio Bi/Zn = 75
25 for BZN, and the ratio Bi/Zn = 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 and Ta/Zn = 75
25 and Ta/Zn = 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 for BZT, respectively.28,29 Another difference between the BZN and BZT structures in the respective CIFs is that the surface of the unit cell of the former contains only metal atoms while the surface of the latter contains only oxygen atoms. Although such a difference after the substitutions, in principle, is only a translation of equivalent representations of the same periodic structure, our calculations show that the end results are modified in a slightly different manner and adopt different crystal symmetries.28,29
25 for BZT, respectively.28,29 Another difference between the BZN and BZT structures in the respective CIFs is that the surface of the unit cell of the former contains only metal atoms while the surface of the latter contains only oxygen atoms. Although such a difference after the substitutions, in principle, is only a translation of equivalent representations of the same periodic structure, our calculations show that the end results are modified in a slightly different manner and adopt different crystal symmetries.28,29
For random solid solutions (BCN(r) and BCT(r), where (r) refers to random distribution of Cd in the crystal structure), calculations have been carried out using crystal structures with fractionally occupied (mixed) cations. After substituting Cd for Zn, the resulting fractionally occupied structures have also been further modified by defining specific sites in the crystal structures, where the Cd substitutions take place (BCN(o) and BCT(o), where (o) refers to ordered solid solution). Schematics of the BCN or BCT random and ordered solid solutions using the CIF of BZT as an initial structure before geometry optimization are displayed in Fig. 1. The ratio of Bi to Cd or Nb(Ta) to Cd is [3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1] within each unit cell, with substitutions running along the 〈211〉 direction as previously described in the literature.34 Atoms are displayed using a ball and stick style, where Bi, Nb(or Ta), Cd (A and B-sites) and O atoms are purple, blue, green, orange and red balls, respectively, and the diameters of the balls are in proportion to ionic radii. Tables with atomic coordinates of all the atoms within the above mentioned unit cells are given in the ESI in Table S1.†
1] within each unit cell, with substitutions running along the 〈211〉 direction as previously described in the literature.34 Atoms are displayed using a ball and stick style, where Bi, Nb(or Ta), Cd (A and B-sites) and O atoms are purple, blue, green, orange and red balls, respectively, and the diameters of the balls are in proportion to ionic radii. Tables with atomic coordinates of all the atoms within the above mentioned unit cells are given in the ESI in Table S1.†
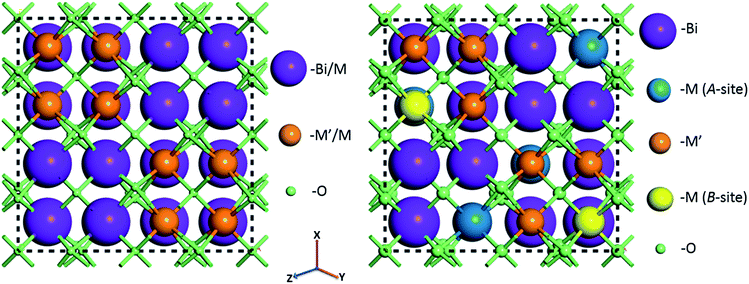 | ||
| Fig. 1 Crystal structures of Bi1.5MM′1.5O7 (M = Zn, Cd; M′ = Ta, Nb) combinations assuming random (left) and ordered (with cations substituted at specific sites) (right) solid solutions before geometry optimization. Full lists with atomic positions are given in ESI (Table S1†). | ||
Structures with ordered substitutions at only a single site (either A or B, while the other site remains fractionally occupied or random) have also been considered as an alternative option for the model structures (BCN(p.o) and BCT(p.o), where (p.o) refers to partial order). Depending on which site the substitution is ordered, the structure is called either A or B-site partially ordered. Details of the structural modifications have been described in our previous publications.28,29
3. Results and discussion
3.1. Crystal structure
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) pyrochlore unit-cell can lead to symmetry-lowering and formation of a rhombohedral (R
m) pyrochlore unit-cell can lead to symmetry-lowering and formation of a rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure, which will be manifest as peak splitting in the diffraction patterns.35
m) structure, which will be manifest as peak splitting in the diffraction patterns.35
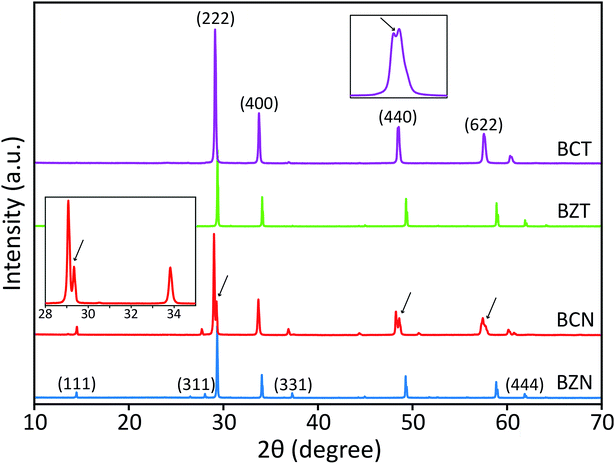
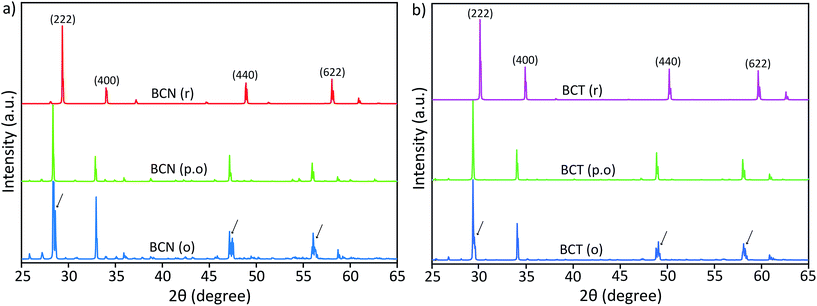
Peak splitting of the most intense peak (for the 222 reflection using cubic indexes) in the diffraction patterns of BCT is not clearly detected at normal scan rates. However, splitting at peaks for (440), (622) and (444) reflections (cubic indices) in the XRD pattern is obtained (see enlarged (440) peak in Fig. 2). The difference between observed BCN and BCT peak patterns may be partly due to a higher sintering temperature (≥1000 °C) required for synthesis of Ta-compounds to a similar level of crystallinity to Nb-compounds.36,37 In fact, the broader full width at half maximum (FWHM) value can be related to crystallites of smaller size using the Scherrer equation.
Moreover, the diffraction patterns for BZN and BZT, refined to cubic structures with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227) using TOPAS, give lattice parameters a = 10.558 and 10.555 Å and fitting coefficients RWP = 3.86 and 3.97%, respectively. The refined unit-cell values for both BZN and BZT are approximated by respective least squares refinements of the (111), (311), (222), (400), (331), (511), (440), (622) and (444) reflections from powder samples as shown in Fig. 2.
m (No. 227) using TOPAS, give lattice parameters a = 10.558 and 10.555 Å and fitting coefficients RWP = 3.86 and 3.97%, respectively. The refined unit-cell values for both BZN and BZT are approximated by respective least squares refinements of the (111), (311), (222), (400), (331), (511), (440), (622) and (444) reflections from powder samples as shown in Fig. 2.
When refinements of the BCN and BCT structures to the cubic structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227) are attempted, they result in lattice constants a = 10.640 and 10.623 Å. The diffraction pattern of BCN fits poorly with RWP = 22.19%, while the pattern of BCT fits more reasonably with RWP = 8.74%. Such poor fitting, particularly for BCN, is due to the large peak splitting at the approximate cubic (222), (440), (622) and (444) reflections in the patterns (see Fig. 2). In this case, the refinement identifies the most intense peak as the (222) reflection for the cubic structure in the diffraction patterns and treats remaining peaks as impurity phases.
m (No. 227) are attempted, they result in lattice constants a = 10.640 and 10.623 Å. The diffraction pattern of BCN fits poorly with RWP = 22.19%, while the pattern of BCT fits more reasonably with RWP = 8.74%. Such poor fitting, particularly for BCN, is due to the large peak splitting at the approximate cubic (222), (440), (622) and (444) reflections in the patterns (see Fig. 2). In this case, the refinement identifies the most intense peak as the (222) reflection for the cubic structure in the diffraction patterns and treats remaining peaks as impurity phases.
Therefore, the possibility of two coexisting cubic structures with slightly different lattice parameters was explored by calculating the expected XRD peak positions for a set of (hkl) Miller indices as shown in Table 1.
| h | k | l | TOPAS refined lattice parameter | Calculated from split (222) peak | ||
|---|---|---|---|---|---|---|
| 2 theta (°) | Distance | 2 theta (°) | Distance | |||
| 1 | 0 | 0 | 8.303 | 10.6402 | 8.360 | 10.5684 |
| 1 | 1 | 0 | 11.753 | 7.5237 | 11.833 | 7.4730 |
| 1 | 1 | 1 | 14.407 | 6.1431 | 14.505 | 6.1017 |
| 2 | 0 | 0 | 16.650 | 5.3201 | 16.764 | 5.2842 |
| 2 | 1 | 0 | 18.632 | 4.7584 | 18.760 | 4.7263 |
| 2 | 2 | 0 | 23.631 | 3.7619 | 23.794 | 3.7365 |
| 3 | 1 | 1 | 27.786 | 3.2081 | 27.978 | 3.1865 |
| 2 | 2 | 2 | 29.048 | 3.0716 | 29.249 | 3.0508 |
| 4 | 0 | 0 | 33.666 | 2.6600 | 33.901 | 2.6421 |
| 4 | 4 | 0 | 48.350 | 1.8809 | 48.700 | 1.8682 |
| 6 | 2 | 2 | 57.399 | 1.6041 | 57.825 | 1.5932 |
Distances are calculated assuming there is a second cubic phase with slightly different lattice parameter. Table 1 shows that if the split peaks around the 2 theta angle (using Cu Kα1 wavelength of 1.54056 Å) around 23.6–23.8° (with (222) indexes) are interpreted as belonging to two cubic lattices with slightly different cubic lattice parameters, other peaks for the same cubic structures (with indexes (400), for instance), should also display similar splitting according to the table, which is not the case experimentally (see inset on the left for the red XRD trace in Fig. 2). This indicates that two coexisting cubic structures are not an explanation for the peak splitting.
A significantly improved refinement of the BCN pattern, with RWP = 11.09%, has been obtained assuming the structure is better approximated as a rhombohedral symmetry with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) crs (No. 167). In this case, all peaks, including those split, are indexed and matched with calculated peaks from the TOPAS refinement. The refined rhombohedral lattice parameters of BCN are a = 10.627 Å and α = 90.37°. Other attempts at refinement with slightly different rhombohedral structures produced fitting parameters as poor as the refinement with a cubic structure. In the case for BCT, both cubic and rhombohedral refinements produce similar quality results, which is due to the absence of obvious peak splitting at the (222) reflection in the diffraction pattern.
crs (No. 167). In this case, all peaks, including those split, are indexed and matched with calculated peaks from the TOPAS refinement. The refined rhombohedral lattice parameters of BCN are a = 10.627 Å and α = 90.37°. Other attempts at refinement with slightly different rhombohedral structures produced fitting parameters as poor as the refinement with a cubic structure. In the case for BCT, both cubic and rhombohedral refinements produce similar quality results, which is due to the absence of obvious peak splitting at the (222) reflection in the diffraction pattern.
Refined lattice parameters for both BCN and BCT assuming both cubic and rhombohedral structures, along with comparative BZN and BZT cubic structures are shown in Table 2. The results for BCT are nearly the same, whether a cubic or a rhombohedral structure is assumed, confirming that the modification of the group symmetry from cubic is minimal (if any). On the other hand, the quality of the fitting for BCN improves in the rhombohedral phase, not only in terms of the overall refinement, but also producing a lattice dimension, which is closer to that of BCT. Both refinements using rhombohedral symmetry are more consistent with the results observed for BZN and BZT compounds.
| Structure | Cubic | Rhombohedral | |||
|---|---|---|---|---|---|
| a (Å) | RWP (%) | a (Å) | α (°) | RWP (%) | |
| BCN | 10.640 | 22.19 | 10.627 | 90.37 | 11.09 |
| BCT | 10.623 | 8.74 | 10.623 | 89.98 | 8.77 |
| BZN | 10.558 | 3.86 | — | — | — |
| BZT | 10.555 | 3.97 | — | — | — |
 | ||
| Fig. 3 Reflex simulated diffraction patterns of (a) BCN and (b) BCT structures with different cation substitutional order (the arrows indicate peak splitting). | ||
Diffraction patterns for random (BCN(r) and BCT(r)) and partially ordered (BCN(p.o)) structures show single peaks with no peak splitting at the (222), (440) and (622) reflections. However, ordered solid solutions, BCN(o) and BCT(o) (keeping the atomic ratios Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 3
Cd = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and Nb (or Ta)
1 and Nb (or Ta)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 3
Cd = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the A and B sites, respectively), have clearly shown double or triple peaks in the simulated diffraction patterns (the arrows indicate peak splitting in Fig. 3). These DFT simulated patterns of BCN(o) and BCT(o) structures in Fig. 3(a) and (b), respectively, closely resemble those obtained from the X-ray diffraction patterns of BCN and BCT samples are shown in Fig. 2. Simulated diffraction patterns of BCT(o) suggest that the peak splitting at major peaks, particularly, at (222) reflections correspond to symmetry modification from the cubic phase and not to a second phase with slightly different cubic lattice parameters.
1 in the A and B sites, respectively), have clearly shown double or triple peaks in the simulated diffraction patterns (the arrows indicate peak splitting in Fig. 3). These DFT simulated patterns of BCN(o) and BCT(o) structures in Fig. 3(a) and (b), respectively, closely resemble those obtained from the X-ray diffraction patterns of BCN and BCT samples are shown in Fig. 2. Simulated diffraction patterns of BCT(o) suggest that the peak splitting at major peaks, particularly, at (222) reflections correspond to symmetry modification from the cubic phase and not to a second phase with slightly different cubic lattice parameters.
Small extra diffraction peaks are also observed in the simulated diffraction pattern for the BCN(o) structure, which are due to the repeated periodicity of Cd cations in the crystal structure. These small peaks are not observed experimentally, indicating that the superlattice order is not as perfect as simulated, and that it may only exist as few nanometre scale domains. This result suggests that the distribution of Cd cations in the crystal structures is not random, but rather located at specific positions with certain order, at least within a several unit cell domain scale.
Lattice parameters for random, partially and completely ordered BCN and BCT structures after full geometry optimization are shown in Table 2, along with those for BZN and BZT structures. Refined lattice parameters for experimental diffraction data using TOPAS (given in Table 2) are also included in Table 3 for comparison.
| Structure | DFT calculated (geometry optimized) lattice parameters | Refined lattice parameters from XRD data | |||||
|---|---|---|---|---|---|---|---|
| Random | Partially ordered (A-site) | Partially ordered (B-site) | Ordered | ||||
| a (Å) | a (Å) | a (Å) | a (Å) | α (°) | a (Å) | α (°) | |
| BCN | 10.532 | 10.495 | 10.895 | 10.867 | 90.33 | 10.627 | 90.37 |
| BCT | 10.273 | 10.173 | 10.536 | 10.520 | 90.25 | 10.623 | 89.98 |
| BZN | 10.492 | 10.566 | 10.822 | 10.767 | 90.11 | 10.558 | 90.00 |
| BZT | 10.223 | 10.214 | 10.442 | 10.418 | 90.13 | 10.555 | 90.00 |
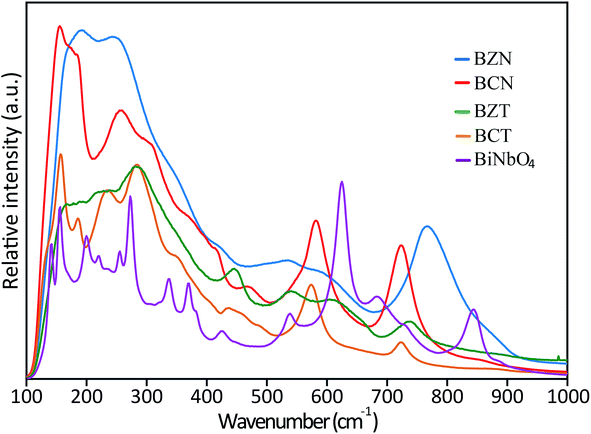 | ||
| Fig. 4 Raman spectra of BZN, BCN, BCT and BZT samples. The spectra of orthorhombic BiNbO4 is also shown for comparison. | ||
FTIR spectra (Fig. S1 in ESI†) for all investigated pyrochlore samples and orthorhombic BiNbO4 have also been collected in the range of 100–1000 cm−1 using 4000 sweeps to reduce noise. Consistent with the Raman results, FTIR spectra for the investigated pyrochlores typically has broader peaks than the spectra for the orthorhombic compounds. These results strongly indicate that the investigated pyrochlore compounds have lower symmetry than cubic or orthorhombic, since they would be displaying less degeneracies in their spectra compared to the more symmetric cubic and orthorhombic structures. Further, the similar appearances and comparable positions between the broad pyrochlore spectra also suggest that these compounds are governed by similar peak position and activity rules, that is, they may belong to the same crystal structure and group symmetry.
| Structure | Enthalpy (eV) | |||
|---|---|---|---|---|
| Random | Partially ordered (A-site) | Partially ordered (B-site) | Ordered | |
| BCN | −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605.61 605.61 |
−55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812.94 812.94 |
−57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363.54 363.54 |
−57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570.16 570.16 |
| BCT | −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523.88 523.88 |
−55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729.18 729.18 |
−57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381.29 381.29 |
−57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590.19 590.19 |
| BZN | −56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059.83 059.83 |
−56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278.83 278.83 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209.31 209.31 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427.47 427.47 |
| BZT | −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.85 972.85 |
−56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188.72 188.72 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228.60 228.60 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449.02 449.02 |
Differences in calculated enthalpies are substantial and appear to indicate that ordered or partially (B-site) ordered structures are more stable than random or partially (A-site) ordered structures. Specifically, the enthalpy values −57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570.16 and −57
570.16 and −57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590.19 eV for BCN(o) and BCT(o), respectively, are considerably lower than the values −55
590.19 eV for BCN(o) and BCT(o), respectively, are considerably lower than the values −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605.61 and −55
605.61 and −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523.88 eV for the BCN(r) and BCT(r), respectively. Thus, there are significant differences of 1964.55 and 2066.31 eV for BCN and BCT, respectively, which corresponds to an averaged difference of more than 22 eV per atom (for 88 atoms in the structure).
523.88 eV for the BCN(r) and BCT(r), respectively. Thus, there are significant differences of 1964.55 and 2066.31 eV for BCN and BCT, respectively, which corresponds to an averaged difference of more than 22 eV per atom (for 88 atoms in the structure).
The situation is similarly stable for the partially ordered solid solutions on the B-site, BCN(p.o) and BCT(p.o), while partial order on the A-site results in enthalpies that are comparable to the random enthalpies. The trends are similar for the BZN and BZT structures as shown in Table 4. Energy minimization is a criterion for geometry optimization and is consistent with the lattice constant comparison discussed in the previous section. Therefore, these results indicate that ordered substitutions of Cd cations in the BCN and BCT at specific sites, followed by slight structural modification from cubic symmetry, minimize the energy.
3.2. Optical properties
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 0.75
Cd = 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 and Nb(Ta)
0.25 and Nb(Ta)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 0.75
Cd = 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 for BCN(r) or BCT(r), have produced metallic-like compounds without electronic band gaps. This situation changes when the substitutions of Cd-cations are assumed to occur at specific, preferential sites in the structures with ratios of Bi
0.25 for BCN(r) or BCT(r), have produced metallic-like compounds without electronic band gaps. This situation changes when the substitutions of Cd-cations are assumed to occur at specific, preferential sites in the structures with ratios of Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 3
Cd = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and Nb(Ta)
1 and Nb(Ta)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd = 3
Cd = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
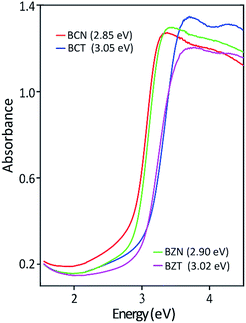
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for BCN(o) or BCT(o). Clear band gaps evolve between the valence bands (VB) and the conduction bands (CB) at the G-point in the Brillouin zones in the electronic band structures of BCN(o) and BCT(o). Calculated band gaps of about 1.73 and 3.06 eV are obtained for the BCN(o) and BCT(o), respectively, using norm-conserving pseudopotentials.
1 for BCN(o) or BCT(o). Clear band gaps evolve between the valence bands (VB) and the conduction bands (CB) at the G-point in the Brillouin zones in the electronic band structures of BCN(o) and BCT(o). Calculated band gaps of about 1.73 and 3.06 eV are obtained for the BCN(o) and BCT(o), respectively, using norm-conserving pseudopotentials.Furthermore, the electronic band structures produce interesting results depending on the site where partial order has been assumed. Similar to random structures, electronic structure calculations assuming A-site partial order do not display any band gaps. In contrast, band gaps comparable to those for completely ordered structures are obtained when the Cd-substitutions are partially ordered at the B-site only. However, the partially ordered structures produce a few localized bands in the electronic structures, which are due to the fractional occupancy of the Bi/Cd-cations in the A-site of BCN(p.o) and BCT(p.o).
The calculated band gap values in this case are 1.65 eV (from the dense VB bands to the localized bands) and 2.02 eV (from the dense VB bands to the dense CB) for the B-site BCN(p.o) and 1.74 eV (from the dense VB to the localized bands) and 3.34 eV (from the dense VB to the dense CB) for the B-site BCT(p.o), respectively. Similar behaviour in the electronic structures for BCN and BCT using all the various degrees of order in the structure has been observed for the BZN and BZT structures, as discussed in our previous reports.28,29
In the investigated structures, Bi in the A-site is in 8-fold coordination, while Nb and Ta (B-site) are in 6-fold coordination.40 Bi has p-orbital character, while Nb, Ta and Cd are transition metals and have d-orbital character. This d-orbital character appears to respond to the surrounding crystal field effects to generate a band gap, when periodicities in the substitutions remain under consideration. Random solid solutions destroy the periodicities of the substitutions, and this seems to be reflected in the absence of a band gap. Therefore, ordered solid solution structures appear to be more reliable with regards to the determination of band gaps in electronic band structure calculations using the full plane wave functions of the CASTEP (MS) than randomly substituted solid solutions with fractionally occupied atomic positions. Further, the closing and opening of the gap between the VB and CB is controlled by the B-site (Nb or Ta) cation order.
Table 5 shows the experimentally measured optical band gaps compared with the theoretically calculated band gaps using various pseudopotentials. It can be seen that computed band gap values vary with the pseudopotential options in the DFT calculations. The optically measured band gap value of 3.05 eV is in excellent agreement with the DFT predicted value of 3.06 eV for the BCT(o) using a norm-conserving pseudopotential. In the case for BCN(o), the theoretical band gaps is 1.73 eV using norm-conserving pseudopotential. The computed band gap of 2.55 eV using ultrasoft pseudopotential is closer to the experimental value of 2.85 eV. This result is probably due to a more adequate Nb ultrasoft pseudopotential, which also predicts a lattice parameter more consistent with the experimental result.
| Structure | Computational data (DFT calculated) | Experimental data | ||||
|---|---|---|---|---|---|---|
| Norm-conserving pseudopotential | Ultrasoft pseudopotential | |||||
| Lattice constant (Å) | Band gap (eV) | Lattice constant (Å) | Band gap (eV) | Lattice constanta (Å) | Band gap (eV) | |
| a TOPAS refined values. | ||||||
| BCN | 10.867 | 1.73 | 10.766 | 2.55 | 10.627 | 2.85 |
| BCT | 10.520 | 3.06 | 10.989 | 2.40 | 10.623 | 3.05 |
| BZN | 10.767 | 1.76 | 10.582 | 2.96 | 10.558 | 2.90 |
| BZT | 10.418 | 3.12 | 10.809 | 2.71 | 10.555 | 3.02 |
3.3. TEM/EDS microstructural characterization
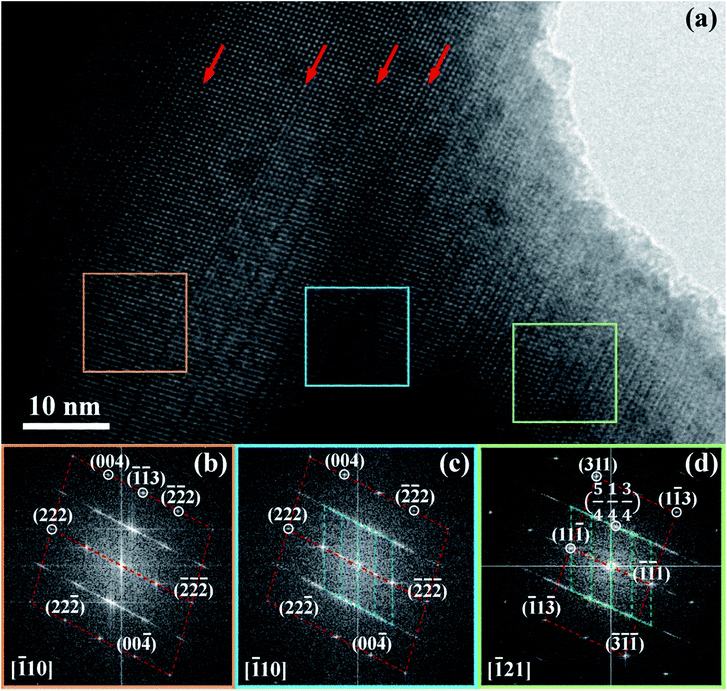
As discussed above, DFT has predicted the largest structural distortion from cubic symmetry will occur in BCN, based on its geometry optimized rhombohedral structure, which has the largest angle. Experimental XRD subsequently has shown that the pattern cannot be matched, let alone refined, to a cubic structure (or to a couple of cubic structures with slightly different lattice parameters). These results identify this material as a prime candidate for further microstructural characterization to confirm the rhombohedral structure and/or to provide evidence of structural distortion.Fig. 6(a) and (b) show bright field TEM micrographs, with low magnification, from representative grains of the BCN powder material supported on a holey carbon film. Most grains display an array of parallel domains or bands with alternating contrast when the crystal orientation is suitably aligned with respect to the incident electron beam. A high resolution TEM micrograph from a similar parallel domain region of another BCN crystal is also shown in Fig. 6(a), where it can be seen that many of the boundary planes between adjacent domains correspond to glide planes (highlighted by arrows). The structure of one domain appears to be shifted by half of the lattice spacing along [110] direction on the boundary plane (as described below), relative to the adjacent domain. Formation of this type of stacking fault is generally a mechanism to reduce strain energy in the crystal. Therefore, the TEM observations confirm that the crystal is distorted from cubic symmetry.
Further analysis of the atomic plane distances and angles at adjacent domains can help determine their crystallographic relationships. Fig. 6(c) shows a high resolution TEM image and the corresponding diffraction pattern obtained from the image. The lack of boundaries between domains suggests that this particular crystal is aligned approximately parallel to the interface planes, like those shown in Fig. 6(a, b) and 7(a). Careful measurement of angles in the Fast Fourier Transform (FFT) diffraction pattern indicates that the unit-cell is rhombohedral. In the FFT pattern along the [01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction, the d-spacing of (222) planes is calculated to be approximately 3.044 Å, which is very close to the d-spacing of 3.047 Å for (222) reflection determined from the TOPAS refinement using a rhombohedral structure.
] direction, the d-spacing of (222) planes is calculated to be approximately 3.044 Å, which is very close to the d-spacing of 3.047 Å for (222) reflection determined from the TOPAS refinement using a rhombohedral structure.
Fig. 7 shows diffraction pattern obtained from regions indicated by the respective coloured boxes. Dotted lines have been added as guides to more easily visualize similarities between different regions and superposition of electron diffraction patterns occurring in the centre and right regions. The diffraction pattern on the left is indexed to a rhombohedral structure. The diffraction pattern in the centre has in the background, approximately the same pattern as that in the left region, but is superimposed by a finer, more diffuse pattern. This finer pattern has been determined to correspond to a localized superlattice structure (being shorter in reciprocal space, the spots correspond to larger distances in real space). The superlattice spots referred to the rhombohedral lattice show fractional indexes. This confirms new periodicities in addition to the original rhombohedral lattice do exist within these crystals. The diffraction pattern in the right shows a different orientation for the rhombohedral pattern in the background. However, the superlattice spots are approximately the same as those in the centre diffraction pattern. Reciprocal lattices coincident with the background rhombohedral lattice and the superlattice spots can be identified in the centre and right diffraction patterns.
The [111] or [11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] directions are perpendicular to the (parallel) interfaces. The [
] directions are perpendicular to the (parallel) interfaces. The [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] and [
10] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 21] or [101] and [
21] or [101] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 21] directions are along the interface plane. Notice that one of these directions is the observation axis and the other one can be obtained as a vector product between the observation axis and the perpendicular to the interface planes. A superlattice periodicity with indices
21] directions are along the interface plane. Notice that one of these directions is the observation axis and the other one can be obtained as a vector product between the observation axis and the perpendicular to the interface planes. A superlattice periodicity with indices 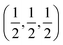 or
or 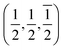 also appears to be present, which corresponds to the double lattice period in the high resolution TEM image in Fig. 6(a). It is interesting to notice that the stacking defects at the interface are along [110] directions, which are relevant to the investigations of local order/disorder in the BZN structure.27 In our previous work, we investigated various choices of substitutional directions. However, the chosen structure in this study is the most representative model.28 The primary directions, where substitution order is assumed, coincide with the major directions contained in the interface plane.
also appears to be present, which corresponds to the double lattice period in the high resolution TEM image in Fig. 6(a). It is interesting to notice that the stacking defects at the interface are along [110] directions, which are relevant to the investigations of local order/disorder in the BZN structure.27 In our previous work, we investigated various choices of substitutional directions. However, the chosen structure in this study is the most representative model.28 The primary directions, where substitution order is assumed, coincide with the major directions contained in the interface plane.
In order to evaluate whether differences in composition are influencing the formation of domains, EDS line scans (graph is not shown) have been carried out approximately across the perpendicular direction to the domain interface planes. The line scan transects several domains in the sample. On average, the composition remains constant within the uncertainty or noise of the measurement. Small precipitates can be observed to form, even under the more moderate exposure during TEM imaging. They increase in number and coarsen significantly with EDS analysis because this method uses a focussed beam. The spikes in Bi concentration become more pronounced as Bi-rich precipitates appear on the track of the EDS line scan.
The TEM results in conjunction with the XRD analyses consistently and unequivocally show that BCN is rhombohedral as predicted by the DFT calculations. The similar positions and broad appearance of the Raman and FTIR spectra seem to suggest that all the family of investigated pyrochlores may belong to the same crystal structure and group symmetry, that is, they are also very likely rhombohedral. These compounds provide an interesting case for further investigation by XRD using synchrotron radiation. Standard XRD has already displayed indications of peak splitting for BCT, therefore, synchrotron radiation may be expected to fully resolve other peaks in this compound. The situation is not as clear cut for the other pyrochlores, which are closer to the cubic structure, however, it is still worthy of investigation, given the potentially far reaching implications for predictions from DFT calculations. DFT may allow for unprecedented checks and balances to conventional peak fitting, refinement approaches, providing a more encompassing picture of the combined geometrical and electronic structures.
4. Conclusions
Theoretical DFT predictions for the existence of electronic band gaps in BCN and BCT, which require ordered substitutions in the B-sites and result in structures slightly modified from cubic symmetry, have been experimentally confirmed using a combination of XRD and TEM characterization. Besides excellent agreement between calculated and experimentally determined electronic band gaps, particularly for BCT, formation enthalpies from DFT calculations strongly favour ordered substitutions and the accompanying modifications from cubic symmetry. DFT calculations also indicate that BCN is the most modified case for this substitutional series. It appears that the level of distortion for BCN exceeds a threshold, where the reduced symmetry from an initially assumed cubic structure, becomes clearly manifested in XRD patterns and in TEM as domain formation, presumed to alleviate increasing build-up of strain. The XRD pattern displays splitting of diffraction peaks and high resolution TEM images and electron diffraction patterns from individual domains are consistent with a rhombohedral structure. Remarkably, TOPAS refinement for BCN using a rhombohedral structure is optimal when the initial parameters are close to those predicted by DFT models.These results are consistent with our previously reported results for BZN28 and BZT29 using identical approaches, which indicate that ordered solid solutions are a better approximation to transition metal substitution in this family of Bi-based multi-component pyrochlores when using the full plane wave models in DFT calculations. For the BCN-case, the large size of the Cd cation has apparently magnified distortion effects on the cubic structure, leading to a well-defined rhombohedral structure. The rhombohedral structure has been confirmed by XRD, high resolution TEM and electron diffraction of synthesized samples, and the presence of local superstructures displaying orientation relationships with the rhombohedral axes. These additional periodicities likely correspond to cation order in the material, since detailed compositional analyses at the scale of the superstructures show constant composition across the interfaces.
Comparison of pseudopotentials appears to indicate that norm-conserving pseudopotentials lead to an excellent match between calculated and experimental lattice parameters and band gaps for BCT and BZT. In contrast, results for BCN and BZN significantly improved when ultrasoft pseudopotentials are used, indicating that currently available norm-conserving pseudopotentials for Nb may not be as adequate as their ultrasoft pseudopotentials counterparts. This work constitutes a significant validation of DFT methods for combined determination of geometric and electronic band structures. In addition, this work provides clarity on XRD refinement procedures particularly with regard to appropriate attribution of fractional occupancy of atomic positions in pyrochlore structures.
Acknowledgements
The authors are thankful for access to research facilities at Queensland University of Technology (QUT). We would also like to thank staff members from The Central Analytical Research Facility (CARF), The Institute for Future Environments (IFE) and The High Performance Computing (HPC) facilities at QUT. Special thanks go to Dr Henry Spratt and Mr Arixin Bo for their technical assistance with TOPAS and Digital Micrograph Software, respectively. Professor Ian Mackinnon is also acknowledged for his valuable comments on the manuscript.References
- D. Huiling and Y. Xi, Ferroelectrics, 2001, 262, 83–88 CrossRef.
- H. Du, X. Yao and H. Wang, Appl. Phys. Lett., 2006, 88, 212901–212903 CrossRef.
- X. Fan, R. Sun and X. Wang, J. Am. Ceram. Soc., 2012, 95(4), 1197–1200 CrossRef CAS.
- A. Qasrawi, B. H. Kmail and A. Mergen, Ceram. Int., 2012, 38, 4181–4187 CrossRef CAS.
- H. Wang, S. Kamba, H. Du, M. Zhang, C. T. Chia, S. Veljko, S. Denisov, F. Kadlec, J. Petzelt and X. Yao, J. Appl. Phys., 2006, 100, 014105–014107 CrossRef.
- M. C. Wu, S. Kamba, V. Bovtun and W. F. Su, J. Am. Ceram. Soc., 2006, 26, 1889–1893 CrossRef CAS.
- K. Sudheendran and K. Raju, Ceram. Int., 2008, 34, 897–900 CrossRef CAS.
- H. Wang and X. Yao, J. Mater. Res., 2001, 16, 83–87 CrossRef.
- Q. Wang, H. Wang and X. Yao, Ceram. Int., 2009, 35, 143–146 CrossRef CAS.
- Z. Zou, J. Ye and H. Arakawa, Mater. Sci. Eng., B, 2001, 79, 83–85 CrossRef.
- L. L. Garza-Tovar, L. M. Torres-Martínez, D. B. Rodríguez, R. Gómez and G. Del Ángel, J. Mol. Catal. A: Chem., 2006, 247, 283–290 CrossRef CAS.
- Y. Li, G. Chen, H. Zhang and Z. Li, Mater. Res. Bull., 2009, 44, 741–746 CrossRef CAS.
- L. Schwertmann, M. Wark and R. Marschall, RSC Adv., 2013, 3, 18908–18915 RSC.
- Q. Liu, M. Xu, Z.-X. Low, W. Zhang, F. Tao, F. Liu and N. Liu, RSC Adv., 2016, 6, 21564–21570 RSC.
- A. Qasrawi and A. Mergen, Ceram. Int., 2012, 38, 581–587 CrossRef CAS.
- L. X. Pang, D. Zhou and H. Wang, Ceram. Int., 2013, 39, S673–S676 CrossRef CAS.
- N. P. Bansal and D. Zhu, Mater. Sci. Eng., A, 2007, 459, 192–195 CrossRef.
- M. Subramanian, G. Aravamudan and G. S. Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef CAS.
- B. C. Chakoumakos, J. Solid State Chem., 1984, 53, 120–129 CrossRef CAS.
- L. M. Daniels, H. Y. Playford, J.-M. Grenèche, A. C. Hannon and R. I. Walton, Inorg. Chem., 2014, 53, 13197–13206 CrossRef CAS PubMed.
- W. Hong, D. Huiling and Y. Xi, Mater. Sci. Eng., B, 2003, 99, 20–24 CrossRef.
- D. Huiling and Y. Xi, J. Mater. Sci.: Mater. Electron., 2004, 15, 613–616 CrossRef.
- H. Wang, R. Elsebrock, T. Schneller, R. Waser and X. Yao, Solid State Commun., 2004, 132, 481–486 CrossRef CAS.
- Y. Liu, R. L. Withers, T. Welberry, H. Wang, H. L. Du and X. Yao, J. Electroceram., 2008, 21, 401–404 CrossRef CAS.
- C. Khaw, C. Lee, Z. Zainal, G. Miles and A. West, J. Am. Ceram. Soc., 2007, 90, 2900–2904 CrossRef CAS.
- X. Wang, H. Wang and X. Yao, J. Am. Ceram. Soc., 1997, 80, 2745–2748 CrossRef CAS.
- R. Withers, T. Welberry, A. K. Larsson, Y. Liu, L. Norén, H. Rundlöf and F. Brink, J. Solid State Chem., 2004, 177, 231–244 CrossRef CAS.
- G. Perenlei, J. A. Alarco, P. C. Talbot and W. N. Martens, Int. J. Photoenergy, 2015, 2015, 575376 Search PubMed.
- G. Perenlei, J. A. Alarco, P. C. Talbot and W. N. Martens, Int. J. Photoenergy, 2015, 2015, 349030 Search PubMed.
- S. Zanetti, S. Da Silva and G. Thim, J. Solid State Chem., 2004, 177, 4546–4551 CrossRef CAS.
- S. M. Zanetti, M. G. S. Pereira and M. C. A. Nono, J. Eur. Ceram. Soc., 2007, 27, 3647–3650 CrossRef CAS.
- J. Sun, G. Chen, J. Pei, R. Jin and Y. Li, Int. J. Hydrogen Energy, 2012, 37, 12960–12966 CrossRef CAS.
- H. Du and X. Yao, J. Mater. Sci., 2007, 42, 979–982 CrossRef CAS.
- B. B. Hinojosa, Atomic structure effects on bulk and surface properties of mixed metal oxides from first principles simulations, University of Florida, 2010 Search PubMed.
- J. B. Thomson, A. R. Armstrong and P. G. Bruce, J. Solid State Chem., 1999, 148, 56–62 CrossRef CAS.
- R. Roth and J. Waring, Am. Mineral., 1963, 48, 1348 CAS.
- B. Aurivillius, Arkiv for Kemi, 1951, 3, 153–161 CAS.
- H.-F. Zhai, X. Qian, J.-Z. Kong, A.-D. Li, Y.-P. Gong, H. Li and D. Wu, J. Alloys Compd., 2011, 509, 10230–10233 CrossRef CAS.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371 CrossRef CAS.
- L. Cai, A. L. Arias and J. C. Nino, J. Mater. Chem., 2011, 21, 3611–3618 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27633d |
| This journal is © The Royal Society of Chemistry 2017 |