Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The molecular mechanism of hPPARα activation†
Bowen Tang,
Boqun Li,
Yuqin Qian,
Mingtao Ao,
Kaiqiang Guo,
Meijuan Fang * and
Zhen Wu*
* and
Zhen Wu*
Fujian Provincial Key Laboratory of Innovative Drug Target Research, School of Pharmaceutical Sciences, Xiamen University, South Xiang-An Road, Xiamen, 361102, China. E-mail: fangmj@xmu.edu.cn; wuzhen@xmu.edu.cn; Fax: +86-592-2189868; Tel: +86-592-2189868
First published on 20th March 2017
Abstract
Human peroxisome proliferator-activated receptor alpha (hPPARα) is a ligand-dependent transcription factor that mainly controls lipid metabolism in the liver. It has drawn wide attention as a significant target for developing new hypoglycaemic drugs. However, a central and largely unresolved question in finding new drugs targeted on hPPARα concerns ligand action mechanism: what makes certain molecules act as antagonists while others behave as agonists in the same binding site? To understand this, we performed a total of 600 ns all-atom molecular dynamics (MD) simulations to explore how four small molecule ligands bind to the hPPARα and play opposite effects. We characterized and compared the protein backbone fluctuation, and investigated the interaction networks and the movements of helixes and loops near binding site during MD simulations. Moreover, by free energy calculation and phylogenetic tree analysis, 11 key residues favouring binding ligands and some other residues playing important roles in inducing the active conformation changing of hPPARα were discovered. The results could help to understand the activation/deactivation of hPPARα by agonists or antagonists, and provide insightful prospective into hPPARα targeted structure-based drug designs.
Introduction
Peroxisome proliferator activated receptors (PPARs) are nuclear receptors that function as transcription factors mediating gene expression.1–6 There are three distinct PPAR subtypes, termed as PPARα, PPARβ/δ and PPARγ. Among these receptors, hPPARα has been the most broadly researched, because it plays important roles in regulating glucose, cholesterol and lipids metabolism as well as in the fatty acid β-oxidation and homeostasis.7 These make hPPARα as an important pharmacological target for the discovery of novel therapeutic agents used for treatment of dyslipidemia and type 2 diabetes mellitus (T2DM).8,9 The increasing data collected by several experimental techniques, including fluorescence anisotropy, NMR and X-ray crystal, together with related computer simulations of PPARs have resolved many key features of structures in the activation approach of PPARs, including molecular switch, ligand-binding specificity and interactions with regualtors.7,10–13 Despite this progress, lots of important mechanistic principles of hPPARα mediating signal transduction are still poorly understood at the molecular level. For example, how can drugs that bind to the same regions of the hPPARα exert opposite responses? Molecular dynamics (MD) simulation could be an important tool to help to solve this issue.14As most available crystal structures concerned about the ligand binding domain (LBD) of hPPARα, we termed hPPARα standing for hPPARα LBD for clear in our study. hPPARα has many agonists and different types of agonists always introduce different effects as Davide Capelli's team reported.15 In this work, we focused on these agonists that bind into the classic ligand binding pocket (LBP) of hPPARα and directly interact with Helix-12. To address mechanistic and structural questions about hPPARα, four complexes as shown in Fig. S1 (see ESI†), hPPARα-YIN, hPPARα-13M and hPPARα-NKS for agonist-bound conformation (PDB: 4CI4, 3VI8 and 3KDU) and hPPARα-471 for antagonist-bound conformation (PDB: 1KKQ) in which 471 is the only one for antagonizing hPPARα in PDB database, were subjected to perform all-atom MD simulations with three parallel runs. Then, the fluctuation of protein backbone, the residue community networks as well as the movements of helices and loops during these MD simulations were characterized respectively. As a result, we discovered that the interaction change of H2′–H3 loop and H11–H12 loop directly induced H12 conformation change during MD simulations. In addition, by energy calculation, 11 hotspots for the four different ligands binding hPPARα complexes and some other key residues causing for hPPARα's activation conformation change were identified. These results could help understand the mechanism of hPPARα activation and design new drugs targeted on hPPARα.
Methods
Preparation for MD
The antagonist-bound structure of hPPARα LBD was solved in complex with 471 (PDB: 1KKQ) at 3.0 Å resolution,16 in which the co-suppressor peptide was removed, and three agonist-bound systems were determined in complexes with agonist Y1N (PDB: 4CI4) at 2.3 Å,7 agonist 13M (PDB: 3vi8) at 1.75 Å and agonist NKS (PDB: 3KDU) at 2.07 Å. The sequence of hPPARα LBD was used from 204 to 467 in these four systems. The missing loops and other missing residues were repaired by using Prime module of Schrodinger suite software.17,18 Crystal water molecules beyond 4 Å of complex were deleted. Hydrogen atoms were added by tleap integrated in AmberTools15.19 All calculation are finished in the house computer workstation based on CPU calculation of Wu's Lab.MD process
MD simulations of the four hPPARα complexes were carried out using Amber14 suit.19 Each complex will be simulated three times at different initial speeds (each 50 ns). A total of 600 ns simulation will be run in our research. The FF14SB force field parameter set was chosen for receptor hPPARα. The electrostatic potential of four ligands was calculated at the B3LYP/6-311G* level using Gaussian 09 D software.20 Then, we used the antechamber package21 to get RESP charge22 values. The molecular force field parameters for agonist and antagonist were using with the general amber force field (GAFF).23 All agonist bound systems were neutralized by adding 3 Na+ ions and antagonist bound system was neutralized by adding 2 Na+ ions, then solvated in a truncated octahedron box with TIP3P water molecules. The distance between any atom in hPPARα-ligand and the edge of the periodic box was set no less than 8 Å. The long-range electrostatic interactions were computed with a non-bonded cut-off of 8 Å by using Particle Mesh Ewald (PME) method,24 and the SHAKE algorithm25 was applied to constrain covalent bonds connecting hydrogen. Energy minimization process used the steepest descent and conjugated gradient methods.26 Systems gradually heated to 300 K during 200 ps using the Langevin thermostat method with the collision frequency 2 ps−1, and followed by 50 ps of density equilibration. Restraints force constant of 2 kcal (mol Å2)−1 were only performed on atoms of receptor–ligand complex in the above flow. Last, all systems were equilibrated with unconstrained MD simulations for total 50 ns in an isothermal-isobaric (NPT) ensemble. The time step was 2.0 fs. The trajectory coordinates and information were kept every 2 ps for results analysis in MD production state.Dynamics correlation network construction and community analysis
Correlated atom positional fluctuations of residues were characterized with Bio3D packages of R as reported elsewhere.27–30 The nodes, which were mapped to different colors and scaled variable sizes by the containing number of residues, represented residual groups in network. Edges, which were weighted and colored by constituent atomic correlation values, connect these clusters. Node centrality, suboptimal paths calculation and community analysis were applied to each network to characterize properties of network and identify residues involved in the dynamic coupling of different sites by using Bio3D packages.Principal components analysis (PCA)
To extract the principal model related to the conformational motions, the collective motions of all systems were investigated by PCA.31 Translational and rotational motions were removed before the covariance matrix calculation with least-squares superposition to the averaged-structure. The covariance matrix of all Cα atoms' coordinates was calculated with the next equation:32| Cij = 〈(ri − 〈rj〉)(rj − 〈ri〉)〉 | (1) |
Binding free energy calculation
The Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) method33 was carried out to calculate free energy of binding for macromolecules by combining molecular mechanics calculations and continuum solvation models. Here was applied to compute the binding free energies of ligands. The free energy of binding ΔGbind was calculated as:| ΔEMM = ΔEinternal + ΔEvdw + ΔEele | (2) |
| ΔGbind = ΔH − TΔS = ΔEMM + ΔGsol − TΔS | (3) |
| ΔGsol = ΔGnonpol + ΔGpol | (4) |
In which ΔEMM, ΔGsol and −TΔS were equivalent to the changes of the gas phase MM energy, the solvation free energy and the conformational entropy on binding. ΔEMM was standard molecular mechanics term including ΔEinternal (bond, angel and dihedral energies) which would be cancelled as we used a single trajectory approach to reduce the noise,33 van der Waals interaction ΔEvdw and electrostatic ΔEele energies. The nonpolar solvation free energy ΔGnonpol was calculated from the area (SASA) using the method of linear combination of pairwise overlaps (LCPO) (ΔGnonpol = 0.0072 × ΔSASA).34 The SASA here was determined with probe radii of 1.4 Å. The electrostatic free energy of solvation ΔGpol was calculated by the generalized Born method (igb = 5) developed by Onufriev et al.35 −TΔS was the conformational entropy change calculated by normal mode analysis on a set of conformational snapshots taken from MD simulation.36
The ΔEMM and ΔGsol calculations were performed using 4000 snapshots striped from the final 40 ns simulation with an interval of 10 ps. The conformational entropy change upon ligand binding (−TΔS) was evaluated with the normal-mode analysis using the nmode program in AmberTools15 package. However, because the entropy calculations for larger systems being extremely computationally expensive, merely 200 snapshots were chosen with an interval of 100 ps during equilibrium state of simulation to calculate −TΔS. All these snapshots were minimized with 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps by using a distance-dependent dielectric constant (dielc = 1.0) and a root-mean-square gradient (drms = 1.0 × 10−4 kcal mol−1 Å−1).
000 steps by using a distance-dependent dielectric constant (dielc = 1.0) and a root-mean-square gradient (drms = 1.0 × 10−4 kcal mol−1 Å−1).
Free energy decomposition to ligand–residue interaction
To quantitatively evaluate the contribution to the two ligands' binding, the total, electrostatic, van der Waals interaction and solvation energies between residues of hPPARα and ligands (Agonists: Y1N, 13M and NKS. Antagonist: 471) were computed based on the Amber force field equation. Each energy component was estimated by using the snapshots from above calculation of ΔEMM and ΔGsol.Phylogenetic tree analysis
Energy contributions of 264 residues to four ligands rendered a 2 dimensional vector. The phylogenetic tree of residues contributing to Y1N, 13M, NKS and 471 in hPPAR-'s LBD was produced with the statistical analysis package R-3.3.1.37 The Manhattan distance38 was selected to calculate similarities among vectors:
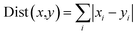 | (5) |
Results and discussion
Simulation convergence
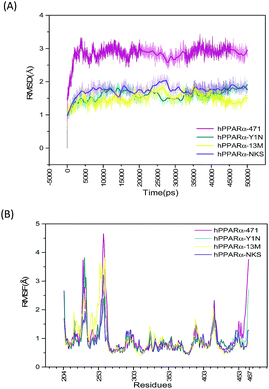
Starting with the agonist-bound (PDB: 4CI4, 3KDU and 3VI8) and the antagonist-bound (PDB: 1KKQ) structures of hPPARα with ligands kept, sufficiently long simulations should generate converged ensembles. The root mean square deviation (RMSD) of protein backbone atoms (O, C, Cα, N) were calculated referring to the repaired structures (Fig. S2, green color structures, see ESI†) in preparation of MD and plotted in Fig. 1(A). The RMSD plot of the backbone atoms for antagonist-bound hPPARa complex (hPPARα-471) displayed a significant degree of structural variation comparing to agonist-bound hPPARα complexes (hPPARα-Y1N, hPPARα-13M and hPPARα-NKS). As illustrated in Fig. 1(A), the RMSD values for hPPARα-Y1N, hPPARα-13M and hPPARα-NKS complexes fluctuate around 1.6, 1.7 and 1.5 Å in the period of 10–50 ns respectively, while the values for hPPARα-471 complex stabilize at about 2.7 Å comparing initial structure after 10 ns. Moreover, we aligned the conformation every 5 ns and the original crystal structure for these four systems as showed in Fig. S2 (see ESI†). As the original co-suppressor removed in hPPARα-471 for better comparing with the agonist-bound hPPARα complexes (hPPARα-Y1N, hPPARα-13M and hPPARα-NKS), H12 changed its conformation to parallel with H3 after the first 2 ns (the video part) and kept this conformation in the rest time. All these data indicated that these four systems had been reached equilibrium state after first 10 ns.The root mean square fluctuation (RMSF), which is another useful method to study the stability of systems, reflects the mobility of certain amino acid residues around their average positions. Fig. 1(B) illustrates the difference of residue flexibility among the four systems. The peaks in the RMSF plot stand for magnitudes of residue flexibility. Residues 256–266 are obviously more flexible in antagonist 471 bounded system in which the RMSF value is above 4 Å than in three agonists bounded systems. These residues constructed a loop connecting H2′ and H3 which are directly involving in building the classic LBP of hPPARα.41 The flexibility change of this loop may relate to hPPARα's ligand recognition and stabilization as Amanda Bernardes' group reported in which they named the loop of residues 256–266 as a part of Ω-loop.41
Residues communication network analysis
To aid in further interpretation and quantification of residues' motions coupling in agonists (Y1N, 13M, NKS) and antagonist 471 bounded system, we constructed residues communication network using the data from the last 40 ns of the production runs as showed in Fig. 2. In the four correlation network plots as displayed in Fig. 2(A)–(D) top parts, each node represents a cluster of residues in close interaction, while the color and the thickness of each connecting edge is weighted and colored by the correlation value between the two clusters. This method has been used successfully to discover motional couplings of residues in many systems.27,42,43 In agonist-bound hPPARα systems (Fig. 2(A)–(C)), there were more nodes than in the antagonist-bound system: 10 nodes were found in hPPARα-Y1N, and 9 nodes were found in both hPPARα-13M and hPPARα-NKS, while only 7 nodes were observed in hPPARα-471. Nodes size and ID number were listed in Table S1 (see ESI†).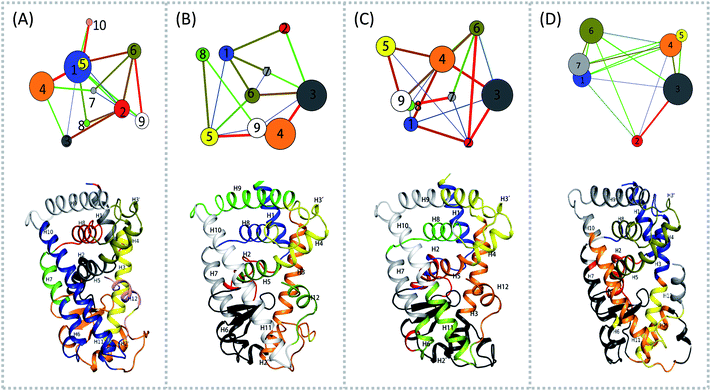 | ||
| Fig. 2 Residues community networks (top) for four hPPARα-ligand complexes and 3D structures with mapping same color and Helix label in hPPARα (bottom). The order of color, blue-green-red related to the change of lines' width from thin to thick. The helixes labeled based on this work.13 (A) hPPARα-YIN, (B) hPPARα-13M, (C) hPPARα-NKS and (D) hPPARα-471. | ||
There were fewer larger nodes in agonist systems than in antagonist system because several smaller nodes had merged after antagonist binding. This finding indicated that there were more discrete local interactions in the active state of the receptor. Specifically, the position of H11–H12 loop (residues 450–456) in the surface region varied with the state of the receptor, leading to a different interaction network. Among antagonist-bound systems, the loop shared the same community network with the head part of H3 which interacting with this loop both colored in yellow as showed in Fig. 2(D) bottom, this interaction related to that inducing H12 to move away from H11 and pack against H3 as an inactive conformation, as H11–H12 loop connected the H12. These findings were in agreement with the experiment result.16 Moreover, the coupling between the head part of H3 and H11–H12 loop disrupted the interaction between H2′–H3 loop (residues 255–256) and H11–H12 loop in 471 bounded system, which was identified by less residues contact (Table S2, see ESI†) and further mass center distance (Fig. S7, see ESI†) between H2′–H3 loop and H11–H12 loop comparing in the three agonists bound systems. As a result, the increasing fluctuation of residues 256–266 was detected in above RMSF of 471 bounded system.
Detecting significant conformational differences from principal component analysis (PCA)
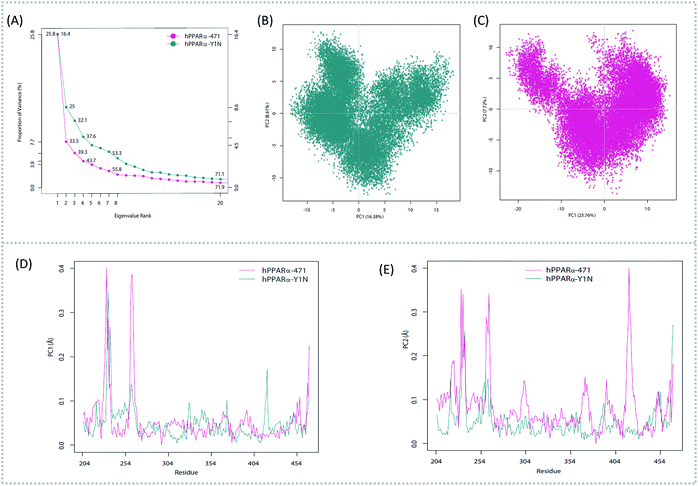
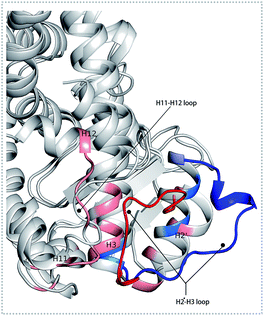
To better understand the complicated conformational motions which may be relevant to the mechanism of hPPARα's activation in the three agonists bounded hPPARα systems and deactivation in hPPARα-471 system, principal component analysis was implemented. For clearly, we firstly comparing the hPPARα-471 and hPPARα-Y1N systems. Fig. 3(A) shows the eigenvalues at the very beginning are relative to larger concerted motions, but decrease quickly and reach more localized fluctuations. These results suggest that the top 20 principal components (PC) could capture 71.9% and 71.1% of total variance during the last 40 ns of the trajectories in 471 and Y1N bounded systems, respectively. Similarly, top 20 PCs could capture 75.4% and 73.3% of total variance in 13M and NKS bounded systems as showed in (see ESI†).The conformational behavior of the two systems, which was projected along the direction of PC1 and PC2, showed difference as plotted in Fig. 3(B) and (C). In order to find the way in which agonist Y1N or antagonist 471 affected the motions described by this two PCs, we calculated the displacements of PC1 and PC2 of the two complexes. The motions of residues 256–266 (located in the loop behind H2′) in antagonist 471 bounded system were obviously higher than Y1N bounded system as described in both Fig. 3(D) and (E). Similarly, both agonists 13M and NKS bounded systems also presented lower values comparing hPPARα-471 from PC1 and PC2 in the peak of residues 256–266 as displayed in Fig. S3(D) and (E) (see ESI†). These results were consistent with the RMSF results and suggested that the H2′–H3 loop was more stable in agonists bounded systems. Detailly, residues 256–266 could interacted with H3 and H11–H12 loop (residues 450–456) by a closed loop form in hPPARα-Y1N (Fig. 4, red loop). We also found the similar phenomenon to hPPARα-13M and hPPARα-NKS as displayed in Fig. S4 (see ESI†). While, H2′–H3 loop (residues 256–266) adopted open form (Fig. 4, blue loop) only interacting with H2′ and small part of H3 head in hPPARα-471 system. As the interaction decreased, which was also identified by the loop contact information in Tables S2 and S3 (see ESI†), the fluctuation of this loop (residues 256–266) increased significantly (Fig. S3(D) and (E)†). On the other hand, the region about residues 414–424 showed different behaviors along PC1 and PC2. It reversed in Fig. 3(D) and (E), while it almost had no peak in hPPARα-NKS (Fig. S3(D) and (E)†). However, the global effect of this region was similar as identified in above RMSF when all results of PCs accumulated.
Analysis of the binding energy
In order to explore the effects caused by the agonist or antagonist on the interaction between hPPARα and ligands, we calculated the individual energy components and the binding free energies by Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) calculation. The predicted binding free energy for hPPARα with agonist Y1N, 13M, NKS and antagonist 471 were −26.86, −37.64, −44.32 and −36.50 kcal mol−1. As shown in Table 1, ΔEvdw, ΔEele and ΔGnonpol mainly contributed to the binding of ligands with hPPARα, while the polar solvent energy (ΔEpol) hampered the binding.| Energy | 4CI4-Y1N | 1KKQ-471 | 3VI8-13M | 3KDU-NKS |
|---|---|---|---|---|
| a ΔEele the electrostatic interaction energies between hPPARα and ligand. ΔEvdw the vander Waals interaction energies between hPPARα and ligand. ΔEpol the polar solvation free energy between hPPARα and ligand. ΔEnonpol the nonpolar solvation free energy between hPPARα and ligand. −TΔS the enthalpic contribution to binding in temperature 300 K. ΔGbind the binding energy between hPPARα and ligand. | ||||
| ΔEvdw | −60.76 ± 2.53 | −72.83 ± 2.42 | −66.48 ± 3.32 | −70.43 ± 3.11 |
| ΔEele | −6.98 ± 1.43 | −11.16 ± 3.12 | −16.36 ± 5.30 | −13.84 ± 6.97 |
| ΔGnonpol | −8.34 ± 0.19 | −9.98 ± 0.25 | −9.01 ± 0.17 | −9.56 ± 0.20 |
| ΔGpol | 22.18 ± 1.60 | 31.70 ± 2.29 | 15.04 ± 7.40 | 25.48 ± 6.42 |
| −TΔS | 27.04 ± 2.45 | 24.64 ± 4.85 | 32.26 ± 4.01 | 31.85 ± 3.92 |
| ΔGbind | −26.86 ± 3.10 | −37.64 ± 2.43 | −44.32 ± 3.74 | −36.50 ± 4.39 |
Phylogenetic tree analysis based on energy decomposition
To overall characterize the residues contribution to the interaction between receptor and ligands, a phylogenetic tree, in which ward algorithm was chosen in hierarchical clustering procedure, was used to identify hot spots from 264 residues based on per-residue MM/GBSA free energy decomposition. In Fig. 5, four groups of residues were found. Residues favoring ligands binding were colored in red. The residue with the highest contribution (−4.764 kcal mol−1) was colored as deep red. The color of the lower contribution was set to fade gradually towards white (almost no contribution). While, the residues obstructing ligand binding were displayed in blue. The highest one was colored as deep blue (0.722 kcal mol−1) and the color of the lower was set to fade gradually towards white. Notably, the residue with the most favoring ligand binding energy is much bigger than the most obstructing the binding.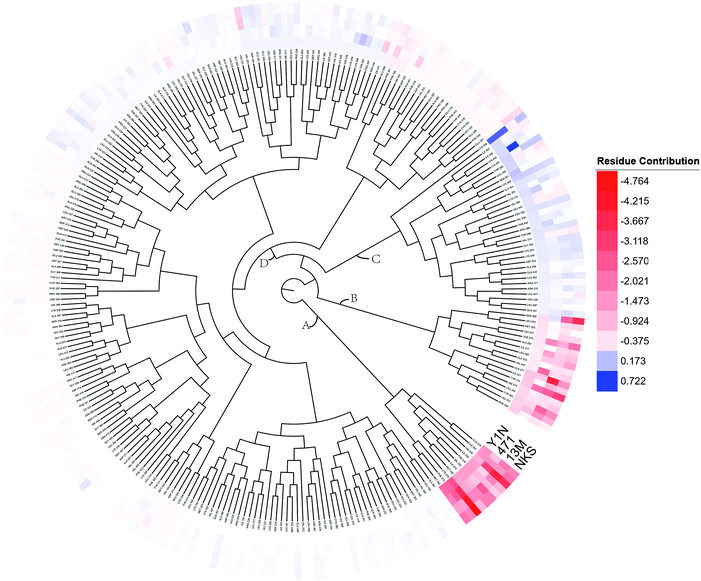 | ||
| Fig. 5 A phylogenetic tree of energy contribution for residues 204–467 in hPPARα ligand binding domain. | ||
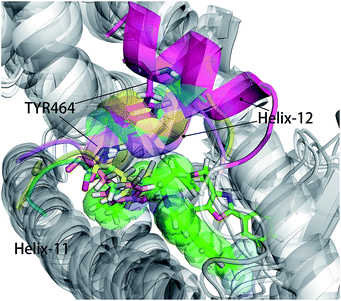
As shown in Fig. 5, energy contribution of group A (MET355, PHE273, CYS276, MET330, ILE272, VAL332, PHE318, ILE339, HIE440, ILE354, CYS275) were consistently higher for four ligands than that group B, C and D, suggesting group A playing a crucial role to bound ligands. Actually, the residues of group A directly construct the ligand pocket7,16 as displayed in Fig. S1 (see ESI†), and the sum of group A's energy contributions accounted for the major part of the total energy (65.52% for Y1N, 54.05% for 471, 51.80% for 13M and 50.80% for NKS). Except HIE440, the rest 10 residues were all hydrophobic amino acids. Those 11 residues revealed a similar pattern in ligand binding which ligands must have a suitable hydrophobic group to fit, and were identified as hot spots for hPPARα's binding. Moreover, the residue CYS276 of H3 showed deepest red (−2.70, −3.41, −4.15 and −4.76 kcal mol−1 for binding Y1N, 471, 13M and NKS respectively) in four systems, indicating that it playing an important role and favoring binding interaction for both agonists (Y1N, 13M, NKS) and antagonist (471). But the interaction modes of these four ligands with CYS276 were different, in which Y1N and 13M adopting L-shaped configuration contacted with this residue, while NKS and 471 wrapped CYS276 liking U-shaped as displayed in Fig. S5 (see ESI†). Based on this information, CYS276 may be a hot site for developing new covalent drugs, as its side chain orientation, close distance to ligand (Fig. S6, see ESI†) and nucleophilic property.44,45 In spite of weak contributions or weak against to binding interaction in cluster C and D, some residues display almost opposite characteristics which were also essential for conformation change with ligand binding. For example, the side chain of residue SER280 (−0.42, −0.66 and −0.46 kcal mol−1 for Y1N, 13M and NKS respectively, as displayed in Fig. S8–S10, see ESI†) formed a hydrogen bond with carboxyl of each agonist in these three agonist-bounded hPPARα systems (Fig. S11(A), S11(C) and S11(D), see ESI†), while it (about 0.08 kcal mol−1) contacted with the hydrophobic fragment of benzene in antagonist 471 (Fig. S11(B), see ESI†). Similarly, VAL437 and ILE447 in antagonist system (−0.37 kcal mol−1 and −0.62 kcal mol−1, as displayed in Fig. S8, see ESI†) favored binding the hydrophobic fragment of 471, which was plotting with sphere in Fig. S11(B) (see ESI†), comparing in these three agonist-bounded hPPARα systems hPPARα-Y1N, hPPARα-13M and hPPARα-NKS (VAL437: 0.015, 0.049 and 0.035 kcal mol−1; ILE447: 0.025, 0.072 and 0.185 kcal mol−1 in Fig. S8–S10, see ESI†). As this hydrophobic interaction existed, H12, where the side chain position of residue TYR464 was occupied by the hydrophobic fragment of 471 plotted in sphere (Fig. 6), were pushed away from H11 to pack against H3. These calculations were consistent with H. Eric Xu's group experiment results.16 Together, these 11 hotspots are essential for the agonists Y1N, 13M and 471, or antagonist 471 binding in the pocket of hPPARα, but these residues with reverse affinity may directly decide the conformation of hPPARα to agonist or antagonist.
Conclusions
MD simulations enable us to visualize the molecular motion with time evolution. In this study, multiple computational methods were integrated to explore the molecular activation mechanism of hPPARα. We found that both antagonist 471 and three agonists (Y1N, 13M and NKS) are favoring with the same 11 residues analyzed in a phylogenetic tree. These 11 hotspots made ligand binding stable, while the binding interaction induced other residues conformation change to fit the ligand. These residues, like SER280, VAL437, ILE447 and TYR464, had a lower contribution for binding ligand comparing 11 hotspots, but were directly involved in inducing receptor conformation change during ligand binding. In the inactive conformation of hPPARα, ILE437 and ILE447 interacted with 471's larger head group, which occupied the space of TYR464 and pushed the H12 packing against H3. As conformation change of H12 decreased the contact between H11–H12 loop and H2′–H3 loop, H11–H12 loop changed motion to coupling with the head part of H3 identified in the residue communication network. Residues 256–266 of H2′–H3 loop were detected more variable in both RMSF and PCA analysis comparing in active stage of the receptor. Finally, based on these series of changes, hPPARα presented active or inactive conformation to fit these three agonists (Y1N, 13M and NKS) or antagonist 471. All these findings provide new insights into the molecular changes and fundamental mechanism of receptor activation. Such insights are help for understanding the activation of hPPARα in the atom level and are valuable guidance for hPPARα targeted drug design.Author contributions
Bowen Tang carried out experiments, analyzed experimental results and drafted the manuscript. Boqun Li, Yuqin Qian, Mingtao Ao and Kaiqiang Guo proposed the protein (hPPARα), prepared the manuscript and revised the literature sources. Zhen Wu and Meijuan Fang supervised whole research project, revised manuscript and did manuscript final version approval. All authors read and approved the manuscript.Acknowledgements
This research was conducted by using the computational resources of the School of Pharmaceutical Sciences and the College of Chemistry and Chemical Engineering, Xiamen University. The work was supported by the National Natural Science Foundation of China (No. 81273400 and No. 81302652). This research was also financially supported by Fujian Science and Technology project (Grant No. 2014N5012).References
- K. Schoonjans, B. Staels and J. Auwerx, J. Lipid Res., 1996, 37, 907 CAS.
- G. Chinetti, J.-C. Fruchart and B. Staels, Inflammation Res., 2000, 49, 497 CrossRef CAS PubMed.
- O. Braissant, F. Foufelle, C. Scotto, M. Dauça and W. Wahli, Endocrinology, 1996, 137, 354 CAS.
- P. Delerive, K. De Bosscher, S. Besnard, W. V. Berghe, J. M. Peters, F. J. Gonzalez, J.-C. Fruchart, A. Tedgui, G. Haegeman and B. Staels, J. Biol. Chem., 1999, 274, 32048 CrossRef CAS PubMed.
- G. V. Dhoke, R. P. Gangwal and A. T. Sangamwar, J. Mol. Struct., 2012, 1028, 22 CrossRef CAS.
- L. Michalik, J. Auwerx, J. P. Berger, V. K. Chatterjee, C. K. Glass, F. J. Gonzalez, P. A. Grimaldi, T. Kadowaki, M. A. Lazar and S. O'Rahilly, Pharmacol. Rev., 2006, 58, 726 CrossRef CAS PubMed.
- J. C. dos Santos, A. Bernardes, L. Giampietro, A. Ammazzalorso, B. De Filippis, R. Amoroso and I. Polikarpov, J. Struct. Biol., 2015, 191, 332 CrossRef PubMed.
- J. J. Acton III, T. E. Akiyama, C. H. Chang, L. Colwell, S. Debenham, T. Doebber, M. Einstein, K. Liu, M. E. McCann and D. E. Moller, J. Med. Chem., 2009, 52, 3846 CrossRef PubMed.
- X. Chen, J. Matthews, L. Zhou, P. Pelton, Y. Liang, J. Xu, M. Yang, E. Cryan, P. Rybczynski and K. Demarest, Metabolism, 2008, 57, 1516 CrossRef CAS PubMed.
- P. Cronet, J. F. Petersen, R. Folmer, N. Blomberg, K. Sjöblom, U. Karlsson, E.-L. Lindstedt and K. Bamberg, Structure, 2001, 9, 699 CrossRef CAS PubMed.
- B. A. Johnson, E. M. Wilson, Y. Li, D. E. Moller, R. G. Smith and G. Zhou, J. Mol. Biol., 2000, 298, 187 CrossRef CAS PubMed.
- B. C. Kallenberger, J. D. Love, V. K. K. Chatterjee and J. W. Schwabe, Nat. Struct. Mol. Biol., 2003, 10, 136 CAS.
- V. Zoete, A. Grosdidier and O. Michielin, Biochim. Biophys. Acta, Mol. Cell Biol. Lipids, 2007, 1771, 915 CrossRef CAS PubMed.
- M. Karplus and J. A. McCammon, Nat. Struct. Mol. Biol., 2002, 9, 646 CAS.
- D. Capelli, C. Cerchia, R. Montanari, F. Loiodice, P. Tortorella, A. Laghezza, L. Cervoni, G. Pochetti and A. Lavecchia, Sci. Rep., 2016, 6, 34792 CrossRef CAS PubMed.
- H. E. Xu, T. B. Stanley, V. G. Montana, M. H. Lambert, B. G. Shearer, J. E. Cobb, D. D. McKee, C. M. Galardi, K. D. Plunket and R. T. Nolte, Nature, 2002, 415, 813 CrossRef CAS PubMed.
- M. P. Jacobson, R. A. Friesner, Z. Xiang and B. Honig, J. Mol. Biol., 2002, 320, 597 CrossRef CAS PubMed.
- M. P. Jacobson, D. L. Pincus, C. S. Rapp, T. J. Day, B. Honig, D. E. Shaw and R. A. Friesner, Proteins: Struct., Funct., Bioinf., 2004, 55, 351 CrossRef CAS PubMed.
- D. Case, J. Berryman, R. Betz, D. Cerutti, T. Cheatham III, T. Darden, R. Duke, T. Giese, H. Gohlke and A. Goetz, AMBER 2015, University of California, San Francisco, 2015 Search PubMed.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Inc., Wallingford, CT, 2009 Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 2001, 222, U403 Search PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952 CrossRef CAS.
- R. Fletcher and M. J. Powell, Comput. J., 1963, 6, 163 CrossRef.
- L. Skjærven, X.-Q. Yao, G. Scarabelli and B. J. Grant, BMC Bioinf., 2014, 15, 399 CrossRef PubMed.
- G. Scarabelli and B. J. Grant, Biophys. J., 2014, 107, 2204 CrossRef CAS PubMed.
- B. J. Grant, A. P. Rodrigues, K. M. ElSawy, J. A. McCammon and L. S. Caves, Bioinformatics, 2006, 22, 2695 CrossRef CAS PubMed.
- L. Skjærven, S. Jariwala, X.-Q. Yao, J. Idé and B. J. Grant, Biophys. J., 2016, 110, 379a CrossRef.
- M. A. Balsera, W. Wriggers, Y. Oono and K. Schulten, J. Phys. Chem., 1996, 100, 2567 CrossRef CAS.
- P. Chandrasekaran and R. Rajasekaran, Mol. BioSyst., 2016, 12, 850 RSC.
- T. Hou, J. Wang, Y. Li and W. Wang, J. Comput. Chem., 2011, 32, 866 CrossRef CAS PubMed.
- J. Weiser, P. S. Shenkin and W. C. Still, J. Comput. Chem., 1999, 20, 217 CrossRef CAS.
- A. Onufriev, D. Bashford and D. A. Case, Proteins: Struct., Funct., Bioinf., 2004, 55, 383 CrossRef CAS PubMed.
- F. Tama and Y.-H. Sanejouand, Protein Eng., 2001, 14, 1–6 CrossRef CAS PubMed.
- S. Tippmann, Nature, 2015, 517, 109 CrossRef CAS PubMed.
- (a) P. E. Black, Dictionary of Algorithms and Data Structures, 2006, vol. 18, p. 2012 Search PubMed; (b) G. Zheng, W. Xue, P. Wang, F. Yang, B. Li, X. Li, Y. Li, X. Yao and F. Zhu, Sci. Rep., 2016, 6, 26883 CrossRef CAS PubMed.
- F. Murtagh and P. Legendre, 2011, arXiv preprint arXiv:1111.6285.
- I. T. O. Life, Bioinformatics, 2007, 23, 127 CrossRef PubMed.
- A. Bernardes, P. C. Souza, J. R. Muniz, C. G. Ricci, S. D. Ayers, N. M. Parekh, A. S. Godoy, D. B. Trivella, P. Reinach and P. Webb, J. Mol. Biol., 2013, 425, 2878 CrossRef CAS PubMed.
- Y. Karami, E. Laine and A. Carbone, BMC Bioinf., 2016, 17, 13 CrossRef PubMed.
- S. Yuan, H. Chan, H. Vogel, S. Filipek, R. C. Stevens and K. Palczewski, Angew. Chem., Int. Ed., 2016, 55, 10331 CrossRef CAS PubMed.
- T. Zhang, N. Kwiatkowski, C. M. Olson, S. E. Dixon-Clarke, B. J. Abraham, A. K. Greifenberg, S. B. Ficarro, J. M. Elkins, Y. Liang and N. M. Hannett, Nat. Chem. Biol., 2016, 12, 876 CrossRef CAS PubMed.
- N. Kwiatkowski, T. Zhang, P. B. Rahl, B. J. Abraham, J. Reddy, S. B. Ficarro, A. Dastur, A. Amzallag, S. Ramaswamy and B. Tesar, Nature, 2014, 511, 616 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27740c |
| This journal is © The Royal Society of Chemistry 2017 |