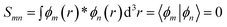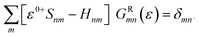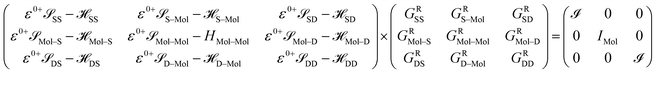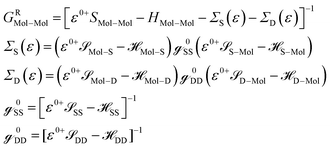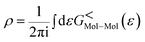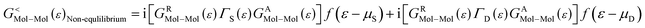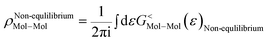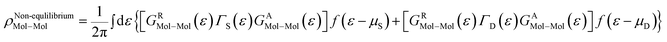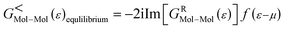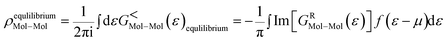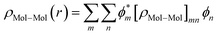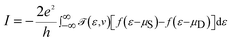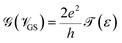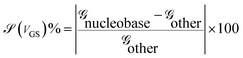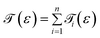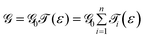Open Access Article
Open Access ArticleQuantum mechanical investigation into the electronic transport properties of a memantine-functionalized gold nanopore biosensor for natural and mutated DNA nucleobase detection
Abhisek Kole and
K. Radhakrishnan *
*
Centre for Micro-/Nano-electronics (NOVITAS), School of Electrical and Electronic Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798. E-mail: eradha@ntu.edu.sg; Fax: +65 67933318
First published on 26th January 2017
Abstract
Quantum mechanical studies of the electronic transport properties of a memantine-functionalized gold nanopore biosensor for natural and mutated DNA nucleobase detection are reported. In this study, a gold electrode was functionalized with a modified diamondoid structure, called memantine, and the tunnelling current arising from nucleobases was investigated as it translated through the functionalized gold nanopore. Non-equilibrium Green's function (NEGF) and density functional theorem (DFT) methods have been used to analyze and calculate the results. The transmission spectrum for each nucleobase is presented. In order to justify that the resonance peaks are originating from the nucleobases, the Projected Densities of States (PDOS) of the nucleobases were plotted and compared with their corresponding transmission spectra. The electronic wave functions relating to transmission and the device sensitivity have also been shown. The proposed device is demonstrated to detect various natural and mutated nucleobases with a sensitivity ranging from 103 to 107. Finally, differential conductance methods have been found to be effective in detecting nucleobases in the case of overlapping transmission peaks.
1. Introduction
Increasing rates of malignant diseases such as cancer and other genetic diseases threaten millions of human lives throughout the world. Fortunately, after years of research and improvement in DNA sequencing techniques, genetics based medicine and cancer treatments are now close to becoming a reality. Since the human genome project first sequenced the human genome, research and development into inexpensive and fast DNA sequencing has been extraordinary. The human genome project was carried out using the classical Sanger method, where the DNA strands were synthesized from a primer sequence using dideoxy deoxyribonucleoside triphosphate (dNTP) in such a way that the last base was known. Then, the strands were separated using gel electrophoresis for nucleobase reading. However, ultra-fast low-cost sequencing technology would revolutionize the field of genetics treatment.Recently, it has been proposed that nanopores in a material can be used to create fast and cheap DNA sequencing technology.1–3 Graphene4,5 and MoS2 (ref. 6) nanopore-based devices are two important developments among several reported proposals. As the DNA bases translate through the nanopores, electron tunneling can identify individual nucleobases in single-stranded DNA (ssDNA) without any amplification. It has also been reported that ssDNA bases can be identified by translating the ssDNA through electrode nanopores.7,8 These kinds of devices involve a nanopore-including brake junction electrode, which measures the tunneling current during the translation of DNA nucleobases.9,10,20 Every single nucleobase gives a different tunneling current signature, and hence DNA nucleobases can be easily identified through observing the tunneling current. This method of sensing can be very efficient, but excellent coupling between the molecule and electrode is still a big issue.11 Also, the overlapping of the transmission spectra of different nucleobases is a huge problem in this method. Recently, it has been reported that modified diamondoid (amantadine) functionalized gold nanopores can be used to detect nucleobases.12 Modified diamondoid can be used as a functionalizing molecule to improve the signatures of the nucleobases. These functionalizing molecules provide hydrogen bonding bridges for the nucleobases. Consequently, the coupling between the nucleobases and the electrode improves, which leads to a better tunneling current and sensitivity.
Four natural nucleobases, namely adenine (A), thymine (T), cytosine (C), and guanine (G), and two epigenetic markers, 5-methylcytosine (5 mC) and 8-oxoguanine (8oG),13 were investigated in this study. In 1948, Rollin and Hotchkiss14 discovered the presence of a methyl group at the 5th position of the cytosine ring. Cytosine methylation during DNA synthesis15–17 is due to the transfer of a methyl group from S-adenosylmethionine (donor) to the fifth position of the cytosine ring. The transformation from natural cytosine to 5-methylcytosine has an enormous impact on reducing gene expansion. This kind of methylation can lead to severe consequences in the development of human malignancies. In our investigation, a modified diamondoid structure, called memantine,18,19 has been used to functionalize gold nanopores to detect nucleobases. We have functionalized both electrodes to obtain optimal coupling between the electrodes through the molecules. For this reason, we have observed very sharp resonance peaks in the transmission spectra, with a specific energy level for each nucleobase, which directly leads to less overlapping of transmission spectra and greater resolving capabilities for the device. Also, we have observed a transmission probability in the order of at least 0.3, which indicates excellent coupling between the molecules and the electrodes. The quantum transport properties have been calculated using non-equilibrium Green's function formalism (NEGF) and the density functional theorem (DFT).
In this work, the transmission spectrum for each nucleobase and the respective projected density of states (PDOS) have been shown. The physics behind these resonance peaks and the electronic wave function have also been investigated. In addition, the molecular-projected self-consistent Hamiltonian (MPSH) eigenstates of the nucleobases have also been determined. The sensitivity of the device has been examined, which indicates how well it can perform in detecting a particular nucleobase over other nucleobases. Finally, we have analyzed the differential conductance of the device with respect to the gate voltage, in order to resolve the overlapping transmission spectra for various nucleobases.
2. Model and methods
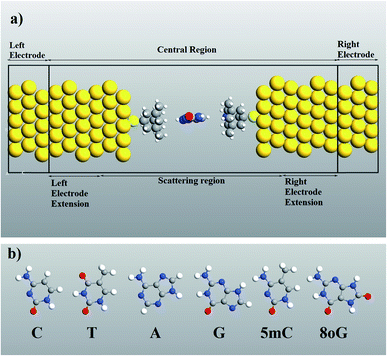
Computer simulations were performed to investigate the quantum mechanical transport phenomenon through memantine functionalized gold electrodes and nucleobases. The tunneling currents arising from various nucleobases were analyzed, and very distinct patterns were observed for each of the nucleobases. A semi-infinite gold (111) electrode was used, and the memantine was attached to the gold surface with a thiol group. The device configuration and the nucleobase structures investigated are shown in Fig. 1(a) and (b), respectively. Since the nucleobases mainly influence the tunneling current and transmission spectra, the phosphate backbone and other factors are not considered in this report. This will also help to minimize the computation time.The quantum transport calculations were carried out using the Atomistix Toolkit package (ATK) based on non-equilibrium Green functions (NEGF)21,22 and density functional theory (DFT).23–25 For the exchange-correlation (XC) functional, the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof26–30 was used. A mesh cutoff energy of 150 Ry and a 5 × 5 × 100 k point mesh with a Monkhorst–Pack scheme were used to obtain better matching between the Fermi level of the electrodes and the central region of the device. While double-ζ polarized (DZP) basis sets were used for nitrogen, hydrogen, carbon, oxygen and sulphur atoms, a single-ζ polarized (SZP) basis set was employed for gold atoms. The geometry optimization and structural relaxations of the central region were performed with sufficient vacuum spacing (a minimum of 12 Å) to prevent interactions between the periodic images. The relaxation procedure was carried out to ensure that the Hellmann–Feynman force acting on the atoms became less than 0.02 eV Å−1.
A molecular device consists of a molecule and two contacts. The molecule is sandwiched between the source (left electrode) and the drain (right electrode) contacts. As can be seen in Fig. 1, we have included some part of the contact in the central region. This is called the extended molecule (EM). μS and μD are the chemical potentials of the source and drain contacts, respectively. Under zero-bias conditions, the electro-chemical potentials of the source and drain are always equal, μD = μS. This can be considered as an equilibrium system. But, as soon as bias is applied between the contacts, the system enters a non-equilibrium state, with μD ≠ μS.
It must be noticed that the system is charge neutral. Now, if we apply a voltage across the device, there will be a shift in the spectrum, and also a potential profile will develop over the extended molecule. The potential must match the lead at the boundary of the EM. If this does not happen, then a discontinuity will appear at the boundary and scattering will be generated. Thus, in order to avoid this problem and to obtain excellent coupling, we need to include some part of the lead in the central region (left and right electrode extension) as shown in Fig. 1(a). Now, the wave function in the lead has the form of a normal plain wave, which can be easily calculated. But, the main problem is in describing the scattering of the plain wave from the source to the drain through the extended molecule. This can be calculated with the Green's function method.
The contacts are assumed to be defect free metals with a regular periodic structure, and the unit cells are in the direction of transport. The Hamiltonian of the whole system can be written as, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , which is also a Hermitian matrix. Here, it is important to introduce the concept of a principle layer (PL). The PL is the smallest cell that repeats itself periodically in the direction of transport, in such a way that it only interacts with the nearest neighboring PL. The source and drain contacts can be divided into (N = 1, 2, 3…) principle layers. Here, HS and HD are an N × N matrix, which describes the interaction inside a PL. Since we are using the same metal for both contacts, HS = HD. Similarly, Hτ,S and Hτ,D are the interaction terms in between the two PLs. Also, Hτ,S = Hτ,D. The matrix HMol describes the Hamiltonian for the extended molecule (EM), which is an M × M matrix. HS–Mol(N × M) is the Hamiltonian that describes the interaction between the source PL and the EM. Similarly, HD–Mol(M × N) is the Hamiltonian for the drain PL and the EM. Hence, the total Hamiltonian can be written as
, which is also a Hermitian matrix. Here, it is important to introduce the concept of a principle layer (PL). The PL is the smallest cell that repeats itself periodically in the direction of transport, in such a way that it only interacts with the nearest neighboring PL. The source and drain contacts can be divided into (N = 1, 2, 3…) principle layers. Here, HS and HD are an N × N matrix, which describes the interaction inside a PL. Since we are using the same metal for both contacts, HS = HD. Similarly, Hτ,S and Hτ,D are the interaction terms in between the two PLs. Also, Hτ,S = Hτ,D. The matrix HMol describes the Hamiltonian for the extended molecule (EM), which is an M × M matrix. HS–Mol(N × M) is the Hamiltonian that describes the interaction between the source PL and the EM. Similarly, HD–Mol(M × N) is the Hamiltonian for the drain PL and the EM. Hence, the total Hamiltonian can be written as
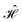 = = 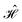 SS + SS + 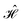 S–Mol + ĤMol–Mol + S–Mol + ĤMol–Mol + 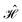 Mol–D + Mol–D + 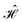 DD DD |
Similarly, we also have the overlap matrix ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , similar to this matrix. It must be noticed that
, similar to this matrix. It must be noticed that ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (calligraphic) is an infinite matrix and H is a finite matrix.
(calligraphic) is an infinite matrix and H is a finite matrix.
In the NEGF + DFT31–36 method, the Hamiltonian of the central region is not known in advance. Thus, it has to be computed using the self-consistent DFT loop for the charge density matrix. Generally, 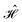 is expanded in terms of localized basis sets, which means the overlap between two localized functions, ϕm(r − R1) and ϕn(r − R2), will be zero if they are separated far enough away from each other. In other words, when |R1 − R2|> a certain distance, the overlapping matrix
is expanded in terms of localized basis sets, which means the overlap between two localized functions, ϕm(r − R1) and ϕn(r − R2), will be zero if they are separated far enough away from each other. In other words, when |R1 − R2|> a certain distance, the overlapping matrix
Therefore, the interaction between the central region and the electrodes is constrained to a limited part of L and R. Hence, the Hamiltonian matrices ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S–Mol and
S–Mol and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) Mol–D are also finite. Direct tunneling from source to drain is also negligible. By using the localized basis set, we can write the Green's function matrix as
Mol–D are also finite. Direct tunneling from source to drain is also negligible. By using the localized basis set, we can write the Green's function matrix as
After dividing our device into three parts, source, drain and extended molecule, the Green's function matrix for the system becomes
Here, we are neglecting direct tunnelling from source to drain. Hence,
ε0+![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) SD − SD − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) SD = ε0+ SD = ε0+![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) DS − DS − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) DS = 0 DS = 0 |
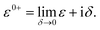
Therefore,
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) Mol–Mol and HMol–Mol are finite matrix terms (extended molecule: M × M). Also, GRMol–Mol is a finite matrix, and
Mol–Mol and HMol–Mol are finite matrix terms (extended molecule: M × M). Also, GRMol–Mol is a finite matrix, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) SS and
SS and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) DD have the diagonal form. From the above matrix equation, we can write
DD have the diagonal form. From the above matrix equation, we can write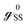 and
and 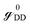 are called surface Green's functions, and they are very much different from GRSS and GRDD.
are called surface Green's functions, and they are very much different from GRSS and GRDD.
The matrix elements of the Hamiltonian of the system are not known initially. But they are functions of the charge density ρ. Hence we obtain ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) [ρ], which can be calculated using the DFT method. When the device is considered without bias (equilibrium), the Hamiltonian of the system can be easily found using standard DFT calculations. But when bias is applied across the contacts, the Hamiltonian of the EM will change, as both the net charge and the polarization are affected by the bias. This will lead to a completely new electrostatic potential profile for the extended molecule. However, since the contacts are charge neutral, the Hamiltonian of the contacts will not change. The Hamiltonian of the extended molecule is given by
[ρ], which can be calculated using the DFT method. When the device is considered without bias (equilibrium), the Hamiltonian of the system can be easily found using standard DFT calculations. But when bias is applied across the contacts, the Hamiltonian of the EM will change, as both the net charge and the polarization are affected by the bias. This will lead to a completely new electrostatic potential profile for the extended molecule. However, since the contacts are charge neutral, the Hamiltonian of the contacts will not change. The Hamiltonian of the extended molecule is given by
| HMol–Mol = HMol–Mol[ρ(r)] |
The total density matrix of the molecule region is given by
As the Green's function has poles in the real energy axis, the integral of the total density is difficult to calculate. But this integral can easily be calculated by adding the two separate parts, ρNon-equlilibriumMol–Mol and ρequlilibriumMol–Mol.
So,
Thus,
| ρMol–Mol = ρequlilibriumMol–Mol + ρNon-equlilibriumMol–Mol |
As the density matrix, ρMol–Mol, is known, we can find out the electron density ρMol–Mol(r) of the molecular region, which is necessary to calculate the new HMol–Mol[ρ(r)]. So,
| HMol–Mol[ρ(r)] = 〈ϕm|HK–S(r)|ϕn〉 |
where
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ε,v) is the transmission probability for the electron to transmit from the source to the drain with the energy ε, and μS and μD are the chemical potentials of the source and drain, respectively. The transmission probability is given by
(ε,v) is the transmission probability for the electron to transmit from the source to the drain with the energy ε, and μS and μD are the chemical potentials of the source and drain, respectively. The transmission probability is given by![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ε,v) = Trace[ΓSGRMol–MolΓDGAMol–Mol] (ε,v) = Trace[ΓSGRMol–MolΓDGAMol–Mol] |
| ΓS,D = i[ΣS,D(ε) − Σ†S,D(ε)] |
| GAMol–Mol = [GRMol–Mol]† |
From GRMol–Mol, one can also define the projected density of states (PDOS) of any molecule as
3. Results and discussion
The fully relaxed structures of the memantine functionalized gold electrode and the nucleobases adenine (A), thymine (T), cytosine (C), guanine (G), 5-methylcytosine (5 mC) and 8-oxoguanine (8oG) are shown in Fig. 2. The hydrogen bonds between the memantine and the nucleobases can be clearly observed. It is also evident that there are no covalent bonds between the nucleobases and the functionalized atoms. The fully relaxed geometry is one of the most important configuration steps in the calculation of quantum mechanical transport phenomena through molecular devices, as it exhibits the optimum coupling between molecules and electrodes. All the calculations have been achieved based on these device configurations.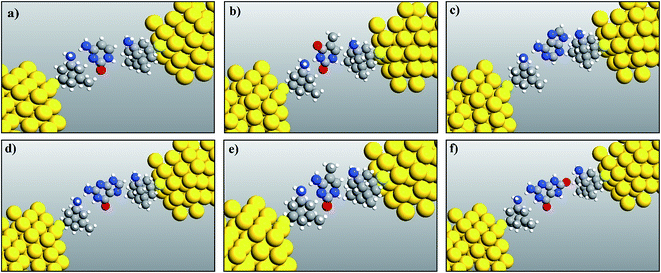 | ||
| Fig. 2 Relaxed geometry structures of functionalized electrodes with the nucleobases: (a) cytosine, (b) thymine, (c) adenine, (d) guanine, (e) 5-methylcytosine, and (f) 8-oxoguanine. | ||
The transmission spectra over the energy range of −1.5 eV to 0 eV, obtained using the DFT + NEGF method, for all the nucleobases are plotted in Fig. 3 along with the PDOS. The very distinct tunneling current signature can be easily observed for all the nucleobases. It is observed that the resonant peaks obtained for different nucleobases are not only different in energy levels but also in transmission probability, T(E). The resonant peak occurs for Cytosine at E = −1.27 eV with T(E) = 0.94, for thymine at E = −1.184 eV with T(E) = 0.97, for Adenine at E = −1.16 eV with T(E) = 0.82, for guanine at E = −1.42 eV with T(E) = 0.407, for 5-methylcytosine at E = −1.22 eV with T(E) = 0.654, and for 8-oxoguanine at E = −0.616 eV with T(E) = 0.34. The transmission probability reduces to the range of 0.0001 to 0.0003, which is far away from the resonant peak of the corresponding nucleobases.
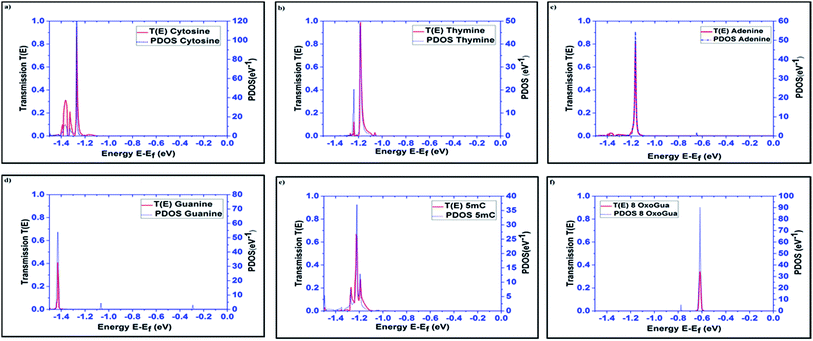 | ||
| Fig. 3 Transmission spectra and PDOS are plotted for all the nucleobases: (a) cytosine (C), (b) thymine (T), (c) adenine (A), (d) guanine (G), (e) 5-methylcytosine (5 mC), and (f) 8-oxoguanine (8oG). | ||
The projected densities of states (PDOS) are projected for the nucleobases in Fig. 3 in order to justify that the resonant peaks are originating from the effects of the nucleobases. By directly comparing the transmission spectrum and PDOS for each nucleobase, it can be concluded that the resonant peaks are originating from the introduction of the DOS from the nucleobases to the system. Precisely, the DOS is the contribution from the combined effect of each eigenchannel from the transmission matrix. This result directly leads to the detection of the nucleobase signature.
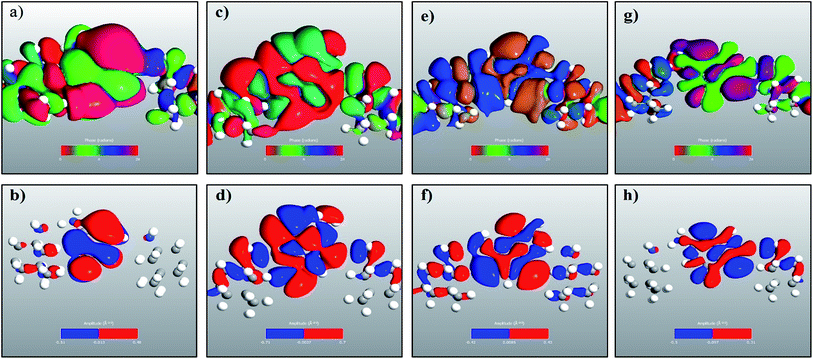
The transmission eigenchannel wave functions (corresponding to the eigenvalues) relating to the resonance peaks of the transmission spectra are plotted in Fig. 4 for all the nucleobases. The transmission eigenchannel wave functions are complex in nature. The same isovalue has been used to plot all the wave functions relating to the nucleobases. The isosurface shows the absolute value of the electronic wave function, and the color of the isosurface shows the phase. The phase change37 in the wave function is due to scattering in the eigenchannels. The periodic color map is used to indicate phase. If a close inspection is made of the electronic wave function, one can see from Fig. 4 that the EWFs38 spread from the source to the drain through the molecule, which indicates very decent coupling over the whole device. It is also shown in Fig. 4 that the transmission pathway for the nucleobases corresponds to the resonance peak in the transmission spectrum. The transmission pathway helps in understanding the exact path of electron flow through the molecule. The arrows in the pathway show the local direction of the flow between two atoms, and the color indicates the magnitude of the electron flow through a path. For example, in the case of thymine, it can be clearly seen in Fig. 4(d) that most of the electrons are flowing through a very dedicated path, and the red and violet arrows identify the path. It may also be noted that the electronic wave function shown in Fig. 4(c) follows the same route in transmitting the wave function from source to drain.
In a molecular device, coupling between the molecule and the electrode is necessary to calculate the quantum transport properties through the molecule. To understand and visualize the energy levels of nucleobases in the presence of electrodes, MPSH39 eigenstates were calculated. The nucleobases and the functionalization molecule were included in calculating the MPSHs. The HOMO and LUMO states of a free nucleobase do not change with its angular orientation. But, when the nucleobase interacts with the functionalized electrode, there will be strong interaction and hybridization between the molecular orbital of the nearest atoms of both the nucleotide and the functionalized molecules. Therefore, the DNA nucleobase will increase the transient local density of states. Consequently, the resonance peak in the transmission spectrum can be seen at the specific energy level. The dominant transmission peaks in the spectrum are also observed to be dependent on the molecular angular orientation. This dependency is due to non-trivial interaction of orbitals between the DNA base and the functionalized molecule. In Fig. 5 (only the natural nucleobases are shown), one can see an excellent resemblance between the transmission eigenstates of the nucleobases and their corresponding MPSH eigenstates, which also correspond to the HOMO states of the nucleobases.
In the following section, a proposal is made for detecting the resonance peaks for all the nucleotides in a real device. A molecular field effect transistor (FET)40,41 device is one of the perfect candidates for this kind of application. A simple schematic diagram of a molecular FET is shown in Fig. 6(a). The molecule is sandwiched between two contacts, the source and the drain. It provides a path for electrons to flow from source to drain. There is also a third contact, serving as the gate terminal, which is completely separated from the central molecular region by an insulator. It is capacitively coupled with the central region and forms a single plate capacitor with the molecule and the terminal. The purpose of the gate is not to transfer charge to the central molecule but to tune the Fermi energy level of the central molecule in such a way that the resonance peak is pushed in between the chemical potential of the drain and the source. As the gate voltage increases, the energy levels of the molecule start to shift relative to the chemical potential of the source and the drain. At a particular applied gate voltage, when the resonance peak energy level is in between the source and drain chemical potentials, an absolute increment of current can be observed. If the gate voltage is increased further, the current will suddenly decrease sharply as the energy levels leave the potential window. Fig. 6(b) shows this scenario graphically where ψ represents the electronic wave, r is the reflected wave, t is the transmitted wave, VGS is the gate voltage, VDS is the source to drain voltage, and μS and μD are the chemical potentials of the source and drain contacts, respectively. Here,
| μS − μD = −eVDS. |
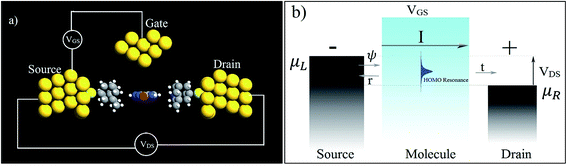 | ||
| Fig. 6 (a) A simple schematic diagram of a three-terminal molecular FET and (b) its working principles. | ||
Hence, it is possible to detect nucleotides by tuning the Fermi level of each nucleobase through applying a gate voltage. For example, Adenine can be detected by adjusting the Fermi level to VGS = −1.16 eV. The gating conductance can be written as a function of VGS in the following fashion:42
The sensitivity can be written for a specific nucleobase with respect to another nucleobase at a particular gating voltage as,
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) nucleobase and
nucleobase and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) other are the conductances of the nucleobase to be detected and that of other nucleobases at the same gate voltage, respectively. This conductance can be written using the transmission resonant peak for the nucleobases from the previous formalism.
other are the conductances of the nucleobase to be detected and that of other nucleobases at the same gate voltage, respectively. This conductance can be written using the transmission resonant peak for the nucleobases from the previous formalism.
In Fig. 7, sensitivity (%) data at various gate voltages are plotted for different nucleobases. This illustration will help to understand how well the device can detect a specific nucleobase at a particular gate voltage. It can be observed that the device sensitivity ranges from 103 to 107. That means that detecting a particular nucleobase at a specific gate voltage is 3 orders of magnitude more resolved than for the other nucleobases at that same gate voltage. In Fig. 7(a), the sensitivity for cytosine is plotted over other nucleobases with a gate voltage of −1.27 V. It can be seen that the sensitivity for cytosine is at least three orders of magnitude higher than for other nucleobases. Thus, the device can easily detect cytosine. Similarly, in Fig. 7(b), the sensitivity toward Thymine at a gate voltage of −1.18 V is found to be at least three orders of magnitude higher than for A, G, C, 5 mC and 8oG. In Fig. 7(f), the sensitivity for 8-oxoguanine is observed to be larger at a gate voltage of −0.62 V, with the sensitivity spread between 106 and 107. So this device can also quickly detect 8-oxoguanine. Moreover, the sensitivity for 5 mC is four orders of magnitude more resolved than for the natural nucleobase cytosine, enabling this device to distinguish between regular nucleobases and an epigenetic marker.
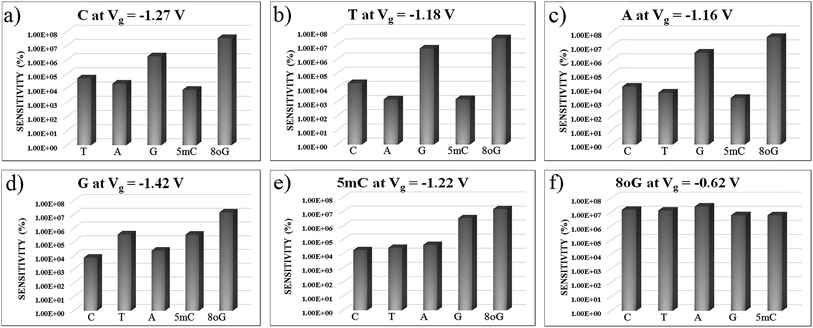 | ||
| Fig. 7 The device sensitivity is plotted with different gate voltages in figures (a) to (f) with respect to other nucleobases. All the plots are in semi-log scale. | ||
In order to understand the physics behind the plots in Fig. 7, one can examine Fig. 7(a) for cytosine at a gate voltage of −1.27 V, and the rest of the plots also follow the same logic. In Fig. 8, all the transmission eigenchannel EWFs for the nucleobases have been plotted for the gate voltage of −1.27 V. Thus, the EWFs for all the nucleobases can be seen at the same voltage. It can be observed that the EWFs cover the whole scattering region of the device only for cytosine at the applied voltage, indicating excellent coupling between the electrodes, the diamondoid and the Cytosine. This behavior will result in transmission resonance, leading to an increase in the current. But for the other nucleobases, the EWFs are mainly concentrated around the source, and the contributions to the nucleobases are almost negligible. In other words, there will be minuscule transmission for other nucleobases, providing an almost negligible amount of current. The transmission pathway (not shown here) for all the nucleobases has been investigated in this report. A dedicated path was observed for cytosine, but this was found to be negligible for the other nucleobases. From this analysis, it can be concluded that this device will be able to detect all normal and mutated nucleobases separately.
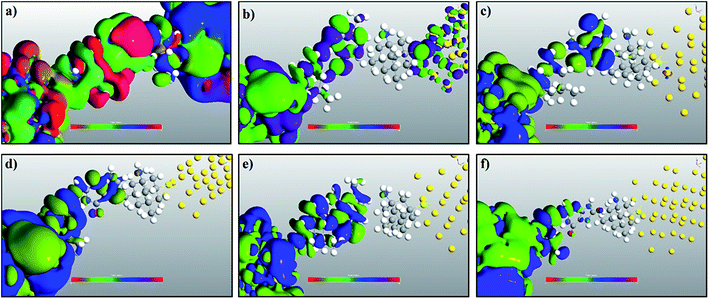 | ||
| Fig. 8 A comparison of the electronic wave functions at −1.27 V for (a) cytosine, (b) thymine, (c) adenine, (d) guanine, (e) 5-methylcytosine, and (f) 8-oxoguanine. | ||
Up to this point, we have showed the detection of nucleobases through tuning the gate voltage for respective nucleobases. In this section, we will introduce another possible way to detect the nucleobases in terms of the differential conductance, 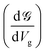 . The transmission coefficient
. The transmission coefficient ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ε) can be written as the sum of all n eigen-channels for a certain energy level as follows:
(ε) can be written as the sum of all n eigen-channels for a certain energy level as follows:
The conductance can be written as
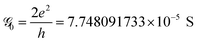 . This is called the quantum conductance. It is clear from the above equation that
. This is called the quantum conductance. It is clear from the above equation that 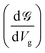 can be expressed in terms of
can be expressed in terms of ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ε). The differential conductance gives us the resolving capability when the peaks are not easily distinguishable. From Fig. 3, we can observe that the transmission peaks for cytosine, thymine, and 5-methylcytosine are very close to each other, and sometimes they overlap with each other. In Fig. 9, we have shown a well resolved plot of the differential conductance for T, C, and 5 mC. It is clear that the differential conductance of T and C does not overlap over the interval of −1.25 V < Vg < −1.15 and −1.30 V < Vg < −1.27. A similar trait can be observed for C and 5 mC (red and black curves). In the range of Vg = 1.35 ± 0.1, the differential conductance for 5 mC is highly resolved. This observation leads us to conclude that the device is capable of differentiating between C and 5 mC, demonstrating the capability of a differential conductance method to detect nucleobases in the case of overlapping transmission peaks.
(ε). The differential conductance gives us the resolving capability when the peaks are not easily distinguishable. From Fig. 3, we can observe that the transmission peaks for cytosine, thymine, and 5-methylcytosine are very close to each other, and sometimes they overlap with each other. In Fig. 9, we have shown a well resolved plot of the differential conductance for T, C, and 5 mC. It is clear that the differential conductance of T and C does not overlap over the interval of −1.25 V < Vg < −1.15 and −1.30 V < Vg < −1.27. A similar trait can be observed for C and 5 mC (red and black curves). In the range of Vg = 1.35 ± 0.1, the differential conductance for 5 mC is highly resolved. This observation leads us to conclude that the device is capable of differentiating between C and 5 mC, demonstrating the capability of a differential conductance method to detect nucleobases in the case of overlapping transmission peaks.
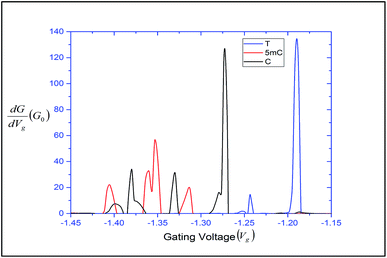 | ||
| Fig. 9 Differential conductance with respect to the gating voltage, plotted for thymine, cytosine and 5-methylcytosine. | ||
4. Conclusions
In this report, the NEGF + DFT method is used to understand the fundamental working principles of a memantine functionalized gold electrode biosensor. The proposed device is demonstrated to detect various natural and mutated nucleobases. The sensitivity of the device spreads over the range of 103 to 107 for all the nucleobases. The transmission spectra for the nucleobases studied are shown and discussed. The observed resonant peaks are at least in the order of 0.3. The underlying physics behind these resonance peaks has been explained through calculating the projected densities of states of the nucleobases and concluding that these resonance peaks originate due to the translation of the nucleobases. The transmission pathways and electronic wave functions, which explain the coupling between the electrode and the molecules, are discussed. The MPSH calculated, in order to understand the energy levels of the nucleobases in the presence of electrodes, gives an excellent overview of the energy levels involved in the transmission resonance peaks for the nucleobases. The comparison between the various EWFs at a gate voltage of −1.27 V reveals the physics behind the excellent resolving and detecting capabilities of the device for various nucleobases. Finally, the differential conductances for various nucleobases were analyzed in order to resolve overlapping transmission spectra. This clearly shows the advantage of functionalizing both electrodes, which leaves less overlap of transmission spectra and gives more resolving capabilities to the device. It is confirmed that the proposed device can resolve the detection of a specific nucleobase with respect to other nucleobases.Acknowledgements
The authors acknowledge the Centre for Micro-/Nano-electronics (NOVITAS), School of Electrical and Electronic Engineering, Nanyang Technological University for the computational resources and help.References
- M. Zwolak and D. Ventra, Rev. Mod. Phys., 2008, 80, 141–165 CrossRef.
- S. Huang, J. He, S. Chang and P. Zhang, et al., Nat. Nanotechnol., 2010, 5, 868–873 CrossRef CAS PubMed.
- S. Chang, S. Huang and J. He, et al., ACS Nano, 2010, 10, 1070–1075 CAS.
- P. H. Chang, H. Liu and B. K. Nikolić, J. Comput. Electron., 2014, 13, 847–856 CrossRef CAS.
- T. Ahmed, J. T. Haraldsen, J.-X. Zhu and A. V. Balatsky, J. Phys. Chem. Lett., 2014, 5, 2601–2607 CrossRef CAS PubMed.
- A. B. Farimani, K. Min and N. R. Aluru, ACS Nano, 2014, 8, 7914–7922 CrossRef CAS PubMed.
- H. S. Kim and Y.-H. Kim, Biosens. Bioelectron., 2015, 69, 186–198 CrossRef CAS PubMed.
- M. Zwolak and M. Di Ventra, Nano Lett., 2005, 5, 421 CrossRef CAS PubMed.
- J. Lagerqvist, M. Zwolak and M. Di Ventra, Nano Lett., 2006, 6, 779 CrossRef CAS PubMed.
- M. Tsutsui, M. Taniguchi, K. Yokota and T. Kawai, Nat. Nanotechnol., 2010, 5, 286 CrossRef CAS PubMed.
- H. Jeong, H. S. Kim, S.-H. Lee, D. Lee, Y. H. Kim and N. Huh, Appl. Phys. Lett., 2013, 103, 023701 CrossRef.
- G. Sivaraman, R. G. Amorim, R. H. Scheicher and M. Fyta, Nanoscale, 2016, 8, 10105–10112 RSC.
- S. Kanvah, J. Joseph, G. B. Schuster, R. N. Barnett, C. L. Cleveland and U. Landman, Acc. Chem. Res., 2010, 43, 280 CrossRef CAS PubMed.
- R. D. Hotchkiss, J. Biol. Chem., 1948, 175, 315–332 CAS.
- P. M. Das and R. Singal, J. Clin. Oncol., 2004, 22, 4632–4642 CrossRef CAS PubMed.
- P. W. Laird, Nat. Rev. Cancer, 2003, 3, 253–266 CrossRef CAS PubMed.
- P. A. Jones and S. B. Baylin, Nat. Rev. Genet., 2002, 3, 415–428 CrossRef CAS PubMed.
- G. Sivaraman and M. Fyta, Nanoscale, 2014, 6, 4225–4232 RSC.
- G. Sivaraman and M. Fyta, EPL, 2014, 108, 17005 CrossRef.
- J. Li, T. Li, Y. Zhou, W. Wu, L. Zhang and H. Li, Phys. Chem. Chem. Phys., 2016, 18, 28217 RSC.
- Y. Meir and N. S. Wingreen, Phys. Rev. Lett., 1992, 68, 2512 CrossRef PubMed.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, England, 1995 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1994 Search PubMed.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1986, 84, 4524 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- Y. Xue, S. Datta and M. A. Ratner, Chem. Phys., 2002, 281, 151 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- S. H. Ke, H. U. Baranger and W. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 085410 CrossRef.
- L. V. Keldysh, J. Exp. Theor. Phys., 1965, 20, 1018–1026 Search PubMed.
- A. R. Rocha, V. M. García-Suárez, S. Bailey, C. Lambert, J. Ferrer and S. Sanvito, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085414 CrossRef.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407 CrossRef.
- M. Buttiker, IBM J. Res. Dev., 1988, 32, 63 CrossRef , eigenchannels are mentioned in Appendix C.
- M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117 CrossRef.
- K. Stokbro, J. Taylor, M. Brandbyge, J. L. Mozos and P. Ordejon, Comput. Mater. Sci., 2003, 27, 151 CrossRef CAS.
- S. Datta, Lessons from Nanoelectronics: A New Perspective on Transport, 2012 Search PubMed.
- S. Datta, Quantum Transport: Atom to Transistor, 2005 Search PubMed.
- S. K. Min, W. Y. Kim, Y. Cho and K. S. Kim, Nat. Nanotechnol., 2011, 6, 162–165 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |