 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Are the experimentally observed 3-dimensional carbon honeycombs all-sp2 structures? The dangling p-orbital instability†
Zacharias G. Fthenakis
Institute of Electronic Structure and Laser, FORTH, P. O. Box 1527, 71110 Heraklio, Crete, Greece. E-mail: fthenak@iesl.forth.gr
First published on 7th February 2017
Abstract
Recently, Krainyukova and Zubarev [Phys. Rev. Lett. 116, 055501 (2016)] reported that they observed a series of all-sp2 3-dimensional carbon honeycomb structures with interesting storage properties. In the present study we show that these structures are unstable, reducing to honeycomb structures with sp3 atoms at the honeycomb junctions. As we show, this instability is due to solitary electrons which occupy the unhybridized p orbitals of the junction atoms, thus violating the octet rule. These orbitals are localized and have all the features that characterize dangling orbitals. This instability, as well as the ability of unhybridized p orbitals to form dangling bonds, has not been reported previously.
1 Introduction
Recently, Krainyukova and Zubarev1 reported that they observed a series of 3-dimensional (3D) all-sp2 carbon honeycomb structures, obtained by deposition of sublimated graphite. For the identification of the structures they used low temperature electron diffraction and electron microscopy methods and they reported that the structures they found could be either random or periodic. The proposed structures are composed of zig–zag terminated graphene nanoribbon (GNR) walls, interconnected through single carbon atoms arranged along a line at the wall’s junctions, as shown in Fig. 1. An important feature of these structures (which was studied and reported by the authors) is that they exhibit a high level of physical absorption of several gases, like Xe, Kr and CO2, which makes them interesting candidates for gas or liquid storage. Moreover, these structures might be of a more general interest, since they are expected to have interesting electronic, transport (thermal and electronic), and mechanical properties, which need further investigation.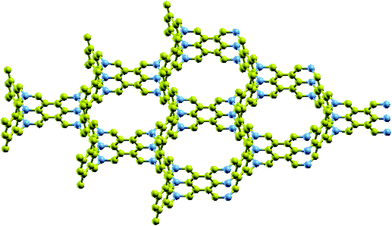 | ||
| Fig. 1 A periodic representative of the 3D all-sp2 honeycomb structure proposed by Krainyukova and Zubarev.1 The junction atoms are shown in dark blue. | ||
The rising interest in these structures, however, is not only because they might have interesting properties, but also because they are supposed to be the first all-sp2 3D carbon honeycomb structures observed (and derived) experimentally. Similar 3D honeycomb structures have been proposed and studied theoretically,2–9 but to the best of our knowledge, none of them are composed entirely of sp2 carbon atoms. They are rather composed of sp2 atoms at the graphitic walls and sp3 atoms at the junctions, and they might also be random or periodic, like the structures proposed by Krainyukova and Zubarev.1 Although these structures have not been observed experimentally, it is reported that they could be produced by collisions of graphene patches, which collide at right angles to each other, resulting in the production of Y-junctions.9 It is worth noting, however, that other all-sp2 3D structures, like bco-C16,10 Rh6,11 cR6 and cT8,12 have been predicted theoretically, but these structures are not 3D honeycombs.
In the present study we show that the all-sp2 3D honeycomb carbon structures proposed by Krainyukova and Zubarev1 are unstable, reducing to mixed sp2/sp3 3D honeycomb structures, with the sp3 carbon atoms at the junctions. For our calculations we utilize the density functional theory (DFT) at both the local density approximation (LDA) and the generalized gradient approximation (GGA) level. We optimize a periodic representative of these structures, shown in Fig. 1, and we show that along a transition path, which converts the unstable (proposed) structure to its stable counterpart, there is no energy barrier, thus leading to the conclusion that the proposed structure is unstable. It is worth noting, however, that there are studies based on phonon band structure calculations, which claim that the proposed all-sp2 structures are stable.13,14 In view of the results presented here, which make clear that the proposed all-sp2 structures are unstable, the results of these studies are very difficult to rationalize.
One might assume that the instability mechanism, which is responsible for the formation of sp2 bonds at the junctions, is similar to the mechanism which converts graphite with AA stacking to hexagonal diamond under pressure normal to the graphitic planes,15 or the mechanism which is partly responsible for the instability of H-6 carbon.16 However, as we show, this is not true. On the contrary, we show that this instability is due to the solitary electrons occupying the unhybridized p orbitals of the junction atoms, thus violating the octet rule. These orbitals are localized and have all the features that characterize dangling orbitals. They cannot interact with their neighboring unhybridized p electrons to form double bonds and they only have one choice for bonding: to hybridize and form single bonds with their neighboring atoms at the junctions, thus stabilizing the structure. This is not the first time that the unhybridized p-orbital orientation has been reported as being responsible for dynamic instability.12,16
Based on the fact that the proposed all-sp2 structures (which were supposed to be experimentally observed) are not stable, the question which arises is what structures are these that were observed experimentally? Are they the optimized structures proposed here, or could they also be similar 3D honeycombs, like those already proposed theoretically (see for instance ref. 3 and 9)? This question, which is posed as a result of the present work, is an open question which has to be answered by experimentalists.
Based on the above, the aim of this study is (i) to make it clear that the proposed all-sp2 structures are unstable, (ii) to act as a theoretical guide for further experimental studies on the structural properties of the 3D carbon honeycombs, (iii) to act as a warning for those intending to study the properties of these unstable structures, thus avoiding an effort which might lead to erroneous results, (iv) to show the instability mechanism which destabilizes these structures and (v) to show the ability of unhybridized p orbitals to form dangling bonds.
2 The method
All the calculations of the present study were performed using the ab initio DFT method as implemented by the SIESTA code,17 utilizing both the local density approximation Ceperley–Adler functional (LDA/CA)18 and the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA/PBE)19 functional. We use a 5 × 5 × 20 Monkhorst–Pack grid20 in the reciprocal space and a 300 Ry mesh cutoff value. For the pseudopotential of C we utilize the norm-conserving Troullier–Martins pseudopotentials21 in the Kleinman–Bylander factorized form.22 The basis for the wavefunction expansion in real space is an atomic-like double-zeta basis with polarization orbitals. For the structure optimizations, which include both the atomic position and lattice relaxations, we use the conjugate gradient method. The structure is considered optimized if the maximum force and stress component is smaller than 0.005 eV Å−1 and 0.01 GPa, respectively. Using these optimization conditions, the energy accuracy of the optimized structure is less than 0.001 eV per atom.We first consider the all-sp2 periodic structure shown in Fig. 1. This is a periodic representative of the structures of interest and has 14 atoms per unit cell. For convenience we will call this structure “structure A”. This 14 atom unit cell, as well as the unit cell vectors a, b and c of the structure, is shown in Fig. 2(a). Fig. 2(a) shows two such unit cells, each containing 2 junction atoms (one in the middle and one at the edge of the unit cell), which are shown in blue.
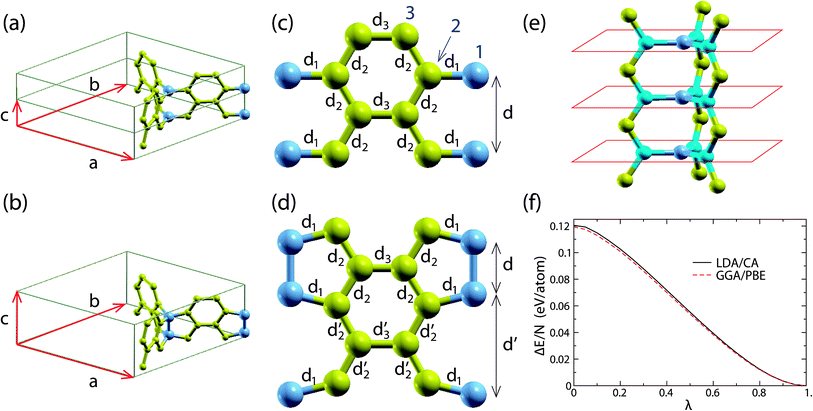 | ||
| Fig. 2 (a) and (b) Unit cells of the optimized A and B structures, respectively, obtained using the LDA/CA functional. Similar structures are obtained using the GGA/PBE functional. The atoms at the junctions are shown in blue. (c) and (d) Walls of the 3D honeycombs for structures A and B, respectively. Bonds with the same bond length are shown with the same d-symbol next to them. The bond length values are shown in Table 1 of the ESI.† The atoms at the junctions are shown in blue. (e) The local planarity at the junctions of structure A. The atoms at the junctions and their first nearest neighbors are shown in dark blue and light blue, respectively. The red lines show schematically the parallel planes, which are locally graphitic with AA stacking. (f) The total energy per atom ΔE/N with respect to the corresponding energy of structure B along the transition path converting structure A to structure B (i.e. as a function of λ of eqn (1)). | ||
The periodicity of this unit cell along the c axis does not allow the atoms at the junction to come closer and form sp3 pairs, as shown in Fig. 2(b). Therefore, the optimized structure A maintains its all-sp2 character. However, if the unit cell is doubled along the c direction, then the formation of these sp3 pairs is not prohibited by the periodicity of the structure. In order to find out whether or not these sp3 pairs are formed, we optimize the structure with the doubled unit cell, as well as structure A (with the single unit cell) for comparison. As we explain in the next section, the optimized double unit cell structure prefers to form those sp3 pairs, instead of maintaining the all-sp2 character of structure A. The 28 atom unit cell of this optimized new structure is shown in Fig. 2(b). For convenience we will call this structure “structure B”.
What we show next is that structure A is unstable. In order to show this, we utilize a simple transformation path that linearly transforms structure A to structure B. To construct this transformation path we consider that the unit cell of the optimized structure A is doubled along the c direction, so that there is a one-to-one correspondence between the atoms of the unit cell of the optimized structure A with those of the optimized structure B. The transformation path is defined by the equation
| ri(λ) = rA,i + λ(rB,i − rA,i), | (1) |
3 Results and discussion
As already mentioned in the above section, we optimized both structures A and B using the DFT with both the LDA/CA and the GGA/PBE functionals. For both optimized structures the unit cell vectors have the form
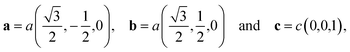 | (2) |
The total energy per atom obtained from the above optimizations using the LDA/CA functional for structures A and B is E(LDA/CA)A = −154.925 eV and E(LDA/CA)B = −155.045 eV, respectively. The corresponding energy values obtained using the GGA/PBE functional are E(GGA/PBE)A = −161.993 eV and E(GGA/PBE)B = −162.112 eV. The energy differences ΔELDA/CA = E(LDA/CA)B − E(LDA/CA)A and ΔEGGA/PBE = E(GGA/PBE)B − E(GGA/PBE)A are ΔELDA/CA = 0.121 eV and ΔEGGA/PBE = 0.119 eV. Therefore, in comparison with structure A, structure B is energetically favorable, for both cases.
Moreover, calculating the energy along the transition path described in the previous section, which converts structure A to structure B, we find that the energy decreases monotonically along the transition pathway, which means that there is no energy barrier along this path. In turn, this means that structure A corresponds to an unstable equilibrium and a very small structural distortion will cause its transformation to structure B. The energy along this path, determined by the parameter λ, is shown in Fig. 2(f) for calculations with both the LDA/CA and GGA/PBE functionals. Consequently, structure A is unstable.
In order to understand the instability mechanism of structure A, let us first focus on its structural features. Structure A is planar along the graphitic walls and each junction atom is coplanar with its three first nearest neighbors (see Fig. 2(e)). The planar structure of the graphitic walls and the local planarity in the vicinity of the junction atoms give rise to sp2 hybridization of the 2s and 2p orbitals of each C atom. The sp2 hybridized orbitals lie along the graphitic wall planes and along the plane formed locally from each junction atom and its first nearest neighbors. The unhybridized p orbitals rise at each atom of the walls normal to the wall, and at each atom of the junctions, normal to the plane locally formed by the junction atoms and its first nearest neighbors.
Thus, due to the parallel arranged unhybridized p orbitals of the walls, each atom of the wall of structure A forms delocalized double bonds with its neighboring wall atoms, as in graphene. In contrast, the unhybridized p orbitals of the junction atoms are perpendicular to the unhybridized p orbitals of their neighboring atoms at the zig–zag edges of the walls, and therefore they do not overlap to form a bond. Thus, the atoms at the zig–zag edges of the walls form single bonds with the junction atoms‡ and the electrons occupying the unhybridized p orbitals of the junction atoms remain as solitary electrons (one electron per unhybridized p orbital), thus violating the octet rule. Therefore, these orbitals form dangling bonds and they are expected to be very reactive. As a consequence, the atoms at the junctions would prefer to form single bonds with each other in pairs (as in structure B) to saturate these dangling bonds, restore the octet rule and stabilize the structure.
The above picture is in agreement with the projected density of states (pDOS) of the orbitals of the atoms of structure A. In Fig. 3(a) we show the pDOS of the s and p orbitals composing the sp2 hybrids of atoms 1, 2 and 3 shown in Fig. 2(b), while in Fig. 3(b) we show the pDOS of the corresponding unhybridized p orbitals. Due to the symmetry of the walls of structure A, only the pDOS of atoms 1, 2 and 3 are different. For the directions of px, py and pz, we have assumed that the wall shown in Fig. 2(c) lays along the xz plane, with the z-axis along the junction line.
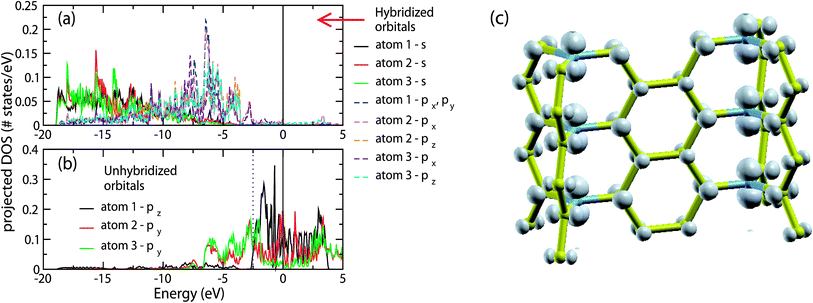 | ||
| Fig. 3 (a) and (b) Partial density of states for the s and p orbitals of atoms 1, 2 and 3 (see Fig. 2(c)) of structure A. The orbitals of (a) correspond to the orbitals composing the sp2 hybrids, while the orbitals of (b) correspond to the unhybridized p orbitals. (c) Local electron density of the electronic eigenstates with energies in the range of −2.5 to 0 eV, corresponding to the unhybridized p orbitals of the junction atoms and partly to the unhybridized p orbitals of the wall atoms. | ||
As we can see, the s and p orbitals composing the sp2 hybrids contribute to the Hamiltonian eigenstates with energies in the range of −19 to −2.5 eV, laying well bellow the Fermi energy, as expected according to the picture shown in Fig. 3. The p unhybridized orbitals contribute to the Hamiltonian eigenstates with energies in the range of −7 to 0 eV, i.e. near the Fermi level. In particular, the pDOS of the unhybridized p orbitals of the junction atoms (atom 1 of Fig. 2(b)) corresponds to the energy range of −2.5 to 0 eV, forming a relatively narrow band. Thus, the unhybridized p orbitals of the junction atoms could interact with only those orbitals which contribute to the Hamiltonian eigenfunctions with an energy in the range of −2.5 to 0 eV. However, despite the unhybridized p orbitals of the junction atoms, only the unhybridized p orbitals of the wall atoms have significant contributions to the Hamiltonian eigenfunctions in this energy range, while the contributions of the s and p orbitals composed of the sp2 orbitals are negligible. Recalling that the unhybridized p orbitals of the wall atoms do not interact with the unhybridized p orbitals of the junctions atoms, we come to the conclusion that the unhybridized p orbitals of the junction atoms do not interact with any of their neighboring orbitals.
However, if this was correct, the pDOS of these orbitals would be just a δ-function, located at the energy Ep of the atomic p orbitals, which does not agree with the band broadening shown in Fig. 3(b). This means that practically there are some weak interactions, which are responsible for this broadening. The most important among them are the interactions with the unhybridized p orbitals of the neighboring junction atoms, which are the second nearest neighbor interactions§ of the ppσ type. The band broadening due to these interactions can be qualitatively estimated using the tight binding approximation (TBA). Assuming interactions only between those orbitals, the energy E(k) (according to the TBA) is E(k) = Ep + 2Vppσ(d) cos(kd), where Ep is the energy of the 2p orbitals of the isolated C atom, Vppσ(d) = 〈2pz(0,0,0)|H|2pz(0,0,d)〉 is the hopping integral for the C orbitals |2pz(0,0,0)〉 and |2pz(0,0,d)〉 located at the positions (0,0,0) and (0,0,d), respectively, and d is the interatomic distance between neighboring junction atoms. Thus, the energy range between the lowest energy of the band (Ep − 2|Vppσ|) and the Fermi level EF (EF = Ep) is ΔE1/2 − 2|Vppσ|. According to Papaconstantopoulos,23 Vppσ(d) = Vppσ(d0)(d0/d)3, where Vppσ(d0) = 0.63 eV is the second nearest neighbor hopping integral at d0 = 2.525 Å, where d0 is the second nearest neighbor distance in diamond. Thus for d = 2.4343 Å in our case (according to our LDA/CA calculation), Vppσ(d0) = 0.70 eV, and therefore ΔE1/2 = 1.40 eV. Qualitatively, therefore, this value is comparable to the corresponding 2.5 eV value of our DFT calculations, and can explain the reason for this broadening, as well as the importance of these interactions in the instability of structure A. Similar broadening occurs in the pDOS of the unhybridized p orbitals of the sp2 terminated carbon foam surfaces,4 due to second nearest neighbor interactions. In Fig. 3(c) we show the local electron density corresponding to the eigenstates with eigenenergies in the range of −2.5 to 0 eV, where the dominant contribution of the unhybridized p electrons of the junction atoms in this energy range is clearly shown.
To the best of our knowledge, p dangling orbitals and the corresponding instability have not been reported previously. Dangling bonds rather refer to sp3 orbitals either on the surface of a crystalline24,25 or in the bulk of an amorphous solid,26 but not to unhybridized p orbitals. What is clearly shown here is that unhybridized p orbitals may also form dangling bonds.
Despite the above described instability mechanism for structure A, and taking into account that the atomic arrangement at the junctions is very similar to the structure of graphite with AA stacking, as shown schematically in Fig. 2(e), one may assume that the instability mechanism of structure A is (also) related to the mechanism that converts graphite with AA stacking to hexagonal diamond under pressure15 and is partly responsible for the instability of H-6 carbon.16 Indeed, this mechanism tends to buckle the structure, as it happens locally at the junctions of structure B, and therefore, the above assumption is reasonable. However, as we show in the ESI,† this is not the instability mechanism of structure A.
4 Conclusions
In the present study, using DFT calculations both at the LDA/CA and the GGA/PBE level, we show that the all-sp2 3D carbon honeycomb structures, recently proposed by Krainyukova and Zubarev1 as experimentally observed structures, are unstable, reducing to mixed sp2/sp3 3D honeycomb structures, with the sp3 atoms at the honeycomb junctions. The instability of these structures is due to the solitary electrons occupying the unhybridized p orbitals of the junction atoms, thus violating the octet rule. These orbitals are localized and have all the features that characterize dangling orbitals. These structures are stabilized when those orbitals hybridize and form single bonds with each other in pairs, thus restoring the octet rule. To the best of our knowledge, this instability mechanism, as well as the ability of unhybridized p orbitals to form dangling bonds, has not been reported previously.The question which is now posed, as a result of the present work, is the following: since the structure of the experimentally observed 3D carbon honeycombs is not the one proposed by Krainyukova and Zubarev,1 what really is the internal structure of the experimentally observed 3D carbon honeycombs? Is it structure B derived from the optimization of structure A, containing not only sp2, but also sp3 atoms? Is it one of the other mixed sp2/sp3 theoretically proposed 3D honeycomb structures,3,9 or is it a structure not yet known? This is an open question, which the experimentalists have to answer.
References
- N. V. Krainyukova and E. N. Zubarev, Phys. Rev. Lett., 2016, 116, 055501 CrossRef PubMed.
- Z. Zhu, Z. G. Fthenakis, J. Guan and D. Tománek, Phys. Rev. Lett., 2014, 112, 026803 CrossRef PubMed.
- A. Kuc and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 214104 CrossRef.
- Z. Zhu and D. Tománek, Phys. Rev. Lett., 2012, 109, 135501 CrossRef PubMed.
- K. Umemoto, S. Saito, S. Berber and D. Tománek, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 193409 CrossRef.
- S.-Z. Chen, F. Xie, F. Ning, Y.-Y. Liu, W.-X. Zhou, J.-F. Yu and K.-Q. Chen, Carbon, 2017, 111, 867–877 CrossRef CAS.
- G. Yu, L. Jiang and Y. Zheng, Appl. Phys. Lett., 2014, 105, 061601 CrossRef.
- A. Martínez-Mesa, L. Zhechkov, S. N. Yurchenko, T. Heine, G. Seifert and J. Rubayo-Soneira, J. Phys. Chem. C, 2012, 116, 19543–19553 Search PubMed.
- T. Kawai, S. Okada, Y. Miyamoto and A. Oshiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035428 CrossRef.
- J.-T. Wang, H. Weng, S. Nie, Z. Fang, Y. Kawazoe and C. Chen, Phys. Rev. Lett., 2016, 116, 195501 CrossRef PubMed.
- J.-T. Wang, C. Chen, E. Wang and Y. Kawazoe, Sci. Rep., 2014, 4, 4339 Search PubMed.
- J.-T. Wang, C. Chen and Y. Kawazoe, Sci. Rep., 2013, 3, 3077 Search PubMed.
- Z. Yang, G. Lan, B. Ouyang, L.-C. Xu, R. Liu, X. Liu and J. Song, Mater. Chem. Phys., 2016, 183, 6–10 CrossRef CAS.
- Y. Gao, Y. Chen, C. Zhong, Z. Zhang, Y. Xie and S. Zhang, Nanoscale, 2016, 8, 12863–12868 RSC.
- S. Fahy, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 7623–7626 CrossRef CAS.
- Z. G. Fthenakis, RSC Adv., 2016, 6, 78187–78193 RSC.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- D. Papaconstantopoulos, Handbook of the band structure of elemental solids, Plenum Press, New York and London, 1986 Search PubMed.
- B. P. Lemke and D. Haneman, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1893–1907 CrossRef CAS.
- S. R. Schofield, P. Studer, C. F. Hirjibehedin, N. J. Curson, G. Aeppli and D. R. Bowler, Nat. Commun., 2013, 4, 1649 CrossRef CAS PubMed.
- R. Biswas, C. Z. Wang, C. T. Chan, K. M. Ho and C. M. Soukoulis, Phys. Rev. Lett., 1989, 63, 1491–1494 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27833g |
| ‡ This explains why their bond length d1 is so long (d1 ≈ 1.49 Å) in comparison with the 1.42 Å bond length of graphene at equilibrium. |
| § Although junction atoms are not second nearest neighbors in terms of atom connectivity, their distance range is in the second nearest distance range, and therefore, they should be considered as second nearest neighbors. |
| This journal is © The Royal Society of Chemistry 2017 |
