Open Access Article
Open Access ArticleFirst-principles investigation of the surface properties of fergusonite-type monoclinic BiVO4 photocatalyst
Guo-Ling Li *
*
School of Physics and Engineering, Henan University of Science and Technology, Luoyang 471023, China. E-mail: guoling.li@gmail.com; liguoling@dicp.ac.cn
First published on 30th January 2017
Abstract
Fergusonite-type monoclinic BiVO4 (fm-BiVO4) is an important semiconductor photocatalyst as an alternative to TiO2 for solar energy conversion and environmental protection. Based upon density functional theory (DFT) calculations, we report the results of a comprehensive study of the surface properties of fm-BiVO4, including surface geometric/electronic structures, surface energy, work function, Bader charge, and oxygen-vacancy formation energy on the (100), (010), (001), (101), (011), (110) and (111) surfaces. The low-index surfaces of fm-BiVO4 are characterized by surface geometric structures terminated with Bi atoms and VO4 groups. There are strongly localized band-gap states at the (110) and (111) surfaces. The calculated surface energies of fm-BiVO4 indicate a surface stability order of {001} > {011} ∼ {101} > {111} > {110} > {010} ∼ {100}. The equilibrium morphology of fm-BiVO4 is predicted as a corner-cut truncated bipyramid with {001}, {101}, {011} and {111} facets exposed, in good agreement with experiments. The dramatic difference in work function may act as the driving force for photogenerated charge separation between {101}/{011} and {001} as observed in experiments. Based on our results, we provide a clue to morphology design for further enhancing the efficiency of charge separation in fm-BiVO4.
1 Introduction
The surface physicochemical properties of semiconductor oxides are crucial in applications such as heterogeneous catalysis, molecule adsorption, gas sensing, and energy conversion and storage.1 To improve the desired physicochemical properties, semiconductor facets can be fine-tuned via morphology control strategies. For example, the {001} facets of anatase TiO2 are known to be especially reactive for photocatalysis. However, the {001} facets are the minority among exposed facets in the equilibrium morphology of anatase. It is desirable to synthesize anatase single crystals with a high percentage of {001} facets in order to improve the photocatalytic activity. Such a strategy has been successfully demonstrated recently.2 The success in morphology control for anatase depends on the knowledge of the surface physics and chemistry of TiO2 that have been extensively studied.3Much attention has been paid to bismuth vanadate BiVO4 due to its novel properties such as ferroelasticity,4 ionic conductivity,5 and acousto-optical6 and photochromic7 effects. With a high chemical stability, BiVO4 could be used as a nontoxic yellow pigment,8 potential cathode material in lithium cells,9 promising gas sensor,10 and good catalyst for the selective oxidation of olefins11 and H2S.12 Especially, under visible light irradiation, BiVO4 can robustly evolve O2 from water in the presence of sacrificial reagents (e.g., Ag+ and Fe3+ ions),13 selectively reduce CO2 into ethanol,14 photochemically decompose organic pollutants and oxidize inorganic chemicals such as NO,15 synthesize H2O2 from water and O2,16 and act as an efficient photoanode in photoelectrochemical cells.17,18 In this sense BiVO4 is considered as an important alternative photocatalyst to TiO2 for solar energy conversion and environmental protection.19
BiVO4 comprises four polymorphs, i.e., pucherite, dreyerite, clinobisvanite, and scheelite-type tetragonal phase.4,20 Among them clinobisvanite, i.e., fergusonite-type monoclinic BiVO4 (fm-BiVO4), is stable at ambient temperature and pressure, and is most often used as a photocatalyst. It has been found that the morphology of fm-BiVO4 has a strong impact on the photocatalytic activity, and much effort has been devoted to the controllable synthesis of fm-BiVO4 with specific morphologies.10,21–24 In particular, it has been confirmed that the photogenerated electrons and holes can be efficiently separated between different crystal facets of fm-BiVO4.25
To reveal the underlying structure–property relationships, density functional theory (DFT) calculations have been carried out for BiVO4, mainly for fm-BiVO4.18,22,26–35 Emphasis is placed on the role of Bi 6s orbitals which contain stereoactive electron lone pairs.26–29 For example, based on the calculated density of states (DOS), the Bi 6s orbitals are found to contribute considerably to the valence band (VB) top, and are inferred to result in a large hole mobility as well as the excellent photocatalytic activity of fm-BiVO4.26 Walsh et al. concluded that fm-BiVO4 is a direct bandgap semiconductor.28,29 However, Zhao et al. calculated fm-BiVO4 as an indirect one.30,31 The optical functions of fm-BiVO4 were calculated,28,30 and the strong optical anisotropy was related to the morphology dependence of photocatalytic activity.30 Doping properties were well studied for fm-BiVO4, based on which the doping impact on the photocatalytic or photoelectrochemical properties was discussed.31–34,36 Zhao et al. also calculated the surface energies of fm-BiVO4.37 The water adsorption properties on the (100) surface of fm-BiVO4 were investigated by a first-principles molecular dynamics approach, indicating that water is adsorbed molecularly at the fivefold-coordinated Bi site where water oxidization is supposed to occur.35
Compared to TiO2, BiVO4 is a much less studied semiconductor oxide, especially with respect to its surface properties. Here we report the comprehensive results of first-principles calculations of surface properties for fm-BiVO4. Low-index surfaces, i.e., (100), (010), (001), (101), (011), (110) and (111), are considered. Structural effects are carefully taken into account to understand the calculated surface properties including surface geometric/electronic structures, surface energy, work function, Bader charge, and oxygen-vacancy formation energy. The predicted equilibrium morphology of fm-BiVO4 is compared with the experimental one. We also discuss the possible driving force for photogenerated charge separation in photocatalysis, and provide clues to morphology design for further enhancing the efficiency of charge separation in fm-BiVO4.
2 Crystal structure and computational methodology
The crystal structure of fm-BiVO4 belongs to point group C62h and space group no. 15 in the international tables for crystallography. As is known, space group no. 15 has one conventional setting C2/c and several nonconventional settings such as I2/a, I2/b and B2/b. For fm-BiVO4, experimentalists were used to the body-centered setting I2/a while theorists preferred the base-centered setting C2/c.28,30,31,34,36,37 However, it is better to take the body-centered setting I2/b for fm-BiVO4 in order to make a direct comparison between the body-centered monoclinic fm-BiVO4 and the body-centered tetragonal BiVO4.4,5,33 In this work, we take the setting I2/b for the bulk and surfaces of fm-BiVO4. For the sake of convenience, we present in Table 1 the corresponding low indices of crystal face in the representation of the settings I2/a, B2/b and C2/c according to transformation matrices between these settings.38| Settings | Low indices of crystal face | ||||||
|---|---|---|---|---|---|---|---|
| I2/b | {100} | {010} | {001} | {101} | {011} | {110} | {111} |
| I2/a | {001} | {100} | {010} | {011} | {110} | {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) } } |
{11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) } } |
| B2/b | {100} | {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10} 10} |
{001} | {101} | {1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1} 1} |
{010} | {01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) } } |
| C2/c | {100} | {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01} 01} |
{010} | {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10} 10} |
{![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11} 11} |
{001} | {011} |
Fig. 1 shows the crystal structure of fm-BiVO4, a body-centered monoclinic cell in the setting I2/b.4,20 In view of centrosymmetry, we can classify fm-BiVO4 as a non-polar oxide. Owing to the weak symmetry breaking in the a–b plane, the crystal structure of fm-BiVO4 can be taken as a slight distortion of the scheelite-type tetragonal structure. Due to the distortion, there are two kinds of inequivalent oxygens, i.e., O(1) and O(2), both coordinated to two Bi atoms and one V atom. The isolated VO4 tetrahedron with the V atom surrounded by four oxygen atoms in a distorted tetrahedral geometry is coordinated to eight neighboring Bi atoms. The Bi atom together with the BiO8 dodecahedron is surrounded by eight VO4 tetrahedra. In addition, the BiO8 dodecahedron shares four edges with neighboring BiO8 dodecahedra but no edges with any VO4 tetrahedra. According to crystal chemistry, the structure of fm-BiVO4 can be regarded as made up of Bi3+ cations and VO43− anions. Table 2 lists the measured structural parameters.20
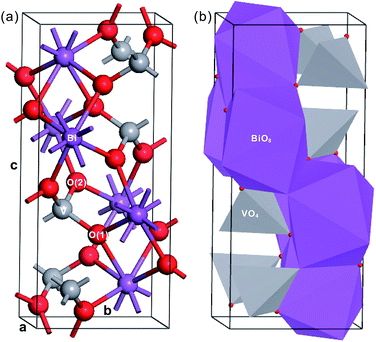 | ||
| Fig. 1 Crystal structure of fm-BiVO4. (a) In the ball-stick model and (b) in the polyhedron model. The Bi, Ti and O atoms are in purple, gray and red, respectively. | ||
| Exp. (295 K)20 | Cal. (GGA-PBE) | |
|---|---|---|
| a (Å) | 5.1935 | 5.177 |
| b (Å) | 5.0898 | 5.145 |
| c (Å) | 11.6972 | 11.769 |
| γ (°) | 90.3870 | 90 |
| Wyckoff | x | y | z | x | y | z | |
|---|---|---|---|---|---|---|---|
| Bi | 4(e) | 0.0000 | 0.2500 | 0.6335 | 0.000 | 0.250 | 0.626 |
| V | 4(e) | 0.0000 | 0.2500 | 0.1300 | 0.000 | 0.250 | 0.127 |
| O(1) | 8(f) | 0.1465 | 0.5077 | 0.2082 | 0.142 | 0.502 | 0.205 |
| O(2) | 8(f) | 0.2606 | 0.3810 | 0.4493 | 0.251 | 0.388 | 0.452 |
DFT calculations are done using the projector-augmented wave method39 and a plane-wave basis set as implemented in the Vienna Ab Initio Simulation Package (VASP).40 The generalized gradient approximation (GGA) formulated by Perdew, Burke and Ernzerhof (PBE) is taken for the exchange–correlation functional.41 The valence configurations are treated as 6s2 6p3 for Bi, 3d3 4s2 for V, and 2s2 2p4 for O. The cutoff energy for plane-wave basis functions is 400 eV. For simplification, the γ angle of fm-BiVO4 is approximated to 90°,26,28 which removes the tiny differences between {11k} and {1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) k} surfaces (k = 0, 1). For bulk structure optimization, calculations are done in a 10 × 10 × 6 Monkhorst–Pack (MP) k-point mesh with lattice parameters a, b, c varied and internal parameters (x, y, z) relaxed, based on which a 5 × 5 × 5 three-dimensional energy grid is obtained. The equilibrium structural parameters are derived from the lowest energy point on the interpolated energy grid. The non-polar (100), (010), (001), (101), (011), (110) and (111) surface slabs with 6, 7, 8, 9 and 10 layers of Bi/V cations are generated from the optimized bulk lattice. A 12 Å vacuum layer is added in the crystallographic planes of interest. We use a 4 × 2 × 1 MP k-point mesh for the (100) and (111) surfaces, 2 × 4 × 1 for the (010) surface, 4 × 4 × 1 for the (110) surface, and 4 × 6 × 1 for the (101) and (011) surfaces. For each surface slab, we use a conjugate-gradient algorithm to relax the atomic positions until forces converge to less than 0.02 eV Å−1 prior to the total energy calculation. It should be noted that the surface slabs with 8 layers of cations are thick enough for calculating surface electronic structures, Bader charges, work functions, and O-vacancy formation energies. The surface slabs with 6, 7, 8, 9 and 10 layers of cations are used to obtain accurate surface energies which are crucial to morphology prediction for fm-BiVO4. For slab calculations, dipole correction is taken into account. All the calculations are non-spin-polarized except those for O-vacancy formation energies.
k} surfaces (k = 0, 1). For bulk structure optimization, calculations are done in a 10 × 10 × 6 Monkhorst–Pack (MP) k-point mesh with lattice parameters a, b, c varied and internal parameters (x, y, z) relaxed, based on which a 5 × 5 × 5 three-dimensional energy grid is obtained. The equilibrium structural parameters are derived from the lowest energy point on the interpolated energy grid. The non-polar (100), (010), (001), (101), (011), (110) and (111) surface slabs with 6, 7, 8, 9 and 10 layers of Bi/V cations are generated from the optimized bulk lattice. A 12 Å vacuum layer is added in the crystallographic planes of interest. We use a 4 × 2 × 1 MP k-point mesh for the (100) and (111) surfaces, 2 × 4 × 1 for the (010) surface, 4 × 4 × 1 for the (110) surface, and 4 × 6 × 1 for the (101) and (011) surfaces. For each surface slab, we use a conjugate-gradient algorithm to relax the atomic positions until forces converge to less than 0.02 eV Å−1 prior to the total energy calculation. It should be noted that the surface slabs with 8 layers of cations are thick enough for calculating surface electronic structures, Bader charges, work functions, and O-vacancy formation energies. The surface slabs with 6, 7, 8, 9 and 10 layers of cations are used to obtain accurate surface energies which are crucial to morphology prediction for fm-BiVO4. For slab calculations, dipole correction is taken into account. All the calculations are non-spin-polarized except those for O-vacancy formation energies.
3 Computational results
3.1 Bulk geometric and electronic structures
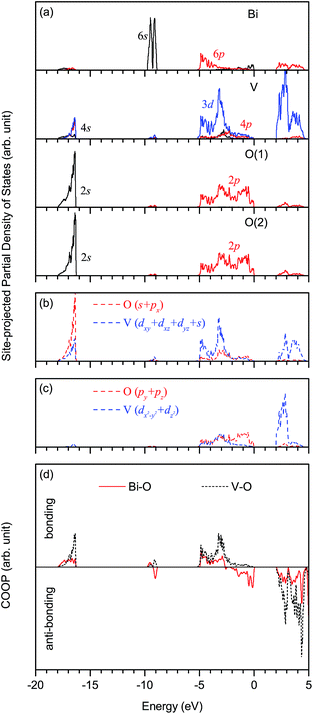
The optimized structural parameters of fm-BiVO4 are presented in Table 2, in good agreement with the experiment.20 In the same representation of space group, our optimized lattice constants a, b and c are quite close to those calculated by Walsh et al.28 The V–O bond lengths dV–O are calculated to be 1.739 and 1.751 Å, and the Bi–O bond lengths dBi–O are 2.432, 2.451, 2.473 and 2.532 Å.Fig. 2 shows the site-projected partial DOS and chemical bonding analysis of fm-BiVO4 in the energy range from −20 eV to 5 eV. Here, Crystal Orbital Overlap Population (COOP) for chemical bonding analysis is done with the computer program LOBSTER,42 based on the PAW results calculated using VASP. The Bi 6s states are located predominantly around −9.3 eV, and partially around −17 eV and between −2.5 to 0 eV. However, the Bi–O bonding magnitude is rather small around −9.3 eV compared to those around −17 eV and between −2.5 to 0 eV. Thus, the Bi 6s orbital can be characterized as strongly non-bonding around −9.3 eV, weakly bonding around −17 eV and anti-bonding between −2.5 to 0 eV. There are notable Bi 6p states below the Fermi level, indicating that the Bi atom is not fully ionized into the expected Bi3+ cation. The mixing between the Bi 6p orbital and the O 2p orbital occurs mainly around −5 to −3 eV (bonding) and above 2 eV (anti-bonding). As in CrO42− and MnO4−,43 the d3s (3dxy, 3dxz, 3dyz, 4s) hybrid orbitals of vanadium in VO43− dominate in the tetrahedral hybridization with considerable mixing among the V 3d and 4p orbitals. The inequivalent O(1) and O(2) have an overall similar DOS with the 2s orbital around −17 eV and the 2p orbital around the Fermi level. As shown in Fig. 2(b), the V d3s hybrid orbitals overlap with the O sp (2s, 2px) hybrid orbitals, forming four σ bonds. In Fig. 2(c), the empty V 3dx2−y2 and 3dz2 orbitals overlap with the O 2py and 2pz orbitals, resulting in two delocalized 5-center-8-electron Π85 bonds.43 The main charge compositions are the O 2p (64.7%) and Bi 6s (12.6%) states at the VB edge, and the V 3d (70.7%) and Bi 6p (11.7%) states at the conduction band (CB) edge. In particular, the O 2py and 2pz orbitals contribute 51.0% at the VB edge, and the V 3dx2−y2 and 3dz2 orbitals 67.0% at the CB edge, implying that the Π85 bonds play the most important role in physical properties determined by band edges. The calculated band gap Eg is 2.07 eV, close to the reported values.26,28,30–34
3.2 Surface cleavage
The surface cleavage of fm-BiVO4 involves Bi–O and/or V–O bond disruption. It has been noted that the V–O bond strength in the rigid VO4 tetrahedron is much stronger than the Bi–O bond strength in the BiO8 dodecahedron.44 Thus, the surface of fm-BiVO4 is likely to consist of Bi cations and VO4 tetrahedra on all faces.11Here we make an estimate of the Bi–O and V–O bond energies. Considering the (100) surface unit cell, there are 12 Bi–O bonds disrupted in the expected termination with Bi–O–V and VO4 groups at the surface.11,26 In another possible termination with Bi–O–Bi and VO3 groups at the surface, there are only 6 Bi–O and 2 V–O bonds disrupted. The latter termination is 1.96 eV higher in energy than the former one for each surface Bi or V atom. Assuming simply that all Bi–O (V–O) bonds are identical, we obtain the Bi–O (V–O) bond energy EBi–O (EV–O) in terms of (Eunrelslab − Ebulk)/2 = NBi–OEBi–O + NV–OEV–O, where Eunrelslab denotes the total energy of the unrelaxed slab, Ebulk is the corresponding total energy of the bulk, and NBi–O (NV–O) is the number of disrupted Bi–O (V–O) bonds at the surface. EBi–O is then estimated to be 0.52 eV and EV–O is estimated as 3.54 eV, indicating that the Bi–O bond strength is much weaker than the V–O bond strength.
Thus, we make sure that the stable surfaces of fm-BiVO4 are terminated with Bi atoms and VO4 groups, directly supporting the above-mentioned argument from crystal chemistry.11,44
3.3 Surface geometric and electronic structures
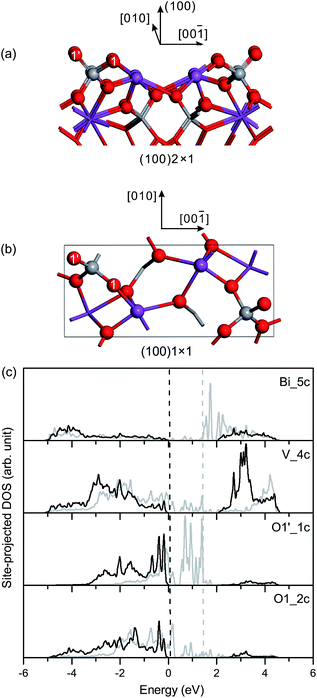
Based on the optimized structural parameters, we constructed the surface slabs of fm-BiVO4. It should be noted that, due to the weak symmetry breaking in the a–b plane, there are only trivial differences between {100} and {010} in the surface geometric structures of fm-BiVO4. It is the same between {101} and {011}. According to the structure–property relationships, physical properties, e.g., surface electronic structures, surface energies and work functions, are expected to be similar for {100}/{010} or {101}/{011}.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond with a bond length of 1.614 Å, as presented in Table 3. The surface V–O bond length is 1.755 Å, close to the bulk values. In the unrelaxed slab of fm-BiVO4 (100), the surface Bi and V atoms are coplanar in the surface plane. In the relaxed slab, the surface Bi atom moves inward 0.13 Å while the surface V atom moves outward 0.07 Å along the [100] direction.
O double bond with a bond length of 1.614 Å, as presented in Table 3. The surface V–O bond length is 1.755 Å, close to the bulk values. In the unrelaxed slab of fm-BiVO4 (100), the surface Bi and V atoms are coplanar in the surface plane. In the relaxed slab, the surface Bi atom moves inward 0.13 Å while the surface V atom moves outward 0.07 Å along the [100] direction.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in Å in the bulk and on the surfaces of fm-BiVO4
O in Å in the bulk and on the surfaces of fm-BiVO4
| Bulk | (100) | (010) | (001) | (101) | (011) | (110) | (111) | |
|---|---|---|---|---|---|---|---|---|
| dV–O | 1.739 | 1.755 | 1.756 | 1.692 | 1.686 | 1.688 | 1.730 | 1.727 |
| 1.751 | 1.718 | 1.718 | 1.667 | 1.679 | ||||
| 1.707 | 1.704 | 1.733 | ||||||
| 1.670 | ||||||||
dV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.614 | 1.614 | 1.629 | 1.630 | ||||
| 1.620 |
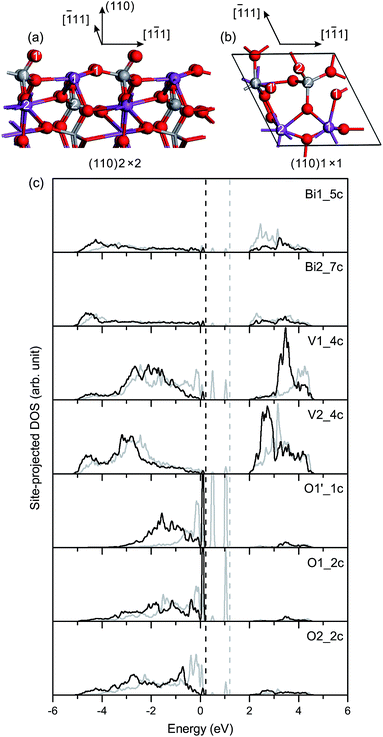
Fig. 3(c) shows the site-projected DOS of specific surface atoms in the relaxed and unrelaxed (100) surface slabs, denoted by black and grey curves, respectively. For the unrelaxed slab, the empty backbond 6p states of the surface Bi atom lie in the bulk band-gap region. The Π85 bonds are totally broken in the surface VO4 group. The occupied backbond 2p states of the surface O1′, overlapping heavily with the V 3d states, are located in the bulk band-gap region too. As is known, surface relaxation often shifts the occupied ideal surface states down and the empty ideal surface states up in energy.45 Thus, for the relaxed slab, surface relaxation makes the band-gap surface states merge into the bulk region. Only O 2p-derived resonances are found in the upper valence band region, and the surface Fermi level almost coincides with the bulk one.
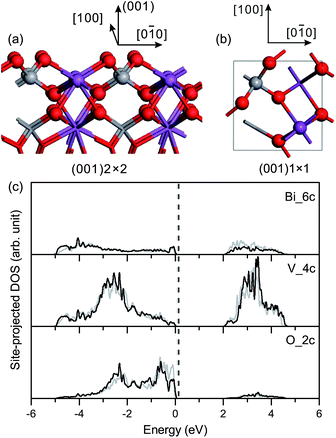
Surface relaxation is negligible for the fm-BiVO4 (001) surface, and the site-projected DOS of specific surface atoms is similar for the relaxed and unrelaxed surface slabs, as shown in Fig. 4(c). The Π85 bonds remain in the surface VO4 group with an increase in the bonding–antibonding splitting. No band-gap states occur in the band-gap region.
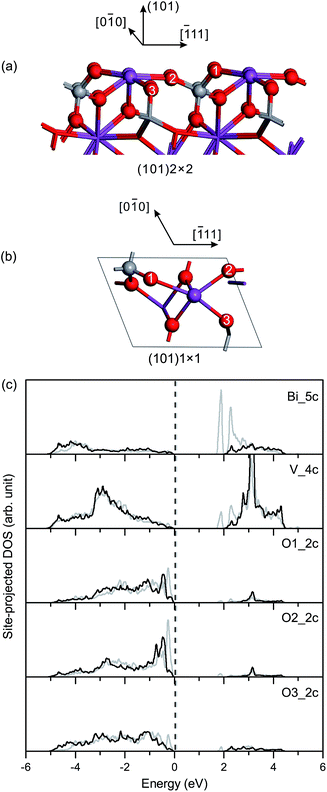
Fig. 5(c) shows the site-projected DOS of specific surface atoms in the relaxed and unrelaxed (101) surface slabs. For the unrelaxed slab, the empty backbond 6p states of the surface Bi atom are located in the bulk band-gap region. The Π85 bonds remain in the surface and subsurface VO4 groups, with an increase in the bonding-antibonding splitting. For the relaxed slab, the surface states of Bi 6p disappear due to surface relaxation, and no band-gap states occur in the band-gap region.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is 1.629 Å at the (110) surface, slightly longer than that at the (100)/(010) surface. In the unrelaxed slab, the Bi1 (Bi2) and V1 (V2) atoms are coplanar in the surface plane. In the relaxed slab, Bi1, Bi2 and V1 atoms move inward 0.15 Å, 0.04 Å and 0.02 Å, respectively, and the V2 atom moves outward 0.04 Å along the [100] direction.
O is 1.629 Å at the (110) surface, slightly longer than that at the (100)/(010) surface. In the unrelaxed slab, the Bi1 (Bi2) and V1 (V2) atoms are coplanar in the surface plane. In the relaxed slab, Bi1, Bi2 and V1 atoms move inward 0.15 Å, 0.04 Å and 0.02 Å, respectively, and the V2 atom moves outward 0.04 Å along the [100] direction.
Fig. 6(c) shows the site-projected DOS of specific surface atoms in the relaxed and unrelaxed (110) surface slabs. The Π85 bonds remain in the surface and subsurface VO4 groups. The bonding–antibonding splitting of Π85 is larger in the surface VO4 than in the subsurface VO4. For the unrelaxed slab, two sharp peaks of occupied dangling-bond states lie in the band-gap region. The two dangling bonds are derived from the Π85 bonds in the surface VO4. Due to surface relaxation, one peak of the dangling-bond states merges into the bulk VB region, and the other is fixed at 0.1–0.2 eV above the VB top. Thus, there are dangling-bond states in the band-gap region of the (110) surface.
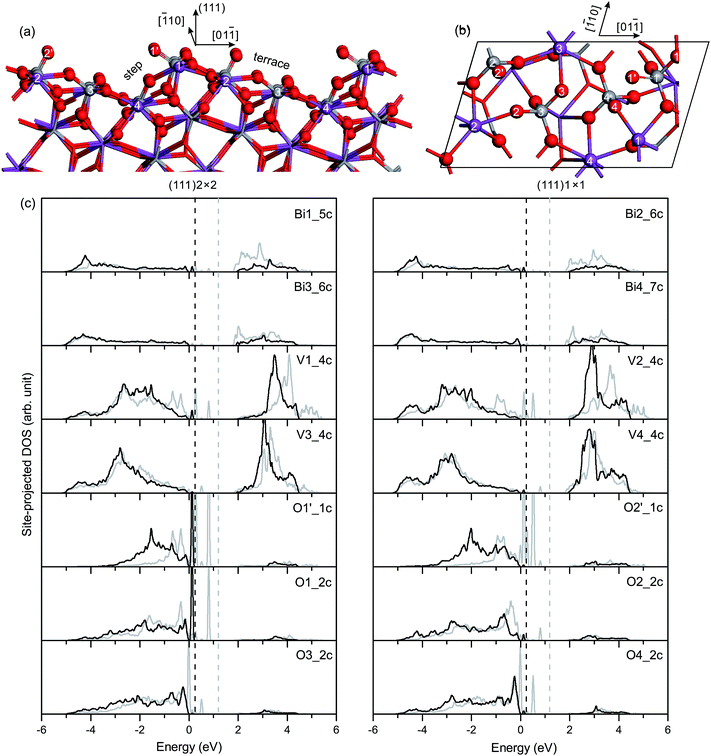
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O on the (111) surface is nearly the same as that on the (110) surface, as given in Table 3. In the unrelaxed slab, the Bi and V atoms are coplanar in the surface plane. In the relaxed slab, Bi1, Bi2, Bi3 and Bi4 atoms move inward 0.11 Å, 0.13 Å, 0.04 Å and 0.07 Å, respectively. However, the four surface V atoms do not move much along the [100] direction (≤0.01 Å).
O on the (111) surface is nearly the same as that on the (110) surface, as given in Table 3. In the unrelaxed slab, the Bi and V atoms are coplanar in the surface plane. In the relaxed slab, Bi1, Bi2, Bi3 and Bi4 atoms move inward 0.11 Å, 0.13 Å, 0.04 Å and 0.07 Å, respectively. However, the four surface V atoms do not move much along the [100] direction (≤0.01 Å).
Fig. 7(c) shows the site-projected DOS of specific surface atoms in the relaxed and unrelaxed (111) surface slabs. The Π85 bonds remain in the surface VO4 groups. For the unrelaxed slab, sharp peaks of occupied dangling-bond states lie in the band-gap region. The dangling bonds are derived from the Π85 bonds in the four surface VO4 groups. Due to surface relaxation, only one peak of the dangling-bond states from the Π85 bonds in the V1O4 group is fixed at 0.1–0.2 eV above the VB top. All other dangling-bond states merge into the bulk VB region. Thus, there are dangling-bond states in the band-gap region of the (111) surface.
3.4 Surface energy and equilibrium morphology
The surface energy σ is defined as
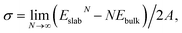 | (1) |
The relaxation energy, i.e., the energy gain due to relaxation of the ideally cut surface, is calculated as Erelax = (Eunrelaxedslab − Erelaxedslab)/2A.47 Here, Erelaxedslab and Eunrelaxedslab denote the total energies of relaxed and unrelaxed slabs, respectively. The unrelaxed surface energy σu is then obtained via σu = σr + Erelax.
The calculated unrelaxed surface energies σu and relaxation energies Erelax for low-index surfaces of fm-BiVO4 can be classified into three groups, as shown in Table 4. The calculated σu (Erelax) are ∼1.7 J m−2 (1.1 J m−2) for the (100)/(010) surfaces, 0.46 J m−2 (0.15 J m−2) for the (001) surface, and ∼1.0 J m−2 (0.6 J m−2) for other surfaces. The calculated relaxed surface energies σr of fm-BiVO4 indicate a surface stability order of {001} > {011} ∼ {101} > {111} > {110} > {010} ∼ {100}, in good agreement with reported results.37 The most stable surface is {001}, in accordance with the fact that fm-BiVO4 exhibits a perfect {001} cleavage.48
| Surface | {100} | {010} | {001} | {101} | {011} | {110} | {111} |
|---|---|---|---|---|---|---|---|
| A | 60.55 | 60.93 | 26.64 | 33.08 | 33.25 | 42.95 | 89.94 |
| NDB | 12 | 12 | 4 | 6 | 6 | 8 | 16 |
| σr | 0.63 | 0.62 | 0.31 | 0.35 | 0.34 | 0.57 | 0.49 |
| 0.8848 (ref. 37) | — | 0.5016 (ref. 37) | 0.5517 (ref. 37) | 0.5496 (ref. 37) | 0.8765 (ref. 37) | — | |
| σu | 1.67 | 1.77 | 0.46 | 0.92 | 0.95 | 1.10 | 1.02 |
| Erelax | 1.04 | 1.15 | 0.15 | 0.57 | 0.61 | 0.53 | 0.53 |
| ϕ | 6.96 | 6.90 | 7.20 | 5.93 | 5.98 | 6.89 | 6.82 |
As is known, the surface energy is associated with the disruption of chemical bonds at the surface. It is therefore reasonable to assume that σr is proportional to the density of disrupted chemical bonds at the surfaces with similar geometric structures. Surfaces except (101) and (011) exhibit a good linear relation between σr and NDB/A, as shown in Fig. 8. Here, NDB is the number of disrupted Bi–O bonds listed in Table 4. The (101) and (011) surfaces are terminated with only Bi atoms while all other surfaces are terminated with both Bi atoms and VO4 groups. Thus, the deviation of (101) and (011) from other surfaces can be ascribed to their distinct surface geometric structures.
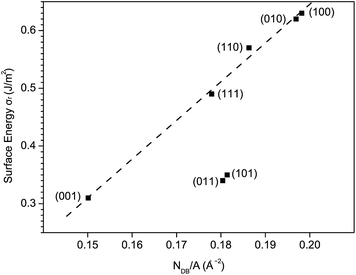 | ||
| Fig. 8 The relaxed surface energy σr vs. surface density of disrupted Bi–O bonds NDB/A for low-index surfaces of fm-BiVO4. | ||
The equilibrium morphology of a crystal can be determined from the calculated surface energies σr via Wulff construction.49 Fig. 9(a) shows an SEM image of fm-BiVO4 samples from our previous work.24 Fig. 9(b) is the predicted equilibrium morphology of fm-BiVO4, a corner-cut truncated bipyramid with {001}, {101}, {011} and {111} facets exposed. The {101}/{011} facets contribute 77.3%, {001} 22.0%, and {111} 0.7% to the total surface region. The magnified insets demonstrate the good agreement between prediction and measurement. The equilibrium morphology of fm-BiVO4 was widely observed in experiments by others.23 Compared to the morphology predicted by Zhao et al., our results reveal the existence of {111} facets for real crystals of fm-BiVO4.
 | ||
| Fig. 9 Equilibrium morphology of fm-BiVO4. (a) The SEM image;24 (b) prediction. | ||
3.5 Work function
The work function ϕ is determined by| ϕ = Ev − EF, | (2) |
The calculated surface-dependent work functions of fm-BiVO4 are presented in Table 4. It should be noted that, due to the existence of occupied band-gap states, the EF of (110) and (111) are 0.2 eV higher in energy than those of other surfaces. Thus, the Fermi level pinning at the surface contributes 0.2 eV to the reduction of the work functions of (110) and (111). Furthermore, the variation in ϕ between the different surfaces of fm-BiVO4 is related to the surface dipole layer. For simplicity, the position of the V atom can be roughly taken as the negative charge center of the VO43− anion, and the position of the Bi atom as the positive charge center of the Bi3+ cation. As mentioned above, for all unrelaxed surface slabs except (101) and (011), the surface Bi and V atoms are coplanar in the surface plane, indicating that the net surface dipole is approximately zero. However, surface relaxation makes a relative displacement Δd between the surface Bi and V atoms along the surface orientation, inducing a positive surface dipole. The Δd values, proportional to the magnitude of the surface dipole, are 0.08 Å, 0.11 Å, 0.11 Å and 0.19 Å for (001), (110), (111) and (100)/(010), respectively. As is known, the larger the positive surface dipole the smaller the value of ϕ. Therefore, if the Fermi level pinning is not included, ϕ would decrease with increasing Δd in the sequence (001), (110), (111) and (100)/(010). If the Fermi level pinning is included, ϕ would decrease in the sequence (001), (100)/(010), (110) and (111), as shown in Table 4.
For the unrelaxed surface slabs of (101) and (011), the outermost layer is the Bi atom, the sublayer and sub-sublayer are the VO4 groups, indicating a large outward-pointing permanent surface dipole. Surface relaxation results in a relative displacement Δd of 0.36 Å between the surface Bi and V atoms along the surface orientation. The induced surface dipole is positive, compensating partially for the loss in the permanent surface dipole. In short, the large surface dipole layer remains at the (101) and (011) surfaces, and causes a dramatic reduction of more than 1 eV in the work function.
3.6 Bader charge analysis
The calculated Bader charges on Bi, V and O atoms in bulk fm-BiVO4 are +2.25e, +2.43e and −1.17e, respectively. Here, e denotes the elementary charge. The Bader charge on the Bi atom is close to the assumed +3 oxidation state of the Bi3+ cation, indicating that the bonding between Bi and O is mainly ionic in nature. In contrast, the Bader charge on the V atoms is much smaller than the expected +5 oxidation state of the V5+ cation, implying that the bonding between V and O is considerably covalent in nature.In Table 5, we present the calculated Bader charges on all specific surface atoms. Due to the ionic nature of bonding, Bader charges on surface Bi atoms remain around +2.20e. In contrast, Bader charges for all surfaces except (001) are reduced to around +2.0e, −1.0e and −0.7e on the V, twofold-coordinated O and onefold-coordinated O atoms, respectively. The reduction in Bader charges originates from charge transfer between V and O at the surfaces. It is worth noting that the Bader charges on Bi, V and O atoms at the (001) surface are rather close to those in the bulk, indicating that the chemical bonding is almost unchanged in the [001] orientation by surface interruption.
| Surface | (100) | (010) | (001) | (101) | (011) | (110) | (111) |
|---|---|---|---|---|---|---|---|
| Q(Bi_5c) | +2.22 | +2.20 | +2.19 | +2.16 | +2.12 | +2.16 | |
| Q(Bi_6c) | +2.26 | +2.09 | |||||
| Q(Bi_6c) | +2.17 | ||||||
| Q(Bi_7c) | +2.19 | +2.22 | |||||
| Q(V_4c) | +2.03 | +2.04 | +2.34 | +1.99 | +2.02 | +2.13 | +2.01 |
| +2.05 | +1.96 | ||||||
| +1.92 | |||||||
| +1.96 | |||||||
| Q(O_1c) | −0.75 | −0.79 | |||||
| −0.70 | −0.69 | −0.70 | |||||
| Q(O_2c) | −1.10 | −1.03 | −1.02 | −0.97 | −0.93 | −0.92 | −1.03 |
| −1.03 | −1.03 | −0.91 | −0.92 | ||||
| −0.99 | −1.04 | −0.98 | |||||
| −0.94 |
3.7 Oxygen vacancy formation energy
Oxygen vacancies, a common defect in the bulk and at the surface, have a strong impact on functional properties of oxides. In particular, oxygen vacancies are crucial to understanding the surface catalysis of oxides. Here, we use the O-vacancy formation energy EOvf defined as53
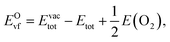 | (3) |
The oxygen vacancy in bulk fm-BiVO4 is modelled in a 2 × 2 × 1 supercell. The calculated bulk EOvf is 4.36 eV for both O(1) and O(2). In Table 6 we present the calculated surface EOvf together with the corresponding surface supercells. At the (100)/(010), (110) and (111) surfaces, the onefold-coordinated O1′ atom is most likely to form an oxygen vacancy. The onefold-coordinated O2′ at the (111) surface, however, is rather stable due to the specific geometry of VO4 sitting in the terrace of (111). At the (101)/(011) surface, the twofold-coordinated O3 atom in the subsurface VO4 group tends to form an O vacancy. At the (001) surface, the surface EOvf is 4.26 eV, quite close to the bulk value.
| Surface | (100) | (010) | (001) | (101) | (011) | (110) | (111) |
|---|---|---|---|---|---|---|---|
| Size | 2 × 1 | 1 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 1 |
| EO_1cvf | 3.38 | 3.36 | 3.41 | 3.40 | |||
| 3.71 | |||||||
| EO_2cvf | 3.81 | 3.76 | 4.26 | 4.36 | 4.33 | 3.78 | 3.66 |
| 4.28 | 4.24 | 4.46 | 3.69 | ||||
| 3.80 | 3.83 | 3.76 | |||||
| 3.81 |
It is interesting to make a comparison of the O-vacancy formation energies between fm-BiVO4 and rutile TiO2. The calculated EOvf for bulk TiO2 is 4.11 eV, comparable to that of fm-BiVO4. However, the EOvf at the TiO2 (110) surface is 2.73 eV, about 0.6–1.5 eV lower in energy than those at the low-index surfaces of fm-BiVO4. As is known, the formation of oxygen vacancies is common at the TiO2 (110) surface. In contrast, the formation of oxygen vacancies is expected to be rather difficult at the low-index surfaces (especially (001)) of fm-BiVO4. Thus, lattice oxygens are not likely to take part in the oxygen evolution reaction at the surfaces of fm-BiVO4.
4 Discussion
As evidenced by experiments,25 spatial charge separation occurs between the {001} and the {101}/{011} facets of fm-BiVO4. Photogenerated holes tend to locate at the {101}/{011} facets while photogenerated electrons locate at the {001} facets. A plausible explanation is that the driving force for charge separation is the huge difference of 1.2 eV in work function between {101}/{011} and {001}. As we know, the larger the work function, the lower the Fermi level or band edges. Thus, electrons prefer to locate on the {001} facets (ϕ = 7.20 eV) while holes prefer to locate on the {101}/{011} facets (ϕ ∼ 6 eV).There are no band-gap states for all surfaces except (110) and (111), and the band-gap states at the (110) and (111) surfaces are very close to the bulk VB top. Thus, whatever facets are exposed in real crystals, the optical absorption of fm-BiVO4 would remain the same.
It should be kept in mind that the occupied band-gap states act as hole acceptors. When photogenerated holes and electrons migrate to the surfaces, only (110) and (111) could make the photogenerated holes localize at the surface. The localization of holes would reduce the possibility of charge recombination and consequently promote spacial charge separation. As mentioned above, the {111} facets exist in real crystals of fm-BiVO4, although the percentage is small among the exposed facets. If the percentage of {111} or {110} can be enhanced by morphology design, the efficiency of charge separation would be further improved for fm-BiVO4.
Under in situ conditions of photocatalytic reactions, the exposed facets of fm-BiVO4 are covered by water and/or cocatalysts. The adsorption of water molecules and/or nanoparticles on the surfaces would modify the intrinsic surface properties of fm-BiVO4, such as the work function and band-gap states. However, to what degree intrinsic surface properties will be modified under in situ conditions is still an open question, and deserves further effort.
5 Conclusions
The low-index surfaces of fm-BiVO4 are characterized by surface geometric structures terminated with Bi atoms and VO4 groups. Similarity in surface geometric structures occurs between (100) and (010) as well as between (101) and (011). There are twofold-coordinated O atoms at the (001), (101) and (011) surfaces, and both onefold- and twofold-coordinated O atoms at the (100), (010), (110) and (111) surfaces. For (101) and (011), surface VO4 groups are underneath the surface Bi atoms. For all other surfaces except (101) and (011), surface Bi atoms and VO4 groups are nearly coplanar in the surface plane. At the (100), (010), (110) and (111) surfaces, there are bridge sites for adsorption between neighboring surface Bi atoms.For the (100), (010), (001), (101) and (011) surfaces, no surface states occur in the band gap region. At the (110) and (111) surfaces, however, there are strongly localized band-gap states derived from the dangling Π85 bonds of surface VO4 group. The band-gap states are occupied and are located at 0.1–0.2 eV above the bulk VB edge. Surface relaxation has a strong impact on the surface electronic structure for all surfaces except (001). The calculated surface energies of fm-BiVO4 indicate a surface stability order of {001} > {011} ∼ {101} > {111} > {110} > {010} ∼ {100}. The equilibrium morphology of fm-BiVO4 is predicted as a corner-cut truncated bipyramid with {001}, {101}, {011} and {111} facets exposed, in good agreement with experiments. The percentages of {101}/{011}, {001} and {111} facets are 77.3%, 22.0% and 0.7%, respectively.
The calculated surface-dependent work functions of fm-BiVO4 could be explained through consideration of the surface dipole effect. In particular, the work functions of (101) and (011) are ∼6 eV, about 1 eV lower in energy than the work functions of other surfaces. The dramatic difference in work function might provide the driving force for charge separation between {101}/{011} and {001} as observed in the experiment. To further improve the efficiency of charge separation in photocatalysis, the strategy of morphology design could be used to increase the percentage of {111} and (110) facets.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (U1404212 and 11404098) and Henan University of Science and Technology (2013ZCX018). G. L. L. thanks W.-X. Li, C. Li, F. Studt, S. Siahrostami, J. K. Nørskov, D.-P. Sun, W.-C. Ding, D. Wang, and H.-X. Ma for their valuable suggestions and kind help.References
- G. Liu, J. C. Yu, G. Q. M. Lu and H.-M. Cheng, Chem. Commun., 2011, 47, 6763–6783 RSC
.
- H. G. Yang, C. H. Sun, S. Z. Qiao, J. Zou, G. Liu, S. C. Smith, H. M. Cheng and G. Q. Lu, Nature, 2008, 453, 638–641 CrossRef CAS PubMed
.
- A. L. Linsebigler, G. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735–758 CrossRef CAS
.
- R. M. Hazen and J. W. E. Mariathasan, Science, 1982, 216, 991–993 CAS
.
- L. Hoffart, U. Heider, R. A. Huggins, W. Witschel, R. Jooss and A. Lentz, Ionics, 1996, 2, 34–38 CrossRef CAS
.
- C. Manolikas and S. Amelinckx, Phys. Status Solidi A, 1980, 60, 167–172 CrossRef CAS
.
- A. Tuücks and H. P. Beck, Dyes Pigm., 2007, 72, 163–177 CrossRef
.
- High Performance Pigments, ed. E. B. Faulkner and R. J. Schwartz, Wiley-VCH, Weinheim, 2nd edn, 2009 Search PubMed
.
- M. Pasquali and G. Pistoia, J. Power Sources, 1989, 27, 29–34 CrossRef CAS
.
- Y. Zhao, Y. Xie, X. Zhu, S. Yan and S. Wang, Chem.–Eur. J., 2008, 14, 1601–1606 CrossRef CAS PubMed
.
- A. W. Sleight and W. J. Linn, Ann. N. Y. Acad. Sci., 1976, 272, 22–44 CrossRef CAS
.
- K.-T. Li, M.-Y. Huang and W.-D. Cheng, Ind. Eng. Chem. Res., 1996, 35, 621–626 CrossRef CAS
.
- A. Kudo, K. Omori and H. Kato, J. Am. Chem. Soc., 1999, 121, 11459–11467 CrossRef CAS
.
- Y. Liu, B. Huang, Y. Dai, X. Zhang, X. Qin, M. Jiang and M.-H. Whangbo, Catal. Commun., 2009, 11, 210–213 CrossRef CAS
.
- G. Li, D. Zhang and J. C. Yu, Chem. Mater., 2008, 20, 3983–3992 CrossRef CAS
.
- H. Hirakawa, S. Shiota, Y. Shiraishi, H. Sakamoto, S. Ichikawa and T. Hirai, ACS Catal., 2016, 6, 4976–4982 CrossRef
.
- K. Sayama, A. Nomura, Z. Zou, R. Abe, Y. Abe and H. Arakawa, Chem. Commun., 2003, 2908–2909 RSC
.
- K. Sayama, A. Nomura, T. Arai, T. Sugita, R. Abe, M. Yanagida, T. Oi, Y. Iwasaki, Y. Abe and H. Sugihara, J. Phys. Chem. B, 2006, 110, 11352–11360 CrossRef CAS PubMed
.
- M. D. Hernández-Alonso, F. Fresno, S. Suárez and J. M. Coronado, Energy Environ. Sci., 2009, 2, 1231–1257 Search PubMed
.
- A. W. Sleight, H. y. Chen, A. Ferretti and D. E. Cox, Mater. Res. Bull., 1979, 14, 1571–1581 CrossRef CAS
.
- G. Xi and J. Ye, Chem. Commun., 2010, 46, 1893–1895 RSC
.
- Y. Sun, C. Wu, R. Long, Y. Cui, S. Zhang and Y. Xie, Chem. Commun., 2009, 4542–4544 RSC
.
- X. Meng, L. Zhang, H. Dai, Z. Zhao, R. Zhang and Y. Liu, Mater. Chem. Phys., 2011, 125, 59–65 CrossRef CAS
.
- D. Wang, H. Jiang, X. Zong, Q. Xu, Y. Ma, G.-L. Li and C. Li, Chem.–Eur. J., 2011, 17, 1275–1282 CrossRef CAS PubMed
.
- J. Zhu, F. Fan, R. Chen, H. An, Z. Feng and C. Li, Angew. Chem., Int. Ed. Engl., 2015, 54, 9111–9114 CrossRef CAS PubMed
.
- M. Oshikiri, M. Boero, J. Ye, Z. Zou and G. Kido, J. Chem. Phys., 2002, 117, 7313–7318 CrossRef CAS
.
- M. W. Stoltzfus, P. M. Woodward, R. Seshadri, J.-H. Klepeis and B. Bursten, Inorg. Chem., 2007, 46, 3839–3850 CrossRef CAS PubMed
.
- A. Walsh, Y. Yan, M. N. Huda, M. M. Al-Jassim and S.-H. Wei, Chem. Mater., 2009, 21, 547–551 CrossRef CAS
.
- D. J. Payne, M. D. M. Robinson, R. G. Egdell, A. Walsh, J. McNulty, K. E. Smith and L. F. J. Piper, Appl. Phys. Lett., 2011, 98, 212110 CrossRef
.
- Z. Zhao, Z. Li and Z. Zou, Phys. Chem. Chem. Phys., 2011, 13, 4746–4753 RSC
.
- Z. Zhao, W. Luo, Z. Li and Z. Zou, Phys. Lett. A, 2010, 374, 4919–4927 CrossRef CAS
.
- M. R. Dolgos, A. M. Paraskos, M. W. Stoltzfus, S. C. Yarnell and P. M. Woodward, J. Solid State Chem., 2009, 182, 1964–1971 CrossRef CAS
.
- S. Yao, K. Ding and Y. Zhang, Theor. Chem. Acc., 2010, 127, 751–757 CrossRef CAS
.
- W.-J. Yin, S.-H. Wei, M. M. Al-Jassim, J. Turner and Y. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155102 CrossRef
.
- M. Oshikiri, M. Boero, A. Matsushita and J. Ye, J. Electroceram., 2009, 22, 114–119 CrossRef CAS
.
- H. S. Park, K. E. Kweon, H. Ye, E. Paek, G. S. Hwang and A. J. Bard, J. Phys. Chem. C, 2011, 115, 17870–17879 CAS
.
- Z. Zhao, Z. Li and Z. Zou, RSC Adv., 2011, 1, 874–883 RSC
.
- http://www.cryst.ehu.es/cryst/get_gen.html.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, R558–R561 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed
.
- A. S. Kunju and G. Krishnan, Group Theory and its Applications in Chemistry, PHI Learning Pvt. Ltd., New Delhi, 2010 Search PubMed
.
- J. W. E. Mariathasana, R. M. Hazenb and L. W. Finger, Phase Transform., 1986, 6, 165–174 CrossRef
.
- I. Ivanov and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 7275–7296 CrossRef CAS
.
- V. Fiorentini and M. Methfessel, J. Phys.: Condens. Matter, 1996, 8, 6525–6529 CrossRef CAS
.
- N. V. Skorodumova, M. Baudin and K. Hermansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075401 CrossRef
.
- O. v. Knorring, T. G. Sahama, M. Lehtinen, P. Rehtijärvi and J. Siivola, Contrib. Mineral. Petrol., 1973, 41, 325–331 CrossRef
.
- M. A. Lovette, A. R. Browning, D. W. Griffin, J. P. Sizemore, R. C. Snyder and M. F. Doherty, Ind. Eng. Chem. Res., 2008, 47, 9812–9833 CrossRef CAS
.
- W. Liu, W. T. Zheng and Q. Jiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235322 CrossRef
.
- A. Groß, Theoretical Surface Science: A Microscopic Perspective, Springer-Verlag, Berlin, 2nd edn, 2009 Search PubMed
.
- T. C. Leung, C. L. Kao, W. S. Su, Y. J. Feng and C. T. Chan, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195408 CrossRef
.
- M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219–270 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2017 |