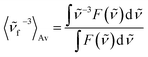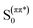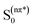Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photophysical properties of betaxanthins: miraxanthin V – insight into the excited-state deactivation mechanism from experiment and computations†
Stanisław Nizińskia,
Monika Wendela,
Michał F. Rode *b,
Dorota Prukałac,
Marek Sikorski
*b,
Dorota Prukałac,
Marek Sikorski c,
Sławomir Wybraniecd and
Gotard Burdziński
c,
Sławomir Wybraniecd and
Gotard Burdziński *a
*a
aQuantum Electronics Laboratory, Faculty of Physics, Adam Mickiewicz University in Poznań, Umultowska 85, Poznań, 61-614, Poland. E-mail: gotardb@amu.edu.pl
bInstitute of Physics, Polish Academy of Sciences, Aleja Lotników 32/46, 02-668 Warsaw, Poland. E-mail: mrode@ifpan.edu.pl
cFaculty of Chemistry, Adam Mickiewicz University in Poznań, Umultowska 89b, 61-614 Poznań, Poland
dFaculty of Chemical Engineering and Technology, Institute C-1, Section of Analytical Chemistry, Cracow University of Technology, Warszawska 24, 31-155 Cracow, Poland
First published on 19th January 2017
Abstract
Miraxanthin V is a betaxanthin dye occurring in Caryophyllales plants. This work describes its photophysical properties in aqueous and alcoholic solutions. After excitation at λexc = 480 nm (2.6 eV), transient absorption spectrum of the excited S1 state was observed (S1 → Sn absorption band at λprobe = 394 nm). The S1 state population decays with two time constants (4.2 ps and 24.2 ps in water) corresponding to the photoexcited miraxanthin V in its two major stereoisomeric forms. The S1 state decay is mainly radiationless, since the fluorescence quantum yield is low (ΦF = 0.003 in water, the smallest value among all of the studied betaxanthins). Strong correlations were obtained between the solvent viscosity and the S1 state lifetime in linear alcohols, as well as in methanolic solutions at low temperatures. These correlations suggest that intramolecular rotation or conformational relaxation precedes the S1 state decay. Full recovery of the electronic ground state S0 was observed after excitations at λexc = 480 nm and 298 nm (4.2 eV), without forming the triplet T1 state or any photoproducts. Experimental results are complemented by the ab initio S0 state calculations using MP2 and DFT methods, and also by the excited-state calculations at the ADC(2) and TD-DFT levels of theory. The ab initio ADC(2) results give insight into the mechanism of the excited-state deactivation through the conical intersection region. We conclude that most probably the excited-state deactivation process is initiated by the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond, present in the chain linking the electron-donor catechol to the electron-acceptor dihydropyridine group, and it is followed by collective geometry changes involving a large rotation about the C
N double bond, present in the chain linking the electron-donor catechol to the electron-acceptor dihydropyridine group, and it is followed by collective geometry changes involving a large rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond. This mechanism seems to be universal for different betaxanthin dyes present in plants, and plays a photoprotective role.
C double bond. This mechanism seems to be universal for different betaxanthin dyes present in plants, and plays a photoprotective role.
Introduction
Betaxanthins are yellow dyes present in Caryophyllales plants.1 Their photophysical properties, such as efficient light to heat conversion, indicate that betaxanthins play a photoprotective role in biological systems.2,3 Recent studies for betaxanthins in solutions show that the major S1 state deactivation path is due to the S1 → S0 internal conversion, while fluorescence contributes only weakly (ΦF < 0.01 in H2O), with neither the S1 → T1 intersystem crossing nor the product formation ever observed.2,3 The internal conversion is likely enhanced by the intramolecular rotations, since an increase in the solvent viscosity causes an increase of the S1 state lifetime and fluorescence quantum yield. Advanced quantum chemical calculations are required for a better understanding of the mechanisms responsible for the efficient internal conversion. Presently, we use miraxanthin V (MIR, Fig. 1) as a model betaxanthin dye, which probably has the highest rate of the internal conversion among betaxanthins, as follows from its lowest fluorescence intensity.4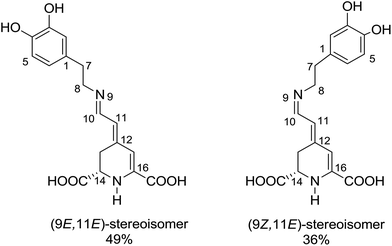 | ||
| Fig. 1 The two dominant stereoisomers of miraxanthin V in aqueous solutions.5 | ||
Stintzing et al. have characterized MIR structure using 13C-NMR spectroscopy.5 Four stereoisomeric forms have been identified, existing in a 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 equilibrium mixture in slightly acidified aqueous solutions. Gandía-Herrero et al. have developed a protocol for semi-synthesis of MIR by condensation of betalamic acid with dopamine, followed by HPLC purification.6 MIR undergoes thermal degradation in solutions, being sufficiently stable for spectroscopic studies at room temperature. It is more stable at low temperatures in the pH range between 4 and 7.7,8 The absorption maximum of MIR in water is at about 472 nm (2.63 eV),9,10 while its fluorescence spectrum peaks at 512 nm (2.42 eV).4 The MIR molar absorption coefficient is expected to be similar to those of other betaxanthins, εmax = 48
7 equilibrium mixture in slightly acidified aqueous solutions. Gandía-Herrero et al. have developed a protocol for semi-synthesis of MIR by condensation of betalamic acid with dopamine, followed by HPLC purification.6 MIR undergoes thermal degradation in solutions, being sufficiently stable for spectroscopic studies at room temperature. It is more stable at low temperatures in the pH range between 4 and 7.7,8 The absorption maximum of MIR in water is at about 472 nm (2.63 eV),9,10 while its fluorescence spectrum peaks at 512 nm (2.42 eV).4 The MIR molar absorption coefficient is expected to be similar to those of other betaxanthins, εmax = 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1.2,3 MIR is the dominant dye in yellow Mirabilis jalapa L., Portulaca oleracea L. and Celosia argentea L. inflorescences,11–13 with flower fluorescence patterns presumably attracting insects pollinators.13,14 MIR has a potential to be used as food colorant.12,15 It might also be used in DSSC (Dye Sensitized Solar Cells),16 where we need to understand the S1 state intramolecular deactivation (the undesirable phenomenon) competing with the electron injection (the desirable phenomenon).
000 M−1 cm−1.2,3 MIR is the dominant dye in yellow Mirabilis jalapa L., Portulaca oleracea L. and Celosia argentea L. inflorescences,11–13 with flower fluorescence patterns presumably attracting insects pollinators.13,14 MIR has a potential to be used as food colorant.12,15 It might also be used in DSSC (Dye Sensitized Solar Cells),16 where we need to understand the S1 state intramolecular deactivation (the undesirable phenomenon) competing with the electron injection (the desirable phenomenon).
The aim of this work is characterization of the MIR photophysical properties using stationary and time-resolved optical spectroscopies. The solvent viscosity is probably an important factor controlling the S1 state deactivation dynamics that will be explored. Theoretical studies will elucidate the mechanistic reasons behind the efficient radiationless S1 → S0 transition, by calculating the excited-state minimum-energy path for the isomerization reaction. The new insights are expected to be important for betaxanthins, and also for betacyanins in general.
Results and discussion
Stationary absorption and fluorescence spectra
The recorded absorption and fluorescence spectra (λexc = 470 nm) of MIR in aqueous and alcoholic solutions are presented in Fig. 2. The absorption band maximum is weakly affected by the solvent, being located around λmaxabs = 475 nm.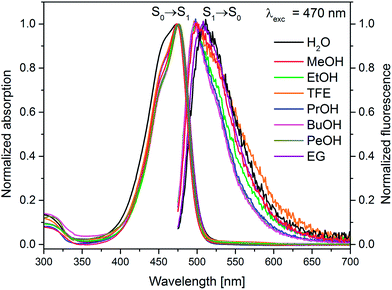 | ||
| Fig. 2 Normalized stationary absorption and fluorescence spectra of miraxanthin V in selected solvents. | ||
These spectra correspond to the S0 → S1 transition, predicted using TD-DFT calculations (see Table S1 in ESI†). The shapes of MIR absorption spectra are all similar in alcoholic solutions, differing slightly in water. This is also confirmed by calculations that predict no significant difference between the absorption spectra of MIR in H2O vs. MeOH (see Table S1†). However, the fluorescence maxima λmaxf show a stronger dependence on solvent. The emission spectra in ethylene glycol and water are red-shifted (λmaxf ≈ 510 nm, Table 1) in comparison to linear alcoholic and TFE solutions (λmaxf ≈ 498 nm). The experimental Stokes shift (Δνs = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) maxabs −
maxabs − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) maxf) reaches the highest value (≈1530 cm−1) in water.
maxf) reaches the highest value (≈1530 cm−1) in water.
| Solvent | Viscositya [cP] | ΦF [×10−3]b | λmaxabs (S0 → S1) [nm] | λmaxf [nm] | Stokes shift [cm−1] |
|---|---|---|---|---|---|
| a The solvent viscosity value at 25 °C taken from CRC Handbook of Chemistry and Physics, 87th ed.b Accuracy: ±15%. | |||||
| Water | 0.89 | 3 | 474 | 511 | 1528 |
| Methanol | 0.54 | 4.7 | 474 | 500 | 1097 |
| Ethanol | 1.07 | 7.6 | 475 | 497 | 932 |
| Trifluoroethanol | 1.73 | 5.8 | 475 | 498 | 972 |
| 1-Propanol | 1.945 | 14 | 476 | 498 | 928 |
| 1-Butanol | 2.54 | 20 | 475 | 497 | 932 |
| 1-Pentanol | 3.619 | 22 | 477 | 497 | 844 |
| Ethylene glycol | 16.1 | 15 | 478 | 508 | 1235 |
The MIR fluorescence excitation spectrum agrees with the absorption spectrum (Fig. S1B†) implying a similarity of the shape of the absorption spectra of two major MIR stereoisomers in H2O, in line with calculations (Table S1†). The contour plot of 3D fluorescence of MIR in water is shown in Fig. S2.† Fluorescence is placed in one zone at 480–640 nm in the emission scale. The peak of the contour plot shows a maximum at λmaxf ≈ 510 nm upon the excitation wavelength λexc ≈ 470 nm. The shapes of the emission spectra weakly depend on the excitation wavelength. The fluorescence quantum yields ΦF, determined with rhodamine 6G as a reference with quantum yield ΦrefF = 0.9,17 are in the range of 3–22 × 10−3 in the solvents tested (Table 1). The clear ΦF dependence on the solvent viscosity in linear alcohols (Fig. S3†) agrees with the excited state behavior of other betaxanthins.2,3 The smallest ΦF value is observed in water (ΦF = 3 × 10−3) which is the lowest value among the betaxanthins studied so far (ΦF = 5.3 and 7.3 × 10−3 for indicaxanthin and vulgaxanthin I in H2O, respectively,2,3 see Table S2†). It also agrees with Gandía-Herrero et al. reporting that the smallest fluorescence intensity is observed for MIR in relation to other betaxanthins.4 The weak fluorescence of MIR has been explained by the lack of electron withdrawing group (such as carboxyl) in the amine and the electron-donating character of the catechol moiety.4
On the basis of the stationary measurements, we determined the radiative rate constant for MIR in water using the Strickler–Berg relation:18
 | (1) |
here, ε(
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) is the molar absorption coefficient, F(
) is the molar absorption coefficient, F(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) the fluorescence intensity,
) the fluorescence intensity, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) the wavenumber, n the refractive index.18 Note, that F(
the wavenumber, n the refractive index.18 Note, that F(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) = λ2F(λ). The resulting calculated value is kr = 2.2 × 108 s−1 for MIR in water. Note that the S0 → S1 absorption band is well-defined, with the molar extinction coefficient εmax ≈ 48
) = λ2F(λ). The resulting calculated value is kr = 2.2 × 108 s−1 for MIR in water. Note that the S0 → S1 absorption band is well-defined, with the molar extinction coefficient εmax ≈ 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1.
000 M−1 cm−1.
Transient absorption spectroscopy
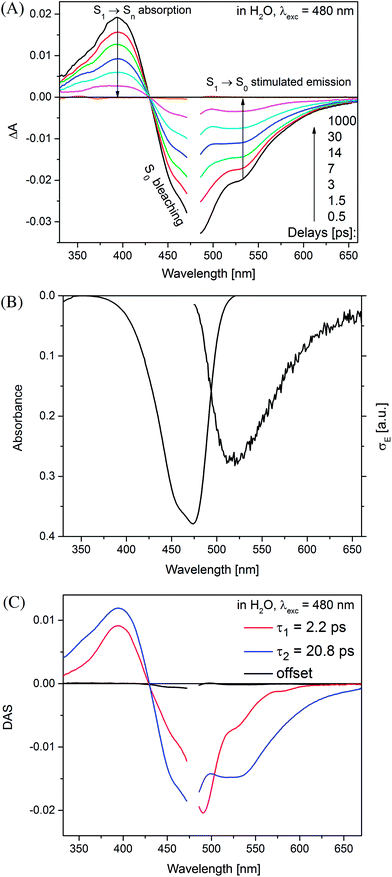
Time-resolved absorption measurements were performed in the spectral range of 330–660 nm with excitation at λexc = 480 nm. Fig. 3 shows typical data obtained for MIR in water. Note that two separate contributions are responsible for the negative band: (i) the bleaching at ≈470 nm caused by the reduced MIR concentration in the ground state S0 upon the sample photoexcitation (ii) the S1 → S0 stimulated emission peaking at ≈530 nm. The shape of the latter band may be well approximated by the spectrum of the stimulated emission cross-section obtained from the stationary fluorescence spectrum scaled by the factor of λ4 (Fig. 3B).The positive band with the maximum at 394 nm (3.14 eV) is mainly assigned to the S1 → Sn absorption, with quite small S0-bleaching contribution at 394 nm. Normalization of the S1 → Sn absorption band shows no spectral shift or band narrowing (Fig. S4†) within our signal-to-noise ratio, thus the contributions from solvation and vibrational cooling are not noticeable. A weak contribution of the solvation was to be expected, based on small Stokes shift values (below 1600 cm−1) obtained in the stationary measurements, and a weak dependence of the Stokes shift on the solvent polarity (compare water to the less polar methanol, Table 1).
In order to retrieve the S1 state lifetime, band integral kinetics were computed using
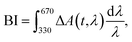 | (2) |
| Solvent | Viscosity [cP] | π* | Positive BI | Negative BI | Global analysis τ1, τ2c [ps] | ||
|---|---|---|---|---|---|---|---|
| A1, A2 | τ1, τ2b [ps] | A1, A2 | τ1, τ2c [ps] | ||||
| a Polarity π* is taken from ref. 65.b Accuracy: ±20%.c Accuracy: ±15%. | |||||||
| Water | 0.89 | 1.09 | 0.42, 0.58 | 3.7, 22.7 | 0.4, 0.6 | 4.2, 24.2 | 2.2, 20.8 |
| Methanol | 0.54 | 0.60 | 0.34, 0.66 | 6.1, 33.3 | 0.35, 0.65 | 6.9, 36.1 | 5.6, 35.9 |
| Ethanol | 1.07 | 0.54 | 0.23, 0.77 | 5.6, 56.7 | 0.24, 0.76 | 6, 58.4 | 5.7, 58.9 |
| Trifluoroethanol | 1.73 | 0.73 | 0.32, 0.68 | 5.3, 40.1 | 0.34, 0.66 | 6.1, 43.4 | 4.5, 40.7 |
| 1-Propanol | 1.945 | 0.52 | 0.22, 0.78 | 8, 79.9 | 0.23, 0.77 | 10.7, 84.2 | 6.2, 80.8 |
| 1-Butanol | 2.54 | 0.47 | 0.23, 0.77 | 7.5, 103.5 | 0.22, 0.78 | 9.3, 106.8 | 5.8, 102.7 |
| 1-Pentanol | 3.619 | 0.40 | 0.27, 0.73 | 8.1, 121.4 | 0.27, 0.73 | 10.4, 127.8 | 7.7, 126.7 |
| Ethylene glycol | 16.1 | 0.92 | 0.36, 0.64 | 9.6, 82.2 | 0.37, 0.63 | 9.5, 83.2 | 7.6, 79 |
The two time constants (τ1 = 4.2 ps, τ2 = 24.2 ps, NBI in water) were tentatively assigned to the S1 state lifetimes of the two major stereoisomers. The ratio of the partial amplitudes with the respective time-constants (0.4 and 0.6, NBI in water) reflects the relative populations of the stereoisomers in the S1 state, which likely coincide with the S0 state equilibrium existing before photoexcitation. Indeed, the ratio 0.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.58 between the two dominant stereoisomers was estimated for MIR in aqueous solutions using the NMR data (Fig. 1).5 Based on their respective abundances, we infer that the EE stereoisomer is associated with the longer time constant, while the ZE stereoisomer with a shorter time constant. Inspection of Table 2 also shows that the relative amplitudes of the two exponential components, describing the band integrals kinetics, depend on solvent. Fig. S6† shows an increase of the partial amplitude A1 with solvent polarity π*. We can expect, that a more polar solvent stabilizes a more polar stereoisomer. Indeed, theoretical predictions show that the ZE form has a larger dipole moment than EE form (Tables S1 and S3†).
0.58 between the two dominant stereoisomers was estimated for MIR in aqueous solutions using the NMR data (Fig. 1).5 Based on their respective abundances, we infer that the EE stereoisomer is associated with the longer time constant, while the ZE stereoisomer with a shorter time constant. Inspection of Table 2 also shows that the relative amplitudes of the two exponential components, describing the band integrals kinetics, depend on solvent. Fig. S6† shows an increase of the partial amplitude A1 with solvent polarity π*. We can expect, that a more polar solvent stabilizes a more polar stereoisomer. Indeed, theoretical predictions show that the ZE form has a larger dipole moment than EE form (Tables S1 and S3†).
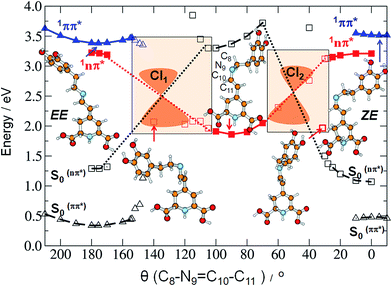
The global analysis of the transient absorption data results in time constants (τ1 = 2.2 ps, τ2 = 20.8 ps, in water) similar to those deduced from the band integral kinetics (Table 2); note similar shapes of the two respective decay-associated spectra (Fig. 3C).
The MIR transient absorption data in H2O (Fig. 3A) were also analyzed by independent fitting of the individual kinetic traces (Fig. S7†). The obtained time constants approximately reproduce the values retrieved in the global analysis (Fig. 3C). The exception is at probe λ = 493 nm where the individual time-constants are too short. This can be explained by contribution from an intermediate absorption,20 indeed species nascent upon S1 → S0 deactivation can be structurally unrelaxed and possess a red-shifted absorption band in relation to the relaxed MIR in the S0 state.
Time-resolved absorption measurements were also performed for MIR in the range of 825–1380 nm (the NIR range) with the excitation at λexc = 485 nm in water (Fig. S8A†). The recorded S1 → Sm (m > 1) absorption band is located around ≈920 nm. The band integral over the entire spectral range (825–1380 nm) was calculated. The two time constants obtained from the double exponential fit: 2.7 ps (0.41) and 21.9 ps (0.59), are in a reasonable agreement with those derived from the global analysis (Fig. S8B†). Thus, the determined amplitude associated spectra (Fig. S8B†) likely reflect respective stereoisomers S1 state absorption bands. Similar transient absorption data are produced for MIR in MeOH (Fig. S9A†), with the amplitude associated spectra resembling those in H2O.
The long-lived stereoisomer in the S1 state mainly contributes to the stationary fluorescence spectra and to the fluorescence quantum yield ΦF. This also agrees with inspection of the strength of the stimulated emission transient bands at longer delay times exceeding 6 ps, Fig. 3A. The radiative rate constant for this stereoisomer was calculated using the standard expression:
| krτ2 = ΦF | (3) |
Very similar spectral shape of transient absorption data (Fig. S11A†) at delays longer than 3 ps was obtained for MIR in water using excitation at λexc = 298 nm instead of 480 nm (Fig. 3A). The decay time-constants retrieved from band integral analysis (NBI, τ1 = 3.8 ps, τ2 = 23.6 ps) are comparable to those obtained with λexc = 480 nm. Inspection of transient absorption kinetics at probe wavelengths 460 nm and 520 nm (Fig. S11E†) shows an extra decay (460 nm) and rise (520 nm) with a time-constant of 0.6 ps. This time-constant likely reflects vibrationally hot population of the S1 state generated through the Sn → S1 internal conversion process, following the initial S0 → Sn (n > 1) state photoexcitation (with λexc = 298 nm). Thus, the vibrationally hot S1 state contributes to the fast decay of the stimulated emission at probe 460 nm. In contrast, probe 520 nm shows the initial growth (0.6 ps) of the stimulated emission signal because the vibrationally relaxed S1 state population increases. The early changes caused by the S1 state vibrational relaxation are virtually absent with a long excitation wavelength (λexc = 480 nm, Fig. S11E†), since under these conditions a small excess of vibrational energy is produced in the S1 state. A very fast heat dissipation capability of MIR can be explained by strong solute–solvent coupling through hydrogen bonding. Note that the vibrational cooling in case of betanin has been also described by a short time-constant (≈0.9 ps in H2O).21
The transient absorption measurements were also performed for MIR in alcoholic solutions with the excitation at λ = 480 nm (Fig. S12†). The time constants deduced from both global and band integral analysis all depend on the solvent viscosity in linear alcohols (Table 2). Note that while the dynamics is affected by the solvent, the shape of the transient absorption spectra remains unchanged (Fig. S12†). Additional measurements were performed at temperatures between 180 and 300 K for MIR methanolic solutions, and again a correlation of the S1 lifetime vs. viscosity η was observed, although the influence of temperature should also be considered (Fig. S13, data in Table S4†). These viscosity-dependent data may be described by a commonly used empirical model.22 Thus, the rates of the S1 decay in methanol as a function of temperature, and also in linear alcohols at T = 22 °C, may all be fitted using the following equation:23–26
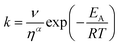 | (4) |
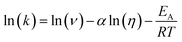 | (5) |
The fitted surface is presented in Fig. S14.† The parameter values α2 = 0.74 ± 0.04, EA2 = 57 ± 33 cm−1, and α1 = 0.25 ± 0.10, EA1 = 350 ± 80 cm−1 were obtained for the long- and short-lived stereoisomers, respectively. As expected,26 the higher barrier (EA1 > EA2) for the internal rotations or conformational relaxation in the singlet excited state should be accompanied by a weaker dependence of the rate k on viscosity (α1 < α2). The activation energy for both stereoisomers is small and comparable to kT value in room temperature (≈210 cm−1), thus the solvent viscosity is the main factor controlling the S1 state lifetime. Comparing the α values (α2 = 0.74 vs. α1 = 0.25), we deduce that the stereoisomer 2 (EE) experiences a stronger friction against the solvent molecules. Indeed, a more hampered rotation around the central bridge bonds is expected for the EE stereoisomer (Fig. 1) due to the increased friction of the dopamine moiety against the solvent molecules.
Quantum chemical calculations
The NMR data indicate that MIR exists in solution in an equilibrium between the two main stereoisomers: EE (9E,11E) and ZE (9Z,11E), which are the most abundant (see Fig. 1).5 The quantum chemical calculations produced the optimized structures of the most abundant stereoisomers shown in Fig. S15.† In both the forms the electron-donating catechol moiety lies in the plane that is approximately parallel to the plane containing the electron-accepting moiety and the C11, C10, N9 and C8 atoms. The two moieties contained in the above-mentioned planes are linked by the C7–C8 single bond bridge – a linkage of a geometry typical for saturated hydrocarbons. Such molecular arrangement makes the potential energy profile asymmetric with respect to the rotations described in this paragraph. Both the B3LYP/cc-pVDZ and MP2/cc-pVDZ calculations in gas phase confirm that the ZE isomer is by ≈0.16 eV higher in energy than the most stable EE form. The calculated excitation energies along with the oscillator strengths for different rotameric forms of MIR (computed with the aid of the TD-DFT method for different solvents and in vacuum) are presented in Tables S1 and S3,† with ADC(2) results given for comparison. The S0 → S1 transition was computed at 401 nm (3.09 eV) with oscillator strength f = 0.20 for EE, and at 422 nm (2.94 eV) with lower intensity for ZE in vacuum (Table S1†). This band gets significantly stronger for both forms in polar solvents (water and alcohols), as its oscillator strength f increases to ≈0.6 (see Table S1†). Moreover, the calculations show that the two absorption peaks for both the EE and ZE forms are even closer in a given solvent (alcohol or water) than in vacuum. This computational result suggests that the photoexcitation at λexc ≈ 480 nm in a given solvent results in an initial population of the isomers in the S1 state that reproduces the equilibrium existing in the S0 state. The molecular orbitals involved in the S0 → S1 transition were plotted with isosurfaces at 0.03 value (Table S5†). The major contribution to this transition is provided by HOMO (π) → LUMO (π*) component, while the second most relevant HOMO−1 (π) → LUMO (π*) contribution is a little smaller for both the forms. The coefficients of electronic configurations contributing to the ADC(2) S1 state wavefunction are given in Table S5.† Note that the S0 → S1 transition has a π,π* character for both the EE and ZE forms. The shape of orbitals indicates that after excitation within the Franck–Condon area in the S1 state, a part of the electron density moves from the electron-donating catechol moiety to the one of the electron-accepting carboxyl groups,27 suggesting that MIR may act as a sensitizer in DSSC. The presence of COOH groups in MIR facilitates anchoring of this dye to the TiO2 layer.28 The difference between the experimental excitation wavelength (474 nm) and its predicted theoretical value (401 nm) is quite significant (3837 cm−1 = 0.48 eV), while still at the level of the mean absolute error for the B3LYP functional (≈0.34 eV for excited singlet states).29 Note that our attempt to use either a CAM-B3LYP functional or a larger aug-cc-pVTZ basis set with B3LYP functional produced no improvements to the TD-DFT results.The strongly absorbing ππ* state is always the lowest excited state in the spectrum. Thus, we presume that this is the initially photoexcited state, active in the photophysics of MIR, however, the second lowest excited state has nπ* character and lies approx. 0.5 eV above the S1(ππ*) state, according to the ADC(2)/cc-pVDZ method (see Table S3†).
As already mentioned, we expect that upon UV excitation of the S0 → S1(ππ*) transition, the initially formed S1(ππ*) state in solution exists in two major forms: S1(EE) and S1(ZE), with the population ratio similar to that of the S0 state. Moreover, the transient absorption data show two characteristic time constants assigned to the S1 state lifetimes. Those two S1(ππ*) state forms are almost isoenergetic in the gas phase, according to the ADC(2)/cc-pVDZ results (compare the adiabatic energies of the 1ππ*-excited states in Table 3). The electronic structure analysis indicates locally-excited character of the respective minima (see Table S5†). Both the electron-donating and accepting orbitals are localized on the dihydropyridine moiety of MIR. However, the experimentally determined S1 state lifetimes (4.2 ps and 24.2 ps in water) are relatively short. This suggests existence of an efficient molecular mechanism for the radiationless decay of the electronic excitation. A possible explanation for the fast excited-state deactivation is given by the existence of a low-lying S1–S0 conical intersection (CI) seam (see the colored beige rectangles in Fig. 4 and bottom-right circle in Fig. 5), where non-adiabatic transition takes place from the excited state (S1) to the (S0) electronic ground state.30,31
| C8–N9 | C10![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N9 N9 |
C10–C11 | C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 C12 |
Ea [eV] | Ef [eV] | μ [D] | f(S1 → S0) | |
|---|---|---|---|---|---|---|---|---|
| S0 EE | 1.455 | 1.299 | 1.454 | 1.374 | 0.00 | 2.8 | ||
| S1 EE ππ* | 1.447 | 1.318 | 1.427 | 1.415 | 3.32 | 2.98 | 5.1 | 0.541 |
| S1 θ = 90° | 1.455 | 1.434 | 1.3334 | 1.486 | 1.83 | −1.55 | 8.3 | 0.000 |
| S1 ZE ππ* | 1.455 | 1.321 | 1.429 | 1.420 | 3.38 | 2.96 | 5.3 | 0.512 |
| S0 ZE | 1.457 | 1.302 | 1.460 | 1.377 | 0.16 | 3.4 |
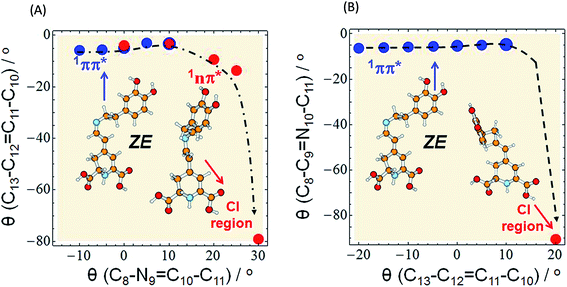 | ||
Fig. 5 Minimum-energy profile of the 1ππ* (blue circles) and 1nπ* (red circles) excited state of miraxanthin plotted as a function of θ(C8–N9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10–C11) and θ(C13–C12 C10–C11) and θ(C13–C12![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C11–C10) coordinates illustrating the deactivation pathway of the ZE form according to two alternative scenarios: (A) the initial rotation about the C C11–C10) coordinates illustrating the deactivation pathway of the ZE form according to two alternative scenarios: (A) the initial rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond (as in Fig. 4) is followed by strong twisting of the C N bond (as in Fig. 4) is followed by strong twisting of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, (B) the initial rotation about the C C bond, (B) the initial rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (as in Fig. S16†) followed by large twisting of the C C bond (as in Fig. S16†) followed by large twisting of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond to enter the CI region. The red circle in the bottom right corner of the surfaces represents the conical intersection region: CI(S0–S1) of a so-called “collapsed” structure. The results were obtained with the aid of the ADC(2)/def-SV(P) method. N bond to enter the CI region. The red circle in the bottom right corner of the surfaces represents the conical intersection region: CI(S0–S1) of a so-called “collapsed” structure. The results were obtained with the aid of the ADC(2)/def-SV(P) method. | ||
Such transitions are the most effective in the geometries where the excited and the ground states become degenerate. In our experiments the dependence of the MIR-S1 state lifetimes on the solvent viscosity was determined (Fig. S14†). This implies that the driving coordinate for the excited-state decay should be a large-amplitude motion described as a rotation about one of the torsional angles. Studying the MIR chemical structure, we may consider several potential reaction coordinates that may drive the system towards the S1–S0 CI region.
There are six torsional angles which should be considered as a driving coordinate. These are two double bonds: C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 and C10
C12 and C10![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N9, shortly referred to as C
N9, shortly referred to as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, and four single bonds: C1–C7, C7–C8, C8–N9, and C10–C11. Single bonds can be immediately excluded from consideration for a following reason; the shape of the minimum energy profile (MEP) of the excited state calculated along the coordinate described as a rotation about a single bond is known to be parallel to the MEP along the same coordinate for the S0 state,30,32–34 thus such rotation would demand overpassing the excited-state energy barrier as it also exists in the S0 state. This implies that single bond rotations cannot lead to the fast deactivation pathway through the CI regions. We are pointing to the conclusion that rotations about double bonds are good candidates for the driving coordinates for fast deactivation process ongoing in the excited state. Why is that?
N, and four single bonds: C1–C7, C7–C8, C8–N9, and C10–C11. Single bonds can be immediately excluded from consideration for a following reason; the shape of the minimum energy profile (MEP) of the excited state calculated along the coordinate described as a rotation about a single bond is known to be parallel to the MEP along the same coordinate for the S0 state,30,32–34 thus such rotation would demand overpassing the excited-state energy barrier as it also exists in the S0 state. This implies that single bond rotations cannot lead to the fast deactivation pathway through the CI regions. We are pointing to the conclusion that rotations about double bonds are good candidates for the driving coordinates for fast deactivation process ongoing in the excited state. Why is that?
There are several known classes of molecules where such excited-state rotations around different type of double bonds are observed, such as azobenzenes where rotation around the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond leads to profound conformational changes.35–38 The excited-state rotation around the C
N double bond leads to profound conformational changes.35–38 The excited-state rotation around the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond occurs in the extensively studied stilbenes (Z/E isomerization),39,40 cyanines,41–43 the 3-hydroxy-picolinic acid,44,45 and the 7HQ46,47 molecule. Quite recently, a new photoswitching molecule N-(3-pyridinyl)-2-pyridinecarboxamide (NPPCA) has been investigated, where excited state rotation occurs about the C
C double bond occurs in the extensively studied stilbenes (Z/E isomerization),39,40 cyanines,41–43 the 3-hydroxy-picolinic acid,44,45 and the 7HQ46,47 molecule. Quite recently, a new photoswitching molecule N-(3-pyridinyl)-2-pyridinecarboxamide (NPPCA) has been investigated, where excited state rotation occurs about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond,48 present also in the MIR chromophore; the same effect was observed in light-switchable peptides.33,39
N double bond,48 present also in the MIR chromophore; the same effect was observed in light-switchable peptides.33,39
Upon UV excitation, a double bond nominally short in the S0 state, may get weaker and longer in the excited state. This effect was detected in a series of derivatives of 7-hydroxy-quinoline (7HQ)47 and salicylidene methylamine.49 Thus, a hindered rotation around a nominally double bond in the S0 state may become allowed in the S1-excited state due to lowering of the barrier, explained by this bond becoming a longer and weaker (single) bond in the S1 state.
Indeed, according to the calculations, comparing the ground- and excited-state equilibrium geometries in MIR, both the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bonds undergo elongation upon excitation, with the single C–C bond simultaneously getting shorter. This is observed for both the EE and ZE rotamers. The respective geometric parameters are compared in Table 3.
N double bonds undergo elongation upon excitation, with the single C–C bond simultaneously getting shorter. This is observed for both the EE and ZE rotamers. The respective geometric parameters are compared in Table 3.
Our calculations indicate an elongation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond by 0.039 and 0.043 Å for the EE and ZE forms, respectively, comparing their equilibrium ground-state geometry to their excited-state equilibrium geometry; similarly, we obtained elongation of the C
C bond by 0.039 and 0.043 Å for the EE and ZE forms, respectively, comparing their equilibrium ground-state geometry to their excited-state equilibrium geometry; similarly, we obtained elongation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond by 0.019 Å for both forms. To get insight into the mechanism of deactivation process of MIR the excited-state MEPs were calculated along two driving coordinates, separately: rotations about the C10
N bond by 0.019 Å for both forms. To get insight into the mechanism of deactivation process of MIR the excited-state MEPs were calculated along two driving coordinates, separately: rotations about the C10![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N9 and C11
N9 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 double bonds. Until the system is in the 1ππ*-state minimum, both planes including two ring moieties are almost parallel to one another. Comparison of the estimated in calculations excited-state barriers, indicates that in the initially photoexcited S1(ππ*) state, the barrier for the rotation about the C10
C12 double bonds. Until the system is in the 1ππ*-state minimum, both planes including two ring moieties are almost parallel to one another. Comparison of the estimated in calculations excited-state barriers, indicates that in the initially photoexcited S1(ππ*) state, the barrier for the rotation about the C10![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N9 bond is lower than analogous barrier for the C11
N9 bond is lower than analogous barrier for the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 and C10–C11 rotations, for a given stereoisomer, especially for EE (cf. 4, S16 and S17†). That is why we may assume that it is a rotation about the C
C12 and C10–C11 rotations, for a given stereoisomer, especially for EE (cf. 4, S16 and S17†). That is why we may assume that it is a rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond that initiates the deactivation process of overpassing the 1ππ*-state barrier. Such evolution of the system toward the 1ππ*-state barrier one may observe in Fig. 5A for which the C
N bond that initiates the deactivation process of overpassing the 1ππ*-state barrier. Such evolution of the system toward the 1ππ*-state barrier one may observe in Fig. 5A for which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond does not change much.
C bond does not change much.
The initial C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C rotation as 1ππ*-state deactivation path can be considered for ZE stereoisomer (Fig. 5B), since the barrier for the C
C rotation as 1ππ*-state deactivation path can be considered for ZE stereoisomer (Fig. 5B), since the barrier for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C rotation is only slightly higher than that for C
C rotation is only slightly higher than that for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N rotation. However in both scenarios (Fig. 5A and B) the initial bond rotation along one coordinate is followed by twisting of the second coordinate before reaching the conical intersection point, where MIR deactivates to the ground state.
N rotation. However in both scenarios (Fig. 5A and B) the initial bond rotation along one coordinate is followed by twisting of the second coordinate before reaching the conical intersection point, where MIR deactivates to the ground state.
The conical intersection region is reached upon the initial rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond of the ZE form by the dihedral angle of ≈30°. The most relevant orbitals that contribute to the nonadiabatic transition between the excited and the ground state in the S1/S0 conical intersection are shown in Table S7.† The most important in this arbitrarily chosen geometry is the nπ* contribution, while the ππ* contribution is also present. However, based on this contribution set we can't state that the conical intersection is purely of the nπ*/S0 nature. Its character is thus a mixture of the two contributions.
N double bond of the ZE form by the dihedral angle of ≈30°. The most relevant orbitals that contribute to the nonadiabatic transition between the excited and the ground state in the S1/S0 conical intersection are shown in Table S7.† The most important in this arbitrarily chosen geometry is the nπ* contribution, while the ππ* contribution is also present. However, based on this contribution set we can't state that the conical intersection is purely of the nπ*/S0 nature. Its character is thus a mixture of the two contributions.
The photophysical deactivation of MIR proceeds as follows. After photoexcitation of the EE form (as well as ZE), the S1(ππ*) state is populated. As shown in Fig. 4, the potential-energy profile of the S1(ππ*) excited state has a small barrier of 0.09 eV for the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond (see blue curve in the upper-left corner of Fig. 4). The analogous S1(ππ*)-state barrier for the ZE form is lower, of 0.04 eV (see the blue curve in the upper-right corner of Fig. 4). Such a small barrier may be easily overcome in experiments undertaken at room temperature. It is also evident that a rotation by just about 25–30°, either from the EE or from the ZE S1(ππ*)-state minimum form, may put the system into a close proximity of the CI region (beige areas). The process is also shown in Fig. 5A which illustrates the deactivation pathway eye-guided along the points presented in the two-coordination space. In this region (θ(C
N bond (see blue curve in the upper-left corner of Fig. 4). The analogous S1(ππ*)-state barrier for the ZE form is lower, of 0.04 eV (see the blue curve in the upper-right corner of Fig. 4). Such a small barrier may be easily overcome in experiments undertaken at room temperature. It is also evident that a rotation by just about 25–30°, either from the EE or from the ZE S1(ππ*)-state minimum form, may put the system into a close proximity of the CI region (beige areas). The process is also shown in Fig. 5A which illustrates the deactivation pathway eye-guided along the points presented in the two-coordination space. In this region (θ(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) ≈ 30°), the S1(ππ*) state meets the descending – 1nπ* state – which was found to be the second excited state in the absorption spectrum both for the EE and ZE forms (Table S3†), and S1(ππ*) populates this 1nπ* state. This intersection of the ππ* and nπ* states is illustrated in Fig. 5A, where at the intersection point the two states have the same driving coordinate values what helps the transition from one state into another because the barrier between the states disappears. In general, however, one may note that the intersection point presented in Fig. 5A is still just an apparent crossing, since the remaining geometry parameters in the two states can differ. As soon as the rotation about the C
N) ≈ 30°), the S1(ππ*) state meets the descending – 1nπ* state – which was found to be the second excited state in the absorption spectrum both for the EE and ZE forms (Table S3†), and S1(ππ*) populates this 1nπ* state. This intersection of the ππ* and nπ* states is illustrated in Fig. 5A, where at the intersection point the two states have the same driving coordinate values what helps the transition from one state into another because the barrier between the states disappears. In general, however, one may note that the intersection point presented in Fig. 5A is still just an apparent crossing, since the remaining geometry parameters in the two states can differ. As soon as the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is allowed, the optimization procedure immediately heads to the “collapsed” structure with the C13–C12
C bond is allowed, the optimization procedure immediately heads to the “collapsed” structure with the C13–C12![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C11–C10 dihedral ≈80° (shown in the bottom right corner of Fig. 5A), which is a structure with ≈60° angle between the two planes of the ring moieties. Upon large amplitude motion, including other degrees of freedom such as rotation about single bonds in the bridge, the energy of the excited state rapidly decreases and collective relaxation immediately drives the system toward the CI(S1–S0) region where the nonadiabatic transition to the S0 state takes place. Unfortunately this leads the ADC(2) method to cease in convergence.
C11–C10 dihedral ≈80° (shown in the bottom right corner of Fig. 5A), which is a structure with ≈60° angle between the two planes of the ring moieties. Upon large amplitude motion, including other degrees of freedom such as rotation about single bonds in the bridge, the energy of the excited state rapidly decreases and collective relaxation immediately drives the system toward the CI(S1–S0) region where the nonadiabatic transition to the S0 state takes place. Unfortunately this leads the ADC(2) method to cease in convergence.
Exactly the same mechanism of excited-state deactivation was made for the EE and ZE tautomers (compare the second left and the second right structures in Fig. 4). Moreover, since after overpassing the 1ππ*-state barrier, the system rotates ≈80° about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, it can be assumed that the system will come back to the same S0 state stereoisomer which was photoexcited (aborted isomerization path), instead of proceeding through the higher-in-energy central path connected with lonely rotation about the C
C bond, it can be assumed that the system will come back to the same S0 state stereoisomer which was photoexcited (aborted isomerization path), instead of proceeding through the higher-in-energy central path connected with lonely rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond, in which the C
N double bond, in which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C rotation is not present.
C rotation is not present.
The involvement of the nπ* state in the overall excited-state deactivation process through the conical intersection region(s) in MIR is an interesting idea. Additional evidence in support is given by the fact that the nπ*-state is found driving the same processes in several other molecules, e.g. for the hydrogen-bonded azo aromatic molecules,37 dyes with the molecular scaffold of 2-hydroxyazobenzene (Sudan I and Orange II),38 and for the picolinic acid derivatives.44,45 In the latter case the 1nπ* state lies below the 1ππ* excited state in all of four tautomeric forms studied. Apparently the electronically excited picolinic acid decays non-radiatively through the conical intersections of the 1nπ* state with the ground state, quenching the fluorescence of all of the tautomeric forms.44
Conclusions
Experimental data show an increase of the MIR S1 state lifetimes with an increase of solvent viscosity in linear alcohols. We postulate that torsional relaxation of the S1(π,π*) state around the central bonds (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and/or C
C and/or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) leads to S1 → S0 radiationless relaxation. This rotational motion is slower in a more viscous solvent, therefore the internal conversion rate is limited by the time required to reach the necessary geometry. The S1 → S0 radiationless relaxation is the main deactivation channel for the S1 state. Fluorescence is a minor relaxation pathway (ΦF < 0.03 in all of the solvents tested), with a secondary role in the overall S1-population deactivation. We obtained no indications of photoproduct or T1 state formation from the S1 state, with the full S0 state recovery observed. The S1 state population exhibit biexponential decays in solution attributed to the presence of two major stereoisomers in the ground state of MIR. While numerous photophysical properties, including stationary UV-vis absorption, fluorescence, spectral locations of the S1 state absorption band and the S1 deactivation paths make MIR similar to other betaxanthins studied so far (see Table S2† for the comparison),2,3 MIR exhibits exceptionally low fluorescence quantum yield ΦF, and relatively short S1 state lifetimes. These features are controlled by structural factors, such as the electron-donating character of the catechol moiety, while the more fluorescent betaxanthins (vulgaxanthin I, indicaxanthin) typically possess an electron-withdrawing group (e.g. carboxyl) in the amine, instead of catechol.
C) leads to S1 → S0 radiationless relaxation. This rotational motion is slower in a more viscous solvent, therefore the internal conversion rate is limited by the time required to reach the necessary geometry. The S1 → S0 radiationless relaxation is the main deactivation channel for the S1 state. Fluorescence is a minor relaxation pathway (ΦF < 0.03 in all of the solvents tested), with a secondary role in the overall S1-population deactivation. We obtained no indications of photoproduct or T1 state formation from the S1 state, with the full S0 state recovery observed. The S1 state population exhibit biexponential decays in solution attributed to the presence of two major stereoisomers in the ground state of MIR. While numerous photophysical properties, including stationary UV-vis absorption, fluorescence, spectral locations of the S1 state absorption band and the S1 deactivation paths make MIR similar to other betaxanthins studied so far (see Table S2† for the comparison),2,3 MIR exhibits exceptionally low fluorescence quantum yield ΦF, and relatively short S1 state lifetimes. These features are controlled by structural factors, such as the electron-donating character of the catechol moiety, while the more fluorescent betaxanthins (vulgaxanthin I, indicaxanthin) typically possess an electron-withdrawing group (e.g. carboxyl) in the amine, instead of catechol.
Ab initio calculations give insight into the mechanism of fast S1 → S0 internal conversion in MIR. Easy access to the CI region through the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds explains fast radiationless deactivation of the singlet excited state and its short lifetime. The rotation about the C
C bonds explains fast radiationless deactivation of the singlet excited state and its short lifetime. The rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond seems to initiate the excited-state deactivation process, with an energy barrier lower than that for the rotation about the C
N double bond seems to initiate the excited-state deactivation process, with an energy barrier lower than that for the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, and much lower than that for the rotation about the C–C single bond in the central bridge of the molecule. However, as soon as the system leaves the initially photoexcited 1ππ*-state minimum, collective geometry changes, foremost the rotation about the C
C bond, and much lower than that for the rotation about the C–C single bond in the central bridge of the molecule. However, as soon as the system leaves the initially photoexcited 1ππ*-state minimum, collective geometry changes, foremost the rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond, drives the system toward the CI region and next to the ground state repopulation, closing the photocycle through the aborted isomerization process. The twisting angle of ≈30° is required for the system to reach the CI region, thus it explains found influence of solvent viscosity on S1 lifetimes and fluorescence quantum yields in solution. Since the other betaxanthins studied so far2,3 also have two distinct values of the S1 state lifetime, we expect them to have a similar S1 state deactivation mechanism, with the S1 state decay rate controlled by structural factors, location of the CI region, and solvent viscosity.
C double bond, drives the system toward the CI region and next to the ground state repopulation, closing the photocycle through the aborted isomerization process. The twisting angle of ≈30° is required for the system to reach the CI region, thus it explains found influence of solvent viscosity on S1 lifetimes and fluorescence quantum yields in solution. Since the other betaxanthins studied so far2,3 also have two distinct values of the S1 state lifetime, we expect them to have a similar S1 state deactivation mechanism, with the S1 state decay rate controlled by structural factors, location of the CI region, and solvent viscosity.
Experimental section
Pure MIR was obtained as proposed by Gandía-Herrero et al.6 Before the semi-synthesis of MIR, a separation of the synthetic substrate, indicaxanthin (IND), from the orange-yellow fruits of Opuntia ficus-indica L. Mill, was performed as described previously.2 During the semi-synthesis, dopamine was added in a 25-fold molar excess to an alkaline solution of betalamic acid obtained directly after IND hydrolysis at pH 11.4 through addition of 25% NH4OH. After 20 min since the addition of dopamine, the solution was acidified to pH 6.5 by formic acid and chromatographically purified by open column chromatography on C18 sorbent (Merck, Darmstadt, Germany).2 Typically, the C18 sorbent was activated with 100% methanol and then rinsed with 1% aqueous formic acid. The samples were applied to a column rinsed again with 1% formic acid and betaxanthin was eluted with methanol. The eluates were pooled and preconcentrated under reduced pressure at 25 °C. Concentrated extract was submitted to semipreparative flash chromatography (preparative HPLC system with LC-20AP pumps, UV-VIS SPD-20AV detector and LabSolutions 5.51 operating software, Shimadzu Corp., Japan) on a C18 flash column (Interchim, France) for the separation of MIR.21 Further purification of the pigment was performed on an semipreparative HPLC column Luna C18(2) 250 × 30 mm i.d., 10 μm (Phenomenex, Torrance, CA, USA).50The details of femtosecond UV-vis-NIR transient absorption spectra have been described elsewhere.2 The ultrafast laser system consists of a short-pulse titanium-sapphire oscillator (Mai-Tai, Spectra Physics, 70 fs) followed by a high-energy titanium-sapphire regenerative amplifier (Spitfire Ace, Spectra Physics, 100 fs). The 800 nm beam was split into two beams to generate: (1) a pump (λexc = 480, 485 or 298 nm) in the optical parametric amplifier (Topas Prime with a NirUVis frequency mixer) and (2) probe pulses – white light continuum in the UV-vis range by using a CaF2 plate (330–660 nm, Ultrafast Systems, Helios) or in the NIR range by using a YAG crystal (830–1390 nm, Ultrafast Systems, Helios). The remaining 800 nm photons in the probe pulse were filtered out before the sample. The pump pulse energy was typically about 0.5–0.8 μJ. In most of the transient absorption experiments the absorbance was about 0.5 at the excitation wavelength in a 2 mm optical path quartz cell. Sample solution was stirred by a Teflon-coated bar. The entire set of pump–probe delay positions was repeated at least four times to ensure data reproducibility. The transient absorption data were corrected for chirp of the white light continuum. The instrument response function (IRF) was about 200 fs (FWHM) in the experiments with 480 nm excitations, and 350 fs (FWHM) with the excitation at 298 nm. The data were analyzed by determination of the band integral kinetics and fitted with a double-exponential function. The convolution with a Gaussian response function was included into the global fitting procedure (ASUFIT program), and satisfactory fits were obtained. Temperature-dependent experiments between 180 and 300 K were performed in a liquid nitrogen cryostat (Janis VPF-100). The solutions were placed into a cuvette consisting of two parallel plastic windows, separated by 1.5 mm distance. The temperature was measured by two thermocouples, located over and under the sample.
Fluorescence emission and excitation spectra were recorded on a Horiba Jobin-Yvon-Spex Fluorolog 3-22 spectrofluorometer. Right-angles geometry was used in all of the steady-state emission measurements. The sample emission and excitation spectra were recorded with three replicates at a reduced scanning rate. The experiments were performed on 3.5 mL of sample solutions contained in a quartz cell (1 cm × 1 cm) with the MIR absorbance not exceeding 0.1 at the excitation wavelength (2 × 10−6 M in water). The excitation wavelength was set at λexc = 470 nm for the fluorescence measurements. Fluorescence spectra were collected with 1 nm excitation and emission slits, using 0.5 s integration time. Fluorescence spectra typically were not corrected for contribution of the solvent Raman scattering (Fig. S1A†).
For the 3D fluorescence spectra, excitation and emission slits were 2 nm; the acquisition interval was 2 nm and the integration time was 0.2 s. 3D emission spectra were collected between 480 to 675 nm in the 355–550 nm range of the excitation wavelengths, spaced by 5 nm intervals in the excitation domain. Stationary UV-vis absorption spectra were recorded using a Jasco V-550 spectrophotometer. Alcohols and rhodamine 6G were purchased from Aldrich, water was purchased from Fluka. Unless otherwise stated, experiments were performed at room temperature (22 °C).
Computational methods
To simulate the UV-absorption spectra of MIR, the equilibrium geometries of the molecular system in its closed-shell ground singlet state (S0) were determined at the level of density functional theory (DFT) with the use of the of the B3LYP51 hybrid correlation–exchange functional in conjunction with the cc-pVDZ52 correlation-consistent basis set as implemented in TURBOMOLE software package.53 In the calculation of the excitation energies, mimicking the absorption spectra, the basis set was augmented with diffuse functions (aug-cc-pVDZ52) and single-point TD-DFT calculations were done on the top of the geometries optimized with the cc-pVDZ basis set. Such calculations are supposed to be in good agreement with the experimental UV-absorption spectra. In the next step, the geometry was optimized in the Conductor-like Screening Model54 (Cosmo) implemented in TURBOMOLE, to have comparison of the UV-absorption spectra obtained in the solvent and vacuum. Such satisfactory comparison was done in our report on betanin,21 based on TD-DFT calculations with the B3LYP functional51 with 6-311++G(3df,3pd) basis set55 (the largest Pople-style basis set) and polarizable continuum model (PCM) for the solvent,56,57 as implemented in Gaussian software package.58 Thus, here we use the same approach for MIR.However, the TD-DFT method is also known to fail in prediction of the excited states with strong charge-transfer,59,60 with small overlap of the two orbitals contributing to the electron excitation (e.g. HOMO and LUMO). To bypass this problem in predicting the excited-state potential energy profile (PE), additional calculations were performed, where the equilibrium geometry of the molecular system in its closed-shell singlet ground state (S0) was determined with the MP2 method.61 Excitation energies, equilibrium geometries, and response properties of the lowest singlet excited states were calculated using the algebraic diagrammatic construction method of the second order, ADC(2).62,63 To get insight into the mechanism of excited-state deactivation process, the minimum-energy reaction path (MEP) along the photophysically relevant reaction coordinates in the lowest excited singlet state were also determined with the ADC(2) method. For a suitably chosen driving coordinate, all other nuclear degrees of freedom were optimized for a given value of the driving coordinate. To allow cost-effective exploration of the high-dimensional potential-energy surfaces, the standard split-valence double-zeta basis set with polarization functions on the heavy atoms (def-SV(P)) was employed in these geometry optimizations.
Ab initio calculations for all of the model systems were performed with the TURBOMOLE program package,53 making use of the Resolution-of-the-Identity (RI) approximation for the evaluation of the electron-repulsion integrals.64
Acknowledgements
This work was supported by the Polish National Science Centre (NCN), within the DEC-2013/09/B/ST4/00273 project. Laser flash photolysis studies were performed at the Center for Ultrafast Laser Spectroscopy at A. Mickiewicz University in Poznan. Gaussian 09 suite of programs were used at the PL-Grid Infrastructure.References
- D. Strack, T. Vogt and W. Schliemann, Phytochemistry, 2003, 62, 247–269 CrossRef CAS PubMed.
- M. Wendel, D. Szot, K. Starzak, D. Tuwalska, D. Prukala, T. Pedzinski, M. Sikorski, S. Wybraniec and G. Burdzinski, Dyes Pigm., 2015, 113, 634–639 CrossRef CAS.
- M. Wendel, D. Szot, K. Starzak, D. Tuwalska, J. Gapinski, R. Naskrecki, D. Prukala, M. Sikorski, S. Wybraniec and G. Burdzinski, J. Lumin., 2015, 167, 289–295 CrossRef CAS.
- F. Gandía-Herrero, F. García-Carmona and J. Escribano, J. Chromatogr. A, 2005, 1078, 83–89 CrossRef.
- F. C. Stintzing, F. Kugler, R. Carle and J. Conrad, Helv. Chim. Acta, 2006, 89, 1008–1016 CrossRef CAS.
- F. Gandía-Herrero, F. García-Carmona and J. Escribano, Phytochem. Anal., 2006, 17, 262–269 CrossRef.
- Y. Cai, M. Sun, W. Schliemann and H. Corke, J. Agric. Food Chem., 2001, 49, 4429–4435 CrossRef CAS PubMed.
- K. M. Herbach, F. C. Stintzing and R. Carle, J. Food Sci., 2006, 71, R41 CrossRef CAS.
- M. Piattelli, L. Minale and R. A. Nicolaus, Phytochemistry, 1965, 4, 817–823 CrossRef CAS.
- G. F. Trezzini and J. P. Zryd, Phytochemistry, 1991, 30, 1901–1903 CrossRef CAS.
- W. Schliemann, Y. Cai, T. Degenkolb, J. Schmidt and H. Corke, Phytochemistry, 2001, 58, 159–165 CrossRef CAS PubMed.
- F. Gandía-Herrero, F. Garcia-Carmona and J. Escribano, Food Res. Int., 2005, 38, 879–884 CrossRef.
- F. Gandía-Herrero, M. Jiménez-Atiénzar, J. Cabanes, J. Escribano and F. García-Carmona, J. Agric. Food Chem., 2009, 57, 2523–2528 CrossRef PubMed.
- F. Gandía-Herrero, F. García-Carmona and J. Escribano, Nature, 2005, 437, 334 CrossRef PubMed.
- F. Gandía-Herrero, J. Escribano and F. Garcia-Carmona, Planta, 2010, 232, 449–460 CrossRef PubMed.
- G. Calogero, J.-H. Yum, A. Sinopoli, G. D. Marco, M. Grätzel and M. K. Nazeeruddin, Sol. Energy, 2012, 86, 1563–1575 CrossRef CAS.
- D. Magde, R. Wong and P. G. Seybold, Photochem. Photobiol., 2002, 75, 327–334 CrossRef CAS PubMed.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- S. A. Kovalenko, R. Schanz, V. M. Farztdinov, H. Hennig and N. P. Ernsting, Chem. Phys. Lett., 2000, 323, 312–322 CrossRef CAS.
- M. Wendel, S. Nizinski, D. Prukala, M. Sikorski, S. Wybraniec and G. Burdzinski, J. Photochem. Photobiol., A, 2017, 332, 602–610 CrossRef CAS.
- M. Wendel, S. Nizinski, D. Tuwalska, K. Starzak, D. Szot, D. Prukala, M. Sikorski, S. Wybraniec and G. Burdzinski, Phys. Chem. Chem. Phys., 2015, 17, 18152–18158 RSC.
- G. R. Fleming, S. H. Courtney and M. W. Balk, J. Stat. Phys., 1986, 42, 83–104 CrossRef.
- B. D. Allen, A. C. Benniston, A. Harriman, S. A. Rostron and C. Yu, Phys. Chem. Chem. Phys., 2005, 7, 3035–3040 RSC.
- C. Singh, B. Modak, J. A. Mondal and D. K. Palit, J. Phys. Chem. A, 2011, 115, 8183–8196 CrossRef CAS PubMed.
- V. I. Stsiapura, A. A. Maskevich, V. A. Kuzmitsky, V. N. Uversky, I. M. Kuznetsova and K. K. Turoverov, J. Phys. Chem. B, 2008, 112, 15893–15902 CrossRef CAS PubMed.
- A. K. Singh, G. Ramakrishna, H. N. Ghosh and D. K. Palit, J. Phys. Chem. A, 2004, 108, 2583–2597 CrossRef CAS.
- W. P. Ozimiński and J. C. Dobrowolski, J. Phys. Org. Chem., 2009, 22, 769–778 CrossRef.
- C. I. Oprea, A. Dumbrava, I. Enache, A. Georgescu and M. A. Girtu, J. Photochem. Photobiol., A, 2012, 240, 5–13 CrossRef CAS.
- S. S. Leang, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2012, 136, 104101 CrossRef PubMed.
- M. F. Rode and A. L. Sobolewski, Chem. Phys., 2008, 347, 413–421 CrossRef CAS.
- W. Domcke, D. R. Yarkony and H. Koppel, Conical Intersections: Theory, Computation and Experiment, World Scientific, 2011 Search PubMed.
- A. L. Sobolewski, W. Domcke and C. Hättig, J. Phys. Chem. A, 2006, 110, 6301–6306 CrossRef CAS PubMed.
- R. Omidyan and M. Iravani, J. Phys. Chem. A, 2016, 120, 1012–1019 CrossRef CAS PubMed.
- A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2006, 8, 3410–3417 RSC.
- R. H. E. Halabieh, O. Mermut and C. J. Barrett, Pure Appl. Chem., 2004, 76, 1445–1465 CrossRef.
- P. Gorostiza and E. Y. Isacoff, Science, 2008, 322, 395–399 CrossRef CAS PubMed.
- G. Cui, P.-J. Guan and W.-H. Fang, J. Phys. Chem. A, 2014, 118, 4732–4739 CrossRef CAS PubMed.
- P.-J. Guan, G. Cui and Q. Fang, ChemPhysChem, 2015, 16, 805–811 CrossRef CAS PubMed.
- S. Kitzig, M. Thilemann, T. Cordes and K. Rueck-Braun, ChemPhysChem, 2016, 17, 1252–1263 CrossRef CAS PubMed.
- A. Szukalski, A. Miniewicz, K. Haupa, B. Przybyl, J. Janczak, A. L. Sobolewski and J. Mysliwiec, J. Phys. Chem. C, 2016, 120, 14813–14819 CAS.
- A. Yartsev, J.-L. Alvarez, U. Aberg and V. Sundstrom, Chem. Phys. Lett., 1995, 243, 281–289 CrossRef CAS.
- B. Dietzek, A. Yartzev and A. N. Tarnovsky, J. Phys. Chem. B, 2007, 111, 4520–4526 CrossRef CAS PubMed.
- Z. Wei, T. Nakamura, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2011, 133, 8205–8210 CrossRef CAS PubMed.
- M. F. Rode and A. L. Sobolewski, Chem. Phys., 2012, 409, 41–48 CrossRef CAS.
- M. F. Rode and A. L. Sobolewski, J. Chem. Phys., 2014, 140, 84301–84314 CrossRef PubMed.
- L. Lapinski, M. J. Nowak, J. Nowacki, M. F. Rode and A. L. Sobolewski, ChemPhysChem, 2009, 10, 2290–2295 CrossRef CAS PubMed.
- M. F. Rode and A. L. Sobolewski, J. Phys. Chem. A, 2010, 114, 11879–11889 CrossRef CAS PubMed.
- J. Bahrenburg, M. F. Rode, A. L. Sobolewski and F. Temps, presented in part at the 19th International Conference on Ultrafast Phenomena, Okinawa Japan, 2014 Search PubMed.
- J. Jankowska, M. F. Rode, J. Sadlej and A. L. Sobolewski, ChemPhysChem, 2014, 15, 1643–1652 CrossRef CAS PubMed.
- S. Wybraniec, K. Starzak, A. Sipinska, B. Nemzer, Z. Pietrzykowski and T. Michalowski, J. Agric. Food Chem., 2013, 61, 6435–6476 CrossRef PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, since 2007, http://www.turbomole.com, V6.3 2011 edn, 1989-2007 Search PubMed.
- A. Klamt and G. Schuumann, J. Chem. Soc., Perkin Trans. 1, 1993, 2, 799–805 RSC.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef CAS.
- R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., in Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- S. N. Steinmann, C. Piemontesi, A. Delacht and C. Corminboeuf, J. Chem. Theory Comput., 2012, 8, 1629–1640 CrossRef CAS PubMed.
- A. Wakai, H. Fukasawa, C. Yang, T. Mori and Y. Inoue, J. Am. Chem. Soc., 2012, 134, 4990–4997 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- J. Schirmer, Phys. Rev. A, 1981, 26, 2395 CrossRef.
- A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299 CrossRef CAS.
- F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340 CrossRef CAS.
- Y. Marcus, The Properties of Solvents, John Wiley & Sons, Chichester, UK, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Results of stationary and time-resolved spectroscopic measurements, the results of quantum chemical calculations. See DOI: 10.1039/c6ra28110a |
| This journal is © The Royal Society of Chemistry 2017 |