Open Access Article
Open Access ArticleSolubility limits in quaternary SnTe-based alloys†
Sebastian Siol‡
 *a,
Aaron Holder
*a,
Aaron Holder ab,
Brenden R. Ortiz
ab,
Brenden R. Ortiz c,
Philip A. Parilla
c,
Philip A. Parilla a,
Eric Toberer
a,
Eric Toberer c,
Stephan Lany
c,
Stephan Lany a and
Andriy Zakutayev
a and
Andriy Zakutayev *a
*a
aNational Renewable Energy Laboratory, Golden, CO 80401, USA. E-mail: siol.sebastian@gmail.com; andriy.zakutayev@nrel.gov
bChemical and Biological Engineering, University of Colorado, Boulder, CO 80309-0596, USA
cColorado School of Mines, Golden, CO 80401, USA
First published on 9th May 2017
Abstract
The controlled decomposition of metastable alloys is an attractive route to form nanostructured thermoelectric materials with reduced thermal conductivity. The ternary SnTe–MnTe and SnTe–SnSe heterostructural alloys have been demonstrated as promising materials for thermoelectric applications. In this work, the quaternary Sn1−yMnyTe1−xSex phase space serves as a relevant model system to explore how a combination of computational and combinatorial-growth methods can be used to study equilibrium and non-equilibrium solubility limits. Results from first principle calculations indicate low equilibrium solubility for x,y < 0.05 that are in good agreement with results obtained from bulk equilibrium synthesis experiments and predict significantly higher spinodal limits. An experimental screening using sputtered combinatorial thin film sample libraries showed a remarkable increase in non-equilibrium solubility for x,y > 0.2. These theoretical and experimental results were used to guide the bulk synthesis of metastable alloys. The ability to reproduce the non-equilibrium solubility levels in bulk materials indicates that such theoretical calculations and combinatorial growth can inform bulk synthetic routes. Further, the large difference between equilibrium and non-equilibrium solubility limits in Sn1−yMnyTe1−xSex indicates these metastable alloys are attractive in terms of nano-precipitate formation for potential thermoelectric applications.
1. Introduction
Thermoelectric (TE) power generation allows the transformation of waste heat into electrical energy and is expected to play an important role in the future of sustainable energy generation.1 While optimization of TE performance requires the control of transport properties of the material, many of the recent advances were achieved by reducing the thermal conductivity.2 The lattice thermal conductivity can be reduced through phonon scattering by introducing secondary phase nanoprecipitates, point defects, grain boundaries and intrinsic bond anharmonicity.3–5 Secondary phase nanoprecipitates to scatter phonons or control the Fermi level6,7 can be incorporated through mechanical and chemical approaches. Mechanical approaches involve the incorporation of non-reactive secondary phases into a matrix phase. Chemical approaches are centered around a supersaturation and precipitation of a secondary phase within a solid matrix. For example, temperature can be used to increase the solubility of an alloy; subsequent quenching yields the formation of nanoparticles due to the decreased solubility on cooling.7,8 Liquid-state quenching provides even greater solubility and can yield very high volume fractions of nanoprecipitates.9 However, in many systems, the change in solubility in the solid state is small and liquid phase quenching is impractical. Nanoprecipitate formation requires an alternative to temperature to achieve metastable compositions. One solution has been to combine mechanical processing (milling to yield metastable powders) with subsequent chemical partitioning.SnTe is a narrow band gap IV–VI semiconductor with demonstrated high ZT.10–13 Promising results have been reported regarding the isoelectronic alloying of SnTe, specifically for (Sn,Mn)Te and Sn(Te,Se). High solubility limits have been observed in previous studies of these systems (MnTe in SnTe < 13%,14,15 SnSe in SnTe < 15% (ref. 5)). For SnTe alloyed with MnTe, the maximum performance occurred at alloying concentrations slightly above the solubility limit and is attributed to an increase in phonon scattering from point defects and secondary phases, as well as changes in the electronic band structure (i.e. band degeneracy and opening of the band gap).14,15
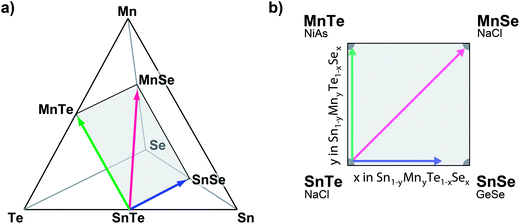
Based on the promising results of ternary SnTe alloys, we investigate the quaternary (Sn,Mn) (Se,Te) alloy system (Fig. 1a). This 3-dimensonal phase space can be constrained by limiting the anion to cation ratio to unity (see Fig. 1b). While the isoelectric alloying with SnSe and MnTe has been successfully demonstrated,15 the choice of MnSe is motivated by its structural and thermodynamic properties. Like SnTe, MnSe crystallizes in the cubic NaCl structure although the atomic volume is roughly 35% smaller than metallic SnTe (see Table 1). The entropic stabilization of the quaternary alloy thus is at odds with the enthalpic forces to separate the composition; both strain and the high stability of MnSe (melting point Tm = 1460 °C (ref. 16)) are expected to yield a ground state that exhibits low MnSe solubility in SnTe.
| AFM-phase | ΔEgs (meV at.−1) | V (Å3 at.−1) | Eg (eV) | Eg-D (eV) | mh (m0) | me (m0) | Eg-exp. (eV) | |
|---|---|---|---|---|---|---|---|---|
| SnTe | NaCl* | 0 | 32.7 | 0.10 | 0.10 | 0.72 | 1.34 | 0.2 (ref. 5) |
| MnTe | NiAs* | 0 | 25.5 | 0.98 | 2.11 | 1.54 | 1.26 | 1.2 (ref. 19) |
| NaCl | 40 | 25.7 | 0.65 | 1.25 | 1.16 | 0.61 | — | |
| SnSe | ORC* | 0 | 28.0 | 0.96 | 1.10 | 1.59 | 0.98 | 0.9 (ref. 20) |
| MnSe | NaCl* | 0 | 20.5 | 2.52 | 3.01 | 1.57 | 0.78 | 2.6 (ref. 21) |
In this work, we present a general computational and high-throughput experimental approach to quickly identify promising material systems with large metastable phase regions amenable to controlled nano-precipitate formation. Here, the equilibrium and metastable solubility limits of Sn1−yMnyTe1−xSex were investigated for ultimate application in spontaneous nanostructure formation through a mixture of first principles calculations, non-equilibrium bulk syntheses, and high-throughput thin film combinatorial sputtering. This structural analysis reveals a large region of metastable Sn1−yMnyTe1−xSex phase space that is accessible by non-equilibrium synthesis methods. This, in turn, should facilitate independent control of alloying concentration and the amount of nano-precipitates in the alloyed material, a strategy that has led to significant enhancement of thermoelectric properties for a variety of promising materials systems.3
2. Results
For an investigation of the composition–structure relationship in the quaternary Sn1−yMnyTe1−xSex alloy system, a combined computational and experimental approach was employed. First principle calculations were used to determine solubility limits and end member compound properties. In parallel, bulk synthesis and high throughput combinatorial thin film deposition were performed to experimentally determine equilibrium and non-equilibrium single-phase boundaries.2.1 Computational results
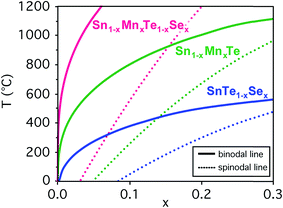
Prior to an investigation of the quaternary Sn1−yMnyTe1−xSex alloy system, the properties of the binary end member compounds SnTe, MnTe, SnSe and MnSe were investigated. Table 1 shows a summary of functional properties calculated for different polymorphs for the respective materials. The reported GW band gaps exclude the effect of spin–orbit coupling (SOC). At the DFT level, SOC reduces the gap of MnTe (NiAs structure) by 0.19 eV. In SnTe, the conventional gap of 0.08 eV becomes an inverted gap of 0.23 eV. The properties provided for the end member binaries calculated for the NaCl structure can provide a general trend how the properties of SnTe would change upon alloying with those materials. For the case of alloying SnTe with SnSe, the orthorhombic (ORC) structure of SnSe can be viewed as a distorted NaCl structure, and is therefore commensurate with the SnTe lattice. Similar to SnS,17,18 SnSe has an inverted band gap in the ideal NaCl structure, but this structure is not stable and a sizable conventional band gap opens due to the orthorhombic distortion (see Table 1).One issue that is limiting the performance of SnTe for thermoelectric applications is its low band gap and high carrier concentration.5 Considering a linear extrapolation of the materials properties from the end member compounds in NaCl structure (see Table 1) alloying with MnSe could increase the SnTe band gap while increasing the hole effective mass. To determine the thermodynamic solubilities for Sn1−yMnyTe1−xSex with x = y as well as Sn1−xMnxTe and SnTe1−xSex first principle calculations were performed for the mixing enthalpies. Fig. 2 shows the binodal and spinodal lines for all three cases, defining the metastable and unstable phase regions, respectively. No significant Mn–Se interaction was found for the quaternary alloy system hence the system can be treated as a random alloy. A significant decrease in solubility is observed upon alloying with MnSe as compared to SnSe or MnTe. This might initially be counterintuitive since an increase in solubility is expected for the isostructural alloy. It can be explained however, by the large difference in atomic volume (35%, see Table 1) that leads to tensile stress in the alloy.
In addition, the co-doping of SnTe with Mn and Se introduces rock salt MnSe as a potential competing phase that is not present in the ternary Sn1−xMnxTe or SnTe1−xSex alloys. The increased relative stability of MnSe compared to the other competing phases, SnSe and MnTe, reduces the solubility limit of the quaternary solid solution despite the increase in configurational entropy compared to the ternary alloys.
2.2 Bulk synthesis
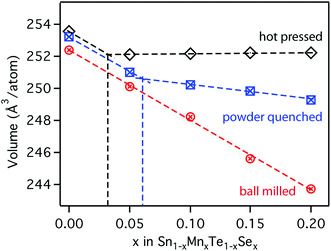
For comparison with first principle calculations, several bulk samples of the quaternary Sn1−yMnyTe1−xSex alloy with x = y were synthesized. Three routes of synthesis were employed to target different degrees of metastability, and five different compositions were investigated (x = y = 0/0.05/0.10/0.15/0.20) for each route.Fig. 3 shows the atomic volume derived from X-ray diffraction (XRD) measurements for the three bulk-processing methods employed herein. Hot pressed samples were processed at temperatures of roughly 600 °C (80% of the melting point Tm for each alloy) and slowly cooled to room temperature. The powder-quenched samples were processed at temperatures of over 700 °C (90% Tm for each alloy) and quenched in water to avoid decomposition of the sample upon cooling. The ball-milled powder received no thermal treatment after ball milling and represents a state of non-equilibrium, due the high kinetic energies in the ball milling apparatus. Experimental details for the synthesis are given in the methods section. A linear shift is expected with increasing alloying concentration according to Vegard's law,22 whereas a change in slope indicates the formation of secondary phases. For the hot pressed sample this change in slope occurs at roughly x = 0.03 alloying concentrations. The powder quench leads to increased solubility of over x = 0.06. Ball milling of the powder on the other hand shows a remarkable increase in solubility of over x = 0.2. Only minor impurities of metallic Sn and Te can be found in the XRD patterns (see ESI, Fig. S1†).
2.3 Combinatorial screening
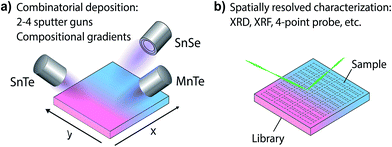
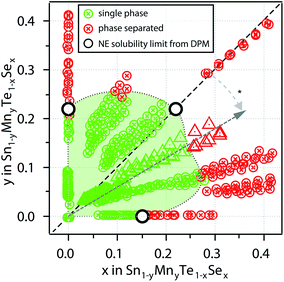
For an investigation of the non-equilibrium solubility in the quaternary alloy system, high-throughput combinatorial experiments were carried out. While high-throughput techniques are commonly used in other areas of materials science (i.e. novel materials for thin film PV23–26 or materials by design27,28) such combinatorial approaches are rather uncommon in TE research.29,30 Combinatorial thin film deposition was performed using radio frequency (RF) magnetron co-sputtering from multiple targets leading to composition gradients along the substrate, and resulting in combinatorial sample libraries (see Fig. 4, details are given in the Methods section). Spatially resolved X-ray fluorescence (XRF) and Θ–2Θ X-ray diffraction (XRD) measurements were performed on multiple libraries deposited at a substrate temperature of 230 °C. This way, a large number of samples could be investigated (>1000 within the Sn1−yMnyTe1−xSex compositional phase space).Fig. 5 shows a phase map of the Sn1−yMnyTe1−xSex with alloying concentrations of x,y < 0.5. The green data points represent samples that are single phase according to XRD. In addition to a simple screening for impurities the disappearing phase method was employed to determine the solubility limits (white points in Fig. 4) for alloys of SnTe with MnTe, MnSe and SnSe (see Fig. S2†). Over the entire composition range high solubility limits of x,y > 0.15 are observed. Solubility limits for the SnTe/MnSe alloy are in good agreement with non-equilibrium solubility limits obtained from ball-milled powder (see Fig. 3).
To investigate the feasibility of the alloy materials for thermoelectric applications a combinatorial screening of the resistivity ρ was carried out. The measurements were taken on combinatorial thin film libraries consisting of alloys of SnTe/MnTe, SnTe/SnSe, as well as SnTe/MnSe at 300 K. Resistivities were found to be in a range of 10−3 Ω cm to 10−4 Ω cm (Fig. S3a†). Besides delamiation that occurred for several samples due to mechanical stress in the film and lack of adhesion on the glass substrates only a minor rise in resistivity can be observed with increasing alloying concentration. In addition, the Seebeck coefficient was measured for individual samples at 300 K. While for the SnTe/SnSe a decrease in Seebeck coefficient can be observed for higher alloying concentrations. Alloys of SnTe with MnTe and MnSe show promising results with the highest Seebeck coefficients of 54 μV K−1 and 41 μV K−1 occurring around y ≈ 0.1 and y, x ≈ 0.1 for the Sn1−yMnyTe and Sn1−yMnyTe1−xSex alloys, respectively (Fig. S3b†). This is in good agreement with literature values for SnTe/MnTe as well as SnTe/SnSe, supporting the feasibility of an initial thin film materials screening for thermoelectric applications.
3. Discussion
A comprehensive analysis of the structure composition relation of the Sn1−yMnyTe1−xSex alloy phase space by theoretical and experimental methods was carried out. Fig. 6 shows a comparison of the single phase boundaries obtained by different methods.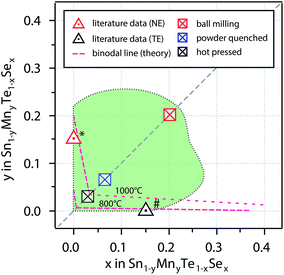 | ||
| Fig. 6 Combination of non-equilibrium solubility limits from sputter deposition (Fig. 5) as well as non-equilibrium (NE) and equilibrium bulk synthesis. The dashed lines represent binodal lines from computational data for 800 °C and 1000 °C. * is taken from ref. 15 (1150 °C + quenching in water), # is taken from ref. 5 (anneal at 900 °C). | ||
Computational results indicate very low equilibrium solubility of x,y < 0.05 for quaternary alloys of SnTe/MnSe in thermodynamic equilibrium. This can be explained by the large difference in atomic volume leading to tensile strain in the material (see Table 1) and is in very good agreement with results from bulk synthesis and values from literature for ternary (Sn,Mn)Te and Sn(Se,Te) alloys. Theoretical predictions for equilibrium solubility limits in these ternary alloys at 1000 °C are only slightly higher than literature values for the ternary samples that were quenched from 1150 °C (ref. 14 and 15) (see Fig. 6). In addition, the solubility limits obtained for the hot pressed SnTe/MnSe quaternary alloy from this work are also within 3% of the theoretical prediction, which is a remarkably good agreement. This favorable comparison highlights the feasibility of an accelerated computational screening of equilibrium solubility limits even in complex alloy systems like the quaternary alloys investigated in this work.
The solubility limits in the SnTe/MnSe can be increased somewhat by quenching the samples in water (powder-quenched). This synthesis route allows for more rapid cooling from a higher-temperature and therefore higher-energy state, than for the hot-pressed samples discussed above. Since the cooling process is fast only little time is available for the decomposition of the alloy in the end member products. For the powder-quenched SnTe/MnSe alloy non-equilibrium solubility limits in the range of 7% could be achieved.
The non-equilibrium solubility limits obtained from the ball milled alloy powder and from sputtered thin films are remarkably higher, exceeding compositional values of x,y > 0.2. The increase in solubility for these methods is due to the more energetic environments during the synthesis processes. The high-energy collisions during ball milling can supply more energy than the heating during hot-pressing or powder-quenching.31 At the same time kinetic energies of the atoms during RF sputtering are comparably high (typically in the eV range32). It is not unusual for thin film alloys deposited at high kinetic energies to show extended single-phase boundaries.27,33 For both of these processes, even at higher alloying concentrations binodal decomposition can be kinetically hindered, as shown in Fig. 6.
An additional interesting result of this study is the evolution of the non-equilibrium solubility line as obtained from combinatorial experiments. Upon alloying of SnTe with MnSe the resulting Sn1−yMnyTe1−xSex films exhibit compositions of x > y indicating preferred anion exchange (see Fig. 5). This can tentatively explained by a reduction of tensile stress in the material as described by Ortiz et al.34 and implies a new design principle for isoelectronic alloying for thermoelectric applications. By carefully choosing the cation and anion alloying elements it should be possible to suppress macroscopic volume changes of the alloy, while maintaining local strain that is necessary to enable enhancements in phonon scattering. Using non-equilibrium bulk synthesis such as spark plasma sintering this promising phase space can be made accessible for thermoelectric applications. In particular, material systems with large accessible metastable composition space are promising for the controlled incorporation of nano-precipitates and secondary phases to increase phonon scattering. Most metastable alloys can withstand heating up to a certain temperature before they undergo binodal-decomposition, i.e. sufficient energy needs to be supplied to overcome kinetic barriers in the decomposition pathway. In turn, this means that the alloy can be designed to achieve the desired concentration of nano-precipitates at the targeted operating temperature of the thermoelectric by carefully adjusting the alloying concentration and therefore the degree of metastability.
4. Conclusion
The integration of unique micro/nanostructures into bulk thermoelectric materials is an attractive way of improving ZT. This work has demonstrated that a combination of combinatorial sputtering and computation can serve as an effective proxy for identifying solubility/metastability boundaries in complex chemical spaces. Furthermore, results from sputtering have been shown to be reproducible in bulk (via high-energy ball milling), allowing the results to be generalized into a form-factor attractive to thermoelectric applications. We have specifically tested this technique on alloys of Sn1−yMnyTe1−xSex, demonstrating that a large region of metastability (0.05 < x,y < 0.20) is present, providing a wide array of potential chemical compositions that can be used to generate nuanced micro/nanostructures in bulk. Our approach serves as a case-study for the rapid generation of alloying data combining computation, combinatorial sputtering, and bulk synthesis to enable controlled partitioning and evolution of micro/nanostructures in thermoelectric materials.5. Methods
5.1 Computational work
The first principles calculations were performed with the VASP code and its implementations of DFT and GW,35,36 using the standard projector augmented wave pseudopotentials distributed with VASP. The GW calculations of the binary electronic properties reported in Table 1 were performed as described in ref. 37. The alloy mixing enthalpies were calculated in DFT+U38,39 with U = 3 eV for Mn-d orbitals and an energy cutoff of 420 eV. To model the alloys, we used the special quasi-random structure (SQS) method40 to generate ideally random alloy structures for each phase and composition. The use of random alloy models for describing the SnTe-rich quaternary alloys is supported by the predicted binding energy between Mn and Se of −0.036 meV, where the law of mass action indicates that for such a small attractive energy the pairs will be predominately dissociated at room temperature or higher. The mixing enthalpy (ΔHm(x)) calculations were performed using 64-atom SQS models. For the Mn containing alloys, we used the lowest energy magnetic configuration of the Mn cations, as determined from magnetic configuration sampling, for computing ΔHm(x). The alloy ΔGm(x) was determined from ΔHm(x) and the configurational entropy of each sub-lattice in the random alloy: ΔS = −kB[x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + (1 − x)ln(1 − x)]. The reported solubility limit (binodal line) are approximated from the dG(T)/dx = 0 condition, and the spinodal line evaluated using the zero-curvature condition.
x + (1 − x)ln(1 − x)]. The reported solubility limit (binodal line) are approximated from the dG(T)/dx = 0 condition, and the spinodal line evaluated using the zero-curvature condition.
5.2 Bulk synthesis
For the bulk synthesis Mn (99.99%), Se (99.999%), Te (99.999%), Sn (99.99%) precursors in shot or chunk form were used. Samples ranging from 0.00–0.20 substitution (x in Sn1−xMnxTe1−xSex) in steps of 5% were prepared. Samples were loaded in stainless-steel vials with 3 0.5′′ stainless-steel balls and milled continuously for 3 h. Powders were subsequently passed through a 106 μm sieve. XRD measurements were performed at this step (ball-milled in Fig. 3). Ball-milled powders were then divided into two batches: one for hot-pressing and one for annealing. For hot-pressing, powders were loaded into a high-density graphite die and placed in an induction, uniaxial hot-press. Samples were heated under vacuum (<5 mT) at 250 °C min−1 to 600 °C and hot pressed for 1 h at 80 MPa. Afterwards, the samples were annealed at 80% Tm (600–691 °C) for 30 min. The samples were cooled to RT in approximately 30 min, sectioned via diamond saw and subsequently analyzed with XRD (hot-pressed in Fig. 3). For the annealing experiment (powder-quenched in Fig. 3), the remaining ball-milled powder was sealed in fused-silica ampoules under rough vacuum. Ampoules were subsequently dropped in pre-heated furnaces (90% Tm, 675–794 °C) and annealed for 72 h. Afterwards the samples were quenched in water and analyzed with XRD. Atomic cell volumes were determined from XRD data using LeBail fits.5.3 Combinatorial screening
Thin-film combinatorial libraries were deposited using orthogonal composition and temperature gradients via RF co-sputtering from ceramic SnTe and MnTe, SnSe or MnSe targets, respectively (see Fig. 1c). By applying intentional and well-controlled gradients on the substrate during combinatorial thin film synthesis, several values of deposition parameters can be covered in a single synthesis experiment.23 For selected experiments a uniform temperature was applied over the whole substrate area and co-sputtering from 3 targets was carried out (SnTe, MnTe and MnSe, or SnTe, SnSe and MnSe, respectively – see Fig. 1c). Several libraries were deposited to cover a broad range of deposition temperatures and produce thin-film samples over the entire alloy composition range. A total of 44 samples were defined on a single library. The samples were analyzed via spatially-resolved X-ray fluorescence (XRF) and XRD with respect to their composition and crystal structure (including disappearing phase analysis), and electrical properties were characterized using 4 point probe mapping. Single point Seebeck measurements were carried out at 300 K on selected samples. A more detailed description of the combinatorial experiments can be found in ESI† and in our prior work.25,41Author contributions
The manuscript was written by SS and AZ with contributions from all authors. AH and SL performed the computational analysis, BO performed the bulk synthesis supervised by ET. SS conducted the high throughput experiments with contributions and supervision from AZ. PAP contributed to the evaluation of data from high throughput experiments. All authors have provided input to the text and given their approval to the final version of the manuscript.Acknowledgements
This work was supported by NREL's Laboratory Directed Research and Development (LDRD) program. In addition, SS and AH gratefully acknowledge funding from the US Department of Energy, Office of Science, Office of Basic Energy Sciences, as part of the Energy Frontier Research Center “Center for Next Generation of Materials by Design” under contract No. DE-AC36-08GO28308 to NREL. The authors declare no competing financial interests.References
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- M. G. Kanatzidis, Chem. Mater., 2010, 22, 648–659 CrossRef CAS.
- Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- A. Banik and K. Biswas, J. Mater. Chem. A, 2014, 2, 9620 CAS.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed.
- G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167 CrossRef CAS PubMed.
- A. Banik, B. Vishal, S. Perumal, R. Datta and K. Biswas, Energy Environ. Sci., 2016, 9, 2011–2019 CAS.
- Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS.
- M. Zhou, Z. M. Gibbs, H. Wang, Y. Han, L. Li and G. Jeffrey Snyder, Appl. Phys. Lett., 2016, 109, 42102 CrossRef.
- G. Tan, W. G. Zeier, F. Shi, P. Wang, G. J. Snyder, V. P. Dravid and M. G. Kanatzidis, Chem. Mater., 2015, 27, 7801–7811 CrossRef CAS.
- M. Zhou, Z. M. Gibbs, H. Wang, Y. Han, C. Xin, L. Li and G. J. Snyder, Phys. Chem. Chem. Phys., 2014, 16, 20741–20748 RSC.
- L. D. Zhao, X. Zhang, H. Wu, G. Tan, Y. Pei, Y. Xiao, C. Chang, D. Wu, H. Chi, L. Zheng, S. Gong, C. Uher, J. He and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 2366–2373 CrossRef CAS PubMed.
- H. Wu, C. Chang, D. Feng, Y. Xiao, X. Zhang, Y. Pei, L. Zheng, D. Wu, S. Gong, Y. Chen, J. He, M. G. Kanatzidis and L.-D. Zhao, Energy Environ. Sci., 2015, 8, 3298–3312 CAS.
- G. Tan, F. Shi, S. Hao, H. Chi, T. P. Bailey, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Valence Band Modification and High Thermoelectric Performance in SnTe Heavily Alloyed with MnTe, J. Am. Chem. Soc., 2015, 137(35), 11507–11516, DOI:10.1021/jacs.5b07284.
- D. L. Perry, Handbook of Inorganic Compounds, CRC Press, Boca Raton, FL, 2nd edn, 2011 Search PubMed.
- R. L. Z. Hoye, P. Schulz, L. T. Schelhas, A. M. Holder, K. H. Stone, J. D. Perkins, D. Vigil-Fowler, S. Siol, D. O. Scanlon, A. Zakutayev, A. Walsh, I. C. Smith, B. C. Melot, R. C. Kurchin, Y. Wang, J. Shi, F. C. Marques, J. J. Berry, W. Tumas, S. Lany, V. Stevanović, M. F. Toney and T. Buonassisi, Chem. Mater., 2017, 29(5), 1964–1988 CrossRef CAS.
- J. Vidal, S. Lany, J. Francis, R. Kokenyesi and J. Tate, J. Appl. Phys., 2014, 115, 113507 CrossRef.
- W. Xie, S. Populoh, K. Gałązka, X. Xiao, L. Sagarna, Y. Liu, M. Trottmann, J. He and A. Weidenkaff, J. Appl. Phys., 2014, 115, 103707 CrossRef.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- N. Moloto, M. J. Moloto, M. Kalenga, S. Govindraju and M. Airo, Opt. Mater., 2013, 36, 31–35 CrossRef CAS.
- K. T. Jacob, S. Raj and L. Rannesh, Int. J. Mater. Res., 2007, 98, 776–779 CrossRef CAS.
- M. L. Green, I. Takeuchi and J. R. Hattrick-Simpers, J. Appl. Phys., 2013, 113, 231101 CrossRef.
- K. Mokurala, L. L. L. Baranowski, F. W. F. W. de Souza Lucas, S. Siol, M. F. A. M. van Hest, S. Mallick, P. Bhargava and A. Zakutayev, ACS Comb. Sci., 2016, 18, 583–589 CrossRef CAS PubMed.
- S. Siol, P. Schulz, M. Young, K. A. Borup, G. Teeter and A. Zakutayev, Adv. Mater. Interfaces, 2016, 3, 1600755 CrossRef.
- A. W. Welch, L. L. Baranowski, P. Zawadzki, C. DeHart, S. Johnston, S. Lany, C. A. Wolden and A. Zakutayev, Prog. Photovoltaics, 2016, 24(7), 929–939 CAS.
- H. Peng, P. F. Ndione, D. S. Ginley, A. Zakutayev and S. Lany, Phys. Rev. X, 2015, 5, 21016 Search PubMed.
- A. M. Holder, S. Siol, P. F. Ndione, H. Peng, A. M. Deml, B. E. Matthews, L. T. Schelhas, M. F. Toney, R. G. Gordon, W. Tumas, J. D. Perkins, D. S. Ginley, B. P. Gorman, J. Tate, A. Zakutayev, S. Lany, 2017, unpublished results.
- M. Otani, K. Itaka, W. Wong-Ng, P. K. Schenck and H. Koinuma, Appl. Surf. Sci., 2007, 254, 765–767 CrossRef CAS.
- J. García-Cañadas, N. J. E. Adkins, S. McCain, B. Hauptstein, A. Brew, D. J. Jarvis and G. Min, ACS Comb. Sci., 2016, 18, 314–319 CrossRef PubMed.
- T. Hashishin, Z. Tan, K. Yamamoto, N. Qiu, J. Kim, C. Numako, T. Naka, J. C. Valmalette and S. Ohara, Sci. Rep., 2014, 4, 4700 CrossRef PubMed.
- D. Depla and S. Mahieu, Reactive Sputter Deposition, Springer-Verlag, Berlin, Heidelberg, 2008, vol. 109 Search PubMed.
- A. Bikowski, A. Holder, H. Peng, S. Siol, A. Norman, S. Lany and A. Zakutayev, Chem. Mater., 2016, 28, 7765–7772 CrossRef CAS.
- B. R. Ortiz, H. Peng, A. Lopez, P. A. Parilla, S. Lany and E. S. Toberer, Phys. Chem. Chem. Phys., 2015, 17, 19410–19423 RSC.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 35101 CrossRef.
- H. Peng and S. Lany, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 201202 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- S. Siol, T. P. Dhakal, G. S. Gudavalli, P. P. Rajbhandari, C. DeHart, L. L. Baranowski and A. Zakutayev, ACS Appl. Mater. Interfaces, 2016, 8, 14004–14011 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28219a |
| ‡ Current address: Empa, Swiss Federal Laboratories for Materials Science and Technology, CH-8600 Dübendorf, Switzerland. |
| This journal is © The Royal Society of Chemistry 2017 |