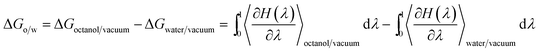Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Prednisolone adsorption on lung surfactant models: insights on the formation of nanoaggregates, monolayer collapse and prednisolone spreading
Evelina D. Estrada-López ,
Erika Murce
,
Erika Murce ,
Matheus P. P. Franca
,
Matheus P. P. Franca and
Andre S. Pimentel
and
Andre S. Pimentel *
*
Departamento de Química, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, RJ 22453-900, Brazil. E-mail: a_pimentel@puc-rio.br
First published on 17th January 2017
Abstract
The adsorption of prednisolone on a lung surfactant model was successfully performed using coarse grained molecular dynamics. The prednisolone coarse grained model was parameterized using a well-established cholesterol model and validated by using calculations of octanol–water partition coefficients and lateral diffusion coefficients. The calculated octanol–water partition coefficient of prednisolone is 3.9. The lateral diffusion coefficient of prednisolone in the DPPC/POPC mixed monolayer is estimated to be (6 ± 4) × 10−7 cm2 s−1 at 20 mN m−1, which is in agreement with that found for cholesterol. The DPPC/POPC mixed monolayer was used as lung surfactant model where prednisolone molecules were adsorbed forming nanoaggregates at surface tension of 0 mN m−1. The nanoaggregates of prednisolone were transferred into the DPPC/POPC mixed monolayer being spread at the surface tension of 20 mN m−1. At 0 mN m−1, the prednisolone nanoaggregates induce the collapse of the DPPC/POPC mixed monolayer forming a bilayer. The implications of this finding are that prednisolone may only be administered with lung surfactant by using low fractions of prednisolone per lipid, and with high fractions, the collapse inactivates the properties of the lung surfactant by forming a bilayer that may be eliminated by the clearance process of the lung.
Introduction
Prednisolone is an active molecule that is a metabolite of prednisone. It is a synthetic glucocorticoid that binds to the glucocorticoid receptor and plays an important role in the glucose metabolism and in synthesis in the adrenal cortex.1 It is part of the feedback mechanism in the immune system which reduces inflammation.2 Therefore, it is used to treat respiratory diseases caused by an overactive immune system such as allergies and asthma.3,4 Potentially harmful side effects, such as behavioral disturbances, impaired immune response, and weight gain, are commonly seen with long term or repetitive treatment.2,5 In fact, the use of steroids has been often linked to adverse effects on the neurological development, contributing to the generalized inhalation or endotracheal administration of steroids.6 Even so, both are on the World Health Organization (WHO) list of the most essential and important medications in the basic health system.7 Consequently, it is important to investigate a less invasive local or topical use than oral administration of prednisone and prednisolone. In this sense, the use of lung surfactant as drug carrier and spreading agent is potential drug delivery strategy on the horizon to treat respiratory distress syndrome and obstructive lung diseases.8,9The properties of the lung surfactant system may be used to rapidly spread and deliver drugs on the alveolar interface and pulmonary epithelium, thus favoring the drug effectivity and reducing the systemic toxicity. Furthermore, the lung surfactant may assist the solubilization of hydrophobic drugs. Therefore, in order to utilize it as a drug deliver system, the interaction of drugs with the lung surfactant must be evaluated in order to understand a possible lung surfactant inactivation. As inflammation may be a primary mediator in the pathogenesis of many diseases, steroids have been the focus of several studies.6 Davies et al. reported that the glucocorticoid budesonide interacts with lung surfactant monolayers by hydrophobic interactions.10 Kuo et al. presented significant reduction of deaths administrating mixed budesonide-lung surfactant in premature infants.11 Dani et al. also reported positive results with beclometasone-lung surfactant mixture.12 Mikolka et al. also found that budesonide mixed with lung surfactant improves the lung function as compared with pure lung surfactant.13
Corticosteroids are also derivatives of cholesterol and share a similar structure and vital role in the phase regulation of phospholipids.14 Zuo et al. compared the effect of cholesterol and budesonide on the surface activity and molecular organization of a lung surfactant.15 Previous studies sustain their results16–18 but contradictory reports also exist.19 Palmer et al. showed that budesonide significantly reduced the surface activity of the lung surfactant although salbutamol did not.19 Wang et al. found that budesonide and beclometasone do not substantially affect the surface activity of a lung surfactant, but the film collapses with higher concentrations.20
In the last 10 years, some challenges on simulating complex lung surfactant models were presented in order to mimick the phase separation, formation of a bilayer fold and a highly curved structure by long time and large size scales using coarse grained simulations.21–34 The coarse grained molecular dynamics (MD) of the adsorption of nanoparticles has also been studied in the literature.35–42 The atomistic MD simulations are also feasible to be investigate these systems on time scales of the order of 200–400 ns.43–52 On the other hand, to the best of our knowledge, the adsorption of drugs on lung surfactant models has not been investigated at all.
This study provides information on the adsorption of prednisolone into mixed phospholipid monolayers composed of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) in the proportion 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 using coarse-grained MD. The chemical structures of these compounds are shown in Fig. 1. The coarse-grained MD is a very useful tool that has been used for modeling of the interaction of drugs with lung surfactant models. Once the tool is applied to the lung surfactant monolayer model, conformational and dynamic information of the system can be drawn from the analysis of the results, such as area per lipid, orientation, order, formation of nanoaggregates, and diffusion. The simulations were performed with different surface tensions to mimic the changes on surface tension during the respiration process. When a human being inflates the lung with air (air inhalation), the surface tension is increased to approximately 20 mN m−1. And, the surface tension decreases to around 0 mN m−1 as air is exhaled. The aim of this study is to understand the behavior of prednisolone in the lung surfactant phospholipid monolayer model.
3 using coarse-grained MD. The chemical structures of these compounds are shown in Fig. 1. The coarse-grained MD is a very useful tool that has been used for modeling of the interaction of drugs with lung surfactant models. Once the tool is applied to the lung surfactant monolayer model, conformational and dynamic information of the system can be drawn from the analysis of the results, such as area per lipid, orientation, order, formation of nanoaggregates, and diffusion. The simulations were performed with different surface tensions to mimic the changes on surface tension during the respiration process. When a human being inflates the lung with air (air inhalation), the surface tension is increased to approximately 20 mN m−1. And, the surface tension decreases to around 0 mN m−1 as air is exhaled. The aim of this study is to understand the behavior of prednisolone in the lung surfactant phospholipid monolayer model.
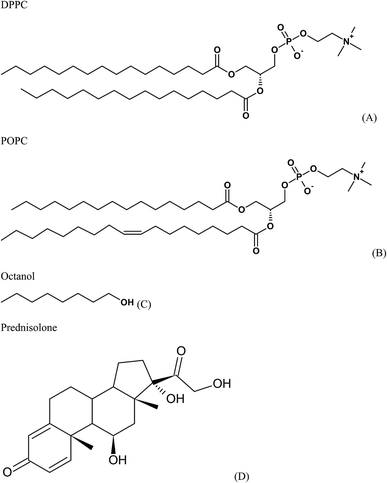 | ||
| Fig. 1 Chemical structures of (A) 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), (B) 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), (C) octanol, and (D) prednisolone. | ||
Methodology
Parameterization
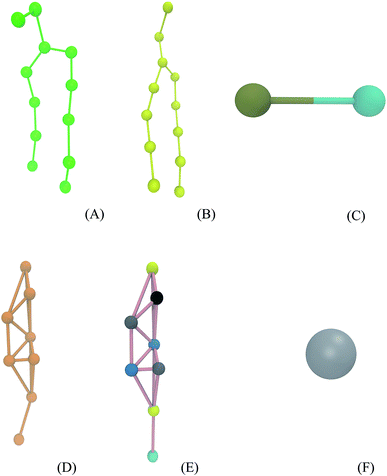
Simulations were performed using the computational package GROMACS 5.0.6.53,54 The Martini force field parameters for DPPC, POPC, octanol, and water were acquired from the literature.55–57 The lipid molecules are represented by particles that group approximately four heavy atoms together (Fig. 2A and B). The octanol molecule is modeled by two groups (one is a hydrophobic hydrocarbon chain and other is a polar head) as shown in Fig. 2C. DPPC and POPC are standard components of this force field.56,57 The prednisolone model (Fig. 2E) was generated using the cholesterol model57 keeping the cholesterol framework as presented in Fig. 2D and Table 1. The water model (Fig. 2F) is a representation of four water molecules.| Group | Cholesterol | Group representation | Prednisolone | Group representation |
|---|---|---|---|---|
| 1 | SP1 | Cyclic alcohol | SNa | Cyclic ketone |
| 2 | SC1 | Cyclic alkane | SC4 | Cyclic diene |
| 3 | SC3 | Cyclic alkene | SC1 | Cyclic alkane |
| 4 | SC1 | Cyclic alkane | SNda | Cyclic alcohol |
| 5 | SC1 | Cyclic alkane | SNda | Cyclic alcohol |
| 6 | SC1 | Cyclic alkane | SC1 | Cyclic alkane |
| 7 | SC1 | Cyclic alkane | SNa | Cyclic ketone |
| 8 | C1 | Alkane | P2 | Aliphatic alcohol |
General procedures
Before all simulations, the energy of the two-phase system was minimized using the steepest descent method in order to eliminate the overlap of atoms during the dimensioning of the system. The minimization was performed until the energy reaches 100 kJ mol−1. This energy is not the minimum energy. It is only a target energy used to attain a better and relaxed configuration system with no overlapped groups. It could be other energy value, but the energy used is standard and very well tested. The time step of all simulations was 20 fs. Also, the cutoffs for Lennard-Jones interactions were shifted to zero between 0.9 and 1.2 nm and Coulomb interactions were shifted to zero between 0 and 1.2 nm, which are the standard cutoffs for the coarse grained force field. The default relative dielectric constant was used, which is 15 for this force field.27,56 The neighbor list for nonbonded interactions was updated evert 10 steps.Thermodynamic integration
Two systems were prepared using a cubic box of 5.1 nm and periodic boundary conditions: (a) 1 molecule of prednisolone and 918 molecules of water; and (b) 1 molecule of prednisolone, 600 molecules of octanol, and 153 molecules of water (in order to achieve a mole fraction of 0.255 for water consistent with the literature58–60). The two systems were used to perform a thermodynamic integration to calculate the free energies for transferring prednisolone from water into octanol/water phase and are presented in Fig. 3. After energy equilibration using the steepest descent algorithm, a leap-frog stochastic dynamics61 was used to further equilibrate this system for 5 ns using NVT ensemble followed by 10 ns with NpT ensemble.62 100 ns stochastic dynamics simulations were run to evaluate the transferring of prednisolone from water into octanol/water phase using a timestep of 20 fs. The pressure was coupled with the Parrinello–Rahman barostat63 using a time constant of 12 ps at 1 bar. Temperature was set to 298 K using a time constant of 1 ps.The Gibbs free energies of transferring prednisolone from water into octanol/water phase (ΔGo/w) were calculated using the thermodynamics integration64 methodology as follows:
Umbrella sampling
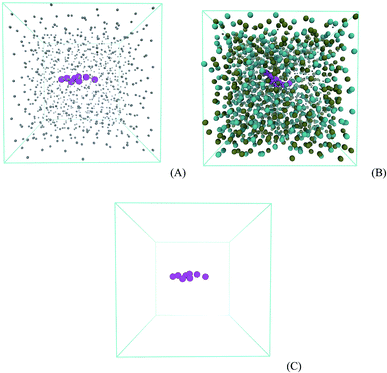
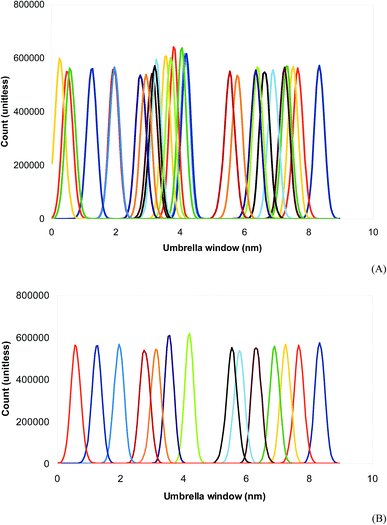
An octanol/water two-phase system was prepared in a rectangular box of dimensions 5 nm × 5 nm × 24 nm in order to perform free energy calculations. The system containing 765 molecules of octanol and 2938 molecules of water is presented in Fig. 4. Prednisolone was inserted in the water phase and later smoothly transferred into the octanol/water phase. Fig. 4A shows the octanol/water two-phase system with the prednisolone molecule placed in the water phase and 4B in octanol/water phase. After the energy minimization using the steepest descent algorithm, this system was further equilibrated for 10 ns with leap-frog algorithm using the temperature v-scale thermostat65 at 298 K using a time constant of 1 ps and the Berendsen pressure barostat62 using a time constant of 3 ps at 1 bar. The temperatures of water, octanol, and prednisolone were coupled separately. A position constraint for prednisolone was used to allow the solvation.Prednisolone was spontaneously shifted in 9 nm from the water phase into the octanol/water phase. Each umbrella window was spaced with 0.2 nm and run for 100 ns with the same equilibration parameters, except the barostat. The pressure was now coupled separately with the Parrinello–Rahman barostat63 using a time constant of 12 ps at 1 bar. The potential mean force was computed as a function of the distance between the center of mass of prednisolone and the center of mass of octanol (each 0.2 nm) using the weighted histogram analysis method.66 The umbrella sampling simulations27,66,67 were performed using force constants between 10 and 1000 kJ mol−1 nm−2 in order to calculate the Gibbs free energy for transferring prednisolone from water phase into octanol/water phase (ΔGo/w).
Equilibrium simulations
The script INSANE55 was used to build the DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POPC (7
POPC (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) bilayer system with 512 phospholipids in each monolayer. The phospholipid bilayer was split in two individual monolayers separated by 6 nm using the program gmx editconf. Then, the water box was built with size dimensions of 17 nm × 17 nm × 6 nm using the program gmx solvate, generating a water slab with around 14
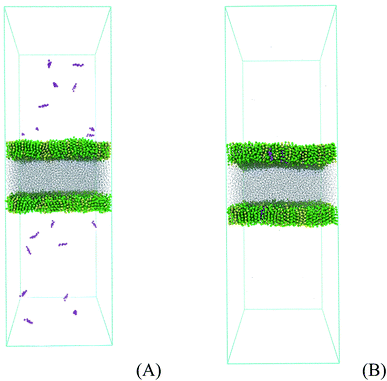
3) bilayer system with 512 phospholipids in each monolayer. The phospholipid bilayer was split in two individual monolayers separated by 6 nm using the program gmx editconf. Then, the water box was built with size dimensions of 17 nm × 17 nm × 6 nm using the program gmx solvate, generating a water slab with around 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules and with a density of 1 kg L−1. This slab was put between the two phospholipid monolayers, allowing 20 nm of vacuum on the top and bottom of the phospholipids. The lipid plane is parallel to the XY plane of the system, and the lipid orientation in this system stands with the polar heads oriented to the water phase. The whole system with 17 nm × 17 nm × 50 nm was placed in a space-filling box, which was replicated periodically in all directions x, y, and z. The empty space (vacuum) is randomly filled with 1, 10, and 120 molecules of prednisolone which gives a fraction of around 0.1, 1, and 10% w/w. Fig. 5 presents the starting system (Fig. 5A) and the system after prednisolone adsorption (Fig. 5B). The system was visualized with the VMD computer program68 to check the overlap between atoms.
000 molecules and with a density of 1 kg L−1. This slab was put between the two phospholipid monolayers, allowing 20 nm of vacuum on the top and bottom of the phospholipids. The lipid plane is parallel to the XY plane of the system, and the lipid orientation in this system stands with the polar heads oriented to the water phase. The whole system with 17 nm × 17 nm × 50 nm was placed in a space-filling box, which was replicated periodically in all directions x, y, and z. The empty space (vacuum) is randomly filled with 1, 10, and 120 molecules of prednisolone which gives a fraction of around 0.1, 1, and 10% w/w. Fig. 5 presents the starting system (Fig. 5A) and the system after prednisolone adsorption (Fig. 5B). The system was visualized with the VMD computer program68 to check the overlap between atoms.
After energy minimization with steepest descent algorithm, the system was also equilibrated with a simulation time of 10 ns using the leap-frog algorithm.69 This step allowed the water to be flexible in order to give more freedom for water molecules to interact with the phospholipid head groups. A production MD run with a simulation time of 2 μs was performed using the leap-frog algorithm.69 The properties were calculated by averaging over the last microsecond of the trajectory. Lipids and water were coupled separately to a temperature of 310 K using the v-scale thermostat65 with a time constant of 1 ps. The surface tension was maintained to 0, 10, and 20 mN m−1 using the surface tension coupling scheme and the Berendsen pressure barostat62 with a time constant of 3 ps. The compressibility of 4.5 × 10−5 bar−1 was used in the xy-plane; the compressibility in the z-axis was set to zero in order to prevent box contraction.
Results and discussions
First of all, it is important to validate the prednisolone parameterization by comparison with experimental results. Using the thermodynamic integration method, the Gibbs free energy of transferring prednisolone from the water phase to octanol/water phase is estimated to be −29 kcal mol−1, which is used to calculate an octanol/water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −ΔGo/w/RT) equal to 5.1 for prednisolone as shown in Table 2. This estimated octanol/water partition coefficient (log
P = −ΔGo/w/RT) equal to 5.1 for prednisolone as shown in Table 2. This estimated octanol/water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) is well above the experimental log
P) is well above the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value of 1.62 for prednisolone,70 as presented in Table 2. The explanation of this disagreement is the difficulty of calculating entropies and Gibbs free energies, which is well known in the literature.71,72
P value of 1.62 for prednisolone,70 as presented in Table 2. The explanation of this disagreement is the difficulty of calculating entropies and Gibbs free energies, which is well known in the literature.71,72
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of prednisolone calculated by thermodynamic integration and umbrella sampling
P) of prednisolone calculated by thermodynamic integration and umbrella sampling
Up to date, the umbrella sampling is one of the most accurate methodologies to evaluate the Gibbs free energy of transferring prednisolone from the water phase to octanol/water phase. The energy cost to displace prednisolone from water phase to octanol/water phase is characterized by the potential mean force, which was calculated separately for each pulled prednisolone using the weighted histogram analysis. However, the force constant was varied from the usual 1000 to 10 kJ mol−1 nm−2. The lowest Gibbs free energy and the most reasonable overlap between the umbrella sampling windows in the weighted histogram analysis were found with the force constant of 100 kJ mol−1 nm−2 as shown in Fig. 6. Using the umbrella sampling, the Gibbs free energy of transferring prednisolone from the water phase to octanol/water phase is estimated to be −22 kcal mol−1. From this value, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for prednisolone is calculated to be 3.9, as presented in Table 2, which is in better agreement with the experimental log
P for prednisolone is calculated to be 3.9, as presented in Table 2, which is in better agreement with the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for prednisolone.70
P for prednisolone.70
The methodology applied in this work has two weaknesses. The three regions (water, interface, and octanol) in Fig. 6 usually have distinct behaviors in terms of interaction forces of the solute–solvent pair, and indeed, require three different force constants in the weighted histogram analysis. Consequently, the sampling generates umbrella windows in the three regions described above. The water and octanol regions have the same amount of windows, which are nicely sampled in the water phase but too overlapped in the octanol/water phase. Moreover, the interface region is poorly sampled since there are only few windows. As this procedure does not provide well overlapped umbrella windows generally produced in one-phase systems, the free energy calculated using this standard methodology gives results above the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P measurements for prednisolone.70 After removing selected windows closely overlapped at the octanol/water phase in the weighted histogram analysis, the Gibbs free energy of transferring prednisolone from the water phase to octanol/water phase is also estimated to be −22 kJ mol−1. Thus, the log
P measurements for prednisolone.70 After removing selected windows closely overlapped at the octanol/water phase in the weighted histogram analysis, the Gibbs free energy of transferring prednisolone from the water phase to octanol/water phase is also estimated to be −22 kJ mol−1. Thus, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for prednisolone is recalculated to be 3.9, which is the same value found previously.
P for prednisolone is recalculated to be 3.9, which is the same value found previously.
The lateral diffusion coefficients of DPPC in membranes and in large vesicles are around 10−7 and 10−8 cm2 s−1, respectively.52,73 From our best knowledge, there is no experimental data for lateral diffusion coefficients of phospholipids in monolayers. The calculated lateral diffusion coefficients for DPPC and POPC molecules in the mixed DPPC/POPC monolayers are (7 ± 2) × 10−7 and (8 ± 1) × 10−7 cm2 s−1, respectively, at 20 mN m−1, and (4 ± 3) × 10−7 cm2 s−1 at 0 mN m−1 as presented in Table 3. The diffusion coefficients at 20 mN m−1 are 1.2 to 2 times larger than those at 0 mN m−1, which is in agreement with the data reported in the literature.27 The lateral diffusion coefficients of phospholipids in monolayers are 10 to 40 times larger than those in bilayers. Generally, the lateral diffusion varies about two orders of magnitude depending on the transition phase, thus we believe that our results are reliable because they fall into the range cited above.
| Surface tension (mN m−1) | D (10−7 cm2 s−1) | |
|---|---|---|
| DPPC | 0 | 4 ± 3 |
| 10 | 7 ± 2 | |
| 20 | 7 ± 2 | |
| POPC | 0 | 4 ± 3 |
| 10 | 8 ± 3 | |
| 20 | 8 ± 1 | |
| Prednisolone | 20 | 6 ± 4 |
The lateral diffusion coefficient of prednisolone in DPPC/POPC mixed monolayers is calculated to be (6 ± 4) × 10−7 cm2 s−1 at 20 mN m−1, as shown in Table 3. The diffusion coefficients of cholesterol, desmosterol, and lanosterol in DPPC bilayers are, respectively, around 2 × 10−8, 5 × 10−8, and 13 × 10−8 cm2 s−1 at 310 K.74 Other measurements for the diffusion coefficients of cholesterol in DPPC bilayers are 5 × 10−8 and 17 × 10−8 cm2 s−1 at 310 K.75 By comparing with the above experimental diffusion coefficients of sterols measured on DPPC bilayers, the lateral coefficient of prednisolone in DPPC/POPC mixed monolayers is estimated to be 3 to 30 times larger than in DPPC bilayers. Laing et al.27 calculated the diffusion coefficients for cholesterol in a phospholipid mixed monolayer and found (3.2 ± 0.3) × 10−7 and (6.5 ± 0.4) × 10−7 cm2 s−1 at 0 and 20 mN m−1, respectively. Our results have an outstanding agreement with those found by Laing et al.27
After verifying the equilibration of the model and validating the methodology by comparison with the experimental results of octanol/water partition coefficient and lateral diffusion, the interactions of prednisolone with the DPPC/POPC mixed monolayer were simulated. Then, the area per lipid, the order parameters of DPPC and POPC, and the formation of prednisolone nanoaggregates were investigated at surface tensions 0, 10 and 20 mN m−1.
The average areas per lipid calculated using coarse grained molecular dynamics are presented in Table 4. The area per lipid in the DPPC/POPC mixed monolayers increases as the surface tension is raised from 0 to 20 mN m−1. As the surface tension increases from 0 to 10 mN m−1, the area increases more as compared from 10 to 20 mN m−1. This trend is in agreement with Langmuir isotherm experiments for phospholipids.76 It is noteworthy to state that the addition of prednisolone molecules in the monolayer does not significantly increase the area per lipid, except in the case of surface tension at 20 mN m−1 with fraction of 10% w/w.
| N | Surface tension (mN m−1) | Area per lipid (Å2 per molecule) |
|---|---|---|
| 0 | 0 | 47.7 ± 0.1 |
| 10 | 55.1 ± 0.3 | |
| 20 | 56.9 ± 0.3 | |
| 10 | 0 | 47.8 ± 0.1 |
| 10 | 55.2 ± 0.4 | |
| 20 | 57.3 ± 0.1 | |
| 120 | 0 | Collapsed |
| 10 | Collapsed | |
| 20 | 61.8 ± 0.2 |
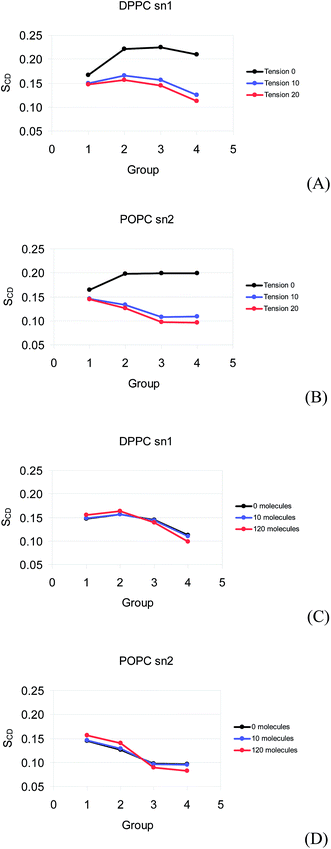
The order parameters for the monolayers calculated using coarse grained molecular dynamics are shown in Fig. 7. It is important to mention that the order parameters of DPPC sn1, DPPC sn2, and POPC sn1 are similar (the last two are not shown in Fig. 7), so the order parameters of POPC sn2 and DPPC sn1 are the only ones presented here. The order of the DPPC and POPC tails presents a strong decrease as the surface tension is raised from 0 to 10 mN m−1. The order slightly decreases from 10 to 20 mN m−1. The order does not change significantly as 10 molecules of prednisolone are inserted to the DPPC/POPC mixed monolayer at 0, 10, and 20 mN m−1. When 120 molecules of prednisolone are added in the monolayer, there is a slight decrease in the tail order and a small increase in the order of hydrocarbon groups close to the head group at 20 mN m−1.
At 0 mN m−1, the adsorption of 120 molecules of prednisolone on the DPPC/POPC monolayer yields the formation of five nanoaggregates as presented in Fig. 8A. The cluster analysis shows that the nanoaggregates are formed by 8, 13, 20, 22, and 39 molecules of prednisolone. After increasing the surface tension to 20 mN m−1, the molecules in the nanoaggregates are transferred to the DPPC/POPC mixed monolayer in about 260 ns as shown in Fig. 8B. If the surface tension is kept at 0 mN m−1, the nanoaggregates are shifted to the interior of the monolayer causing instability. Then, the DPPC/POPC mixed monolayer collapses into a bilayer in the presence of the nanoaggregates of prednisolone as presented in Fig. 8C. The sizes of the prednisolone aggregates are between 1 and 3 nm.
Zuo et al.15 compared the effect of cholesterol and budesonide on the surface activity and molecular organization of a lung surfactant. They found that both similarly behave with concentrations of up to 1% on the fluidization of the lung surfactant film. Therefore, as the concentration increases to 10%, cholesterol induces an unique phase transition that suppresses the surface activity of the film. This suppression may also be related to the monolayer collapse presented above. However, 10% of budesonide simply fluidizes the film, producing limited effects under the surface activity.15 Previous studies sustain these results.16–18 Therefore, the literature also presents a contradictory report about the budesonide effect on the surfactant properties.19 Palmer et al. showed that a small amount of budesonide (0.6%) significantly reduced the surface activity of the lung surfactant although salbutamol did not.19 Wang et al. explained that a concentration of less than 1% budesonide or 10% beclometasone do not substantially affect the surface activity of a natural lung surfactant; the film collapses for higher concentrations than those due to the film fluidization.20
Implications
The dynamics of prednisolone interacting with the lung surfactant models seems to be very similar to that for cholesterol. Several simulations for the prodrug prednisone that is metabolized into the pharmacologically active drug prednisolone gives similar results. Therefore, it may be possible to generalize the fate of sterols in the lung surfactant because there is a large structural similarity. It is also worthy to mention that the interaction of sterols in the lung surfactant is strong enough to make them remaining for long times (at least 2 μs) in the hydrocarbon tail region of the lung surfactant.The hydrophobicity of prednisolone causes the formation of nanoaggregates on the lung surfactant when the prednisolone fraction is around 10% w/w. However, prednisolone may also form nanoaggregates in droplets of aerosols that have normally been introduced in the respiratory system by inhalation during treatment of lung diseases, resulting in collapse of the lung surfactant. Consequently, the molecules of prednisolone dispersed in the lung surfactant at 20 mN m−1 may cause the collapse of the lung surfactant after compressing to 0 mN m−1. According to that, the prednisolone administered in high fractions (∼10% w/w) may also induce the collapse of the lung surfactant and inactivate it. However, lower fractions of prednisolone may be administrated by inhalation without losing the surface activity of the lung surfactant. The lung surfactant has the property of spreading the prednisolone in it, and when applied on the respiratory system, prednisolone may also be spread on the high surface area of the lung. If the lung surfactant has collapsed by formation of prednisolone nanoaggregates, the clearance process takes place to eliminate the phospholipid-prednisolone bilayers formed in the collapse. The implications of this study are very important to the pharmaceutical industry in order to develop a new treatment for preterm babies suffering of respiratory distress syndrome and adults with asthma.
Conclusion
Coarse grained molecular dynamics simulation was successfully applied to understand the stability of lung surfactant models interacting with prednisolone. The lung surfactant was modeled using a DPPC/POPC mixed monolayer with the Martini force field. The force field parameters were validated using calculations of Gibbs free energies of transferring the prednisolone from the water phase to the octanol/water phase. The octanol/water partitioning coefficient was calculated to be 3.9, which is in reasonable agreement with experimental data considering the difficulty of calculating free energies. The lateral diffusion coefficient of lipids in the mixed monolayer was also calculated in order to validate the model parameters. The calculated lateral diffusion coefficients of DPPC and POPC in the DPPC/POPC mixed monolayer are of order of 10−7 cm2 s−1, larger than those found for bilayers. The lateral diffusion coefficient of prednisolone in the DPPC/POPC mixed monolayer is calculated to be (6 ± 4) × 10−7 cm2 s−1 at 20 mN m−1, which is larger than that found for cholesterol in DPPC bilayers and in excellent agreement with the theoretical value for phospholipid mixed monolayers. The molecules of prednisolone were placed in the gas phase in order to simulate the adsorption process on the lung surfactant model. Prednisolone at low fractions (0.1 and 1% w/w) may not affect the stability of the lung surfactant. However, high fractions of prednisolone (∼10% w/w) may cause collapse of the lung surfactant due to the formation of prednisolone nanoaggregates on it at 0 mN m−1. At 20 mN m−1, prednisolone molecules in the nanoaggregates transfer to the DPPC/POPC mixed monolayer and spread out. The implications for the possible effect of prednisolone on the lung surfactant model are discussed in terms of its administration by inhalation to treat lung diseases such as asthma and respiratory distress syndrome.Acknowledgements
The authors thank the Brazilian funding agencies CNPq (Grant No. 465259/2014-6) and FAPERJ (Grant No. 210.558/2015, and E-26/010.001241/2016) for financial support. E. D. E. L. thanks FAPERJ for a graduate fellowship. E. M. and M. P. P. F. acknowledge CNPq for an undergraduate research fellowship.References
- A. C. Pelt, Glucocorticoids: effects, action mechanisms, and therapeutic uses, Hauppauge, N.Y., Nova Science, 2011, ISBN 978-1617287589 Search PubMed.
- T. Rhen and J. A. Cidlowski, Antiinflammatory action of glucocorticoids-new mechanisms for old drugs, N. Engl. J. Med., 2005, 353(16), 1711–1723 CrossRef CAS PubMed.
- D. Czock, F. Keller, F. M. Rasche and U. Häussler, Pharmacokinetics and pharmacodynamics of systemically administered glucocorticoids, Clin. Pharmacokinet., 2005, 44(1), 61–98 CrossRef CAS PubMed.
- M. Davis, R. Williams, J. Chakraborty, J. English, V. Marks, G. Ideo and S. Tempini, Prednisone or prednisolone for the treatment of chronic active hepatitis? A comparison of plasma availability, Br. J. Clin. Pharmacol., 1978, 5(6), 501–505 CrossRef CAS PubMed.
- B. Frey, Pharmacokinetics of 3 prednisolone prodrugs. Evidence of therapeutic inequivalence in renal transplant patients with rejection, Transplantation, 1985, 39, 270–274 CrossRef CAS PubMed.
- D. Bassler, Inhalation or Instillation of Steroids for the Prevention of Bronchopulmonary Dysplasia, Neonatology, 2015, 107(4), 358–359 CrossRef CAS PubMed.
- 19th WHO Model List of Essential Medicines April 2015, WHO, April 2015, Retrieved August 23, 2016.
- A. Hidalgo, A. Cruz and J. Pérez-Gil, Barrier or carrier? Pulmonary surfactant and drug delivery, Eur. J. Pharm. Biopharm., 2015, 95, 117–127 CrossRef CAS PubMed.
- M. Griese, Pulmonary surfactant in health and human lung diseases: state of the art, Eur. Respir. J., 1999, 13(6), 1455–1476 CrossRef CAS PubMed.
- M. J. Davies, A. Brindley, X. Chen, S. W. Doughty, M. Marlow and C. J. Roberts, A quantitative assessment of inhaled drug particle-pulmonary surfactant interaction by atomic force microscopy, Colloids Surf., B, 2009, 73(1), 97–102 CrossRef CAS PubMed.
- H. T. Kuo, H. C. Lin, C. H. Tsai, I. C. Chouc and T. F. Yeh, A follow-up study of preterm infants given budesonide using surfactant as a vehicle to prevent chronic lung disease in preterm infants, J. Pediatr., 2010, 156(4), 537–541 CrossRef CAS PubMed.
- C. Dani, I. Corsini, S. Burchielli, V. Cangiamila, M. Longini, F. Paternostro, G. Buonocore and F. F. Rubaltelli, Natural surfactant combined with beclomethasone decreases oxidative lung injury in the preterm lamb, Pediatr. Pulmonol., 2009, 44(12), 1159–1167 CrossRef PubMed.
- P. Mikolka, D. Mokrá, J. Kopincová, L. Tomčíková-Mikušiaková and A. Calkovská, Budesonide added to modified porcine surfactant Curosurf may additionally improve the lung functions in meconium aspiration syndrome, Physiol. Res., 2013, 62(Suppl 1), S191–S200 CAS.
- Y. Wang, P. Gkeka, J. E. Fuchs, K. R. Liedl and Z. Cournia, DPPC-cholesterol phase diagram using coarse-grained MD simulations, BBA-Biomembranes, 2016, 1858(11), 2846–2857 CrossRef CAS PubMed.
- Y. Y. Zuo, Y. E. Wang, C. R. Neal and Y. Y. Zuo, Differential effects of cholesterol and budesonide on biophysical properties of clinical surfactant, Pediatr. Res., 2012, 71, 316–323 CrossRef PubMed.
- E. Keating, L. Rahman, J. Francis, A. Petersen, F. Possmayer, R. Veldhuizen and N. O. Petersen, Effect of cholesterol on the biophysical and physiological properties of a clinical pulmonary surfactant, Biophys. J., 2007, 93(4), 1391–1401 CrossRef CAS PubMed.
- Z. Leonenko, E. Finot, V. Vassiliev and M. Amrein, Effect of cholesterol on the physical properties of pulmonary surfactant films: atomic force measurements study, Ultramicroscopy, 2006, 106(8–9), 687–694 CrossRef CAS PubMed.
- L. Gunasekara, S. Schürch, W. M. Schoel, K. Nag, Z. Leonenko, M. Haufs and M. Amrein, Pulmonary surfactant function is abolished by an elevated proportion of cholesterol, Biochim. Biophys. Acta, 2005, 1737(1), 27–35 CrossRef CAS PubMed.
- D. Palmer, S. Schurch and J. Belik, Effect of budesonide and salbutamol on surfactant properties, J. Appl. Physiol., 2000, 89(3), 884–890 CAS.
- Y. E. Wang, H. Zhang, Q. Fan, C. R. Neal and Y. Y. Zuo, Biophysical interaction between corticosteroids and natural surfactant preparation: implications for pulmonary drug delivery using surfactant as a carrier, Soft Matter, 2012, 8(2), 504–511 RSC.
- Y. N. Kaznessis, S. Kim and R. G. Larson, Specific mode of interaction between components of model pulmonary surfactants using computer simulations, J. Mol. Biol., 2002, 322(3), 569–582 CrossRef CAS PubMed.
- H. Lee, S. K. Kandasamy and R. G. Larson, Molecular dynamics simulations of the anchoring and tilting of the lung-surfactant peptide SP-B1–25 in palmitic acid monolayers, Biophys. J., 2005, 89(6), 3807–3821 CrossRef CAS PubMed.
- S. K. Kandasamy and R. G. Larson, Molecular dynamics study of the lung surfactant peptide SP-B1–25 with DPPC monolayers: insights into interactions and peptide position and orientation, Biophys. J., 2005, 88(3), 1577–1592 CrossRef CAS PubMed.
- S. Baoukina, L. Monticelli, M. Amrein and D. P. Tieleman, The Molecular Mechanism of Monolayer-Bilayer Transformations of Lung Surfactant from Molecular Dynamics Simulations, Biophys. J., 2007, 93, 3775–3782 CrossRef CAS PubMed.
- S. Baoukina, L. Monticelli, S. J. Marrink and D. P. Tieleman, Pressure-Area Isotherm of a Lipid Monolayer from Molecular Dynamics Simulations, Langmuir, 2007, 23, 12617–12623 CrossRef CAS PubMed.
- S. Baoukina, L. Monticelli, H. J. Risselada, S. J. Marrink and D. P. Tieleman, The molecular mechanism of lipid monolayer collapse, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(31), 10803–10808 CrossRef CAS PubMed.
- C. Laing, S. Baoukina and D. P. Tieleman, Molecular dynamics study of the effect of cholesterol on the properties of lipid monolayers at low surface tensions, Phys. Chem. Chem. Phys., 2009, 11, 1916–1922 RSC.
- S. Baoukina and D. P. Tieleman, Direct simulation of protein-mediated vesicle fusion: lung surfactant protein B, Biophys. J., 2010, 99(7), 2134–2142 CrossRef CAS PubMed.
- S. L. Duncan and R. G. Larson, Folding of lipid monolayers containing lung surfactant proteins SP-B1–25 and SP-C studied via coarse-grained molecular dynamics simulations, Biochim. Biophys. Acta, 2010, 1798, 1632–1650 CrossRef CAS PubMed.
- S. Baoukina and D. P. Tieleman, Lung Surfactant Protein SP-B Promotes Formation of Bilayer Reservoirs from Monolayer and Lipid Transfer between the Interface and Subphase, Biophys. J., 2011, 100, 1678–1687 CrossRef CAS PubMed.
- S. L. Duncan, I. S. Dalal and R. G. Larson, Molecular dynamics simulation of phase transitions in model lung surfactant monolayers, Biochim. Biophys. Acta, 2011, 1808, 2450–2465 CrossRef CAS PubMed.
- E. Mendez-Villuendas, S. Baoukina and D. P. Tieleman, Challenges in analysing and visualizing large-scale molecular dynamics simulations: domain and defect formation in lung surfactant monolayers, J. Phys.: Conf. Ser., 2012, 385, 012002 CrossRef.
- S. Baoukina, E. Mendez-Villuendas and D. P. Tieleman, Molecular View of Phase Coexistence in Lipid Monolayers, J. Am. Chem. Soc., 2012, 134, 17543–17553 CrossRef CAS PubMed.
- S. Baoukina, D. Rozmanov, E. Mendez-Villuendas and D. P. Tieleman, The Mechanism of Collapse of Heterogeneous Lipid Monolayers, Biophys. J., 2014, 107, 1136–1145 CrossRef CAS PubMed.
- S. Choe, R. Chang, J. Jeon and A. Violi, Molecular dynamics simulation study of a pulmonary surfactant film interacting with a carbonaceous nanoparticle, Biophys. J., 2008, 95(9), 4102–4114 CrossRef CAS PubMed.
- M. Schneemilch and N. Quirke, Molecular dynamics of nanoparticle translocation at lipid interfaces, Mol. Simul., 2010, 36(11), 831–835 CrossRef CAS.
- X. Lin, Y. Li and N. Gu, Molecular dynamics simulations of the interactions of charge-neutral PAMAM dendrimers with pulmonary surfactant, Soft Matter, 2011, 7(8), 3882–3888 RSC.
- C.-C. Chiu, W. Shinoda, R. H. DeVane and S. O. Nielsen, Effects of spherical fullerene nanoparticles on a dipalmitoyl phosphatidylcholine lipid monolayer: a coarse grain molecular dynamics approach, Soft Matter, 2012, 8, 9610–9616 RSC.
- X. Lin, T. Bai, Y. Y. Zuo and N. Gu, Promote potential applications of nanoparticles as respiratory drug carrier: insights from molecular dynamics simulations, Nanoscale, 2014, 6, 2759 RSC.
- J. Barnoud, L. Urbini and L. Monticelli, C60 fullerene promotes lung monolayer collapse, J. R. Soc., Interface, 2015, 12, 20140931 CrossRef PubMed.
- N. Nisoh, M. Karttunen, L. Monticelli and J. Wong-Ekkabut, Lipid monolayer disruption caused by aggregated carbon nanoparticles, RSC Adv., 2015, 5, 11676 RSC.
- T. Yue, X. Wang, X. Zhang and F. Huang, Molecular modeling of interaction between lipid monolayer and graphene nanosheets: implications for pulmonary nanotoxicity and pulmonary drug delivery, RSC Adv., 2015, 5, 30092 RSC.
- J. A. Freites, Y. Choi and D. J. Tobias, Molecular Dynamics Simulations of a Pulmonary Surfactant Protein B Peptide in a Lipid Monolayer, Biophys. J., 2003, 84(4), 2169–2180 CrossRef CAS PubMed.
- D. Rose, J. Rendell, D. Lee, K. Nag and V. Booth, Molecular dynamics simulations of lung surfactant lipid monolayers, Biophys. Chem., 2008, 138(3), 67–77 CrossRef CAS PubMed.
- M. Javanainen, L. Monticelli, J. B. de la Serna and I. Vattulainen, Free volume theory applied to lateral diffusion in Langmuir monolayers: atomistic simulations for a protein-free model of lung surfactant, Langmuir, 2010, 26(19), 15436–15444 CrossRef CAS PubMed.
- H. I. Kim, H. Kim, Y. S. Shin, L. W. Beegle, S. S. Jang, E. L. Neidholdt, W. A. Goddard, J. R. Heath, I. Kanik and J. L. Beauchamp, Interfacial Reactions of Ozone with Surfactant Protein B in a Model Lung Surfactant System, J. Am. Chem. Soc., 2010, 132(7), 2254–2263 CrossRef CAS PubMed.
- T. R. Sosnowski, M. Kolinski and L. Gradon, Interactions of Benzo[a]pyrene and Diesel Exhaust Particulate Matter with the Lung Surfactant System, Ann. Occup. Hyg., 2011, 55(3), 329–338 CrossRef CAS PubMed.
- T. R. Sosnowski, M. Kolinski and L. Gradon, Alteration of surface properties of dipalmitoyl phosphatidylcholine by benzo[a]pyrene: a model of pulmonary effects of diesel exhaust inhalation, J. Biomed. Nanotechnol., 2012, 8(5), 818–825 CrossRef CAS PubMed.
- M. Khabiri, M. Roeselova and L. Cwiklik, Properties of oxidized phospholipid monolayers: an atomistic molecular dynamics study, Chem. Phys. Lett., 2012, 519–520, 93–99 CrossRef CAS.
- P. Bertani, V. Vidovic, T. C. Yang, J. Rendell, L. M. Gordon, A. J. Waring, B. Bechinger and V. Booth, Orientation and depth of surfactant protein B C-terminal helix in lung surfactant bilayers, Biochim. Biophys. Acta, Biomembr., 2012, 1818(5), 1165–1172 CrossRef CAS PubMed.
- E. C. Griffith, T. R. C. Guizado, A. S. Pimentel, G. S. Tyndall and V. Vaida, Oxidized aromatic–aliphatic mixed films at the air–aqueous solution interface, J. Phys. Chem. C, 2013, 117, 22341–22350 CAS.
- H. I. Padilla-Chavarria, T. R. C. Guizado and A. S. Pimentel, Molecular dynamics of dibenz[a,h]anthracene and its metabolite interacting with lung surfactant phospholipid bilayers, Phys. Chem. Chem. Phys., 2015, 17, 20912 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 CrossRef.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindhal, GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447 CrossRef CAS PubMed.
- T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, Computational lipidomics with insane: a versatile tool for generating custom membranes for molecular simulations, J. Chem. Theory Comput., 2015, 11, 2144–2155 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. Vries, The MARTINI force field: coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- M. N. Melo, H. I. Ingólfsson and S. J. Marrink, Parameters for Martini sterols and hopanoids based on a virtual-site description, J. Chem. Phys., 2015, 143, 243152 CAS.
- S. E. Debolt and P. A. Kollman, Investigation of Structure, Dynamics, and Solvation in 1-Octanol and Its Water-Saturated Solution: Molecular Dynamics and Free-Energy Perturbation Studies, J. Am. Chem. Soc., 1995, 117(19), 5316–5340 CrossRef CAS.
- J. L. Maccallum and D. P. Tieleman, Structures of neat and hydrated 1-octanol from computer simulations, J. Am. Chem. Soc., 2002, 124(50), 15085–15093 CrossRef CAS PubMed.
- P. Sassi, M. Paolantoni, R. S. Cataliotti, F. Palombo and A. Morresi, Water/alcohol mixtures: a spectroscopic study of the water-saturated 1-octanol solution, J. Phys. Chem. B, 2004, 108(50), 19557–19565 CrossRef CAS.
- W. F. van Gunsteren and H. J. C. Berendsen, A Leap-frog Algorithm for Stochastic Dynamics, Mol. Simul., 1988, 1, 173–185 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. J. Marrink, A. H. de Vries, T. A. Harroun, J. Katsaras and S. R. Wassall, Cholesterol Shows Preference for the Interior of Polyunsaturated Lipid Membranes, J. Am. Chem. Soc., 2008, 130, 10–11 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling, J. Comp. Physiol., 1977, 23, 187–199 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- R. W. Hockney, S. P. Goel and J. Eastwood, Quiet High-Resolution Computer Models of a Plasma, J. Comp. Physiol., 1974, 14, 148–158 Search PubMed.
- C. Hansch, A. Leo and D. Hoekman, in Exploring QSAR. Hydrophobic, Electronic and Steric Constants, American Chemical Society, Washington, DC, 1995 Search PubMed.
- H. Meirovitch, S. Cheluvaraja and R. P. White, Methods for calculating the entropy and free energy and their application to problems involving protein flexibility and ligand binding, Curr. Protein Pept. Sci., 2009, 10, 229–243 CrossRef CAS PubMed.
- J. Kästner, Umbrella sampling, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 CrossRef.
- P. F. Fahey and W. W. Webb, Lateral diffusion in phospholipid bilayer membranes and multilamellar liquid crystals, Biochemistry, 1978, 17, 3046–3053 CrossRef CAS PubMed.
- H. A. Scheidt, D. Huster and K. Gawrisch, Diffusion of Cholesterol and Its Precursors in Lipid Membranes Studied by 1H Pulsed Field Gradient Magic Angle Spinning NMR, Biophys. J., 2005, 89, 2504–2512 CrossRef CAS PubMed.
- C. Gliss, O. Randel, H. Casalta, E. Sackmann, R. Zorn and T. Bayerl, Anisotropic Motion of Cholesterol in Oriented DPPC Bilayers Studied by Quasielastic Neutron Scattering: The Liquid-Ordered Phase, Biophys. J., 1999, 77, 331–340 CrossRef CAS PubMed.
- A. A. Hidalgo, A. S. Pimentel, M. Tabak and O. N. Oliveira Jr, Thermodynamic and Infrared Analyses of the Interaction of Chlorpromazine with Phospholipid Monolayers, J. Phys. Chem. B, 2006, 110, 19637–19646 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |