Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bio ionic liquids and water mixtures: a structural study†
Lorenzo Gontrani *,
Eleonora Scarpellini,
Ruggero Caminiti and
Marco Campetella
*,
Eleonora Scarpellini,
Ruggero Caminiti and
Marco Campetella *
*
Department of Chemistry, “La Sapienza” University of Rome, P.le Aldo Moro 5, 00185 Rome, Italy. E-mail: lorenzo.gontrani@uniroma1.it; eleonora.scarpellini@uniroma1.it; ruggero.caminiti@uniroma1.it; marco.campetella@uniroma1.it
First published on 31st March 2017
Abstract
In this study we have explored, by means of ab initio molecular dynamics, a subset of three different water/cho+–phe− mixtures. We present both structural and dynamical information of these mixtures as revealed by accurate ab initio computations of the forces acting on the atoms. We highlight the presence of a strong hydrogen bond network between the anions, and the persistence of such interaction even at very high water concentration. Furthermore, we show that the water molecules favour the establishment of hydrogen bond contacts with IL ions, up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 IL/water molar ratio. Finally we point out the possible bridging role of a water molecule, namely it can insert between a cation and an anion and give rise to a three-body adduct.
1.5 IL/water molar ratio. Finally we point out the possible bridging role of a water molecule, namely it can insert between a cation and an anion and give rise to a three-body adduct.
1 Introduction
Ionic liquids (ILs) are a class of useful and interesting materials, for both fundamental and applied research.1–3 Their properties, that include low volatility, thermal stability, great solvation capabilities and high versatility, have raised high expectations for industrial applications, spurring a vast research effort.4 An interesting and studied family of ionic liquids is that of Protic Ionic Liquids (PILs).5,6 They can be obtained by the easy reaction between Brönsted acids and bases.7 In PILs, proton transfer occurs from the acid (donor) to the base (acceptor), leading to the formation of a pure liquid made up of ion pairs, where proton acceptor and donor sites eventually generate a hydrogen-bond network.8–10 We focus here on another family of ionic liquids, the so-called “Bio-Ionic Liquids” (Bio-ILs). In these compounds, the classical inorganic ions, like Cl−/Br−, NO− or BF4−, are replaced by bio-organic molecules.11–14 In particular, we describe two examples of the choline–aminoacid (cho–AA) ILs class. These compounds are constituted by a choline cation cho+ and various deprotonated aminoacids as anions: alanine, valine, isoleucine etc.15 and share the presence of an acid hydrogen on the cation with the more common PILs. Since their constituents are also involved in several metabolic processes, it has been proved that choAA Bio-ILs are quite bio-degradable, non-toxic for the humans and for the environment16,17 and can be employed in a large range of bio-related applications.18,19 Given the large number of available choline–aminoacid combinations, it is possible to achieve ionic liquids with different and tunable chemical physical properties. These liquids have opened new routes in the pharmacological and biomedical fields and, in general, in green-chemistry processes.20,21 To further expand the applications, ionic liquids-based mixed solvents have been proposed in recent years, and it has been shown that the presence of co-solvents such as water can affect the physical and chemical features of ionic liquids as well as the global solvation properties.22–24 In the field of protic ionic liquids, in particular, several papers by our and other research groups have appeared recently describing the mixtures with molecular solvents like water,25–27 alcohols28,29 and non-amphiphilic compounds.30,31 In this paper, we present a systematic study of the structural properties of three different solutions of choline (cho+)–phenylalanine (phe−) in water. The sketch of the molecules are reported in Fig. 1.The different molar concentrations of IL in water considered are: 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9. For simplicity we will refer to such mixtures as: SolA, SolB and SolC respectively. Their relative compositions are: SolA, 12 ILs couples and 3 water molecules; SolB, 10 ILs couples and 15 water molecules; SolC, 6 ILs couples and 54 water molecules. The introduction of polarization effects in the simulation studies are essential for a good description of the hydrogen bond and ring–ring stacking interactions in cho+–phe−,32,33 so the classical two-body force fields fail in describing the bulk properties of the mixtures.34,35 As a consequence, we have adopted a more sophisticated computation tool to reach a reliable nanoscopic interpretation of these materials, namely ab initio molecular dynamics (AIMD). The theoretical model was validated with accurate experimental measurements of the liquid internal structure. The main objective of this work is therefore the description of the nanoscopic structure of these mixtures, within the short-medium distance range allowed by AIMD, namely up to 8 Å.
9. For simplicity we will refer to such mixtures as: SolA, SolB and SolC respectively. Their relative compositions are: SolA, 12 ILs couples and 3 water molecules; SolB, 10 ILs couples and 15 water molecules; SolC, 6 ILs couples and 54 water molecules. The introduction of polarization effects in the simulation studies are essential for a good description of the hydrogen bond and ring–ring stacking interactions in cho+–phe−,32,33 so the classical two-body force fields fail in describing the bulk properties of the mixtures.34,35 As a consequence, we have adopted a more sophisticated computation tool to reach a reliable nanoscopic interpretation of these materials, namely ab initio molecular dynamics (AIMD). The theoretical model was validated with accurate experimental measurements of the liquid internal structure. The main objective of this work is therefore the description of the nanoscopic structure of these mixtures, within the short-medium distance range allowed by AIMD, namely up to 8 Å.
2 Results
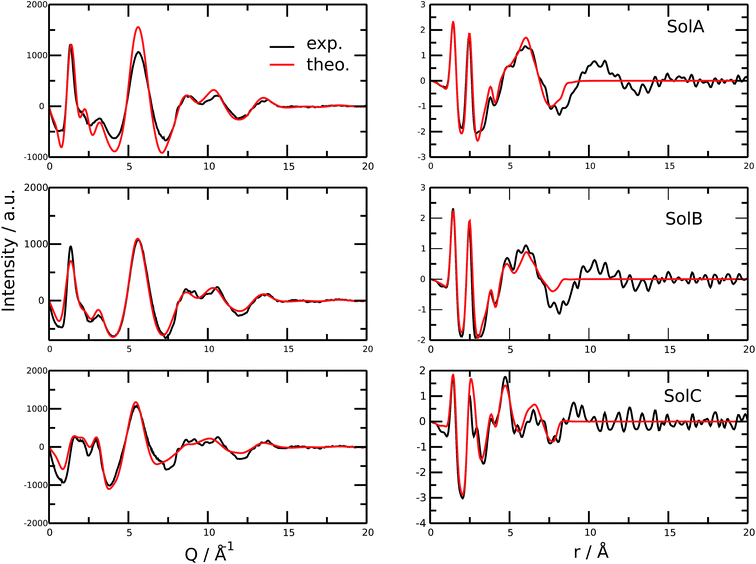
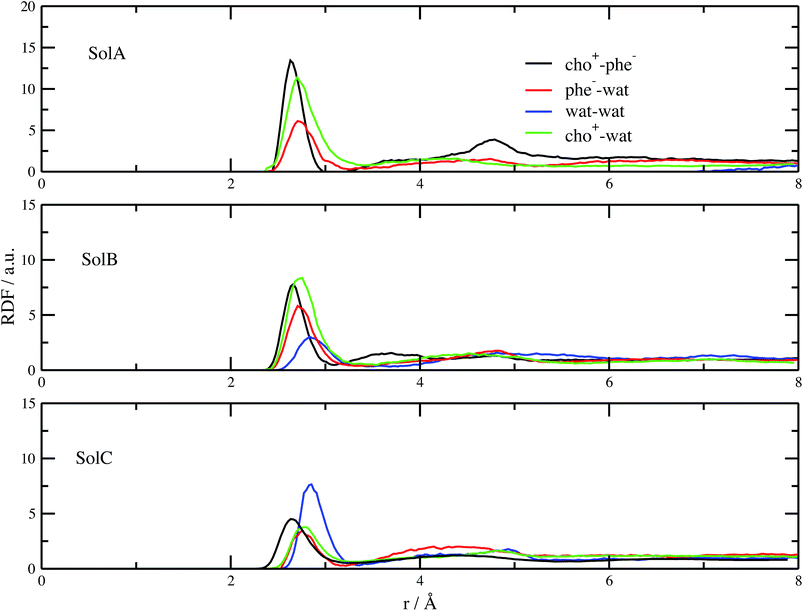
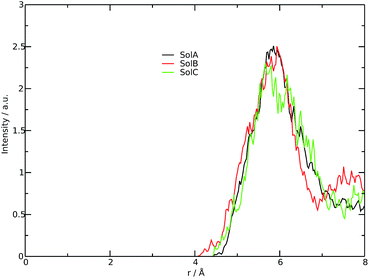
Fig. 2 shows the measured and calculated structure factors [QI(Q)M(Q), left] and differential radial distribution function [as “Differential distribution function”, Diff(r), right] of the three cho+phe−/water mixtures. In ESI† the relative theoretical function obtained from classical molecular dynamics are reported. It can be clearly seen that classical MD cannot reproduce any of the two experimental functions in all of the solutions. In particular, we can notice that the classical MD is reliable only in describing solutions with the largest concentration of water. Hence, this fact endorses that standard force fields cannot reproduce in a satisfactory way the electrostatic interactions present in this kind of ILS. On the contrary, excellent agreement is obtained across the relevant scale of distances involved with AIMD. For this reason, hereafter we will consider only the results obtained from the QM-trajectory. It is noteworthy to remark three different aspects: the first one is the absence of physical meanings for theoretical data below 0.5 Å−1 due to the finite size of our simulation cells. The second one is the fact that QI(Q)M(Q) (and consequently its relative Fourier transform Diff(r)) are very sensitive to liquid structural parameters, if compared with structure functions in other formulations like I(Q) or S(Q); therefore it is usually difficult to reproduce them in a satisfactory way. The last but not least issue is that even in the less concentrated solution the experimental structure factor does not exhibit the pre-peak observed in neat cho+–phe− at low Q values.36 In other words, the presence of water prevents the formation of the nanoscopic average aggregates that give rise to a repetitive (effective) distance of 16.5 Å. The diffraction pattern results from the average over all the configurations of all the inter-atomic distances; for this reason it is difficult to assign each peak present in the plot. At any rate, it is possible to distinguish between two different regions, that can be attributed to intramolecular contacts (above 5 Å−1) and intermolecular ones below. As we can see, the agreement in the intramolecular region is excellent and is certainly due to the accuracy of the ab initio computation of the geometry and of the forces. The agreement is also very good (both in terms of position and height of the peaks) for the intermolecular region below 3 Å−1. In this region, we find the principal peak that falls at 1.43 Å−1, both for SolA and SolB. Such result is in agreement with the previous one obtained for neat cho+phe−.33 It is related to correlation distances ranging from 3.0 to 6.0 Å. This peak is due to the alternating pattern of cations and anions in the liquid and represents a clear fingerprint of the local structure of RTILs in general. Even if the principal peaks are located at the same Q value, for SolA and SolB, the relative intensities are different. In particular, we can see how the increase in water content leads to the reduction peak height in SolB, that is the partial disruption of the ion pair correlation. A separate mention should be made for SolC. In this case the principal peak disappears and two distinct peaks related to the bulk structure of pure water come out. It means that the alternating pattern of cations and anions is absent in this case, owing to the surplus of water. The less evident peak appearing at the right of the main one, around 2.2–2.4 Å−1 is mostly due to the O⋯O correlation due to hydrogen bonding whose peak falls between 2.6 and 2.8 Å in the direct space, depending on the interacting atoms.In order to get a clearer picture, we investigated the morphology (at least the short-range geometrical features) of the three mixtures by calculating the radial distribution functions (RDFs) between the oxygen atoms of cho+, phe− and water (see Fig. 3). All RDFs show the same sharp peak located at 2.6 Å, due to the H-bond interaction between the carboxylate group of the anion and the hydroxyl group of the cation. Those peaks are symmetric around their maxima thereby signaling a very strong H-bond in which the proton is exclusively localized on the cation. The height of those peaks ranges from 10.5 to 6.5 and decreases passing from SolA to SolC. Namely IL couples do not tend to cluster with each other when water concentration rises. On the contrary, we point out that in SolA waters do not interact, but they prefer to give rise to an H-bond interaction centered at 2.7 Å, both with the cation and the anion. This distance is in the middle point between the O(cat)⋯O(ani) and the O(wat)⋯O(wat) equilibrium distances. In all the solutions considered, the water molecules tend to form a more stable H-bond interaction with the cation, with respect to the anion. This finding is in partial disagreement with a recent study by some of us,37 where water–anion interactions were deemed responsible for the disruption of the hydrogen bond network of butylammonium butanoate. Likely, the partially bidentate interaction between choline and aminoacid anion (hydroxyl-quaternary ammonium⋯carboxylate),38 is stronger than the simpler ammonium–carboxylate correlation. In addition to the atomic RDF, we have also calculated the radial distributions between the ring centers of the cation. Such RDF has been calculated in order to investigate the possible effect of phenyl–phenyl stacking. The relative RDFs are reported in Fig. 4. In all cases, the distribution shows the presence of a broad peak centered at about 5.8 Å, that might suggest the occurrence of phenyl stacking on the long range. Unfortunately, due to the wat–IL interaction, this kind of interaction is not sufficient to establish long range aggregation phenomena, as shown for the neat liquid in previous works.36,39 To better characterize the H-bond network of the simulated boxes, we have extracted the H-bonds contacts lifetime from the trajectories. For the calculation, we exploited the autocorrelation function tool of TRAVIS,40 and the distance/angle values chosen to parameterize the H-bonds were: distance between ethero atoms, ranging between 2 and 3.5 Å and N–H⋯O angle from 135° to 180°. The relative autocorrelation function was fitted to the function 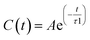 . In the previous formula, t is the time, A is a constant that determines the probability of the specific process, τ1 is the characteristic life-time of the two dimer formation.
. In the previous formula, t is the time, A is a constant that determines the probability of the specific process, τ1 is the characteristic life-time of the two dimer formation.
The relative values of τ1 are reported in Table 1. From this analysis we confirm the results just reported for the RDFs. The first point is the decrease of IL pair formation with the water concentration increase, but in SolA and SolC it is the most stable dimer. Another aspect is the absence of wat–wat interaction in SolA, that is in dilute concentration the water molecules prefer to establish H-bond contacts with the phe− or cho+, with the hydroxyl group as the favourite docking point of the cation for SolA and SolB. At high dilution, water interacts in the same way with all the other species present in the mixture, namely cho+, phe− and water itself. Since water molecules form very stable H-bond contacts with either ions, to better characterize the water–IL interaction, the relative Combined Distribution Function (CDF) was calculated. This CDF distribution correlates the O(wat)⋯O(ani) and O(wat)⋯O(cat) distances; the corresponding function for SolA is shown in Fig. 5.
| Mixture | Wat–phe− | Wat–cho+ | Wat–wat | Cho+–phe− |
|---|---|---|---|---|
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
11.2 ± 0.4 | 14.2 ± 0.9 | 0.0 | 19.3 ± 0.9 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
8.5 ± 0.3 | 10.2 ± 0.8 | 7.6 ± 0.3 | 17.4 ± 0.6 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
5.5 ± 0.3 | 5.5 ± 0.4 | 4.6 ± 0.3 | 12.6 ± 0.5 |
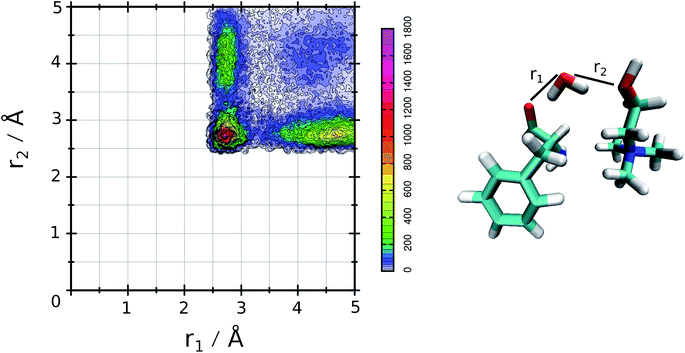 | ||
| Fig. 5 CDF for SolA, combining the two ethero atoms distances that characterize the three body adduct. | ||
This figure shows a tall peak with maximum at about 2.7 Å/2.7 Å, resulting from the formation of a three body adduct during the simulation. The other two mixtures have a similar CDF, for this is reason the relative curves are not reported.
3 Conclusions
In this work, the comparison among structural and dynamical properties of three different water/cho+–phe− mixtures is reported. The aim of this work was to determine the effect of water concentration on the structural properties of the IL. We found the presence of a strong and stable hydrogen bond between the cation and the anion in all the studied mixtures, with the equilibrium distance falling at 2.6 Å. The presence of water does not affect this interaction significantly. It is important to notice that in SolA and SolB, namely up to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 molar ratio between IL and water, the water molecules prefer to establish H-bonds with the cations. This finding correlates nicely with our previous studies on other choline–aminoacid liquids that have shown the particularly strong H-bond correlation; at very high water contents (SolC), though, the wat–cat, wat–ani and wat–wat become competitive with each other. Furthermore we have shown the presence of possible three-body adducts, in which the one water molecule acts as bridge between the cation and the anion.
1.5 molar ratio between IL and water, the water molecules prefer to establish H-bonds with the cations. This finding correlates nicely with our previous studies on other choline–aminoacid liquids that have shown the particularly strong H-bond correlation; at very high water contents (SolC), though, the wat–cat, wat–ani and wat–wat become competitive with each other. Furthermore we have shown the presence of possible three-body adducts, in which the one water molecule acts as bridge between the cation and the anion.
4 Methods
To explore the bulk properties of the three mixtures, we performed simulations of three different cells, each having an edge of about 17 Å. The computational protocol, applied for all the simulation boxes, is:• Generation of the starting configuration with PACKMOL software.41
• Pre-equilibration, performed with classical molecular dynamics within periodic boundary conditions, using the AMBER42 program package with the Gaff43,44 force field.
• The final configuration of the classical trajectory was used as the starting structure for AIMD, that was performed with the program package CP2k.45
During the classical MD, an equilibration phase of about 5 ns in the NPT ensemble was performed. The final theoretical densities were very similar to the experimental ones, differing by less than 5%. The relative densities were 1.02 g cm−3, 1.06 g cm−3 and 1.11 g cm−3 for SolA, SolB and SolC respectively. The ab initio molecular dynamics exploits the Quickstep module46 and the orbital transformation47 for faster convergence. The electronic structure was calculated in the framework of density functional theory,48,49 using the PBE50 functional, with the explicit van der Waals terms according to the empirical dispersion correction (D3) by Grimme.51 MOLOPT-DZVP-SR-GTH52 basis sets and GTH pseudopotentials53,54 were applied; the time step chosen was 0.5 fs and the simulation temperature was set at 310 K by a Nosé–Hoover chain thermostat. Before obtaining the productive 80 ps NVT dynamics, we performed a QM-equilibration of about 10 ps. The timescale and the number of atoms were chosen in order to guarantee a corrected starting configuration and a reliable productive trajectory.13,24,33 Furthermore, in previous works,10,12 it has been shown how this timescale was sufficient for a realistic the description of the first/second coordination shell in protic ILs.
The X-ray experiments (WAXS) were carried out on a new energy-dispersive diffractometer recently set up in our lab at the University “La Sapienza” of Rome. The instrument has a novel horizontal design that allows to perform the data acquisitions at the three/four fixed angular configurations needed by the technique55–57 very rapidly and at large momentum transfer range (0.5–24 Å−1). Owing to the marked increase of the intensity, in fact, a complete diffraction pattern (see below) at high statistics viz. more than 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts, can be collected in at most 6 hours.
000 counts, can be collected in at most 6 hours.
After the corrections for background and sample absorption and the subtraction of the independent atomic scattering that does not depend on the structure 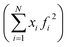 from raw data (IEXP(Q)), the “total static structure function” I(Q), in electron units, is obtained (eqn (1)):
from raw data (IEXP(Q)), the “total static structure function” I(Q), in electron units, is obtained (eqn (1)):
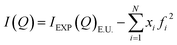 | (1) |
The structure function is the structurally sensitive part of the scattered intensity, and originates from the interference contributions from different atoms; the “scattering variable” Q is the magnitude of the transferred momentum, and depends on the scattering angle (2θ), according to the relation 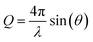 , which is equal to Q ≈ 1.0136E
, which is equal to Q ≈ 1.0136E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, when E is expressed in keV and Q in Å−1. Furthermore, the function I(Q) is related to the partial radial distribution functions g(r)'s descriptive of the structure and obtainable from molecular simulations, on the basis of the following equation:
θ, when E is expressed in keV and Q in Å−1. Furthermore, the function I(Q) is related to the partial radial distribution functions g(r)'s descriptive of the structure and obtainable from molecular simulations, on the basis of the following equation:
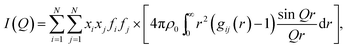 | (2) |
In the formulae above, xi are the numerical concentrations of the species, fi their Q-dependent X-ray scattering factors and ρ0 is the bulk number density of the system. Eqn (2) is thus the link between experimental and model data. Both the experimental and the theoretical structure functions were multiplied by a sharpening function M(Q), necessary to improve the curve resolution at high Q, and to decrease the truncation error when I(Q) is Fourier-transformed in the distance domain, according to the relation
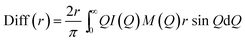 | (3) |
In the differential correlation form of the total radial distribution (eqn (3)), only the structural contributions are present, since the “uniform” contribution is left out. For a comprehensive report of all the formulas, see ref. 58 and 59. Summarizing, the comparison between experiment and simulations will be carried out using both reciprocal space (QI(Q)M(Q)) and distance space (Diff(r) plus the partial correlation functions gij(r)) patterns. This methodology has been successfully applied to the study of molecular60,61 and ionic liquids,6 as well as solutions.62
Acknowledgements
M. C. and L. G. thank Prof. Ruggero Caminiti (Sapienza University of Rome, Chemistry Department) for providing free usage of Narten computing cluster facility.References
- J. S. Wilkes, Green Chem., 2002, 4, 73–80 RSC.
- E. W. Castner Jr and J. F. Wishart, J. Chem. Phys., 2010, 132, 120901 CrossRef PubMed.
- P. Wasserscheid and W. Keim, Angew. Chem., Int. Ed., 2000, 39, 3772–3789 CrossRef CAS PubMed.
- R. D. Rogers and K. R. Seddon, A. C. S. symposium series, 2002 Search PubMed.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- M. Campetella, L. Gontrani, E. Bodo, F. Ceccacci, F. Marincola and R. Caminiti, J. Chem. Phys., 2013, 138, 184506 CrossRef PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- A. Mariani, R. Caminiti, M. Campetella and L. Gontrani, Phys. Chem. Chem. Phys., 2016, 18, 2297–2302 RSC.
- M. Campetella, L. Gontrani, F. Leonelli, L. Bencivenni and R. Caminiti, ChemPhysChem, 2015, 16, 197–203 CrossRef CAS PubMed.
- M. Campetella, D. Bovi, R. Caminiti, L. Guidoni, L. Bencivenni and L. Gontrani, J. Chem. Phys., 2016, 145, 024507 CrossRef CAS PubMed.
- K. Fukumoto, M. Yoshizawa and H. Ohno, J. Am. Chem. Soc., 2005, 127, 2398–2399 CrossRef CAS PubMed.
- M. Campetella, E. Bodo, R. Caminiti, A. Martino, F. D'Apuzzo, S. Lupi and L. Gontrani, J. Chem. Phys., 2015, 142, 234502 CrossRef CAS PubMed.
- B. Bhargava and S. Balasubramanian, Chem. Phys. Lett., 2006, 417, 486–491 CrossRef CAS.
- A. Bagno, F. D'Amico and G. Saielli, ChemPhysChem, 2007, 8, 873–881 CrossRef CAS PubMed.
- S. De Santis, G. Masci, F. Casciotta, R. Caminiti, E. Scarpellini, M. Campetella and L. Gontrani, Phys. Chem. Chem. Phys., 2015, 17, 20687–20698 RSC.
- X.-D. Hou, Q.-P. Liu, T. J. Smith, N. Li and M.-H. Zong, PLoS One, 2013, 8, e59145 CAS.
- K. D. Weaver, H. J. Kim, J. Sun, D. R. MacFarlane and G. D. Elliott, Green Chem., 2010, 12, 507–513 RSC.
- J.-C. Plaquevent, J. Levillain, F. Guillen, C. Malhiac and A.-C. Gaumont, Chem. Rev., 2008, 108, 5035–5060 CrossRef CAS PubMed.
- M. Petkovic, J. L. Ferguson, H. N. Gunaratne, R. Ferreira, M. C. Leitao, K. R. Seddon, L. P. N. Rebelo and C. S. Pereira, Green Chem., 2010, 12, 643–649 RSC.
- J. Stoimenovski, P. M. Dean, E. I. Izgorodina and D. R. MacFarlane, Faraday Discuss., 2012, 154, 335–352 RSC.
- Y. Yu, X. Lu, Q. Zhou, K. Dong, H. Yao and S. Zhang, Chem. - Eur. J., 2008, 14, 11174–11182 CrossRef CAS PubMed.
- H. Shekaari and E. Armanfar, J. Chem. Eng. Data, 2009, 55, 765–772 CrossRef.
- T. Singh, M. Drechsler, A. H. Müeller, I. Mukhopadhyay and A. Kumar, Phys. Chem. Chem. Phys., 2010, 12, 11728–11735 RSC.
- Q.-G. Zhang, N.-N. Wang and Z.-W. Yu, J. Phys. Chem. B, 2010, 114, 4747–4754 CrossRef CAS PubMed.
- U. Salma, P. Ballirano, M. Usula, R. Caminiti, N. V. Plechkova, K. R. Seddon and L. Gontrani, Phys. Chem. Chem. Phys., 2016, 18, 11497–11502 RSC.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef CAS PubMed.
- C. Spickermann, J. Thar, S. Lehmann, S. Zahn, J. Hunger, R. Buchner, P. Hunt, T. Welton and B. Kirchner, J. Chem. Phys., 2008, 129, 104505 CrossRef CAS PubMed.
- A. Mariani, M. Campetella, C. Fasolato, M. Daniele, F. Capitani, L. Bencivenni, P. Postorino, S. Lupi, R. Caminiti and L. Gontrani, J. Mol. Liq., 2017, 226, 2–8 CrossRef CAS.
- W. Schroer, A. Triolo and O. Russina, J. Phys. Chem. B, 2016, 120, 2638–2643 CrossRef CAS PubMed.
- A. Mariani, R. Dattani, R. Caminiti and L. Gontrani, J. Phys. Chem. B, 2016, 120, 10540–10546 CrossRef CAS PubMed.
- K. Marsh, J. Boxall and R. Lichtenthaler, Fluid Phase Equilib., 2004, 219, 93–98 CrossRef CAS.
- E. Bodo, A. Sferrazza, R. Caminiti, S. Mangialardo and P. Postorino, J. Chem. Phys., 2013, 139, 144309 CrossRef CAS PubMed.
- M. Campetella, E. Bodo, M. Montagna, S. De Santis and L. Gontrani, J. Chem. Phys., 2016, 144, 104504 CrossRef PubMed.
- L. Tanzi, F. Ramondo, R. Caminiti, M. Campetella, A. Di Luca and L. Gontrani, J. Chem. Phys., 2015, 143, 114506 CrossRef PubMed.
- G. Prampolini, M. Campetella, N. De Mitri, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2016, 12, 5525 CrossRef CAS PubMed.
- M. Campetella, D. Martino, E. Scarpellini and L. Gontrani, Chem. Phys. Lett., 2016, 660, 99–101 CrossRef CAS.
- U. Salma, M. Usula, R. Caminiti, L. Gontrani, N. V. Plechkova and K. R. Seddon, Phys. Chem. Chem. Phys., 2017, 19, 1975–1981 RSC.
- A. Benedetto, E. Bodo, L. Gontrani, P. Ballone and R. Caminiti, J. Phys. Chem. B, 2014, 118, 2471–2486 CrossRef CAS PubMed.
- M. Campetella, S. De Santis, R. Caminiti, P. Ballirano, C. Sadun, L. Tanzi and L. Gontrani, RSC Adv., 2015, 5, 50938–50941 RSC.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- V. R. Albertini, L. Bencivenni, R. Caminiti, F. Cilloco and C. Sadun, J. Macromol. Sci., Part B: Phys., 1996, 35, 199–213 CrossRef.
- M. Carbone, R. Caminiti and C. Sadun, J. Mater. Chem., 1996, 6, 1709–1716 RSC.
- L. Gontrani, O. Russina, F. C. Marincola and R. Caminiti, J. Chem. Phys., 2009, 131, 244503 CrossRef PubMed.
- R. Caminiti, M. Carbone, G. Mancini and C. Sadun, J. Mater. Chem., 1997, 7, 1331–1337 RSC.
- D. A. Keen, J. Appl. Crystallogr., 2001, 34, 172–177 CrossRef CAS.
- L. Gontrani, F. Ramondo, G. Caracciolo and R. Caminiti, J. Mol. Liq., 2008, 139, 23–28 CrossRef CAS.
- L. Gontrani, F. Ramondo and R. Caminiti, Chem. Phys. Lett., 2006, 417, 200–205 CrossRef CAS.
- M. Usula, F. Mocci, F. C. Marincola, S. Porcedda, L. Gontrani and R. Caminiti, J. Chem. Phys., 2014, 140, 124503 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28545g |
| This journal is © The Royal Society of Chemistry 2017 |