One-step fabricated wettable gradient surface for controlled directional underwater oil-droplet transport

Abstract

A wettable gradient surface for underwater oil is fabricated by a one-step anodic oxidation method on a graphite plate and self-propulsion of an underwater oil droplet is achieved on it. Moreover, the transport distance could be further controlled and predicted via the initial position of the droplet and/or tilted angle of the graphite plate. Such surfaces with a continuous wettable gradient for underwater oil may be used for the construction of new smart devices.

---

Manipulating a liquid droplet to move along a given direction is an important technique and widely employed in various fields, such as microfluidic devices,¹ no-loss transportation,² chemical reactions,³ etc. Over the past few years, several strategies have been adopted to manipulate the directional movement of a liquid droplet on a solid surface,^4–6 among which fabricating a surface with a wettable gradient is widely used.^7–9 Recently, manipulating a liquid droplet in aqueous media is also becoming an emerging field due to its remarkable role in various phenomena and wide promising applications in many fields.^10,11 However, different from the environment in air, the underwater environment is more complicated. More phases may be involved (air/water/solid) and many factors may have an influence on underwater liquid manipulation. Besides, it is hard to manipulate an oil droplet underwater due to the higher underwater movement resistance and ultra-low surface tension of oil. Jiang et al.¹² revealed the mechanism of the special underwater superoleophobicity of fish scales. Inspired by these findings, some works have been expended on the manipulation of underwater oil droplets via wettability and adhesion.^13,14 Yong et al. reported the transfer of underwater oil droplets achieved between glass surfaces with different wettability and adhesion fabricated by femtosecond laser.¹⁵ Zhang et al. realized underwater oil droplets transport by using highly adhesive superoleophobic surface as a “mechanical hand”.¹⁶ Although the transport of underwater oil droplet has been realized, most of works focus on the transport between different surfaces with different wettability or adhesion through complicated methods.¹⁷ It remains a challenge to develop a facile and cost-efficient approach to achieve controllable underwater oil droplet transport on one single surface. Here, we adopt a one-step anodic oxidation method to fabricate a surface with wettable and adhesion gradient on a graphite plate and self-propelling of underwater oil droplets is achieved on it. The results indicate that hydrophobic (for great wettable gradient) and underwater oleophobic (for low adhesion) of a graphite plate surface are necessary for realizing the self-propelling of an underwater oil droplet. Interestingly, the transport distance of oil droplet could be extended further via introducing the gravity, which could be controlled and predicted according to the initial position of droplet and/or tilted angle of graphite plate. The fabricating method adopted in this work is scalable that it can be broadened to some other substrate materials such as carbon materials and metal materials. Such surfaces with continuous wettable gradient for underwater oil may be used for the construction of new smart devices.

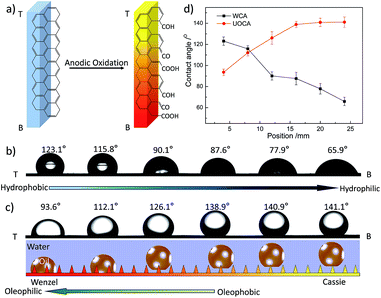
In this experiment, a wettable gradient on a graphite plate is fabricated by an improved one-step anodic oxidation (AO) method via the current and oxidation time gradient¹⁸ (see Experimental section and Fig. S1, ESI†). Generally, carbon (C) is the only detectable element on the untreated graphite plate surface. After AO, oxygen element (O) is introduced onto the surface.¹⁹ X-ray photoelectron spectroscopy (XPS) analysis is carried out on different areas of the sample AO treated under current 0.4 A and volume flow of electrolyte 2.7 L h⁻¹. According to the results, the O 1s/C 1s ratio of different areas increases significantly along the direction from T to B (T: top area and B: bottom area of graphite plate during the perpendicularly anodic oxidation process) (see Fig. S2, ESI†). Deconvolution of the C 1s spectra gives four peaks representing graphitic carbon (peak I, 284.6 eV), carbon presents in alcohol or ether groups (peak II, 286.1–286.3 eV), carbonyl groups (peak III, 287.3–287.6 eV) and carboxylic acid or ester groups (peak IV, 288.4–288.9 eV).²⁰ The spectral contribution of the carboxylic carbon peak increases from about 0.5 to 14%, and the carbonyl content increases from about 1.5 to 27% (Fig. S2, ESI†). Therefore the increase in O 1s/C 1s ratio is attributed to an increase in the carboxylic and carbonyl carbon contents. An oxidation extent gradient is formed on the graphite plate surface and more polar oxygen-containing groups are introduced at the bottom part, resulting in a chemical gradient (Fig. 1a). However, the scanning electron microscopy (SEM) and corresponding atomic force microscopy (AFM) images of different areas of the AO graphite plate surface (from T to B) show little difference between each other. The root-mean-square (RMS) roughness barely changes from ∼272.8 nm to ∼285.3 nm. The results of water contact angle (WCA) measurement indicates that, after AO, the surface wettability changes from hydrophobic (123.1°) to hydrophilic (65.9°) and a wettable gradient (2.86° mm⁻¹) for water is formed on the whole graphite plate (Fig. 1b). Based on the results above, we mainly ascribe the formation of the wettable gradient to the change of the surface chemical composition. As for underwater oil contact angle (UOCA), although a wettable gradient is also formed, from 93.6° (T) to 141.1° (B) gradually (Fig. 1c), the change trend is different from that of WCA. As shown in Fig. 1d, when WCA is more than 90° (hydrophobic), UOCA increases gradually with the decease of WCA. However, when WCA comes to less than 90° (hydrophilic), the change of UOCA is very little. In other words, obvious wettable gradient for underwater oil is only formed on hydrophobic area. Furthermore, repeated cycling measurement of WCA and UOCA on the AO graphite plate surface indicates excellent reproducibility and stability (Fig. S4, ESI†), and the surface properties have no significant change at room temperature in a month.

Fig. 1 (a) Schematic models of surface changes of the graphite plates. Explanation for the formation of chemical composition gradient. (b) The change of WCAs along the direction from T to B. (c) UOCAs (chloroform) from T to B. (d) The WCAs and UOCAs on different areas of AO graphite plate. The results indicate that, when WCA is more than 90°, UOCA increases gradually with the decease of WCA. However, when WCA comes to less than 90°, the change of UOCA is very little. T: top area and B: bottom area of graphite plate during the perpendicularly anodic oxidation process.

It is well known that surface wettability is attributed to the surface morphology and chemical composition. Commonly, the contact angles (CAs) of an oil/water/solid three-phase system can be calculated from the Young's equation.²¹ According to that, the UOCA should increase with the decrease of WCA, leading to opposite gradient directions. However, the measurement demonstrates that the UOCAs here do not follow the law strictly. When WCA comes to less than 90° (hydrophilic), the change rate of UOCA becomes little (Fig. 1c). Actually, here, intrusion pressure (IP) should be taken into consideration, due to rough microstructures of the graphite plate surface (Fig. S3, ESI†). IP would prevent the droplet spontaneous transporting from Cassie state to Wenzel state on a solid surface, which could be described as the following equation^22,23

IP = 2γ/R = −cγ(cos θ)/A (1)

where γ is the interface tension, R is the radius of meniscus, c is the circumference of the pore, A is the cross-sectional area of the pore, and θ is the CA. When a hydrophobic graphite plate is submerged into water, water is hard to intrude the pores. Thus, oil droplet could occupy the most of pores as it contacts the surface of graphite plate, exhibiting a Wenzel state with high adhesion (Fig. 1c and S5, ESI†). With the decrease of WCA, IP becomes smaller and smaller, and more water would penetrate the pores to occupy some surface of graphite plate, which would induce the gradual increase of UOCA.²⁴ Here, IP of water on the AO graphite plate changes from ∼24.03 kPa to ∼−17.94 kPa (WCA from 123.1° to 65.9°) with an average pore cross-sectional area of ∼33.68 μm². When the surface becomes hydrophilic, IP becomes negative and the water can penetrate the pores more easily. Consequently water occupies most surface of graphite plate, which prevents the oil from effectively contacting with the surface of graphite plate forming an oil/water/solid interface instead of the oil/solid interface.^25,26 As a result, oil droplet is suspended by the water layers trapped in the microstructures, exhibiting a Cassie state with low adhesion due to extremely discontinuous three-phase contact line (Fig. 1c and S5, ESI†). In this case, UOCA is mostly attributed to the strong repellency of water molecules to oil molecules rather than the intrinsic wettability of the surface. Accordingly, with the decrease of WCA, UOCA changes little (∼140°). Fig. S5† shows the adhesion forces of underwater oil on different wettability surfaces. Clearly, the hydrophobic (underwater oleophilic) surface has much larger adhesion force than that of hydrophilic (underwater oleophobic) surface, which is consistent with the theoretical analysis above. Therefore, in order to form a wettable gradient for underwater oil to realize the movement control of oil droplet underwater, the surface of graphite plate should be hydrophobic (for great wettable gradient) and underwater oleophobic (for low adhesion).

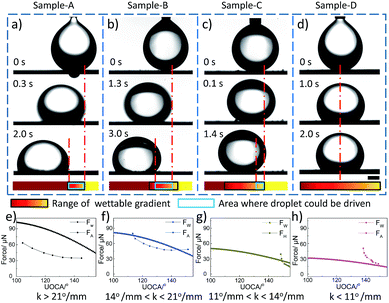
Based on the analysis above, hydrophobic and underwater oleophobic surfaces with different wettable gradient are fabricated (by adjusting the oxidation conditions, wettable gradient for underwater oil can be controlled from 1.08° mm⁻¹ to 43.20° mm⁻¹ easily) and the movement behaviours of underwater oil droplets on different wettable gradient surfaces are investigated. We found the movement behaviours of underwater oil droplets could be divided into four cases. Fig. 2 shows typical representatives of different movement behaviours. First, when the wettable gradient (k) for underwater oil is great (k > 21° mm⁻¹), although the range of wettable gradient is short, the oil droplet could be driven on the whole area of wettable gradient. For example, as for Sample-A (current: 0.6 A, volume flow of electrolyte: 2.4 L h⁻¹, Fig. 2a), the wettable gradient is 26° mm⁻¹, the movement distance reaches 1.57 mm. Second, when 14° mm⁻¹ < k < 21° mm⁻¹, the oil droplet could be driven only on the middle area of wettable gradient range. The movement distance is 1.75 mm for wettable gradient of 20° mm⁻¹ (Sample-B, current: 0.5 A, volume flow of electrolyte: 2.7 L h⁻¹, Fig. 2b). Third, when 11° mm⁻¹ < k < 14° mm⁻¹, the oil droplet could be driven only on the one end of wettable gradient range, but could not on the other end. An oil droplet dripped on the less wettable end of graphite plate with 13° mm⁻¹ moves about 0.65 mm (Sample-C, current: 0.6 A, volume flow of electrolyte: 3.4 L h⁻¹, Fig. 2c). Fourth, when the value of k is small (k < 11° mm⁻¹), the oil droplet could not be driven on the whole wettable gradient range. For Sample-D with 8° mm⁻¹, no significant movement is observed (current: 0.6 A, volume flow of electrolyte: 1.1 L h⁻¹, Fig. 2d).

Fig. 2 (a–d) Movement behaviours of underwater oil droplet (chloroform) on the horizontal AO graphite plate surfaces with different wettable gradient (k). (a) Sample-A: 26° mm⁻¹. (b) Sample-B: 20° mm⁻¹. (c) Sample-C: 14° mm⁻¹. and (d) Sample-D: 8° mm⁻¹. The volume of the oil droplet is 10 μL and the scale bar is 1 mm. (e–h) Comparison of wettable gradient force (F_W) and adhesion force (F_A) on different samples. For Sample-A, the value of F_W is larger than that of F_A in the whole range of wettable gradient (e). For Sample-B, the value of F_W is larger than that of F_A in the middle area of wettable gradient range (f). For Sample-C, only when the UOCA is below 150°, F_W is larger than F_A (g). For Sample-D, F_W is always smaller than F_A (h).

In order to gain better understanding of the unique phenomenon, we analysed the forces exerted on the droplets. There are three main forces influencing the movement behaviours of underwater oil: wettable gradient force (F_W), hysteresis force (F_H)¹⁸ and underwater movement resistance force (F_R). Due to low movement velocity and short transport distance, F_R could be regarded as a constant during the movement process. Thus, the values of F_W and F_H would determine the movement behaviours of oil droplet. F_W drives oil droplet towards the more wettable region of the surface, which is described as^8,27

F_W = πγR²k sin θ (2)

where R is the base radius of the droplet, γ is the surface tension of oil, k is the wettable gradient and θ is the position-responsive sessile CA of the droplet. For an oil droplet of 10 μL, R could be seen as a constant (1 mm) and we could get the value of F_W at different values of k and θ (Fig. 2e–h).

In fact, it is hard to obtain accurate values of hysteresis force (F_H), as the oil droplet would move immediately when it contacts with the surface due to high wettable gradient. Considering that the CA hysteresis is a direct measure of the adhesion force,²⁸ we used the adhesion forces (F_A) (along the direction of the wettable gradient) of samples to estimate the values of F_H. As shown in Fig. 2e, for Sample-A, the value of F_W is larger than that of F_A in the whole range of wettable gradient. For Sample-B, the value of F_W is larger than that of F_A in the middle area of wettable gradient range, i.e., from 145° to 114° (Fig. 2f). For Sample-C, only when the UOCA is below 150°, F_W is larger than F_A (Fig. 2g). And on the surface of Sample-D, the value of F_W is always smaller than that of F_A (Fig. 2h). Clearly, the result of force analysis is consistent with the actual observation. Therefore, according to the results and theory analysis above, we deduce that the movement of the underwater oil droplet on the AO surface must meet two necessary conditions. On one hand, the surface of graphite plate should be hydrophobic (for great wettable gradient of underwater oil) and underwater oleophobic (for low adhesion). For example, an oil droplet is dripped on the position with the UOCA of 83.1°, although the wettable gradient reaches 23° mm⁻¹ in a short distance, oil droplet can only spread directionally on the surface due to the high adhesion between the oil and the surface (see Fig. S6, ESI†). On the other hand, the wettable gradient for underwater oil should be more than 11° mm⁻¹. Because the movement resistance underwater is hundreds of times larger than that in air, the surface must have high wettable gradient to get large driving force. Clearly, we realize the self-propelling of underwater oil droplet by the one-step anodic oxidation and the movement distance could be adjusted via wettability and wettable gradient effectively.

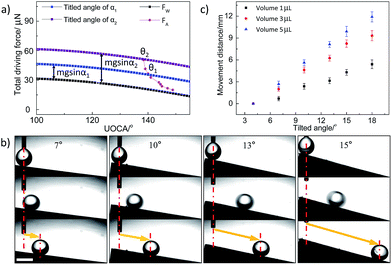
In the experiment above, although we realize the self-propelling of oil droplet underwater, the movement distance is very limited. Here, in order to control the movement behaviour of underwater oil droplets effectively, the gravity as an external force is introduced by tilting the surface with some angle (no significant movement of underwater oil droplets is observed on an untreated graphite plate even vertically positioned) and the total driving force (F_TD) could be described as the sum of wettable gradient force and the component of gravity (F_G) in the titled surface:

F_TD = F_W + F_G = F_W + mg sin α (3)

where, m is the mass, g is the acceleration and α is the titled angle. Here, we could adjust the total driving force via the mass of droplet and the titled angle of plate to change the balance position and control the movement distance of the droplet (θ₁, θ₂, in Fig. 3a). Fig. 3b shows the movement behaviours of underwater oil droplets on the Sample-D surface at different tilted angles. In order to enhance the controllability of underwater oil droplet, small droplet of 4 μL is used. As the oil droplet is dripped on the less wettable end, it rolls off along the direction of the wettable gradient, and is finally pinned on a fixed position for a given titled angle. With the increase of titled angle, the movement distance increases gradually, i.e., the movement distance increases from 2.00 mm (at tilted angle 7°) to 8.98 mm (at tilted angle 15°). And the underwater oil droplet would totally roll off the surface due to large F_G when the tilted angle reaches 30° (Fig. S7, ESI†). Besides titled angle, we could also adjust the movement distance via changing the mass of the oil droplet. The relationship between the movement distance and the titled angle of graphite plate at different volumes is shown in Fig. 3c.

Fig. 3 (a) Force analysis of underwater oil on AO graphite plate with different titled angles. (b) Movement behaviours of underwater oil droplets on the Sample-D surface at different tilted angles. The result indicates that the movement distance could be controlled via adjusting tilted angle. The scale bar is 2 mm. (c) The relationships between the movement distance and the tilted angle at different volumes. It is clear that the movement distance increases with the tilted angle and the volume of droplet. Obviously, we could control the movement distance of underwater oil easily via titled angle and volume of droplet.

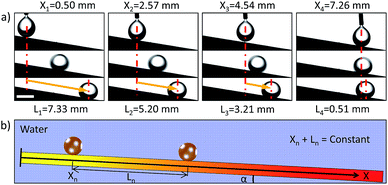
We can see that the movement distance increases with the tilted angle (within 30°) and the volume of oil droplet. For example, for a droplet of 5 μL, the movement distance increases to 11.91 mm at titled angle 18°. Obviously, we could control the movement distance (from 2.00 mm to 11.91 mm) of underwater oil droplets easily via titled angle (from 7° to 18°) and volume of the oil droplets (from 1 μL to 5 μL) on Sample-D. Furthermore, a special phenomenon is also observed, i.e., there seems to be a fixed balance position for a given titled angle and oil droplets always stop at the same position for the given titled angle wherever it is dripped (within the balance position). Fig. 4 shows the movement behaviours of underwater oil droplets dripped on different positions on Sample-D at titled angle of 9°. For initial positions 0.50, 2.57, 4.54, 7.26 mm, the movement distances reach 7.33, 5.20, 3.21, 0.51 mm. The results indicate that oil droplets are unexceptionally pinned at almost the same position eventually no matter where they are placed, i.e., X + L = constant = ∼7.80 mm (X is the initial position and L is the movement distance of droplet. The zero position (X = 0) is defined as bottom end of AO graphite plate during the oxidation treatment). In this case, the total force (F) is, F = F_W + F_G − F_R − F_A, for a given titled angle, the component of gravity (F_G = mg sin α) is a constant. Due to low movement velocity and short transport distance, F_R could also be regarded as a constant. So F is regarded as a function of the position of oil droplet (x), i.e., F = F_W + F_G − F_R − F_A = F(x) (F_W and F_A are only function of position (x)). At the beginning, F > 0, the oil droplet rolls off along the surface. In this process, F_W and F_A increase gradually with the movement distance (L), but F_A grows faster than F_W (Fig. 3a). As a result, the total force (F) decreases during the movement process. When it reaches the balance position where F(x) = 0, the oil droplet would stop and be pinned on the surface. Therefore, the droplets always stop at the same position (F(x) = 0) for a given titled angle wherever it is dripped (within the balance position). Clearly, we could realize the transport of an underwater oil droplet from one point to another accurately via initial position and/or titled angle. Besides, the method adopted in this work could be broadened to some other substrate materials such as carbon materials and metal materials.

Fig. 4 The movement behaviours of underwater oil droplets dripped on different initial positions of the Sample-D surface with a tilted angle of 9°. There seems to be a balance position on the surface for the given titled angle wherever the oil droplet is dripped, i.e., X_n + L_n = constant (X is the initial position and L is the movement distance of oil droplet. The zero position (X = 0) is defined as the bottom end of AO graphite plate during the oxidation treatment process). It further indicates that the movement distance of the oil droplet could be controlled via initial position. The scale bar is 2 mm.

Conclusions

In summary, a graphite plate surface with a wettable gradient for underwater oil is fabricated by a one-step anodic oxidation method, which is facile, scalable and cost-efficient. We realize the transport of an underwater oil droplet from one point to another accurately. The transport distance could be controlled and predicted according to the initial position of droplet and/or tilted angle of graphite plate. The study has promising application in microfluidics, submerged antifouling systems, no loss oil microdroplet transport, clean oil proof materials underwater and so on.^29,30

Acknowledgements

This work was supported by National Key Basic Research Program of China (2013CB933000), National Natural Science Foundation of China (21673015, 21234001, 51203006, 21473007), Fundamental Research Funds for Central Universities (YWF-15-HHXY-017, YWF-16-JCTD-A-01) and Aeronautical Science Foundation of China (2015ZF51060).

Notes and references

1. K. Suzuno, D. Ueyama, M. Branicki, R. Tóth, A. Braun and I. Lagzi, Langmuir, 2014, 30, 9251.
2. Y. Liu, M. Andrew, L. Jing, J. M. Yeomans and Z. Wang, Nat. Commun., 2015, 6, 10034.
3. K. John, M. Bär and U. Thiele, Eur. Phys. J. E, 2005, 18, 183.
4. C. Schlaich, C. L. Cuellar, L. Yu, K. Achazi, Q. Wei and R. Haag, ACS Appl. Mater. Interfaces, 2016, 8, 29117.
5. K. O. Zamuruyev, H. K. Bardaweel, C. J. Carron, N. J. Kenyon, O. Brand, J. P. Delplanque and C. E. Davis, Langmuir, 2014, 30, 10133.
6. S. Datta, A. K. Das and P. K. Das, Langmuir, 2015, 31, 10190.
7. S. L. Feng, S. J. Wang, C. C. Liu, Y. M. Zheng and Y. P. Hou, Chem. Commun., 2015, 51, 6010.
8. M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539.
9. N. Dorri, P. Shahbazi and A. Kiani, Langmuir, 2014, 30, 1376.
10. L. Lin, M. J. Liu, L. Chen, P. P. Chen, J. Ma, D. Han and L. Jiang, Adv. Mater., 2010, 22, 4826.
11. J. A. Halldorsson, S. J. Little, D. Diamond, G. Spinks and G. Wallace, Langmuir, 2009, 25, 11137.
12. M. J. Liu, S. T. Wang, Z. X. Wei, Y. L. Song and L. Jiang, Adv. Mater., 2009, 21, 665.
13. I. E. Palamá, S. D'Amone, M. Biasiucci, G. Gigli and B. Cortese, J. Mater. Chem. A, 2014, 2, 17666.
14. T. Q. Guo, M. C. Li, L. P. Heng and L. Jiang, RSC Adv., 2015, 5, 62078.
15. J. L. Yong, F. Chen, Q. Yang, U. Farooq, H. Bian, G. Q. Du and X. Hou, Appl. Phys. A: Mater. Sci. Process., 2015, 119, 837.
16. E. S. Zhang, Z. J. Cheng, T. Lv, L. Li and Y. Y. Liu, Nanoscale, 2015, 7, 19293.
17. Y. Chu and Q. M. Pan, Chem. Commun., 2014, 50, 13817.
18. S. L. Feng, S. J. Wang, L. C. Gao, G. J. Li, Y. P. Hou and Y. M. Zheng, Angew. Chem., Int. Ed., 2014, 53, 6163.
19. A. G. Pandolfo and A. F. Hollenkamp, J. Power Sources, 2006, 157, 11.
20. Z. R. Yue, W. Jiang, L. Wang, S. D. Gardner and C. U. Pittman Jr, Carbon, 1999, 37, 1797.
21. Y. C. Jung and B. Bhushan, Langmuir, 2009, 25, 14165.
22. H. Mei, D. Luo, P. Guo, C. Song, C. C. Liu, Y. M. Zheng and L. Jiang, Soft Matter, 2011, 7, 10569.
23. C. W. Extrand and S. I. Moon, Langmuir, 2012, 28, 3503.
24. M. H. Jin, S. S. Li, J. Wang, Z. X. Xue, M. Y. Liao and S. T. Wang, Chem. Commun., 2012, 48, 11745.
25. I. E. Palamà, S. D'Amone, V. Arcadio, D. Caschera, R. G. Toro, G. Gigli and B. Cortese, J. Mater. Chem. A, 2015, 3, 3854.
26. S. S. Li, M. Y. Liao and M. H. Jin, Chem. Res. Chin. Univ., 2014, 30, 518.
27. H. Bai, X. Tian, Y. Zheng, J. Ju, Y. Zhao and L. Jiang, Adv. Mater., 2010, 22, 5521.
28. W. Li and A. Amirfazli, Adv. Mater., 2007, 19, 3421.
29. R. L. Agapov, J. B. Boreyko, D. P. Briggs, B. R. Srijanto, S. T. Retterer, C. P. Collier and N. V. Lavrik, ACS Nano, 2013, 8, 860.
30. K. Manabe, T. Matsubayashi, M. Tenjimbayashi, T. Moriya, Y. Tsuge, K. H. Kyung and S. Shiratori, ACS Nano, 2016, 10, 9387.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S7. Experimental apparatus, XPS analysis and SEM images of AO graphite plate surface, cycling measurement of WCA and UOCA on AO graphite plate surface, adhesion force on untreated and AO graphite plate surfaces, spreading process of underwater oil droplet, movement behaviours of underwater oil droplets on Sample-D at tilted angle 30°. See DOI: 10.1039/c6ra28710g

---