 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Confinement of hydrogen and hydroxyl radicals in water cages: a density functional theory study†
Liuxie Liua,
Shuang Maoa,
Quan Li*a,
Xiaolan Wanga,
Mingli Yang b and
Laicai Li
b and
Laicai Li *a
*a
aCollege of Chemistry and Materials Science, Sichuan Normal University, Chengdu 610068, China. E-mail: liquan6688@163.com; lilcmail@163.com
bInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
First published on 6th March 2017
Abstract
Density functional theory calculations with D3 empirical dispersion correction reveal that hydrogen and hydroxyl radicals encapsulated in typical water cages found in clathrate hydrates exhibit similar structures and properties in their confined states to those in their corresponding free states, including atomic charges, spin densities, and electronic configurations. Diffusion studies reveal that energy barriers exist for these radicals to approach or exit these water cages. Energy decomposition analyses further reveal that coulombic repulsion between the radical and water cage is responsible for these energy barriers and the inability of these species to react with cage water molecules. This study provides insight into mechanisms for the storage of free radicals, which is normally extremely difficult because of their high reactivities toward many substances.
Introduction
Clathrate hydrates are crystalline solid compounds that exist widely in ocean sediments, permafrost regions, and comets and on certain planets.1–9 Interest in clathrate hydrates arose due to of two aspects. First, their ability to store methane on a large scale, both underground and in the ocean, means that they might become a major source of energy in the future. It has been shown that the methane reserves in these hydrates are perhaps twice as abundant as those in other proven fossil fuel sources, including oil, gas, and coal.10–16 The other important aspect is that clathrate hydrates can be used as nano-containers for confining radicals, which are of great significance in chemical reactions,17–21 biological systems,22–25 and ageing processes.26,27 Free radicals, which contain one or more unpaired electrons, are reactive and usually exist as transient reaction intermediates.28 They are key constituents that initiate many chemical reactions, but are difficult to contain for subsequent use because of their high reactivities. The containment of free radicals is of particular interest in synthetic and catalytic chemistry.Over the past few years, a number of experiments have revealed that radicals can exist in clathrate hydrates with extended lifetimes.29–31 Yeon et al.30 observed stably entrapped hydrogen radical (H·) in clathrate hydrates by electron spin resonance (ESR) and nuclear magnetic resonance (NMR) spectroscopies. Cha et al.31 studied O2 + Me4NOH in these hydrates at a 60 kGy irradiation dose and various temperatures and demonstrated the stable existence of superoxide radical anions in clathrate hydrates by magnetic property measurement system (MPMS) studies and ESR spectroscopy. Clathrate hydrates have cage-like structures that can encapsulate small molecules such as CH4 and CO2.10–16 These species, however, are chemically inert compared to reactive radicals. Encapsulating radicals in water cages and moderating their reactivities are therefore interesting issues for the design and development of nano-containers and nano-reactors. In this article, we present our theoretical study on the status of H· and hydroxyl radicals (OH·) in the water cages and reveal that coulombic interactions between these radicals and the water cages prevent them from combining. Moreover, the curvature of these water cages contributes to the enhancement of coulombic interactions.
The hydrates are thermodynamically stable when guest molecules occupy the host cages to a certain minimum level, and the interactions between the host and guest involve mainly van der Waals forces (noncovalent interactions).32,33 To study the stability, Lebsir et al. and Khan computed the stabilization energy (SEk) of one cage occupied by different gases using Hartree–Fock (HF) and second-order Møller–Plesset perturbation theory (MP2). Their results showed that ab initio quantum chemical methods provide independent and accurate means of reaching a good understanding of the nature of hydrates and their host–guest interactions.34–36 The HF method is somewhat less accurate, while MP2 is more expensive for larger molecules and tends to overestimate noncovalent interactions. More accurate and economical methods that correctly describe noncovalent interactions are therefore required. For a long time, density functional theory (DFT) was disregarded as a reliable method for the description of noncovalent interactions. In particular, for dispersion-dominated complexes that require a non-localized energy description, GGA functionals are inadequate as they do not explicitly describe these dispersion phenomena.37 Numerous ways for overcoming these disadvantages of DFT currently exist: the use of DFT-D methods, which have empirical dispersion corrections added to their functionals, is one example. A significant amount of work has been directed toward validating the performance of the DFT-D3 method,38 which has been shown to be reliable for describing noncovalent interactions.38–41
In this work, we employ DFT-D3 to study whether or not H· and OH· radical are stable in typical clathrate hydrate structures I and/or II and focus on variations in the SEk of the hydrates, charges and spin densities of the encapsulated free radicals, and energy barriers for radical transfer between cages.
Computational methods
There are three common clathrate hydrate structures: structure I, structure II, and structure H, which respectively contain 512–51262, 512–51264, and 512−435663−51268 cages.3,42,43 The third cage, structure H, has seldom been studied. Therefore, this work focused on the first two structures. Two types of water cages, s1 and s2, with the structural motifs of structures I and II, respectively, were constructed. The first, s1, consists of one 512 cage linked to another 51262 cage, while s2 contains one 512 and one 51264 cage, as shown in Fig. 1. The initial coordinates of the O atoms were taken from previous studies,36,44–46 however, some of the H atoms are oriented differently.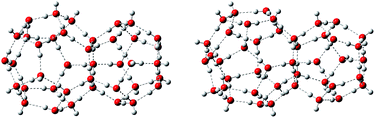 | ||
| Fig. 1 Prototypical hydrate structures s1 (left) and s2 (right). O atoms are red, and H atoms are gray. | ||
The structures of empty s1 and s2 were optimized within the DFT framework using the B97D,47 B3LYP,48 BLYP,48 and PBE49 exchange-correlation functionals with Grimme's D3 dispersion correction.38 The triple-ζ basis set def-TZVP,50 which includes polarized function, as implemented in the Turbomole suite,51 was used. These four methods produce similar geometries for the empty s1 and s2 cages. To further validate our computational strategy, we also optimized the cage structure of the water hexamer, W6, at the MP2/def-TZVP52 level, and compared the results obtained with DFT-D3 method. The calculated bond lengths are given in Table S1,† while the binding energies computed at the four DFT-D3 levels are listed in Table S2.† It is clear that the four DFT-D3 methods provide results that are in reasonable agreement with those of MP2. In particular, B97D-D3 provides the best agreement with MP2. The largest structural discrepancy, 0.01 Å, was found for an H⋯O bond. Hence, B97D-D3 was mainly used in further calculations.
The two free radicals, H· and OH·, were separately placed at the centers of these cages to study the encapsulation of free radicals in clathrate hydrates, and the resulting structures were fully optimized without any constraints. The H· and OH· radicals were placed in either cage (s1 or s2) and all possible variations were optimized for comparison. Tetrahydrofuran (THF) is commonly used during the preparation of many clathrate hydrates to stabilize their structures.4,30 The influence of THF was studied by placing each radical in the small cage and THF in the large one. In addition, we studied the stability of H· and OH· at different locations, which is useful for the understanding of their movements, and diffusion inside, and between cages. Harmonic vibrational frequencies were computed to ensure the located stationary structures are true minima on their respective potential energy surfaces. In the self-consistent field (SCF) calculations, the density tolerance was set to 10−6 a.u. during geometry optimization. The resolution-of-identity (RI) approximation53,54 and multipole accelerated RI (MARI) approach55 were employed to speed up the computations.
Results and discussion
Structures of H· and OH· hydrates
The structures of the s1 and s2 water cages were optimized at the DFT-D3/def-TZVP level. The maximum and minimum values of the O–H bond lengths and hydrogen-bond lengths are listed in Table S5.† Using the B97D-D3 functional, for example, the O–H bond length, which is linked to other O atom by hydrogen bonding, is in the range 0.974–1.035 Å for s1 and 0.973–1.039 Å for s2. The O–H bond length, without hydrogen bonding, is about 0.966 Å for s1 and s2. In addition, the hydrogen-bond length is in the range 1.560–1.971 Å for s1 and 1.509–1.987 Å for s2. These results are similar to those of Chattaraj et al.,56 and are listed for comparison in Table S5.†The structures of the eight radical-included clathrate hydrates, with the radical either in the small or large cage for s1 or s2, were optimized at the unrestricted DFT-D3/def-TZVP level. Furthermore, to check for the spin contamination57 in the open-shell species, the 〈S2〉 values were determined and are listed in Table S6.† None of the clathrate hydrates are significantly affected by spin contamination (after allowing 10% variation58). Optimized structures are depicted in Fig. S1.† For the four H-included clathrate hydrates, the structures of the optimized water-cage frameworks are essentially the same as those of the cages devoid of the encapsulant. The inter- and intramolecular distances and angles are almost unchanged for the water molecules. H· always sits at around center of the cage, with distances of about 3.70–4.80 Å to the O atoms of the (cage) water molecules. Alavi et al. examined the movement of H· within 512 and 51264 water cages, and found that structures in which the H· was located at the center of the small or large cage were energetically more favorable than other conformers.59 The structures of the cages of the four OH-included clathrate hydrates are similar to those of their H-included counterparts. The encapsulation of OH· has little effect on the water cages, with the exception that one of the water molecules moves inward to form a hydrogen bond with OH·. Consequently, OH· is displaced about 1.5 Å from the center of the cage. The shortest distance between OH· and the surrounding water molecules is about 2.02–2.44 Å in the four hydrates. Only small changes in the O–H bond length are noted, about −0.005–0.006 Å, compared to free OH· in the gas phase.
Table 1 lists the stabilization energies (SEs) of the H- and OH-included hydrates. For these systems, two kinds of SE can be defined. The first takes the stabilization energy among the water molecules into account, and it is computed by SEa = E(hydrate) − E(guest) − N × E(water), where E(X) is the total energy of the encapsulated hydrate, free guest radical, or free water molecule, respectively, and N is the number of water molecules. The second emphasizes the interaction between the guest and the water cage, and is computed by SEb = E(hydrate) − E(guest) − E(water cage). All SE values have been subjected to basis set superposition error (BSSE) correction, using the counterpoise method of Boys and Bernardi.60 In addition, all SE values have been zero-point energy (ZPE) corrected.
| SEa | SEb | ||||
|---|---|---|---|---|---|
| UB97D-D3 | UB97D-D3 | UB3LYP-D3 | UBLYP-D3 | UPBE-D3 | |
| H· | |||||
| s1-L | −326.3 | 2.2 | −1.1 | −1.0 | −0.9 |
| s1-S | −325.2 | 3.8 | −1.2 | −1.3 | −1.2 |
| s2-L | −342.6 | 2.7 | −0.9 | −0.9 | −0.9 |
| s2-S | −341.5 | 4.3 | −1.5 | −1.4 | −1.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| OH· | |||||
| s1-L | −332.0 | −4.8 | −5.1 | −7.8 | −10.7 |
| s1-S | −333.5 | −6.2 | −7.9 | −10.0 | −10.4 |
| s2-L | −349.4 | −4.8 | −6.0 | −7.8 | −8.0 |
| s2-S | −352.4 | −7.1 | −7.1 | −10.4 | −10.6 |
| s1 | −328.6 | ||||
| s2 | −346.6 | ||||
The SEb values for H· in s1 and s2 are very small in magnitude. Positive values are predicted with UB97D-D3, while UB3LYP-D3, UBLYP-D3, and UPBE-D3 produce small negative SEb values. For OH·, the computed SEb values are negative using all four functionals. In addition, the SEb values of OH· are larger than those of H·. However, for both H· and OH· radicals, there are no differences evident in the SEb values between the s1 and s2 structures, or between the small and large cages. In contrast, the SEa of H· and OH· in s1 and s2 are large and negative, and this can be attributed mainly to the stabilization energy of the water cage. The stabilities of the H- and OH-included hydrates are reflected by their large SEa, although their encapsulation leads to very small SEb values. For comparison, the SEa of empty s1 and s2 are also given in Table 1. It is apparent that more than 93% of the SEa of H· and OH·, in s1 or s2, comes from the SEa of the water molecules. Vikas et al.61 investigated the effect of D3, so the UB97D functional is further used, the results of which are listed in Table S7.† The UB97D results and UB97D-D3 are similar. Therefore, we can conclude that the water cages themselves help stabilize the encapsulation of H· and OH·, indicating that these water cages serve as stabilizers for these active radicals.
Status of H· and OH· inside the water cages
We further studied the status of H· and OH· radicals in these water cages. Table 2 lists the net charges and spin densities of H· and OH·, which were evaluated by natural bond orbital (NBO) analyses.62 The net charge on H· is very small, less than −0.014, regardless of the hydrate structure and cage size, indicating that little charge is exchanged between H· and the water cage. However, the net charge on OH· varies in the range of −0.123 to −0.165. Compared to the isolated OH·, the negative charge on the O atom increases, and the positive charge on the H atom also increases. The encapsulated OH· is clearly more polar than its isolated, gas-phase form. It is clear that very small amounts of charge flow from the water cage toward the OH·. The weak hydrogen bond between the OH· and the cage serves as a bridge for this flow of charge. Further analysis reveals that the transferred charge comes not only from the directly connected water molecule, but also from some of the other neighboring molecules, through the hydrogen bonding network, however, this contribution is rather small. In other words, the encapsulated H· and OH· retain almost the same charge states as their isolated forms.| H· | OH· | |||
|---|---|---|---|---|
| Net charge | Spin density | Net charge | Spin density | |
| s1-L | −0.006 | 0.987 | −0.135 | 0.836 |
| s1-S | −0.014 | 0.970 | −0.132 | 0.857 |
| s2-L | 0 | 1.000 | −0.123 | 0.858 |
| s2-S | −0.013 | 0.971 | −0.165 | 0.800 |
The H· and OH· hydrate systems are found to be stable as doublet states. For the four H-containing hydrates, almost all (close to unity) of the spin density is located on the central H·, indicating that it maintains the spin state of its gas-phase form. On the other hand, the spin density of OH· lies in the range of 0.800–0.858, and a small part of the spin is distributed to the nearby water molecules. These spin distributions are also reflected in their electronic configurations, as shown in Table 3. The H· keeps its 1s1.00 configuration in these cages, while the H atom in OH· is configured to be 1s0.57–0.58, close to that of free OH· (1s0.61). The O atom in OH· is configured to be 2s1.882p4.64−4.693p0.00–0.01, also close to that observed for free OH· (2s1.892p4.49). These spin density and electronic configuration analyses confirm that, when encapsulated, both H· and OH· retain most of the radical characteristics of their (free) gas-phase forms.
| H· | OH· | ||||
|---|---|---|---|---|---|
| H | O | ||||
| 1s | 1s | 2s | 2p | 3p | |
| s1-L | 1.00 | 0.59 | 1.88 | 4.65 | 0.01 |
| s1-S | 1.01 | 0.57 | 1.88 | 4.67 | |
| s2-L | 1.00 | 0.58 | 1.88 | 4.64 | |
| s2-S | 1.01 | 0.58 | 1.88 | 4.69 | 0.01 |
| Gaseous | 1.00 | 0.61 | 1.89 | 4.49 | |
In this study, the influence of THF on the status of H· and OH· in these water cages was examined. THF normally occupies the larger cage of s1 and s2 because of its volume, while only the small cages are available for radicals. Using similar methods to those described above, we optimized structures in which H· or OH· occupies the small cage, while the large cage is occupied by THF, the results are given in Table 4. In all optimized structures THF is located at the center of the large cage with the shortest distance between its H atoms and the surrounding O atoms, in the s1 or s2 structure, calculated to be about 2.20 Å. In the presence of THF, very small variations in positions are noted for the H· and OH· radicals, compared to the structures devoid of THF. The H· is still located the center of the small cage for s1 and s2, and the average distance between H· and the surrounding water molecules is shorter than that without THF, by about 0.06 Å, while the shortest distance between OH· and the surrounding water molecules is shorter by about 0.1 Å. The changes in stabilization are less than 2.1 kcal mol−1 for SEa and 22.2 kcal mol−1 for SEb, regardless of the nature of the hydrate (s1 or s2). The corresponding changes in spin densities are less than 0.029 au for H· and 0.045 au for OH·. The net charges on H· and OH· remain almost the same, with corresponding changes of less than 0.001 for H· and 0.002 for OH·. In other words, although THF plays an important role in stabilizing these clathrate structures, it has little effect on the status of H· or OH· in the adjacent cage. Both H· and OH· are found to retain their radical characteristics in the presence of THF.
| SEa | SEb | Net charge | Spin density | |
|---|---|---|---|---|
| H· | ||||
| s1-S | −334.7 | 2.6 | −0.013 | 0.972 |
| s2-S | −364.8 | 2.4 | −0.013 | 0.971 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| OH· | ||||
| s1-S | −341.5 | −4.9 | −0.131 | 0.858 |
| s2-S | −368.6 | −6.9 | −0.163 | 0.813 |
Diffusion of H· and OH· radical between the water cages
When the radicals are confined in the clathrate structures, their movements are localized within the cages. We further studied the diffusion of H· and OH· radical between the water cages, as shown in Fig. S2.† In the s1 and s2 structures, the small (512) and large (51262 or 51264) cages share a pentagonal face. The energy profiles for radical diffusion between the cages are shown in Fig. 2, at different distances from the outer pentagonal face of the 512 cage, to the center of the 512 cage, to the center of the 51262 or 51264 cage, and finally to near the edge of the 51262 or 51264 cage.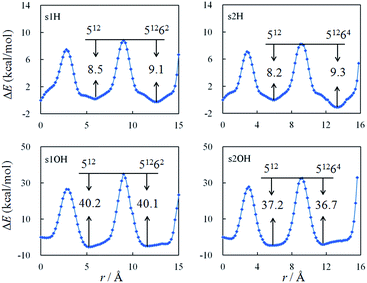 | ||
| Fig. 2 Energy profiles for H· and OH· diffusion between cages in the s1 and s2 structures calculated with the UB97D-D3 functional. | ||
The barriers for the diffusion of the H· radical from outside these hydrates through the pentagonal face of the 512 cage are calculated to be 8.5 and 8.3 kcal mol−1 for the s1 and s2 structures, respectively, and they are essentially the same as the barriers for the reverse process, which are 8.5 and 8.2 kcal mol−1 for the s1 and s2 structures, respectively. Alavi et al. studied the migration of H· through one 512 cage at the MP2 and B3LYP levels with the 6-311++G(d,p) basis set. One-dimensional barriers of 14.80 and 10.98 kcal mol−1, respectively, were calculated.59 The barriers for OH· radical diffusion are calculated to be larger than those for H·, at 25.4 and 26.0 kcal mol−1 for movement from outside the pentagonal face of each of the s1 and s2 structures, respectively.
From the center of the small cage to the center of the large cage in the s1 and s2 structures, the radicals migrate through another pentagonal face. Calculations predict that the barriers for diffusion from the center of the small cage, through the pentagonal face, to the center of the large cage are always similar to those for the reverse pathway. The differences are less than 1.1 kcal mol−1. Finally, as the radicals approach the furthest edges of these hydrates, the barriers increase enormously. This means that if a radical is confined by a water cage, it is very difficult for it to escape from the cage, or approach the cage edges.
Stabilization mechanism of H· and OH· inside the water cages
Several authors have studied the reactions of H2O with H· or OH·.63–65 These studies show that H· attacks the O atom in H2O to form H3O·, with C3v symmetry, while the O atom in OH· bonds to one of the H atoms in H2O. In contrast to free H2O, the water molecules in these cage structures are inactive toward the encapsulated H· or OH· radicals.Fig. 3 depicts the interactions of H· and OH· radicals with the water cage. Firstly, one needs to note the specific structure that comes from water cage. The water molecules constitute a network in which the positively charged H atoms and the negatively charged O atoms are arranged alternatively with ∠H–O–H ≈ 106°, ∠O–H⋯O ≈ 175°, and ∠H–O⋯H ≈ 111° along the surface, to simulate the arrangements of water molecules in cages. For H·, the angles θ between the radical and O atom in water molecules 1, 2, and 3 are 67° without optimization, as shown in Fig. S3a.† The positions of water molecules 1, 2 and 3 are then adjusted, and angles θ between H· radical and the O atoms of water molecules are respectively 67°, 72°, 77°, 82°, and 90°. Obviously, if r and θ are reduced, the H· becomes positioned closer to the water molecules. When H· approaches any of the atoms in an H2O molecule, it is polarized by the charge of the interacting O or H atom, and an opposing charge is developed on the interacting side, which is however of the same sign as those of the atoms near the interacting atom. Coulombic repulsion from these atoms results in an increase in energy, and consequently, the H· is unable to approach the cage structure any closer. To further study this effect, energies were computed without optimization at CCSD(T)66/6-311++G(d,p)67 and UB97D-D3/6-311++G(d,p) levels of theory, and the results of which are shown in Fig. S4,† both methods show the same tendency in behavior. At the various angles, the energies are all calculated to increase as the distances, r, between the radical and the water molecules decrease. On the other hand, when r is fixed, energies are observed to increase with decreasing θ. This means that if the H· is close to the water molecules, the overall energy increases.
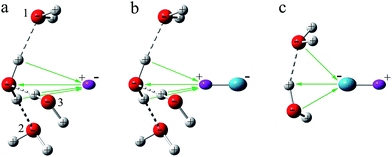 | ||
| Fig. 3 Schematic diagram showing the interaction of H· and OH· with the water cage. H· and the H atom in the OH· radical are purple, the O atom in OH· is blue-green. | ||
Through localized molecular orbital energy decomposition analysis (LMOEDA),68 implemented in GAMESS,69 energy decomposition analyses was performed at CCSD(T)/6-311++G(d,p) level, in order to better understand why these energies increase, the results of this study are listed in Fig. S5.† The interaction energies were decomposed into electrostatic energy, exchange energy, polarization energy and repulsion energy. Except for repulsion energy, which increases with reduced r, the other three energy terms are all reduced with decreasing r. Moreover, the changes observed in the repulsion and exchange energies with r are larger than the changes in the electrostatic and polarization energies. Fig. 4a shows the total energy and energy decomposition analyses for H· at an angle of θ = 67°. When r is reduced, in other words H· is close to the water molecules, repulsion energies clearly become larger, while the exchange energies are decreased more than the electrostatic and polarization energies. The changes in interaction energy are led by the coulombic repulsion and exchange energies, with coulombic repulsion energy being the major factor for the observed increases in interaction energy.
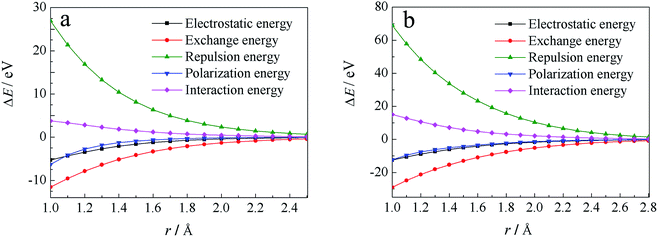 | ||
| Fig. 4 Energy decomposition analysis for H· radical attack at θ = 67° (a) and OH· radical at θ = 155° (b) using LMOEDA analysis. | ||
Similar analyses can be made for the OH· radical, as depicted in Fig. 3c and S3c,† at θ = 155°, 160°, 165°, 170°. Energies were also calculated at the CCSD(T)/6-311++G(d,p) and UB97D-D3/6-311++G(d,p) levels, the results of which are shown in Fig. S4.† At both levels, the approaching of OH· toward the cage results in increases in energy. LMOEDA analyses were also performed, as shown in Fig. S6† and 4b. Once again, the coulombic repulsion energy is a major factor for the observed increases in interaction energy.
As shown in Fig. S5 and S6,† repulsion energies increase with decreasing θ. In the water cage, there are specific angles between the water molecules. As a result, the curvatures of the s1 and s2 water cages contribute to the increases in repulsion energies. Coulombic repulsion makes H· and OH· unable to approach the water cage edges, or react with water molecules, and this results in these radicals having relatively long survival times.
Conclusions
By combining a D3 empirical dispersion correction to DFT functionals, we have modeled the confinement of hydrogen and hydroxyl radicals in typical water cages, s1 and s2, found in clathrate hydrates. After optimization, H· and OH· were found to be located near the center of the water cages, and these cages assist their encapsulation. Both radicals exhibit similar structures and properties to their corresponding free forms, including atomic charges, spin densities, and electronic configurations. Inter-cage diffusion studies reveal that energy barriers exist for these radicals to leave or approach the cage edges. LMOEDA energy decomposition analyses reveal that the changes in energy are mainly led by coulombic repulsion and exchange energies, with the coulombic repulsion energy between the radical and the water cage being the major factor for the observed increases in energy. The curvatures of the s1 and s2 water cages contribute to the increases in repulsion energies. Therefore, radicals are unable to approach or leave the water cage, and they cannot react with the water molecules of the cage. These studies provide insight into mechanisms for the prolonged capture of free radicals, with applications to synthetic and catalytic chemistry.Acknowledgements
We acknowledge the Education Committee of Sichuan Province (16ZB0067) for financial support.References
- E. D. Sloan, Energy Fuels, 1998, 12, 191–196 CrossRef CAS.
- W. L. Mao, H. Mao, A. F. Goncharov, V. V. Struzhkin, Q. Guo, J. Hu, J. Shu, R. J. Hemley, M. Somayazulu and Y. Zhao, Science, 2002, 297, 2247–2249 CrossRef CAS PubMed.
- E. D. Sloan, Nature, 2003, 426, 353–359 CrossRef CAS PubMed.
- L. J. Florusse, C. J. Peters, J. Schoonman, K. C. Hester, C. A. Koh, S. F. Dec, K. N. Marsh and E. D. Sloan, Science, 2004, 306, 469–471 CrossRef CAS PubMed.
- H. Lu, Y. Seo, J. Lee, I. Moudrakovski, J. A. Ripmeester, N. R. Chapman, R. B. Coffin, G. Gardner and J. Pohlman, Nature, 2007, 445, 303–306 CrossRef CAS PubMed.
- M. R. Walsh, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Science, 2009, 326, 1095–1098 CrossRef CAS PubMed.
- A. Falenty, T. C. Hansen and W. F. Kuhs, Nature, 2014, 516, 231–233 CrossRef CAS PubMed.
- Y. Huang, C. Zhu, L. Wang, X. Cao, Y. Su, X. Jiang, S. Meng, J. Zhao and X. C. Zeng, Sci. Adv., 2016, 2, e1501010 Search PubMed.
- M. Muraoka, N. Susuki and Y. Yamamoto, RSC Adv., 2016, 6, 63880–63885 RSC.
- P. G. Debenedetti and S. Sarupria, Science, 2009, 326, 1070–1071 CrossRef PubMed.
- A. Boetius and E. Suess, Chem. Geol., 2004, 205, 291–310 CrossRef CAS.
- R. Boswell, Science, 2009, 325, 957–958 CrossRef CAS PubMed.
- J. Zhu, S. Du, X. Yu, J. Zhang, H. Xu, S. C. Vogel, T. C. Gremann, J. S. Francisco, F. Izumi, K. Momma, Y. Kawamura, C. Jin and Y. Zhao, Nat. Commun., 2014, 5, 4128–4137 CAS.
- C.-G. Xu and X.-S. Li, RSC Adv., 2015, 5, 54672–54699 RSC.
- J. R. Cendagorta, A. Powers, T. J. H. Hele, O. Marsalek, Z. Bačić and M. E. Tukeman, Phys. Chem. Chem. Phys., 2016, 18, 32169–32177 RSC.
- H. D. Nagashima, S. Takeya, T. Uchida and R. Ohmura, Sci. Rep., 2016, 6, 19345–19354 CrossRef PubMed.
- S. Matsuishi, K. Hayashi, M. Hirano, I. Tanaka and H. Hosono, J. Phys. Chem. B, 2004, 108, 18557–18568 CrossRef CAS.
- J. Yu, J. Chen, C. Li, X. Wang, B. Zhang and H. Ding, J. Phys. Chem. B, 2004, 108, 2781–2783 CrossRef CAS.
- E. Carter, A. F. Carley and D. M. Murphy, J. Phys. Chem. C, 2007, 111, 10630–10638 CAS.
- C. R. Becer, R. Hoogenboom and U. S. Schubert, Angew. Chem., Int. Ed., 2009, 48, 4900–4908 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- E. Cadenas and K. J. Davies, Free Radical Biol. Med., 2000, 29, 222–230 CrossRef CAS PubMed.
- S. Leon, Nature, 2009, 461, 358–359 CrossRef PubMed.
- M. Diehn, R. W. Cho, N. A. Lobo, T. Kalisky, M. J. Dorie, A. N. Kulp, D. Qian, J. S. Lam, L. E. Ailles, M. Wong, B. Joshua, M. J. Kaplan, I. Wapnir, F. M. Dirbas, G. Somlo, C. Garberoglio, B. Paz, J. Shen, S. K. Lau, S. R. Quake, J. M. Brown, I. L. Weissman and M. F. Clarke, Nature, 2009, 458, 780–783 CrossRef CAS PubMed.
- A. T. Hoye, J. E. Davoren, P. Wipf, M. P. Fink and V. E. Kagan, Acc. Chem. Res., 2008, 41, 87–97 CrossRef CAS PubMed.
- W. Dröge, Physiol. Rev., 2002, 82, 47–95 CrossRef PubMed.
- D. P. Jones, Am. J. Physiol.: Cell Physiol., 2008, 295, C849–C868 CrossRef CAS PubMed.
- M. Valko, D. Leibfritz, J. Moncol, M. T. D. Cronin, M. Mazur and J. Telser, Int. J. Biochem. Cell Biol., 2007, 39, 44–48 CrossRef CAS PubMed.
- K. Ohgaki, K. Nakatsuji, K. Takeya, A. Tani and T. Sugahara, Phys. Chem. Chem. Phys., 2008, 10, 80–82 RSC.
- S.-H. Yeon, J. Seol, Y. Park, D.-Y. Koh, Y. S. Kang and H. Lee, J. Am. Chem. Soc., 2008, 130, 9208–9209 CrossRef CAS PubMed.
- M. Cha, K. Shin, M. Kwon, D.-Y. Koh, B. Sung and H. Lee, J. Am. Chem. Soc., 2010, 132, 3694–3696 CrossRef CAS PubMed.
- K. Yasuda, S. Takeya, M. Sakashita, H. Yamawaki and R. Ohmura, J. Phys. Chem. C, 2009, 113, 12598–12601 CAS.
- L. C. Jacobson, W. Hujo and V. Molinero, J. Phys. Chem. B, 2010, 114, 13796–13807 CrossRef CAS PubMed.
- A. Khan, J. Phys. Chem. A, 2001, 105, 7429–7434 CrossRef CAS.
- A. Khan, J. Chem. Phys., 2002, 116, 6628 CrossRef CAS.
- F. Lebsir, A. Bouyacoub, D. Bormann and A. Krallafa, J. Mol. Struct.: THEOCHEM, 2008, 864, 42–49 CrossRef CAS.
- K. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203 CrossRef CAS PubMed.
- P. Ghosh and P. Banerjee, Phys. Chem. Chem. Phys., 2016, 18, 22805–22815 RSC.
- Z. Jian, X. Yang, D. Chen and Y. Qian, RSC Adv., 2016, 6, 114560–114565 RSC.
- J. Vatamanu and P. G. Kusalik, J. Am. Chem. Soc., 2006, 128, 15588–15589 CrossRef CAS PubMed.
- S. Takeya, K. A. Udachin, I. L. Moudrakovski, R. Susilo and J. A. Ripmeester, J. Am. Chem. Soc., 2010, 132, 524–531 CrossRef CAS PubMed.
- J. Vatamanu and P. G. Kusalik, J. Phys. Chem. B, 2006, 110, 15896–15904 CrossRef CAS PubMed.
- D. A. G. Gualdrón and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 15554–15564 Search PubMed.
- N. I. Papadimitriou, I. N. Tsimpanogiannis, A. T. Papaioannou and A. K. Stubos, J. Phys. Chem. C, 2008, 112, 10294–10302 CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- J. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- F. Weigend, M. Haser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- TURBOMOLE V5-9-1, University of Karlsruhe, 2007 Search PubMed.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Oehm, M. Haeser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 CrossRef CAS.
- M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136 CrossRef CAS.
- P. K. Chattaraj, S. Bandaru and S. Mondal, J. Phys. Chem. A, 2011, 115, 187–193 CrossRef CAS PubMed.
- M. W. Wong and L. Radom, J. Phys. Chem., 1995, 99, 8582–8588 CrossRef CAS.
- R. Kaur and Vikas, RSC Adv., 2016, 6, 29080–29098 RSC.
- S. Alavi and J. A. Ripmeester, Chem. Phys. Lett., 2009, 479, 234–237 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- P. Sangwan and Vikas, J. Chem. Phys., 2016, 144, 044305 CrossRef PubMed.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- D. H. Zhang, M. A. Collins and S.-Y. Lee, Science, 2000, 290, 961–963 CrossRef CAS PubMed.
- M. Brouard, P. O'Keeffe and C. Vallance, J. Phys. Chem. A, 2002, 106, 3629–3641 CrossRef CAS.
- T. Uchimaru, A. K. Chandra, S. Tsuzuki, M. Sugie and A. Sekiya, J. Comput. Chem., 2003, 24, 1538–1548 CrossRef CAS PubMed.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef.
- P. F. Su and H. Li, J. Chem. Phys., 2009, 131, 014102–014115 CrossRef PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Bond lengths (Å) and binding energies of the optimized water cluster W6 computed at different levels; the coordination energies of water cages s1 and s2; energies for water approach by and H· or OH·; and LMOEDA energy decomposition analyses for H· and OH· radical attack at waters. See DOI: 10.1039/c6ra28804a |
| This journal is © The Royal Society of Chemistry 2017 |
