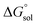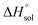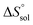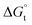DOI:
10.1039/C7RA00038C
(Paper)
RSC Adv., 2017,
7, 14776-14789
Solubility temperature and solvent dependence and preferential solvation of citrus flavonoid naringin in aqueous DMSO mixtures: an experimental and molecular dynamics simulation study
Received
2nd January 2017
, Accepted 27th February 2017
First published on 6th March 2017
Abstract
This study describes the thermodynamics of dissolution of flavonoid naringin in different aqueous solutions of dimethyl sulfoxide (DMSO) containing 0–100% (w/w) under atmospheric pressure and over a temperature range of 298.15 to 325.15 K. The temperature dependence of solubility of naringin was analyzed using the modified Apelblat equation model, ideal model, and the λH equation model. In a mean harmonic temperature, the dissolution thermodynamic parameters of naringin containing 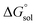 ,
, 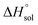 and
and 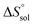 were also calculated. Furthermore, the effects of solvent composition on the solubility of this flavonoid were analyzed in terms of Hildebrand's solubility parameter (δH) and Kamlet, Abboud and Taft (KAT) solvatochromic parameters (α, β, and π*). Finally, the preferential solvation parameters of the flavonoid naringin by DMSO (δxDMSO,S) were determined from experimental solubility data using the inverse Kirkwood–Buff integrals (IKBIs). It was found that water preferentially solvates naringin in water-rich mixtures while DMSO forms local solvation shells in compositions from 50% (w/w) or xDMSO = 0.19 up to pure co-solvent. Moreover, the structure of solvation shells of naringin in the under study mixtures was obtained by molecular dynamics (MD) simulations. The computational results showed that in the compositions xDMSO > 0.20, the probability of presence of the DMSO molecules in vicinity of naringin is more than water molecules. These findings are compatible with the available IKBI data.
were also calculated. Furthermore, the effects of solvent composition on the solubility of this flavonoid were analyzed in terms of Hildebrand's solubility parameter (δH) and Kamlet, Abboud and Taft (KAT) solvatochromic parameters (α, β, and π*). Finally, the preferential solvation parameters of the flavonoid naringin by DMSO (δxDMSO,S) were determined from experimental solubility data using the inverse Kirkwood–Buff integrals (IKBIs). It was found that water preferentially solvates naringin in water-rich mixtures while DMSO forms local solvation shells in compositions from 50% (w/w) or xDMSO = 0.19 up to pure co-solvent. Moreover, the structure of solvation shells of naringin in the under study mixtures was obtained by molecular dynamics (MD) simulations. The computational results showed that in the compositions xDMSO > 0.20, the probability of presence of the DMSO molecules in vicinity of naringin is more than water molecules. These findings are compatible with the available IKBI data.
Introduction
Naringin (C27H32O14) with the chemical name 4′,5,7-trihydroxyflavanone-7-rhamnoglucoside, is a flavanone glycoside that is frequently found in many citrus fruits especially grapefruit and lemon, such that it is responsible for the fruit's bitter taste.1 It has been reported that naringin can show biological effects like antioxidant, anti-inflammatory, anti-cancer (breast cancer), anti-allergic, anti-diabetic, anti-angiogenesis and cholesterol-lowering activities.1–3 As a plant flavonoid, naringin, has attracted significant scientific and public interest in recent years due to its versatile health-promoting effects.4 However, due to very poor solubility of naringin in water at room temperature, its bioavailability is low and this hinders further studies on its pharmacological applications.2
The experimental solubility measurement of bioactive compounds in the solution as a function of solvent composition and temperature is valuable particularly for the pharmaceutical and industrial product design, and also to obtain complete information about physicochemical characteristics of pharmaceutical dissolutions.5,6 Furthermore, the solubility data of solutes in different solvents are necessary for determining the appropriate solvents for extraction, separation, production, and purification of organic compounds.1 There are various mathematical and empirical models to correlate and predict the solubility of drug compounds in different solvents and temperatures. These models can solve issues such as expensive cost and long time in the solubility determination process.1 Dependence of the solubility on the temperature allows thermodynamic analysis to give us information about the mechanisms involved in the dissolution process.7
In addition to solubility, preferential solvation phenomenon in which the solute is surrounded preferably by the component of the solvent mixture has not been studied in many pharmaceutical compounds so far. The phenomenon can help in understanding the molecular interactions involved in the dissolution process. Therefore, the present study first focuses on measuring the equilibrium solubility of antioxidant flavonoid naringin in aqueous co-solvent systems of DMSO (0–100% by w/w) and different temperatures (298.15 to 325.15 K) using an isothermal dissolution equilibrium method. It is noteworthy that the co-solvent DMSO is an important polar aprotic solvent with very low toxic and immense biological importance.6 It dissolves both polar and nonpolar compounds and is miscible in a wide range of organic solvents as well as water. In the following step, the effect of temperature on the solubility of naringin in the binary aqueous mixtures is analyzed to evaluate the thermodynamic quantities involved in the process of solubility. It is important to emphasize that the temperature range used in this work covers different room conditions as well as the normal human body temperature. We also determined the influence of co-solvent composition on the solubility of naringin by means of KAT equations. Finally, the inverse Kirkwood–Buff integrals (IKBI) approach is applied to evaluate the preferential solvation of naringin in the binary mixtures examined. On the other hand, the molecular dynamics (MD) simulations which are based on a range of complementary computational approaches provide a very powerful tool for investigating the solvation phenomenon, especially preferential solvation, directly using computed radial distribution function (RDF).8–10 We also characterized the structure of the solvation shell of the naringin molecule (preferential solvation) in the aqueous DMSO mixtures by calculating the RDFs. The results of preferential solvation are then compared with the data obtained from the inverse Kirkwood–Buff integrals (IKBI) approach.
Experimental section
Chemicals and apparatus
The flavonoid used as solute in the experiments, naringin, was purchased from Acros as analytical reagent (≥97.0% purity) and was not purified prior to use. The molecular structure of this flavonoid is presented in Scheme 1. The organic solvent DMSO was obtained from Merck, with pro analysis grade (≥99.0% purity). All solutions were freshly prepared using ultrapure water (with a specific resistance more than 18.2 MΩ cm) throughout. Absorbance measurements were conducted on a Perkin-Elmer (Lambda 25) UV-Vis spectrophotometer in conjunction with a LabTech LCB-R08 thermo-circulator, using quartz cells of 10 mm optical path.
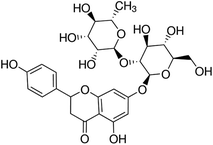 |
| | Scheme 1 Molecular structure of flavonoid naringin. | |
Measurement of naringin solubility
First, the saturated solutions of naringin in each mass percentage of the co-solvent DMSO (0–100%) were prepared in a 20 mL dual-wall glass flask by adding an excess amount of the flavonoid naringin to the flask containing a known volume of the pure or mixed solvents (5–10 mL). Then, the suspensions were constantly stirred at temperatures 298.15, 303.15, 310.15, 315.15, 320.15, 325.15 K under atmospheric pressure of 0.1 MPa using a Teflon-coated magnetic stirring bar running at 450 rpm for at least 4 h plus 2 h of settling in order to achieve the solid–liquid equilibrium. These times were chosen based on previous investigations.1,2 Between the outer and inner walls of the flask was filled by temperature controlled circulating water. However, the actual temperature measurement was made using a mercury thermometer with an uncertainty of ±0.1 K that was inserted in the solution. After equilibration, three samples were taken out carefully from the upper parts of the suspensions each with different volumes and were filtered and transferred to volumetric tubes. In the next step, the solvent was evaporated under reduced pressure and then the dried residue was dissolved with a known volume of the pure co-solvent. Finally, in order to determine the flavonoid concentration, absorbance spectrum of the solutions was recorded using a UV-Vis spectrophotometer in the wavelength range of 200 to 450 nm and with 0.1 nm intervals. All the solubility experiments were run at least in triplicates and the mean values were reported.
Before preparation of the saturated solutions, a calibration curve was constructed using standard solutions of naringin over an appropriate concentration range in the pure co-solvent DMSO to determine the molar absorbance coefficient (ε) of naringin (λmax = 326.6 nm). From the regression equation of the linear calibration plot, the value obtained for ε was 1.2726 × 104 L mol−1 cm−1. The value of molar absorbance coefficient was used for quantitation of naringin in different co-solvent mixtures analyzed.
Theoretical calculations
The Kirkwood–Buff approach
In a binary co-solvent mixture like water/DMSO system, the preferential solvation parameter of the solute (flavonoid naringin) by co-solvent (DMSO) can be defined according to the following equation:11| |
|
δxDMSO,S = xLDMSO,S − xDMSO,S
| (1) |
where xDMSO,S is the mole fraction of co-solvent DMSO in the bulk solution and xLDMSO,S is the local mole fraction of co-solvent in the environment near to the solute (solvation sphere). The δxDMSO,S parameter represents the excess or deficiency of organic co-solvent of the aqueous–organic mixture in the local region. Such that the solute is preferentially solvated by co-solvent, when δxDMSO,S > 0, while in case δxDMSO,S < 0, the solute is said to be preferentially solvated by water. Nevertheless, if xLDMSO,S ≈ 1, then complete solvation of the solute is performed by the co-solvent. The parameter δxDMSO,S in co-solvent systems can be obtained from the inverse Kirkwood–Buff integrals (IKBI) for each solvent component as follows:12,13| |
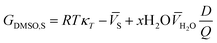 | (2) |
| |
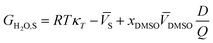 | (3) |
In these equations, κT is the isothermal compressibility of binary water/DMSO mixtures free of the solute (in GPa−1). The dependence of κT on composition of solvent mixture can be approximated from individual isothermal compressibilities of components as:14
| |
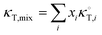 | (4) |
Here,
xi is the mole fraction of solvent
i in the mixture and
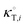
is the isothermal compressibility of the pure solvent
i with the values 0.524 and 0.457 GPa
−1, for DMSO and water, respectively.
13
In eqn (2) and (3), ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) DMSO and
DMSO and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) H2O are the partial molar volumes of the solvents in the binary mixture (in cm3 mol−1). Also,
H2O are the partial molar volumes of the solvents in the binary mixture (in cm3 mol−1). Also, ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) S is the partial molar volume of the solute in these mixtures with the value 349.72 cm3 mol−1 for naringin. The partial molar volumes of water and the co-solvent can be calculated based on the following expressions:
S is the partial molar volume of the solute in these mixtures with the value 349.72 cm3 mol−1 for naringin. The partial molar volumes of water and the co-solvent can be calculated based on the following expressions:
| |
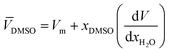 | (5) |
| |
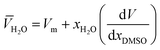 | (6) |
where
Vm is the molar volume of the mixtures and it is calculated as
Vm = (
xDMSO·
MDMSO +
xH2O·
MH2O)/
dmix. The values of
MDMSO and
MH2O are 78.13 and 18.02 g mol
−1, respectively. The density of the binary mixtures analyzed (
dmix) has been gathered from the literature.
15,16
In eqn (2) and (3), the parameter D is the first derivative of the standard molar Gibbs energies of transfer of the solute from pure water to binary water/DMSO mixtures 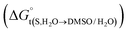 with respect to the co-solvent composition (in kJ mol−1):
with respect to the co-solvent composition (in kJ mol−1):
| |
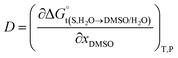 | (7) |
The standard molar Gibbs energy of transfer of the flavonoid naringin, 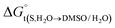 , is calculated from the naringin solubility data and then correlated to specific polynomials as:
, is calculated from the naringin solubility data and then correlated to specific polynomials as:
| |
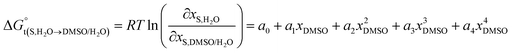 | (8) |
Thus, the D values are obtained from the first derivative of the above polynomial as follows:
| |
|
D = a1 + 2a2xDMSO + 3a3x2DMSO + 4a4x3DMSO
| (9) |
The parameter Q in eqn (2) and (3) involves the second derivative of the excess molar Gibbs energy of mixing of the two solvents 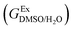 with respect to the water proportion in the mixtures (in kJ mol−1):14
with respect to the water proportion in the mixtures (in kJ mol−1):14
| |
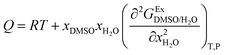 | (10) |
In order to calculate the Q values, first the excess molar Gibbs energies of mixing, 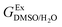 , should be evaluated at all the temperatures considered. In this way,
, should be evaluated at all the temperatures considered. In this way, 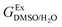 values (in kJ mol−1) are calculated at 298.15 K by means of eqn (11) as reported by Marcus.11 Then, the
values (in kJ mol−1) are calculated at 298.15 K by means of eqn (11) as reported by Marcus.11 Then, the 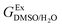 values at the other temperatures can be calculated by means of eqn (12):
values at the other temperatures can be calculated by means of eqn (12):
| |
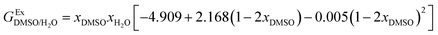 | (11) |
| |
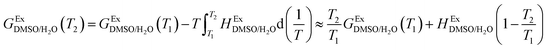 | (12) |
where
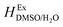
is the excess molar enthalpy of the co-solvent mixtures,
T1 is 298.15 K and
T2 is one of the other temperatures under study. At
T1 = 298.15 K,
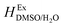
function is calculated according to the following equation:
11| |
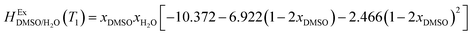 | (13) |
The preferential solvation parameter, δxDMSO,S, can be calculated from the Kirkwood–Buff integrals by means of the following expression which proposed initially by Ben-Naim:17
| |
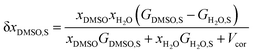 | (14) |
where
Vcor represents the correlation volume and can be obtained as the following empirical equation:
11| |
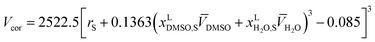 | (15) |
In this equation, rS is the radius of the solute (in nm) which is calculated as:
| |
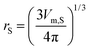 | (16) |
where
Vm,S is the molecular volume of the solute with the value 0.5816 nm
3 for naringin. It is calculated as
Vm,S = 10
21MS/
dSNAv in which
MS and
dS are the molar mass and the density of the solute, respectively and
NAv is the Avogadro number. Since the definitive correlation volume depends on the local mole fractions of the solvents (
eqn (15)), it requires iteration.
The molecular dynamics (MD) simulation
MD simulations were performed using GROMACS 4.5.4.18–20 GROMOS96 force field has been used for DMSO,21 whereas water is modelled by SPC model.22 Force field parameters and their geometries were generated using PRODRG2 server (http://davapc1.bioch.dundee.ac.uk/cgi-bin/prodrg_beta).
The energy of the system was minimized using 100 ps of the steepest descent method.23 Then 200 ps position restraint simulations were performed to relieve close contacts before the actual simulations. Finally, 5 ns MD simulations were accomplished at the isothermal–isobaric (NPT) canonical ensemble.24 The temperature was kept constant at 298.15 K by modified V-rescale thermostat with the coupling constants of 0.1 and pressure was controlled at 0.1 MPa by Parrinello–Rahman barosta25 with the coupling constants of 2.0. The system was under the periodic boundary conditions by applying the leap-frog algorithm26 with a time step of 2 fs and bond lengths constrained using the LINCS algorithm.27,28 Electrostatic interactions were determined using the particle mesh Ewald approach,29 with a 1.0 nm cut off for electrostatics and a 1.0 nm cut off for van der Waals interactions.
Results and discussion
Solubility data of naringin
The solubility of flavonoid naringin in different aqueous mixtures of DMSO was calculated in terms of molar concentrations of the solute (molar solubility, Sm) by using the absorbance data obtained for the saturated solutions as well as the molar absorbance coefficient of naringin. The solubility was also obtained in terms of mole fraction of the solute (mole fraction solubility) using molar solubility data as follows:| |
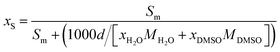 | (17) |
where d is the density of the solvent mixtures free of the flavonoid which was taken from the literature,15,16 xH2O and xDMSO are the mole fraction of water and the co-solvent DMSO, MH2O and MDMSO, respectively, represent the molar mass of water and the co-solvent. The experimental solubility values for naringin in various aqueous DMSO mixtures at temperature ranges of 298.15 to 325.15 K are given in Table 1. The obtained results demonstrate that the equilibrium solubility of naringin increases with the increasing the proportion of DMSO in the binary mixture and by increasing the temperature from 298.15 to 325.15 K. On the other hand, due to very low solubility of naringin in water, it was not possible to measure it with simplicity and enough precision. Unfortunately, no data for the solubility of this flavonoid in aqueous mixtures of DMSO have so far been reported in the literature for comparison.
Table 1 Experimental solubilities of naringin in molarity (Sm) and mole fraction (xS) at different temperatures under atmospheric pressure p = 0.1 MPa in aqueous DMSO mixturesa
| %WDMSOb |
xDMSOb |
Sm (mol dm−3) |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| Standard uncertainties u are u(T) = 0.1 K, u(p) = 0.003 MPa and u(W) = 0.0004; average relative standard uncertainty in solubility, ur(xS) and ur(Sm) are 3.6%. WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively. |
| 0 |
0.0000 |
0.1069 × 10−5 |
0.1540 × 10−5 |
0.2251 × 10−5 |
0.2958 × 10−5 |
0.3672 × 10−5 |
0.4479 × 10−5 |
| 10 |
0.0250 |
0.1581 × 10−5 |
0.2083 × 10−5 |
0.4380 × 10−5 |
0.5226 × 10−5 |
0.6041 × 10−5 |
0.8011 × 10−5 |
| 20 |
0.0545 |
0.2970 × 10−5 |
0.3724 × 10−5 |
0.6127 × 10−5 |
0.8791 × 10−5 |
0.9737 × 10−5 |
0.1344 × 10−4 |
| 30 |
0.0874 |
0.4152 × 10−5 |
0.5073 × 10−5 |
0.8369 × 10−5 |
0.1470 × 10−4 |
0.1433 × 10−4 |
0.2074 × 10−4 |
| 40 |
0.1470 |
0.6278 × 10−5 |
0.7851 × 10−5 |
0.2660 × 10−4 |
0.3789 × 10−4 |
0.4714 × 10−4 |
0.5601 × 10−4 |
| 50 |
0.1890 |
0.9661 × 10−5 |
0.1728 × 10−4 |
0.2921 × 10−4 |
0.4321 × 10−4 |
0.6651 × 10−4 |
0.8660 × 10−4 |
| 60 |
0.2560 |
0.1413 × 10−4 |
0.2414 × 10−4 |
0.5703 × 10−4 |
0.6870 × 10−4 |
0.8348 × 10−4 |
0.1272 × 10−3 |
| 70 |
0.3520 |
0.3940 × 10−4 |
0.5131 × 10−4 |
0.9623 × 10−4 |
0.1691 × 10−3 |
0.2171 × 10−3 |
0.2940 × 10−3 |
| 80 |
0.4880 |
0.8389 × 10−4 |
0.1260 × 10−3 |
0.3647 × 10−3 |
0.4823 × 10−3 |
0.5953 × 10−3 |
0.7131 × 10−3 |
| 90 |
0.6900 |
0.4957 × 10−3 |
0.5912 × 10−3 |
0.1241 × 10−2 |
0.1562 × 10−2 |
0.1850 × 10−2 |
0.2488 × 10−2 |
| 95 |
0.8398 |
0.7760 × 10−3 |
0.1191 × 10−2 |
0.2410 × 10−2 |
0.3181 × 10−2 |
0.3894 × 10−2 |
0.4321 × 10−2 |
| 100 |
1.0000 |
0.1252 × 10−2 |
0.2032 × 10−2 |
0.3779 × 10−2 |
0.4650 × 10−2 |
0.5315 × 10−2 |
0.5994 × 10−2 |
| %WDMSOb |
xDMSOb |
xS |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| 0 |
0.0000 |
0.1932 × 10−7 |
0.2786 × 10−7 |
0.4077 × 10−7 |
0.5372 × 10−7 |
0.6941 × 10−7 |
0.8599 × 10−7 |
| 10 |
0.0250 |
0.3050 × 10−7 |
0.4021 × 10−7 |
0.8479 × 10−7 |
0.1014 × 10−6 |
0.1230 × 10−6 |
0.1645 × 10−6 |
| 20 |
0.0545 |
0.6169 × 10−7 |
0.7737 × 10−7 |
0.1276 × 10−6 |
0.1831 × 10−6 |
0.2106 × 10−6 |
0.2941 × 10−6 |
| 30 |
0.0874 |
0.9296 × 10−7 |
0.1137 × 10−6 |
0.1879 × 10−6 |
0.3301 × 10−6 |
0.3220 × 10−6 |
0.4764 × 10−6 |
| 40 |
0.1470 |
0.1593 × 10−6 |
0.1993 × 10−6 |
0.6758 × 10−6 |
0.9631 × 10−6 |
0.1219 × 10−5 |
0.1459 × 10−5 |
| 50 |
0.1890 |
0.2653 × 10−6 |
0.4757 × 10−6 |
0.8034 × 10−6 |
0.1189 × 10−5 |
0.1862 × 10−5 |
0.2434 × 10−5 |
| 60 |
0.2560 |
0.4352 × 10−6 |
0.7448 × 10−6 |
0.1763 × 10−5 |
0.2126 × 10−5 |
0.2633 × 10−5 |
0.4023 × 10−5 |
| 70 |
0.3520 |
0.1412 × 10−5 |
0.1841 × 10−5 |
0.3457 × 10−5 |
0.6079 × 10−5 |
0.7964 × 10−5 |
0.1086 × 10−4 |
| 80 |
0.4880 |
0.3615 × 10−5 |
0.5440 × 10−5 |
0.1579 × 10−4 |
0.2088 × 10−4 |
0.2625 × 10−4 |
0.3178 × 10−4 |
| 90 |
0.6900 |
0.2685 × 10−4 |
0.3207 × 10−4 |
0.6746 × 10−4 |
0.8510 × 10−4 |
0.1021 × 10−3 |
0.1391 × 10−3 |
| 95 |
0.8398 |
0.4840 × 10−4 |
0.7447 × 10−4 |
0.1513 × 10−3 |
0.2003 × 10−3 |
0.2469 × 10−3 |
0.2772 × 10−3 |
| 100 |
1.0000 |
0.8917 × 10−4 |
0.1455 × 10−3 |
0.2722 × 10−3 |
0.3363 × 10−3 |
0.3842 × 10−3 |
0.4375 × 10−3 |
Apparent thermodynamic functions of dissolution process
It is understood that thermodynamic properties of the compound dissolved in co-solvent mixtures has important practical significance for analyzing the dissolution process. In this work, for calculating apparent thermodynamic functions of naringin solution, all of them were estimated at mean harmonic temperature (Thm), which itself is defined by means of eqn (18)7,30| |
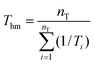 | (18) |
where nT is the number of temperatures analyzed. According to this equation, Thm is equal with 311.70 K in the present work. The molar standard enthalpy change of solution 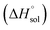 is calculated at Thm by the following equation:2
is calculated at Thm by the following equation:2| |
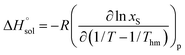 | (19) |
where R is the universal gas constant (8.3145 J K−1 mol−1), T is absolute temperature (K) and xS is the mole fraction solubility of solute. As examples, Fig. 1 shows the linear behavior of some co-solvent mixtures with compositions WDMSO = 0, 20, 50, 70, 90 and 100%. In all cases, the correlation coefficient (r2) of the linear regressions is more than 0.99.
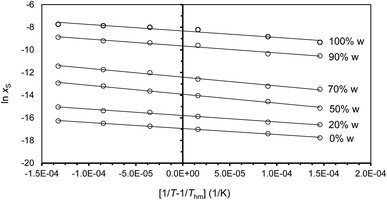 |
| | Fig. 1 van't Hoff plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS versus (1/T − 1/Thm) for naringin in water/DMSO co-solvent mixtures. Lines correspond to the best linear regression analyses. xS versus (1/T − 1/Thm) for naringin in water/DMSO co-solvent mixtures. Lines correspond to the best linear regression analyses. | |
The molar standard Gibbs energy change for the solution process, 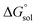 , can be calculated at Thm from the following thermodynamic relationship:6,7
, can be calculated at Thm from the following thermodynamic relationship:6,7
| |
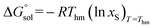 | (20) |
in which, (ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS
xS)
T=Thm is value of the intercept of the plot of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS versus
xS versus (1/
T − 1/
Thm). Finally, the standard molar dissolution entropic change
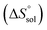
is obtained at
Thm as follows:
| |
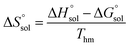 | (21) |
Table 2 represents values of the standard molar dissolution functions for naringin in the aqueous co-solvent mixtures containing 0–100% (w/w) of DMSO. The standard Gibbs energy of naringin dissolution is positive in all cases, just as also are the dissolution enthalpy and entropy. Therefore, it follows that the dissolution process of this flavonoid in water/DMSO mixed solvents is an endothermic and entropy-driven course over the temperature range investigated. According to Table 2, the addition of DMSO to water first increases the 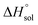 and
and 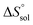 values (up to 40% by w/w DMSO) and then decreases them to a minimum in pure co-solvent DMSO. This behavior may be related to the breaking of the ordered structure of water (hydrogen bonds) around the apolar moieties of naringin, which increases first both the enthalpy and the entropy of the system;31 whereas by raising the DMSO proportion, due to formation of ordered structure of the co-solvent around naringin after it’s solvated by DMSO, the enthalpy and entropy of the system continuously decrease.
values (up to 40% by w/w DMSO) and then decreases them to a minimum in pure co-solvent DMSO. This behavior may be related to the breaking of the ordered structure of water (hydrogen bonds) around the apolar moieties of naringin, which increases first both the enthalpy and the entropy of the system;31 whereas by raising the DMSO proportion, due to formation of ordered structure of the co-solvent around naringin after it’s solvated by DMSO, the enthalpy and entropy of the system continuously decrease.
Table 2 Apparent standard thermodynamic functions of dissolution of naringin in water/DMSO mixed systems at Thm = 311.70 K and local atmospheric pressure p = 0.1 MPaa
Temperature and solvent effects
Fig. 2 graphically represents the solubility behavior of naringin in different temperatures and solvent compositions under study. It is observed that the solubility of naringin increases with increasing temperature and mass fraction of DMSO in the co-solvent mixtures, so that the maximum solubility of naringin is observed in pure DMSO and the highest temperature examined.
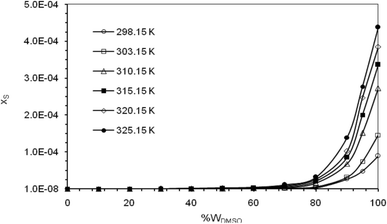 |
| | Fig. 2 Plots of mole fraction solubility (xS) of naringin versus mass percentage in water/DMSO mixed solvents and several temperatures under local atmospheric pressure of 0.1 MPa. | |
The temperature dependence of equilibrium naringin solubility in water/DMSO mixtures can be represented by three solution models: (1) the modified Apelblat equation, (2) the simplified universal equation (ideal model), and (3) the λH equation. The first model (modified Apelblat equation) is given as the following expression:5,32
| |
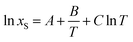 | (22) |
where
xS is the mole fraction solubility of naringin,
T is the absolute temperature (K), and
A,
B, and
C are the parameters whose values were determined by nonlinear multivariate regression analysis of experimental solubilities reported in
Table 1.
Other model that can represent the temperature dependence of naringin solubility is the simplified universal equation (ideal model):1
| |
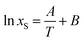 | (23) |
where
xS denotes the mole fraction solubility of solute,
T is the absolute temperature (K), and
A and
B are the parameters whose values can be obtained by fitting.
Finally, the λH equation which proposed firstly by Buchowski et al.33 is also used as an optional model for correlation of the solubility of naringin with temperature. The Buchowski λH equation is included only two adjustable parameters; λ and H, and is expressed as:
| |
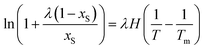 | (24) |
Here
xS is also the mole fraction solubility of solute.
T stands for the absolute temperature and
Tm represents the normal melting temperature, for naringin
Tm = 439.15 K.
34 The quantities
λ and
H are the model parameters whose values can also be obtained by the fitting.
The deviations between the experimental solubility (xexpS) and the calculated solubility by above models (xcalS) were determined in terms of root-mean-square deviations (RMSD). RMSD was calculated using eqn (25):
| |
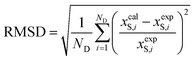 | (25) |
where
ND is the number of experimental data points. The values of the parameters
A,
B, and
C of
eqn (22); the parameters
A and
B of
eqn (23); and the parameters
λ and
H of
eqn (24) are listed in
Table 3 along with RMSD values. Considering the RMSD values, the three models are a good fit for the naringin data. However, the data exhibit that the modified Apelblat model is more suitable for describing the dependence of naringin solubility on temperature (RMSD = 0.072–1.032) than the ideal model (RMSD = 0.154–1.671) and the
λH equation model (RMSD = 0.537–2.642).
Table 3 Parameters of modified Apelblat, ideal and λH equation model for the solute naringin in aqueous co-solvents mixtures of DMSO
| Parameters |
%WDMSOa |
| 0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
95 |
100 |
| WDMSO is the mass fraction of DMSO in the binary water/DMSO mixtures. |
| Modified Apelblat model |
| A |
419.16 |
1152.02 |
138.28 |
318.93 |
2659.51 |
626.62 |
1787.06 |
212.88 |
2881.40 |
738.10 |
2264.24 |
2474.98 |
| B |
−24670.32 |
−59158.62 |
−11961.45 |
−20583.39 |
−130829.64 |
−36305.48 |
−89702.09 |
−16970.16 |
−140493.56 |
−39719.67 |
−110452.07 |
−119491.59 |
| C |
−62.16 |
−170.41 |
−20.15 |
−46.71 |
−392.54 |
−91.26 |
−263.42 |
−29.75 |
−425.23 |
−108.02 |
−334.13 |
−365.69 |
| RMSD (%) |
0.072 |
0.452 |
0.317 |
0.706 |
1.032 |
0.289 |
0.677 |
0.596 |
0.856 |
0.838 |
0.419 |
0.356 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Ideal model |
| A |
−5319.49 |
−6101.96 |
−5688.71 |
−6040.11 |
−8575.78 |
−7881.21 |
−7651.89 |
−7704.22 |
−8017.37 |
−6071.84 |
−6355.47 |
−5567.50 |
| B |
0.12 |
3.20 |
2.45 |
4.03 |
13.15 |
11.37 |
11.16 |
12.31 |
14.50 |
9.83 |
11.52 |
9.54 |
| RMSD (%) |
0.154 |
0.596 |
0.320 |
0.715 |
1.451 |
0.378 |
0.999 |
0.603 |
1.652 |
0.937 |
1.463 |
1.671 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| λH equation model |
| λ |
0.00000598 |
0.00002431 |
0.00002758 |
0.00007201 |
0.00265608 |
0.00138638 |
0.00223581 |
0.00561940 |
0.03449658 |
0.01982048 |
0.06522654 |
0.05785392 |
| H |
885654272.14 |
254336740.70 |
206671344.44 |
86767634.76 |
3411354.73 |
5687596.41 |
3502156.07 |
1381886.19 |
244915.18 |
310968.71 |
101254.43 |
101776.83 |
| RMSD (%) |
0.537 |
1.724 |
0.967 |
1.985 |
2.569 |
0.717 |
1.869 |
1.042 |
2.455 |
1.581 |
2.187 |
2.642 |
At a constant temperature, the solubility process of a solute in a solvent or a solvent mixture depends on the physicochemical properties of solvent as well as the various interaction types between the solute and the solvent system. In order to study the role played by different types of molecular interaction on the solubility, a multiple linear regression analysis (MLRA) involving various solvent parameters was used.7 The most ambitious and also most successful quantitative treatment of solvent effects has been introduced by Kamlet, Abboud, and Taft (KAT equation):35,36
| |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = A0 + aα + bβ + pπ* + hδ2H xS = A0 + aα + bβ + pπ* + hδ2H
| (26) |
where
A0 represents the regression value of log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS
xS in a hypothetical solvent with
α =
β =
π* = 0, the
δ2H represents Hildebrand's solubility parameter squared of solvent and corresponds to the energy associated with the intermolecular solvent–solvent interactions. The
π* parameter is the index of the solvent dipolarity/polarizability, which is a measure of the ability of a solvent to stabilize a charge or a dipole by its own dielectric effects. The
α parameter represents the solvent hydrogen-bond donor (HBD) acidity, in other words it describes the ability of a solvent to donate a proton in a solvent to a solute hydrogen-bond. The
β quantity is a measure of solvent hydrogen-bond acceptor (HBA) basicity, and describes the ability of a solvent to accept a proton from a solute molecule.
37 The regression coefficients
a,
b,
p and
h in
eqn (26) are measures of the relative susceptibilities of the solubility to the indicated solvent parameters.
Table 4 shows the values of KAT solvatochromic parameters as well as Hildebrand's solubility parameter in different compositions of the water/DMSO co-solvent mixture. These values were compiled from the plots of each property versus the mole fraction of the organic solvent of the values that have been previously reported in the literature.38,39
Table 4 The KAT solvatochromic parameters and the Hildebrand's solubility parameters (δH) of aqueous DMSO mixturesa
| %WDMSOb |
α |
β |
π* |
δH (MPa1/2) |
| The KAT solvatochromic parameters include α: HBD ability, β: HBA ability and π*: polarity/polarizability. WDMSO is the mass fraction of DMSO in the binary water/DMSO mixtures. |
| 0 |
1.170 |
0.4700 |
1.090 |
47.967 |
| 10 |
1.052 |
0.4804 |
1.102 |
47.373 |
| 20 |
0.9572 |
0.5128 |
1.112 |
46.657 |
| 30 |
0.8614 |
0.5436 |
1.118 |
45.880 |
| 40 |
0.7123 |
0.5870 |
1.122 |
44.489 |
| 50 |
0.6245 |
0.6099 |
1.120 |
43.528 |
| 60 |
0.5106 |
0.6364 |
1.110 |
41.994 |
| 70 |
0.3947 |
0.6602 |
1.087 |
39.846 |
| 80 |
0.2992 |
0.6824 |
1.051 |
36.901 |
| 90 |
0.2241 |
0.7226 |
1.012 |
32.687 |
| 95 |
0.1487 |
0.7636 |
0.9983 |
29.721 |
| 100 |
0.0000 |
0.8010 |
0.9800 |
26.591 |
In order to explain the solubility values obtained through the KAT solvent parameters, the solubilities (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS) were correlated with solvent properties by means of single-, dual- and multi-parameter linear regression analysis by a suitable computer program in Excel environment (LINEST). A stepwise procedure and least-squares analysis were applied to select the significant solvent properties to be influenced in the model and to obtain the final expression for the solubilities. The LINEST program used can determine the A0, a, b, p, h values of eqn (26) and some statistical parameters including the r2 coefficient, the standard deviation of each parameter, the overall standard error (ose) of log
xS) were correlated with solvent properties by means of single-, dual- and multi-parameter linear regression analysis by a suitable computer program in Excel environment (LINEST). A stepwise procedure and least-squares analysis were applied to select the significant solvent properties to be influenced in the model and to obtain the final expression for the solubilities. The LINEST program used can determine the A0, a, b, p, h values of eqn (26) and some statistical parameters including the r2 coefficient, the standard deviation of each parameter, the overall standard error (ose) of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS and the residual sum of the squares of errors (rss). The linear regression analysis of solubility of naringin with the dual-parameter equations (α and δH) indicates significant improvement with regard to the single- and multi-parameter models and yield the lowest standard deviation and possess very good coefficients of determination in all cases. The expressions of the KAT equation at the temperatures analyzed are given in Table 5 based on two solvatochromic parameters (α and δH). In these equations, the negative sign of α and δH indicates a decrease in the hydrogen-bond donor acidity and the Hildebrand's solubility parameter of the solvent increases the solubility of the solute. Consequently, the solubility increases when these parameters decrease. The magnitude of the coefficients a and h in Table 5 are in the order of h > a. This suggests that the Hildebrand's solubility parameter of the solvent is the most important for solubility, and the hydrogen-bond donor acidity parameter plays a relatively small role in changing the solubility of naringin in various aqueous DMSO solutions.
xS and the residual sum of the squares of errors (rss). The linear regression analysis of solubility of naringin with the dual-parameter equations (α and δH) indicates significant improvement with regard to the single- and multi-parameter models and yield the lowest standard deviation and possess very good coefficients of determination in all cases. The expressions of the KAT equation at the temperatures analyzed are given in Table 5 based on two solvatochromic parameters (α and δH). In these equations, the negative sign of α and δH indicates a decrease in the hydrogen-bond donor acidity and the Hildebrand's solubility parameter of the solvent increases the solubility of the solute. Consequently, the solubility increases when these parameters decrease. The magnitude of the coefficients a and h in Table 5 are in the order of h > a. This suggests that the Hildebrand's solubility parameter of the solvent is the most important for solubility, and the hydrogen-bond donor acidity parameter plays a relatively small role in changing the solubility of naringin in various aqueous DMSO solutions.
Table 5 Expressions of KAT equations (dual-parameters) for the solubility of naringin in different aqueous DMSO mixtures at various temperatures
| T (K) |
KAT equationa |
r2b |
F-Value |
rssc |
osed |
| Standard error associated to values is given in parentheses. Coefficient of determination. Residual sum of the squares errors. Overall standard error. |
| 298.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.45(±0.18) − 0.32(±0.29)α − 2.08(±0.20)δ2H xS = −2.45(±0.18) − 0.32(±0.29)α − 2.08(±0.20)δ2H |
0.995 |
980.08 |
8.09 × 10−2 |
9.48 × 10−2 |
| 303.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.32(±0.14) − 0.45(±0.22)α − 2.02(±0.15)δ2H xS = −2.32(±0.14) − 0.45(±0.22)α − 2.02(±0.15)δ2H |
0.997 |
1796.1 |
4.54 × 10−2 |
7.10 × 10−2 |
| 310.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.20(±0.18) − 0.93(±0.29)α − 1.74(±0.20)δ2H xS = −2.20(±0.18) − 0.93(±0.29)α − 1.74(±0.20)δ2H |
0.996 |
1065.6 |
7.94 × 10−2 |
9.39 × 10−2 |
| 315.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.23(±0.17) − 1.16(±0.28)α − 1.56(±0.19)δ2H xS = −2.23(±0.17) − 1.16(±0.28)α − 1.56(±0.19)δ2H |
0.996 |
1136.2 |
7.29 × 10−2 |
9.00 × 10−2 |
| 320.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.23(±0.19) − 1.32(±0.31)α − 1.46(±0.21)δ2H xS = −2.23(±0.19) − 1.32(±0.31)α − 1.46(±0.21)δ2H |
0.995 |
923.11 |
8.97 × 10−2 |
9.98 × 10−2 |
| 325.15 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.26(±0.17) − 1.48(±0.28)α − 1.31(±0.19)δ2H xS = −2.26(±0.17) − 1.48(±0.28)α − 1.31(±0.19)δ2H |
0.996 |
1088.2 |
7.38 × 10−2 |
9.05 × 10−2 |
Preferential solvation of naringin
The Kirkwood–Buff approach. By using the experimental data of mole fraction solubility of naringin (Table 1), the numerical values of 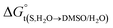 for naringin are obtained (eqn (8)) at different temperatures and are given in Table 6. The variations of
for naringin are obtained (eqn (8)) at different temperatures and are given in Table 6. The variations of 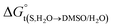 with organic co-solvent composition (xDMSO) at different temperatures corresponding to a regular polynomial are shown in Fig. 3. The D values were calculated from the first derivative of the polynomial models obtained.
with organic co-solvent composition (xDMSO) at different temperatures corresponding to a regular polynomial are shown in Fig. 3. The D values were calculated from the first derivative of the polynomial models obtained.
Table 6 Values of Gibbs energy of transfer 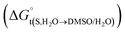 for naringin in different aqueous mixtures of DMSO and various temperatures
for naringin in different aqueous mixtures of DMSO and various temperatures
| %WDMSOa |
xDMSOa |
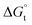
(kJ mol−1) |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively. |
| 0 |
0.0000 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
| 10 |
0.0250 |
−1.13 |
−0.93 |
−1.89 |
−1.66 |
−1.52 |
−1.75 |
| 20 |
0.0545 |
−2.88 |
−2.57 |
−2.94 |
−3.21 |
−2.95 |
−3.32 |
| 30 |
0.0874 |
−3.89 |
−3.55 |
−3.94 |
−4.76 |
−4.08 |
−4.63 |
| 40 |
0.1470 |
−5.23 |
−4.96 |
−7.24 |
−7.56 |
−7.63 |
−7.65 |
| 50 |
0.1890 |
−6.49 |
−7.15 |
−7.69 |
−8.11 |
−8.75 |
−9.04 |
| 60 |
0.2560 |
−7.72 |
−8.28 |
−9.71 |
−9.64 |
−9.68 |
−10.4 |
| 70 |
0.3520 |
−10.6 |
−10.6 |
−11.4 |
−12.4 |
−12.6 |
−13.1 |
| 80 |
0.4880 |
−13.0 |
−13.3 |
−15.4 |
−15.6 |
−15.8 |
−16.0 |
| 90 |
0.6900 |
−17.9 |
−17.8 |
−19.1 |
−19.3 |
−19.4 |
−20.0 |
| 95 |
0.8398 |
−19.4 |
−19.9 |
−21.2 |
−21.5 |
−21.8 |
−21.8 |
| 100 |
1.0000 |
−20.9 |
−21.6 |
−22.7 |
−22.9 |
−22.9 |
−23.1 |
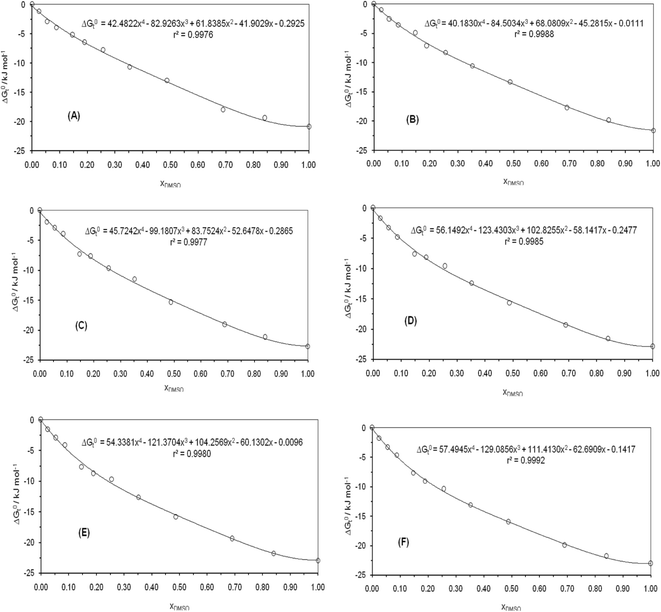 |
| | Fig. 3 Variation of standard Gibbs energy of transfer of naringin from pure water to binary water/DMSO mixtures as function of xDMSO at (A) 298.15 K, (B) 303.15 K, (C) 310.15 K, (D) 315.15 K, (E) 320.15 K, (F) 325.15 K. | |
Table 7 presents the GH2O,S and GDMSO,S values obtained for naringin in all co-solvent compositions. The negative values of these parameters (Kirkwood–Buff integrals) indicate that this flavonoid exhibits affinity for both solvents present in the mixture.
Table 7 GDMSO,S and GH2O,S values for naringin in water/DMSO co-solvent mixtures at several temperatures
| %WDMSOa |
xDMSOa |
GDMSO,S (cm3 mol−1) |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively. |
| 0 |
0.0000 |
−653.9 |
−673.5 |
−718.5 |
−739.9 |
−775.8 |
−793.7 |
| 10 |
0.0250 |
−631.0 |
−648.3 |
−688.2 |
−706.6 |
−742.7 |
−755.9 |
| 20 |
0.0545 |
−602.3 |
−616.7 |
−650.4 |
−665.2 |
−692.2 |
−705.3 |
| 30 |
0.0874 |
−569.8 |
−581.1 |
−608.1 |
−619.1 |
−629.1 |
−641.4 |
| 40 |
0.1470 |
−515.4 |
−522.0 |
−538.5 |
−544.0 |
−553.6 |
−556.8 |
| 50 |
0.1890 |
−483.7 |
−487.6 |
−498.6 |
−501.4 |
−507.6 |
−508.4 |
| 60 |
0.2560 |
−445.4 |
−446.5 |
−451.6 |
−451.9 |
−455.6 |
−455.0 |
| 70 |
0.3520 |
−411.5 |
−410.7 |
−411.9 |
−410.8 |
−412.8 |
−411.9 |
| 80 |
0.4880 |
−386.6 |
−385.4 |
−385.1 |
−384.0 |
−385.4 |
−384.9 |
| 90 |
0.6900 |
−366.9 |
−366.9 |
−366.5 |
−366.1 |
−367.1 |
−367.0 |
| 95 |
0.8398 |
−355.8 |
−356.7 |
−356.2 |
−356.1 |
−356.4 |
−356.2 |
| 100 |
1.0000 |
−348.4 |
−348.4 |
−348.4 |
−348.4 |
−348.3 |
−348.3 |
| %WDMSOa |
xDMSOa |
GH2O,S (cm3 mol−1) |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| 0 |
0.0000 |
−348.6 |
−348.6 |
−348.5 |
−348.5 |
−348.5 |
−348.5 |
| 10 |
0.0250 |
−377.2 |
−379.1 |
−383.2 |
−385.2 |
−387.1 |
−388.4 |
| 20 |
0.0545 |
−406.7 |
−410.2 |
−418.1 |
−421.8 |
−425.1 |
−427.7 |
| 30 |
0.0874 |
−433.2 |
−437.9 |
−448.6 |
−453.3 |
−456.2 |
−459.7 |
| 40 |
0.1470 |
−464.5 |
−469.5 |
−481.7 |
−486.3 |
−489.2 |
−491.8 |
| 50 |
0.1890 |
−476.2 |
−480.5 |
−491.7 |
−495.2 |
−497.0 |
−498.7 |
| 60 |
0.2560 |
−484.5 |
−486.8 |
−495.0 |
−496.3 |
−496.4 |
−496.6 |
| 70 |
0.3520 |
−488.9 |
−487.9 |
−491.6 |
−490.1 |
−488.7 |
−487.4 |
| 80 |
0.4880 |
−497.4 |
−493.7 |
−493.4 |
−490.2 |
−489.0 |
−487.2 |
| 90 |
0.6900 |
−514.4 |
−515.9 |
−513.1 |
−511.0 |
−512.8 |
−511.6 |
| 95 |
0.8398 |
−501.8 |
−523.0 |
−513.9 |
−513.4 |
−513.2 |
−508.6 |
| 100 |
1.0000 |
−264.7 |
−401.3 |
−343.1 |
−337.9 |
−303.7 |
−270.5 |
We done three iterations by using eqn (1), (14) and (15) to obtain an almost non-variant value of the correlation volume (Vcor) just like those that are reported in Table 8.
Table 8 Correlation volume (Vcor) and δxDMSO,S values of naringin in binary water/DMSO mixtures
| %WDMSOa |
xDMSOa |
Vcor (cm3 mol−1) |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively. |
| 0 |
0.0000 |
1245 |
1246 |
1247 |
1247 |
1271 |
1280 |
| 10 |
0.0250 |
1272 |
1272 |
1271 |
1271 |
1300 |
1304 |
| 20 |
0.0545 |
1309 |
1309 |
1307 |
1306 |
1328 |
1336 |
| 30 |
0.0874 |
1356 |
1356 |
1354 |
1353 |
1354 |
1367 |
| 40 |
0.1470 |
1449 |
1449 |
1449 |
1448 |
1460 |
1465 |
| 50 |
0.1890 |
1514 |
1515 |
1516 |
1516 |
1528 |
1531 |
| 60 |
0.2560 |
1614 |
1616 |
1617 |
1618 |
1632 |
1636 |
| 70 |
0.3520 |
1749 |
1750 |
1752 |
1753 |
1769 |
1774 |
| 80 |
0.4880 |
1927 |
1928 |
1930 |
1931 |
1948 |
1959 |
| 90 |
0.6900 |
2171 |
2174 |
2177 |
2180 |
2194 |
2208 |
| 95 |
0.8398 |
2336 |
2342 |
2345 |
2349 |
2360 |
2373 |
| 100 |
1.0000 |
2507 |
2514 |
2521 |
2527 |
2527 |
2541 |
| %WDMSOa |
xDMSOa |
δxDMSO,S × 102 |
| 298.15 K |
303.15 K |
310.15 K |
315.15 K |
320.15 K |
325.15 K |
| 0 |
0.0000 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
| 10 |
0.0250 |
−0.70 |
−0.74 |
−0.84 |
−0.89 |
−0.96 |
−0.99 |
| 20 |
0.0545 |
−1.13 |
−1.20 |
−1.37 |
−1.44 |
−1.55 |
−1.60 |
| 30 |
0.0874 |
−1.20 |
−1.26 |
−1.43 |
−1.49 |
−1.56 |
−1.63 |
| 40 |
0.1470 |
−0.65 |
−0.68 |
−0.74 |
−0.76 |
−0.84 |
−0.85 |
| 50 |
0.1890 |
−0.11 |
−0.11 |
−0.10 |
−0.09 |
−0.16 |
−0.14 |
| 60 |
0.2560 |
0.65 |
0.67 |
0.73 |
0.75 |
0.68 |
0.69 |
| 70 |
0.3520 |
1.37 |
1.37 |
1.41 |
1.40 |
1.32 |
1.31 |
| 80 |
0.4880 |
1.87 |
1.82 |
1.82 |
1.78 |
1.71 |
1.68 |
| 90 |
0.6900 |
1.79 |
1.81 |
1.78 |
1.75 |
1.75 |
1.72 |
| 95 |
0.8398 |
1.00 |
1.14 |
1.08 |
1.07 |
1.07 |
1.03 |
| 100 |
1.0000 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
The δxDMSO,S values for naringin in the co-solvent systems and various temperatures under consideration are given in Table 8. Furthermore, Fig. 4 shows the variation of the values of δxDMSO,S for naringin versus different compositions of the co-solvent in binary mixture. As has been seen in Fig. 4, addition of DMSO to aqueous solution of naringin causes to being negative the δxDMSO,S values from the pure water up to the mixture with composition xDMSO = 0.19 reaching minimum values in the mixture with 0.09 in mole fraction of DMSO. The negative values of δxDMSO,S indicate that water is preferred over the organic co-solvent in the solvation shell. This is possibly explained by the ordered structure of water molecules around the apolar groups of this flavonoid (aromatic rings, Scheme 1), which is formed via hydrophobic hydration in water-rich mixtures.40,41 However, in the mixtures with composition xDMSO = 0.19 to 1.00, the δxDMSO,S values are positive, so that the δxDMSO,S reaches a maximum value in xDMSO = 0.49 at all the temperatures. This behavior probably be related to the breaking of the same ordered structure of water around the apolar moieties of the flavonoid.40,41
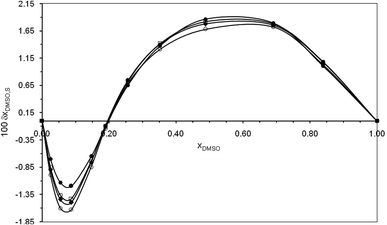 |
| | Fig. 4 Changes of δxDMSO,S parameter for naringin versus mole fraction of co-solvent in water/DMSO mixtures and the temperatures (●) 298.15, (□) 310.15 K, (♦) 315.15 K, and (○) 325.15 K. | |
From Fig. 4, it is noteworthy that increasing the temperature from 298.15 K to 325.15 K, leads to increase the preferential solvation of naringin by water molecules in aqueous-rich mixtures; while by increasing the temperature, the preferential solvation action of the flavonoid by DMSO decreases in intermediate compositions to cosolvent-rich regions. However, the influence of temperature on preferential solvation in intermediate compositions to cosolvent-rich regions is relatively small.
Due to the hydrogen atoms in its hydroxyl groups, the flavonoid naringin, Scheme 1, mainly acts as a Lewis acid in solution to interact with the proton-acceptor solvents via hydrogen bonds. In addition, this flavonoid can act as a Lewis base due to lone electron pairs on oxygen atoms of –OH, ≧O and –O– groups, to interact with hydrogen atoms in a protic solvent. The preferential solvation results show that in water-rich mixtures (xDMSO = 0.00–0.19), where the flavonoid is preferentially solvated by water, it acts mainly as a Lewis base in the presence of water because the Kamlet–Abboud–Taft (KAT) acidity parameters are α = 1.17 for water, 0.00 for DMSO.37 On the other hand, in the co-solvent mixtures with mole fraction xDMSO = 0.19 to 1.00, naringin acts as a Lewis acid in its hydrogen bonding interactions with DMSO molecules. Because the co-solvent DMSO has more basicity than water, according to the KAT basicity parameters which are β = 0.76 and 0.47 for DMSO and water, respectively.37 In addition to these specific interactions, the non-specific interactions of solute–solvent such as London forces can also involve in the solvation process.
The molecular dynamics (MD) simulation
Molecular dynamics simulations of naringin solvation were performed in a wide composition range of water/DMSO mixture (0.02 < xDMSO < 0.85) according to Table 9. In order to run simulation of the naringin in various compositions of the co-solvent mixture, the one naringin molecule was placed in the center of a cubic box with volume of 24.24 nm3. The details of the chosen solvent mixtures are given in Table 9.
Table 9 Mole fraction and the number of solvent molecules of water and DMSO in different composition used in the MD simulations
| Composition |
xDMSO |
xwater |
nDMSO |
nwater |
| 1 |
0.02 |
0.98 |
20 |
672 |
| 2 |
0.10 |
0.90 |
60 |
517 |
| 3 |
0.20 |
0.80 |
95 |
360 |
| 4 |
0.35 |
0.65 |
133 |
241 |
| 5 |
0.40 |
0.60 |
117 |
286 |
| 6 |
0.42 |
0.58 |
145 |
197 |
| 7 |
0.52 |
0.48 |
149 |
137 |
| 8 |
055 |
0.45 |
164 |
132 |
| 9 |
0.60 |
0.40 |
159 |
102 |
| 10 |
0.63 |
0.37 |
182 |
105 |
| 11 |
0.74 |
0.26 |
177 |
65 |
| 12 |
0.85 |
0.15 |
172 |
30 |
The nature of solvation shells for naringin molecule has been studied by calculating the radial distribution functions (RDFs) of the flavonoid molecules at different mole fractions of DMSO as has been shown in Fig. 5. The value of RDF, g(r), converges to 1 at larger distances. According to Fig. 5, g(r) values of the water solvent at xDMSO < 0.20 are higher than g(r) values of DMSO, whereas at higher mole fractions of the co-solvent DMSO, this status is reversed. These results show when the mole fraction of DMSO is less than 0.20, water molecules form the solvation shell around naringin, however, at the higher mole fractions, the co-solvent DMSO molecules occupy most space of the solvation shell.
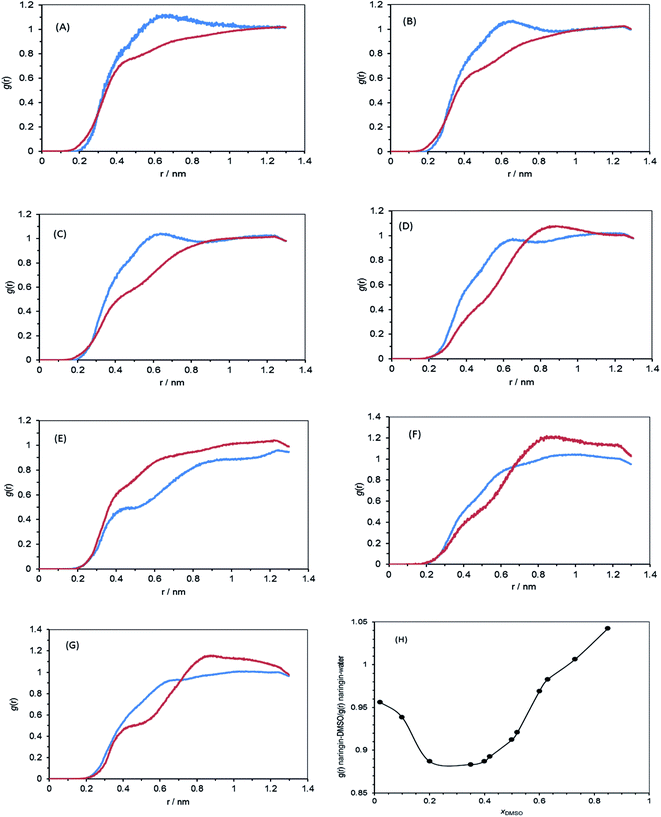 |
| | Fig. 5 Radial distribution functions, g(r), between naringin and water (blue), naringin and DMSO (red) in different mole fractions of DMSO (A) 0.02, (B) 0.10, (C) 0.20, (D) 0.42, (E) 0.60, (F) 0.73, (G) 0.85, and (H) the average g(r)naringin–DMSO/average g(r)naringin–water ratio versus mole fraction of DMSO. | |
The variation of solvation shell can also be represented by ratio of RDF related to naringin–DMSO to RDF of naringin–water system in different mole fractions of DMSO. The results are presented in Fig. 5H. According to Fig. 5H, in compositions less than 0.20 in the mole fractions of DMSO, the function g(r) of the co-solvent DMSO is lower than water, indicating the water molecules are more in vicinity of naringin. Thereafter, in mixtures with compositions from 0.20 in mole fraction of DMSO to pure DMSO, the number of DMSO molecules is increased in the solvation shell and g(r) of the solvent DMSO is increased, too. By comparing this figure and Fig. 4, it is conjecturable that these findings are in good agreement with the data obtained from the inverse Kirkwood–Buff integrals (IKBI) method.
Fig. 6 shows the solute molecule naringin and solvent molecules within 10 Å from the center of mass of naringin and the hydrogen bonds between the solute and solvent for xDMSO = 0.02, 0.1, 0.20, 0.42, 0.60 and 0.85. The snapshots show random distribution of the closest solvent molecules around naringin and they have been illustrated in view that all solvent molecules clearly are observed. At xDMSO = 0.02, thirty-two molecules of water and two molecules of DMSO exist around naringin in the solvation shell and naringin forms two hydrogen bonds with the surrounding water molecules. Along with the increasing of mole fraction of DMSO, number of water molecules is reduced in solvation shell, and instead the number of molecules of DMSO is increased. The number of solvent molecules in solvation shell as well as the hydrogen bonds involved in solvation process of naringin are given in Table 10.
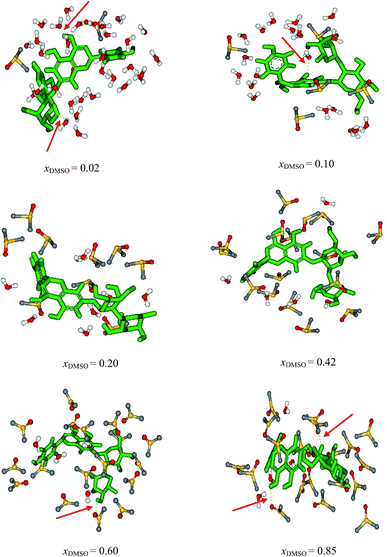 |
| | Fig. 6 Snapshots of the solvation shell for the naringin in different mole fraction of DMSO based on the last configuration of the MD calculations. | |
Table 10 The number of solvent molecules in the solvation shell around naringin based on the MD calculations
| xDMSO |
NH2Oa |
NDMSOa |
NH-H2Ob |
NH-DMSOb |
| NH2O and NDMSO are number of water and DMSO molecules in the solvation shell of naringin. NH-H2O and NH-DMSO are number of hydrogen bonds between the solute naringin and water and DMSO solvents, respectively. |
| 0.02 |
32 |
2 |
2 |
0 |
| 0.10 |
26 |
5 |
1 |
0 |
| 0.20 |
8 |
9 |
0 |
0 |
| 0.42 |
5 |
16 |
0 |
0 |
| 0.60 |
4 |
18 |
0 |
1 |
| 0.85 |
4 |
19 |
0 |
2 |
The conformational changes of the naringin–solvent system during MD simulations were monitored by the root mean square deviation (RMSD) as follows:
| |
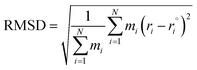 | (27) |
where
mi is the mass of atom
i and
and
ri are the coordinates of atom
i at the reference state and during MD simulations, respectively. RMSDs were calculated for the trajectories from the starting structures of the system as a function of time for naringin–water and naringin–DMSO and are shown in
Fig. 7A and B, respectively. The RMSD of a system is an important criterion for monitoring its stability. When the RMSD curve has not fluctuations and so it is flat and smooth, it indicates that the system studied is in the steady state. In this case, data sampling can be performed in flat region and the last period of times. Moreover, RMSD is the measure of the average distance between the atoms, so the average of each RMSD was obtained in different mole fractions of DMSO and was plotted against mole fraction of DMSO (see
Fig. 7C). As shown in
Fig. 7C, by increasing the mole fraction of the co-solvent DMSO, the distance between naringin and DMSO molecules is reduced, while the distance between naringin molecule and water is increased. RMSD is not only the function of solvent transport properties, but also, and to a larger extent, it is depended on specific chemical interactions between the solute molecule and solvent system.
42 Fig. 7D shows the difference between average RMSD of naringin–DMSO and naringin–water
versus mole fraction of DMSO. According to this figure, in mole fractions less than 0.20 of DMSO, RMSD shows a decreasing trend with increasing
xDMSO and falls into the negative area, so that it indicates the chemical interaction between naringin molecule and water solvent is more in this area. In the mole fraction higher than 0.20 of DMSO, values of RMSD are greater than zero. This result proves that the naringin molecules have found tendency to DMSO solvent and have more interaction with it. This figure is comparable with
Fig. 4 and
5H.
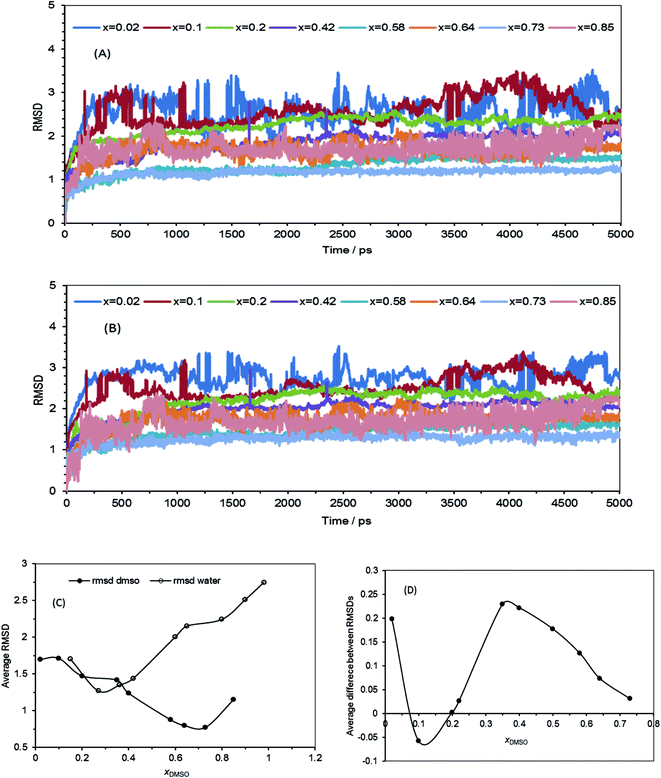 |
| | Fig. 7 (A) RMSD for naringin–water, (B) RMSD for naringin–DMSO, (C) plot of average RMSDs of water and DMSO versus the mole fraction of DMSO and (D) plot of the average difference between RMSD of naringin–DMSO and naringin–water as function of the mole fraction of DMSO. | |
Conclusions
From the results obtained in this study, it was found that (1) the equilibrium solubility of the flavonoid naringin in water/DMSO mixtures (0–100% by w/w) increases when amount of the organic co-solvent DMSO and also the temperature increase, (2) the standard Gibbs energy, the enthalpy and entropy of dissolution process of naringin is positive in all the solvent systems investigated, (3) the analysis of solvent effect on the solubility values of naringin by dual-parameter KAT equations (α and δH) represents the best linear correlation with regard to the single- and multi-parameter models, (4) the flavonoid naringin is preferentially solvated by water in water-rich mixtures while it is preferentially solvated by the co-solvent DMSO in mixtures with intermediate and rich composition of the co-solvent. This is due to the existence of interactions between the solute and solvent system such as the hydrophobic hydration, H-bonding interaction, etc., and finally (5) the MD simulation results of the preferential solvation of the flavonoid naringin showed that at xDMSO > 0.20, the naringin molecule prefer to be in vicinity of the DMSO and solvated by it. These results are in good agreement with the data obtained from the IKBI approach.
Acknowledgements
The authors gratefully acknowledge the Research Council of Damghan University for providing the laboratory facilities.
References
- L. Zhang, L. Song, P. Zhang, T. Liu, L. Zhou, G. Yang and R. Lin, J. Chem. Eng. Data, 2015, 60, 932–940 CrossRef CAS.
- J. Zhang, P. Zhang, T. Liu, L. Zhou, L. Zhang, R. Lin, G. Yang, W. Wang and Y. Li, J. Mol. Liq., 2015, 203, 98–103 CrossRef CAS.
- M. Jain and H. S. Parmar, Inflammation Res., 2011, 60, 483–491 CrossRef CAS PubMed.
- H. Ccedilelik, M. Kosar and E. Arinc, Toxicology, 2013, 308, 34–40 CrossRef PubMed.
- P. Zhang, R. Lin, G. Yang, J. Zhang, L. Zhou and T. Liu, J. Chem. Eng. Data, 2013, 58, 2402–2404 CrossRef CAS.
- A. Hossain, S. Roy, S. Ghosh, S. Mondala and B. K. Dolui, RSC Adv., 2015, 5, 69839–69847 RSC.
- M. A. Filippa and E. I. Gasull, Fluid Phase Equilib., 2013, 354, 185–190 CrossRef CAS.
- A. Vishnyakov, G. Widmalm and A. Laaksonen, Angew. Chem., Int. Ed., 2000, 39, 140–142 CrossRef CAS PubMed.
- G. Saiellia and A. Bagno, Phys. Chem. Chem. Phys., 2010, 12, 2981–2988 RSC.
- G. N. Pallewela and E. P. Smith, J. Phys. Chem. B, 2015, 119, 15706–15717 CrossRef CAS PubMed.
- Y. Marcus, Solvent mixtures: properties and selective solvation, Marcel Dekker, Inc., New York, 2002 Search PubMed.
- Y. Marcus, Acta Chim. Slov., 2009, 56, 40–44 CAS.
- S. Feizi, M. Jabbari and A. Farajtabar, J. Mol. Liq., 2016, 220, 478–483 CrossRef CAS.
- D. R. Delgado and F. Martinez, J. Mol. Liq., 2014, 193, 152–159 CrossRef CAS.
- T. Zamir, S. Tasleem, F. Uddin and S. Durrani, J. Chem. Eng. Data, 2010, 55, 666–672 CrossRef CAS.
- L. M. Omota, O. Iulian, F. Omota and O. Ciocirlan, Rev. Roum. Chim., 2009, 54, 63–73 CAS.
- A. Ben-Naim, Cell Biophys., 1988, 12, 255–269 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- H. Liu, F. Mueller-Plathe and W. F. van Gunsteren, J. Am. Chem. Soc., 1995, 117, 4363–4366 CrossRef CAS.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. P. Hirshman and J. Whitson, Phys. Fluids, 1983, 26, 3553–3568 CrossRef.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- W. Van Gunsteren and H. Berendsen, Mol. Simul., 1988, 1, 173–185 CrossRef.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. R. Krug, W. G. Hunter and R. A. Grieger, J. Phys. Chem., 1976, 80, 2341–2351 CrossRef CAS.
- S. Romero, A. Reillo, B. Escalera and P. Bustamante, Chem. Pharm. Bull., 1996, 44, 1061–1066 CrossRef CAS.
- A. Apelblat and E. Manzurola, J. Chem. Thermodyn., 1999, 31, 85–91 CrossRef CAS.
- H. Buchowski and A. Khiat, Fluid Phase Equilib., 1986, 25, 273–278 CrossRef CAS.
- A. Nussinovitch, Polymer macro- and micro-gel beads: Fundamentals and applications, Springer, New York, 2010 Search PubMed.
- M. J. Kamlet, J. L. M. Abboud and R. W. Taft, Prog. Phys. Org. Chem., 1981, 13, 485–630 CrossRef CAS.
- M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, VCH, New York, 4th edn, 2011 Search PubMed.
- Y. Migron and Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 1339–1343 RSC.
- I. S. Shehatta, A. H. El-Askalany and E. A. Gomaa, Thermochim. Acta, 1993, 219, 65–72 CrossRef CAS.
- F. Franks, Water: a matrix of life, Royal Society of Chemistry, Cambridge, 2nd edn, 2000 Search PubMed.
- Y. Matsumoto, H. Touhara, K. Nakanishi and N. Watanabe, J. Chem. Thermodyn., 1977, 9, 801–805 CrossRef CAS.
- G. Chevrot, E. E. Fileti and V. V. Chaban, J. Comput. Chem., 2015, 36, 2044–2051 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Negar Khosravi,
Mina Feizabadi and
Davood Ajloo
*,
Negar Khosravi,
Mina Feizabadi and
Davood Ajloo
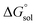 ,
, 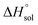 and
and 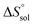 were also calculated. Furthermore, the effects of solvent composition on the solubility of this flavonoid were analyzed in terms of Hildebrand's solubility parameter (δH) and Kamlet, Abboud and Taft (KAT) solvatochromic parameters (α, β, and π*). Finally, the preferential solvation parameters of the flavonoid naringin by DMSO (δxDMSO,S) were determined from experimental solubility data using the inverse Kirkwood–Buff integrals (IKBIs). It was found that water preferentially solvates naringin in water-rich mixtures while DMSO forms local solvation shells in compositions from 50% (w/w) or xDMSO = 0.19 up to pure co-solvent. Moreover, the structure of solvation shells of naringin in the under study mixtures was obtained by molecular dynamics (MD) simulations. The computational results showed that in the compositions xDMSO > 0.20, the probability of presence of the DMSO molecules in vicinity of naringin is more than water molecules. These findings are compatible with the available IKBI data.
were also calculated. Furthermore, the effects of solvent composition on the solubility of this flavonoid were analyzed in terms of Hildebrand's solubility parameter (δH) and Kamlet, Abboud and Taft (KAT) solvatochromic parameters (α, β, and π*). Finally, the preferential solvation parameters of the flavonoid naringin by DMSO (δxDMSO,S) were determined from experimental solubility data using the inverse Kirkwood–Buff integrals (IKBIs). It was found that water preferentially solvates naringin in water-rich mixtures while DMSO forms local solvation shells in compositions from 50% (w/w) or xDMSO = 0.19 up to pure co-solvent. Moreover, the structure of solvation shells of naringin in the under study mixtures was obtained by molecular dynamics (MD) simulations. The computational results showed that in the compositions xDMSO > 0.20, the probability of presence of the DMSO molecules in vicinity of naringin is more than water molecules. These findings are compatible with the available IKBI data.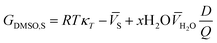
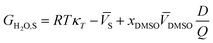
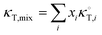
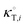 is the isothermal compressibility of the pure solvent i with the values 0.524 and 0.457 GPa−1, for DMSO and water, respectively.13
is the isothermal compressibility of the pure solvent i with the values 0.524 and 0.457 GPa−1, for DMSO and water, respectively.13
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) DMSO and
DMSO and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) H2O are the partial molar volumes of the solvents in the binary mixture (in cm3 mol−1). Also,
H2O are the partial molar volumes of the solvents in the binary mixture (in cm3 mol−1). Also, ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) S is the partial molar volume of the solute in these mixtures with the value 349.72 cm3 mol−1 for naringin. The partial molar volumes of water and the co-solvent can be calculated based on the following expressions:
S is the partial molar volume of the solute in these mixtures with the value 349.72 cm3 mol−1 for naringin. The partial molar volumes of water and the co-solvent can be calculated based on the following expressions: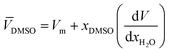
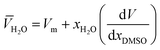
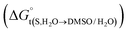 with respect to the co-solvent composition (in kJ mol−1):
with respect to the co-solvent composition (in kJ mol−1):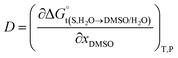
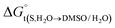 , is calculated from the naringin solubility data and then correlated to specific polynomials as:
, is calculated from the naringin solubility data and then correlated to specific polynomials as: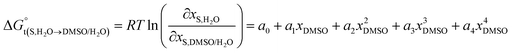
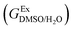 with respect to the water proportion in the mixtures (in kJ mol−1):14
with respect to the water proportion in the mixtures (in kJ mol−1):14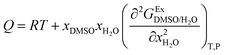
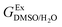 , should be evaluated at all the temperatures considered. In this way,
, should be evaluated at all the temperatures considered. In this way, 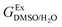 values (in kJ mol−1) are calculated at 298.15 K by means of eqn (11) as reported by Marcus.11 Then, the
values (in kJ mol−1) are calculated at 298.15 K by means of eqn (11) as reported by Marcus.11 Then, the 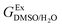 values at the other temperatures can be calculated by means of eqn (12):
values at the other temperatures can be calculated by means of eqn (12):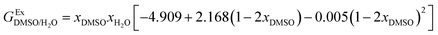
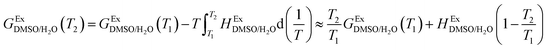
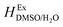 is the excess molar enthalpy of the co-solvent mixtures, T1 is 298.15 K and T2 is one of the other temperatures under study. At T1 = 298.15 K,
is the excess molar enthalpy of the co-solvent mixtures, T1 is 298.15 K and T2 is one of the other temperatures under study. At T1 = 298.15 K, 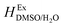 function is calculated according to the following equation:11
function is calculated according to the following equation:11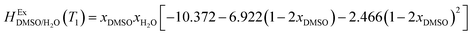
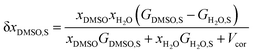
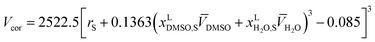
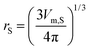
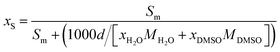
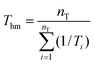
 is calculated at Thm by the following equation:2
is calculated at Thm by the following equation:2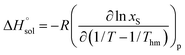

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS versus (1/T − 1/Thm) for naringin in water/DMSO co-solvent mixtures. Lines correspond to the best linear regression analyses.
xS versus (1/T − 1/Thm) for naringin in water/DMSO co-solvent mixtures. Lines correspond to the best linear regression analyses.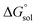 , can be calculated at Thm from the following thermodynamic relationship:6,7
, can be calculated at Thm from the following thermodynamic relationship:6,7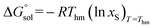
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS)T=Thm is value of the intercept of the plot of ln
xS)T=Thm is value of the intercept of the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS versus (1/T − 1/Thm). Finally, the standard molar dissolution entropic change
xS versus (1/T − 1/Thm). Finally, the standard molar dissolution entropic change 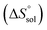 is obtained at Thm as follows:
is obtained at Thm as follows: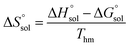
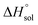 and
and 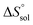 values (up to 40% by w/w DMSO) and then decreases them to a minimum in pure co-solvent DMSO. This behavior may be related to the breaking of the ordered structure of water (hydrogen bonds) around the apolar moieties of naringin, which increases first both the enthalpy and the entropy of the system;31 whereas by raising the DMSO proportion, due to formation of ordered structure of the co-solvent around naringin after it’s solvated by DMSO, the enthalpy and entropy of the system continuously decrease.
values (up to 40% by w/w DMSO) and then decreases them to a minimum in pure co-solvent DMSO. This behavior may be related to the breaking of the ordered structure of water (hydrogen bonds) around the apolar moieties of naringin, which increases first both the enthalpy and the entropy of the system;31 whereas by raising the DMSO proportion, due to formation of ordered structure of the co-solvent around naringin after it’s solvated by DMSO, the enthalpy and entropy of the system continuously decrease.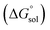 , ur
, ur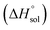 and ur
and ur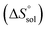 are 4.1%, 4.3% and 4.9%, respectively.b WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively.
are 4.1%, 4.3% and 4.9%, respectively.b WDMSO and xDMSO are the mass fraction and the mole fraction of DMSO in the binary water/DMSO mixtures, respectively.
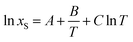
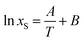
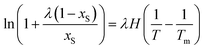
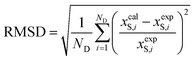
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = A0 + aα + bβ + pπ* + hδ2H
xS = A0 + aα + bβ + pπ* + hδ2H
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS in a hypothetical solvent with α = β = π* = 0, the δ2H represents Hildebrand's solubility parameter squared of solvent and corresponds to the energy associated with the intermolecular solvent–solvent interactions. The π* parameter is the index of the solvent dipolarity/polarizability, which is a measure of the ability of a solvent to stabilize a charge or a dipole by its own dielectric effects. The α parameter represents the solvent hydrogen-bond donor (HBD) acidity, in other words it describes the ability of a solvent to donate a proton in a solvent to a solute hydrogen-bond. The β quantity is a measure of solvent hydrogen-bond acceptor (HBA) basicity, and describes the ability of a solvent to accept a proton from a solute molecule.37 The regression coefficients a, b, p and h in eqn (26) are measures of the relative susceptibilities of the solubility to the indicated solvent parameters.
xS in a hypothetical solvent with α = β = π* = 0, the δ2H represents Hildebrand's solubility parameter squared of solvent and corresponds to the energy associated with the intermolecular solvent–solvent interactions. The π* parameter is the index of the solvent dipolarity/polarizability, which is a measure of the ability of a solvent to stabilize a charge or a dipole by its own dielectric effects. The α parameter represents the solvent hydrogen-bond donor (HBD) acidity, in other words it describes the ability of a solvent to donate a proton in a solvent to a solute hydrogen-bond. The β quantity is a measure of solvent hydrogen-bond acceptor (HBA) basicity, and describes the ability of a solvent to accept a proton from a solute molecule.37 The regression coefficients a, b, p and h in eqn (26) are measures of the relative susceptibilities of the solubility to the indicated solvent parameters.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS) were correlated with solvent properties by means of single-, dual- and multi-parameter linear regression analysis by a suitable computer program in Excel environment (LINEST). A stepwise procedure and least-squares analysis were applied to select the significant solvent properties to be influenced in the model and to obtain the final expression for the solubilities. The LINEST program used can determine the A0, a, b, p, h values of eqn (26) and some statistical parameters including the r2 coefficient, the standard deviation of each parameter, the overall standard error (ose) of log
xS) were correlated with solvent properties by means of single-, dual- and multi-parameter linear regression analysis by a suitable computer program in Excel environment (LINEST). A stepwise procedure and least-squares analysis were applied to select the significant solvent properties to be influenced in the model and to obtain the final expression for the solubilities. The LINEST program used can determine the A0, a, b, p, h values of eqn (26) and some statistical parameters including the r2 coefficient, the standard deviation of each parameter, the overall standard error (ose) of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS and the residual sum of the squares of errors (rss). The linear regression analysis of solubility of naringin with the dual-parameter equations (α and δH) indicates significant improvement with regard to the single- and multi-parameter models and yield the lowest standard deviation and possess very good coefficients of determination in all cases. The expressions of the KAT equation at the temperatures analyzed are given in Table 5 based on two solvatochromic parameters (α and δH). In these equations, the negative sign of α and δH indicates a decrease in the hydrogen-bond donor acidity and the Hildebrand's solubility parameter of the solvent increases the solubility of the solute. Consequently, the solubility increases when these parameters decrease. The magnitude of the coefficients a and h in Table 5 are in the order of h > a. This suggests that the Hildebrand's solubility parameter of the solvent is the most important for solubility, and the hydrogen-bond donor acidity parameter plays a relatively small role in changing the solubility of naringin in various aqueous DMSO solutions.
xS and the residual sum of the squares of errors (rss). The linear regression analysis of solubility of naringin with the dual-parameter equations (α and δH) indicates significant improvement with regard to the single- and multi-parameter models and yield the lowest standard deviation and possess very good coefficients of determination in all cases. The expressions of the KAT equation at the temperatures analyzed are given in Table 5 based on two solvatochromic parameters (α and δH). In these equations, the negative sign of α and δH indicates a decrease in the hydrogen-bond donor acidity and the Hildebrand's solubility parameter of the solvent increases the solubility of the solute. Consequently, the solubility increases when these parameters decrease. The magnitude of the coefficients a and h in Table 5 are in the order of h > a. This suggests that the Hildebrand's solubility parameter of the solvent is the most important for solubility, and the hydrogen-bond donor acidity parameter plays a relatively small role in changing the solubility of naringin in various aqueous DMSO solutions.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.45(±0.18) − 0.32(±0.29)α − 2.08(±0.20)δ2H
xS = −2.45(±0.18) − 0.32(±0.29)α − 2.08(±0.20)δ2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.32(±0.14) − 0.45(±0.22)α − 2.02(±0.15)δ2H
xS = −2.32(±0.14) − 0.45(±0.22)α − 2.02(±0.15)δ2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.20(±0.18) − 0.93(±0.29)α − 1.74(±0.20)δ2H
xS = −2.20(±0.18) − 0.93(±0.29)α − 1.74(±0.20)δ2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.23(±0.17) − 1.16(±0.28)α − 1.56(±0.19)δ2H
xS = −2.23(±0.17) − 1.16(±0.28)α − 1.56(±0.19)δ2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.23(±0.19) − 1.32(±0.31)α − 1.46(±0.21)δ2H
xS = −2.23(±0.19) − 1.32(±0.31)α − 1.46(±0.21)δ2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xS = −2.26(±0.17) − 1.48(±0.28)α − 1.31(±0.19)δ2H
xS = −2.26(±0.17) − 1.48(±0.28)α − 1.31(±0.19)δ2H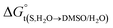 for naringin are obtained (eqn (8)) at different temperatures and are given in Table 6. The variations of
for naringin are obtained (eqn (8)) at different temperatures and are given in Table 6. The variations of 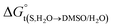 with organic co-solvent composition (xDMSO) at different temperatures corresponding to a regular polynomial are shown in Fig. 3. The D values were calculated from the first derivative of the polynomial models obtained.
with organic co-solvent composition (xDMSO) at different temperatures corresponding to a regular polynomial are shown in Fig. 3. The D values were calculated from the first derivative of the polynomial models obtained.
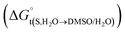 for naringin in different aqueous mixtures of DMSO and various temperatures
for naringin in different aqueous mixtures of DMSO and various temperatures


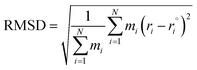
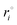 and ri are the coordinates of atom i at the reference state and during MD simulations, respectively. RMSDs were calculated for the trajectories from the starting structures of the system as a function of time for naringin–water and naringin–DMSO and are shown in Fig. 7A and B, respectively. The RMSD of a system is an important criterion for monitoring its stability. When the RMSD curve has not fluctuations and so it is flat and smooth, it indicates that the system studied is in the steady state. In this case, data sampling can be performed in flat region and the last period of times. Moreover, RMSD is the measure of the average distance between the atoms, so the average of each RMSD was obtained in different mole fractions of DMSO and was plotted against mole fraction of DMSO (see Fig. 7C). As shown in Fig. 7C, by increasing the mole fraction of the co-solvent DMSO, the distance between naringin and DMSO molecules is reduced, while the distance between naringin molecule and water is increased. RMSD is not only the function of solvent transport properties, but also, and to a larger extent, it is depended on specific chemical interactions between the solute molecule and solvent system.42 Fig. 7D shows the difference between average RMSD of naringin–DMSO and naringin–water versus mole fraction of DMSO. According to this figure, in mole fractions less than 0.20 of DMSO, RMSD shows a decreasing trend with increasing xDMSO and falls into the negative area, so that it indicates the chemical interaction between naringin molecule and water solvent is more in this area. In the mole fraction higher than 0.20 of DMSO, values of RMSD are greater than zero. This result proves that the naringin molecules have found tendency to DMSO solvent and have more interaction with it. This figure is comparable with Fig. 4 and 5H.
and ri are the coordinates of atom i at the reference state and during MD simulations, respectively. RMSDs were calculated for the trajectories from the starting structures of the system as a function of time for naringin–water and naringin–DMSO and are shown in Fig. 7A and B, respectively. The RMSD of a system is an important criterion for monitoring its stability. When the RMSD curve has not fluctuations and so it is flat and smooth, it indicates that the system studied is in the steady state. In this case, data sampling can be performed in flat region and the last period of times. Moreover, RMSD is the measure of the average distance between the atoms, so the average of each RMSD was obtained in different mole fractions of DMSO and was plotted against mole fraction of DMSO (see Fig. 7C). As shown in Fig. 7C, by increasing the mole fraction of the co-solvent DMSO, the distance between naringin and DMSO molecules is reduced, while the distance between naringin molecule and water is increased. RMSD is not only the function of solvent transport properties, but also, and to a larger extent, it is depended on specific chemical interactions between the solute molecule and solvent system.42 Fig. 7D shows the difference between average RMSD of naringin–DMSO and naringin–water versus mole fraction of DMSO. According to this figure, in mole fractions less than 0.20 of DMSO, RMSD shows a decreasing trend with increasing xDMSO and falls into the negative area, so that it indicates the chemical interaction between naringin molecule and water solvent is more in this area. In the mole fraction higher than 0.20 of DMSO, values of RMSD are greater than zero. This result proves that the naringin molecules have found tendency to DMSO solvent and have more interaction with it. This figure is comparable with Fig. 4 and 5H.