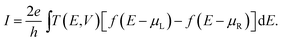Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Obvious modulation of rectifying performance by conjugation breaking of the bridging fragment in donor–bridge–acceptor molecular diodes†
Wen-Xia Sua,
Xi Zuoa,
Zhen Xiea,
Guang-Ping Zhang *ab and
Chuan-Kui Wang*a
*ab and
Chuan-Kui Wang*a
aShandong Province Key Laboratory of Medical Physics and Image Processing Technology, School of Physics and Electronics, Shandong Normal University, Jinan 250014, China. E-mail: zhangguangping@sdnu.edu.cn; ckwang@sdnu.edu.cn
bInstitute of Materials and Clean Energy, Shandong Normal University, Jinan 250014, China
First published on 2nd March 2017
Abstract
The rectifying properties of three donor–bridge–acceptor (D–B–A) type thiolated arylethynylene diodes designed by replacing one of the thiol anchoring groups to cyano, where the central bridging fragment is varied from cross-conjugated 9,10-anthraquinone (AQ), linearly-conjugated anthracene (AC) to broken-conjugated 9,10-dihydroanthracene (AH), are theoretically investigated using a non-equilibrium Green's function (NEGF) method combined with density functional theory (DFT). The numerical results reveal that both the rectifying performance and rectification direction of the D–B–A diodes are closely related with the conjugation type of the central bridging segment. The rectification performance is improved and the rectifying direction is inverted when the central bridge is changed from cross-conjugated AQ to linearly-conjugated AC. Moreover, when conjugation of the bridge part is broken, i.e., AH, the rectification performance is further enhanced remarkably. Further analysis reveals that the asymmetric evolution of strongly localized frontier molecular orbitals under positive and negative bias voltages, induced by conjugation breaking, is responsible for the great enhancement in rectification ratio for AH. This work is helpful for rational design of molecular diodes with diverse rectification performance.
1. Introduction
Molecular rectifiers, one of the most important molecular devices,1–5 have been drawing considerable theoretical and experimental attention since they were first proposed by Aviram and Ratner.6 Geometric asymmetry7 is a fundamental requirement for a molecular junction to behave as a rectifier.8 However, asymmetry created from the interfaces between molecule and electrodes is a great challenge to control. Therefore, the molecule containing intrinsic asymmetry9 is believed to play a more vital role in designing molecular diodes. Among all the asymmetric molecules, donor–bridge–acceptor (D–B–A) type molecules are especially intriguing and have attracted more focuses.8–10 It has been revealed that the rectifying properties of molecular diodes can be fine-tuned by changing the molecular length,11–14 terminal anchoring group,15–17 side groups,14,18,19 molecule-electrode contact configurations,20–22 the PH value of solution,23,24 the external potential field.25Besides, the properties of the donor, acceptor and especially the bridge segment in the D–B–A type molecule also play a crucial role in determining its rectifying performance. Therefore, bridging the properties of target molecules and their rectifying characteristics is of importance in designing molecular diodes from both experimental and theoretical points of view. Fracasso et al. have studied three arylethynylene thiolate molecules using different types of bridging segments, and they found all the three molecules exhibited clear but weak rectifying behaviors resulting from the asymmetric molecule–electrode interface.26 Since it is a nontrivial task to control the interface between the molecule and electrodes, it needs to create intrinsic asymmetries in the molecule itself to obtain stable and more evident rectification in this series of molecules. For this aim, we have designed D–B–A type molecules through side group substitution based on these arylethynylene thiolate molecules.18 And we have found that conjugation breaking of the bridge fragment will lead to an enhancement of the rectifying performance. This suggests that the rectifying properties of D–B–A diodes are closely affected by the properties of bridge segment. However, Liu et al. have demonstrated that a better intramolecular coupling between two tandem diodes by a π-bridge facilitates the rectification compared with that connected by a σ-bridge.27 Therefore, discrepant observations for the effect of bridge type on rectification performance exist. In our work of ref. 18, the rectifying performance is also not so evident. In 2009, Lee et al. have found that the rectification direction can be reversed by replacing one of the terminal thiol groups with an isocyano group in dipyrimidinyl-diphenyl co-oligomer diode.16 This phenomenon has been verified by our subsequent theoretical study, and the results have also predicted a further enhanced rectification by synergetic contributions of dipyrimidinyl-diphenyl itself and the thiol-isocyano terminal groups.17 More recently, Dyck and Ratner have proved that the combination of thiol and cyano anchoring groups for two conjugated fragments connected through a saturated σ-bridge can create an excellent molecular diode.28 Therefore, it is interesting to check whether the combination of thiol and cyano ending groups can realize high performance molecular diodes in arylethynylene thiolate molecules, and to further examine the effect of conjugation type of the bridge segment on the rectifying performance in D–B–A molecular diodes.
With these two aims in mind, we have restudied the arylethynylene molecules and D–B–A type molecular diodes are designed by substituting one of the thiol anchoring groups to cyano. The conjugation type effect of the bridging fragment on rectifying performance of D–B–A arylethynylene molecular diodes is also rechecked. Our first-principles calculations again confirmed that the rectifying performance of junctions correlates negatively with the conjugation of bridging segment. That is, a much more pronounced rectification behavior is observed for molecule with a broken-conjugated dihydroanthracene bridge (AH) than the counterpart with a linearly-conjugated anthracene (AC) or cross-conjugated anthraquinone (AQ). Meanwhile, it is demonstrated that the thiol and cyano anchoring group is indeed an excellent combination for providing a more efficient asymmetry in molecular rectifiers compared with the side group substituting of hydrogen atom by cyano group. More interestingly, we have observed an inversion of the rectifying direction by changing the conjugation type of the bridge fragment in D–B–A arylethynylene molecular diodes.
2. Theoretical model and computational details
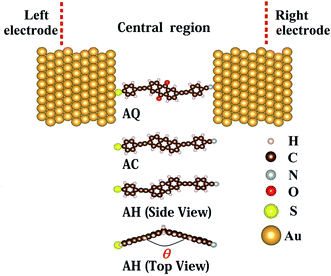
The molecular junctions are modeled within ATK29–31 methodology and illustrated in Fig. 1. The entire molecular junction is divided into three regions: the left electrode, the central region, and the right electrode. Each semi-infinite Au(111) electrode is simulated by a 5 × 5 × 3 super cell with periodic boundary condition. In the central region, a single arylethynylene molecule with different molecular core is anchored to two Au(111) electrodes through thiol group at the left side and cyano group at the right side. The conjugation type of the molecular core is varied from a cross-conjugated 9,10-anthraquinone (AQ), or linearly-conjugated anthracene (AC) to the broken-conjugated 9,10-dihydroanthracene (AH). The sulfur atom of thiol ending group at the left side is located at the hollow site of Au(111) surface while the nitrogen atom of cyano anchoring group at the right side resides on the top site.The structure of the bare molecule is optimized first in the Atomistix ToolKit package with a maximum residual force of 0.05 eV Å−1 (see the ESI†). Then, the molecule is coupled to the Au(111) electrodes to form the single-molecule junction and the central region of the junction is optimized again (see the ESI†). During this optimization, all atoms in the molecule and the adjacent two layers of Au(111) electrodes at both sides are fully optimized. Other atoms in the Au(111) layers in the central region are restricted to move rigidly along the transport direction to allow relaxation of the distance between two electrodes. In the optimization and following electron transport calculations, the improved Troullier–Martins type norm-conserving pseudopotentials32 are used to describe the core electrons and the Perdew–Burke–Ernzerhof (PBE)33 generalized gradient approximation (GGA) is adopted for the exchange–correlation functional.34 A single-ζ plus single polarization (SZP) basis set is employed for Au atoms while a double-ζ plus single polarization (DZP) basis set for other atoms. A 300 Ry mesh cutoff for the real space grid is chosen. The convergence criterion for Hamiltonian matrix is chosen as 1.0 × 10−4 Hartree. A 6 × 6 k-point grid is used for the Brillouin-zone (BZ) sampling after an extensive convergence analysis.
The electron transport properties are investigated using the non-equilibrium Green's function (NEGF) method combined with density functional theory (DFT) implemented in the Atomistix ToolKit package. The current through the molecular junction is calculated according to the Landauer–Büttiker formula,35
3. Results and discussion
We first investigate the effect of conjugation type of the bridge fragment on geometric structures in D–B–A arylethynylene molecular diodes. From Table 1, we can see the S–Au bond length d1 at the left interface is not evidently changed from the cross-conjugated AQ to linearly-conjugated AC. When the molecular conjugation is broken, that is, the broken-conjugated AH, there is a slight decrease for the S–Au bond by 0.035 Å on average compared to that in the conjugated AQ and AC. Meanwhile, there is no obvious variation for the N–Au bond length d2 at the right side when conjugation of the bridge segment is broken. This indicates that the coupling between the molecule and electrodes will not be evidently modified by alternation of the conjugation type for central bridge moiety. However, one can observe a significant effect of the conjugation type on the planarity of molecular backbone. For the conjugated AQ and AC, the molecule is almost in a plane due to the π-conjugation effect. But for the non-conjugated AH, there is a large dihedral angle of about 38 degree with respect to the axis defined by the two saturated carbon atoms in the dihydroanthracene core as shown in Fig. 1. The destruction of the molecular planarity due to conjugation breaking in AH is expected to bring remarkable impact on the spatial localization of the molecular wavefunctions and hence the conductance of AH.| θ/deg | d1/Å | d2/Å | |
|---|---|---|---|
| AQ | 0.16 | 2.545 | 2.258 |
| AC | 0.09 | 2.541 | 2.264 |
| AH | 38.24 | 2.506 | 2.257 |
Then current–voltage (I–V) characteristics of the three junctions are studied self-consistently by using the DFT based NEGF method, which are presented in Fig. 2. As seen from the I–V curve of AQ shown in Fig. 2a, there is hardly any current in the bias voltage range of [−0.4, 0.4 V], that is, there is a threshold bias of about 0.4 V for AQ. When the magnitude of bias voltage exceeds this threshold, the current is enhanced rapidly as the bias voltage increases. And the magnitude of current reaches about to 0.9 μA at the bias voltage of 1.6 V while it is 0.68 μA at −1.6 V, which is not symmetric since an asymmetric combination of thiol and cyano anchoring groups is used. The asymmetry of the I–V curve and hence the rectifying performance of molecular junctions can be well characterized by the bias dependent rectification ratio R defined as R(V) = |I(V)/I(−V)| or the inverted rectification ratio 1/R as 1/R(V) = |I(−V)/I(V)|. As depicted in the inset of Fig. 2a, the rectification ratio R varies with the bias voltage and the largest R for AQ is only 1.2 at 1.6 V, which means the current prefers to flow from the left electrode to the right one. In analogy to semiconducting p–n junctions, the electron donor thiol group resembles the n-doping part while electron acceptor cyano group is like the p-doping part. Then, one will find the forward current flows from the donor to acceptor in AQ, which is opposite to the case of p–n junction. This indicates more versatile and fascinating functionalities can be obtained in molecular devices. When it goes to the linearly-conjugated AC, it is noted that the magnitude of the current is largely enhanced for both positive and negative bias voltages compared to AQ. For instance, the current under −1.6 V reaches up to 2.48 μA while it gets as large as 1.28 μA at 1.6 V. More interestingly, the rectifying direction of AC is reversed to the negative bias voltage, and the rectification performance is also improved with the largest inverted rectification ratio 1/R(V) of 3.7 at the bias voltage of 1.0 V. When the central bridge part becomes non-conjugated, that is AH, the current is largely reduced by forty times in comparison with that of AC. It only has a value of 53.5 nA at −1.6 V. However, the current under positive bias voltage is more dramatically suppressed with a value of 1.48 nA at 1.6 V. Hence, it still keeps an inverted rectification direction and a much more pronounced rectifying effect is observed for conjugation-broken AH with a maximum 1/R(V) of 58.2 at 1.2 V. Therefore, we conclude that changing the central bridge from a π-conjugated segment to a non-conjugated one will greatly promote the rectifying performance in the D–B–A arylethynylene diodes, which is in agreement with our previous results. And at the same time the combination of thiol and cyano anchoring groups is better than the side group substitution by cyano to create a D–B–A arylethynylene molecular diode.
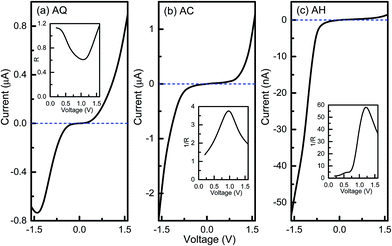 | ||
| Fig. 2 Current–voltage curves for molecular junctions AQ, AC, and AH. The insets are the bias-dependent (inverted) rectification ratios. | ||
As known, available molecular orbital with delocalized spatial distribution in the bias window is the essential requirement for a molecular junction to have a large current. Therefore, to obtain an intuitive understanding of the rectifying mechanisms for the three molecular junctions, an analysis of the molecular orbital is implemented by diagonalizing the molecular projected self-consistent Hamiltonian (MPSH) at each bias voltage, which is proved to be a powerful tool in previous studies.17,36 Fig. 3 shows the evolutions of MPSH eigenvalues under bias voltages for AQ, AC and AH. It is seen that the current of AQ may be contributed by LUMO and HOMO since they are around the Fermi energy (EF). The perturbed LUMO has a nearly symmetric evolution under positive and negative bias voltages. As the magnitude of bias voltage increases, it enters into the bias windows at higher bias voltages contributing to the current. On the contrary, the energy of HOMO varies monotonically with the bias voltage, i.e., it moves far away from the bias window under positive bias voltages while it approaches to the bias window under negative voltages and gets involved in the bias window at −1.6 V. From the evolutions of HOMO and LUMO, it seems that the current under negative bias voltage should be larger than that under positive bias voltage, which is opposite to the observation in the I–V curve. This indicates that it is necessary to have a further inspection of the spatial distributions for MPSH eigenstates to obtain a deep and precise understanding of the rectifying mechanism. The evolutions of HOMO and LUMO for AC are very similar with the case of AQ. Therefore, it is easy to understand why AQ has a rectifying direction along the negative bias voltage. However, for the non-conjugated AH as shown in Fig. 3c, the HOMO and LUMO have very monotonic and opposite evolutions under bias voltages, which should be attributed to the high localization to either part of the molecule in spatial distributions of the wavefunctions. The monotonic shift of HOMO and LUMO under bias voltages results in the entrances into the bias window at higher negative bias voltages while both of them are excluded out of the bias window. Naturally, an evident rectifying effect with an inverted rectification direction is observed for AH.
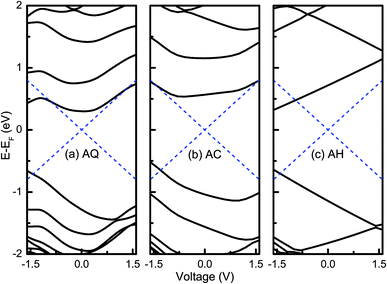 | ||
| Fig. 3 Evolution of MPSH eigenvalues under bias voltages for (a) AQ, (b) AC, and (c) AH. The dashed blue lines indicate the bias window. | ||
As discussed above, the evolutions of HOMO and LUMO under bias voltages seem to conflict with the I–V characteristics for AQ. Therefore, to obtain a well understand of the rectifying mechanism for the three molecular junctions, spatial distributions of the frontier molecular orbitals are explored and presented in Fig. 4. First of all, it is noted that after substituting one of the terminal thiol groups by a cyano group, the frontier molecular orbitals are no longer symmetrically distributed over the molecule backbones compared to those for the symmetric counterparts,9 which provides one of the prerequisites for rectification under bias voltages. It is clearly seen that the LUMO of AQ is localized on the right moiety under zero bias voltage and becomes more localized at −1.6 V. Instead, it turns to be delocalized all over the molecule at 1.6 V. So, LUMO will contribute a larger current under higher positive bias voltages than negative biases. For the HOMO of AQ, it is localized on the left block of the molecule under zero bias voltage, and still keeps localized under negative bias voltages, which leads to little contributions to the current although it enters into the bias windows at higher negative bias voltages. At this point, it is easy to understand why AQ has a larger current under positive bias voltage than under negative bias voltage. Differently, the spatial distributions of HOMO and LUMO for linear-conjugated AC are more delocalized at zero bias voltage as well as when an external bias voltage is applied. That is to say, the magnitude of current under bias voltages is mainly dominated by whether there is molecular orbital included in the bias windows. Thereby, a larger current under negative bias voltages should be clearly shown for AC. When it goes to the conjugation-broken AH, one can see the wavefunctions of HOMO and LUMO are highly localized on the donor and acceptor segment of the molecule respectively, as is always seen in D–A type molecule. The spatially localizations of HOMO and LUMO are responsible for the rigidly shift along the Fermi level of the adjacent electrode under bias voltage and further the enhanced rectification ratio for AH. By now, we can see a distinct modulation on the spatial distributions of frontier molecular orbitals and hence the rectifying performance by changing conjugation type of the bridge segment in D–B–A arylethynylene molecular diodes.
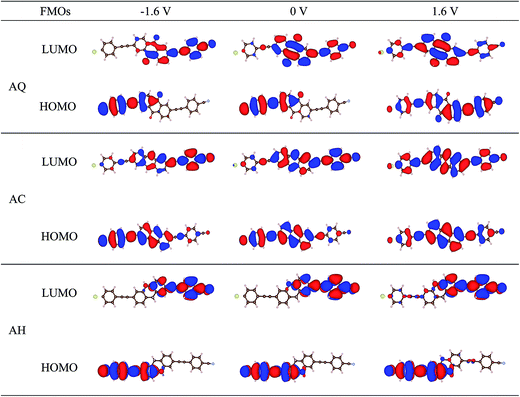 | ||
| Fig. 4 Spatial distributions of the perturbed frontier molecular orbitals (FMOs) for molecular junction AQ, AC, and AH at the bias voltages of −1.6, 0, and 1.6 V. | ||
The rectifying effect of each molecular junction is finally verified directly by the bias-dependent transmission spectra, which are plotted in Fig. 5. From Fig. 5a, we can see the current of AQ is mainly dominated by the LUMO contributed transmission peak locating at 0.3 eV above EF at zero bias voltage. When either a positive or negative bias voltage applied, it moves away from EF, but it is included in the bias windows at a larger magnitude of bias voltage. However, as it is shown in Fig. 5a, the intensity of this peak is quickly suppressed as the increase of the negative bias voltage, which results in a rectification along the positive bias voltage. For the linearly-conjugated AC, the LUMO originated transmission peak makes nearly equal contribution to the current under −1.6 V and 1.6 V. Rather oppositely, there is a transmission peak at around 0.7 eV below EF arising from HOMO also makes a contribution to the current at −1.6 V while this peak is excluded outside of the bias window, which leads to an inverted rectification along the negative bias voltage. When it turns to the broken-conjugated AH, there is only a transmission peak with intensity of 0.004 at 0.75 eV around EF at zero bias voltage, which can be attributed to LUMO. This peak moves along with EF of the right electrode under bias voltages, which results in the entrance into the bias window at higher negative bias voltages while exclusion out of the bias window at positive bias voltages. Therefore, an inverted rectifying direction as well as a large rectification ratio is present.
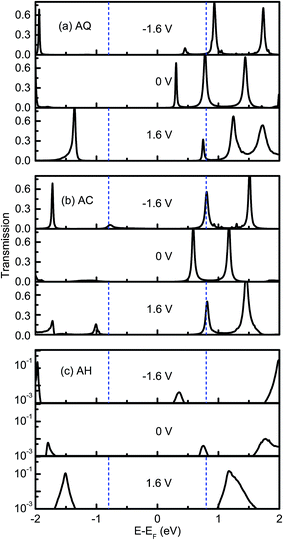 | ||
| Fig. 5 Electronic transmission spectra for (a) AQ, (b) AC and (c) AH at −1.6, 0, 1.6 V. The dashed blue lines indicate the bias window. | ||
4. Conclusions
Three donor–bridge–acceptor (D–B–A) type molecular diodes are designed by replacing one of the thiol anchoring groups to cyano in symmetric thiolated arylethynylene molecule. By using the first-principles method, conjugation effects on the rectifying properties of the three D–B–A arylethynylene diodes are theoretically investigated, where the center bridging fragment is varied from cross-conjugated 9,10-anthraquinone (AQ), linearly-conjugated anthracene (AC) to broken-conjugated 9,10-dihydroanthracene (AH). It is found that both the rectifying performance and rectification direction are highly dependent on the conjugation type of the central bridging segment. The rectification performance is improved and the rectifying direction is inverted when the central bridge is changed from cross-conjugated AQ to linearly-conjugated AC. More interestingly, when the conjugation of the bridge fragment is broken for AH, the rectification performance is further enhanced remarkably. Analysis of the molecular eigenstates as well as the transmission spectra reveals that the asymmetric evolution of strongly localized frontier molecular orbitals under positive and negative bias voltages, induced by conjugation breaking, is responsible for the great enhancement in rectification ratio for AH.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11374195 and 11547252). Thanks to the supporting of Taishan scholar project of Shandong Province.References
- A. Troisi and M. A. Ratner, Nano Lett., 2004, 4, 591–595 CrossRef CAS.
- S. J. Tans, A. R. Verschueren and C. Dekker, Nature, 1998, 393, 49–52 CrossRef CAS.
- D.-Q. Zou, Y. Song, Z. Xie, Z.-L. Li and C.-K. Wang, Phys. Lett. A, 2015, 379, 1842–1846 CrossRef CAS.
- G. Ji, B. Cui, Y. Xu, W. Zhao, D. Li, D. Liu and C. Fang, RSC Adv., 2014, 4, 16537–16544 RSC.
- C. Cheng, H. Hu, Z. Zhang and H. Zhang, RSC Adv., 2016, 6, 7042–7047 RSC.
- A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283 CrossRef CAS.
- C. S. Kumarasinghe, M. Premaratne, S. D. Gunapala and G. P. Agrawal, Sci. Rep., 2016, 6, 21470 CrossRef CAS PubMed.
- H. He, R. Pandey, G. Mallick and S. P. Karna, J. Phys. Chem. C, 2009, 113, 1575–1579 CAS.
- H. Valkenier, C. M. Guédon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Phys. Chem. Chem. Phys., 2014, 16, 653–662 RSC.
- A. B. Ricks, G. C. Solomon, M. T. Colvin, A. M. Scott, K. Chen, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 15427–15434 CrossRef CAS PubMed.
- G. Hu, G. Zhang, J. Ren, C. Wang and S. Xie, Appl. Phys. Lett., 2011, 99, 082105 CrossRef.
- X. Deng, Z. Zhang, J. Zhou, M. Qiu and G. Tang, J. Chem. Phys., 2010, 132, 124107 CrossRef PubMed.
- G.-P. Zhang, Z. Xie, Y. Song, G.-C. Hu and C.-K. Wang, Chem. Phys. Lett., 2014, 591, 296–300 CrossRef CAS.
- X.-X. Fu, R.-Q. Zhang, G.-P. Zhang and Z.-L. Li, Sci. Rep., 2014, 4, 6357 CrossRef CAS PubMed.
- Z. Li and D. S. Kosov, J. Phys. Chem. B, 2006, 110, 19116–19120 CrossRef CAS PubMed.
- Y. Lee, B. Carsten and L. Yu, Langmuir, 2008, 25, 1495–1499 CrossRef PubMed.
- G.-P. Zhang, G.-C. Hu, Y. Song, Z.-L. Li and C.-K. Wang, J. Phys. Chem. C, 2012, 116, 22009–22014 CAS.
- X. Zuo, L. Chu, G.-P. Zhang and C.-K. Wang, Chem. Phys. Lett., 2016, 663, 74–78 CrossRef CAS.
- H. Liu, P. Li, J. Zhao, X. Yin and H. Zhang, J. Chem. Phys., 2008, 129, 224704 CrossRef PubMed.
- G.-P. Zhang, G.-C. Hu, Z.-L. Li and C.-K. Wang, Chin. Phys. B, 2011, 20, 127304 CrossRef.
- H. Nakamura, Y. Asai, J. Hihath, C. Bruot and N. Tao, J. Phys. Chem. C, 2011, 115, 19931–19938 CAS.
- J. Zhao, C. Yu, N. Wang and H. Liu, J. Phys. Chem. C, 2010, 114, 4135–4141 CAS.
- G.-P. Zhang, G.-C. Hu, Z.-L. Li and C.-K. Wang, J. Phys. Chem. C, 2012, 116, 3773–3778 CAS.
- G. M. Morales, P. Jiang, S. Yuan, Y. Lee, A. Sanchez, W. You and L. Yu, J. Am. Chem. Soc., 2005, 127, 10456–10457 CrossRef CAS PubMed.
- T. Kostyrko, V. M. García-Suárez, C. J. Lambert and B. R. Bułka, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085308 CrossRef.
- D. Fracasso, H. Valkenier, J. C. Hummelen, G. C. Solomon and R. C. Chiechi, J. Am. Chem. Soc., 2011, 133, 9556–9563 CrossRef CAS PubMed.
- H. Liu, N. Wang, P. Li, X. Yin, C. Yu, N. Gao and J. Zhao, Phys. Chem. Chem. Phys., 2011, 13, 1301–1306 RSC.
- C. Van Dyck and M. A. Ratner, Nano Lett., 2015, 15, 1577–1584 CrossRef CAS PubMed.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- Atomistix ToolKit version 2015.1, QuantumWise A/S, http://www.quantumwise.com Search PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. C. Payne, M. P. Teter, D. C. Allan, T. Arias and J. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045 CrossRef CAS.
- S. Datta, Electronic transport in mesoscopic systems, Cambridge University Press, 1997 Search PubMed.
- G.-P. Zhang, G.-C. Hu, Y. Song, Z. Xie and C.-K. Wang, J. Chem. Phys., 2013, 139, 094702 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00254h |
| This journal is © The Royal Society of Chemistry 2017 |