Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An approach for correlating the structural and electrical properties of Zr4+-modified SrBi4Ti4O15/SBT ceramic
Priyambada Nayak *a,
Tanmaya Badapandab,
Anil Kumar Singha and
Simanchalo Panigrahia
*a,
Tanmaya Badapandab,
Anil Kumar Singha and
Simanchalo Panigrahia
aDepartment of Physics and Astronomy, National Institute of Technology, Rourkela, Odisha-769008, India. E-mail: priyambada.pce@gmail.com; Fax: +91-661-2464723; Tel: +91-9861260253
bDepartment of Physics, C.V. Raman College of Engineering, Bhubaneswar, Odisha-752054, India
First published on 14th March 2017
Abstract
In the present work, B-site modified layer-structured strontium bismuth titanate (SBT) ceramics with the nominal formula SrBi4Ti4−xZrxO15 were prepared by solid state reaction route and the tailoring effects of zirconium (Zr) were investigated thoroughly. The X-ray diffraction analysis shows that the substitution leads to the formation of a single phase layered perovskite up to x ≤ 0.15 and a ZrO2-based secondary phase was detected for higher Zr-doped compositions. The higher grain-growth rate induced by the larger ionic radius of Zr4+ than Ti4+ was supported by the field emission scanning electron microscopy (FESEM) results. The transition temperature increases slightly for the Zr-modified compositions, which can be described in terms of structural distortion due to the internal stresses developed within the ceramics. The Cole–Cole plot analysis of impedance spectra enabled to distinguish two relaxation behaviours that were assigned to originate from grains and grain boundaries. It was also observed that the remnant polarization and piezoelectric coefficient increases up to the solubility limit of Zr and then decreases with higher doping content. The temperature dependent piezoelectric coefficient was also studied, and was found to be stable up to the transition temperature in all compositions. All these results were explained on the basis of occupancy of the Zr4+ ion at the B-site and for the higher composition ZrO2 secondary phase. Even the composition x = 0.15 exhibited low conductivity, a moderate dielectric constant and a highly stable d33 value, demonstrating that the ceramic is an excellent material for high-temperature piezoelectric application. The possible reason for the enhancement of the electrical properties in the Zr-modified ceramic was discussed based on the structural analysis, which may be used for designing and/or modifying properties of SBT-related ceramics.
1. Introduction
The layered perovskite family, including many titanates, has been extensively studied in recent years due to their remarkable electrical properties, which can be widely used for the manufacture of ferroelectric random-access memory and high-temperature piezoelectric sensors.1,2 The structure of these compounds can be described as pseudo-perovskite (Am−1BmO3m+1)2− slabs separated by (Bi2O2)2+ layers along the crystallographic c-axis.3 The 12-fold co-ordinated A-site can be occupied by mono-, di-, or tri-valent metallic cations, while the octahedral coordinated B-site can be occupied by tetra-, penta-, or hexa-valent metallic cations. The number of octahedral sites along the c-axis between two neighbouring (Bi2O2)2+ layers is indicated by m. The origin of ferroelectricity in these ceramic systems is the displacement of A-site cations of the perovskite block with cooperative tilting of the BO6 octahedra shown in Fig. 1(a). Among the layered family members, strontium bismuth titanate SrBi4Ti4O15 (SBT) is the most versatile; it presents a mobile unit in an orthorhombic structure, described by the C2v12(A21am) space group, exhibits unique properties, such as high Curie temperature (∼530 °C), high dielectric constant (∼200 at room temperature), high dielectric breakdown, low dielectric loss (0.017), high anisotropy and many other properties, suitable for use in acoustic and stress sensor devices working at high temperature.4,5 However, compared with traditional piezoelectric ceramics, such as lead zirconate titanate (PZT) and BaTiO3, SBT has a low piezoelectric coefficient (15 pC/N) and electromechanical coupling factors with a high coercive field because the rotation of the spontaneous polarization is restricted to the a–b plane. High electronic conductivity (105 S cm−1) due to the volatilization of bismuth at high temperature should be attributed to defects mainly related to oxygen vacancies. Still, there has been increasing interest in SBT-doped systems because of the fact that their electrical properties can be controlled within a wide range by means of mixed crystal formation and doping. For instance, partial replacement of Bi by other elements of the lanthanide series has been investigated systematically mainly in bulk ceramics. Properties of La3+-, Dy3+- and Er3+-modified SBT ceramics, which lead to structural distortion, induced strain and significantly modifed electrical properties, were also reported by Chen et al.,6 Mamatha et al.7 and Peng et al.8 At the same time, a decrease in the remnant polarisation (Pr) and Curie temperature (TC) was reported due to the effect of foreign atoms at the Bi-site of SBT. Several reports are also available for A-, B- and both A- and B-site doped SBT, which have attracted surging attention owing to their enhancement of electrical properties.9,10 It has been reported that the ferroelectricity of the titanate-based layer perovskite structure, highly depends on the hybridization of the valence states between the O- ion and the B-site ion, and which can be enhanced by the distortion of the B–O interaction. Therefore, many reports are available on doping at the B-site of SBT ceramics, which tends to enhance the properties. However, modification at the B-site has mainly been focused on aliovalent cation doping, such as V5+ and W6+, as a substitution for Ti4+.11,12 Moreover, it is noted that the aliovalent cations (V5+ and W6+) will induce other additional space charges, and can decrease the oxygen vacancy considering the charge compensation mechanism. Consequently, studying the effect of B-site doping by cations with the same valence on the structural and electrical properties of SBT is interesting.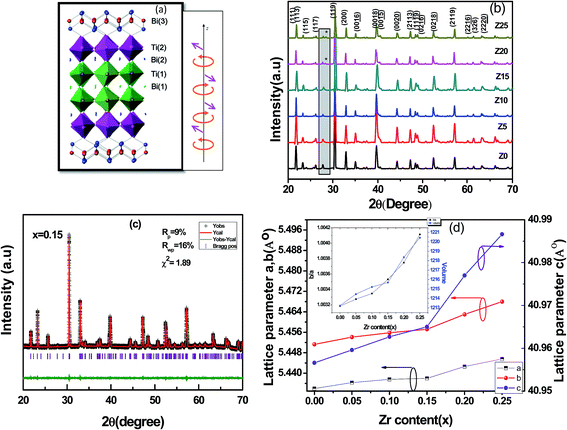 | ||
| Fig. 1 (a) Crystal structure of SBT system. (b) XRD patterns of SBTZ-x ceramics at RT. (c) Rietveld refinement of x = 0.15 specimen. (d) Variation of lattice constants (a–c) in SBTZ-x ceramics. | ||
Recently, Ba (ZrxTi1−x)O3 (BZT) has been choosen for the fabrication of ceramic capacitors because Zr4+ is chemically more stable than Ti4+.13 Similarly, the detailed structural analysis of perovskites Pb(ZrxTi1−x)O3 (PZT) and BLSF ceramics such as Bi4Ti3O12 and BaBi4Ti4O15 has shown that the substitution of Ti by Zr4+ can make the material respond to the external field more easily.14–16 Hennings et al. suggested that incorporation of zirconia particles into barium titanate can form a core–shell structure and the desired temperature-stability of the dielectric properties is achieved by formation of core–shell grains.17 Jesurani et al. showed that the substitution of Zr in place of Ti causes fine-grained and dense microstructure, which changes the electrical properties of CCTO ceramics.18 It is well known that the inhomogeneous composition due to the doping element and internal stress within the microstructure are matters of concern because they greatly influence the electrical properties. Previous reports from the complex impedance plot of SBT analysis shows that two microelements, namely, bulk and grain boundary, contribute to the conduction process that affects the electrical properties.19 It has been argued that the plate-like grains are separated by a grain boundary formed along the low energy bismuth oxide layers and these grain boundaries are visible in the complex impedance plot.20 So, concerning all the factors, in the present work we report the effects of Zr4+ doping on the microstructure, ferroelectric, dielectric and piezoelectric properties of the SBT system. We believe that as Zr4+ possesses a different state (2d) than that of Ti4+ (3d) and the introduction of Zr4+ would bring in Zr–O with a different valence band distance from that of Ti–O, it can lead to the enhancement of the electrical properties. We also investigate the grain and grain boundary effects on the electrical properties of Zr-doped SBT ceramics using complex impedance spectroscopy technique.
2. Experimental
2.1 Synthesis
The Zr-modified SBT ceramics with general formula SrBi4Ti4−xZrxO15 ((SBTZ) with x = 0.00, 0.05, 0.1, 0.15, 0.2, and 0.25, named as Z05, Z10, Z15, Z20, and Z25, respectively) were fabricated by solid-state reaction route using high-purity (>99.9%) oxides: SrCO3, Bi2O3, TiO2 and ZrO2. The powders were weighed in stoichiometric ratio and mixed thoroughly by ball milling in acetone medium for 24 h. After the slurry was dried, the mixture was calcined at 900 °C for 3 h in a covered corundum crucible. The obtained powders were mixed with 3 wt% binder (PVA) and compacted into disk-shaped pellets with diameter of 10.0 mm and thickness of 1.0 mm at 5 MPa. Finally, the pellets were sintered at 1050 °C for 2 h in a conventional furnace at a heating and cooling rate of 5 °C min−1.2.2 Characterization
The phase(s) of the final products were analysed by using X-ray diffraction (XRD) patterns collected by X-ray powder diffractometer (Rigaku Ultima IV) with CuKα radiation (λ = 1.5405 Å) at a scanning rate of 2° min−1 from 20° to 80°. The surface morphology and micro-structural features of the sintered pellets were obtained using a field emission scanning electron microscope (JEOL\T-330). The density of the samples was measured by Archimedes' principle. The dielectric and impedance (frequency range 100 Hz to 1 MHz) data were collected using a Wayne Kerr impedance analyser, while keeping the electrode pellets in sandwich geometry. The electrical polarization of the poled samples was measured using ferroelectric loop-tracer (Radiant Technology). For the piezoelectric measurements, the samples were poled by DC electric field of 10 kV cm−1 for 30 min at 250 °C and the piezoelectric constant d33 was measured using a YE2730A piezometer.3. Results and discussion
3.1 Structural characterization
The room temperature X-ray diffraction (XRD) patterns of the SBTZ ceramics (x = 0.00–0.25) in the 2θ range of 20–70° are shown in Fig. 1(b). As can be seen in Fig. 1(b), the Aurivillius structure was identified by indexing all the diffraction peaks on the basis of an orthorhombic cell with a space group A21am (JCPDS no. 43-0973), indicating that the Zr4+ ions diffused into the B-site lattice and formed solid solutions, as expected. Meanwhile, it is obvious that the highest diffraction peak in the SBTZ ceramics corresponds to the (119) orientation, which is consistent with the fact that it is the strongest diffraction peak in BLSFs with m = 4.21–23 To confirm the purity of the layer perovskite phase, Rietveld refinement was carried out on the XRD data of the x = 0.15 sample, as shown in Fig. 1(c). The final refinement convergence was achieved with Rp = 9%, Rwp = 16% and χ2 = 1.89. However, a subtle crystallographic evolution of the SBTZ ceramics occurred along with the increasing Zr doping content (x). Firstly, the average crystallite sizes for the samples increased with the increase of Zr content, as presented in Table 1. The Zr4+ incorporation changed the type of bonding of Ti–O to Zr–O, which may be the reason for changes in the crystallite size. Secondly, with the increase in doping concentration, the peaks at (119), (200) and (0016) are shifted towards lower 2θ values, which is expected because of the larger ionic radius of Zr4+ (0.72 Å) as compared to Ti4+ (0.60 Å). Thirdly, as marked in the XRD patterns, minor amounts of a secondary phase of ZrO2 were detected in the compositions with x = 0.2 and 0.25. Therefore, it is considered that the solid solubility limit is ∼0.15. The shifting of the diffraction peaks with Zr4+ substitution indicates the change in the lattice parameters. Therefore, the subtle changes in these characteristic peaks illustrate a crystallographic evolution of the SBTZ ceramics, which can be described as the lattice distortion induced by the Zr4+ substitution for Ti4+.| Compound | Measured density (g cm−3) | Percentage of theoretical density | Orthorhombicity [2(a − b)/(a + b)] | Tetragonality, c/a | Particle size (Å) | Grain size (μm) | εr at 100 kHz | TC (°C) |
|---|---|---|---|---|---|---|---|---|
| x = 0.00 | 7.23 | 90.48 | 3.1 | 7.5370 | 447 | 2.549 | 1573 | 535 |
| x = 0.05 | 7.34 | 91.86 | 3.2 | 7.5344 | 472 | 3.435 | 1609 | 537 |
| x = 0.1 | 7.51 | 93.99 | 3.3 | 7.5332 | 495 | 3.776 | 1706 | 537 |
| x = 0.15 | 7.68 | 96.12 | 3.5 | 7.5332 | 512 | 4.653 | 1835 | 537 |
| x = 0.2 | 7.7 | 96.37 | 3.7 | 7.5288 | 525 | 4.969 | 1130 | 555 |
| x = 0.25 | 7.73 | 96.74 | 4.1 | 7.5271 | 589 | 5.308 | 1019 | 560 |
In order to further investigate the effect of Zr doping on the crystallographic modification in the SBT system, the lattice parameters and cell volumes of the samples were calculated and are plotted as a function of doping content (Zr), as shown in Fig. 1(d). It can be clearly seen that the crystallite size as well as lattice constants and unit cell volume V increase monotonically with the increasing x, resulting in an expansion of the lattice constant. This expansion implies that the incorporation of Zr produces the lattice distortion in the pseudo-perovskite block. Therefore, the volume of the unit cell increased with substitution and the effect of Zr4+ substitution on orthorhombic distortion was evaluated by using the formula 2(a − b)/(a + b), which slightly increases with the increase in Zr content (Table 1). As the solid solubility limit of zirconia is ≤0.15, there is a contradictory result of expansion of volume and crystallite size in the x = 0.2 and 0.25 compositions. It may be because of the excess zirconia-containing phase present at the grain boundary of those ceramics. The sintered density, obtained by the Archimedes method, increased from 7.23 to 7.74 g cm−3 with increasing zirconium content up to x = 0.25, indicating that the zirconium modifications enhanced the densification of the SBT ceramics. Related to the theoretical density (ρ = 7.99 g cm−3, derived from JCPDS 43-0973 and X-ray diffraction), the percentages of the theoretical densities ‘ρ’ of the unmodified and zirconium-modified SBT ceramics were obtained, and are listed in Table 1. The ρ of the zirconium-modified SBT ceramics were higher than 96% of the theoretical density, indicating acceptable densification during the sintering process.
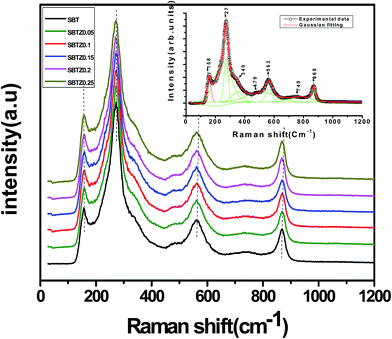
3.2 Raman analysis
Raman spectroscopy was used to probe the subtle changes in the local structure of the modified system under investigation, which can be correlated with the structural study performed by X-ray diffraction. The room temperature Raman spectra of the Zr modified SBT ceramics from 100–1200 cm−1 are shown in Fig. 2. It is reported that SBT ceramics have around seven Raman active modes.24 In order to determine the exact peak frequencies of the different Raman active modes, we fitted the Raman data of the unmodified SBT with the sum of seven peaks by Gaussian fit, which is inserted in Fig. 2. The thin solid lines shown in the fitted graph are of the individual modes and the thick solid line shows the total fit to the experimental data (open circle). In the undoped SBT system, vibrational modes were observed due to the presence of the referred type of Ti–O, Bi–O, Sr–O bond. It can be seen from the figure that the Raman spectra of all specimens exhibit the same phonon modes at approximately 158, 272, 340, 449, 563, 749 and 868 cm−1, which are related to the orthorhombic phase (A21am space group).25,26 The low frequency vibrational modes are ascribed to the Bi3+ ion at the A-site, generally occurring in the range below 200 cm−1. The vibrational mode at 158 cm−1 is the characteristic feature of the layered structures and corresponds to the vibrations as a whole. The vibrational modes related to the Ti–O bonds are located at wave numbers beyond 200 cm−1 (272, 563 and 749 cm−1). The mode at 272 cm−1 corresponds to the torsional bending of the TiO6 octahedra, which is because of B1g mode, and the modes at 563 and 749 cm−1 correspond to the TiO6 stretching mode, which corresponds to B2g and B3g modes.12 The mode at 868 cm−1 is probably ascribed to the vibrations of the A–O bond.25 Compared with the Raman spectra of the SBT ceramic system, it is observed that the modes at 272, 563 and 749 cm−1 remain undeviated up to x ≤ 0.15. For higher concentrations, a clear downshift and peak broadening was observed with increasing Zr content. The anisotropic crystal structure of SBT where the c-lattice parameter is significantly larger than the in-plane lattice parameters a and b, ensures that the x–y vibrations of the Ti atoms are affected much more strongly by the size of the substitutive atom as compared to the z-axis vibrations. This explains the shifting of the mode that corresponds to the x–y vibration of apical oxygen atoms of TiO6 octahedra towards the lower frequency. The large shift in the Z20 and Z25 compositions seems to originate from the ionic difference between the Ti and Zr atoms, which alters the environment around the TiO6 octahedra in an anisotropic manner.3.3 Microstructural analysis
The FESEM micrographs of the SBTZ sintered samples are shown in Fig. 3. The micro-structure reveals tightly bonded well-defined grains with no obvious porosity, corresponding to the high relative density of up to 96% discussed in the previous section. The grain sizes were measured by linear intercept method and are listed in Table 1. The average length of the plate-like grains significantly increased from 2.549 μm to 5.308 μm, but the thickness varies from 0.50 μm to 0.38 μm for pure SBT and SBTZ25 ceramics, respectively. This shows that the aspect ratio L/T (length/thickness) is controlled by the Zr-dopants. The Zr modifications increase the grain growth rate in the direction perpendicular to the c-axis and result in the highly anisotropic microstructure of the SBTZ-25 ceramic. The increase in grain size with Zr4+ substitutions seems to be related to the higher grain-growth rate induced by the larger ionic radius of Zr than Ti.273.4 Dielectric study
Fig. 4 illustrates the frequency dependence of the real (ε′) and imaginary part dielectric constant (ε′′) of all the ceramics at 600 °C. The dielectric constants for all the samples show dispersion at lower frequencies and become constant at higher frequencies. This behaviour may be explained on the basis of Maxwell Wagner type interfacial polarization in agreement with Koop's theory.28 According to this model, polycrystalline ceramics have a heterogeneous microstructure that can be imagined to consist of semiconducting grains separated by insulating grain boundaries, also depicted in the Nyquist plots (discussed later). Free charges build up owing to the defects; that is, oxygen vacancies present in the sample create space charges at the interface between the sample and the electrode's space-charge polarization, whose polarization responds to the applied electric field. At low frequencies these charges have enough time to move longer distances in the sample, creating larger electronic polarization and therefore a high value of dielectric constant. As the frequency increases, the charge carriers are unable to follow the applied external field and so there is a decrease in polarizability. On the other hand, it has been observed that the value of ε′ was found to increase up to x = 0.15. In a grain boundary barrier layer system, the dielectric constant of the materials is linearly proportional to the average value of grain size and inversely proportional to the grain boundary thickness.29 As the grain size increases due to Zr doping, so the dielectric constant increases up to x = 0.15. However, for higher values of x, the grain boundary thickness increases due to the presence of the secondary phase, which reduces the dielectric constant.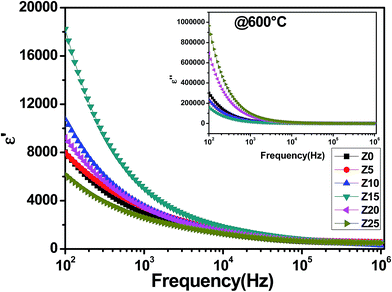 | ||
| Fig. 4 Frequency dependence of the real (ε′) and imaginary parts of the permittivity (ε′′) of SBT and the modified system at 600 °C. | ||
The insert of Fig. 4 shows variation of loss factor (ε′′) with frequency. The loss factor (ε′′) decreases continuously with increasing frequency. As grain boundaries have high resistance, more energy is required for the motion of charge carriers in the low frequency region, hence the energy loss is high. Conversely, less energy is required for the motion of charge carriers in the high frequency region due to the lower resistance, which reduces the loss. It can also be observed from the figure that the dielectric loss decreases with increasing Zr substitution up to x = 15 then increases with further doping. The increment in the dielectric loss at higher doping may be attributed to the poor electric insulation of the impurity phases.30
To further elucidate the temperature-dependent dielectric properties, the relative permittivity (εr) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at 100 kHz frequency as a function of temperature are presented in Fig. 5. The phase transition in the present modification (from Fig. 5(a)) is slightly higher than that of SBT (TC = ∼530 °C) and the variation is within 25° (listed in Table 1). In BLSF ceramics, isovalent substitution at the B-site changes the lattice distortion. The structural distortion is explained in terms of a lattice mismatch between the BO2 and AO planes in the perovskite-type unit, and the tolerance factor (t) of the perovskite-layer units is given by:
δ) at 100 kHz frequency as a function of temperature are presented in Fig. 5. The phase transition in the present modification (from Fig. 5(a)) is slightly higher than that of SBT (TC = ∼530 °C) and the variation is within 25° (listed in Table 1). In BLSF ceramics, isovalent substitution at the B-site changes the lattice distortion. The structural distortion is explained in terms of a lattice mismatch between the BO2 and AO planes in the perovskite-type unit, and the tolerance factor (t) of the perovskite-layer units is given by:
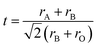 | (1) |
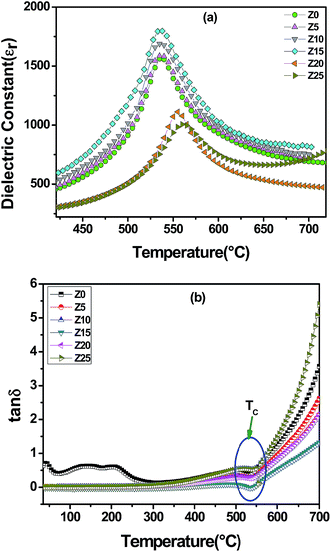 | ||
Fig. 5 (a) Temperature dependence of dielectric constant (εr). (b) Dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of SBTZ-x ceramic at frequency of 100 kHz. δ) of SBTZ-x ceramic at frequency of 100 kHz. | ||
The variation of loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) as a function of temperature is given in Fig. 5(b). The dielectric loss (tan
δ) as a function of temperature is given in Fig. 5(b). The dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for zirconium-modified SBT ceramics was found to be more stable than that of the unmodified SBT samples. The figure shows a kink, observed in all the ceramics, which separates the ferroelectric and paraelectric phase transition mechanisms. This kind of sharp peak occurs when the hopping frequency of the electric charge carriers becomes approximately equal to that of the external applied AC electric field.32
δ) for zirconium-modified SBT ceramics was found to be more stable than that of the unmodified SBT samples. The figure shows a kink, observed in all the ceramics, which separates the ferroelectric and paraelectric phase transition mechanisms. This kind of sharp peak occurs when the hopping frequency of the electric charge carriers becomes approximately equal to that of the external applied AC electric field.32
3.5 Relaxation behaviour and electrical properties
The impedance spectroscopy method is widely used to characterize the electrical properties of materials and give us data regarding both the resistive (real part i.e. Z′ = Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and reactive (imaginary part i.e. Z′′ = −Z
θ) and reactive (imaginary part i.e. Z′′ = −Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
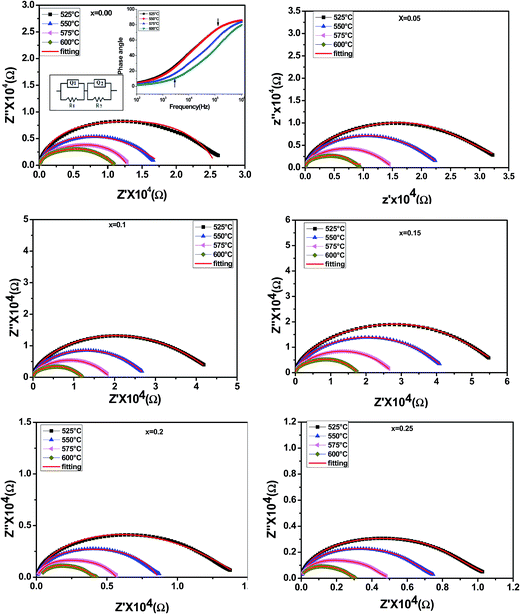
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) components with various transport mechanisms operating within the microstructure of the material. The Cole–Cole plots (Nyquist plots) of SBTZ samples plotted at various temperatures are shown in Fig. 6. The low temperature plots become straight lines with a large slope, indicating the high insulating nature, whereas with increasing temperature, the curves bow toward the abscissa axes to form semi-circular arcs observed in all samples. Further, at higher temperature the radii of the semi-circular arcs become smaller, indicating lower values of resistance. The semi-circular arcs show a slight distortion, indicating deviation from the Debye relaxation mechanism, which may be due to the presence of multi-relaxation processes in the material. The inset of Fig. 6 (for x = 0.00) shows the Bode-phase diagram with frequency for the Z0 ceramic as a representative curve. The arrows show step-like changes in the curves, which suggests that there are at least two relaxation behaviours in the ceramics. But to make it more clear about the relaxation process, the complex impedance data were simulated with an equivalent circuit as inserted in Fig. 6 (x = 0.00) using ‘ZSimpWin’ software. The equivalent circuit contains two resistors in series, each shunted by a constant phase element (CPE). The impedance of CPE given by Abram et al.33 is:
θ) components with various transport mechanisms operating within the microstructure of the material. The Cole–Cole plots (Nyquist plots) of SBTZ samples plotted at various temperatures are shown in Fig. 6. The low temperature plots become straight lines with a large slope, indicating the high insulating nature, whereas with increasing temperature, the curves bow toward the abscissa axes to form semi-circular arcs observed in all samples. Further, at higher temperature the radii of the semi-circular arcs become smaller, indicating lower values of resistance. The semi-circular arcs show a slight distortion, indicating deviation from the Debye relaxation mechanism, which may be due to the presence of multi-relaxation processes in the material. The inset of Fig. 6 (for x = 0.00) shows the Bode-phase diagram with frequency for the Z0 ceramic as a representative curve. The arrows show step-like changes in the curves, which suggests that there are at least two relaxation behaviours in the ceramics. But to make it more clear about the relaxation process, the complex impedance data were simulated with an equivalent circuit as inserted in Fig. 6 (x = 0.00) using ‘ZSimpWin’ software. The equivalent circuit contains two resistors in series, each shunted by a constant phase element (CPE). The impedance of CPE given by Abram et al.33 is:
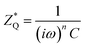 | (2) |
| Compound | Temperature (°C) | Z′′ activation energy (Ea) in eV | Pr (μC cm−2) | d33 (pC/N) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 525 | 550 | 575 | 600 | 450–525 °C | 550–700 °C | ||||
| x = 0.00 | Rg | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410 |
9154 | 0.44 | 0.59 | 0.533 | 11 |
| Rgb | 6909 | 3361 | 2389 | 1730 | |||||
| x = 0.05 | Rg | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 640 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
4043 | 0.6 | 0.72 | 0.3421 | 12 |
| Rgb | 5817 | 1165 | 1529 | 3619 | |||||
| x = 0.10 | Rg | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 950 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
0.65 | 0.80 | 0.3323 | 14 |
| Rgb | 1606 | 1473 | 1728 | 1423 | |||||
| x = 0.15 | Rg | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
0.72 | 0.84 | 0.3280 | 16 |
| Rgb | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 910 |
1798 | 1788 | 1468 | |||||
| x = 0.2 | Rg | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
6715 | 4431 | 2961 | 0.58 | 0.62 | 0.319 | 13 |
| Rgb | 5139 | 1910 | 1223 | 3292 | |||||
| x = 0.25 | Rg | 9731 | 6989 | 4459 | 2859 | 0.51 | 0.47 | 0.279 | 12 |
| Rgb | 1262 | 893.8 | 592.8 | 2972.8 | |||||
The variation of the imaginary part of impedance (Z′′) with frequency for SBTZ ceramics at various temperatures is shown in Fig. 7. It can be observed from the figure that all the curves merge at a frequency greater than 100 kHz. This is owing to the fact that at higher frequencies the dispersion due to grains dominates and the space charge effect decreases. It is also observed that the peak in each graph shifts towards higher frequency and the magnitude of the peak decreases as the temperature is raised. This can be ascribed to the temperature dependent relaxation process in the samples and the peaks broaden with rise in temperature due to multiple relaxations in the samples. The maximum value of the imaginary part of impedance (Z′′max) increases with increasing Zr concentration up to x ≤ 0.15 and for higher concentrations it decreases. This is in well agreement with the interpretation of the conductivity results presented in the next section. Relaxation time (t) is calculated from the peak position of Z′′max vs. frequency plots using the relation 2πfmaxτ = 1, where fmax is the relaxation frequency. The variation of relaxation time with the inverse of temperature is presented in Fig. 8. The activation energy is calculated from the linear fit to the slope of the curve based on the equation:
τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT) exp(−Ea/kBT)
| (3) |
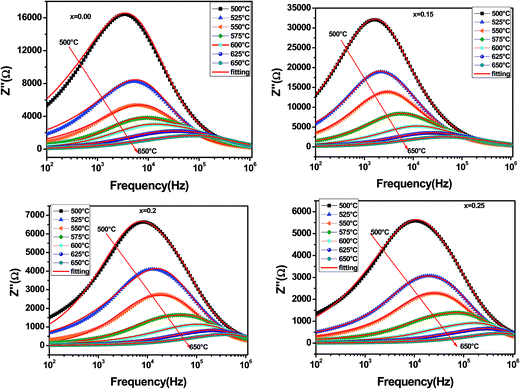 | ||
| Fig. 7 Frequency dependence of the imaginary part of impedance (Z′′) for SBT and the modified systems at selected temperatures. | ||
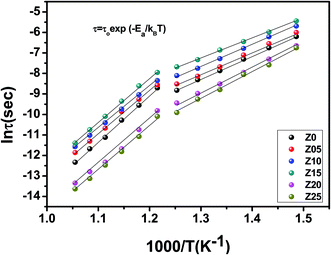 | ||
Fig. 8 The variation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1000/T (Arrhenius plot) with the imaginary impedance (Z′′) of SBTZ ceramic. τ vs. 1000/T (Arrhenius plot) with the imaginary impedance (Z′′) of SBTZ ceramic. | ||
3.6 Conduction mechanism
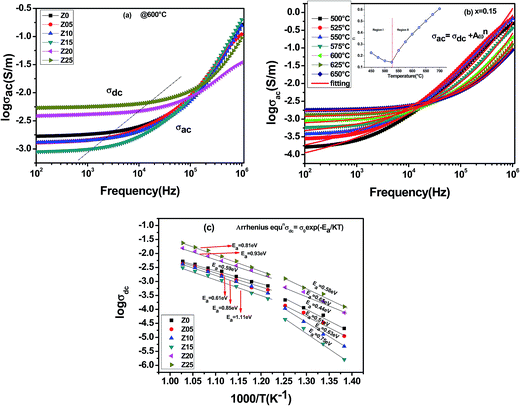
In order to understand the transport behaviour of the modified system, the samples were further characterized by frequency and temperature dependence of AC conductivity. Fig. 9(a) depicts the variation of AC conductivity (σac) with frequency for all the compositions at 600 °C. It is observed that the Zr substitution reduces the conductivity up to x ≤ 0.15, then increases with further increases in doping content (in the Z20 and Z25 ceramic systems). In the SBT system, the conduction mechanism of the leakage current involves (a) a space charge-limited conduction related to oxygen vacancies and (b) a field-assisted ionic conduction related polaron hopping between Ti4+ and Ti3+.36 Hence the reason behind lowering the conductivity of the sample with Zr doping may be attributed to the lowering of the Ti4+ concentration by Zr4+ substitution, or it can be described by the incorporation of Zr4+ with larger ionic radius may bring in a large distortion of TiO6. Nevertheless, when the Zr4+ doping content is modified to >15 mol%, the extra zirconia containing phase occurs at the grain boundary, related to the impurity phase and decreased electrical insulation. From the Cole–Cole plot at 600 °C for Z20 and Z25 samples, we showed that the grain contribution effect decreases and the grain boundary contribution effect increases. This may be owing to an increase in the grain boundary volume and a proportionate increase in disorder introduced into the sample, which supports the conductivity data.We studied the temperature dependence of the AC conductivity behaviour for all compositions, but a representative plot of the conductivity spectrum of the Z15 system at a few selected temperatures is shown in Fig. 9 (b). The total conductivity is simulated by Jonscher's power law37 and is given as
| σac = σdc + Aωn | (4) |
In the case of small polaron (the self-trapped electronic charge with spatial extension comparable to one unit cell) hopping, n increases with temperature (Region II), while for large polaron (spatial extension of charged quasi particle comparable to several unit cells) hopping, n decreases with increasing temperature (Region I).38,39 According to the small polaron model, the small polaron wells of two sites overlap, which reduces the polaron hopping energy after Zr modification.40 This fact indicates that the conductivity in this sample form may be assured by the small polaron hopping conduction at high temperature.
In order to provide the ions that are responsible for the mechanism of conduction in this material, we looked into the structural arrangement. For bismuth layer-structured compounds, the (An−1BnO3n+1)2− slabs and the (Bi2O2)2+ slabs along the c axis are connected by the strong Bi–O bond. The Zr ions was observed to preferably occupy the Ti site of the perovskite layers, as depicted in Fig. 1(a). The substitution of larger Zr ions induces stronger structural distortion by the shortest Bi–O bond lengths and the buckling of Ti–O oxygen octahedrons. It is accepted that the strong structural distortion in SBTZ results from the expected larger interstrain between the perovskite blocks and Bi2O2 slabs. The compressive stress on the perovskite blocks would drive the larger Zr ions away from the oxygen octahedrons adjacent to the Bi2O2 slabs.
The variation of DC conductivity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σdc) as a function of temperature for all SBTZ compositions is illustrated in Fig. 9(c). The solid lines represents the linear fit to the data points, suggesting the Arrhenius like charge transport mechanism within the investigated temperature range. From this figure, it can be observed that the conductivity of all the specimens increased linearly with increasing temperature and the two regions are clearly identified with a change in slope around the dielectric anomalies. The activation energy values of conductivity were calculated according to the Arrhenius type conduction process:
σdc) as a function of temperature for all SBTZ compositions is illustrated in Fig. 9(c). The solid lines represents the linear fit to the data points, suggesting the Arrhenius like charge transport mechanism within the investigated temperature range. From this figure, it can be observed that the conductivity of all the specimens increased linearly with increasing temperature and the two regions are clearly identified with a change in slope around the dielectric anomalies. The activation energy values of conductivity were calculated according to the Arrhenius type conduction process:
σdc = σo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−Ea/kBT e−Ea/kBT
| (5) |
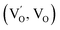 , ionisation of which creates conducting electrons as:
, ionisation of which creates conducting electrons as:
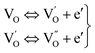 | (6) |
The conduction activation energies below TC (EaI) lie in the range of 0.44 eV to 0.75 eV and above TC (EaII) in the range of 0.59 eV to 1.12 eV. A recent calculation suggests that the activation energy value for conduction are very close to the activation energy value of oxygen vacancies in layer perovskite ferroelectric oxides and the values are associated with 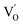 and
and 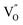 , respectively.23 At low temperatures, the EaI values for SBZT indicate that the first ionization of oxygen vacancies and electron hopping are responsible for conduction because these Ea values are much less than that of the second-ionization of oxygen vacancies.41 At high temperatures, the EaII values increases, which shows that the electrical conduction is governed by the thermal excitation of carriers from the second ionization of oxygen vacancies. Thus, it can be concluded that the electrical conductivity is dominated by the oxygen vacancies migration, changing from a single to a doubly ionized mechanism around the ferroelectric phase transition. One of the conducting electrons is created by the oxygen vacancy ionization and the other from the Ti3+ and Ti4+ valence fluctuations. The created electrons would be trapped at defects, such as boundaries, dislocations, and lattice vacancies, and might hop between the neighbouring transition metal ions as Ti4+ and Ti3+. In addition, the low conductivity and high activation energy of the Z15 specimen indicate that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain pinning. In other words, the oxygen vacancies can easily be released out and no space charge is built up.
, respectively.23 At low temperatures, the EaI values for SBZT indicate that the first ionization of oxygen vacancies and electron hopping are responsible for conduction because these Ea values are much less than that of the second-ionization of oxygen vacancies.41 At high temperatures, the EaII values increases, which shows that the electrical conduction is governed by the thermal excitation of carriers from the second ionization of oxygen vacancies. Thus, it can be concluded that the electrical conductivity is dominated by the oxygen vacancies migration, changing from a single to a doubly ionized mechanism around the ferroelectric phase transition. One of the conducting electrons is created by the oxygen vacancy ionization and the other from the Ti3+ and Ti4+ valence fluctuations. The created electrons would be trapped at defects, such as boundaries, dislocations, and lattice vacancies, and might hop between the neighbouring transition metal ions as Ti4+ and Ti3+. In addition, the low conductivity and high activation energy of the Z15 specimen indicate that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain pinning. In other words, the oxygen vacancies can easily be released out and no space charge is built up.
3.7 Ferroelectric and piezoelectric properties
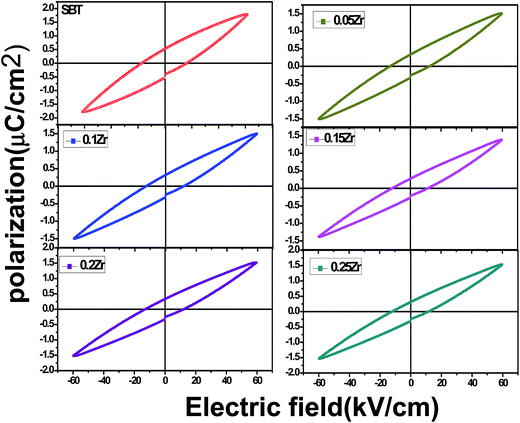
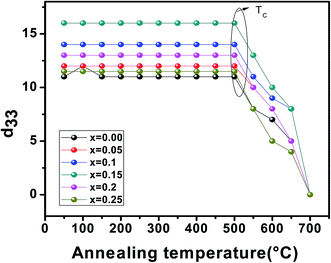
Fig. 10 displays the polarization–electrical field (P–E) hysteresis loops of the SBTZ ceramics, which were recorded at room temperature with the maximum applied voltage of about 60 kV cm−1. The parameters obtained from the hysteresis loop are listed in Table 2. It is observed that with increasing Zr-content, the Pr value decreases and the loop becomes slim. The Pr value is closely related to the orthorhombic distortion and the XRD results reveal that the orthorhombic distortion increases with increasing Zr content. Larger structural distortion generally leads to a large Pr value, which seems to contradict the current experimental results. However, it is noted that the hybridization between Ti-3d states and O-2p states decreases as Zr content increases, since the Zr4+ ion has a stronger metallicity than Ti4+, which tends to form ion bonds with O2− easier. This may be the reason for the decrement of Pr value. Compared with previous reports about the polycrystalline zirconium-modified bismuth titanate (BTO) system, similar types of results were obtained, which may correlate with the present case.42 The variation of piezoelectric constant (d33) with x for the SBTZ ceramics is listed in Table 2. The observed d33 value increases linearly as x increases up to x ≤ 0.15 and giving a maximum value of 16 pC/N for the x = 0.15 composition, then after it decreases drastically with increased Zr content. This suggests that after the substitutions of Zr4+, the ceramics become “softened”, thus giving rise to significant improvements in the d33 value, which makes the poling become more efficient because of less tangent loss. However, in Z20 and Z25 compositions, the loss of the sample increases due to secondary phases, which reduces the d33 value. It is reported that the piezoelectric activity in ceramics can be enhanced to different degrees by constructing phase boundaries and modifying the microstructure of a material, while its piezoelectric activity is strongly sensitive to the phase boundary types. In this section, we further clarify the relationship between phase boundary and piezoelectric activity. It was proposed that the general grain growth observed in oxide-doped samples should be attributed to enhanced atomic mobility; dramatic grain growth can be induced by the difference in surface free energies between the grains.43 The enhancement in the grain size increases the d33 values, but for higher concentrations (x > 0.15) as the secondary phase exists at the grain boundary the piezoelectric coefficient decreases. Again, the enhanced d33 originates from the combined effects caused by the lattice distortion and the decreasing concentrations of oxygen vacancies.The effect of the thermal annealing behaviour on the piezoelectric constant (d33) of the Zr modified specimens is shown in Fig. 11. The values of d33 become almost constant up to the transition temperature and then decrease with increasing temperature. This can be explained as the movement of non-180° domain walls can produce a contribution to the piezoelectric property.44 Moreover, it shows that the piezoelectric constant (d33) of Z15 ceramic remains almost unchanged (16 pC/N) at temperatures below 550 °C, indicating that the ceramic has excellent temperature stability so it is very tolerant to thermal annealing and might be an appropriate candidate for high-temperature applications.
4. Conclusion
It is concluded that B-site modification of SBT-based materials by zirconium was achieved using conventional solid-state processing. X-ray diffraction and Raman studies confirmed the formation of a single phase for Zr4+ substituted SBT up to x ≤ 0.15 and for x = 0.2 and 0.25 (Z20, Z25) compositions, ZrO2 based impurity phases are detected. An increase in the grain size was observed due to Zr modification. The internal stresses developed within the SBTZ ceramics by substitution varies the transition temperature. The impedance spectroscopy analysis revealed that both grain and grain boundary are responsible for the conduction mechanism. The modification resulted in an increase in resistance of the material up to x = 0.15 because of reduction of oxygen vacancies. AC conductivity analysis indicated that small and large polaron mechanisms take place in the Zr-substituted SBT ceramic. The transport mechanism study revealed that the oxygen vacancies are mainly responsible for the conduction. The decrement of the Pr value in the Zr-modified samples is due to the stronger metallicity of the Zr4+ ion compared to Ti4+. Among all the compositions, x = 0.15 showed enhanced ferroelectric and piezoelectric properties, so could be suitable for high-temperature piezoelectric applications.Acknowledgements
One of the authors (Priyambada Nayak) acknowledges the Department of Science and Technology, India (Reference number SR/WOS-A/PM-1003/2014(G)) for providing financial support.References
- H. kodama, F. izumi and A. watanabe, New Members of a Family of Layered Bismuth Compounds, J. Solid State Chem., 1981, 36, 349–355 CrossRef CAS.
- E. C. Subbarao, ferroelectricity in Bi4Ti3O12 and its solid solutions, Phys. Rev., 1961, 122, 804–807 CrossRef CAS.
- A. P. Araujo, J. D. Cuchiaro, L. D. McMillan, M. C. Scott and J. F. Scott, Nature, 1995, 374, 627 CrossRef.
- I. M. Reaney and D. Damjanovic, Crystal structure and domain-wall contributions to the piezoelectric properties of strontium bismuth titanate ceramics, J. Appl. Phys., 1996, 80(7), 4223–4225 CrossRef CAS.
- A. R. James, Effect of oxygen assisted sintering on piezoelectric properties of SrBi4Ti4O15 ceramics prepared via high energy mechano chemical processing, Ceram. Int., 2015, 41, 5100–5106 CrossRef CAS.
- Y. P. Chen, Y. Y. Yao, Z. H. Bao, P. Bao, J. S. Zhu and Y. N. Wang, Study on ferroelectric and dielectric properties of La-doped SrBi4Ti4O15 ceramics, Mater. Lett., 2003, 57, 3623–3628 CrossRef CAS.
- B. Mamatha and P. Sarah, Effect of dysprosium substitution on electrical properties of SrBi4Ti4O15, Mater. Chem. Phys., 2014, 147, 375–381 CrossRef CAS.
- D. Peng, H. Zou, C. Xu, X. Wang, X. Yao, J. Lin and T. Sun, Upconversion luminescence, ferroelectrics and piezoelectrics of Er Doped SrBi4Ti4O15, AIP Adv., 2012, 1–10, 042187 CrossRef.
- P. Nayak, S. R. Mohapatra, P. Kumar and S. Panigrahi, Effect of Ba2+ substitution on the structural and electrical properties of SrBi4Ti4O15 ceramic, Ceram. Int., 2015, 41, 9361–9372 CrossRef CAS.
- H. Hao, H. Liu and S. Ouyang, Structure and ferroelectric property of Nb-doped SrBi4Ti4O15 ceramics, J. Electroceram., 2009, 22, 357–362 CrossRef CAS.
- J. Zhu, X. Y. Mao and X. B. Chen, Properties of vanadium-doped SrBi4Ti4O15 ferroelectric ceramics, Solid State Commun., 2004, 129, 707–710 CrossRef CAS.
- P. Nayak, T. Badapanda and S. Panigrahi, Dielectric, ferroelectric and conduction behaviour of tungsten modified SrBi4Ti4O15 ceramic, J. Mater. Sci.: Mater. Electron., 2016, 27, 1217–1226 CrossRef CAS.
- M. Aghayana, A. Khors, M. Behdania and A. M. Hashimc, Sol–gel combustion synthesis of Zr-doped BaTiO3 nanopowders and ceramics: Dielectric and ferroelectric studies, Ceram. Int., 2014, 40, 16141–16146 CrossRef.
- A. Ulcinas, M. Es-Souni and V. Snitka, Investigation of microstructure and piezoelectric properties of Zr- and Sm doped PbTiO3 nanostructured thin films derived by sol–gel technology, Sens. Actuators, B, 2005, 109, 97–101 CrossRef CAS.
- J. Chen, Q. Yun, W. Gao, Y. Bai, C. Nie and S. Zhao, Improved ferroelectric and fatigue properties in Zr doped Bi4Ti3O12 thin films, Mater. Lett., 2014, 136, 11–14 CrossRef CAS.
- A. Chakrabarti and J. Bera, Structure and relaxor behaviour of BaBi4Ti4−xZrxO15 ceramics, Curr. Appl. Phys., 2010, 10, 574–579 CrossRef.
- D. Hennings, A. Schnell and G. Simon, Diffuse Ferroelectric Phase Transitions in Ba(Ti1−yZry)O3 Ceramics, J. Am. Ceram. Soc., 2006, 65(11), 539–544 CrossRef.
- S. Jesurani, S. Kanagesan, M. Hashim and I. Ismail, Dielectric properties of Zr doped CaCu3Ti4O12 synthesized by sol–gel route, J. Alloys Compd., 2013, 551, 456–462 CrossRef CAS.
- S. K. Rout, A. Hussian, J. S. Lee, I. W. Kim and S. I. Woo, Impedance spectroscopy and morphology of SrBi4Ti4O15 ceramics prepared by soft chemical method, J. Alloys Compd., 2009, 477, 706–711 CrossRef CAS.
- E. V. Ramana, M. P. F. Graça, M. A. Valente and T. Bhima Sankaram, Improved ferroelectric and pyroelectric properties of Pb-doped SrBi4Ti4O15 ceramics for high temperature applications, J. Alloys Compd., 2014, 583, 198–205 CrossRef.
- E. C. Subbarao, J. Chem. Phys., 1961, 34, 695–696 CrossRef CAS.
- C. Hervoches, A. Snedden, R. Riggs, S. H. Kilcoyne, P. Manuel and P. Lightfoot, Structural Behavior of the Four-Layer Aurivillius-Phase Ferroelectrics SrBi4Ti4O15and Bi5Ti3FeO15, J. Solid State Chem., 2002, 164, 280–291 CrossRef CAS.
- F. Rehman, H. Jin and J. Li, Effect of reduction/oxidation annealing on the dielectric relaxation and electrical properties of Aurivillius Na0.5Gd0.5Bi4Ti4O15 ceramics, RSC Adv., 2016, 6, 35102 RSC.
- A. l. Abassi, N. Kallel, S. Kallel, K. Khirouni and O. Peña, Electrical conductivity and complex impedance analysis of La0.7−xNdx Sr0.3Mn0.7Ti0.3O3 (x < 0.30) Perovskite, J. Magn. Magn. Mater., 2016, 401, 853–859 CrossRef CAS.
- H. Hao, H. X. Liu, M. H. Cao, X. M. Min and S. X. Ouyang, Study of A-site doping of SrBi4Ti4O15 Bi-layered compounds using micro-Raman spectroscopy, Appl. Phys. A, 2006, 85, 69–73 CrossRef CAS.
- J. Zhu, X. B. Chen, J. H. He and J. C. Shen, Raman scattering investigations on lanthanum-doped Bi4Ti3O12–SrBi4Ti4O15 intergrowth ferroelectrics, J. Solid State Chem., 2005, 178, 2832–2837 CrossRef CAS.
- K. W. Kwok and H. Y. Wong, Piezoelectric and pyroelectric properties of Cu-doped CaBi4Ti4O15 lead-free ferroelectric ceramics, J. Phys. D: Appl. Phys., 2009, 42, 0954191–0954195 Search PubMed.
- C. L. Du, S. T. Zhang, G. X. Cheng, M. H. Lu, Z. B. Gu, J. Wang and Y. F. Chen, Composition-dependent structures and properties of Bi4Ti3−xZrxO12 ceramics, Phys. B, 2005, 368, 157–162 CrossRef CAS.
- P. K. Patel, K. L. Yadav, H. Singh and A. K. Yadav, Origin of giant dielectric constant and magnetodielectric study in Ba(Fe0.5Nb0.5)O3 nanoceramics, J. Alloys Compd., 2014, 591, 224–229 CrossRef CAS.
- O. Raymond, Frequency-temperature response of ferroelectromagnetic PbFe1/2Nb1/2O3 ceramics obtained by different precursors. Part II. Impedance spectroscopy characterization, J. Appl. Phys., 2005, 97, 084108 CrossRef , 1–8.
- C. Long, H. Fan, M. Li, P. Ren and Y. Cai, candidate for lead-free ultrahigh-temperature piezoelectrics: the excellent electro-mechanical properties of Aurivillius oxides, Ca1−5xLi2xNd2x−xBi2Nb2−2xScxWxO9−1.5x, CrystEngComm, 2013, 15, 10212 RSC.
- M. Sindhu, N. Ahlawat, S. Sanghi, A. Agarwal, R. Dahiya and N. N. Ahlawat, Rietveld refinement and impedance spectroscopy of calcium titanate, Curr. Appl. Phys., 2012, 12, 1429–1435 CrossRef.
- E. J. Abram and D. C. Sinclair, A Strategy for Analysis and Modelling of Impedance Spectroscopy Data of Electroceramics: Doped Lanthanum Gallate, J. Electroceram., 2003, 10, 165–177 CrossRef CAS.
- D. Mancic, V. Paunovic, M. Vijatovic, B. Stojanovic and L. Zivkovic, Electrical Characterization and Impedance Response of Lanthanum Doped Barium Titanate Ceramics, Sci. Sintering, 2008, 40, 283–294 CrossRef CAS.
- C. E. Ciomaga, M. T. Buscaglia, V. Buscaglia and L. Mitoseriu, Oxygen deficiency and grain boundary-related giant relaxation in Ba (Zr, Ti) O3 ceramics, J. Appl. Phys., 2011, 110, 114110 CrossRef.
- A. Pelaiz-Barranco, Dielectric relaxation and electrical conductivity in ferroelectric ceramic/polymer composites around the glass transition, Appl. Phys. Lett., 2012, 100, 212903 CrossRef.
- M. Sindhu, N. Ahlawat, S. Sanghi, R. Kumari and A. Agarwal, Effect of Zr substitution on phase transformation and dielectric properties of Ba0.9Ca0.1TiO3 ceramics, J. Appl. Phys., 2013, 114, 164106 CrossRef.
- I. Coondoo, A. K. Jha and S. K. Agarwal, Enhancement of dielectric characteristics in donor doped Aurivillius SrBi2Ta2O9 ferroelectric ceramics, J. Eur. Ceram. Soc., 2007, 27, 253–260 CrossRef CAS.
- A. Singh, K. Amarnath, K. Prasad and A. Prasad, Impedance, Electrical Conductivity and Piezoelectric Studies on Nb5+ doped (Bi0.5Na0.5)0.94Ba0.06TiO3–PVDF0–3 composites, IOSR Journal of Applied Physics, 2015, 7, 17–26 Search PubMed.
- H. M. Usama, A. Sharif, M. A. Zubair, M. A. Gafur and S. M. Hoque, Structural transition and its effect in La, Zr co-substituted mono-domain BiFeO3, J. Appl. Phys., 2016, 120, 214106 CrossRef.
- J. Wu and J. Wang, Ferroelectric and Impedance Behavior of La- and Ti-Co doped BiFeO3 Thin Films, J. Am. Ceram. Soc., 2010, 93(9), 2795–2803 CrossRef CAS.
- O. Subohi, G. S. Kumar, M. M. Malik and R. Kurchania, Effect of B-site isovalent doping on electrical and ferroelectric properties of lead free bismuth titanate ceramics, J. Phys. Chem. Solids, 2016, 93, 91–99 CrossRef CAS.
- J. Wu, D. Xiao and J. Zhu, Potassium–Sodium Niobate Lead-Free Piezoelectric Materials: Past, Present, and Future of Phase Boundaries, Chem. Rev., 2015, 115(7), 2559–2595 CrossRef CAS PubMed.
- C. Long and H. Fan, Effect of lanthanum substitution at A site on structure and enhanced properties of new Aurivillius oxide K0.25Na0.25La0.5Bi2Nb2O9, Dalton Trans., 2012, 41, 11046 RSC.
| This journal is © The Royal Society of Chemistry 2017 |