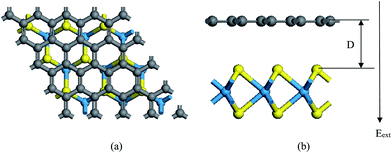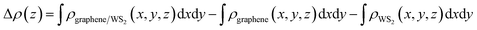Tuning the Schottky contacts at the graphene/WS₂ interface by electric field

Abstract

Using the first-principle calculations, we study the electronic structures of graphene/WS₂ van der Waals (vdW) heterostructures by applying an external electric field (E_ext) perpendicular to the heterobilayers. It is demonstrated that the intrinsic electronic properties of graphene and WS₂ are quite well preserved due to the weak vdW contact. We find that n-type Schottky contacts with a significantly small Schottky barrier are formed at the graphene/WS₂ interface and p-type (hole) doping in graphene occurs during the formation of graphene/WS₂ heterostructures. Moreover, the E_ext is effective to tune the Schottky contacts, which can transform the n-type into p-type and ohmic contact. Meanwhile, p-type (hole) doping in graphene is enhanced under negative E_ext and a large positive E_ext is required to achieve n-type (electron) doping in graphene. The E_ext can control not only the amount of charge transfer but also the direction of charge transfer at the graphene/WS₂ interface. The present study would open a new avenue for application of ultrathin graphene/WS₂ heterostructures in future nano- and optoelectronics.

---

1. Introduction

Two-dimensional (2D) ultrathin materials have received considerable attention recently owing to their outstanding mechanical, thermal, optical, electronic and chemical properties, which make these materials promising for next-generation nanoelectronic and optoelectronic devices.^1–7 Graphene, a 2D sp²-hybridized ¹carbon monolayer has been reported as one of the most fascinating 2D materials^8–11 because of its extraordinary properties including massless Dirac fermions, high carrier mobility and intriguing quantum Hall effect.^12,13 However, the absence of a bandgap restrains its wide application in electronic devices, particularly for logic circuits.^14,15 Subsequently to the graphene isolation, a whole new class of 2D materials has been investigated, such as the transition metal dichalchogenides (TMDs). However, in contrast to the gapless graphene, the semiconducting TMDs possess a finite bandgap.¹⁶ Tungsten disulfide (WS₂), one of the members in the TMDs family, has been recently studied for various electronic devices applications.^17,18 WS₂ belongs to the P6₃/mmc space group (a = 3.155, c = 12.36), and has a vdW layered structure where each layer consists of a slab S–W–S sandwich.¹⁹ Bulk WS₂ is an indirect gap semiconductor, it has a bandgap of 1.3 eV.²⁰ However, studies demonstrate that with decreasing number of layers, WS₂ transforms from indirect gap (in bulk) into direct gap (in monolayer).²¹ Moreover, the monolayer WS₂ possess a sufficiently high in-plane carrier mobility and a high on/off current ratio, which can be applied in photodetectors, field-effect transistors, and electronic devices.^22,23

Currently, vertical heterostructures based on 2D vdW materials, especially heterobilayers made layer by layer from 2D monolayers, are being considered as a promising method to construct devices that integrate the properties of their respective components^24–26 with ideal properties to be applied in nanoelectronics and optoelectronics. Many 2D vertical ultrathin vdW heterostructures, have been widely studied experimentally and theoretically, such as graphene/MoS₂,^27–30 graphene/h-BN,^31–33 BN/TMD,^34,35 phosphorene/TMD,³⁶ TMD/TMD^37–39 and phosphorene/graphene.^40,41 These vdW heterostructures show many new optoelectronic properties far beyond individual components. Moreover, due to the lack of dangling bonds and the weak electron coupling at the interface of vdW heterobilayers, their intrinsic electronic properties are well preserved without any degradation. Among these vdW heterobilayers, graphene-based vdW heterostructures have attracted considerable interest. Hu et al.⁴² reported that interlayer interactions in graphene/silicene heterostructure induce tunable p-type and n-type doping of silicene and graphene, respectively, indicating their doping carrier concentrations can be tuned by their interfacial spacing. Graphene on h-BN substrates have mobilities and carrier inhomogeneities that are almost an order of magnitude better than devices on SiO₂, which show reduced roughness, intrinsic doping and chemical reactivity.³⁶ Tan et al.⁴³ showed that photoirradiation of the WS₂ on graphene region caused further Dirac point shifts, indicative of a reduction in the p-type doping levels of graphene, revealing that the photogenerated excitons in WS₂ are split across the heterostructure by electron transfer from WS₂ to graphene.

Recently, a new generation of field-effect transistors where 2D WS₂ serves as an atomically thin barrier between two layers of mechanically exfoliated graphene have been constructed successfully.⁴⁴ In comparision with MoS₂, WS₂ allows for switching between tunneling and thermionic transport regimes, resulting in much better transistor characteristics and thus allowing for much higher ON/OFF ratios and much larger ON current. The performance of vertical field-effect transistor based on graphene–WS₂ heterostructures depends on the tunability of the Schottky barrier via a shift in the Fermi level of the graphene and changes in the height and type of the barrier. Our recent work⁴⁵ have demonstrated that the E_ext can not only control the Schottky barrier height but also the Schottky contacts (n-type and p-type) and ohmic contacts (n-type) at the interface of arsenene/graphene vdW heterostructures. Therefore, an interesting question arise: whether E_ext for Schottky barrier tuning can also be employed in graphene/WS₂ vdW heterostructure? Therefore, in the present work, we investigate the electronic properties of graphene/WS₂ vdW heterostructure by first-principles calculations, but the main points are the electrically tunable Schottky barriers of graphene/WS₂ heterobilayer.

2. Computational methods and models

We use density functional theory (DFT) calculations implemented in the Vienna Ab-Initio Simulation Package (VASP).⁴⁶ The generalized gradient approximation (GGA) by the Perdew–Burke–Ernzerhof (PBE) functional is utilized as the exchange–correlation functional.⁴⁷ The non-bonding vdW interaction is incorporated by adding a semi-empirical dispersion potential to the conventional Kohn–Sham DFT energy, through a pair-wise force field following Grimme's DFT-D3 method.⁴⁸ The projected augmented wave (PAW) potential⁴⁹ is employed to describe the electron-ion potential. We set the energy cutoff as 500 eV. A 9 × 9 × 1 Monkhorst–Pack mesh was used for relaxation calculations and a 15 × 15 × 1 Monkhorst–Pack mesh was used post-relaxation for static electronic structure calculations. All atoms are allowed to be fully relaxed until the atomic Hellmann–Feynman forces are smaller than 0.01 eV Å⁻¹ and the convergence criterion of energy in the self-consistency process is set to 10⁻⁵ eV. A vacuum space of 20 Å in the z direction is used to avoid the interactions between neighboring slabs. The E_ext is introduced in the VASP by the dipole layer method with the dipole placed in the vacuum region of the periodic supercell.⁵⁰ In addition, the spin-orbital coupling (SOC) effects are included in the self-consistent calculations of electronic structures to verify its effects in the heterostructures.

The calculated lattice parameters of the pristine monolayer WS₂ and graphene are 3.18 Å and 2.46 Å, respectively. We choose WS₂ as a substrate to match with graphene. The supercell of our system is composed of 4 × 4 primitive graphene cells (32 carbon atoms) and 3 × 3 WS₂ primitive cells (18 sulfur and 9 tungsten atoms) along the x and y directions. The lattice mismatch is 3.1% for the composed configuration. The equilibrium geometry of the system is shown in Fig. 1(a) and (b).

Fig. 1 Top view (a) and side view (b) of the graphene/WS₂ vdW heterostructure. The gray, blue and yellow balls are for carbon, tungsten and sulfur atoms, respectively. A vertical E_ext is applied perpendicular to the layers. The interlayer distance D between graphene and WS₂ is marked.

3. Results and discussion

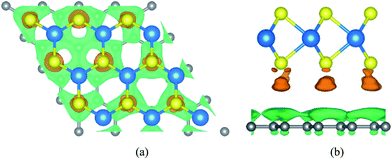
In order to get the equilibrium position of the monolayer WS₂ with respect to the graphene layer, we calculated the binding energy between the monolayer WS₂ and graphene. After fixing the WS₂ layer, we move the WS₂ layer with respect to the graphene layer to make sure this is really the minimum binding energy. The binding energy (E_b) per carbon atom between the graphene sheet and the monolayer WS₂ is calculated as E_b = [E_graphene/WS2 − (E_graphene + E_WS2)]/N, where E_graphene/WS2 is the total energy of the graphene/WS₂ vdW heterostructure, E_graphene is the total energy of the isolated graphene layer, E_WS2 is the total energy of the isolated WS₂ monolayer, and N = 32 is the number of carbon atoms in the supercell. For the graphene/WS₂ heterobilayer, the calculated binding energy per carbon atom is −26.8 meV with an equilibrium interlayer distance of 3.49 Å. The negligible binding energy and the large interlayer distance (much larger than the sum of the covalent radii of the carbon and sulfur atoms) indicate that weak vdW interactions dominate in the graphene/WS₂ heterobilayer, similar to other 2D vdW graphene-based heterostructures.^51,52

To further explore the bonding of graphene and WS₂ monolayer, we studied the charge density difference of the graphene/WS₂ heterostructure, as indicated in Fig. 2. The charge density difference is defined as:

Δρ = ρ_graphene/WS2(r) − ρ_graphene(r) − ρ_WS2(r)

where ρ_graphene/WS2(r), ρ_graphene(r), and ρ_WS2(r) are the charge densities of the relaxed graphene/WS₂, graphene, and WS₂ monolayer, respectively. The orange regions represent charge accumulation while the green represents charge depletion. All the charge densities here are calculated by using the same supercell for the heterostructure. Such a Δρ can clearly demonstrate the charge transfer between graphene and WS₂ monolayer in the heterostructure. As can be seen from Fig. 2, there is a tiny charge accumulation near the WS₂ monolayer. The charge depletion occurs at the graphene sheet. A small amount of electron transfer from graphene layer to WS₂ layer is distinctly recognizable in Fig. 2. Thus, graphene combines with WS₂ by the weak vdW interactions. The relatively weak bonding of graphene and WS₂ have also been deduced by the binding energy calculations.

Fig. 2 Top view (a) and side view (b) of differential charge density of the graphene/WS₂ heterostructure. The gray, blue and yellow balls are for carbon, tungsten and sulfur atoms, respectively. Orange and green isosurfaces correspond to the accumulation and depletion of electronic densities (the isovalue is 4.1 an10⁻⁵ e Å⁻³).

In heterostructures based on vertical stacking of monolayer materials, strain will be present due to lattice mismatches. In the graphene/WS₂ heterostructure there is a 3.1% lattice mismatch, so there is artificial tensile strain on WS₂ and compressive strain on graphene. To correct the artificial strain effect, we investigate uniaxial absolute deformation potentials, which relate the strain to the shifts of individual band edges. The uniaxial absolute deformation potentials can be defined as 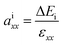, , 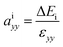where aⁱ is the deformation potential of a given state, ΔE_i is the shift of its energy under strain, and ε_xx, ε_yy are the normal strains in x and y directions. In our electronic structure calculations, we use the vacuum level to align the energies of the electronic states. The calculated absolute deformation potentials of the CBM and VBM of WS₂ and the Dirac point of graphene are presented in Table 1. The absolute deformation potentials allow one to directly obtain the energy shifts of the individual band edges upon application of strain to achieve correcting the artificial strain effect.

Table 1 Absolute deformation potentials (in eV) of the CBM and VBM of WS₂ and the Dirac point of graphene

	a^VBMΓ	a^CBMΓ	a^DiracK
xx	1.56	6.79	0.023
yy	1.68	6.91	0.021

---

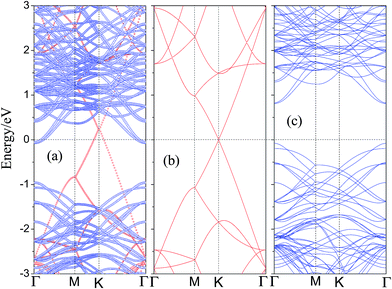
To understand the electronic properties of graphene/WS₂ heterostructure, the electronic structures of pristine graphene and monolayer WS₂ are checked and their energy band structures are plotted in Fig. 3(b) and (c), respectively. It shows that graphene has a zero bandgap and retains its metallic character, which is consistent with previous theoretical studies.^53,54 Considering the SOC effects, Fig. 3(c) presents that the pristine WS₂ monolayer is a direct semiconductor at the Γ point with a bandgap of 0.91 eV, and the valence band splits by 115 meV, while the conduction band is not obviously split. Compared with the band structures of monolayer WS₂ primitive cell, the conduction band minimum (CBM) and the valence band maximum (VBM) of the 3 VB3 monolayer WS₂ supercell are mapped to the Γ point. The reason is that the inequivalent K and K′ points are folded and coupled into the same Γ-point when a 3 × 3 monolayer WS₂ supercell is studied. Then, we investigate the electronic structure of the graphene/WS₂ vdW heterostructure. The calculated band structure of the graphene/WS₂ heterostructure including the SOC effect at the equilibrium interlayer distance is shown in Fig. 3(a). Red and blue denote the contributions from graphene and WS₂ layer, respectively. Compared with the electronic band structures of the pristine graphene and monolayer WS₂ shown in Fig. 3(b) and (c), respectively, the band structure of the graphene/WS₂ heterostructure seems to be a simple sum of each component. The overall shape of band structure of graphene/WS₂ heterostructure is basically in accord with the sum of the pristine graphene and monolayer WS₂. Furthermore, it indicates that a vacuum space of 20 Å in the z direction is sufficient to avoid the interactions between neighboring sheets. The band contributed by graphene illustrates that the graphene layer remains its metallic character, and the band contributed by WS₂ illustrates that the WS₂ layer retains the direct bandgap at the Γ point with a bandgap of 0.91 eV. Thus, the main dominant sorts of binding forces of graphene/WS₂ heterostructure are vdW interaction. The graphene/WS₂ heterostructure can preserve the intrinsic excellent electronic properties of the individual materials. Fig. 3(b) shows that the Dirac point of the isolated graphene is at the Fermi level, however, the Fermi level of graphene/WS₂ heterostructure moves down to below the Dirac point of graphene layer, which results in p-type (hole) doping in graphene. Because the electronic states around Fermi level at K point are all contributed from graphene layer (displayed in Fig. 3(a)), the move of Fermi level demonstrates that graphene layer lose electrons during the formation of graphene/WS₂ heterostructure.

Fig. 3 The projected band structure of (a) graphene/WS₂ heterostructure, projection to graphene by red circles and WS₂ layer is denoted by blue circles. Band structures of (b) pristine graphene and (c) pristine monolayer WS₂. The Fermi level is set to zero and marked by black dashed lines.

Interestingly, we found that a Schottky contact can be formed between metallic graphene and semiconducting WS₂, the graphene/WS₂ configuration is a representative metal–semiconductor heterostructure. From a device point of view, when using graphene as the metal contact and WS₂ monolayer as the channel, the electrical current flow across the metal–semiconductor interface is usually non-linear against the applied bias voltage. For n-type semiconductors, electrons near the CBM carry the most of the current, and for p-type semiconductors, holes near the VBM are mainly responsible for electrical conduction. At the metal–semiconductor interface, the electrons near the CBM for n-type semiconductors can spontaneously flow to the metal. When electronic transport occurs across the metal–semiconductor interface, the states will be offset and the Fermi level is located above the midgap (CBM + VBM)/2, known as the n-type Schottky barrier and the n-type Schottky barrier (Φ_Bn) is defined as: Φ_Bn = E_C − E_F, where E_C and E_F are the CBM and the Fermi level, respectively. A rectifying behavior occurs between the n-type semiconductor and metal due to the n-type Schottky barrier. If the p-type semiconductor is in contact with the metal, the Fermi level is located below the midgap (CBM + VBM)/2, known as the p-type Schottky barrier and the p-type Schottky barrier (Φ_Bp) is defined as: Φ_Bp = E_F − E_V, where E_F and E_V are the Fermi level and the VBM, respectively. The current flow across the metal–semiconductor interface depends on the magnitude of the Schottky barrier height, so it is necessary to study the Schottky barrier of the graphene/WS₂ interface. After analysis of the band structure of the graphene/WS₂ heterostructure, shown in Fig. 3(a), we find that the ohmic contact is formed at the graphene/WS₂ interface with the Fermi level through the conduction band of WS₂ (Φ_Bn < 0).

For the performance of graphene/WS₂ based field effect transistors, determination of the effect of E_ext on the electronic properties of the graphene/WS₂ heterobilayer is important. Therefore we study the effect of E_ext on the interface electronic properties of graphene/WS₂ heterostructure. The projected band structures of graphene/WS₂ heterostructures under different E_ext are shown in Fig. 4. In Fig. 4, with the negative E_ext varies from 0 to −2 V nm⁻¹, the CBM of WS₂ below the Fermi level declines gradually, the ohmic contact is still preserved. Nevertheless, with the positive E_ext varies from 0 to 1 V nm⁻¹, the CBM of WS₂ shifts upward and across the Fermi level, which indicates the n-type Schottky contact is formed. For graphene/WS₂ heterostructure under an E_ext of 1 V nm⁻¹, the CBM of WS₂ is closer to the Fermi level than the VBM of WS₂, giving rise to the n-type Schottky barrier. As can be seen from Fig. 4, the Fermi level shifts from the CBM to the VBM of WS₂ when the positive E_ext increases from 1 V nm⁻¹ to 2 V nm⁻¹. The n-type Schottky barrier height exceeds p-type Schottky barrier height gradually, which demonstrates the positive E_ext transforms the n-type Schottky contact into the p-type Schottky contact at the graphene/WS₂ interface. When the positive E_ext increases from 2 V nm⁻¹ to 3 V nm⁻¹, the valence band of WS₂ moves upward and cross the Fermi level (Φ_Bp < 0), the ohmic contact is obtained again. What is more, as already pointed out, the Fermi level shifts down to below the Dirac point of graphene during the formation of graphene/WS₂ heterostructure, leading to p-type (hole) doping in graphene as shown in Fig. 3. More electrons transfer from graphene's Dirac point to WS₂'s conduction band when the heterobilayer is subjected to a negative E_ext, the shifts (ΔE_D) of graphene's Dirac point relative to the Fermi level in the graphene/WS₂ heterostructure are 0.23, 0.58 and 0.96 eV under the E_ext of 0 V nm⁻¹, −1 V nm⁻¹ and −2 V nm⁻¹, respectively, p-type (hole) doping in graphene is enhanced under the negative E_ext. On the contrary, the large positive E_ext is needed to make the electrons overcome the bandgap (0.91 eV) of WS₂ and then transfer electrons from WS₂'s valence band to graphene's Dirac point. Therefore, the shifts (ΔE_D) of graphene's Dirac point relative to the Fermi level retain almost zero under the positive E_ext, n-type (electron) doping in graphene occurs until the positive E_ext exceeds 2.4 V nm⁻¹.

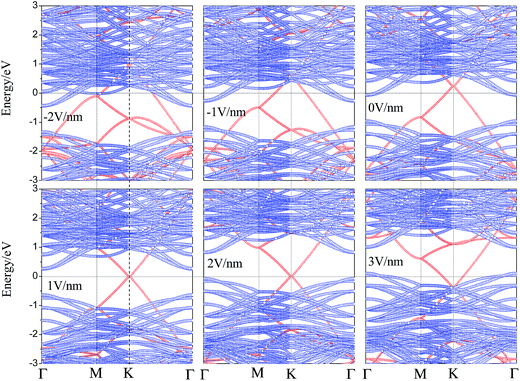Fig. 4 The projected band structures of graphene/WS₂ heterostructures under different E_ext, projection to graphene layer is denoted by red circles and to WS₂ by blue circles.

To quantitatively characterize the Schottky barrier height and Schottky doping of graphene/WS₂ heterobilayer, the evolutions of Φ_Bp and Φ_Bn of graphene/WS₂ heterostructure as a function of E_ext are shown in Fig. 5. When the heterobilayer is subjected to the positive E_ext, the electrons transfer from WS₂ to graphene, the CBM of WS₂ moves upward and across the Fermi level, which results in the form of n-type Schottky contact. With the further increase of the positive E_ext, the valence (conduction) band of WS₂ shifts toward (away from) the Fermi level, the magnitude of Φ_Bp gradually decreases and the magnitude of Φ_Bn gradually increases. As a result, the lines of Φ_Bp and Φ_Bn intersect at 1.35 V nm⁻¹, where the n-type Schottky contact is changed to p-type Schottky contact. As the positive E_ext increases more than 2.4 V nm⁻¹, the valence band of WS₂ will shift up and cross the Fermi level (Φ_Bp < 0), which demonstrates that ohmic contact is formed in the graphene/WS₂ heterostructure. When the heterobilayer is subjected to the negative E_ext, the electrons are transferred from graphene to WS₂, the graphene/WS₂ heterobilayer remains the ohmic contact. Therefore, the E_ext is effective to tune the Schottky contacts, which can transform the n-type into p-type and ohmic contact.

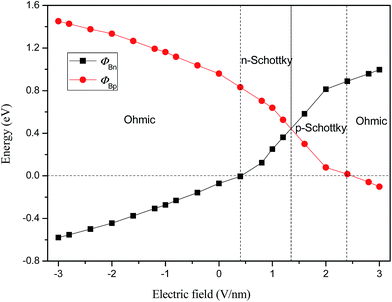Fig. 5 Evolution of Schottky barriers of Φ_Bp and Φ_Bn in graphene/WS₂ heterostructurer as a function of E_ext.

Although the graphene layers and the WS₂ layers binding together via vdW force, the distribution of interfacial charge will be altered in the graphene/WS₂ heterostructure under different E_ext, which may result in the Schottky barrier transition. To visualize the charge redistribution and further understand charge transfer mechanism between graphene and WS₂ layer in the vdW heterobilayer, we plot the plane-averaged charge density difference Δρ(z) along the vertical direction to the heterobilayer, which can provide a quantitative picture of the charge redistribution at the interface. The plane-averaged charge density difference along the z direction is defined as:

where ρ_graphene/WS2(x, y, z), ρ_graphene(x, y, z) and ρ_WS2(x, y, z) are the plane-averaged charge density at the (x, y, z) point in graphene/WS₂ heterostructure, graphene and WS₂ monolayer, respectively, which are calculated by freezing the atomic positions of the respective components in the hybrid system. Thus, positive values demonstrate charge accumulation at the position, and negative values indicate the charge depletion. The vertical red dash line implies the intermediate position for the interface of the monolayers. The results indicate that the charge redistribution is mainly on the surface of graphene and WS₂ layers. It can be seen from Fig. 6(a) that a small amount of electrons are depleted on the graphene side, while they are accumulated on WS₂ side, therefore the charge rearrangement occurs at the interface of the graphene/WS₂ heterostructure. Fig. 6(b) and (c) show that the positive and negative E_ext have different effects on charge transfer at the interface of graphene/WS₂ heterostructure. When applying the positive E_ext, electrons tend to transfer from WS₂ to graphene (Fig. 6(b)), shifting down the Fermi level close to the valence band of WS₂ as shown in Fig. 4. Nevertheless, the negative E_ext induce electrons transfer from graphene to WS₂ (Fig. 6(c)), shifting up the Fermi level close to the conduction band of WS₂ as shown in Fig. 4. The amount of transferring electrons increases with the strength of the E_ext, no matter what the direction of the E_ext is. More charge transfer between graphene and WS₂ demonstrates a stronger interlayer interaction, giving rise to the shift of Fermi level. Therefore, the interfacial charge transfer and the Fermi level shift are the reasons of the transformation of Schottky barrier from n-type Schottky contact to p-type Schottky contact and ohmic contact in the graphene/WS₂ heterobilayer under various E_ext.

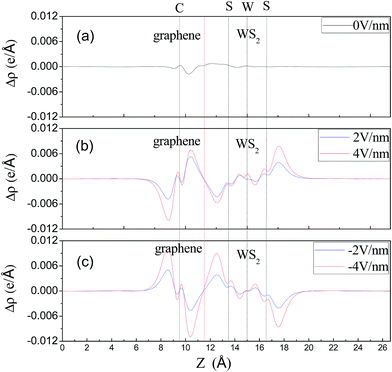Fig. 6 Plots of the plane-averaged charge density difference along z direction under various E_ext. The red vertical dashed line denotes the intermediate position of the two monolayers.

Finally, we would like to point out that conventional PBE methods underestimate the bandgap and Schottky barrier height of the heterostructures, but the HSE or quasi particle self-consistent GW methods are not still considered to correct it for all considered systems in this work due to their tremendously computational costs. We emphasize that our goal here is not to determine precise bandgaps and Schottky barrier heights but to illustrate the phenomenon of Schottky contacts tuning by external electric fields and to uncover the underlying physics. Moreover, PBE methods are good at predicting correct trends and physical mechanisms, which possesses guiding function for future experimental studies. Thus, for future related experimental studies, the numbers obtained in this work should be taken with care since it is likely that the obtained physical quantity should be underestimated.

4. Conclusions

In summary, the electronic properties of graphene/WS₂ vdW heterostructures under different E_ext are investigated by means of the first-principle calculations. We find that graphene interacts weakly with WS₂ via weak vdW interactions and both the intrinsic electronic properties of graphene and WS₂ are quite well preserved at the equilibrium interlayer distance. The n-type Schottky contacts with the significantly small Schottky barrier are formed in the graphene/WS₂ heterostructure and p-type (hole) doping in graphene occurs during the formation of graphene/WS₂ heterostructure. When the heterobilayer is subjected to the positive E_ext, a transition from n-type to p-type Schottky contacts occurs at 1.35 V nm⁻¹, then to ohmic contacts at 3 V nm⁻¹. The graphene/WS₂ heterostructure remains the n-type Schottky contact under the negative E_ext less than −0.55 V nm⁻¹. When the negative E_ext exceeds −0.55 V nm⁻¹, the ohmic contact is obtained again. p-Type (hole) doping in graphene is enhanced under the negative E_ext and the large positive E_ext is required to achieve n-type (electron) doping in graphene. The E_ext can control not only the amount of charge transfer but also the direction of charge transfer at the graphene/WS₂ interface. Our work is expected to promote the application of ultrathin graphene/WS₂ heterostructure in the next-generation nanoelectronic and photonics devices.

Acknowledgements

We acknowledge support from the National Natural Science Foundation of China (Grant No. 61674053, 11504092, U1404109 and 11504334) and the High Performance Computing Center of Henan Normal University.

References

1. J. Du, C. X. Xia, Y. M. Liu, X. P. Li, Y. T. Peng and S. Y. Wei, Appl. Surf. Sci., 2017, 401, 114–119.
2. J. Du, C. X. Xia, T. X. Wang, X. Zhao, X. M. Tan and S. Y. Wei, Appl. Surf. Sci., 2016, 378, 350–356.
3. H. Zhang, C. X. Xia, X. Zhao, T. X. Wang and J. B. Li, Appl. Surf. Sci., 2015, 356, 1200–1206.
4. X. Zhao, C. X. Xia, T. X. Wang, X. Q. Dai and L. Yang, J. Alloys Compd., 2016, 689, 302–306.
5. W. Q. Xiong, C. X. Xia, X. Zhao, T. X. Wang and Y. Jia, Carbon, 2016, 109, 737–746.
6. X. Zhao, T. X. Wang, G. T. Wang, X. Q. Dai, C. X. Xia and L. Yang, Appl. Surf. Sci., 2016, 383, 151–158.
7. P. Chen, X. Zhao, T. X. Wang, X. Q. Dai and C. X. Xia, J. Alloys Compd., 2016, 680, 659–664.
8. A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191.
9. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
10. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
11. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
12. D. B. Farmer, H. Y. Chiu, Y. M. Lin, K. A. Jenkins, F. N. Xia and P. Avouris, Nano Lett., 2009, 9, 4474–4478.
13. Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204.
14. M. Sprinkle, D. Siegel, Y. Hu, J. Hicks, A. Tejeda, A. Taleb-Ibrahimi, P. Le Fevre, F. Bertran, S. Vizzini, H. Enriquez, S. Chiang, P. Soukiassian, C. Berger, W. A. de Heer, A. Lanzara and E. H. Conrad, Phys. Rev. Lett., 2009, 103, 226803.
15. Y. Q. Wu, Y. M. Lin, A. A. Bol, K. A. Jenkins, F. N. Xia, D. B. Farmer, Y. Zhu and P. Avouris, Nature, 2011, 472, 74–78.
16. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
17. R. Gatensby, N. McEvoy, K. Lee, T. Hallam, N. C. Berner, E. Rezvani, S. Winters, M. O'Brien and G. S. Duesberg, Appl. Surf. Sci., 2014, 297, 139–146.
18. L.-Y. Gan, Q. Zhang, Y. Cheng and U. Schwingenschlögl, J. Phys. Chem. Lett., 2014, 5, 1445–1449.
19. W. J. Schutte, J. L. Deboer and F. Jellinek, J. Solid State Chem., 1987, 70, 207–209.
20. G. L. Frey, R. Tenne, M. J. Matthews, M. S. Dresselhaus and G. Dresselhaus, J. Mater. Res., 1998, 13, 2412–2417.
21. Y. D. Ma, Y. Dai, M. Guo, C. W. Niu, J. B. Lu and B. B. Huang, Phys. Chem. Chem. Phys., 2011, 13, 15546–15553.
22. H. Liu, A. T. Neal and P. D. Ye, ACS Nano, 2012, 6, 8563–8569.
23. D. Jariwala, V. K. Sangwan, D. J. Late, J. E. Johns, V. P. Dravid, T. J. Marks, L. J. Lauhon and M. C. Hersam, Appl. Phys. Lett., 2013, 102, 173107.
24. J. M. Hamm and O. Hess, Science, 2013, 340, 1298–1299.
25. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
26. G. Gao, W. Gao, E. Cannuccia, J. Taha-Tijerina, L. Balicas, A. Mathkar, T. N. Narayanan, Z. Liu, B. K. Gupta, J. Peng, Y. Yin, A. Rubio and P. M. Ajayan, Nano Lett., 2012, 12, 3518–3525.
27. Y. D. Ma, Y. Dai, M. Guo, C. W. Niu and B. B. Huang, Nanoscale, 2011, 3, 3883–3887.
28. X. D. Li, S. Yu, S. Q. Wu, Y. H. Wen, S. Zhou and Z. Z. Zhu, J. Phys. Chem. C, 2013, 117, 15347–15353.
29. L. Britnell, R. M. Ribeiro, A. Eckmann, R. Jalil, B. D. Belle, A. Mishchenko, Y. J. Kim, R. V. Gorbachev, T. Georgiou, S. V. Morozov, A. N. Grigorenko, A. K. Geim, C. Casiraghi, A. H. Castro Neto and K. S. Novoselov, Science, 2013, 340, 1311–1314.
30. H. Tian, Z. Tan, C. Wu, X. M. Wang, M. A. Mohammad, D. Xie, Y. Yang, J. Wang, L. J. Li, J. Xu and T. L. Ren, Sci. Rep., 2014, 4, 5951.
31. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726.
32. X. Lin, Y. Xu, A. A. Hakro, T. Hasan, R. Hao, B. L. Zhang and H. S. Chen, J. Mater. Chem. C, 2013, 1, 1618–1627.
33. J. M. Xue, J. Sanchez-Yamagishi, D. Bulmash, P. Jacquod, A. Deshpande, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero and B. J. Leroy, Nat. Mater., 2011, 10, 282–285.
34. R. Gillen, J. Robertson and J. Maultzsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075437.
35. Z. Y. Huang, X. Qi, H. Yang, C. Y. He, X. L. Wei, X. Y. Peng and J. X. Zhong, J. Phys. D: Appl. Phys., 2015, 48, 205302.
36. Y. X. Deng, Z. Luo, N. J. Conrad, H. Liu, Y. J. Gong, S. Najmaei, P. M. Ajayan, J. Lou, X. F. Xu and P. D. Ye, ACS Nano, 2014, 8, 8292–8299.
37. N. J. Huo, J. H. Yang, L. Huang, Z. M. Wei, S. S. Li, S. H. Wei and J. B. Li, Small, 2015, 11, 5430–5438.
38. G. C. Constantinescu and N. D. M. Hine, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195416.
39. T. Roy, M. Tosun, X. Cao, H. Fang, D. H. Lien, P. D. Zhao, Y. Z. Chen, Y. L. Chueh, J. Guo and A. Javey, ACS Nano, 2015, 9, 2071–2079.
40. J. E. Padilha, A. Fazzio and A. J. R. da Silva, Phys. Rev. Lett., 2015, 114, 066803.
41. W. Hu, T. Wang and J. L. Yang, J. Mater. Chem. C, 2015, 3, 4756–4761.
42. W. Hu, Z. Li and J. Yang, J. Chem. Phys., 2013, 139, 154704.
43. H. J. Tan, Y. Fan, Y. M. Rong, B. Porter, C. S. Lau, Y. Q. Zhou, Z. Y. He, S. S. Wang, H. Bhaskaran and J. H. Warner, ACS Appl. Mater. Interfaces, 2016, 8, 1644–1652.
44. T. Georgiou, R. Jalil, B. D. Belle, L. Britnell, R. V. Gorbachev, S. V. Morozov, Y. J. Kim, A. Gholinia, S. J. Haigh, O. Makarovsky, L. Eaves, L. A. Ponomarenko, A. K. Geim, K. S. Novoselov and A. Mishchenko, Nat. Nanotechnol., 2013, 8, 100–103.
45. W. Li, T. X. Wang, X. Q. Dai, X. L. Wang, Y. Q. Ma, S. S. Chang and Y. N. Tang, Phys. E, 2017, 88, 6–10.
46. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
47. L. Y. Gan, Q. Y. Zhang, Y. C. Cheng and U. Schwingenschlogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235310.
48. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
50. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067.
51. G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. van den Brink, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073103.
52. A. Du, S. Sanvito, Z. Li, D. Wang, Y. Jiao, T. Liao, A. Sun, Y. H. Ng, Z. Zhu, R. Amal and S. C. Smith, J. Am. Chem. Soc., 2012, 134, 4393–4397.
53. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
54. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.

---