Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicted structural evolution and detailed insight into configuration correlation, mechanical properties of silicon–boron binary compounds†
Bo Zhang a,
Lailei Wub and
Zhihong Li*a
a,
Lailei Wub and
Zhihong Li*a
aKey Laboratory of Advanced Ceramics and Machining Technology of Ministry of Education, School of Materials Science and Engineering, Tianjin University, Tianjin 300072, China. E-mail: lizhihong@tju.edu.cn; Tel: +86 22 27404260
bKey Laboratory of Metastable Materials Science and Technology, College of Material Science and Engineering, Yanshan University, Qinhuangdao 066004, China
First published on 13th March 2017
Abstract
The crystal structures, phase stability, mechanical and electronic structures of silicon–boron binaries have been investigated systematically using first-principles of pseudopotential calculations. The calculated formation enthalpies of α-SiB3, SiB6 and SiBn follow the sequence: ΔHf (α-SiB3) > ΔHf (SiB6) > ΔHf (SiBn), which is in good agreement with the previous experimental results. Monoclinic SiB6 with P21/m symmetry and hexagonal SiB36 with a B80 unit (a ring linked by diametrically located 2 × B28, 2 × B12) are suggested as the more energetically and mechanically favorable phases by our calculations. The predicted bulk modulus of Si–B binaries is between 120 and 180 GPa, while there is a dramatic drop for two kinds of α-SiB3 in the shear modulus from 130.3 GPa (SiB3) to 71.1 GPa (SiB4). We infer that the additional centered boron atoms, located long the spatial diagonal in SiB4, is responsible for the weakness along this direction. In addition to β-SiB3, the new proposed P21/m-SiB6 and R3m-SiB6 is found to be semiconducting with 0.41 eV indirect and 1.654 eV direct band gap, respectively. There is no band gap provided by band structures of SiB4 and SiB36, as well as their DOS values are quite large at Fermi level, indicating they are energetically unstable under 0 K and GPa.
1. Introduction
Boron-rich borides are classical refractory materials: lightweight, extremely hard, and exceptionally thermal stability.1,2 Even more importantly, boron-rich compounds have attracted extensive attention for their high melting-points, semi-metallic/metallic, ascending Seebeck coefficients and electrical conductivities with increasing temperature.3–5 Excellent electrical conductivity combined with weak thermal conductivity contributes to generate good thermoelectric properties in borides. In particular the silicon borides, possessing extremely higher chemical and thermal stabilities, have great potential for thermoelectric materials in extreme conditions (high-temperature, strong chemical corrosion, etc.).6,7 After reviewing the whole Si–B system, there are mainly three kinds of binary compounds, usually referred to as SiB3, SiB6 and SiBn. To be precise, “SiB3” is the stoichiometry designation for Si–B compounds ranging from SiB2.8 to SiB4.8–15 This range is taken as an indication of a wide homogeneity phase region for a solid with the SiB3 structure. Another probable confusion should be noticed that SiB3 here is more accurately α-SiB3, since an orthorhombic phase, termed β-SiB3, has been obtained in gallium flux conditions at lower temperatures by J. R. Salvador et al.16 Unless otherwise noted, α-SiB3 is used in this paper to designate the phase with that kind of crystal structure and not to indicate a specific composition. Usually, α-SiB3 is synthesized by melting a mixture of boron (5–10 weight%) and silicon in a furnace, however, it is barely possible to obtain it purely, always being accompanied with SiB6 products.8–11,13,14 α-SiB3 has the same structure as boron carbide (B4C or B12C2), and other borides belonging to a class of icosahedral boron-rich solids that includes α-rhombohedral (α-rh) boron.7,17,18 In 1956, Zhuravlev firstly found that SiB6 was a cubic phase through the X-ray structure analysis.19 Another different structure of SiB6 was determined by M. Vlasse using single-crystal X-ray diffraction,20 it has a complex crystal structure with about 43 silicon atoms and 238 boron atoms in its orthorhombic unit cell, containing interconnected icosahedra, icosihexahedra, as well as several isolated boron and silicon atoms. Similar to α-SiB3, the ratio of B/Si = 6/1 is stoichiometry approximation for the Si–B binaries ranging from SiB5.7 to SiB6.1 contributed by interchanging silicon and boron atoms within the multiple sites.17,20 SiBn is obtained through the peritectic reaction: liquid + β-boron solid solution = SiBn at 2293 K,6 and was first synthesized by Giese et al., known as SiB14.21 However, the value width of n has been a controversy so far that previous study claimed that n ranges from 16 to 26;22 ten years later, T. B. Massalski et al. enlarged the n values to the limits between 13.9 and 32.3;23 after another decade, a wider value range of n was introduced by Y. Imai et al.7 that the Si-rich solubility limit at 1873 K is 5.4 at%, corresponding to SiB17.5, and the probable maximum value of n reached up to 60.First-principles calculation is a valuable prediction approach to understand crystal parameters, thermodynamic properties and studying their structural transformations.7,24,25 Band calculations of electronic densities of states and total energies of the Si–B system have been attempted by Y. Imai7 using first-principles pseudopotential method within local density approximation. The theoretical achievements about Si–B compounds were reviewed by B. Albert and H. Hillebrecht,25 crystal structures of this system and the structural features between the specific Si–B compounds and their structurally related borides were summarized and sorted. β-Rhombohedral boron (β-rh B) has been an attractive topic of calculation researches for decades.24–29 The crystal structure, thermodynamic stability, specific heat and electronic structure of β-rh B were introduced by T. Ogitsu et al.24 including experimental and theoretical calculation efforts. Shang et al.29 considered that β-rh B obtained several different atomic densities: 105–110 atoms per rhombohedral cell through examining the total energy of β-rh B as a function of atomic density. For the tetragonal configuration of boron,30–36 the crystal and electronic structures of α-tetragonal (α-t or I-t) B (B50, 50 atoms per cell) were investigated by Hayami and Otani31 from first-principles, while the other unstable β-tetragonal (β-t or II-t) B is probably obtained through nonequilibrium growth based on the research of surface energy and crystal growth.35 α-rh B (B12), the significant basic icosahedral boron unit, has also been focused by researchers employing means of first-principles calculations,29,36–38 and it is shown that α-rh B is a semiconductor with an indirect band gap of 1.70 eV in the study of D. Li et al.36 The majority of the research emphases were about the structures and properties of the elementary boron, and thermodynamic properties of the Si–B compounds. However, to our knowledge, there are no comparative investigations on the mechanical properties and underlying relations between the phases of Si–B system. Therefore, using means of first-principles calculations based on density functional theory, in this paper, we report the enthalpies of formation, elastic constants and electron structures of the Si–B system and other related phases: α-SiB3 (SiB3, SiB4), β-SiB3, SiB6, SiB36. The relevant data of α-rhombohedral boron (α-rh B), β-rhombohedral boron (β-rh B), α-tetragonal boron (α-t B), and γ-B28 (high pressure phases) are also available in ESI† for comparison and comprehensive understanding.
2. Computational details
First-principles calculations were performed using CASTEP code based on Density Functional Theory (DFT).39 The exchange and correlation functions were treated by generalized gradient approximation with the parameterization by Perdew–Burke–Ernzerhof (GGA-PBE).40,41 The electronic configurations of each element were 2s22p1 for B and 3s23p2 for Si, respectively. The mass of B atom is 10.81 and Si atom is 28.085. The oxidation state of any atom is 0, and none temperature factors were set on atoms. The convergence of calculations was initially checked by a 5 × 10 × 10 k-point and cutoff energy of 310 eV. The ground state and elastic constants (Cij) of all considered Si–B phases are then calculated for each fully relaxed structure. Bulk and shear moduli were estimated based on Voight–Reuss–Hill (VRH) approximation.42 Elastic moduli (E) and Poisson's ratio (ν) were obtained based on the relationship: E = 9BG/(3B + G), ν = (3B − 2G)/(6B + 2G). The universal elastic anisotropy index (AU)43 is obtained from the B and G of Voigt and Reuss with the equation: AU = 5GV/GR + BV/BR − 6.3. Results and discussions
3.1. Structural stability
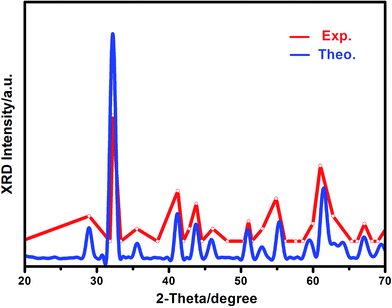
Mechanical stability, a necessary condition for a stable phase to exist in experiments, was firstly checked for all of the Si–B system crystals according to the Born–Huang criterion.44,45 If all the individual elastic moduli of a specific phase are satisfied, the mechanical stability criteria indicate its stability. The calculated elastic constants of Si–B system phases are listed in Table 1, and it can be found that α-SiB3 (SiB3, SiB4), β-SiB3 and SiB36 satisfy the Born–Huang criterion, indicating their mechanical stabilities. However, cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m-SiB6 (ref. 19) (C44 = −4.13 GPa) is mechanically unstable. To get a further understanding of the structural configuration of SiB6, we have employed the in-house developed CALYPSO46,47 structure prediction methodology to conduct the structure search for SiB6. Our search identified 20 stable structures: SiB6-01_01, SiB6-02_01,…, SiB6-19_01, SiB6-20_01. Monoclinic P21/m-type (space group number: 11) SiB6-01_01 with the lowest energy is founded to be the most energetically favorable among the 20 configurations, calculated energy of these 20 structures are available in the ESI.† Hexagonal R3m-type (space group number: 160) SiB6-08_01 is also considered in this study because of its special structure (it will be discussed in the following sections). For convenience, SiB6-01_01 denotes as SiB6 and SiB6-08_01 is abbreviated as SiB6-81. According to Table 1, monoclinic P21/m-SiB6 and hexagonal R3m-SiB6-81 are qualified for mechanical stability. To furtherly prove the reliability of the new suggested structure of SiB6, the XRD pattern was calculated. As shown in Fig. 1, it can be found that our theoretical results are in generally accordance with the experimental XRD data17,48,49 in consideration of only isolated data provided from the previous work,48 which the XRD peaks of Si, SiB3 and other Si–B compounds have been eliminated from based on available reports.17,49
m-SiB6 (ref. 19) (C44 = −4.13 GPa) is mechanically unstable. To get a further understanding of the structural configuration of SiB6, we have employed the in-house developed CALYPSO46,47 structure prediction methodology to conduct the structure search for SiB6. Our search identified 20 stable structures: SiB6-01_01, SiB6-02_01,…, SiB6-19_01, SiB6-20_01. Monoclinic P21/m-type (space group number: 11) SiB6-01_01 with the lowest energy is founded to be the most energetically favorable among the 20 configurations, calculated energy of these 20 structures are available in the ESI.† Hexagonal R3m-type (space group number: 160) SiB6-08_01 is also considered in this study because of its special structure (it will be discussed in the following sections). For convenience, SiB6-01_01 denotes as SiB6 and SiB6-08_01 is abbreviated as SiB6-81. According to Table 1, monoclinic P21/m-SiB6 and hexagonal R3m-SiB6-81 are qualified for mechanical stability. To furtherly prove the reliability of the new suggested structure of SiB6, the XRD pattern was calculated. As shown in Fig. 1, it can be found that our theoretical results are in generally accordance with the experimental XRD data17,48,49 in consideration of only isolated data provided from the previous work,48 which the XRD peaks of Si, SiB3 and other Si–B compounds have been eliminated from based on available reports.17,49
| Phase | S.G. | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C14 |
|---|---|---|---|---|---|---|---|---|---|---|
| SiB3 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
326.0 | 349.3 | 144.0 | 86.3 | 92.1 | −2.47 | |||
| SiB4 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
259.0 | 373.5 | 51.7 | 125.8 | 104.3 | −37.9 | |||
| SiB6 | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
402.6 | −4.13 | 19.31 | ||||||
| P21/m | 373.6 | 351.6 | 432.5 | 127.2 | 176.4 | 174.8 | 101.5 | 101.4 | ||
| 29.5(C23) | 16.0(C15) | −5.8(C25) | −23.7(C35) | −20.5(C46) | ||||||
| SiB6-81 | R3m | 187.8 | 196.1 | 117.3 | 74.0 | 93.3 | 74.9 | |||
| SiB36 | R3m | 419.3 | 431.5 | 146.8 | 72.9 | 75.6 | 36.7 | |||
| β-SiB3 | Imma | 288.8 | 369.6 | 357.4 | 123.3 | 134.6 | 130.8 | 51.5 | 64.3 | |
| 72.6(C23) | ||||||||||
To verify the thermodynamic stability of the considered phases in the Si–B system, the formation enthalpies (ΔHf) are calculated as listed in Table 2 and compared with available experimental results.22,50 The formation enthalpy of SixBy phase can be defined as
| ΔHf = Etotal(SixBy) − (xEtotal(Si) + yEtotal(B)) | (1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m-SiB6 and SiB6-81, since ΔHf of the former one is less than the latter ones. α-SiB3 (SiB3, SiB4) and γ-B28 is structurally related to α-rh B, from Table 2 and ESI,† it can be found that α-rh B is the most thermodynamic stable phase of those related structures and it is naturally interpreted as foreign atoms (Si atoms) disturbing the original charge distribution, thus more energy being needed to maintain equilibrium of the crystal system. However, the ΔHf of SiB36 whose structure is based on the framework of β-rh B is much more negative than β-rh B. Different from the previous condition, introducing Si atoms to the complicated polyatomic β-rh B crystal is helpful to reduce internal energy of the structure. The rigorous synthesis and stability conditions, that β-SiB3 needs producing from a lower temperature reaction (1000–850 °C) in metallic flux to permit the total bypass of the compound α-SiB3,16 indicate the highest ΔHf of β-SiB3 in Table 2.
m-SiB6 and SiB6-81, since ΔHf of the former one is less than the latter ones. α-SiB3 (SiB3, SiB4) and γ-B28 is structurally related to α-rh B, from Table 2 and ESI,† it can be found that α-rh B is the most thermodynamic stable phase of those related structures and it is naturally interpreted as foreign atoms (Si atoms) disturbing the original charge distribution, thus more energy being needed to maintain equilibrium of the crystal system. However, the ΔHf of SiB36 whose structure is based on the framework of β-rh B is much more negative than β-rh B. Different from the previous condition, introducing Si atoms to the complicated polyatomic β-rh B crystal is helpful to reduce internal energy of the structure. The rigorous synthesis and stability conditions, that β-SiB3 needs producing from a lower temperature reaction (1000–850 °C) in metallic flux to permit the total bypass of the compound α-SiB3,16 indicate the highest ΔHf of β-SiB3 in Table 2.
| Phase | S.G. | ΔHf (eV per atom) | ΔHf (kJ per mol per atom) | ΔHf (Exp.) (kJ per mol per atom) |
|---|---|---|---|---|
| SiB3 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
−1.196 | −115.449 | −109.4 (ref. 48) |
| SiB4 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
−1.133 | −109.336 | −109.4 (ref. 48) |
| SiB6 | Cub.(Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
−1.218 | −117.486 | 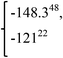 |
| Mon.(P21/m) | −1.267 | −122.233 | ||
| SiB6-81 | Hex.(R3m) | −1.248 | −120.458 | |
| SiB36 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
−2.883 | −278.161 | |
| β-SiB3 | Ort.(Imma) | −0.0699 | −6.746 |
The calculated structural parameters and Wyckoff positions of different crystals, after full stress and position relaxation, are shown in Table 3 and ESI.† In general, our results are in good accordance with previous theoretical and experimental results as shown in Table 3.9,11,16,19,52
| Phase | Structure | Lattice parameter (Å) | |||||
|---|---|---|---|---|---|---|---|
| Theory (this work) | Experiment (ref.) | ||||||
| a | b | c | a | b | c | ||
| SiB3 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
6.319 | 6.319 | 12.71 | 6.32 | 6.32 | 12.71 (ref. 11) |
| SiB4 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
6.319 | 6.319 | 12.71 | 6.33 | 6.33 | 12.74 (ref. 9) |
| SiB6 | Cub.(Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
4.13 | 4.13 | 4.13 | 4.13 | 4.13 | 4.13 (ref. 19) |
| Mon.(P21/m) | 6.26 | 6.22 | 3.07 | ||||
| (β = 90.03°) | |||||||
| SiB6-81 | Hex.(R3m) | 5.85 | 5.85 | 7.48 | |||
| SiB36 | Hex.(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
11.01 | 11.01 | 23.90 | 10.98 | 10.98 | 23.86 (ref. 51) |
| β-SiB3 | Ort.(Imma) | 8.39 | 12.57 | 6.21 | 8.39 | 12.57 | 6.21 (ref. 16) |
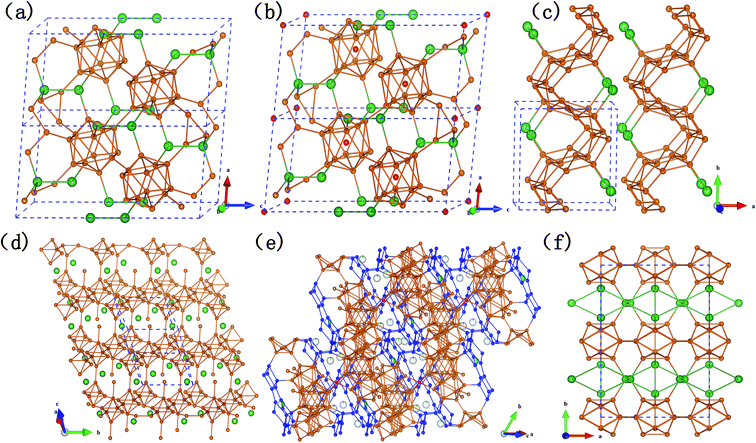
As shown in Fig. 2, B12 icosahedra, as the single primary unit of α-rh B, is an indispensable structural element for most of the Si–B compounds. It can be found that SiB3 (Fig. 2a) and SiB4 (Fig. 2b) are established with B12 icosahedra as the framework. The B12 units are situated on the corners of a rhombohedron just as in α-rh B (two 18h sites in hexagonal arrangement), Si atoms are located on the spatial diagonal of the rhombohedron and link three icosahedra each of one layer (6c site), as a result, the remaining valence electron of Si atom contribute to bonding a pair of close Si atoms to form a Si2 group. Thus, the 2e3c boron bonds (B–B distance: 1.67 Å) in α-rh B are replaced by 2e2c silicon bonds (Si–Si distance: 2.39 Å for SiB3 and 2.29 Å for SiB4), causing a distinct reduction of the c/a ratio (12.56/4.908 for α-rh B in hexagonal arrangement). Overall, it is the partial incorporation, which results from silicon atoms going into the polar position of the icosahedron, that leads to the high silicon content and the relatively large lattice parameters.
The remarkable difference between SiB3 and SiB4 is that there is an additional B atom (3a site) in SiB4 lattice located in the center of each icosahedron, accordingly, which induce slight variations of the bond lengths of inter- and intra-icosahedral boron atoms. However, such little change did not affect the lattice parameters in our calculated results (as shown in Table 3). It also can be explained that in α-SiB3, some Si atoms are randomly distributed in the B12 cages resulting in very distorted icosahedra,18 according to different situation of inside Si atoms of B12-cages in these two α-SiB3 phases. In contrast, Si atoms in β-SiB3 are rigorously excluded from the cages (as shown in Fig. 2f), thus resulting in more regular icosahedra. It was even considered as the first Si–B binary phase that is fully crystallographically ordered without any Si/B mixed sites or disorder.16
The structures of two SiB6 compounds are quite different. In Fig. 2d, the hexagonal crystal (R3m-SiB6-81) belongs to layered-like structure based on the B6 octahedron unit composed of eight boron atoms, and with silicon atoms located in interstitial spaces; however, configuration of the monoclinic one (P21/m-SiB6) is built on zig-zag networks bonded by boron atoms in Fig. 2c.
Comparing the Si–B binaries (Fig. 2a–f), it can be noticed that the structures bonded with boron atoms become more and more complex along with the increasing content of boron. For example, B28 triply fused icosahedra (three condensed icosahedra in Fig. 2e) were formed in SiB36 by 28 boron atoms in addition to B12 icosahedra-the only polyhedron in α-SiB3. Si atoms partially occupy the interstitial sites between the polyhedrons in SiB36 instead of being located in the 6c sites completely in α-SiB3. With regard to the structural influence on the B–B bond lengths of inter- and intra-icosahedra, we find that the distances are all beyond 1.85 Å in the B12 units of two α-SiB3 structures, while they reduce to around 1.70 Å in SiB36.
As the last two phases in the boron-rich end of the Si–B phase diagram, SiB36 and β-rh B have a similar formation based on B28 triply fused icosahedra as the boron framework. Differing to previous structures of SiB36 (ref. 25 and 53) those could be analogized as β-rh B framework with interstitial sites between polyhedrons and B atoms in icosahedra partly occupied by Si atoms, however, in this work there is a new found boron B6 unit comprised with 6 boron atoms. To be specific, as highlighted by blue atoms in Fig. 2e, two quadrilateral-B4 connect with each other by a shared B–B bond (B7–B9, bond length: 1.79 Å) producing two included angle: 121.62° and 115.64°. The linked B6 units together with B atoms of B28 units form a layer being vertical to the spatial diagonal. There are four kinds of boron positions in a B6 unit, B1: bonded with two neighbor B atoms of its own B6 unit and a B atom of the neighbor B6 unit in the same layer; B2: bonded with one B atom of B28 unit, one of the neighbor parallel layer, in addition to two intra-B6 unit B–B bonds; B7: three intra-B6 unit B–B bonds and a B–B bond with a B atom in a icosahedron; B9: similar to B7 except the bond with icosahedral atom, however, linked with a B atom of B28 unit. The lengths of B–B bond intra-B6 unit are B1–B2: 1.71 Å, B2–B7: 1.79 Å, B1–B9: 1.82 Å, B7–B9: 1.79 Å, respectively. The bond lengths of between intra- and inter-B6 unit are layer–layer: B2–B2 = 1.78 Å, intra-B6 with B28: B9–B10 = 1.69 Å and B2–B3 = 1.73 Å, intra-B6 with B12: B7–B5 = 1.67 Å.
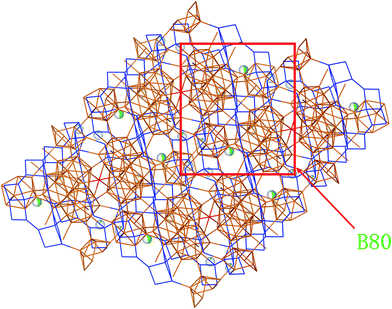
From Fig. 2e and 3, we can find that two layers constituted with B80 units (B80, a ring linked by diametrically located 2 × B28, 2 × B12) are connected by two neighbor parallel B6 layers, in addition to be covalently bound through junctional atom B15 (highlighted as red atoms in Fig. 2e). Therefore, it can be considered as B80 layers and B6 layers being stacked vertically to the spatial diagonal make the framework of SiB36, and Si atoms are partially located at interstitial sites in the space surrounded by the joint B6 layers.
3.2. Elastic properties
The calculated individual elastic constants within the strain–stress method are listed in Table 1 for considered Si–B system crystals. In general, all of the mechanically stable phases show the considerably higher values of C11, C22 and C33 than that of C44, indicating relatively higher incompressibility along a-, b-and c-axis. Furthermore, among all the individual elastic constants, C33 (432.5 GPa) of P21/m-SiB6 is the largest one suggesting its specially low compressibility along c-axis. Additionally, the C11 value of SiB36 reaches up to 419.3 GPa confirming its outstanding incompressibility along a-axis; meanwhile, its C33 is 431.5 GPa, the second highest value, predicting the excellent elastic properties of SiB36.To further demonstrate the elastic properties of Si–B crystals, bulk modulus, shear modulus, Young's modulus, Poisson's ratio and universal elastic anisotropy index (AU) were estimated from the calculated individual elastic constants (as shown in Table 4), the previous available results are also listed for comparison and verifying the reliability of our calculation (as shown in ESI†). In general, our calculated results are in reasonable accordance with the reported data, however, it should not be ignored that the bulk moduli (181.3 GPa) of β-rh B is 11% less than the theoretical result (203.5 GPa) predicted by Masago, et al.37 The different approximation methods may induce the deviation between the two considered values, since local-density approximation (LDA) was employed in ref. 37 while our ab initio calculation adopted GGA as the approximation method. In consideration of first-principles calculation for elastic properties (elastic constant, bulk/shear moduli, etc.), LDA results are probably larger than the actual values, on the other hand, GGA method is likely to complete tasks with underestimation, which can also explain the fact that our results are relatively smaller than the experimental data. According to Table 4, the bulk modulus (183.5 GPa) of SiB36 is the largest B, while SiB6 has the largest G (153.8 GPa) and E (358.8 GPa). The intensity parameters of the other phases are just slightly lower, also indicating their comparative hardness. However, it is unexpected that the shear moduli of SiB4 drops to 55.4 GPa, for its structure is particularly similar to SiB3 (G = 129.8 GPa) and their bulk modulus are very close (172.1 GPa for SiB4, 171.2 GPa for SiB3). Comparing the two structures in Fig. 2, we infer that the additional boron atoms in SiB4 lattice, contrast to SiB3, are just right located long the spatial diagonal so as to disturb the original electronic division and impair the original bonding strength, that finally induce the conspicuous weakness along this direction which be responsible for the shear performance of crystals.
| Phase | S.G. | B | BV | BR | G | GV | GR | E | ν | B/G | AU |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SiB3 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
171.2 | 171.4 | 171.1 | 129.8 | 130.3 | 129.3 | 310.8 | 0.20 | 1.32 | 0.041 |
| SiB4 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
172.1 | 173.4 | 170.7 | 55.4 | 71.1 | 39.6 | 150.0 | 0.35 | 3.11 | 4.00 |
| SiB6 | P21/m | 179.2 | 180.3 | 178.1 | 153.8 | 157.4 | 150.3 | 358.8 | 0.17 | 1.17 | 0.25 |
| SiB6-81 | R3m | 121.1 | 121.4 | 120.8 | 64.3 | 79.0 | 49.5 | 163.8 | 0.27 | 1.88 | 2.99 |
| SiB36 | R3m | 183.5 | 186.1 | 180.9 | 152.4 | 153.2 | 151.6 | 358.1 | 0.17 | 1.20 | 0.082 |
| β-SiB3 | Imma | 153.6 | 154.7 | 152.5 | 132.5 | 132.9 | 132.0 | 308.6 | 0.17 | 1.16 | 0.048 |
It could not be ignored that not only the elastic performances of P21/m-SiB6 and R3m-SiB6-81 are quite different, but also the elastic modulus of R3m-SiB6-81 are much lower than the other Si–B compounds. After analyzing the structures in Fig. 2c and d and 4, we can conclude that the hexagonal crystal (R3m-SiB6-81) belongs to layered-like structure based on the B6 octahedron unit composed of eight boron atoms, and with silicon atoms located in interstitial spaces; however, configuration of the monoclinic one (P21/m-SiB6) seems to be more complex with relative more covalent networks not only between boron atoms but also silicon ones involved, which avoiding layers' sliding in the lattice structure of R3m-SiB6-81 and providing P21/m-SiB6 stronger elastic properties.
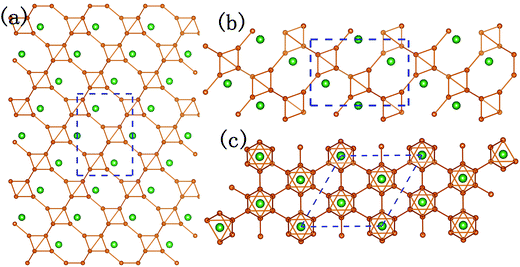 | ||
| Fig. 4 Crystal structure of hexagonal SiB6-81. (a), (b) and (c) are along a-, b- and c-axis, respectively. | ||
The above few fluctuations can't impede us to find these general trends that both the bulk and shear modulus decreased gradually with the increasing Si concentration. Those are possibly induced by that B–B bond distance ranges are lengthened from 1.67–1.92 Å in monatomic boron to 1.84–2.04 Å so as to weaken the bond strength, in addition to the balance of electron distribution is broken and the new Si–Si, Si–B bonds are inferior to B–B bonds in hardness, contributed by the incorporation of Si atoms into the stable structure bonded by B atoms.
The ratio between the shear and bulk modulus (B/G) has been proposed by Pugh54 to predict brittle or ductile behavior of materials. According to the Pugh criterion, a high B/G value indicates a tendency for ductility, while a low B/G value is associated with brittleness. From Table 4, SiB4 (2.80), SiB6-81 (1.88) are recognized with B/G value larger than the critical value (1.75) suggesting their ductile behaviors, while the other phases are expected to perform brittleness. The elastic anisotropy index (AU) represents a universal measure to quantify the single crystal elastic anisotropy. As shown in Table 4, SiB3 is the relatively most isotropic phase, with the lowest AU value (0.041) in the whole Si–B system, contrarily, SiB4 (AU = 4.00) is predicted as most anisotropy crystal.
3.3. Electronic properties
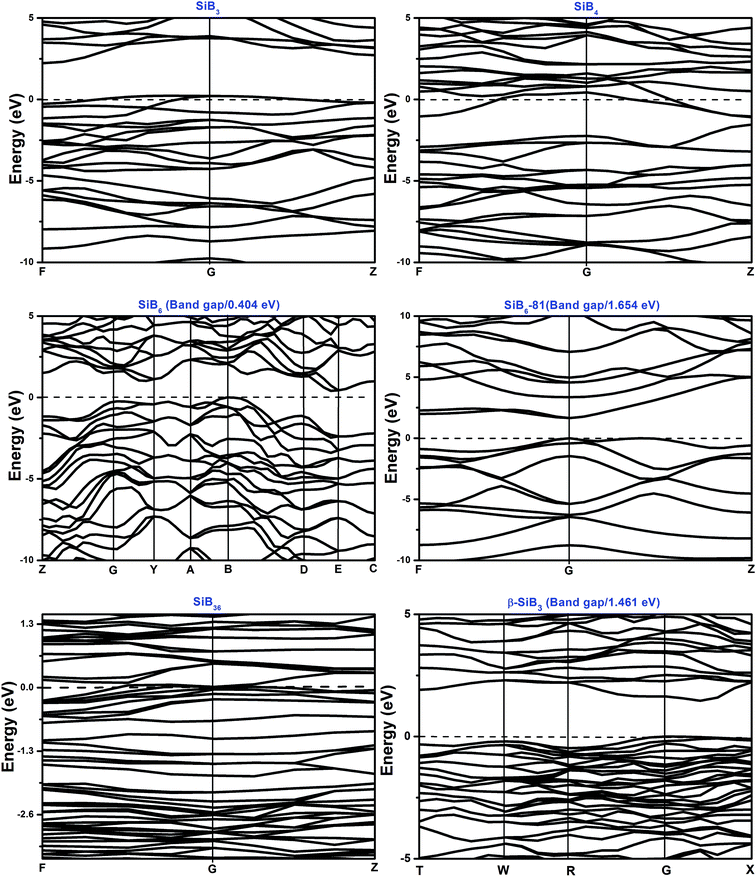
The total and partial density of states (DOS) for the Si–B crystals are displayed in Fig. 5. Analyzing all the DOS patterns, we found that there are three phases: P21/m-SiB6, R3m-SiB6-81 and β-SiB3 showing the semiconducting features. Incorporated with the calculated band structures of those 3 compounds (shown in Fig. 6), we collected the indirect band gaps for P21/m-SiB6 and β-SiB3 with energy values (eV): 0.41 and 1.461; direct band gaps for R3m-SiB6-81 (1.654 eV), respectively. The calculated result of β-SiB3 is in good accordance with the previously work16 which showed an indirect band gap of ∼1.5 eV from theoretical calculations and 2.0 eV optically determined, in addition, our calculated band gaps of α-rh B (1.533 eV) and γ-B28 (1.580 eV) in ESI† are in good agreement with previously theoretical results: 1.54 eV (ref. 25) and 1.7 eV,55 therefore our calculation of electronic properties is dependable. The estimated band gap of SiB6 by Feigelson and Kingery is about 1.2 eV (ref. 56) and our calculated value is 0.41 eV. Since the general tendency is allowed that the generalized gradient approximation gives narrower band gap than the observed one, the estimated value seems to be reasonable. The temperature dependence of the electrical conductivity of SiB3 was measured in ref. 56 and it was concluded that SiB3 is a semiconductor with the energy gap of 1.2 eV, which does not agree to the present work. We infer that the increase in electric conductivity with the temperature observed by Feigelson and Kingery56 is due to the rising hopping probability of the localized state at higher temperature, which is possibly induced by disordered arrangement of the atoms, but due to the semiconducting band conduction. R3m-SiB6-81 has a wide band gap of 1.654 eV, this new theoretically suggested material might be useful as a refractory n-type semiconductor capable of operating in extreme environments, so the results reported herein warrant future investigations of synthesizing this Si–B compound.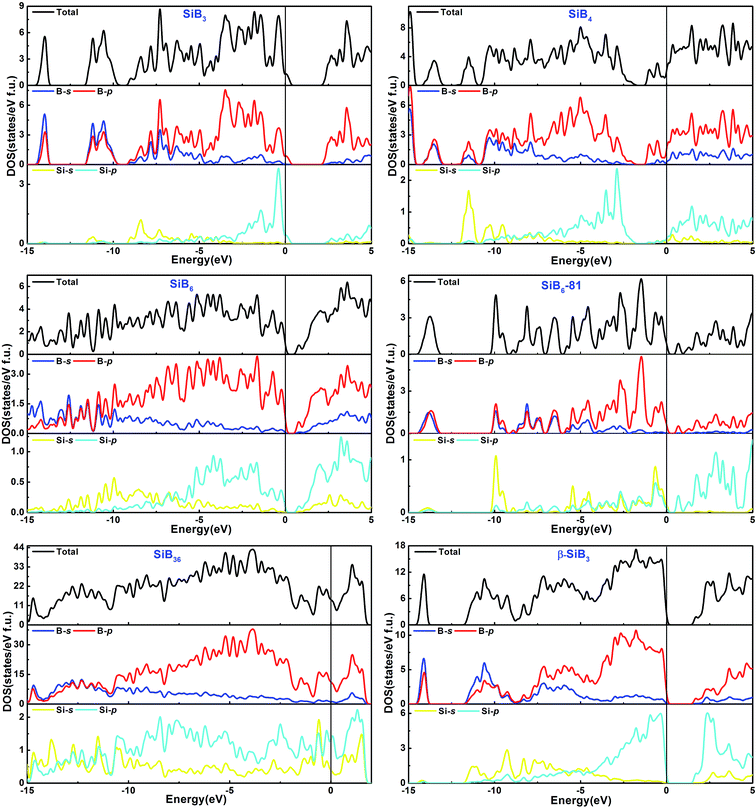 | ||
| Fig. 5 Calculated total and partial density of states of phases in Si–B system. Fermi energy level is indicated by a vertical line. | ||
Since it is widely accepted that the DFT-GGA approximation probably underestimates the band gap of solids,24,32 DFT-LDA approximation was also applied to study the electronic structures and verify the GGA calculation results. The LDA calculation results indicate that the band gaps are 0.371 eV, 1.621 eV and 1.502 eV for SiB6, SiB6-81 and β-SiB3, respectively. Those reasonable differences between GGA and LDA calculations solidify our conclusions in electronic properties research. The DOS and band structures results from DFT-LDA calculations are available in ESI.†
There is no band gap provided by band structures of SiB4 and SiB36 in Fig. 6, as well as their DOS values are relatively large at Fermi level, indicating they are energetically unstable under 0 K and GPa. It can be found that there is a wide overlap between B-s state and B-p state of SiB3, SiB4, SiB6, SiB6-81, SiB36 and β-SiB3 from −14 eV to −5 eV, respectively, demonstrating the strong sp3 hybridization of covalent bonds, which mainly accounts for their relatively good performances in bulk modulus. It is interesting to notice that for SiB3 and SiB4, there are two sharp peaks in both sides of the Fermi level and DOS between the peaks are not 0 eV, which implying pseudogap exists in both of these two phases. Those pseudogap valleys show stronger covalent interaction in the structures. Moreover, there is a general feature for the Si–B binaries that below the Fermi level, the valence bands were dominated by B states with both B-s and B-p states at lower band while B-p states at higher band. Nevertheless, as shown in Fig. 5, the contributions to the total DOS of Si–B compounds from the Si states are not significant because Si atoms donate electrons to B–B network to stabilize the structure, for example, about 0.96 electron transformed from one Si atom to B–B network for SiB6 by analyzing the atomic Mulliken overlap populations.
In addition to the calculated values of two indirect band gaps and one direct band gap, in the band structures of these six Si–B binaries (shown in Fig. 6), it can also be noticed that the distributions of band structures of P21/m-SiB6, SiB36 and β-SiB3 are more concentrated than those of the other three phases; and each energy band at different points fluctuates less drastically. Those details account for that electron localizations of the energy bands of SiB6, SiB36 and β-SiB3 are more intensive and effective mass of an electron is relatively larger; in contrast, energy bands of SiB3, SiB4 and R3m-SiB6-81 display more electron nonlocality.
4. Conclusions
We systematically investigated the crystal structures, phase stability, mechanical properties and electronic structures of silicon–boron system by using first-principles calculations of density functional theory. Previously suggested phase: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m-SiB6 is found to be mechanically unstable, and the new structure of P21/m-SiB6 is proposed in this paper. Another new structure of SiB36 is suggested, in which two layers constituted with B80 unit are connected by two neighbor parallel B6 layers, in addition to be covalently bound through junctional atom B15 while Si atoms are partially located at interstitial sites in the space surrounded by the joint B6 layers. We find the general trends that both the bulk and shear modulus decreased gradually with the increasing Si concentration, because the introduced Si–Si and Si–B bonds are weaker than the original B–B network. Although the elastic properties of β-SiB3 are slightly inferior to α-SiB3, its wide band gap (1.461 eV) makes β-SiB3 a potential p-type semiconductor. In addition to β-SiB3, P21/m-SiB6 is found to be with an indirect band gap of 0.41 eV; while R3m-SiB6-81 has a direct band gap of 1.654 eV, this new theoretically suggested material might be useful as a refractory n-type semiconductor capable of operating in extreme environments that deserving more efforts in research of this Si–B compound.
m-SiB6 is found to be mechanically unstable, and the new structure of P21/m-SiB6 is proposed in this paper. Another new structure of SiB36 is suggested, in which two layers constituted with B80 unit are connected by two neighbor parallel B6 layers, in addition to be covalently bound through junctional atom B15 while Si atoms are partially located at interstitial sites in the space surrounded by the joint B6 layers. We find the general trends that both the bulk and shear modulus decreased gradually with the increasing Si concentration, because the introduced Si–Si and Si–B bonds are weaker than the original B–B network. Although the elastic properties of β-SiB3 are slightly inferior to α-SiB3, its wide band gap (1.461 eV) makes β-SiB3 a potential p-type semiconductor. In addition to β-SiB3, P21/m-SiB6 is found to be with an indirect band gap of 0.41 eV; while R3m-SiB6-81 has a direct band gap of 1.654 eV, this new theoretically suggested material might be useful as a refractory n-type semiconductor capable of operating in extreme environments that deserving more efforts in research of this Si–B compound.
References
- R. Riedel, Adv. Mater., 1994, 6, 549–560 CrossRef CAS.
- Mechanical properties and their relation to microstructure, D. Sherman and D. Brandon, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2000 Search PubMed.
- C. Wood, Mater. Res. Soc. Symp. Proc., 1987, 97, 335–346 CrossRef CAS.
- J.-M. Darolles, T. Lepetre and J.-M. Dusseau, Phys. Status Solidi A, 1980, 58, K71–K75 CrossRef CAS.
- M. Mukaida, T. Tsunoda, M. Ueda and Y. Imai, Proc. 19th Int. Conf. Thermoelectrics, 2000, p. 255 Search PubMed.
- J. Wu, W. Ma, D. Tang, B. Jia, B. Yang, D. Liu and Y. Dai, Procedia Eng., 2012, 31, 297–301 CrossRef CAS.
- Y. Imai, M. Mukaida, M. Ueda and A. Watanabe, J. Alloys Compd., 2002, 347, 244–251 CrossRef CAS.
- C. Brosset and B. Magnusson, Nature, 1960, 187, 54–55 CrossRef CAS.
- V. I. Matkovich, Acta Crystallogr., 1960, 13, 679–680 CrossRef CAS.
- H. F. Rizzo and L. R. Bidwell, J. Am. Ceram. Soc., 1960, 43, 550–552 CrossRef CAS.
- B. Magnusson and C. Brosset, Acta Chem. Scand., 1962, 16, 449–455 CrossRef CAS.
- On refractory boron compounds crystallizing in B4C-type structures, ed. T. Lundstrom and H. Bolmgren, Jpn. J. Appl. Phys. Ser., 1994, vol. 10, pp. 1–4 Search PubMed.
- E. Colton, J. Am. Chem. Soc., 1960, 82, 1002 CrossRef CAS.
- C. F. Cline and D. E. Sands, Nature, 1960, 185, 456 CrossRef CAS.
- R. Tremblay and R. Angers, Ceram. Int., 1989, 15, 73–78 CrossRef CAS.
- J. R. Salvador, D. Bilc, S. D. Mahanti and M. G. Kanatzidis, Angew. Chem., 2003, 115, 1973–1976 CrossRef.
- T. L. Aselage, J. Mater. Res., 1998, 13, 1786–1794 CrossRef CAS.
- T. L. Aselage and D. R. Tallant, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2675–2678 CrossRef CAS.
- N. N. Zhuravlev, Kristallografiya, 1956, 1, 666–668 CAS.
- M. Vlasse, G. A. Slack, M. Garbauskas, J. S. Kasper and J. C. Viala, J. Solid State Chem., 1986, 63, 31–45 CrossRef CAS.
- R. F. Giese, J. Economy and V. I. Matkovich, Z. Kristallogr., 1965, 122, 144–147 CrossRef.
- B. Armas, G. Male, D. Salanoubat, C. Chatillon and M. Allibert, J. Less-Common Met., 1981, 82, 245–254 CrossRef CAS.
- T. B. Massalski, H. Okamoto, P. R. Subramanian and L. Kacprzak, Binary alloy phases diagrams, ASM, Materials Park, OH, 2nd edn, 1990 Search PubMed.
- T. Ogitsu, E. Schwegler and G. Galli, Chem. Rev., 2013, 113, 3425–3449 CrossRef CAS PubMed.
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef CAS PubMed.
- B. Callmer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1951–1954 Search PubMed.
- D. L. V. K. Prasad, M. M. Balakrishnarajan and E. D. Jemmis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195102 CrossRef.
- T. Ogitsu, F. Gygi, J. Reed and Y. Motome, J. Am. Chem. Soc., 2009, 131, 1903–1909 CrossRef CAS PubMed.
- S. Shang, Y. Wang, R. Arroyave and Z. K. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 092101 CrossRef.
- S. Lee, D. Bylander, S. Kim and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 3248–3251 CrossRef CAS.
- W. Hayami and S. Otani, J. Solid State Chem., 2010, 183, 1521–1528 CrossRef CAS.
- S. Aydin and M. Simsek, J. Alloys Compd., 2011, 509, 5219–5229 CrossRef CAS.
- J. L. Hoard, R. E. Hughes and D. E. Sands, J. Am. Chem. Soc., 1958, 80, 4507–4515 CrossRef CAS.
- G. Will and K. Ploog, Nature, 1974, 251, 406–408 CrossRef CAS.
- W. Hayami and S. Otani, J. Phys. Chem. C, 2007, 111, 10394–10397 CAS.
- D. Li, Y. N. Xu and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 5895–5905 CrossRef CAS.
- A. Masago, K. Shirai and H. Katayama-Yoshida, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104102 CrossRef.
- M. A. White, A. B. Cerqueira, C. A. Whitman, M. B. Johnson and T. Ogitsu, Angew. Chem., Int. Ed., 2015, 54, 3626–3629 CrossRef CAS PubMed.
- P. J. D. L. M. D Segall, M. J Probert, C. J Pickard, P. J Hasnip, S. J Clark and M. C Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- R. Hill, Proc. Phys. Soc., 1952, 65, 349–354 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Oxford University Press, Oxford, 1954 Search PubMed.
- J. F. Nye, Physical properties of crystals, Oxford University Press, Oxford, 1985 Search PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- C. F. Cline, J. Electrochem. Soc., 1959, 106, 322–325 CrossRef CAS.
- JCPDS pattern #35-777, International Centre for Diffraction Data, Newton Square, PA.
- A. I. Zaitsev and A. A. Kodentsov, J. Phase Equilib., 2001, 22, 126–135 CrossRef CAS.
- R. W. Olesinski and G. J. Abbaschian, Bull. Alloy Phase Diagrams, 1984, 5, 478–484 CrossRef.
- B. G. Arabey, Izv. Akad. Nauk SSSR, Neorg. Mater., 1979, 15, 1589–1592 Search PubMed.
- J. Roger, V. Babizhetskyy, J.-F. Halet and R. Guérin, J. Solid State Chem., 2004, 177, 4167–4174 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45(7), 823–843 CrossRef CAS.
- E. Zarechnaya, L. Dubrovinsky, N. Dubrovinskaia, Y. Filinchuk, D. Chernyshov, V. Dmitriev, N. Miyajima, A. El Goresy, H. Braun, S. Van Smaalen, I. Kantor, A. Kantor, V. Prakapenka, M. Hanfland, A. Mikhaylushkin, I. Abrikosov and S. Simak, Phys. Rev. Lett., 2009, 102, 185501 CrossRef PubMed.
- R. S. Feigelson and W. D. Kingery, Ceram. Bull., 1963, 42, 688 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00592j |
| This journal is © The Royal Society of Chemistry 2017 |