Open Access Article
Open Access ArticleTheoretical investigation on the effect of ancillary ligand modification for highly efficient phosphorescent platinum(II) complex design†
Hong-Wei Fan,
Fu-Quan Bai *,
Zhi-Xiang Zhang,
Yu Wang,
Ze-Xing Qu,
Rong-Lin Zhong and
Hong-Xing Zhang*
*,
Zhi-Xiang Zhang,
Yu Wang,
Ze-Xing Qu,
Rong-Lin Zhong and
Hong-Xing Zhang*
International Joint Research Laboratory of Nano-Micro Architecture Chemistry, Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130023, China. E-mail: baifq@jlu.edu.cn; zhanghx@mail.jlu.edu.cn
First published on 20th March 2017
Abstract
In this study, density functional theory (DFT) and time-dependent density functional theory (TDDFT) calculations were employed to investigate the geometries, electronic structures, reorganization energy (λ) and photophysical properties of four cyclometalated Pt(II) complexes (bzq)Pt(dpm) (1), (bzq)Pt(ppy) (2), (bzq)Pt(Ncaz) (3) and (bzq)Pt(Ndbt) (4) (where bzq = benzo[h]quinoline, dpm = dipivolylmethanoate, ppy = 2-phenylpyridine, Ncaz = N-substituted carbazole and Ndbt = N-substituted dibenzothiophene). In addition, the radiative decay processes and zero-field splitting were calculated based on the spin–orbit coupling (SOC) effect, and nonradiative decay pathways were discussed to evaluate the phosphorescence efficiency qualitatively. All the complexes retain the bzq as a cyclometalated ligand and our research focuses on the role recognition of another ancillary ligand modification theoretically. According to the results, in complexes 2–4 replacing the dpm with different ligands shows better rigidity which may weaken the nonradiative decay pathways and enhance the capability of charge transfer. Furthermore, complexes 1–4 tend to be bluish-green luminescent materials, and the emission wavelengths of 1, 2 and 4 are close to each other due to the similar excited state energy levels and electronic density distribution. Compared with complex 1, the radiative decay rate constants (kr) of 2–4 are greatly increased. Therefore, the designed complexes would be potential phosphorescence materials because of their high phosphorescence quantum efficiency and complex 3 can also serve as a promising bipolar transporting material due to its better charge transfer balance character.
1 Introduction
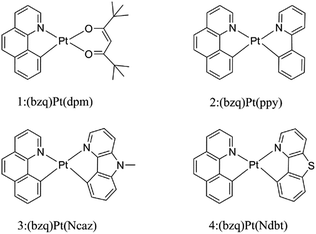
Over the past decades, organic light emitting diodes (OLEDs) have obtained a great deal of attention due to their flexibility in flat-panel displays.1,2 They are widely used in digital products and solid-state lighting devices.3–6 Phosphorescent transition-metal compounds have excellent performances as triplet dopant emitters in OLED emission layers, especially those of Ir(iii) and Pt(II) complexes. They are heavy metal atoms that can induce strong spin–orbit coupling (SOC) and promote an effective intersystem crossing (ISC), which results in higher quantum efficiency.7–11 Platinum which has the second largest SOC constant, tends to form planar structure due to the d8-electron configuration of the Pt(II) ion. The ligand of cyclometalated Pt(II) complexes can be designed as bidentate, tridentate and tetradentate. The diversity of these ligands can greatly affect the phosphorescence properties.12–16 As we know, the singlet excited states convert to the triplet states through ISC due to the SOC and then the triplet excited states return to the ground state, phosphorescence can be achieved through the radiative decay process. Nevertheless, if nonradiative decay holds a large proportion in the whole decay process, there will be weak or no phosphorescence.17 Therefore, the key to improve the efficiency of electroluminescent emitters are to increase the radiative decay rate constants and decrease the nonradiative decay rate constants.18Generally, chelating ligands of transition-metal complexes, which play a critical role in the OLEDs, include the cyclometalated ligands and ancillary ligands. The cyclometalated ligands have influence on the charge transition between metal and ligand (MLCT) at the excited states, and then alter the emission wavelengths.19 Moreover, ancillary ligands provide the ligand fields and affect the relative energy of metal center, such as β-diketonate and picolinate.20,21 Previous researches have demonstrated that the phosphorescence properties would be easily tuned mostly by the variation of cyclometalated ligands, while the change of ancillary ligands has little influence.22,23 Recently, ancillary ligands can affect the phosphorescence efficiency evidently through altering the properties of excited-state was recorded.24 Thus, the modification of ancillary ligands becomes the focus for the highly efficient of transition-metal complexes.25,26 In this respect, the heteroleptic C^N ligands such as phenyl-pyrazole (ppy) and phenyl-pyrazole (ppz) were widely applied in transition metal complexes.27–30 The C^N ligand can bind to metals forming a five-membered chelate through the N atom of pyridine ring and C atom of phenyl. The anionic C atom related to the metal centre is a strong σ-donor while the pyridyl ring maintains a favourable π-acceptor. The C^N ligands provide the metal ion a strong ligand field which leads to a higher energy of deactivating d–d states and reduces the thermal quenching compared to homologous N^N ligands.31,32 Lately, the carbazole group has been used to improve the rigidity and performance of complexes. As reported by Hang and co-workers, a series of highly efficient cyclometalated Pt(II) complexes were synthesized and the maximum external quantum efficiency value as high as 23.7% were achieved by introducing a carbazole group in ligand.33 Based on this knowledge, the N atom on the carbazole group is substituted by the S atom to foresee new structure. Recent research in Thompson group, they have synthesized and reported a series of novel bidentate Pt(II) complexes.34 Among these complexes, the suitable complex 1 has still the small value of nonradiative decay rate constant. Based on the complex 1, complexes 2–4 in Fig. 1 are tried to be designed by replacing the dpm ligand with different ancillary ligands mentioned above to seek the better candidates. Herein, as the highly efficient phosphorescent OLED materials, the newly designed complexes are expected to improve the radiative decay rate constant and strengthen the stability.
In order to gain a deep insight into the effects of ancillary ligands on the photophysical properties and quantum efficiency of these complexes, DFT and TDDFT methods have been adopted to investigate the electronic structures, charge transport abilities and emission properties of the complexes 1–4. The radiative decay rate (kr) and zero-filed splitting values are quantitatively evaluated by the calculation of SOC matrix elements; nonradiative decay rate (knr) is qualitatively discussed via energy gap law and the relative energy between metal-centered (3MC) state and minimum energy crossing point (MECP).17,35,36 Reorganization energy (λ) is an important factor in evaluating the balance between the electron and hole transport of the luminescent materials. The theoretical calculation results reveal that complexes 2 and 4 would be better phosphorescent materials for the high phosphorescence quantum efficiency and complex 3 can serve as promising bipolar candidate due to the balanced charge carrier injection and transport feature. We hope that our preliminary study could provide useful information for the further design and application of highly efficient luminescent material in OLEDs.
2 Theory of computation
2.1 Theoretical background
Generally speaking, the phosphorescence quantum efficiency of transition metals is decided by radiative decay and nonradiative decay rates. According to the energy gap law, the nonradiative decay rate constant (knr) from Tm to S0 states can be evaluated by the equation:37,38| knr(Tm → S0) ∝ exp{−β[E(Tm) − E(S0)]} | (1) |
The parameter β is involved with the structural distortion between the ground and correlative excited triplet states. [E(Tm) − E(S0)] is the energy gap between excited state and ground state. Hence, the smaller structural distortion and larger energy gap between excited triplet and ground state would be beneficial to decrease the nonradiative decay rate.
On the basis of Born–Oppenheimer approximation and the first order perturbation theory, the phosphorescent radiative decay rate constant (kr) that from Tm to S0 can be expressed as follows:39,40
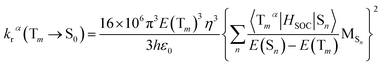 | (2) |
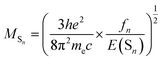 | (3) |
It is obvious that the MSn is connected with the oscillator strength (fn) and transition energy (E(Sn)). Where e is the electron charge; me and c are the mass of an electron and light speed. Combined with the eqn (2) and (3), the kr is represented in the form:
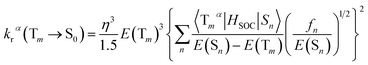 | (4) |
Under the Boltzmann statistics distribution, the triplet sublevels are postulated at thermal equilibrium. Thus, the kr can be calculated as the vectorial summation of krα values as follows:41,42
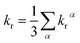 | (5) |
As we all know, the triplet state splits into three spin triplet sublevels duo to the SOC effect. Zero-field splitting (ZFS) is defined as the energy splitting between the first and third sublevel, which is related to the composition of MLCT in emission excited and the magnitude of kr values.43,44 The ΔE(ZFS) can be described in the form:
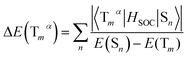 | (6) |
2.2 Computational details
All the calculations were performed by the Gaussian 09 software package with a tight self-consistent convergence threshold to ensure optimization and wave functions convergence.45 The geometry optimization and phosphorescent properties were evaluated by DFT and TDDFT. In the process of optimization, vibrational frequencies were calculated with no imaginary frequencies, indicating the optimized structures are at the minima of the potential energy surface. Since the experimental data was obtained in cyclohexane solution, the solvent effect by utilizing the Polarizable Continuum Model (PCM) was taken into account in the geometry optimization and phosphorescence properties.46,47 In addition, Hay and Wadt's48 quasi-relativistic effective core potential (ECP) with 18 valence electrons as well as the “double-ζ” quality basis set LANL2DZ were adopted for platinum atom and the 6-31G(d) basis set was applied to the non-metallic atoms such as C, H, O, N and S atoms.It is important to choose a reliable exchange–correlation functional for the current system. Considering the charge-transfer of ligand to metal in transition metal complexes, five widely used exchange–correlation functionals containing the B3LYP,49 B3P86,50 PBE0,51 M062X,52 and CAM-B3LYP53 were employed for the singlet ground state of complex 1 compared to its crystal X-ray structure. The corresponding parameters of the optimized ground state geometry together with experimental values are listed in Table 1. The results show that PBE0 can give an accurate geometry structure among these functionals because its average relative error is the smallest. Thus, the optimization of the ground states and the lowest triplet excited states for complexes 1–4 were calculated with PBE0 functional in the studied system.
| Item | Expta | PBE0 | Relative error | B3LYP | Relative error | B3P86 | Relative error | M062X | Relative error | CAM- B3LYP | Relative error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The experimental data is obtained from ref. 34. | |||||||||||
| Pt–N1 | 1.983 | 2.013 | 1.5% | 2.039 | 2.8% | 2.016 | 1.7% | 2.039 | 2.8% | 2.030 | 2.4% |
| Pt–C2 | 1.990 | 1.978 | 0.6% | 1.996 | 0.3% | 1.978 | 0.6% | 1.967 | 1.2% | 1.988 | 0.1% |
| Pt–O3 | 2.029 | 2.015 | 0.7% | 2.034 | 0.3% | 2.014 | 0.7% | 2.037 | 0.4% | 2.018 | 0.6% |
| Pt–O4 | 2.032 | 2.110 | 3.8% | 2.137 | 5.2% | 2.113 | 4.0% | 2.157 | 6.2% | 2.115 | 4.1% |
| C7–C8 | 1.428 | 1.417 | 0.7% | 1.420 | 0.6% | 1.414 | 1.0% | 1.423 | 0.4% | 1.420 | 0.6% |
| Average relative error | 1.46% | — | 1.84% | — | 1.60% | — | 2.20% | — | 1.56% | ||
Owing to spin flipped in triplet states, we also find a responsible method to predict the emission properties, five different functionals were performed on the lowest-lying emission wavelength of triplet state for complex 1. On one hand, through the calculation of five functionals, the transition properties of lowest triplet excited state (T1) are similar. On the other hand, the calculated lowest-lying emission wavelengths are 697 nm, 667 nm, 739 nm, 658 nm, 537 nm with PBE0, B3P86, CAM-B3LYP, B3LYP, M06-2X functionals, respectively. From the result, the wavelength calculated by M06-2X functional is in good agreement with the experimental value of 505 nm. Besides, for the assessment of singlet–triplet transition energies based on the TDDFT, M06-2X is regarded as the most accurate functional which can adopt inner track to estimate with the mean absolute error close to 0.25 eV in most cases.54 In short, the PBE0 functional was used to optimize the singlet ground state and the triplet state geometric structures for all complexes in the current system, while the emission energies were analyzed by M06-2X functional.
3 Results and discussion
3.1 Geometries in ground and lowest-lying triplet excited states
The optimized structures at ground-state along with some atomic labels of the complexes are shown in Fig. 2. It can be seen that these Pt(II) complexes with d8 configuration present a square geometry. To gain a better understanding of the influence about different ligands, some changes of geometry parameters for all complexes are discussed in both S0 and T1 states. The main bond distances and angles between metal center Pt(II) and relevant atoms as well as dihedral angle at S0 and T1 states are listed in Table 2.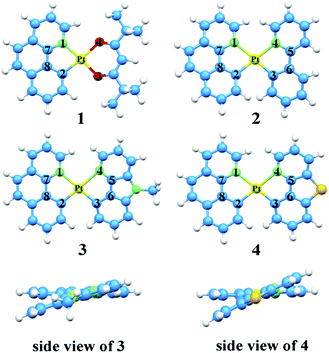 | ||
| Fig. 2 Vertical view of the optimized geometries for 1–4 with the side view for 3 and 4 at the singlet ground state. | ||
| Item | 1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|---|
| S0 | T1 | S0 | T1 | S0 | T1 | S0 | T1 | |
| Bond length (Å) | ||||||||
| Pt–N1 | 2.013 | 2.010 | 2.178 | 2.169 | 2.138 | 2.134 | 2.150 | 2.143 |
| Pt–C2 | 1.978 | 1.970 | 1.996 | 1.989 | 1.971 | 1.965 | 1.981 | 1.975 |
| Pt–O/C3 | 2.015 | 2.019 | 1.989 | 1.994 | 2.021 | 2.027 | 2.012 | 2.018 |
| Pt–O/N4 | 2.110 | 2.102 | 2.153 | 2.151 | 2.404 | 2.395 | 2.282 | 2.277 |
| C5–C6 | — | — | 1.460 | 1.462 | 1.403 | 1.403 | 1.414 | 1.415 |
| C7–C8 | 1.417 | 1.430 | 1.425 | 1.440 | 1.424 | 1.439 | 1.423 | 1.400 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Bond angle [degree] | ||||||||
| C2–Pt–N1 | 82.16 | 81.48 | 79.94 | 79.48 | 81.24 | 80.65 | 80.77 | 80.24 |
| N1–Pt–O1/N4 | 92.86 | 93.58 | 103.4 | 103.3 | 97.80 | 98.12 | 100.4 | 100.4 |
| N/O4–Pt–O/C3 | 91.65 | 91.29 | 79.51 | 79.55 | 82.89 | 82.89 | 81.85 | 81.85 |
| C/O3–Pt–C2 | 93.33 | 93.65 | 100.5 | 101.0 | 99.13 | 99.60 | 98.90 | 99.49 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Dihedral angle [degree] | ||||||||
| N4–C3–Pt–N1 | 0.04 | −0.01 | 103.9 | 103.8 | 95.96 | 98.02 | 103.4 | 103.6 |
From the results, the bond lengths of Pt–N1 are about 0.182 Å longer than Pt–C2 in complexes 1–4, indicating that the coordinated bond between atoms C and Pt is stronger than the Pt–N. Meanwhile, the Pt–N3 and Pt–C4 are also consistent with the above property. At the S0 state, the Pt–N1 bond lengths of 2–4 are elongated by 0.125–0.165 Å compared with complex 1, which can be attributed to the trans effect in different ligands.55,56 In addition, compared with complexes 3–4, the bond lengths of Pt–C3 and Pt–N4 on the ppy ligand of 2 are shorter, while Pt–N1 and Pt–C2 bond lengths on the bzq ligand are elongated. These values reveal that the introduction of ppy ligand can increase its interaction with the metal atom and decrease the interaction between other ligand and metal atom. Obviously, the bond length of C5–C6 in 3 and 4 are shortened by 0.046–0.057 Å, due to the substitution of ppy in the positions of both beta carbons by N and S atom to form Ncaz and Ndbt, which may strengthen the ligand internal–conjugation interaction. While, for C7–C8, the slight change within 0.008 Å can be ignored. For the relevant bond angles of Pt and two ligands, except for the C2–Pt–N1, the difference of others are induced by the five-member rings between Pt and ancillary ligands.
Since the S0 and T1 states participate in the process of phosphorescence, the geometry structures of T1 state worth noticing. The bond lengths of Pt–N1 and Pt–C2 for all complexes are shorter than the ground state. In other words, the bonds between metal and ligands are strengthened, which is likely to promote the charge transfer transition from metal centre to ligands. While the bond angles from S0 to T1 states have no distinct variation, especially for the designated complexes 2–4. The dihedral angle differences between S0 and T1 states for all complexes are less than 2.0°. It is turned out that the complexes show better rigidity, which brings about a smaller nonradiative rate (knr).35
3.2 Frontier molecular orbital properties
In order to clearly reveal the electronic excitation of these Pt(II) complexes, it is essential to further investigate the frontier molecular orbital (FMOs), especially the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). The relevant orbital analysis along with the energy gaps at the S0 state are displayed in Fig. 3. The orbital compositions and distributions of selected FMOs are presented in Tables S2–S5 and Fig. S1.†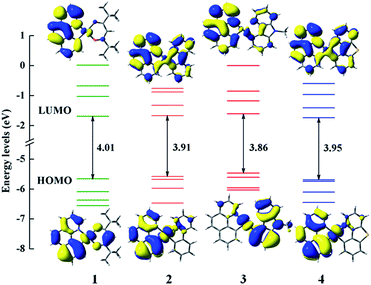 | ||
| Fig. 3 Frontier molecular orbital energy levels, energy gaps (in eV) and orbital composition distributions of the HOMO and LUMO at the S0 state for 1–4. | ||
For the electron density distributions of the HOMO, complex 1 is mainly located in 5d(Pt) orbitals, the π orbitals of bzq and dpm ligands. Obviously, the electron density distributions of HOMO for complexes 2 and 4 are rather similar, which are resided on the 5d(Pt) orbitals and bzq ligand. Complex 3 is predominantly centralized on the 5d(Pt) orbitals and the π orbitals of Ncaz ligand. It is worth noting that the energy differences between HOMO and HOMO−1 of complexes 1–4 are 0.43 (1), 0.10 (2), 0.14 (3) and 0.04 eV (4) with the order of 4 < 2 < 3 < 1. It has been confirmed that the HSOC matrix element will be increased when the two highest occupied orbitals get close, which leads to a large radiative decay rate.14 Obviously, there are obvious differences in LUMO distributions of 2–4 compared with 1. The LUMO of 2 and 4 are delocalized on all ligands, while that in 1 is mainly centralized on the π* orbitals of bzq and a smaller contribution from 5d orbitals of metal center. Combined with the diagram and data, metal 5d(Pt) orbitals provide much contribution for the HOMO and the ligands constitute the majority of LUMO in all complexes, which demonstrates the transition nature from the HOMO to LUMO are metal-to-ligand transfer (MLCT) mixed with ligand-to-ligand (LLCT). As presented in the Fig. 3, the HOMO–LUMO gaps of complexes 2–4 are smaller owing to introducing the different ligands. So the transition from HOMO to LUMO is effective and the higher HOMO energy leads to a better ability of hole-injection compared with 1. In addition, the LUMO energy level of 4 is calculated to be −1.743 eV, which is lower than other complexes. The lower LUMO energy level could be caused by the better electron delocalization in the entire molecule to stabilize the unoccupied molecular orbitals. According to the calculated results, different ancillary ligands have significant influence on the distribution of FMOs, which may alter the energy gap and phosphorescence efficiency.
3.3 Charge transportation properties
It is known that low energy barrier for the injection and transport balance between the hole and electron of luminescent complexes are pivotal for the high performance OLEDs. In order to quantitatively discuss the charge injection properties, the ionization potential (IP) and electron affinity (EA) have been calculated by DFT method, which are closely related to the HOMO and LUMO, respectively.55 In addition, there are vertical (IPv/EAv) and adiabatic (IPa/EAa) two processes. For photoluminescent materials, a smaller IP value implies easier hole injection ability. On the other hand, a larger EA value facilitates the electrons injection capacity. The hole extraction potential (HEP) and electron extraction potential (EEP) are studied to evaluate the extraction potentials of the hole and electron.According to the semiclassical Marcus theory,57 the intermolecular charge (hole and electron) transfer rate (Ket) can be expressed as follows:
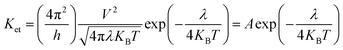 | (7) |
| λh = λ0 + λ+ = IPv − HEP | (8) |
| λe = λ0 + λ− = EEP − EAv | (9) |
All the relevant calculation values of complexes 1–4 are shown in Table 3.
| IP(V) | IP(a) | HEP | EA(v) | EA(a) | EEP | λhole | λe | |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.85 | 6.77 | 6.68 | 0.29 | 0.42 | 0.56 | 0.17 | 0.27 |
| 2 | 6.74 | 6.57 | 6.19 | 0.43 | 0.52 | 0.61 | 0.54 | 0.18 |
| 3 | 6.62 | 6.51 | 6.39 | 0.32 | 0.41 | 0.50 | 0.23 | 0.18 |
| 4 | 6.82 | 6.75 | 6.44 | 0.54 | 0.62 | 0.71 | 0.38 | 0.17 |
As can be seen in Table 3, complexes 2 and 3 have smaller IP values which are related to their higher HOMO energy levels than complex 1. Namely, the complexes 2 and 3 have better hole injection ability due to the introduction of ppy and Ncaz ligands. Meanwhile, the EA values of complexes 2 and 4 are larger than others, which can enhance electron injection ability and agree with their lower LUMO energy. From the Table 3, the reorganization energies of electron (λe) transport of all complexes are smaller than their hole (λh) except for 1. Therefore, the complexes replaced the dpm with different ligands tend to be electron transporting materials. In addition, complex 3 is the promising bipolar transporting material because the difference between hole and electron reorganization values are quite small (0.05 eV), which is an important factor for the OLEDs devices. Generally speaking, the ancillary ligands can not only increase the abilities of hole and electron injection but also affect the balance of charge transfer.
3.4 Phosphorescence emission properties
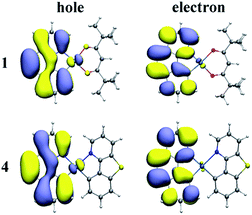
On the basis of the optimized lowest triplet excited-state geometries, the phosphorescence properties of all the investigated complexes were calculated. The results including the lowest energy emission wavelengths and transition characters are shown in Table 4. The natural transition orbitals (NTOs) of complexes 1–4 are plotted in Fig. 4 and S2.† The unoccupied NTOs refer to the as “electron” transition orbitals while the occupied NTOs mean the “hole” transition orbitals. Furthermore, the orbital compositions distribution related to phosphorescence emission of complexes 1–4 are summarized in Table S6.†| States | λ (nm)/E (eV) | λexpt (nm) | Main configuration | Assignment | |
|---|---|---|---|---|---|
| 1 | T1 | 537/2.31 | 505 | H → L (72%) | MLCT/ILCT |
| H-2 → L (14%) | MLCT/ILCT | ||||
| 2 | T1 | 535/2.32 | H → L (67%) | MLCT/ILCT | |
| H → L + 1 (10%) | MLCT/ILCT | ||||
| 3 | T1 | 529/2.34 | H → L (52%) | MLCT/LLCT | |
| H-1 → L (17%) | MLCT/LLCT | ||||
| 4 | T1 | 532/2.33 | H → L (65%) | MLCT/ILCT | |
| H → L + 1 (10%) | MLCT/LLCT |
As we can know from the Table 4, the calculated emission wavelength is 537 nm for complex 1, which matches well with the experimental value of 505 nm. The phosphorescence emissions of 2–4 at 535, 529, and 532 nm are slightly hypochromatic shifted (2–8 nm) compared with that of 1, which reveals that the designed complexes 2–4 have a great trend to be bluish-green luminescent materials. Meanwhile, the emission wavelengths of complexes 1, 2 and 4 are nearly the same due to the similar electronic density distribution between HOMO and LUMO. Additionally, the T1 states of these complexes are originated largely from HOMO to LUMO. As shown in Fig. 4 and S2,† for complexes 1–4, the NTO hole is largely distributed in the metal Pt and bzq ligand, while the NTO electron is delocalized in the bzq ligand. Thus, the transition natures of the investigated complexes at T1 state are assigned as 3MLCT/3LCbzq. In Table S6,† the compositions of 5d(Pt) orbitals have not much differences and be retained for these new complexes, and the LUMO of the studied complexes are all located in bzq ligand, indicating the bzq ligand is the main ligand in this system. For complexes 1, 2 and 4, the HOMO orbitals are centred on the 5d(Pt) orbitals and bzq moieties. The transition of H → L is assigned as [d(Pt) + π(bzq) → π*(bzq)] with 3MLCT/3ILCT (inter-ligand charge transfer) transition characters. However, it can be found that the HOMO of complex 3 is localized on 5d(Pt) orbitals, bzq and Ncaz ligands, it is described as [d(Pt) + π(bzq) +π(C^N) → π*(bzq)] with 3MLCT/3LLCT transition characters.
3.5 Radiative decay rate
Phosphorescence efficiency (ΦPL) of OLEDs is determined by the radiative decay rate constant (kr) and non-radiative decay rate constant (knr), hence the theoretical analysis of kr is imperative. Based on the optimized geometries of emissive states for all complexes, kr and ZFS parameters are evaluated by TDDFT with the eqn (4) and (6). According to the eqn (4), the value of kr is controlled by three factors including the SOC matrix elements between the Sn and Tm states, the oscillator strength fn of Sn and the energy gap among the coupled states. To ensure the effective coupling, only the first 10 singlet excited states and the low-lying triplet excited states Tm which locate below the S1 are taken into consideration. The calculated values of kr and ZFS for all complexes are shown in Table 5.| krz | kry | krx | kr | kr,exp | ΔE(ZFS) | |
|---|---|---|---|---|---|---|
| 1 | 13.45 | 0.39 | 0.09 | 4.64 | 1.0 | 15.34 |
| 2 | 84.58 | 9.99 | 30.45 | 41.67 | — | 40.55 |
| 3 | 11.04 | 3.40 | 3.99 | 6.14 | — | 14.84 |
| 4 | 90.58 | 17.00 | 4.20 | 37.26 | — | 20.27 |
Through the complete comparison, the kr of complex 1 is in the same order of magnitude with the experimental value, indicating that the theoretical method used here is credible. The complexes 2–4 have sizable kr compared with 1 implying that our design is reasonable for OLED materials. It is obvious that the replacement of ancillary ligands is beneficial to the radiative decay process, because the increased conjugation and rigidity of different ligands in cyclometalated Pt(II) complexes can lead to a large kr. In addition, the tendency of ΔE(ZFS) parameters are nearly consistent with the kr, except for 3. The abnormal phenomenon of complex 3 is induced by the energy shifts of three near-equal substates.
In order to further analyze radiative decay process, the diagrams of involved Sn and Tm are collected in Fig. 5 and the relevant information is listed in Tables S7–S10.† The effective SOC can be achieved when 1MLCT and 3MLCT excitation configurations related to the Sn and Tm states possess the different occupied 5d(Pt) orbitals and identical unoccupied π* orbitals. From the Fig. 5, the T1 state of complex 1 has three coupling Sn states, S3, S4, and S5 and three states (S3, S4 and S5) coupling with T3 state. There are four states coupling with T1 state and six states coupling with T3 state in complex 3. As for the complex 2, there are five utilizable singlet-excited states working on T1 state and six states can be coupled with T3 state. What is more, the intersystem crossing (ISC) from S1 state to T3 state is enhanced by the strong SOC process due to the transition from T3 state to Sn states is able to borrow intensity from the S1 state.62 Namely, the H-1 to L transition of T3 state has the similar effect with the H to L transition. As a result, the S1 state is allowed to coupling with T3 state and the vertical excitation energy gap between the two coupled excited states is the closest, which also holds the same with 4. Therefore, the newly designed complexes 2 and 4 have the larger radiative decay rate constants markedly.
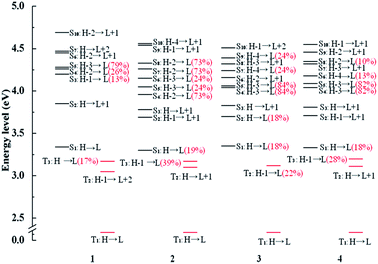 | ||
| Fig. 5 Energy level diagrams of selected excited states between the triplet excited states Tm and singlet excited states Sn with the MLCT composition of major orbitals for complexes 1–4. | ||
3.6 Nonradiative decay rate
The nonradiative decay rate (knr) is the other factor to govern the ΦPL. There are temperature-independent and temperature-dependent nonradiative decay processes. According to the energy gap law, the key to qualitative evaluation of the temperature-independent nonradiative decay rate are the energy gap between T1 and S0 states and the structural distortion that can be measured by Stokes shift.63 The more rigid the complex structure, the smaller the Stokes shift value. The corresponding values of Stokes shift are 0.84, 0.66, 0.68 and 0.67 eV. It demonstrates that the introduction of different ligands is able to enhance the rigidity and reduce the structural distortion. The energy difference between T1 and S0 states is large and then the nonradiative decay pathway is less accessible. The calculated parameters of energy gaps for all complexes are 2.05, 2.03, 2.03 and 2.04 eV, respectively. As mentioned above, the temperature-independent nonradiative decay rates of 2–4 are smaller than 1.There is another significant process called temperature-dependent nonradiative decay pathway. Concretely speaking, the triplet excited state (3ES) gets to short-lived metal-centred (3MC) by the thermal population and then returns back to the ground state (1GS) through the minimum energy crossing point (MECP) in the relevant potential energy surfaces. From the previous studies, the temperature-dependent nonradiative decay rate constant will be decreased by the two factors: (1) a big activation barrier between the 3ES and 3MC states; (2) a higher relative energy of MECP. The MECP were constructed through the code developed by Harvey et al.64,65 The spin density plots of the studied complexes are depicted in Fig. 6 and S3.† The detailed description related to the spin density of complexes 1–4 for all ligands and metal Pt are listed in Table S11.† Besides, the intrinsic potential energy curves are shown in Fig. S4–S7.† At the lowest triplet excited state (3ES), the spin density distributions of all complexes are mainly concentrated on the bzq ligand (93.85–95.50%) and metal Pt (3.98–4.60%). The electronic configurations of 3MC states can be acquired by distorting the geometric structures. And the most distinctive feature of 3MC states is that the spin density plots are mainly concentrated on the metal Pt. As shown in Fig. 6 and Table S11,† at the 3MC states of complexes 1–4, there are about 65–75% contribution from the metal Pt. The distributions of MECP are similar with the 3MC states, which are also centralized on the metal Pt. Unfortunately, the transition states (TS) between the 3ES and 3MC states have not been found out possibly due to the enhancement of molecular rigidity, so the schematics of the potential energy curves from 3ES to 3MC are smooth. The relative energies between the 3MC and MECP are 4.24, 4.78, 4.86 and 4.43 kcal mol−1, respectively. There are no obvious differences of the energy gaps for all complexes, which indicate the temperature-dependent nonradiative decay rates of complexes 1–4 will not have too much difference.
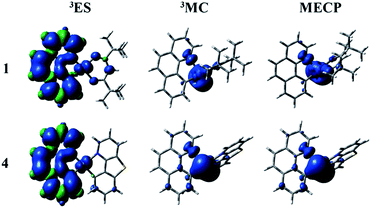 | ||
| Fig. 6 The spin density of the lowest triplet excited state (left), 3MC (middle) and MECP (right) states for complexes 1 and 4. | ||
4 Conclusions
The geometric structures, charge transfer performance, electronic and photophysical properties of four cyclometalated platinum(II) complexes 1–4 are systematically investigated by employing DFT and TDDFT methods. It should be noted that the bond lengths and angles of complexes 2–4 with different ligands instead of dpm ligand have no obvious differences from S0 to T1 state. Thus, complexes 2–4 have better molecular rigidity which can decrease the nonradiative decay rate. The newly designed complex 3 has balanced charge carrier injection/transport performance which is important for OLED materials. As for the phosphorescence properties, the 3MLCT/3LLCT character is assigned for 3, while complexes 1, 2 and 4 are assigned as 3MLCT/3ILCT. The radiative decay rate constants are presented in the following trend: 2 > 4 > 3 > 1. Hence, it is inferred that complexes 2 and 4 may be excellent phosphorescent materials for the higher phosphorescence quantum efficiency. Combined with the above analysis, we come to the conclusion that reasonable modification and variation of the ancillary ligand will be beneficial to improve the phosphorescence quantum efficiency of complexes for the highly efficient OLED emitting materials.Acknowledgements
This work was supported by the State Key Development Program for Basic Research of China (Grant No. 2013CB834801) and the Natural Science Foundation of China (Grant No. 21573088) and Young Scholar Training Program of Jilin University and Open Project Founding of Beijing National Laboratory for Molecular Sciences (BNLMS).Notes and references
- L.-H. Xu, Q.-D. Ou, Y.-Q. Li, Y.-B. Zhang, X.-D. Zhao, H.-Y. Xiang, J.-D. Chen, L. Zhou, S.-T. Lee and J.-X. Tang, ACS Nano, 2016, 10, 1625–1632 CrossRef CAS PubMed.
- C.-W. Hsu, K. T. Ly, W.-K. Lee, C.-C. Wu, L.-C. Wu, J.-J. Lee, T.-C. Lin, S.-H. Liu, P.-T. Chou, G.-H. Lee and Y. Chi, ACS Appl. Mater. Interfaces, 2016, 8, 33888–33898 CAS.
- R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef CAS PubMed.
- Y. Wu, G.-G. Shan, H.-B. Li, S.-X. Wu, X.-Y. Ren, Y. Geng and Z.-M. Su, Phys. Chem. Chem. Phys., 2015, 17, 2438–2446 RSC.
- L. Xiao, Z. Chen, B. Qu, J. Luo, S. Kong, Q. Gong and J. Kido, Adv. Mater., 2011, 23, 926–952 CrossRef CAS PubMed.
- S. Reineke, F. Lindner, G. Schwartz, N. Seidler, K. Walzer, B. Lussem and K. Leo, Nature, 2009, 459, 234–238 CrossRef CAS PubMed.
- L.-M. Xie, F.-Q. Bai, W. Li, Z.-X. Zhang and H.-X. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 10014–10021 RSC.
- F.-Q. Bai, J. Wang, B.-H. Xia, Q.-J. Pan and H.-X. Zhang, Dalton Trans., 2012, 41, 8441–8446 RSC.
- K. O. Kirlikovali, J. C. Axtell, A. Gonzalez, A. C. Phung, S. I. Khan and A. M. Spokoyny, Chem. Sci., 2016, 7, 5132–5138 RSC.
- A.-H. Liang, F.-Q. Bai, J. Wang, J.-B. Ma and H.-X. Zhang, Aust. J. Chem., 2014, 67, 1522–1531 CrossRef CAS.
- B.-Q. Liu, L. Wang, D.-Y. Gao, J.-H. Zou, H.-L. Ning, J.-B. Peng and Y. Cao, Light: Sci. Appl., 2016, 5, e16137 CrossRef CAS.
- A. Tronnier, S. Metz, G. Wagenblast, I. Muenster and T. Strassner, Dalton Trans., 2014, 43, 3297–3305 RSC.
- P. Pinter, H. Mangold, I. Stengel, I. Munster and T. Strassner, Organometallics, 2016, 35, 673–680 CrossRef CAS.
- A. F. Rausch, L. Murphy, J. A. G. Williams and H. Yersin, Inorg. Chem., 2012, 51, 312–319 CrossRef CAS PubMed.
- F.-Q. Bai, X. Zhou, B.-H. Xia, T. Liu, J.-P. Zhang and H.-X. Zhang, J. Organomet. Chem., 2009, 694, 1848–1860 CrossRef CAS.
- X.-Q. Zhang, Y.-M. Xie, Y.-H. Zheng, F. Liang, B. Wang, J. Fan and L.-S. Liao, Org. Electron., 2016, 32, 120–125 CrossRef CAS.
- B. Yang, S. Huang, J. Zhong and H. Zhang, Org. Electron., 2015, 19, 7–14 CrossRef CAS.
- J.-H. Du, Y.-F. Luo, X.-H. Xie, W.-H. Hu and W. Shen, Mol. Simul., 2016, 42, 1035–1041 CrossRef CAS.
- S.-Y. Chang, Y.-M. Cheng, Y. Chi, Y. C. Lin, C.-M. Jiang, G.-H. Lee and P.-T. Chou, Dalton Trans., 2008, 48, 6901–6911 RSC.
- Y. Chi and P.-T. Chou, Chem. Soc. Rev., 2010, 39, 638–655 RSC.
- S.-B. Ko, J.-S. Lu, Y. Kang and S. Wang, Organometallics, 2013, 32, 599–608 CrossRef CAS.
- F. M. Hwang, H.-Y. Chen, P.-S. Chen, C.-S. Liu, Y. Chi, C.-F. Shu, F.-L. Wu, P.-T. Chou, S.-M. Peng and G.-H. Lee, Inorg. Chem., 2005, 44, 1344–1353 CrossRef CAS PubMed.
- T. Tsuzuki, N. Shirasawa, T. Suzuki and S. Tokito, Adv. Mater., 2003, 15, 1455–1458 CrossRef CAS.
- X.-N. Li, Z.-J. Wu, Z.-J. Si, H.-J. Zhang, L. Zhou and X.-J. Liu, Inorg. Chem., 2009, 48, 7740–7749 CrossRef CAS PubMed.
- Y. C. Chiu, Y. Chi, J.-Y. Hung, Y.-M. Cheng, Y.-C. Yu, M.-W. Chung, G.-H. Lee, P.-T. Chou, C.-C. Chen, C.-C. Wu and H. Y. Hsieh, ACS Appl. Mater. Interfaces, 2009, 1, 433–442 CAS.
- C.-H. Yang, Y.-M. Cheng, Y. Chi, C.-J. Hsu, F.-C. Fang, K.-T. Wong, P.-T. Chou, C.-H. Chang, M.-H. Tsai and C.-C. Wu, Angew. Chem., Int. Ed., 2007, 46, 2418–2421 CrossRef CAS PubMed.
- S. Haneder, E. Da Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. Munster, C. Schildknecht and G. Wagenblast, Adv. Mater., 2008, 20, 3325–3330 CrossRef CAS.
- Y. Unger, D. Meyer, O. Molt, C. Schildknecht, I. Münster, G. Wagenblast and T. Strassner, Angew. Chem., Int. Ed., 2010, 122, 10412–10414 CrossRef.
- J. C. H. Chan, W. H. Lam, H.-L. Wong, N.-Y. Zhu, W.-T. Wong and V. W. W. Yam, J. Am. Chem. Soc., 2011, 133, 12690–12705 CrossRef CAS PubMed.
- W. Wu, W. Wu, S. Ji, H. Guo, P. Song, K. Han, L. Chi, J. Shao and J. Zhao, J. Mater. Chem., 2010, 20, 9775–9786 RSC.
- J. A. G. Williams, S. Develay, D. L. Rochester and L. Murphy, Coord. Chem. Rev., 2008, 252, 2596–2611 CrossRef.
- M.-C. Tang, A. K.-W. Chan, M.-Y. Chan and V. W.-W. Yam, Top. Curr. Chem., 2016, 374, 46 CrossRef PubMed.
- X. C. Hang, T. Fleetham, E. Turner, J. Brooks and J. Li, Angew. Chem., Int. Ed., 2013, 52, 6753–6756 CrossRef CAS PubMed.
- A. Bossi, A. F. Rausch, M. J. Leitl, R. Czerwieniec, M. T. Whited, P. I. Djurovich, H. Yersin and M. E. Thompson, Inorg. Chem., 2013, 52, 12403–12415 CrossRef CAS PubMed.
- W. H. Lam, E. S. H. Lam and V. W. W. Yam, J. Am. Chem. Soc., 2013, 135, 15135–15143 CrossRef CAS PubMed.
- Y.-F. Luo, Y.-Y. Xu, W.-T. Zhang, M. Li, R.-X. He and W. Shen, ChemPhysChem, 2016, 17, 69–77 CrossRef CAS PubMed.
- J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Kohler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS PubMed.
- Y. Kataoka, Y. Kitagawa, T. Kawakami and M. Okumura, J. Organomet. Chem., 2013, 743, 163–169 CrossRef CAS.
- Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378 CrossRef CAS PubMed.
- S. Obara, M. Itabashi, F. Okuda, S. Tamaki, Y. Tanabe, Y. Ishii, K. Nozaki and M.-a. Haga, Inorg. Chem., 2006, 45, 8907–8921 CrossRef CAS PubMed.
- S. Lee, S. O. Kim, H. Shin, H. J. Yun, K. Yang, S. K. Kwon, J. J. Kim and Y. H. Kim, J. Am. Chem. Soc., 2013, 135, 14321–14328 CrossRef CAS PubMed.
- J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723 CAS.
- H. Yersin, W. Humbs and J. Strasser, Coord. Chem. Rev., 1997, 159, 325–358 CrossRef CAS.
- H. Yersin, W. Humbs and J. Strasser, Electronic and Vibronic Spectra of Transition Metal Complexes II, Springer, Berlin Heidelberg, 1997, vol. 191, pp. 153–249 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, J. M. Bearpark, J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- D. Jacquemin, E. A. Perpete, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537 CrossRef CAS PubMed.
- T.-T. Feng, F.-Q. Bai, L.-M. Xie, Y. Tang and H.-X. Zhang, RSC Adv., 2016, 6, 11648–11656 RSC.
- M. K. Nazeeruddin, R. Humphry-Baker, D. Berner, S. Rivier, L. Zuppiroli and M. Graetzel, J. Am. Chem. Soc., 2003, 125, 8790–8797 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- X.-L. Ding, L.-Y. Zou, M.-S. Ma, H.-X. Zhang, Y.-X. Cheng and A.-M. Ren, Org. Electron., 2016, 31, 111–119 CrossRef CAS.
- B.-C. Lin, C.-P. Cheng and Z. P. M. Lao, J. Phys. Chem. A, 2003, 107, 5241–5251 CrossRef CAS.
- M. Malagoli and J. L. Bredas, Chem. Phys. Lett., 2000, 327, 13–17 CrossRef CAS.
- E. Jansson, B. Minaev, S. Schrader and H. Agren, Chem. Phys., 2007, 333, 157–167 CrossRef CAS.
- N. I. Nijegorodov and W. S. Downey, J. Phys. Chem., 1994, 98, 5639–5643 CrossRef CAS.
- J. N. Harvey and M. Aschi, Phys. Chem. Chem. Phys., 1999, 1, 5555–5563 RSC.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of calculated molecular orbital (MO) compositions, NTOs, the coupling energy levels and transition characters analysis between singlet excited states and triplet excited states for complexes 1–4. See DOI: 10.1039/c7ra00705a |
| This journal is © The Royal Society of Chemistry 2017 |