Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards life in hydrocarbons: aggregation behaviour of “reverse” surfactants in cyclohexane†
M. Facchin ,
A. Scarso,
M. Selva
,
A. Scarso,
M. Selva ,
A. Perosa
,
A. Perosa * and
P. Riello
* and
P. Riello *
*
Dipartimento di Scienze Molecolari e Nanosistemi, Laboratorio di Sistemi Chimici Complessi, Università Ca' Foscari Venezia, Via Torino 155, 30172 Venezia Mestre, Italy
First published on 7th March 2017
Abstract
Unconventional life forms based on membranes able to self-assemble in hydrocarbons instead of water might in principle exist in the hydrocarbon-rich environments on Earth and in the methane lakes of Saturn's moon, Titan. This reversed paradigm for life would require that these membranes should be constituted of “reverse” surfactants. We here describe the synthesis of reverse amphiphilic molecules with a geometry similar to conventional surfactants but with an opposite topological configuration: lipophilic heads and lipophobic tails. Their self-assembly in cyclohexane was studied by 1H 2D DOSY-NMR and SAXS. We present experimental evidence of the self-assembly of these reverse surfactants to yield typical micelles in a hydrocarbon solvent.
“As the search for life in the solar system expands, it is important to know what exactly to search for”.1 Until now the search for extra-terrestrial life has mainly focused on the search for water and consequently for water-based organisms. Even when searching for life in hydrocarbon-rich environments on Earth such as for example in pitch lakes2,3 or in methane clathrates,4,5 scientists have looked for water-based biological activity. We instead asked ourselves the question whether “unconventional” life forms might be possible in pure liquid hydrocarbon environments – even perhaps on extra-terrestrial planetary bodies – where water is absent but that are rich, for example, in methane, such as Titan.6 Organisms in such environments could either fall into the category of water-based life forms adapted to anaerobically oxidize methane to carbon dioxide, or, more imaginatively, there might exist hydrocarbon-based organisms whose cellular membranes self-assemble in hydrocarbons as liquid medium. The latter hypothesis would require that cellular membranes be made by yet unknown “reverse” surfactants (lipophilic head–lipophobic tail) able to self-assemble in hydrocarbons rather than water.
Previous reports of vesicle formation in non-aqueous environments already exist. Bryant, Atkin and Warr,7 proved that phospholipids self-assemble to form vesicles in a choline chloride–urea deep eutectic solvent system; again, Gayet8 and collaborators studied vesicle formation of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) in ionic liquids. Both these reports demonstrated the possibility of aggregate formation in a non-aqueous environment but still involve highly polar solvents and typical surfactants (lipophobic head–lipophilic tail).
Up to date, one attempt to define the parameters at the basis of the formation of self-assembled aggregates of non-conventional “reverse” surfactants in hydrocarbons was made computationally by Cornell scientists. They calculated the thermodynamics of self-assembly of organic nitrogen-containing compounds such as acrylonitrile and concluded that these could aggregate to yield reverse vesicles, dubbed “azotosomes”, that could exist in liquid methane at 94 K (the temperature of Titan's methane lakes). Modelling suggested that they would possess stability and flexibility similar to liposomes on Earth.9
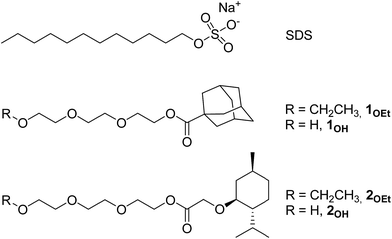
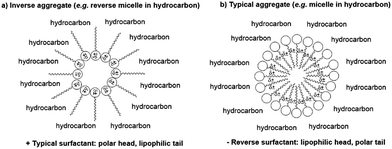
In water, the driving force for aggregation of typical surfactants with lipophilic tails such as sodium dodecylsulfate10 (SDS, Fig. 1) is minimizing the hydrocarbon tail–water interfacial area. This effect is referred to as the “hydrophobic effect”11 and it is the principal contributor to the formation of typical micelles and to the formation of membranes in living cells. In a hydrocarbon solvent instead, typical surfactants (such as sodium di-2-ethylhexylsulfosuccinate12 or SDS10) assemble into reverse micelles (Fig. 2a) that are generally weakly held together by van der Waals forces and often require traces of water to stabilize the hydrophilic core through hydrogen-bonding and thus drive self-assembly.13
For this work we synthesized two pairs of surfactants 1OEt, 2OEt and 1OH, 2OH (Fig. 1), having in common a small and rigid lipophilic head and a long and floppy lipophobic tail. While the lipophobic tail of 1OEt and 2OEt terminated with an ethoxide group, instead 1OH and 2OH possessed a terminal hydroxyl group. We imagined that these could form micellar aggregates in a hydrocarbon solvent with the same configuration of typical micelles in water, i.e. with tightly packed lipophilic heads facing outwards (Fig. 2b) and with the long lipophilic tails aggregated in the core so as to minimize the interaction with the hydrocarbon solvent. We investigated aggregation of 1OEt, 2OEt, 1OH and 2OH experimentally in cyclohexane as a model liquid hydrocarbon by Nuclear Magnetic Resonance (NMR) and Small Angle X-ray Scattering (SAXS). These spectroscopic techniques could first of all show aggregation and in a second stage also give an estimate of the sizes of the aggregates, of the effect of surfactant concentration, of the form of the aggregates (micelles, bilayers or vesicles) and of critical aggregate concentrations. The study shows evidence for the existence of organized molecular aggregates and indicates for the first time that “reverse” surfactants can form micellar aggregates in a hydrocarbon solvent with the same geometrical configuration of typical micelles in water.
The structure of the reverse surfactants was designed by mimicking size and shape of typical surfactants that are known to self-assemble in water and based on the geometry of phospholipids that form typical cell membrane double layers in water: these have two lipophilic tails and a length of approximately 2 nm that would lead to an overall bilayer thickness of 4 nm.14 We prepared both pairs of surfactants 1OEt, 2OEt and 1OH, 2OH (Fig. 1) with similar length (≈2 nm) but simpler geometry: i.e. a small lipophilic head and a single lipophobic tail. Triethylene glycol (TEG) was chosen for the lipophobic tail due to its ability to give polar interactions, to its insolubility in cyclohexane and – in the case of 1OH and 2OH due to the presence of a terminal hydroxyl group able to act as hydrogen bond donor and acceptor.
A preliminary screening of the first pair of surfactants indicated that, albeit soluble in cyclohexane, neither 1OEt or 2OEt showed any sign of self-assembly by NMR or SAXS. On the contrary 1OH and 2OH showed clear evidence of aggregation. In this paper, we therefore describe the syntheses and aggregation study of the “reverse” surfactants 1OH and 2OH (Fig. 1) possessing the terminal hydroxyl group apt to hydrogen-bond. We investigated aggregation experimentally in cyclohexane as a model liquid hydrocarbon to demonstrate our hypothesis.
The structure of the aggregates generally also depends on the geometry of the surfactants and on their interaction with the solvent. A parameter that correlates the properties of the assembly with that of the monomer is the geometric packing parameter (GPP), defined as the ratio of the tail volume to the volume projected by the optimal head group area (GPP = vc/(aolc) where vc = chain volume, ao = optimal headgroup area, lc = critical chain length).15 Small GPPs lead to highly curved aggregates (e.g. spheres) whereas larger GPPs lead to aggregates with reduced curvature (e.g. vesicles or bilayers). The choice of the geometry of the new surfactants 1OH and 2OH was dictated in a first approximation by previous experience on analogous surfactants. For example, a large C60-fullerene head with a short aminoacidic tail16 is characterized by an excessively small GPP.
We therefore chose lipophilic, compact and rigid menthyl and adamantane moieties for the lipophilic head groups. The former is flat while the latter is more spherical.
The two surfactants 1OH and 2OH were synthesized in high isolated yields by acid-catalysed esterification reactions between menthyloxyacetic acid or adamantanoic acid and TEG (see ESI for complete Experimental details†). Special care was taken in the final dehydration of the surfactants in order to minimise the possible interference of water in the subsequent studies of the aggregation. It should be underlined that, while TEG itself is not soluble in cyclohexane, the reverse surfactants 1OH and 2OH form clear colourless solutions up to a 50/50 volume ratio. We analysed the aggregation of surfactants 1OH and 2OH in cyclohexane by NMR and SAXS.
The self-assembly of 1OH and 2OH in cyclohexane was initially studied by measuring the diffusion coefficient of the species in solution by 1H 2D-DOSY NMR (2-Dimensional Diffusion Ordered SpectroscopY) in the concentration range 5–260 mM. For each sample, the diffusion coefficients of the resonances of the surfactant and of the solvent were determined at 303 K and plotted as a function of the concentration of each surfactant.
Fig. 3 shows the diffusion coefficients of cyclohexane in itself (⋄) and of surfactant 1OH (●) at increasing concentrations of 1OH. The diffusion coefficient for cyclohexane at 298 K observed by direct DOSY measurements as an average value among the different solutions of 1OH and 2OH was 1.48 × 10−5 cm2 s−1 which is in good agreement with the value reported in the literature17 corresponding to 1.43 × 10−5 cm2 s−1. Moreover, in the range of concentrations considered, the solvent showed a rather constant diffusion coefficient, indicating that the viscosity of the solution was not affected significantly by changing the concentration of 1OH. As clearly observed in Fig. 3, while the diffusion coefficient of cyclohexane remained constant, the profile of log(D) for the surfactant 1OH as a function of the concentration (5–250 mM) decreased monotonically down to the value of −9.3 at 250 mM. In particular, considering the ratios between the diffusion coefficients of 1OH and of the solvent cyclohexane for the different solutions, it is clear that the average hydrodynamic radius of the surfactant tended to increase with increasing concentration, up to about 5.0 × 10−10 cm2 s−1 at 250 mM. This result is strong indication of aggregation. At a concentration of 250 mM the ratio between the hydrodynamic radius of 1OH and that of the solvent cyclohexane was about 3.5. Measurement of log(D) of surfactant 2OH (in the concentration range 25–250 mM) by 2D-DOSY NMR showed a behaviour analogous to 1OH (see Fig. 4), indicative of aggregation, albeit less pronounced. In this case, the ratio between the hydrodynamic radii of 2OH and cyclohexane was about 2.0.
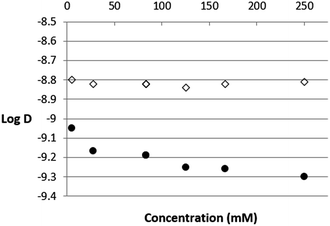 | ||
| Fig. 3 Plot of log(D) vs. concentration of 1OH measured by 2D-DOSY experiments. (●) Surfactant 1OH, (⋄) cyclohexane. | ||
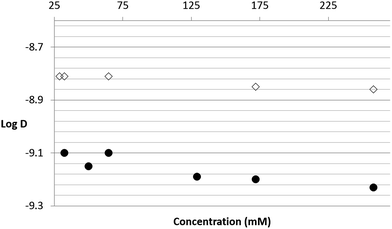 | ||
| Fig. 4 Plot of log(D) vs. concentration of 2OH measured by 2D-DOSY experiments. (●) Surfactant 2OH, (⋄) cyclohexane. | ||
The 2D-DOSY NMR experiments provided diffusion coefficients of the aggregates with respect to the solvent that were consistent with the magnitude of the proposed self-assembled structures. However, it should be kept in mind that these measures afforded experimental log(D) values that were a weighted average between log[(D)free surfactant] and log[(D)aggregate] because the aggregates were in equilibrium with each surfactant 1OH and 2OH in solution and because the aggregation equilibrium was fast with respect to the NMR timescale. This led to an underestimated average hydrodynamic radius of the aggregates.
Having obtained evidence of aggregation of surfactants 1OH and 2OH by NMR, we then focused on SAXS measures for a more detailed characterization of the aggregates. We therefore investigated the behaviour of 1OH and 2OH in cyclohexane by SAXS at different concentrations (50, 75, 100, 200, 300, 500 mM, 298 K). Anhydrous cyclohexane was used (≤0.001% water, Karl Fischer) in order to minimize possible interferences on their aggregation due to traces water.
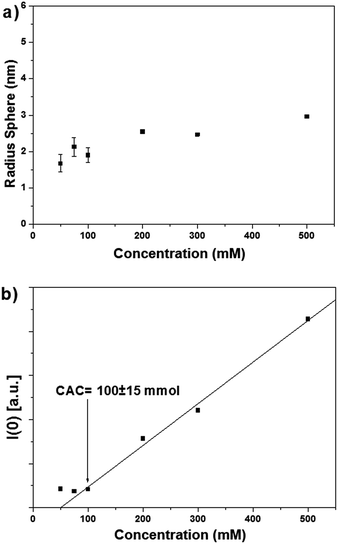
The scattering spectrum of surfactant 1OH in cyclohexane at different concentrations is shown in Fig. 5a. All the intensities are reported in arbitrary units (a.u.). The SAXS intensities were concentration-dependent and showed the presence of self-assembled structures as indicated by the increase in intensity of the signal in the region 0.1–1.0 nm−1.
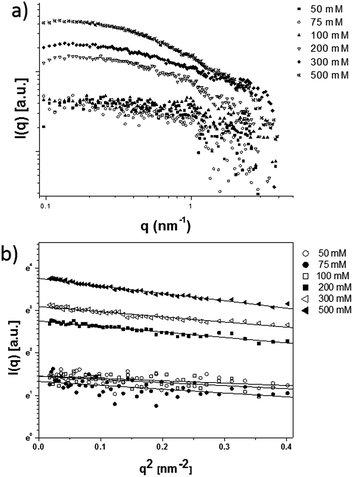 | ||
| Fig. 5 SAXS intensities (arbitrary units) of compound 1OH in solution at different concentrations (a) and Guinier plot of SAXS intensities (b). | ||
The Guinier plot of the intensities subtracted of the solvent contribution are shown in Fig. 5b. The slope of the linear fit of the Guinier plot allowed to calculate the radius of gyration (Rg) as detailed in the ESI section.† Over the range of concentrations, all the slopes and therefore the Rg's of 1OH were very similar. Assuming spherical aggregates, the geometric radii (R) were calculated using equation R2 = 5Rg2/3. The values of R are plotted in Fig. 7a as a function of the surfactant concentration and, assuming a spherical shape of the aggregates, averaged between 1.7 and 2.5 nm. The aggregate sizes complied with the consistence restraint for the Guinier plot that requires that the linear fit must be carried out in the region q2 < 1/Rg2 ≈ 0.35 nm−2. Since the estimated length of surfactant 1OH was approximately 2 nm by molecular mechanics, the radius of the aggregates was consistent with the length of the surfactant.
Critical aggregation concentration (CAC) – i.e. the concentration above which aggregation of the surfactant in cyclohexane takes place – represents a phase separation between diluted surfactant molecules and surfactant aggregates in dynamic equilibrium.18 Since all the aggregates were approximately of the same size (see Fig. 5a), the intensity I(0) obtained by extrapolation to q = 0 of the scattering curve was proportional to the number of aggregates. The plot of I(0) vs. concentration in Fig. 5b showed an abrupt rise of I(0) above 100 mM, indicative of critical aggregate concentration being reached. An interesting feature of our system is that even at very high concentrations such as 500 mM a homogeneous and optically transparent solution was obtained that did not show any sign of phase separation by precipitation nor of gelation. This was further confirmed considering the almost constant diffusion coefficient of the solvent observed during the DOSY experiments in all the range of concentrations of surfactants 1OH and 2OH and by considering that there was no significant change in the shape of the SAXS intensities, a phenomenon normally observed during gelation.
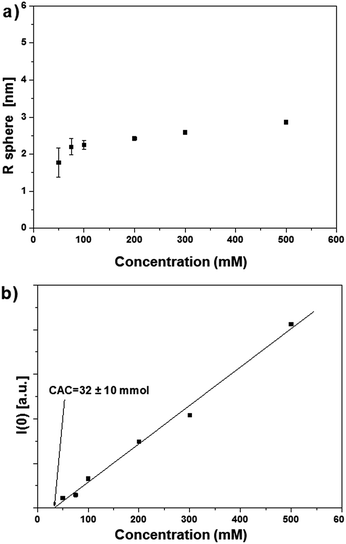
The SAXS data of surfactant 2OH in cyclohexane confirmed the results described for 1OH and are reported in Fig. 6.
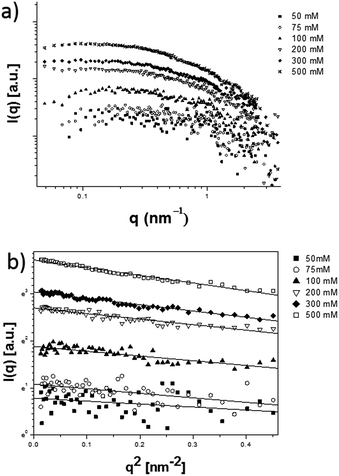 | ||
| Fig. 6 SAXS intensities (arbitrary units) of compound 2OH in solution at different concentrations (a) and Guinier plot of SAXS intensities (b). | ||
SAXS provided insight into the size and number of aggregates as a function of the concentration of surfactants 1OH and 2OH without interference by the free surfactants. The radius of the aggregates was approximately 1.7–2.5 nm for both surfactants, it changed very little over a wide range of concentrations (Fig. 7a and 8a) and it was coherent with the length of each molecule (estimated by simple molecular modelling).
Aggregates of 1OH and 2OH were observed above a critical concentration that was extrapolated from the SAXS intensities. For 1OH this value was around CAC[1OH] = 100 ± 15 mM (see Fig. 7b), while for 2OH, the CAC value was less noticeable and could only be estimated roughly to be at best in a similar range to 1OH: around CAC[2OH]= 30 ± 10 mM (Fig. 8b). Unfortunately, aggregation measures below these concentrations were not possible with the available techniques.
Nonetheless, the geometry of the surfactants 1OH and 2OH and the fact that the size of the aggregates was approximately double that of the surfactant were consistent with the formation of spherical or ellipsoidal micellar-type structures.
In conventional micelles in water, self-assembly is driven by the hydrophobic effect, i.e. a mainly entropic contribution to minimizing free energy.19 In the present case instead, as is well known for reverse micelles, the contribution is likely to be mainly enthalpic and the explanation for aggregation could lie both in the dipole–dipole interactions between the PEG chains as well as on hydrogen-bonding of the hydroxyl moieties in the core of the micelles.20,21 It is well known that the formation of reverse micelles is favoured by the presence of water in the core. In the present case instead, having excluded water, we are confident that self-assembly was driven exclusively by the non-covalent intermolecular forces between the surfactants. In fact, preliminary SAXS evidence shows a correlation between the size of the aggregates and increasing amounts of water.
In conclusion, the definitions of typical and reverse micelles are based only on the solvent (water or organic solvent, respectively) while they do not consider the geometry of the amphiphile and its mode of aggregation. Based solely on this definition, our aggregates would be considered as reverse micelles. However, if one considers that the reverse surfactants here described are constituted by a small and rigid lipophilic head and a long and floppy lipophobic tail, then their aggregation in cyclohexane might be considered structurally more akin to typical micelles such as the one depicted in Fig. 2a. Whatever the definition – reverse or typical – nonetheless, to the best of our knowledge this study provides the first experimental evidence of micellar structures in a hydrocarbon solvent possessing tightly packed rigid lipophilic heads facing outwards and floppy hydrophilic tails in the core. In perspective, they could potentially represent a means for the solubilisation of hydrophilic species into hydrocarbon solvents or for their transport through the lipid layer of cellular membranes.
Notes and references
- Report on The Limits of Organic Life in Planetary Systems by the National Research Council of the National Academies, National Academy of Sciences, 2007.
- D. Schulze-Makuch, S. Haque, M. R. de Sousa Antonio, D. Ali, R. Hosein, Y. C. Song, J. Yang, E. Zaikova, D. M. Beckles, E. Guinan, H. J. Lehto and S. J. Hallam, Astrobiology, 2011, 11, 241–258 CrossRef PubMed.
- C. Uribe-Alvarez, M. Ayala, L. Perezgasga, L. Naranjo, H. Urbina and R. Vazquez-Duhalt, Microb. Biotechnol., 2011, 4, 663–672 CrossRef CAS PubMed.
- C. R. Fisher, I. R. MacDonald, R. Sassen, C. M. Young, S. A. Macko, S. Hourdez, R. S. Carney, S. Joye and E. McMullin, Naturwissenschaften, 2000, 87, 184–187 CrossRef CAS PubMed.
- J. B. Glass, H. Yu, J. A. Steele, K. S. Dawson, S. Sun, K. Chourey, C. Pan, R. L. Hettich and V. J. Orphan, Environ. Microbiol., 2014, 16, 1592–1611 CrossRef CAS PubMed.
- L. H. Norman, Astron. Geophys., 2011, 52, 1.39–31.42 CrossRef.
- S. J. Bryant, R. Atkin and G. G. Warr, Soft Matter, 2016, 12, 1645–1648 RSC.
- F. Gayet, J.-D. Marty, A. Brûlet and N. L.-d. Viguerie, Langmuir, 2011, 27, 9706–9710 CrossRef CAS PubMed.
- J. Stevenson, J. Lunine and P. Clancy, Sci. Adv., 2015, 1, e1400067 Search PubMed.
- A. Khoshnood and A. Firoozabadi, Langmuir, 2015, 31, 5982–5991 CrossRef CAS PubMed.
- (a) C. Tanford, Science, 1978, 200, 1012–1018 CAS; (b) F. Biedermann, W. M. Nau and H.-J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171 CrossRef CAS PubMed.
- H. F. Eicke and J. Rehak, Helv. Chim. Acta, 1976, 59, 2883–2891 CrossRef CAS.
- H. F. Eicke and H. Christen, Helv. Chim. Acta, 1978, 61, 2258–2263 CrossRef CAS.
- S. Krimm, J. Polym. Sci., Part B: Polym. Lett., 1980, 18, 687 CrossRef.
- J. N. Israelachvili, in Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, San Diego, 3rd edn, 2011, pp. 535–576 Search PubMed.
- P. Tundo, A. Perosa, M. Selva, L. Valli and C. Giannini, Colloids Surf., A, 2001, 190, 295–303 CrossRef CAS.
- N. Akio, K. Yoshinobu and O. Yasumichi, Bull. Chem. Soc. Jpn., 1971, 44, 2855–2856 CrossRef.
- D. Yu, F. Huang and H. Xu, Anal. Methods, 2012, 4, 47–49 RSC.
- E. Fisicaro, C. Compari, E. Duce, M. Biemmi, M. Peroni and A. Braibanti, Phys. Chem. Chem. Phys., 2008, 10, 3903–3914 RSC.
- J. H. Fendler, Acc. Chem. Res., 1976, 9, 153–161 CrossRef CAS.
- E. L. Michor and J. C. Berg, Langmuir, 2015, 31, 9602–9607 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01027c |
| This journal is © The Royal Society of Chemistry 2017 |