Open Access Article
Open Access ArticleParticle size effects on structural and optical properties of BaF2 nanoparticles
Adriano B. Andrade *a,
Nilson S. Ferreiraab and
Mário E. G. Valerioa
*a,
Nilson S. Ferreiraab and
Mário E. G. Valerioa
aPhysics Department, Federal University of Sergipe, 49100-000, São Cristovão, SE, Brazil. E-mail: abandrade1@gmail.com; Tel: +55-79-2105-6630
bPhysics Department, Federal University of Amapá, 68902-280, Macapá, AP, Brazil
First published on 19th May 2017
Abstract
Barium fluoride (BaF2) nanoparticles (NPs) with different sizes were produced through a hydrothermal microwave method (HTMW). The microstructural and electronic properties of the synthesized BaF2 NPs were investigated using X-ray powder diffraction combined with the Rietveld refinement method and Williamson–Hall formalism, X-ray photoemission spectroscopy (XPS) and scanning electron microscopy (SEM). From the Rietveld method, we have found that the lattice parameter of BaF2 NPs is smaller than that observed for BaF2 in its crystal bulk form. These results demonstrated that the lattice parameter shows dependence on size of particle, increasing for larger particles, reducing strain-surface effects. XPS analyses showed that no other elements were present in the material. Photoluminescence (PL) studies in the vacuum ultraviolet (VUV) and visible (VIS) range were also performed to investigate the luminescence properties. The PL results showed a slight shift in the self-trapped exciton (STE) edge for samples with higher particle sizes. In addition, the band gap energy (Eg) was found to be around 10.5 eV for all samples. The observed lattice contraction/expansion was in concordance with the bond-order-length strength (BOLS) correlation mechanism. Therefore, we concluded that this behavior was purely due to surface stress as a result of particle size decreasing.
1 Introduction
The application of alkaline-earth fluorides in optical devices has been well established for a long time, mainly due to their wide optical band gap, larger than 10.0 eV. Moreover, BaF2 is also a high-density luminescent material, with likely characteristics for α-ray and elementary particle detection.1 BaF2 bulk crystals have been extensively studied in recent years, showing useful applications as optical lenses for high vacuum ultraviolet (HVU) systems and, more recently, have been used as a lens material for short-wavelength lithographic applications.2,3 Additionally, BaF2 displays an intrinsically faster luminescent emission for use in scintillator applications. When doped with transition metals or rare earth ions, BaF2 shows better performance as a scintillator, displaying high luminescence efficiency while retaining a fast response.4,5 BaF2 also shows good chemical stability and low hygroscopicity.6Studies with fluoride nanoparticles (NPs) have been carried out quite recently.5 Their unique size-dependent properties (optical, electrical, magnetic and mechanical) are very different from those of their equivalent bulk materials;7 e.g. the crystallites are affected by the high-energy surface of the nanoparticles and by the quantum confinement of the electronic states, which may modify the light absorption, providing new properties.
For applications, the knowledge of certain physical characteristics, such as strain and temperature or pressure effects, is important.2 Studies on the effect of pressure and particle size in these materials have received attention due to the changes observed on the crystallographic structure and, consequently, on the optical properties. Studies on the changes in the optical and structural properties of the BaF2 bulk crystal under high hydrostatic pressure were performed by Leger.8 Using X-ray diffraction under high hydrostatic pressure conditions, the author showed that BaF2 displays an induced phase transition from cubic to orthorhombic up to 1.5 GPa, and to hexagonal up to 8.7 GPa.8 The author also showed that after decompression at atmospheric pressure, the cubic and orthorhombic phases are present in the mixture structure.8 The phase transition takes into account the dynamic behavior of the ions in the crystal lattice of this material; this evidence was reported through experimental studies carried out by Samara.9 This author showed that BaF2 has a small elastic constant, which is the origin of the induced strain and phase transition in this material.9
The strain effect in the crystal lattice at the nanoscale has been explained by the high surface energy of the nanoparticles.10 This assumption takes into account that materials at the nanoscale possess a large fraction of under-coordinated surface atoms presenting a bond order deficiency compared to their bulk equivalent form.11,12 This effect induces the compression of the lattice parameters and unit cell, increasing the internal pressure as the particle size decreases. Despite this, the relationships between the surface energy and lattice strain in nanoparticle systems are not yet well understood.13 Recent studies have shown that the luminescence intensity emission and STE creation on BaF2 NPs exhibit a dependence on particle size.14
This paper is dedicated to studying the effect of particle size on the lattice parameter, microstrain (ε), optical band gap energy (Eg) and self-trapped exciton energy (STE) of BaF2 nanoparticles. The results are compared to literature data, showing good agreement for the optical band gap measurements. On the other hand, the structural analysis by Rietveld refinement and vacuum ultraviolet measurements showed an interesting relationship between strain, particle size and self-trapped exciton energies as a function of the particle size for BaF2 NPs. We also have used a theoretical model based on the bond strength between atoms in nanoparticles to describe the experimental behavior observed from lattice strain in BaF2 NPs with a main average particle size of 40–90 nm. By using this method, it was possible to suggest that BaF2 NPs produced through a hydrothermally assisted microwave method (HTMW) had a large fraction of under-coordinated surface atoms, presenting an order deficiency compared to the bulk form.
2 Experimental
BaF2 NPs were synthesized using Ba(NO3)2 99.9%, Geatec and NH4F 99.9%, and neon as a starting precursor, separately dissolved in deionized water at room temperature. Ethylenediamine (EDA) solution was added to barium solution; subsequently, ammonium fluoride solution was dropwise added into the mixture, forming a colloidal suspension. The final solution was maintained under vigorous stirring for about 30 minutes. The final pH was about 10.0–11.0. After stirring, the suspension was finally transferred into a 110 ml bottle Teflon autoclave, reaching 90% of its volume to provide maximum pressure efficiency, which was sealed and placed in a hydrothermal microwave system (HTMW)15 using 2.54 GHz microwave radiation with a power of 800 W. It was heated to 140 °C at a rate of 10 °C s−1, and maintained at this temperature for 5, 15 and 30 min under an autogenous pressure of 0.4 MPa at the maximum temperature. After the heat cycle, the system was then naturally cooled down to room temperature. The precipitate powders were washed with deionized water three times until the pH was adjusted to 7 to eliminate residues of the reaction and then dried on a hot plate at 90 °C for 2 h. The colloidal suspension, without microwave treatment, was also washed and dried; this sample will hereafter be called “without hydrothermal treatment” (WHT).X-ray powder diffraction (XRD) measurements were carried out in a conventional D8 advanced Brucker diffractometer using Cu Kα radiation, operating at 40 kV and 40 mA, in the 2θ range from 20–80° with steps of 0.02° at room temperature and atmospheric pressure. The crystalline phase was identified using the International Center for Diffraction Data (ICDD). All diffraction full-profiles were refined using the Rietveld method, using FullProf v2.05 software.16 The peak shape was modeled using the Thompson–Cox–Hastings approximation with the independent variation of contributions from Gaussian and Lorentzian line shapes.17 For structural refinement, the background was adjusted using linear interpolation between selected background points. Afterwards, the following parameters were refined: scale factor, unit-cell parameters, the zero-point shift, pseudo-Voigt peak profile parameters (including the full width at half-maximum), peak asymmetry parameters, occupancy factors and the overall isotropic temperature factor.
The Rietveld-refined value of all diffraction peaks was corrected for instrumental broadening using standard silicon powder according to eqn (1):18,19
 | (1) |
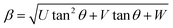 | (2) |
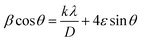 | (3) |
The chemical composition of the BaF2 nanoparticles was investigated using XPS with a Thermo Fisher Scientific XPS instrument using standard monochromatic Al-Kα radiation (1486.7 eV). The measurements were performed at a working pressure of 2.7 × 10−7 mbar. The calibration was based on the binding energy (BE) of the Au4f7/2 line at 83.9 eV with respect to the Fermi level and the standard deviation for the BE values was 0.15 eV. The BEs for all the spectra were corrected for charging effects, assigning the BE value of 286.4 eV to the C 1s line of carbon. Survey scans were obtained in the 0–1000 eV range, whereas detailed scans were recorded for the O 1s, C 1s, Ba 3d and F 1s regions.
The shape and size of the BaF2 NPs were characterized using field emission gun scanning electron microscopy (FEG-SEM), using a JEOL JSM-7500F in secondary electron detection mode. Size distribution studies were performed from SEM image analysis using ImageJ22 commercial software. From each particle size analysis, the median size and size dispersion were estimated through lognormal function fitting using eqn (4).
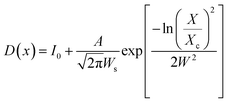 | (4) |
Luminescence measurements with high vacuum ultraviolet (HVUV) photons were performed to investigate the band gap energy absorption, self-trapped exciton energy and dependence of these optical properties on the particle size of BaF2 NPs. Synchrotron radiation at the Brazilian light source synchrotron radiation (LNLS) in the Thoroidal Grating Monochromator (TGM) beamline was used for these experiments. Excitation spectra between 8.0 and 15.0 eV were obtained in a vacuum chamber under 10−9 mbar pressure. The luminescence sample was collected using an optical fiber coupled to a Hamamatsu R928 photomultiplier tube (PMT) as a function of excitation energy. The signal was converted and stored on a computer. The excitation monochromator was calibrated using Xe and Kr atomic absorptions. The sample intensity response was normalized using the absorption of a standard aluminum sheet at the same position of the sample to avoid temporal variation of the HVU incident photon intensity.23–25
3 Results
3.1 Structural analysis
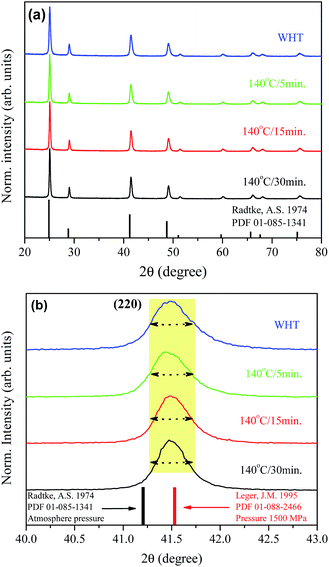
Fig. 1(a) shows XRD patterns of the BaF2 nanoparticles produced at different times of hydrothermal treatment. All of the diffraction peaks, corresponding to the (111), (200), (220), (311), (222), (400), (331), (420) and (422) crystallographic planes, can be indexed to the BaF2 cubic fluorite-type belonging to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m group (PDF# 01-085-1341). No additional diffraction peaks were observed, which eliminated the possibility of any secondary phases. Further examination of the relevant diffraction patterns in Fig. 1(a) was performed by scaling up the diffraction patterns of line (220) for all samples, as shown in Fig. 1(b).
m group (PDF# 01-085-1341). No additional diffraction peaks were observed, which eliminated the possibility of any secondary phases. Further examination of the relevant diffraction patterns in Fig. 1(a) was performed by scaling up the diffraction patterns of line (220) for all samples, as shown in Fig. 1(b).
One can also see that all diffraction lines became narrower with increasing hydrothermal treatment time. This behavior could be attributed to either the particle size increasing or the strain effect, which could also contribute to the peak broadening of the XRD patterns. Besides these observations, one can also see that the Bragg position, from 2θ 41.47° to 41.49°, does not match well to those of the standard reference pattern data reported by Radtke and Brown,26 measured under atmospheric pressure and the same conditions used in this work. However, our Bragg positions match better with the data of Leger et al.8 for samples analyzed using XRD measurements under high pressure conditions of about 1500 MPa. To elucidate the main reason for the peak broadening and shift of diffractions peaks, we calculated the lattice parameters using Rietveld refinements over the raw XRD data, as shown in Fig. 2.
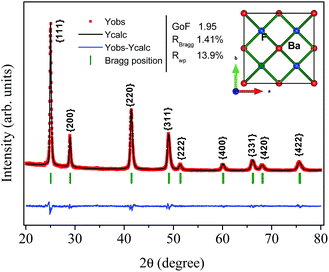 | ||
| Fig. 2 Illustrative typical Rietveld refined XRD pattern for the BaF2 (WHT) sample. The inset shows the BaF2 crystal structure. | ||
The parameters of the refinement, lattice parameters and unit cell volume are presented in Table 1 as a function of the hydrothermal treatment time for all samples.
| Annealing time (min) | Lattice parameter (Å) | χ2 (–) | RBraag (%) | RWP (%) | Unit cel. (Å)3 |
|---|---|---|---|---|---|
| 0 | 6.1564(2) | 1.95 | 1.41 | 13.9 | 233.342(10) |
| 5 | 6.1586(1) | 2.18 | 2.35 | 13.7 | 233.593(9) |
| 15 | 6.1591(1) | 1.72 | 1.21 | 13.0 | 233.638(7) |
| 30 | 6.1603(1) | 2.16 | 2.30 | 13.1 | 233.788(7) |
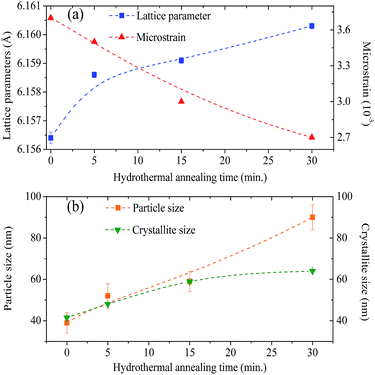
The values of the lattice parameters increased continuously from 6.1564 Å to 6.1603 Å when the hydrothermal treatment time of the sample preparation was increased from 0 to 30 min, with the unit cell volume following the same trend. It is worth highlighting that the lattice parameters for these BaF2 nanoparticles are slightly smaller than the equilibrium values of 1.1964 Å for the single crystal as reported by Radtke and Brown26 (PDF# 01-085-1341).
Furthermore, XRD peak broadening also has a contribution from the self-induced strain (ε) developed in crystallites during the growth that is effective in the nanoparticles.19 Thus, we also calculated the crystallite size and strain for all samples, considering the contribution from crystallites and strain to peak broadening, using the Williamson–Hall formalism21 (eqn (3)).
Fig. 3 shows plots of β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus sin
θ versus sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (W–H plot) for the BaF2 nanoparticles synthesized at different hydrothermal treatment times. It is possible to observe that the straight line intercepts all points, indicating a homogeneous crystallite size distribution and the presence of a homogeneous microstrain.18,19 The results revealed that the estimated crystallite size was about 41.5 ± 0.3 nm for the WTH sample. However, the size of the crystallite increases from 47.9 ± 0.3 to 64.0 ± 0.4 nm with the hydrothermal treatment time increasing from 5 to 30 min. This behavior is attributed to the long times of hydrothermal treatment, which provide crystallite growth by diffusion, related to increases of the probability of collisions between particles due to the pressure system i.e. crystallization rate of the solid phases. As a result, a greater movement of atoms is attained, which facilitates the rapid arrangement of the crystalline structure and subsequent coalescence of the chemical species to form particle agglomeration.27
θ (W–H plot) for the BaF2 nanoparticles synthesized at different hydrothermal treatment times. It is possible to observe that the straight line intercepts all points, indicating a homogeneous crystallite size distribution and the presence of a homogeneous microstrain.18,19 The results revealed that the estimated crystallite size was about 41.5 ± 0.3 nm for the WTH sample. However, the size of the crystallite increases from 47.9 ± 0.3 to 64.0 ± 0.4 nm with the hydrothermal treatment time increasing from 5 to 30 min. This behavior is attributed to the long times of hydrothermal treatment, which provide crystallite growth by diffusion, related to increases of the probability of collisions between particles due to the pressure system i.e. crystallization rate of the solid phases. As a result, a greater movement of atoms is attained, which facilitates the rapid arrangement of the crystalline structure and subsequent coalescence of the chemical species to form particle agglomeration.27
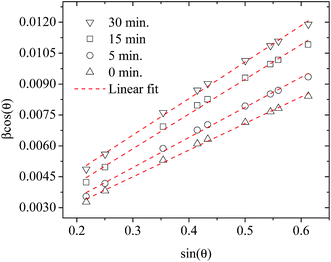 | ||
| Fig. 3 Representative Williamson–Hall plots of the BaF2 nanoparticles prepared using different hydrothermal treatment times. | ||
The lattice microstrain of each sample obtained using the Williamson–Hall method displays a positive value, indicating lattice expansion.19 We also observe that the microstrain decreases with increasing hydrothermal treatment time, showing a reduction for higher hydrothermal treatment times. The obtained microstrain value for the WHT sample was about 2.0 × 10−3, which gradually decreased, varying from 1.9 × 10−3 to −1.3 × 10−3 with increasing hydrothermal treatment time from 5 to 30 minutes. We expected that longer hydrothermal treatment times could result in a particle coalescence effect with subsequent increasing of the crystallite size, causing relaxation in the unit cell volume of the BaF2 nanocrystals. The microstrain decrease with increasing particle size due to the long annealing time has also been reported elsewhere, in a study of CoFe2O4 nanoparticles.28 The calculated crystallite size and microstrain values for all samples are shown in Table 2. A detailed microstructural analysis will be presented later.
| Annealing time (min) | Crystallite size (nm) | Microstrain (arb. unit) |
|---|---|---|
| 0 | 41.5(3) | 2.0 × 10−3 |
| 5 | 47.9(3) | 1.9 × 10−3 |
| 15 | 58.9(4) | 1.6 × 10−3 |
| 30 | 64.0(4) | 1.3 × 10−3 |
The increasing of crystallite size and decreasing of microstrain leads to the growth of particle size, as presented in the electron micrographs analyses in Fig. 4 for the FEG-SEM images of all samples. The BaF2 nanoparticles exhibited different shapes and particle sizes. From Fig. 4(a), it is possible to see that the WHT sample presents a well-defined cubic shape, which is a characteristic fluorite-type structure. However, samples produced at hydrothermal treatment times of 5 and 15 minutes, as shown in Fig. 4(b) and (c), respectively, showed the coexistence of cubic and spherical shapes, indicating an evident coalescence process due to the hydrothermal treatment. Furthermore, the sample produced at a hydrothermal treatment time of 30 minutes shows particles formed mainly of a spherical shape (see Fig. 4(d)), as a result of excessive hydrothermal treatment time. This duration was sufficiently long to change the particles’ shape fully, from cubic to spherical form.
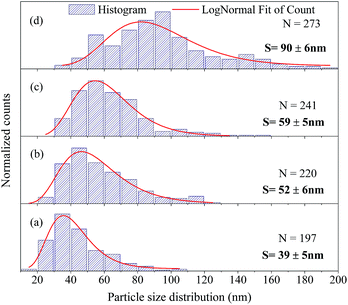
The FEG-SEM images were also used to estimate the average size of BaF2 nanoparticles. Fig. 5 shows histograms of the particle size distributions for samples synthesized without hydrothermal treatment and using different hydrothermal treatment times, as described before. The size distribution was fitted using a log-normal function and the standard deviation used also refers to the best fit to the experimental data using the log-normal function, as shown in eqn (4) where N represents the number of analyzed particles and S is the maximum median size. The histograms indicated that the main particle size for the sample prepared without hydrothermal treatment was about 39 ± 5 nm. Furthermore, the main particle size for the samples increases with hydrothermal treatment time from 52 ± 6 nm at 5 minutes to 90 ± 6 nm for the sample produced using 30 minutes of hydrothermal treatment. These results are higher than the crystallite size estimated from XRD data using the Williamson–Hall formalism (Table 2). The large discrepancies observed among the sizes obtained by these two methods is not surprising, as it is a common effect observed in materials as particles are formed by several crystallites.29
3.2 Electronic and surface analysis
The electronic structure and composition of the BaF2 nanoparticles were also analyzed using X-ray Photoelectron Spectroscopy (XPS). A representative XPS spectrum of the WHT sample, i.e. without hydrothermal treatment, is showed in Fig. 6(a). The XPS survey spectrum confirms the presence of no other elements besides Ba, F, O, and C (the presence of O and C is attributed to the carbon tape used as a sample holder). The high-resolution XPS spectra taken from the Ba 3d, F 1s and O 1s regions are shown in Fig. 6(b)–(d), respectively.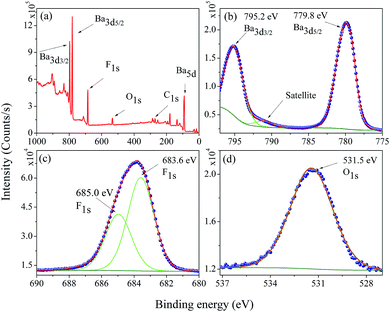 | ||
| Fig. 6 Representative XPS survey low resolution spectra analysis (a), high-resolution spectra for (b) Ba 3d, (c) F 1s, and (d) O 1s in the WHT BaF2 nanoparticles. | ||
The core-level peaks presented in Fig. 6(b) for the Ba 3d region consist of two well-separated spin–orbit components (δ = 15.4 eV), which are characteristic of Ba in the Ba2+ valence state; in addition, a shake-up satellite peak was also observed. The larger binding energy of 795.2 eV corresponds to the Ba 3d3/2 core level; and the peak of 779.8 eV corresponds to the Ba 3d5/2 core level. These values are closer to the value reported for Ba 3d for BaFe2As2 (795.1 eV – Ba 3d3/2 and 779.7 eV – Ba 3d5/2).30 The peak at 779.8 eV corresponding to Ba 3d5/2 is consistent to that of Gauzzi et al.31 for Ba–F bonds. The F 1s peak can be decomposed into two components of Gaussian profile (see Fig. 6(c)), with the lower binding energy component centered at about 683.6 eV, corresponding closely to the binding energy reported in Ba–F bonds for a BaF2 reference compound (683.7 eV).32–34 The other, lying at a higher binding energy of 685.0 eV, cannot be attributed to a chemical shift in the F 1s region, since the sample has only one chemical group. On the other hand, for ions close to the nanoparticle’s surface, the number of ions bonding may be slightly different, inducing a different chemical potential in the particle’s surface than in the bulk of the particle. The O 1s region at 531.6 eV presented in Fig. 6(d) was assigned to C–O bonds; and this is most likely due to the X-ray interaction with the carbon tape used as a sample holder.
From the XPS spectra of the selected regions for all samples (not shown here), the amount of each detected element was calculated (the uncertainty in the amounts in the calculations is estimated to be around 2%).35 For comparison, XPS analyses were also performed for high-quality BaF2 powder from a crystal produced using the Czochralski method. From Table 3, it can be seen that there is no significant difference in composition between the samples produced using or not using the hydrothermal method and crystal BaF2 samples, from the point view of chemical quality; therefore, the XPS results corroborate the XRD measurements, i.e. BaF2 in the fluorite phase was successfully produced. Moreover, these analyses show that the effect of compression in the crystal lattice cannot be attributed to strange chemical elements; for example small amounts of M2+ (M = Sr or Ca) in the crystal lattice, since these elements have a smaller ionic radius than that of a Ba2+ ion.
| Sample | Atomic mass (%) | ||
|---|---|---|---|
| Ba | F | O | |
| 0 | 25.21 | 60.18 | 14.61 |
| 5 | 25.88 | 58.97 | 15.14 |
| 30 | 25.88 | 61.07 | 13.04 |
| Std BaF2 | 26.73 | 58.81 | 14.46 |
3.3 Luminescence analysis
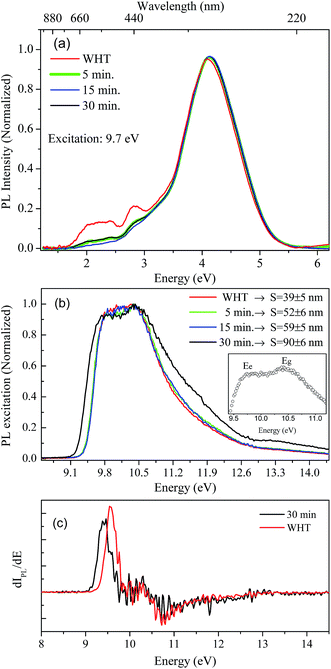
Luminescence studies in nanoparticles of fluoride materials have shown that luminescence properties like excitation and emission quantum efficiency depend on the particle size.14,36 Based on density functional theory calculations (DFT), Schmalzl showed that in BaF2, the band gap energy may shift due to structural changes in the crystal lattice parameters.2 From these affirmations, we investigated, using measurements in the VUV region, the luminescence and excitation luminescence spectra of BaF2 nanoparticles with different particle sizes produced using different hydrothermal treatment times.The STE emission spectra for BaF2 nanoparticles, under 9.7 eV excitation energy at room temperature (300 K), and for samples with different particle sizes, are shown in Fig. 7(a). The STE emission in BaF2 originates from trapped electron–hole pair recombination when the sample is excited with energy hν ≤ Eg or due to recombination of the free charge carriers for hν ≥ Eg. The resultant exciton becomes self-trapped and recombines radiatively, giving rise to the well-known large emission peak at around 4.1 eV (300 nm).14 This emission is similar to that observed for the BaF2 bulk crystal.37 Furthermore, all BaF2 nanoparticles also showed at least two weak emission bands at around 1.7–2.5 eV and 2.5–3.0 eV that were more evident for samples with minor average particle sizes (39 ± 5 nm). Vistovskyy et al. also found a similar behavior for CaF2 nanoparticles.36 The authors found a weak emission band at around 2.5–3.5 eV for nanoparticles with smaller sizes up to 20 nm; for larger particles up to 60–140 nm, the emission was less evident36 (as also observed for BaF2). According to Kirm et al., BaF2 displays fast component emission at around 1.2–2.5 eV, corresponding to intra band luminescence.37 This happens when electron transition occurs inside the conduction band and/or inside the valance band.
Fig. 7(b) shows the excitation spectra measured at 300 K in BaF2 nanoparticles considering the integrated luminescence emission spectra as shown in Fig. 7(a). All spectra were normalized in terms of the maximum intensity, to make the profile spectra analysis concise. The excitation spectrum can be divided into three parts: a region with hν < Eg characteristic for STE creation; a region with hν ≈ Eg, when the fundamental absorption in BaF2 occurs due to band-to-band transition (band gap); and the region for Eg < hν < 2Eg, when electron pair creation occurs.36,37 In the inset in Fig. 7(b), the maximum excitation points for BaF2 with an average particle size of 90 ± 6 nm are highlighted. Two bands are observed: one at 9.8 eV and the other at 10.5 eV, attributed to STE creation (Ee) and band gap (Eg), respectively.38 Furthermore, a slight shift in the STE edge (hν < Eg region) was observed just for the BaF2 sample with higher particle sizes (Fig. 7(b)). This behavior can be more easily seen in Fig. 7(c), which shows the first derivative of the excitation curve for samples with smaller (39 ± 5) and greater (90 ± 6) average particle sizes. The STE creation energy is shifted by approximately 0.2 eV for smaller particles; on the other hand, the Eg region does not shift for any sample. This behavior was also predicted for BaF2 (ref. 14) and CaF2 (ref. 36) nanoparticles, respectively. The authors explain that this slight shift in the STE excitation edge is attributed to the reduction of light absorption by the small nanoparticles, indicating that for smaller particles, the exciting light is not completely absorbed.
4 Discussion
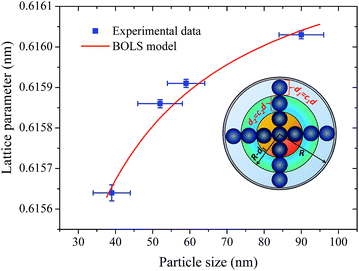
Let us now discuss the origin of the lattice contraction of BaF2 nanoparticles based on the values of lattice parameters, crystallite size, unit cell volume and expansive microstrain of each sample obtained from the structural analyses, as presented in Tables 1 and 2.The lattice strain in all the samples was calculated as shown in Fig. 3. There is a monotonous decrease in the lattice strain with increasing average crystallite size. The high strain in the crystal lattice may lead to lattice contraction in order to relieve the strain. A recent report showed that crystal growth rate depends on the lattice strain.39 Therefore, it is suggestive that this decrease in microstrain could be associated with an increasing of the BaF2 lattice parameters. In fact, it is evident from Fig. 8(a) that the lattice parameter of the BaF2 nanoparticles indeed increases with hydrothermal treatment time and crystallite size (Fig. 8(b)).
Recent studies have shown that the increase in the lattice of oxide nanoparticles is attributed mainly to the superposition of long-range Coulomb attraction and short-range repulsion (Madelung model), in which this balance is altered by particle surfaces at the nanoscale.40,41 The Madelung model has been used to explain the lattice parameter contraction in oxides with particle sizes ranging from 4 to 20 nm.40 However, we cannot use this model to investigate the lattice contraction/expansion of the BaF2 nanoparticles studied here, because our particles have a main size in the range of 39 to 90 nm, as shown before in Fig. 5. Moreover, there are several models that describe the correlation of the lattice parameter contraction with the nanoparticle size based on the surface energy of the nanoparticles,42,43 and also on the variation of the lattice parameters with the shape of the nanoparticles,44 or the lack of outermost bonding of the surface atoms45 and intra-crystalline pressure.46,47
According to Huang et al.,10 the decrease in the lattice parameter of the BaF2 nanoparticles can be attributed to elastic deformation of the BaF2 lattice induced by the surface tension effect. In fact, it is reasonable to consider, based on the microstructural results from XRD and FEG-SEM measurements, that decreasing particle sizes result in an increase of the surface-to-volume ratio, which results in lattice contraction and, subsequently, the inducing of microstrain in the crystalline lattice.
In fact, no reliable studies reporting experimental measurements of the surface stress of BaF2 nanoparticles are available in the literature. Furthermore, there is a lack of studies that consistently report on the possible mechanisms of lattice parameter contraction in BaF2 nanoparticles and their effects. Therefore, we have found, based on these assumptions, that the observed reduction of the lattice parameter is ascribed to the bond-order-length-strength (BOLS) correlation mechanism.12 According to this mechanism, materials at the nanoscale possess a large fraction of under-coordinated surface atoms presenting a bond order deficiency compared to their bulk counterparts.11,12 Thus, the key idea is that lattice strain in an under-coordinated atom in the i-th surface layer is given by the following expression:
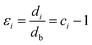 | (5) |
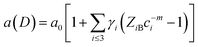 | (6) |
The fitting curves depict the size-dependent behavior of the lattice parameters well; therefore, the results of this calculation suggest that this anomalous lattice parameter contraction of the BaF2 nanoparticles may be explained by the combined effect of defect formation and negative surface stress. It should be pointed out that the large differences in the diffusion coefficients of Ba and F ions (approximately two orders of magnitude) lead to Ba ions diffusing slower than F ions during the BaF2 nanoparticles’ growth.49 This can lead to a more easy and rapid increase in the F–F bond length than that of the Ba–F bond,50 resulting in a high density of fluorine vacancies in the (111) surface of the BaF2 nanoparticles.51 As a result, this can lead to a notable surface-induced tensile strain, discussed elsewhere.52 Thus, it is favorable that the neighboring F atoms located in the third sublayer of the first surface layer are attracted to a surface F center with a displacement magnitude larger than that in the bulk F center case.51 This gives rise to the obtained correlation of the lattice parameter with the particle in BaF2 nanoparticles synthesized through the hydrothermal method being reasonably well evidenced by the BOLS correlation mechanism.
5 Conclusions
Nanoparticles of BaF2 with different sizes have been produced using control precipitated and hydrothermal microwave assisted method. The structural results showed that this method can be used to produce a large range of particle sizes through controlling the synthesis time. We have found that structural and optical properties like strain and self-trapped exciton depends on the particle size. Results from the Rietveld refinement showed that BaF2 nanoparticles are submitted to a strain induced by the surface stress of the nanoparticles. This effect induces reduction of the lattice parameters of the crystalline cell of BaF2. We also investigate using high-resolution electron microscopy, the effect of hydrothermal synthesis time on the growing size of the particles. The analysis shows that prolonged synthesis time gave larger particles and changed the shape of the particles, from a typical cubic to a spherical form. The obtained particles were around 39 nm for smaller sizes and up to 90 nm for higher sizes, which lead to the observation that for higher particles, the strain is lower on then.The electronic structure and elemental composition analyzed using X-ray photon electron spectra showed that there are no contaminant elements in the studied samples. The results were compared to standard crystal results to investigate whether the composition ratio between Ba and F ions is different for BaF2 nanoparticles. The values obtained do not show a significant difference between the crystal and nanoparticle compositions.
From optical studies using vacuum ultraviolet excitation, we were able to investigate the self-trapped exciton and band gap of the BaF2 as a function of the particle size. We showed that self-trapped exciton creation displays an interesting relationship with particle size; for smaller nanoparticles, the self-trapped exciton is higher than for larger BaF2 particles, indicating that the binding energy of STE is higher for smaller particle sizes. Moreover, the band gap was found to be ∼10.5 eV for all samples, not depending on particle size.
We also have used a theoretical model based on the bond-order-length-strength (BOLS) to explain the origin of strain on the particles. The results showed that the BOLS model depicts the size-dependent behavior of lattice parameters well, suggesting that the anomalous lattice parameter of BaF2 nanoparticles may be explained by the combined effect of defect formation and negative surface stress.
Acknowledgements
The authors gratefully acknowledge financial support from the CAPES and CNPq, Brazilian agencies. The authors thank the Brazilian National Laboratories, Synchrotron Light Laboratory (LNLS) and Nanotechnology Laboratory (LNNano) under research proposals TGM – No. 16209/13, TGM – No. 17070/14 and XPS – No. 17752. The authors also thank the Multiuser Center for Nanotechnology of the Federal University of Sergipe (CMNano/UFS), under proposals # 35 – JSM7500F and # 56 – JSM7500F. Adriano B. Andrade thanks Dr Eduardo G. Yukihara for discussions about the text structure.References
- M. J. Weber, P. Lecoq, R. C. Ruchti, C. Woody, W. M. Yen and R. Y. Zhu, Materials Research Society Symposium Proceedings, Pittsburgh, 1994 Search PubMed.
- K. Schmalzl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 014306 CrossRef.
- H. Shi, R. Jia and R. I. Eglitis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195101 CrossRef.
- G. De, W. Qin, J. Zhang, J. Zhang, Y. Wang, C. Cao and Y. Cui, J. Solid State Chem., 2006, 179, 955–958 CrossRef CAS.
- S. Sathyamurthy, E. Tuncer, K. L. More, B. Gu, I. Sauers and M. P. Paranthaman, Appl. Phys. A: Mater. Sci. Process., 2012, 106, 661–667 CrossRef CAS.
- C. M. Bender, J. M. Burlitch, D. Barber and C. Pollock, Chem. Mater., 2000, 12, 1969–1976 CrossRef CAS.
- Z. Kang, M. Barta, J. Nadler, B. Wagner, R. Rosson and B. Kahn, J. Lumin., 2011, 131, 2140–2143 CrossRef CAS.
- J. M. Leger, J. Haines, A. Atouf, O. Schulte and S. Hull, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 13247–13256 CrossRef CAS.
- G. A. Samara, Phys. Rev. B: Solid State, 1970, 2, 4194–4198 CrossRef.
- Z. Huang, P. Thomson and S. Di, J. Phys. Chem. Solids, 2007, 68, 530–535 CrossRef CAS.
- C. Q. Sun, B. K. Tay, X. T. Zeng, S. Li, T. P. Chen, J. Zhou, H. L. Bai and E. Y. Jiang, J. Phys.: Condens. Matter, 2002, 14, 7781 CrossRef CAS.
- C. Q. Sun, Prog. Solid State Chem., 2007, 35, 1–159 CrossRef CAS.
- B. Gilbert, H. Zhang, B. Chen, M. Kunz, F. Huang and J. F. Banfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115405 CrossRef.
- V. V. Vistovskyy, A. V. Zhyshkovych, Y. M. Chornodolskyy, O. S. Myagkota, A. Gloskovskii, A. V. Gektin, A. N. Vasil’ev, P. A. Rodnyi and A. S. Voloshinovskii, J. Appl. Phys., 2013, 114, 194306 CrossRef.
- S. Komarneni, R. Roy and Q. H. Li, Mater. Res. Bull., 1992, 27, 1393–1405 CrossRef CAS.
- J. R. G. Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79–83 CrossRef CAS.
- A. K. Zak, W. A. Majid, M. Abrishami and R. Yousefi, Solid State Sci., 2011, 13, 251–256 CrossRef.
- N. Gonçalves, J. Carvalho, Z. Lima and J. Sasaki, Mater. Lett., 2012, 72, 36–38 CrossRef.
- G. Caglioti, A. Paoletti and F. Ricci, Nucl. Instrum., 1958, 3, 223–228 CrossRef CAS.
- G. Williamson and W. Hall, Acta Metall. Mater., 1953, 1, 22–31 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- A. B. Andrade and M. E. G. Valerio, Radiat. Meas., 2014, 71, 55–60 CrossRef CAS.
- C. d. S. Bezerra and M. E.G. Valerio, Phys. B, 2016, 501, 106–112 CrossRef CAS.
- G. F. C. Bispo, A. B. Andrade, C. d. S. Bezerra, V. C. Teixeira, D. Galante and M. E. G. Valerio, Phys. B, 2017, 507, 119–130 CrossRef CAS.
- A. S. Radtke and G. E. Brown, Am. Mineral., 1974, 59, 885–888 CAS.
- S. H. Ehrman, J. Colloid Interface Sci., 1999, 213, 258–261 CrossRef CAS PubMed.
- M. M. El-Okr, M. A. Salem, M. S. Salim, R. M. El-Okr, M. Ashoush and H. M. Talaat, J. Magn. Magn. Mater., 2011, 323, 920–926 CrossRef CAS.
- W.-N. Wang, W. Widiyastuti, T. Ogi, I. W. Lenggoro and K. OkuyamaO, Chem. Mater., 2007, 19, 1723–1730 CrossRef CAS.
- S. de Jong, Y. Huang, R. Huisman, F. Massee, S. Thirupathaiah, M. Gorgoi, F. Schaefers, R. Follath, J. Goedkoop and M. Golden, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115125 CrossRef.
- A. Gauzzi, H. Mathieu, J. James and B. Kellett, Vacuum, 1990, 41, 870–874 CrossRef CAS.
- C. D. Wagner and G. E. Muilenberg, Handbook of X-ray photoelectron spectroscopy: a reference book of standard data for use in x-ray photoelectron spectroscopy, Physical Electronics Division, Perkin-Elmer Corp., 1979 Search PubMed.
- G. E. Murch and R. J. Thorn, J. Phys. Chem. Solids, 1980, 41, 785–791 CrossRef CAS.
- R. Hessabi and D. S. Urch, J. Chem. Soc., Faraday Trans., 1990, 86, 247–252 RSC.
- P. Gao, Y. Xie and Z. Li, Eur. J. Inorg. Chem., 2006, 2006, 3261–3265 CrossRef.
- V. V. Vistovskyy, A. V. Zhyshkovych, N. E. Mitina, A. S. Zaichenko, A. V. Gektin, A. N. Vasil’ev and A. S. Voloshinovskii, J. Appl. Phys., 2012, 112, 024325 CrossRef.
- M. Kirm, A. Lushchik, C. Lushchik, A. I. Nepomnyashikh and F. Savikhin, Radiat. Meas., 2001, 33, 515–519 CrossRef CAS.
- P. A. Rodnyi, G. B. Stryganyuk, C. W. E. van Eijk and A. S. Voloshinovskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195112 CrossRef.
- J. H. Harding, C. L. Freeman and D. M. Duffy, CrystEngComm, 2014, 16, 1430–1438 RSC.
- V. Perebeinos, S.-W. Chan and F. Zhang, Solid State Commun., 2002, 123, 295–297 CrossRef CAS.
- A. E. Sokolov, A. E. Baranchikov, D. O. Gil, V. K. Ivanov, G. P. Kopitsa, A. A. Petrunin and E. V. Fomin, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech., 2014, 8, 997–1001 CrossRef CAS.
- J. Woltersdorf, A. S. Nepijko and E. Pippel, Surf. Sci., 1981, 106, 64–69 CrossRef CAS.
- Q. Jiang, L. Liang and D. Zhao, J. Phys. Chem. B, 2001, 105, 6275–6277 CrossRef CAS.
- W. H. Qi and M. P. Wang, J. Nanopart. Res., 2005, 7, 51–57 CrossRef CAS.
- M. Fukuhara, Phys. Lett. A, 2003, 313, 427–430 CrossRef CAS.
- C. Herring, Phys. Rev., 1951, 82, 87–93 CrossRef CAS.
- G. Iyer, D. De, A. Kumar, R. Pala and A. Subramaniam, Appl. Surf. Sci., 2016, 371, 343–348 CrossRef CAS.
- W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Nat. Mater., 2008, 7, 308–313 CrossRef CAS PubMed.
- I. Avramov, C. Rüssel, N. Kolkovska and I. Georgiev, J. Phys.: Condens. Matter, 2008, 20, 335203 CrossRef.
- W. Pong, C. S. Inouye and S. K. Okada, Phys. Rev. B: Solid State, 1978, 18, 4422–4425 CrossRef CAS.
- H. Shi, R. Eglitis and G. Borstel, J. Phys.: Condens. Matter, 2006, 18, 8367 CrossRef CAS.
- N. Tsakiris, P. Argyrakis, I. Avramov, C. Bocker and C. Rüssel, Europhys. Lett., 2010, 89, 18004 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |