Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Observing different modes of mobility in lithium titanate spinel by nuclear magnetic resonance
Magnus F. Graf *a,
Hermann Tempel
*a,
Hermann Tempel a,
Simone S. Köcher
a,
Simone S. Köcher ab,
Roland Schierholz
ab,
Roland Schierholz a,
Christoph Scheurerb,
Hans Kungla,
Rüdiger-A. Eichel
a,
Christoph Scheurerb,
Hans Kungla,
Rüdiger-A. Eichel acd and
Josef Granwehr
acd and
Josef Granwehr ae
ae
aInstitute of Energy and Climate Research (IEK-9), Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: j.granwehr@fz-juelich.de
bLehrstuhl für Theoretische Chemie, Technische Universität München, Garching, Germany
cRWTH Aachen University, Institute of Physical Chemistry, Aachen, Germany
dJülich Aachen Research Alliance (JARA), Section JARA-Energy, Aachen, Germany
eRWTH Aachen University, Institute of Technical and Macromolecular Chemistry, Aachen, Germany
First published on 10th May 2017
Abstract
Lithium titanate (LTO) is a spinel material that is able to reversibly intercalate Li ions with minimal changes of the unit cell dimensions (“zero-strain”), making it an attractive choice as anode material for Li ion batteries. However, the nature of the Li transport in this material is still not fully understood. Here, the Li mobility in Li4+xTi5O12 with x = 0 and x ≈ 1.6 is investigated. By regularized inversion of nuclear magnetic resonance (NMR) relaxation and spin alignment echo (SAE) data and supported by DFT simulations, solid-state NMR spectra were analyzed as a function of the respective relaxation times and correlation time constants. A clear correlation between mobility and NMR spectral features was observed, suggesting the presence of local domains with high Li ion mobility. The long-range mobility is limited by the much slower hopping between such domains and appears to be faster for either larger or less ordered local domains. For x ≈ 1.6, spectral features indicate the formation of separate stoichiometric and overlithiated phases rather than a solid solution, yet no segregation into a fast and a slow component was observed in the relaxation and in the SAE dimension, which points towards an entangling of the two phases on a microscopic scale.
1 Introduction
Major challenges for future battery generations are the improvement of cycle life and the reduction of the total cost of ownership. Many promising materials with potential use as anodes or solid electrolytes belong to the spinel family (AB2O4).1–5 One of them is lithium titanate (LTO, Li4Ti5O12),6 a “zero-strain” Li host with a flat and relatively high potential of ∼1.55 V vs. Li/Li+ for reversible Li intercalation and a better cyclability than graphite.7,8 The stoichiometric compound has the chemical formula (Li3)8a(LiTi5)16d(O12)32e with the 16d sites randomly occupied by Ti (5/6th) and Li (1/6th).9 Altering the structure, e.g. by changing the defect chemistry, by raising the temperature, or by overlithiation to form Li4+xTi5O12 (x ≤ 3) significantly influences the ionic and electronic conductivity.10–13 Upon electrochemical overlithiation, Li is inserted into 16c positions with additional Li in equivalent number moving into 16c from 8a to form a rocksalt structure.9 During this process, two-phase separation is observed,14,15 with only a small fraction of solid solution forming.16 On the other hand, chemical overlithiation was reported to form an inserted spinel structure,17,18 with chemically inserted Li ions found to be trapped in 48f sites. Furthermore, different site occupation ratios for Li have been reported for different synthesis routes of LTO and overlithiated LTO (e.g. ref. 19–22).For rational materials design the understanding of dynamical and electrochemical processes taking place in LTO is of utmost importance to establish structure–property relationships by complementing the static structural picture with dynamic information. Initial models of dynamic processes were made based on structural changes.9 Li diffusion in LTO depends on the size of LTO particles, with evidence for kinetic23 as well as surface equilibrium causes.24 Li diffusion has been studied by neutron diffraction,23,25 impedance spectroscopy18 and chronoamperometry.26 The “ultra slow” regime was analyzed via spin alignment echo (SAE) nuclear magnetic resonance (NMR), where changes of the electric field gradient (EFG) seen by a nucleus via its quadrupolar coupling constant CQ are probed.27 The echo decay is characterized by a correlation time constant τC that may be identified as a hopping time between sites, provided that the origin and the destination of a jump are not electrically equivalent. In LTO all jumps occur between inequivalent sites with different EFGs and are therefore contributing to the SAE decay.12 Furthermore, due to the random occupancy of 16d sites by Ti and Li ions (Fig. 1), even nominally identical sites show a distribution of EFG values. The complete intensity decay curve as a function of mixing time tm in an SAE experiment is usually described by one or the sum of several stretched exponential functions. The stretched nature of these functions is generally believed to result from a distribution of time constants with an underlying exponential kernel.28
Temperature dependent measurements of conductivity29 or NMR relaxation times12 were used to obtain activation energies Ea for jumps of Li ions. So far the mechanism of Li conductivity could not be fully resolved.30,31 One reason was provided by a recent theoretical study where it was concluded that jump rates are not primarily limited by activation energies, but a combination of Ea and the availability of jump targets.32 Thus, Ea derived in temperature dependent experiments are merely effective parameters and cannot generally be interpreted as actual physical barriers of ion motion.
Inverting relaxation and diffusion data using an exponential kernel instead of fitting it with a particular model has become a routine tool in NMR.33–35 However, the common regularization with a non-negativity constraint is not physically justified once exchange processes become relevant for the dynamics of a spin system.36–40 Amorphous and multisite crystalline solid-state systems are affected in particular due to their highly branched interaction network,28 which requires a different approach for data inversion. One suggestion was to analyze the data in the time domain, without actually inverting it.40 Here, the applicability of uniform penalty (UP) regularization in combination with a penalty to prevent unnecessary oscillations41 is demonstrated for the inversion of solid-state NMR data. The suitability of the algorithm for averaging in a non-inverted dimension is shown, facilitating spectral separation of the static NMR spectrum with respect to the SAE time constant. Using this technique and supported by ab initio density functional theory (DFT) calculations, the dynamics of stoichiometric and chemically overlithiated LTO is investigated.
2 Methods
2.1 Sample preparation and characterization
Stoichiometric Li4Ti5O12 was purchased from Sigma-Aldrich (>99%). Li4+xTi5O12 with x ≈ 1.6 was prepared by dispersing 10 mmol of the commercial Li4Ti5O12 in 30 ml hexane with subsequent slow addition of 2 ml of 11 M butyllithium (3 mmol). The color of the dispersion changed immediately from white to dark blue when adding the butyllithium. The dispersion was stirred for at least 24 hours, dried under vacuum, washed three times with fresh hexane and then dried again. Complete transition of the Li from the butyllithium to the lithium titanate results in formation of Li4+xTi5O12 with x ≈ 1.6. All sample preparation steps were done in a glove box under argon. A sample with a lower degree of lithiation (x ≈ 0.2) was prepared in the same way, using 0.4 mmol butyllithium.X-ray diffraction was measured in transmission mode with Cu K-alpha radiation (40 kV, 40 mA) with an Empyrean diffractometer (Panalytical, Netherlands) with the powder placed between two mylar foils. Microscopy was performed with a CM 20 transmission electron microscope (Philips, Netherlands) operated at 200 kV. In the glovebox the powder was placed on lacey carbon grids which were sealed in aluminium foil for transport. The bags were opened, the grids were placed in the holder and the holder was inserted into the TEM to minimize the exposure of the samples to air (max. 1 minute). PowderCell (Bundesanstalt für Materialforschung und prüfung)42 was used to simulate diffraction patterns for stoichiometric LTO (ICSD 160655) and fully overlithiated LTO (x = 3, ICSD 160655 but Li on 16c).
2.2 NMR spectroscopy
All NMR measurements were recorded on a Bruker AVANCE III HD 400 spectrometer at a 7Li frequency of ω0/2π = 155.5 MHz.SAE NMR employs the Jeener–Broekaert pulse sequence β1 − tp − β2 − tm − β3 − td, where β represents radio frequency pulses, tp is the evolution time, tm the mixing time and td the detection transient.43 It results in an echo with an intensity relative to the correlation between the quadrupolar precession frequency ωQ during the evolution time and during the detection transient at time tm later. A correlation function can be mapped directly by repeating this sequence with variable tm if the correlation time constant, τC, is shorter than the spin–lattice relaxation with time constant T1, the decay of quadrupolar order with time constant T1Q, and temperature-independent spin diffusion processes.27 SAE NMR measurements of stoichiometric and overlithiated LTO were recorded at different temperatures between 10 °C and 45 °C using a 32 step phase cycle44 and a fixed evolution time tp of 10 μs. A saturation pulse train and a suitable delay time were used between measurements to ensure consistent initial conditions. In all the experiments with a static sample, 90°-pulse lengths were around 6.5 μs. The sample temperature was controlled by a Bruker BCU-20 cooling unit and was recorded using a Bruker B-SVT system. The temperature was stable within ±1 K. The reported temperatures are averaged values over the experiment time.
T1 of the overlithiated samples was measured spectrally resolved using the saturation recovery (SR) experiment with magic angle sample spinning (MAS). For this experiment the 90°-pulse duration was 1.1 μs and the 1.3 mm rotor was set to a speed of 65 kHz. The sample temperature was controlled with a flow of heated nitrogen.
2.3 NMR data analysis
A distribution of τC from SAE experiments and of T1 from SR experiments is obtained using regularized inversion with UP regularization in combination with a penalty for zero crossing of the density function to prevent it from exhibiting unnecessary oscillations by minimizing the number of sign changes. At the same time, neither sign of the density function amplitude is preferred over the other.41The spectral NMR information contained in the SAE13 and in the SR experiments are obtained by Fourier transformation of the transient echo signal and the free induction decay, respectively. Since a spectral density in the inverted dimension is determined from the echo decay as a function of tm rather than fitting a particular τC or T1 to the data, the NMR spectrum corresponding to different τC and T1 can be obtained in a second dimension that is contained in the transiently recorded data already. This facilitates the independent mobility characterization of ions in different lattice sites or with different local environments whose spectrum and correlation time both vary considerably. Although the data is inverted in one dimension only, the full two-dimensional data set for T1 and the full three-dimensional data set for τC are used when performing the regularized inversion. In the spectral and in the (inverse) temperature dimension, a unity kernel is employed, hence regularization acts as a smoothing filter along the non-inverted dimensions. The advantage compared to the application of smoothing after inversion of independent one-dimensional data sets is that an algorithm acting on multi-dimensional data leads to potentially narrower features along the inverted dimension since the sensitivity-enhancing smoothing is performed simultaneously with data inversion.45
The regularization parameters for the inversion have been chosen as detailed in ref. 41.
2.4 Computational details of DFT simulations
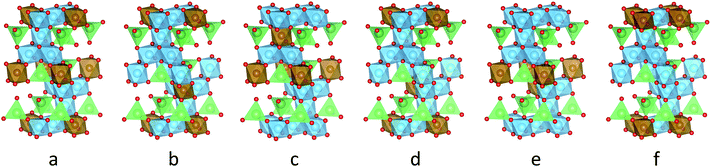
To approximate the occupational disorder of Li4Ti5O12, the stoichiometric representation Li8Ti10O24 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) was studied. All possible occupations of the unit cell reduce to six symmetry-inequivalent structures similar in total energy, shown in Fig. 1. The geometry of the six unit cells was optimized with CASTEP 7.01 (ref. 46) using the default ultra-soft, on-the-fly-generated pseudo-potentials and the PBE exchange–correlation functional. The forces were converged to 3 meV with a cut-off energy of 600 eV and a k-point grid of 4 × 4 × 2.
m) was studied. All possible occupations of the unit cell reduce to six symmetry-inequivalent structures similar in total energy, shown in Fig. 1. The geometry of the six unit cells was optimized with CASTEP 7.01 (ref. 46) using the default ultra-soft, on-the-fly-generated pseudo-potentials and the PBE exchange–correlation functional. The forces were converged to 3 meV with a cut-off energy of 600 eV and a k-point grid of 4 × 4 × 2.
The quadrupolar coupling constants CQ for the optimized geometries were calculated with CASTEP 8.0,46 the default ultra-soft, on-the-fly-generated pseudo-potentials, and the LDA exchange–correlation functional. For the structure with minimum energy (supercell a), the convergence criterion of 0.1 kHz for CQ was met with a cut-off energy of 1.3 keV and a k-point grid of 8 × 8 × 4, which was adopted for the calculation of the CQ of the other LTO unit cells. Modifications in the pseudo-potentials (especially in the Li pseudo-potential) resulted in changes of up to 25 kHz for the absolute value of CQ in supercell a, whereas the replacement of the LDA exchange–correlation functional with PBE only yielded negligible changes of up to 0.5 kHz.
3 Results
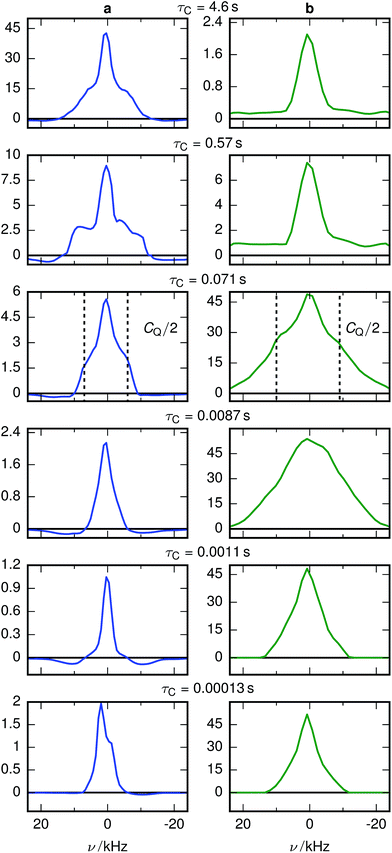
The X-ray diffractograms of the prepared samples (Fig. 2a) are consistent with literature.17,22 While they do not allow a quantification of Li content, they are qualitatively in agreement with simulations as I311/I111 increases, I400/I111 decreases and I220 almost disappears with overlithiation. The average grain sizes of the product as well as the educt are below 100 nm (Fig. 2b) with different crystallite orientations per grain (Fig. 2c).Fig. 3 shows the spectrally resolved density of the SAE correlation time constant τC at different temperatures. Individual spectra for selected τC are shown in Fig. 4.
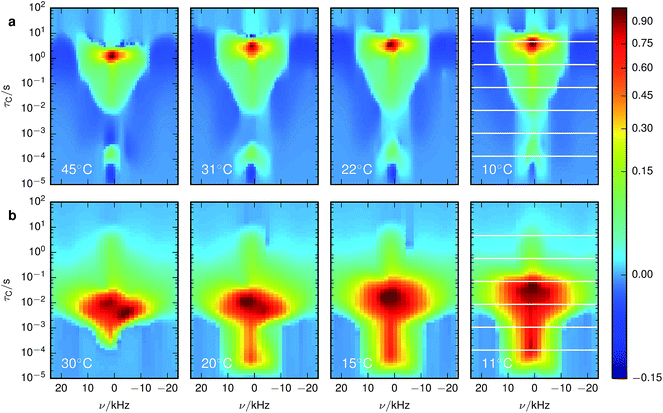 | ||
| Fig. 3 Inversion of 7Li SAE spectra recorded at different temperatures for (a) stoichiometric and (b) overlithiated LTO. The plots show the density of the correlation time τC from relatively fast processes (small τC) to very slow processes (large τC). The spectral dimension facilitates the individual NMR lineshape analysis of Li species with different mobilities. The white lines in the lowest temperature figures identify the slices shown in Fig. 4. | ||
3.1 Stoichiometric LTO
For stoichiometric LTO (Fig. 3a) the pattern of the spectrally resolved correlation time density is similar at all temperatures. However, a temperature increase does not lead to a simple shift of these patterns, as would be expected for dynamic processes following an Arrhenius law with a single Ea.12 Instead, fast processes are almost temperature independent, indicating a small Ea, while temperature dependence is increasing for slower processes, suggesting a higher Ea.Signal components with a negative amplitude, which proved to be necessary for an accurate fit of the data, can be observed at τC ≈ 10 μs and off-center in the spectral dimension on both sides of the main signal components along the whole τC axis. The former might result from spin–spin (T2) relaxation effects, allowing unwanted coherences to contribute to the NMR signal.44 Hence the signal decay may contain some Gaussian contribution. Inverting a Gaussian function with an exponential kernel leads to signal contributions with negative amplitude. The origin of the latter component cannot be identified unequivocally. One possibility could be relaxation induced violations of coherence transfer selection rules, which could lead to such negative amplitudes on either side of a resonance.47
The change of the spectral features as a function of τC is quite pronounced. Although broadened, the spectra display the pattern expected for quadrupolar interactions of a spin 3/2 nucleus (Fig. 4a). With the exception of the fastest correlation times probed, the width of these features exceeds τC−1, hence it is unlikely that processes exhibiting a correlation time τC are the cause for this line narrowing. We can thus assume that the width of the spectra represents the averaged magnitude of the EFG seen by the signal-inducing nuclei and that an estimate of the quadrupolar interaction is possible. Since no reference data of quadrupolar coupling constants of 7Li ions in LTO are available, ab initio calculations were performed to estimate EFG values at lattice sites occupied by Li+. Because such a calculation needs to consider the stochastic occupancy of the 16d sites in LTO even in the absence of defects, a set of supercells with systematic variation of Li and Ti on 16d sites has been utilized (Fig. 1). Simulated CQ values for the six different unit cells are summarized in Table 1.
| Li position | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 8a | 61.3 | 62.7 | 14.4 | 46.6 | 285.4 | 280.6 |
| 8a | 61.3 | 95.1 | 207.0 | 118.5 | 18.5 | 280.6 |
| 8a | 16.2 | 95.1 | 204.8 | 118.7 | 288.1 | 14.6 |
| 8a | 84.2 | 61.3 | 12.1 | 46.2 | 300.8 | 350.2 |
| 8a | 83.7 | 160.3 | 238.8 | 146.9 | 32.0 | 350.6 |
| 8a | 16.0 | 160.2 | 237.3 | 146.7 | 277.9 | 14.6 |
| 16d | 34.1 | 71.5 | 36.2 | 54.1 | 99.2 | 145.0 |
| 16d | 70.7 | 67.8 | 33.3 | 54.3 | 68.6 | 144.9 |
3.2 Overlithiated LTO
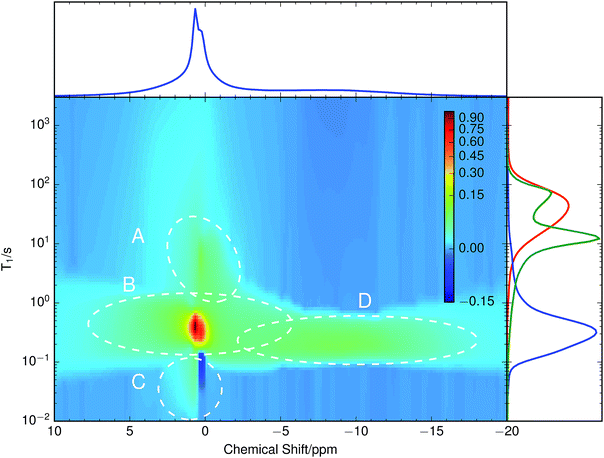
A chemically overlithiated sample was used to study the impact of electronic defects, such as polaronic Ti3+ states, on the Li mobility in LTO. In Fig. 3b the correlation between τC and the static NMR spectrum is shown for overlithiated LTO. The general trends and patterns are similar to the stoichiometric LTO, but τC of the dominant signal components are about two orders of magnitude shorter and the spectra are considerably broader. A quadrupolar origin of the line broadening is supported by the shape of the spectra, which again show – albeit additionally broadened – features as expected for static quadrupolar spectra of spin 3/2 nuclei (Fig. 4b).It can be seen that a fraction of the overlithiated LTO shows a signal with similar τC as the stoichiometric LTO. This is expected for two-phase formation upon overlithiation.14–16 However, the signal fraction exhibiting such a reduced mobility in overlithiated LTO is smaller than the fraction of stoichiometric LTO if a strict two-phase separation according to Li4+xTi5O12 = (1 − x/3)Li4Ti5O12 + (x/3)Li7Ti5O12 is assumed.22 To distinguish different resonances, the spectrally resolved distribution of spin–lattice relaxation times T1 of overlithiated LTO using an SR experiment with MAS was determined (Fig. 5). Two different spectral features are observed: a set of poorly resolved resonances with different T1 at about 0 ppm (regions A–C) and a broad line centered at about −10 ppm (region D). The frequencies of the former are overlapping with the resonances observed in stoichiometric LTO.19 The latter is due to the presence of paramagnetic Ti3+.48 The spectral separation is likely caused by the formation of different phases rather than a solid solution upon chemical overlithiation. This is in agreement with microscopy results,15 where clear boundaries between overlithiated and stoichiometric phases were observed. Nonetheless, both signals show a short relaxation component for 100 ms ≲ T1 ≲ 1 s (regions B and D). This is considerably shorter than T1 of stoichiometric LTO, whose projected distribution is shown in Fig. 5, and is indicative of Li ions in the vicinity of paramagnetic Ti3+.
The resonances at 0 ppm show additional clearly distinguished relaxation components. The one at T1 ≈ 10 s (region A), which is only moderately reduced compared to T1 of stoichiometric LTO, could be explained by some Li+ exchange with overlithiated phases, yet considerably reduced compared to the above-mentioned component with fast T1. Alternatively, such an increase could be caused by a variation of Li ion mobility, without the presence of paramagnetic centers in the region sampled by a Li ion. Either way, the reduction of T1 shows that these phases are not macroscopically separated due to non-uniform sample overlithiation, which would cause a contribution with identical T1 as in stoichiometric LTO. It also indicates that there is some heterogeneity in the distribution of mobility or size of the phases, otherwise a continuous distribution of T1 would be expected. Finally, the component at T1 ≈ 20 ms (region C) is rather unusual. It does not show a considerable chemical shift, and it is in the immediate neighborhood of a peak with negative sign. It is likely that both peaks are caused by exchange, since we know from the SAE that corresponding mobility processes are taking place.
Overlithiation in the limit of small x was probed using a sample with x ≈ 0.2. This sample does not show a feature around −10 ppm and the resonances around 0 ppm are much narrower than for x ≈ 1.6 and even slighty narrower than for x = 0, consistent with data shown by Schmidt et al.13 Its T1 distribution, shown in the side panel of Fig. 5 (green curve) consists of two clearly separated peaks at T1 ≈ 80 s and T1 ≈ 10 s as well as a long, low tail towards shorter relaxation times. The peak at longer T1 coincides with the long T1 edge of the stoichiometric LTO. The peak with shorter T1 is somewhat reduced compared to the edge at short T1 of the stoichiometric LTO, which would be consistent with a T1 reduction due to accelerated motion,13 but not with the considerable relaxivity enhancement induced by paramagnetic Ti3+. This latter effect is likely responsible for the long, weak tail towards short T1, which shows the onset of the features observed for the quickly relaxing signals (including the negative signal in region C) of the sample with x ≈ 1.6.
4 Discussion
4.1 Mobility modes of Li ions
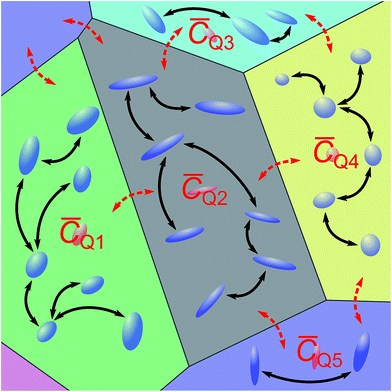
Experimentally observed (∼10–40 kHz) and theoretically simulated (∼20–300 kHz) CQ values differ by a factor of between two and eight. Even though the first-principles simulated values show a rather large methodical error of up to 25 kHz, the differences cannot be attributed to this methodical error alone. In particular, the simulated values systematically overestimate experimental values. In contrast to the common way of interpretation, the experimentally observed CQ might not result from microscopic, local EFGs on individual Li sites. Instead, consistent with molecular dynamics simulations,19 this suggests microscopic Li hopping between a limited number of sites on a much shorter timescale than the experimentally accessible timescale of ∼10−5 s, causing a partial, anisotropic averaging of the individual EFGs. This results in an experimentally observed residual quadrupolar coupling,49–51 which is illustrated in Fig. 6. Notice that at τC ≳ 10 s the spectrum gets considerably broader, more consistent with the values obtained for CQ from simulations. Considering the distribution of the spin–lattice relaxation time constant T1 shown in the side panel of Fig. 5, it is likely that this signal contribution with long τC is caused by immobile Li ions that are relaxing with the relaxation time constant of quadrupolar order, T1Q ≈ T1/3, in an SAE experiment.28Similar averaging effects, yet more pronounced due to the observed sharp quadrupolar pattern, have been found for fast ionic conductors.52 For LTO, this implies that to quantify ion mobility, two intrinsically different influences need to be considered – fast local mobility leading to the observation of residual quadrupolar coupling, and slower long-range mobility over larger distances between local domains, which gets probed by SAE NMR.
Since isotropic chemical shifts of Li in diamagnetic environments are distributed over a frequency range that is considerably narrower than typical values of CQ, such fast local mobility that causes a narrowing of quadrupolar patterns would also lead to an averaging of the isotropic chemical shift among the sites that form a local mobility domain in an experiment with MAS. Hence the conventional interpretation of isotropic6,7Li chemical shifts of LTO in terms of static Li occupancy of certain crystallographic sites20,22,53 could be incomplete or even unsuitable, and discrepancies of site populations between NMR and other techniques would be a consequence.19
4.2 Incorporation of additional Li by overlithiation
The observed differences in the SAE NMR spectrum between the stoichiometric and the overlithiated LTO sample (Fig. 3 and 4) arise from the presence of paramagnetic centers generated upon incorporation of additional Li+ into LTO, which is charge-compensated primarily by reduction of diamagnetic Ti4+ to paramagnetic Ti3+. A high local concentration of Ti3+ ions causes a paramagnetic shift or a Knight shift and induces a considerable line broadening due to reduced T2 relaxation time constants.48 Furthermore, both Ti3+ as well as the additionally incorporated Li+ could change the EFG with a corresponding alteration of CQ. The increased mobility of Li ions in the overlithiated LTO, which is reflected by the reduced τC, can be linked directly with their vicinity to reduced Ti3+ centers. Notice that τC for overlithiated LTO may also be affected by polaronic hopping of an electron between Ti ions rather than motion of the Li ion itself. Hence care must be taken when attempting a quantitative analysis of SAE experiments with potentially non-stationary paramagnetic centers.A possible explanation for the increased average EFG probed by CQ could be the presence of the additionally incorporated Li ions and a shorter average distance to the titanium due to a smaller repulsion caused by the reduced nominal Ti charge. This makes it easier for Li to approach Ti ions, thereby also speeding up ion transport. Alternatively, an increased average EFG may also be caused by smaller local domains, which would show poorer averaging.
A trend observed for stoichiometric as well as overlithiated LTO is the triangular shape of the spectrally resolved τC pattern, which is narrowing towards shorter τC. Assuming that better averaging of the quadrupolar interaction is obtained for locally sampled domains with a larger number of sites, then this pattern would indicate that local mobility dispersed over more sites also causes faster motion between different domains. In other words, the more restricted the local mobility, the slower is the global mobility. An explanation could be that larger local domains also offer more anchors for jumps out of a domain. With more available jumping targets, i.e. Li vacancies or interstitial sites, the probability of a jump increases and τC decreases, as observed. Alternatively, such an improved averaging could also be explained by poorer ordering within local domains, causing smaller residual quadrupolar couplings.
In the T1 distribution shown in Fig. 5, region B is clearly affected by paramagnetic centers, which would contradict the two-phase model. A possible explanation could be densely entangled overlithiated and stoichiometric phases of small dimensions, which is consistent with data showing an exchange time constant of τ ≈ 2 ms between the resonances.22 This is two to three orders of magnitude shorter than T1 found in the distribution. Hence an equalization of T1 is realistic for the majority of the two phases. An alternative interpretation could be a displacement of phase boundaries by simultaneous Li motion and polaronic electron hopping between neighboring Ti ions. However, such a model is incompatible with an observation of two-phase separation by microscopy techniques,15 which requires a much longer lifetime for phase boundaries to be detectable.
An explanation for the apparent discrepancy with results in the literature that suggest the formation of a solid solution upon overlithiation13 can be deduced from the T1 experiment with the sample at x ≈ 0.2. In this case only a very minor fraction of the Li is influenced by Ti3+, while a considerable fraction appears to show a slightly accelerated T1 that would be consistent with an increased Li ion mobility. If charge of the additionally incorporated Li+ ions is not compensated by reduction of Ti4+ to Ti3+, then it is conceivable that in the early stages of overlithiation the additional Li may be charge-compensated by removing oxygen atoms close to the grain surfaces. Since LTO is not an oxygen conductor at room temperature, initially a core–shell structure would be formed with the additional Li incorporated in the shell, possibly in the form of a solid solution. Ti4+ reduction would set in as soon as the surface regions of the LTO are oxygen depleted, leading to the two-phase configuration suggested above. From the overlap of T1 of region A in Fig. 5 and the slightly accelerated T1 component of the sample with x ≈ 0.2, it seems possible that such a core–shell configuration, but with a considerably reduced shell volume, is maintained in the sample with x ≈ 1.6. To quantitatively understand the evolution of the T1 distribution, further experiments with a larger number of different overlithiation steps and a direct quantification of Ti3+ by electron paramagnetic resonance10 will be necessary.
5 Conclusions
A novel analysis technique for the inversion of solid-state NMR relaxation and SAE data was used to qualitatively study the mobility of Li ions in stoichiometric and chemically overlithiated LTO. Such an analysis facilitates, in analogy to established liquid-state NMR techniques, the separation of static or MAS NMR spectra into different components according to their T1 or their τC. By employing an algorithm that does not depend on a non-negativity constraint, it is not necessary to assume that, for example, no exchange is taking place between different signal contributions. For the datasets shown in this work, the negative components proved to be necessary for a good fit to the experimental data. Although this method cannot be implemented as computationally efficient as the non-negativity constrained Tikhonov regularization,36 it is still possible to use it for two- and even three-dimensional inversion problems.For LTO it was found that the 7Li NMR spectra show a pronounced τC dependence. From the discrepancy between experimentally observed quadrupolar couplings and numerical simulations it was concluded that fast local mobility of lithium ions between a limited number of sites is taking place and that the observed coupling constants represent residual quadrupolar couplings. Such a hypothesis also implies that resonances at different isotropic chemical shifts, as observed by MAS NMR experiments, may not be caused by static occupation of certain crystallographic sites. Furthermore, this means that SAE NMR is not suitable to directly quantify long-range ion motion in LTO as long as the size of the local domains is not known. Even NMR relaxation time measurements need to be assessed critically for their suitability for such a quantification, since multiple relaxation modes can be expected, which are potentially difficult to disentangle or for which it is not necessarily clear whether relaxation is dominated by long-range or short-range motion. However, effective parameters from NMR relaxation or SAE experiments may be well suited to compare differently synthesized samples of the same material or systematic material variations, for example by doping or variation of the stoichiometry.
Different contributions to the spectrally resolved SAE distribution show different temperature dependence, hence Li mobility cannot be described by a single activation energy or a small number of activation energies for jumps between particular crystallographic sites. Instead it is necessary to consider the stochastically occupied local environment of ions, as was predicted theoretically by DFT simulations.32 Our results indicate that it is not sufficient to simulate unit cells or small supercells with periodic boundary conditions accessible by DFT calculations, but that an intrinsically multiscalar simulation approach is required to cover local domains showing enhanced Li mobility as well as jumps between such domains.
For a more conclusive interpretation of the observed chemical shift values and time constant distributions, a refinement of simulations as well as additional spectroscopic and imaging experiments will be needed. In particular, atomistic as well as systematically coarse-grained simulations capable of capturing the essential dynamical processes of extended sample volumes appear promising, since the observed features in the relaxation time distribution indicate that relevant volume sizes even for the description of the two-phase behavior of overlithiated LTO could be within reach of current multiscale simulation methods. Preliminary results from simple kinetic Monte Carlo simulations with a single rate constant32 and randomized quadrupolar frequency distribution support the hypothesis of an averaging process on a timescale smaller than experimentally accessible (approx. 10−5 s). Expanding the configurations (Fig. 1) sampled for quadrupolar frequencies by Li-16c defect structures results in a kinetically averaged CQ much closer to experimental values.
Acknowledgements
We are grateful to Dr Peter Jakes and Steffen Kayser, M.Sc. of Forschungszentrum Jülich, Andreas Garhammer, B.Sc. and Hendrik Heenen, M.Sc. of Technische Universität München, and Dr Saskia Stegmaier of SUNCAT, SLAC for their technical assistance and fruitful discussions. Funding from the German Federal Ministry of Education and Research (BMBF project DESIREE, grant number 03SF0477A) is gratefully acknowledged.References
- M. V. Reddy, G. V. Subba Rao and B. V. R. Chowdari, Chem. Rev., 2013, 113, 5364–5457 CrossRef CAS PubMed.
- X. Sun, P. V. Radovanovic and B. Cui, New J. Chem., 2015, 39, 38–63 RSC.
- Z. Yang, D. Choi, S. Kerisit, K. M. Rosso, D. Wang, J. Zhang, G. Graff and J. Liu, J. Power Sources, 2009, 192, 588–598 CrossRef CAS.
- C. Sandhya, B. John and C. Gouri, Ionics, 2014, 20, 601–620 CrossRef CAS.
- C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef CAS PubMed.
- A. Deschanvres, B. Raveau and Z. Sekkal, Mater. Res. Bull., 1971, 6, 699–704 CrossRef CAS.
- Y.-B. He, M. Liu, Z.-D. Huang, B. Zhang, Y. Yu, B. Li, F. Kang and J.-K. Kim, J. Power Sources, 2013, 239, 269–276 CrossRef CAS.
- Z. Chen, I. Belharouak, Y.-K. Sun and K. Amine, Adv. Funct. Mater., 2012, 23, 959–969 CrossRef.
- T. Ohzuku, A. Ueda and N. Yamamoto, J. Electrochem. Soc., 1995, 142, 1431–1435 CrossRef CAS.
- P. Jakes, J. Granwehr, H. Kungl and R.-A. Eichel, Z. Phys. Chem., 2015, 229, 1439–1450 CrossRef CAS.
- I. Leonidov, O. Leonidova, L. Perelyaeva, R. Samigullina, S. Kovyazina and M. Patrakeev, Phys. Solid State, 2003, 45, 2183–2188 CrossRef CAS.
- M. Wilkening, R. Amade, W. Iwaniak and P. Heitjans, Phys. Chem. Chem. Phys., 2007, 9, 1239 RSC.
- W. Schmidt, P. Bottke, M. Sternad, P. Gollob, V. Hennige and M. Wilkening, Chem. Mater., 2015, 27, 1740–1750 CrossRef CAS.
- S. Scharner, W. Weppner and P. Schmid-Beurmann, J. Electrochem. Soc., 1999, 146, 857–861 CrossRef CAS.
- M. Kitta, T. Akita, S. Tanaka and M. Kohyama, J. Power Sources, 2014, 257, 120–125 CrossRef CAS.
- D. Safronov, S. Novikova, A. Skundin and A. Yaroslavtsev, Inorg. Mater., 2012, 48, 57–61 CrossRef CAS.
- L. Aldon, P. Kubiak, M. Womes, J. Jumas, J. Olivier-Fourcade, J. Tirado, J. Corredor and C. Pérez Vicente, Chem. Mater., 2004, 16, 5721–5725 CrossRef CAS.
- J. Qiu, C. Lai, E. Gray, S. Li, S. Qiu, E. Strounina, C. Sun, H. Zhao and S. Zhang, J. Mater. Chem. A, 2014, 2, 6353–6358 CAS.
- M. Vijayakumar, S. Kerisit, K. M. Rosso, S. D. Burton, J. A. Sears, Z. Yang, G. L. Graff, J. Liu and J. Hu, J. Power Sources, 2011, 196, 2211–2220 CrossRef CAS.
- P. Krtil, J. Dědeček, T. Kostlánová and J. Brus, Electrochem. Solid-State Lett., 2004, 7, A163–A166 CrossRef CAS.
- W. Schmidt and M. Wilkening, J. Phys. Chem. C, 2016, 120, 11372–11381 CAS.
- H. Hain, M. Scheuermann, R. Heinzmann, L. Wünsche, H. Hahn and S. Indris, Solid State Nucl. Magn. Reson., 2012, 42, 9–16 CrossRef CAS PubMed.
- W. K. Pang, V. K. Peterson, N. Sharma, J.-J. Shiu and S.-h. Wu, Chem. Mater., 2014, 26, 2318–2326 CrossRef CAS.
- X. Lu, L. Gu, Y.-S. Hu, H.-C. Chiu, H. Li, G. P. Demopoulos and L. Chen, J. Am. Chem. Soc., 2015, 137, 1581–1586 CrossRef CAS PubMed.
- A. Laumann, H. Boysen, M. Bremholm, K. T. Fehr, M. Hoelzel and M. Holzapfel, Chem. Mater., 2011, 23, 2753–2759 CrossRef CAS.
- N. Takami, K. Hoshina and H. Inagaki, J. Electrochem. Soc., 2011, 158, A725–A730 CrossRef CAS.
- A. Kuhn, V. Epp, G. Schmidt, S. Narayanan, V. Thangadurai and M. Wilkening, J. Phys.: Condens. Matter, 2012, 24, 035901 CrossRef CAS PubMed.
- R. Böhmer, K. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87–174 CrossRef.
- Ģ. Vītiņš, G. Ķizāne, A. Lūsis and J. Tīliks, J. Solid State Electrochem., 2002, 6, 311–319 CrossRef.
- B. Ruprecht, M. Wilkening, R. Uecker and P. Heitjans, Phys. Chem. Chem. Phys., 2012, 14, 11974 RSC.
- M. Vijayakumar, S. Kerisit, Z. Yang, G. L. Graff, J. Liu, J. A. Sears, S. D. Burton, K. M. Rosso and J. Hu, J. Phys. Chem. C, 2009, 113, 20108–20116 CAS.
- B. Ziebarth, M. Klinsmann, T. Eckl and C. Elsässer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174301 CrossRef.
- G. Borgia, R. Brown and P. Fantazzini, J. Magn. Reson., 1998, 132, 65–77 CrossRef CAS PubMed.
- P. T. Callaghan, C. H. Arns, P. Galvosas, M. W. Hunter, Y. Qiao and K. E. Washburn, Magn. Reson. Imaging, 2007, 25, 441–444 CrossRef PubMed.
- A. Lupulescu, M. Kotecha and L. Frydman, J. Am. Chem. Soc., 2003, 125, 3376–3383 CrossRef CAS PubMed.
- L. Venkataramanan, Y. Song and M. Hurlimann, IEEE Trans. Acoust., Speech, Signal Process., 2002, 50, 1017–1026 CrossRef.
- G. Bodenhausen and R. R. Ernst, Mol. Phys., 1982, 47, 319–328 CrossRef CAS.
- S. Rodts and D. Bytchenkoff, J. Magn. Reson., 2010, 205, 315–318 CrossRef CAS PubMed.
- P. Fantazzini, F. Galassi, V. Bortolotti, R. Brown and F. Vittur, New J. Phys., 2011, 13, 065007 CrossRef.
- Y.-Q. Song, G. Carneiro, L. M. Schwartz and D. L. Johnson, Phys. Rev. Lett., 2014, 113, 235503 CrossRef PubMed.
- J. Granwehr and P. J. Roberts, J. Chem. Theory Comput., 2012, 8, 3473–3482 CrossRef CAS PubMed.
- W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301–303 CrossRef CAS.
- J. Jeener and P. Broekaert, Phys. Rev., 1967, 157, 232–240 CrossRef CAS.
- F. Qi, G. Diezemann, H. Böhm, J. Lambert and R. Böhmer, J. Magn. Reson., 2004, 169, 225–239 CrossRef CAS PubMed.
- M. Levitt, G. Bodenhausen and R. Ernst, J. Magn. Reson., 1984, 58, 462–472 CAS.
- S. Clark, M. Segall, C. Pickard, P. Hasnip, M. Probert, K. Refson and M. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- N. Müller, G. Bodenhausen and R. R. Ernst, J. Magn. Reson., 1987, 75, 297–334 Search PubMed.
- T. Kostlánová, J. Dědeček and P. Krtil, Electrochim. Acta, 2007, 52, 1847–1856 CrossRef.
- M. Vogel and E. Rössler, J. Magn. Reson., 2000, 147, 43–58 CrossRef CAS PubMed.
- M. Vogel, C. Brinkmann, H. Eckert and A. Heuer, Solid State Nucl. Magn. Reson., 2002, 22, 344–362 CrossRef CAS PubMed.
- S. C. Shekar, J. A. Tang and A. Jerschow, Concepts Magn. Reson., Part A, 2010, 36, 362–387 CrossRef.
- R. Bertermann and W. Müller-Warmuth, Z. Naturforsch., A: Phys. Sci., 1998, 53, 863–873 CAS.
- M. Wagemaker, E. R. H. van Eck, A. P. M. Kentgens and F. M. Mulder, J. Phys. Chem. B, 2009, 113, 224–230 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |