Graphene oxide and nanodiamond: same carboxylic groups, different complexation properties

Abstract

DFT calculations (PBE functional with the empirical correction by Grimme) were employed to explain why our attempts to coordinatively functionalize nanodiamond (ND) with tetraazamacrocyclic cations [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺, and to generate paramagnetic hybrid materials in this way, failed, contrary to the successful functionalization of graphene oxide (GO) reported previously (Appl. Surf. Sci., 2016, 371, 16–27). The explanation offered is based on the comparison of binding energies for low-spin (singlet) and high-spin (triplet) complexes of model carboxylate ions GO⁻ and ND⁻ with the two tetraazamacrocycles. The formation energies were interpreted in terms of ΔΔE₃₋₁ values, which characterize the difference in stability for the triplet and singlet complexes (negative values mean that triplet state is more stable, and positive, that singlet state is more stable). While the results obtained do not rule out completely the possibility of forming high-spin [Ni(cyclam)]²⁺ carboxylate derivatives on ND, in the case of [Ni(tet b)]²⁺ comparison of the ΔΔE₃₋₁ values explicitly demonstrated that the formation of high-spin complex is highly unfavorable with ND⁻ contrary to GO⁻ model: ΔΔE₃₋₁ values obtained are 13.22 and −4.64 kcal mol⁻¹, respectively. For comparison, similar data are presented for a series of simpler carboxylates. In addition to binding energies and ΔΔE₃₋₁ values, for all the systems studied we analyzed Ni–O distances, spin density plots and HOMO−LUMO parameters.

---

1. Introduction

Chemical functionalization is widely used to modify electronic and magnetic characteristics of carbon nanomaterials, including carbon nanotubes (CNTs), nanodiamond (ND), graphene and graphene oxide (GO). In particular, in the case of graphene and related materials, it is considered important for the design of new solar energy conversion systems, sensors, photoluminescent, nanoelectronic and spintronic devices, contrast agents for biomedical imaging, efficient heterogeneous catalysts, among others.^1–7 Azamacrocyclic ligands (usually porphyrins and phthalocyanins) and their transition metal complexes are among most important functionalizing reagents, due to the following two factors: (1) their electronic structure, magnetic, spectroscopic and redox properties can be adjusted by changing the central metal ion; (2) macrocyclic structure of the ligands implies superior stability of their complexes, preventing potential leakage of the metal ion. To attach macrocyclic molecules to graphene and GO, a broad spectrum of interactions can be employed, from amide or other covalent bonding to noncovalent (π–π stacking and van der Waals) and electrostatic interactions.^{1,2,4–6,8–16} The existence of carboxylic groups is an especially attractive property of GO, since it allows not only for the covalent functionalization through amide linkage with amino-substituted azamacrocycles,^1,2,4,10 but also offers the possibility of complexation between the oxygen-containing groups and coordinatively unsaturated central metal atoms of macrocyclic complexes.^17,18

Graphene and GO nanohybrids functionalized with tetraazamacrocyclic complexes possessing magnetic properties are materials of special interest, mainly from the point of view of organic spin electronic (or spintronic) devices. The disadvantages of depositing single magnetic metal atoms on surfaces is that they tend to coalesce (aggregate) without forming regular patterns, as well as can exhibit a decreased magnetic response due to the interaction with support surface.¹⁹ On the other hand, when magnetic metal atoms are deposited in the form of complexes with organic ligands, magnetic nanohybrids with regular and stable networks of magnetic units can be obtained. Different combinations of organic ligands and paramagnetic central metal ions were shown to be useful for their fabrication, from the complexes with relatively simple bidentate and tridentate ligands^20,21 to those with tetraazamacrocyclic porphyrin^12,22–24 and phthalocyanine ligands,^19,25–27 where most commonly employed complexes incorporate 3d metal atoms such as iron(II)^19,23,25,26 and cobalt(II).^22,24

Among other possible application areas for graphene and GO-supported magnetic tetraazamacrocyclic complexes, one can mention magnetic resonance imaging (MRI). For example, Hung et al.²⁸ performed GO functionalization through noncovalent attachment of gadolinium(III) complexes with a series of fifteen substituted saturated tetraazamacrocyclic ligands, in order to enhance the contrast properties of Gd(III) ions for cellular MRI.

One should emphasize that all the research reports mentioned above employ the same, rather straightforward strategy, in which functionalizing complex molecules already possess magnetic properties due to paramagnetic central metal ions: in other words, graphene or GO-based magnetic materials are obtained by combining a paramagnetic complex with a diamagnetic support. Nevertheless, this is not the only approach possible. As we recently suggested,²⁹ there is a possibility to in situ generate magnetic properties in GO hybrids by using some diamagnetic tetraazamacrocyclic complexes of 3d transition metal ions such as nickel(II). The ligands suitable for this purpose include saturated 14-membered tetraazamacrocycles, which can be exemplified by 1,4,8,11-tetraazacyclotetradecane and rac-5,5,7,12,12,14-hexamethyl-1,4,8,11-tetraazacyclotetradecane, commonly called for simplicity cyclam and tet b, respectively (see review³⁰ and literature cited therein). Conformational flexibility of the saturated tetraazamacrocyclic ligands makes their transition metal complexes very different from rigid planar hyperconjugated porphyrin and phthalocyanine analogues. In particular, the unique property of Ni(II) complexes with cyclam and tet b, important in the present context, is that low-spin square-planar cations [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ in basic media can additionally coordinate carboxylate ions as bidentate ligands, thus transforming into high-spin pseudooctahedral complexes (Scheme 1), in which the macrocycle adopts a folded conformation.^30–33

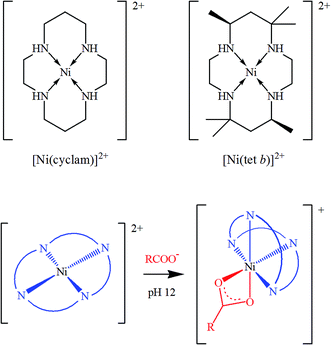Scheme 1 Low-spin square planar tetraazamacrocyclic complexes of Ni(II) (top) and their conversion into respective high-spin octahedral carboxylates (bottom).

Given the fact that carboxyls are among dominating functional groups in GO, it seems logical to expect that they are capable of coordinating to [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ square-planar tetraazamacrocyclic cations. This motivated us²⁹ to test a novel approach to GO functionalization, which would allow for facile generation of a paramagnetic material by combining two diamagnetic components. Indeed, we found that the coordination coupling can be easily performed under basic conditions in a water–ethanol mixture, without the need for high temperatures and/or other harsh conditions and reagents. The conversion of Ni(II) coordination geometry from square-planar tetracoordinated to pseudooctahedral hexacoordinated one resulted in the change from low-spin to high-spin state of nickel ions. The content of tetraazamacrocyclic complexes in functionalized GO samples turned to be rather low (Ni content of about 1 wt%), nevertheless, magnetic susceptibility measurements easily confirmed the generation of paramagnetic properties in both nanohybrids.

Despite of some evident (especially morphological) differences, another carbon nanomaterial, nanodiamond, has much in common with GO. ND has rather complex structure including a diamond core composed of sp³-hybridized carbon atoms, a fullerene-like shell of sp²-hybridized C atoms, and finally an outer surface in which carbon atoms form a variety of oxygenated functional groups. Like in the case of GO, carboxylic functionalities are found among the most abundant groups identified on ND surface, and therefore, it is not surprising that the functionalization of ND^34–40 is based on essentially the same chemical strategies and protocols as those employed for GO.

Based on the above general considerations, we attempted coordination functionalization of ND with the same [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ tetraazamacrocyclic cations, under the same conditions as in the case of GO.²⁹ Nevertheless, the results were frustrating, since despite of the presence of small amounts of Ni detected by traditional elemental analysis and energy dispersive X-ray spectroscopy, other analytical data (in particular, those of thermogravimetric analysis, infrared and X-ray photoelectron spectroscopy) turned to be unconvincing. And, what is especially important, magnetic susceptibility measurements suggested that the ND samples remain diamagnetic. The conclusion is unambiguous: for some reason, low-spin square-planar cations [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ are unable to coordinate to COOH groups of ND and thus to form high-spin pseudooctahedral complexes.

The differences in topology of GO sheet edges and ND particle surfaces, and therefore in spatial accessibility of COOH groups for their complexation with the tetraazamacrocyclic cations, seemed to us the most likely explanation. Accordingly, the goal of the present theoretical work was to verify whether such steric factors indeed exist.

2. Theoretical calculations

The theoretical analysis of geometries and energies of tetraazamacrocycle–carboxylate complexes and their components was performed in the frame of density functional theory (DFT). For all the calculations, we used the numerical-based DFT module DMol3, which forms part of the Materials Studio 6.0 software package (Accelrys Inc).^41–44 The computational methodology we chose was a general gradient approximation correlation functional by Perdew–Burke–Ernzerhof⁴⁵ (PBE) in conjunction with the empirical correction by Grimme⁴⁶ to account for dispersion effects. The double numerical basis set DNP⁴⁴ employed has a polarization d-function added on all non-hydrogen atoms and a polarization p-function added on all H atoms. This computational methodology was shown to be efficient for the description of noncovalent interactions between tetraazamacrocyclic compounds with different carbon nanoclusters (fullerenes, fulleroid nanotube models and oxidized graphene sheets).^29,47–49 Full geometry optimization and calculation of electronic parameters was performed with the following settings: ‘fine’ quality and convergence criteria, all-electron core treatment, a global orbital cutoff of 4.5 Å and Fermi orbital occupancy (no thermal smearing).

The formation energies ΔE_C+Ni for C + [Ni(cyclam)] and C + [Ni(tet b)] complexes were calculated by using the following formula:

ΔE_C+Ni = E_C+Ni − (E_Ni + E_C)

where E_C is the corresponding absolute energy for anionic carboxylate ligand (C = R–COO⁻), and E_Ni, for [Ni(cyclam)]²⁺ or [Ni(tet b)]²⁺ cations.

3. Results and discussion

3.1. Models

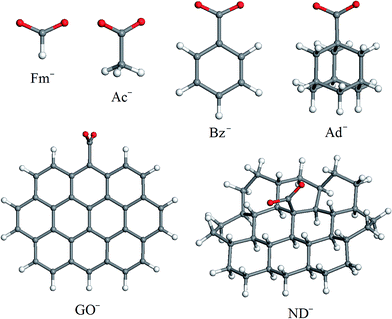
To investigate how steric factors influence the capability of carboxylic groups on carbon nanoparticles to coordinate [Ni(cyclam)]²⁺ or [Ni(tet b)]²⁺ cations, we found it necessary to analyze how the optimized geometries of coordination sphere and formation energies of high-spin tetraazamacrocycle–carboxylate complexes change upon the gradual increase of substituent R (Scheme 1). For this purpose, we selected a series of carboxylate anions shown in Fig. 1. The smallest carboxylate possible is formate (Fm⁻; R = H) followed by acetate (Ac⁻; R = CH₃). Since both GO and ND are essentially polycyclic hydrocarbon systems, the remaining carboxylate models included different types of cyclic fragments. The smallest one, structurally more related to GO, is benzoate (Bz⁻; R = C₆H₅). The next anion, structurally more related to ND, is 1-adamantanecarboxylate (Ad⁻). And finally, two models were necessary to simulate GO and ND. When choosing them, we bore in mind two considerations. First, these models have to match the most important topological differences of the two carbon nanomaterials: GO is composed of oxidized graphene sheets with COOH groups distributed predominantly on their edges, whereas in ND, carboxylic groups are situated on slightly convex (one can say, nearly flat) surface of a few-nanometer size primary particles. Second, the exact chemical environment of COOH groups in both GO and ND is impossible to know. Both models (GO⁻ and ND⁻, respectively; Fig. 1) of choice were based on ten fused ring system: in the case of GO⁻, all carbon atoms of the backbone have sp² hybridization state, whereas for ND⁻, they are sp³-hybridized. In the case of GO⁻, one COO⁻ group was placed at the graphene sheet edge, whereas in ND⁻ model, it was placed at the 'face'. Apart from one COO⁻ group, both models included only hydrogen atoms in order to fill dangling bonds.

Fig. 1 Optimized geometries of organic anions employed for DFT calculations: Fm⁻, formate; Ac⁻, acetate; Bz⁻, benzoate; Ad⁻, 1-adamantanecarboxylate; GO⁻, sp²-hybridized ten fused ring system with COO⁻ substituent at the edge simulating graphene oxide; ND⁻, sp³-hybridized ten fused ring system with COO⁻ substituent at the face simulating nanodiamond. Atom colors: grey, carbon; white, hydrogen; red, oxygen.

The main results presented in this work refer to the high-spin complexes of [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ cations with carboxylates. However, for comparison, we also performed the same set of calculations for low-spin (singlet) analogues of hexacoordinated tetraazamacrocycle–carboxylate complexes.

3.2. Energies of complexation

The calculated total energies for carboxylate components, tetraazamacrocyclic dications and the corresponding macrocycle-carboxylates in both low and high-spin states, along with formation energies ΔE for the latter complexes are presented in Table 1. One more important set of values which can be found here is the energies ΔΔE₃₋₁, which were calculated as the difference in ΔE values for the triplet and singlet states: when negative, triplet state is more stable, whereas positive value means that singlet state is more stable.

Table 1 Total energies (in Ha) for carboxylate components (Fm⁻, Ac⁻, Bz⁻, Ad⁻, GO⁻ and ND⁻),^a macrocyclic dications [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺, macrocycle–carboxylate complexes in both low^b and high-spin states,^c formation energies ΔE (in kcal mol⁻¹) for the complexes along with the respective HOMO, LUMO and HOMO–LUMO gap energies (in eV) and the Ni–O distances (in Å) between carboxylic O and central Ni atoms, calculated with PBE GGA functional with dispersion correction by Grimme, in conjunction with DNP basis set. ΔΔE₃₋₁ values (in kcal mol⁻¹) in parenthesis after formation energies mean the difference in ΔE values for the triplet and singlet states (if negative, triplet state is more stable; if positive, singlet state is more stable)

Compound	Etotal, Ha	ΔE (ΔΔE3−1), kcal mol^−1	EHOMO, eV	ELUMO, eV	Egap, eV	Ni–O distances, Å
a Fm^−, formate; Ac^−, acetate; Bz^−, benzoate; Ad^−, 1-adamantanecarboxylate.b In low-spin (singlet) complexes [Ni(cyclam)]^2+Fm^−, [Ni(cyclam)]^2+Ac^−, [Ni(cyclam)]^2+Bz^−, [Ni(cyclam)]^2+Ad^−, [Ni(cyclam)]^2+GO^−, [Ni(cyclam)]^2+ND^−, [Ni(tet b)]^2+Fm^−, [Ni(tet b)]^2+Ac^−, [Ni(tet b)]^2+Bz^− and [Ni(tet b)]^2+Ad^−, one of carboxylic O atoms fills the fifth coordination site of Ni atom; only in [Ni(tet b)]^2+GO^− and [Ni(tet b)]^2+ND^−, carboxylate anion does not enter the coordination sphere.c High-spin (triplet) complexes [Ni(cyclam)Fm]^+, [Ni(cyclam)Ac]^+, [Ni(cyclam)Bz]^+, [Ni(cyclam)Ad]^+, [Ni(cyclam)GO]^+, [Ni(cyclam)ND]^+, [Ni(tet b)Fm]^+, [Ni(tet b)Ac]^+, [Ni(tet b)Bz]^+, [Ni(tet b)Ad]^+, [Ni(tet b)GO]^+ and [Ni(tet b)ND]^+ acquire octahedral geometry of the coordination sphere.
Fm^−	−189.091514		0.740	6.308	5.568
Ac^−	−228.370008		0.830	5.970	5.140
Bz^−	−419.955009		−0.016	2.386	2.402
Ad^−	−578.277388		0.180	3.682	3.502
GO^−	−1414.877581		−1.459	−0.291	1.168
ND^−	−1433.961008		−0.582	3.048	3.630
[Ni(cyclam)]^2+	−2121.723230		−12.506	−10.319	2.187
[Ni(cyclam)]^2+Fm^−	−2311.119804	−191.43	−7.173	−6.019	1.154	2.014, 2.704
[Ni(cyclam)Fm]^+	−2311.134553	−200.68 (−9.25)	−7.505	−5.763	1.742	2.133, 2.171
[Ni(cyclam)]^2+Ac^−	−2350.404378	−195.24	−6.980	−5.837	1.143	2.023, 2.527
[Ni(cyclam)Ac]^+	−2350.420948	−205.64 (−10.40)	−7.339	−5.508	1.831	2.117, 2.147
[Ni(cyclam)]^2+Bz^−	−2541.978424	−188.37	−6.944	−5.777	1.167	2.011, 2.534
[Ni(cyclam)Bz]^+	−2541.994669	−198.56 (−10.19)	−7.271	−5.450	1.821	2.102, 2.149
[Ni(cyclam)]^2+Ad^−	−2700.310175	−194.25	−6.852	−5.643	1.209	1.983, 2.573
[Ni(cyclam)Ad]^+	−2700.323532	−202.63 (−8.38)	−7.187	−5.352	1.835	2.119, 2.122
[Ni(cyclam)]^2+GO^−	−3536.878488	−174.24	−6.500	−5.635	0.865	2.118, 2.248
[Ni(cyclam)GO]^+	−3536.895254	−184.76 (−10.52)	−6.572	−5.323	1.249	2.111, 2.127
[Ni(cyclam)]^2+ND^−	−3555.991187	−192.61	−6.642	−5.505	1.137	1.964, 2.578
[Ni(cyclam)ND]^+	−3556.005448	−201.56 (−8.95)	−7.010	−5.227	1.783	2.065, 2.153
[Ni(tet b)]^2+	−2357.411642		−11.832	−9.753	2.079
[Ni(tet b)]^2+Fm^−	−2546.801972	−187.51	−7.151	−5.801	1.350	2.491, 3.414
[Ni(tet b)Fm]^+	−2546.798288	−185.20 (2.31)	−7.287	−5.687	1.600	2.153, 2.215
[Ni(tet b)]^2+Ac^−	−2586.085377	−190.59	−6.993	−5.693	1.300	2.455, 3.398
[Ni(tet b)Ac]^+	−2586.087855	−192.14 (−1.55)	−7.045	−5.246	1.799	2.113, 2.191
[Ni(tet b)]^2+Bz^−	−2777.657923	−182.77	−7.070	−5.695	1.375	2.497, 3.355
[Ni(tet b)Bz]^+	−2777.657466	−182.49 (0.28)	−7.089	−5.404	1.685	2.111, 2.207
[Ni(tet b)]^2+Ad^−	−2935.987737	−187.44	−6.988	−5.663	1.325	2.421, 3.461
[Ni(tet b)Ad]^+	−2935.988188	−187.72 (−0.28)	−7.004	−5.298	1.706	2.119, 2.183
[Ni(tet b)]^2+GO^−	−3772.551052	−164.30	−6.253	−5.826	0.427	2.811, 2.972
[Ni(tet b)GO]^+	−3772.558443	−168.94 (−4.64)	−6.547	−5.323	1.224	2.121, 2.185
[Ni(tet b)]^2+ND^−	−3791.693078	−201.07	−6.751	−5.510	1.241	2.369, 3.394
[Ni(tet b)ND]^+	−3791.672013	−187.85 (13.22)	−6.868	−5.189	1.679	2.119, 2.139

---

One can see that ΔE values are very low, roughly around −2 × 10² kcal mol⁻¹: such a strong binding is quite natural due to the interaction between oppositely charged ions. On average, carboxylate complexes of [Ni(cyclam)]²⁺ are noticeably stronger than their counterparts with [Ni(tet b)]²⁺. The most likely reason is that cyclam ligand does not have substituents in the macrocyclic ring, contrary to tet b having six methyl groups, which create some steric hindrance for carboxylate to approach Ni²⁺ ion. More specifically, for high-spin complexes with [Ni(cyclam)]²⁺, ΔE values span from −184.76 to −205.64 kcal mol⁻¹, and with [Ni(tet b)]²⁺, from −168.94 to −192.14 kcal mol⁻¹. The binding strength decreases in the order of Ac⁻ > Ad⁻ > ND⁻ > Fm⁻ > Bz⁻ > GO⁻ and Ac⁻ > ND⁻ ≈ Ad⁻ > Fm⁻ > Bz⁻ > GO⁻, respectively. Interestingly, formate is not the anion which forms the strongest complexes, despite of its smallest size. This fact might imply a notable contribution of the van der Waals interactions between macrocyclic ligands and substituent R (which is H in Fm⁻) of carboxylate to the complex stability (stronger acidity of formic acid, resulting in lower basicity of formate, can be another reason, with a contribution of electronic effects due to R = H instead of a hydrocarbon substituent). Furthermore, apparently for the same reason, macrocycle complexation is predicted to be stronger with ND⁻ than with GO⁻ model anion.

As regards the singlet analogues, for the complexes with [Ni(cyclam)]²⁺, the calculated ΔE values are found between −174.24 and −195.24 kcal mol⁻¹; with [Ni(tet b)]²⁺, between −164.30 and −201.07 kcal mol⁻¹. The binding strength decreases in the order of Ac⁻ > Ad⁻ > ND⁻ > Fm⁻ > Bz⁻ > GO⁻ and ND⁻ > Ac⁻ > Fm⁻ ≈ Ad⁻ > Bz⁻ > GO⁻, respectively. One can make two observations. First, the order of binding strength for carboxylate complexes with [Ni(cyclam)]²⁺ remains the same for their singlet and triplet states. Second, in the case of [Ni(tet b)]²⁺, not only the order changes, but [Ni(tet b)]²⁺ND⁻ becomes the most stable, and [Ni(tet b)]²⁺GO⁻, the least stable low-spin complex.

As it was mentioned above, we calculated one more key parameter, ΔΔE₃₋₁, which characterizes the difference in stability for the triplet and singlet complexes. In the case of [Ni(cyclam)]²⁺ complexation, all ΔΔE₃₋₁ values are negative (Table 1), which means that triplet is always more stable than singlet state. The difference in their stability decreases in the order of GO⁻ > Ac⁻ > Bz⁻ > Fm⁻ > ND⁻ > Ad⁻, where the largest negative value is −10.52 kcal mol⁻¹ for GO⁻, and the least negative value of −8.38 kcal for Ad⁻ is only insignificantly different from that for ND⁻, of −8.95 kcal mol⁻¹.

A strikingly different picture can be observed for the interaction of carboxylates with [Ni(tet b)]²⁺. Here, only three ΔΔE₃₋₁ differences are negative, of −4.64, −1.55 and −0.28 kcal mol⁻¹ for GO⁻, Ac⁻ and Ad⁻, respectively: their absolute values are very low as compared to the case of [Ni(cyclam)]²⁺. For Bz⁻, Fm⁻ and ND⁻, ΔΔE₃₋₁ values are increasingly positive of 0.28, 2.31 and 13.22 kcal mol⁻¹, that is, singlet state is more stable for the complexes with these anions. As a whole, the stability of high-spin complexes as compared to their low-spin counterparts decreases in the order of GO⁻ > Ac⁻ > Ad⁻ > Bz⁻ > Fm⁻ > ND⁻. These results explicitly imply that the formation of high-spin complex for [Ni(tet b)]²⁺ is unfavorable on ND⁻, contrary to GO⁻. In the case of [Ni(cyclam)]²⁺, one can conclude that the formation of triplet state is less favorable with ND⁻ than with GO⁻, but in both case it remains more stable than the corresponding singlet state.

3.3. Geometry of coordination sphere

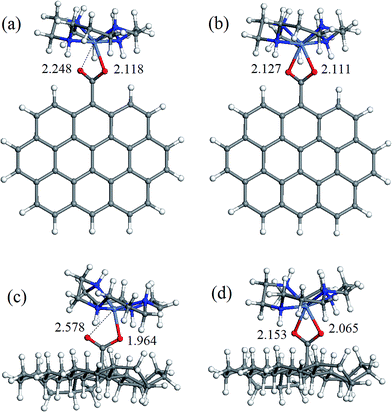
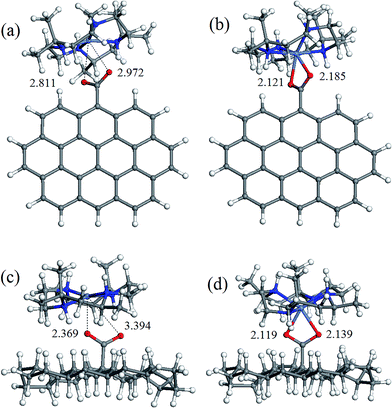
The geometry of coordination sphere was analyzed in terms of two Ni–O distances (corresponding to two carboxylic O atoms), which has the most direct relevance for the conversion of square-planar tetraazamacrocyclic complexes to high-spin pseudooctahedral carboxylates. They are presented in Table 1. Additionally, for the complexes of special interest, that is, with GO⁻ and ND⁻ model anions, optimized geometries are presented in Fig. 2 and 3 for [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺, respectively.

Fig. 2 Optimized geometries of coordination complexes: (a) singlet [Ni(cyclam)]²⁺GO⁻; (b) triplet [Ni(cyclam)GO]⁺; (c) singlet [Ni(cyclam)]²⁺ND⁻; (d) triplet [Ni(cyclam)ND]⁺. The values specified are Ni–O distances (in Å). Atom colors: grey, carbon; white, hydrogen; red, oxygen; blue, nitrogen; violet blue, nickel.

Fig. 3 Optimized geometries of coordination complexes: (a) singlet [Ni(tet b)]²⁺GO⁻; (b) triplet [Ni(tet b)GO]⁺; (c) singlet [Ni(tet b)]²⁺ND⁻; (d) triplet [Ni(tet b)ND]⁺. The values specified are Ni–O distances (in Å). Atom colors: grey, carbon; white, hydrogen; red, oxygen; blue, nitrogen; violet blue, nickel.

As can be seen from Table 1, the Ni–O distances vary within a very broad range: the smallest value of 1.964 Å was found in low-spin complex [Ni(cyclam)]²⁺ND⁻, and the longest distance of 3.414 Å, in low-spin [Ni(tet b)]²⁺Fm⁻ complex. Here it is appropriate to mention that the Ni–O distances in the crystalline high-spin [Ni(tet b)]²⁺ nicotinate complex were found to be almost equal, of 2.153 and 2.156 Å,³³ and slightly differing in its bridged pyridinedicarboxylate analogue, of 2.123 and 2.255 Å.³² The non-equivalence of Ni–O distances in the latter case was attributed to steric hindrance between one [Ni(tet b)]²⁺ cation and the remaining part of the bulky bridged complex,³² therefore the distance of 2.255 Å can be considered as a typical length for coordination Ni–O bond in high-spin complexes. So, to classify Ni–O distances observed in the present case, we chose a slightly shorter and more realistic cutoff value of 2.220 Å for this type of bond.

Based on the latter, all the macrocycle–carboxylate complexes can be subdivided into three categories, which can be described as follows: (1) both Ni–O distances are shorter than 2.220 Å, and thus correspond to coordination bonds; (2) one bond is coordination, and one Ni–O distance is longer than 2.220 Å; (3) both Ni–O distances are too long to be considered as coordination bonds. As it could be expected, all the high-spin carboxylate complexes, for both [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ cations, have two Ni–O coordination bonds, and thus belong to the first category (see, for example, Fig. 2b, d and 3b, d). The second category includes exclusively low-spin carboxylates of [Ni(cyclam)]²⁺ (exemplified for GO⁻ and ND⁻ in Fig. 2a and c). This fact implies that, even though the complex is found in singlet state, filling the fifth coordination site of Ni ion causes significant distortion of NiN₄ macrocyclic system from square-planar geometry. As regards the second, non-coordinated O atom, it is interesting to note that the longest Ni–O distance of 2.704 Å (Table 1) does not correspond to the most bulky carboxylates (i.e., GO⁻ or ND⁻), but to the most compact one, Fm⁻. And vice versa, the shortest Ni–O distance of 2.248 Å corresponds to one of the most bulky carboxylates, namely GO⁻ (Fig. 2a).

The latter observation has obviously to do with easier accessibility for additional coordination of Ni ion incorporated into tetraazamacrocyclic ring of cyclam ligand, which has no substituents. On the contrary, tet b has six methyl substituents in the macrocyclic ring, creating significant steric hindrance for carboxylate to approach Ni²⁺ ion. Therefore, the fact that in all low-spin carboxylate complexes of [Ni(tet b)]²⁺ (constituting the third category) both Ni–O distances are too long to be considered as coordination bonds seems quite natural (exemplified for GO⁻ and ND⁻ in Fig. 3a and c). They vary in a very broad range from 2.369 to 3.461 Å (Table 1), as observed in [Ni(tet b)]²⁺ND⁻ and [Ni(tet b)]²⁺Ad⁻, respectively. And again, it is interesting to note that the shortest Ni–O separation of 2.369 Å corresponds to one of the most bulky carboxylates, ND⁻ (Fig. 3c), whereas the longest Ni–O separation of 3.461 Å was found for Ad⁻, which has R substituent of intermediate size.

3.4. Spin density and frontier orbitals

Logically, spin density plots must show the existence of unpaired electrons for the triplet tetraazamacrocycle–carboxylate complexes, and their absence for all the singlet states. As regards the triplet carboxylates, indeed, for all of them a significant unpaired electron density can be observed (as exemplified for [Ni(cyclam)GO]⁺, [Ni(cyclam)ND]⁺, [Ni(tet b)GO]⁺ and [Ni(tet b)ND]⁺ in Fig. 4). It is associated with the paramagnetic Ni(II) centers together with all N and O donor atoms (in other words, with the NiN₄O₂ coordination sphere), with a minor fraction found on other atoms of the macrocyclic ligands. In the case of both triplet complexes with GO⁻, one should note that no appreciable spin density can be found on the atoms of graphene sheet, despite of its hyperconjugated nature. This fact suggests the absence of ferromagnetic coupling, which agrees very well with the experimental results of magnetic susceptibility measurements for paramagnetic nanohybrids of [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ with GO.²⁹

Fig. 4 Spin density plots (isosurfaces at 0.005 a.u.) for low and high-spin complexes of [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ with GO⁻ and ND⁻ models.

The results obtained for low-spin tetraazamacrocycle–carboxylate complexes were in some sense unexpected. It turned out that these complexes fall into two categories, just like they do when considering Ni–O distances (Section 3.3). Note that ‘singlet’ state was explicitly specified in the calculation settings. Nevertheless, for all 'low-spin' carboxylates of [Ni(cyclam)]²⁺ we found a considerable density of unpaired electrons, as exemplified in Fig. 4 for [Ni(cyclam)]²⁺GO⁻ and [Ni(cyclam)]²⁺ND⁻. On the other hand, its distribution is more constrained as compared to the one for triplet carboxylates: besides central Ni ion, it is basically limited to only one carboxylic O atom (coordinated to Ni ion) and only one N atom of tetraazamacrocyclic ring. In the case of all low-spin carboxylates of [Ni(tet b)]²⁺, no similar phenomenon was observed (exemplified in Fig. 4 for [Ni(tet b)]²⁺GO⁻ and [Ni(tet b)]²⁺ND⁻), that is, no traces of unpaired electrons was detected: this correlates with the long Ni–O distances.

The general appearance of HOMO and LUMO plots in most cases was found to be qualitatively similar, where both HOMO and LUMO are associated with NiN₄ system and COO⁻ groups (mainly O atoms) of carboxylate component: this is exemplified in Fig. 5 for [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ complexes with ND⁻, in both low-spin and high-spin state. The four exceptions found were their counterparts with GO⁻ (Fig. 5), in which HOMO tends to be localized on the anion with a variable degree of extension to central Ni ion and its adjacent atoms (especially in the case of [Ni(cyclam)]²⁺GO⁻). As regards LUMO, its distribution remains to be limited to NiN₄ system along with carboxylate O atoms, like for all other tetraazamacrocycle–carboxylate complexes.

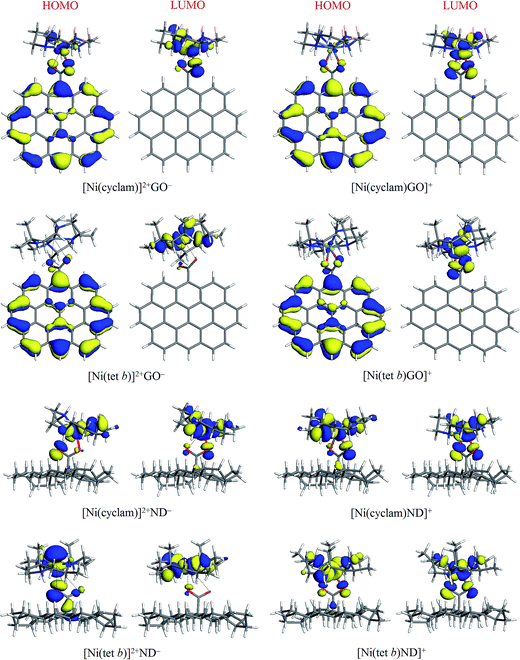Fig. 5 HOMO and LUMO plots (isosurfaces at 0.03 a.u.) for low and high-spin complexes of [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺ with GO⁻ and ND⁻ models.

In quantitative terms, we also calculated HOMO, LUMO and HOMO−LUMO gap energies for all the complexes (as well as for separated ions) studied; the corresponding values are presented in Table 1. High-spin complexes exhibit systematically higher values, ranging from 1.224 (for [Ni(tet b)GO]⁺) to 1.835 eV (for [Ni(cyclam)Ad]⁺), as compared to low-spin complexes, where the lowest HOMO−LUMO gap of 0.427 eV was obtained for [Ni(tet b)]²⁺GO⁻, and the highest value of 1.375 eV, for [Ni(tet b)]²⁺Bz⁻. No evident correlation was found between this parameter and formation energy of the complexes or Ni–O distances in them.

4. Conclusions

The results of DFT calculations can explain why our attempts to coordinatively functionalize nanodiamond with tetraazamacrocyclic cations [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺, and to generate paramagnetic hybrid materials in this way failed, contrary to the successful functionalization of graphene oxide.²⁹ The explanation offered is based on the comparison of binding energies for low-spin (singlet) and high-spin (triplet) complexes of model carboxylate ions GO⁻ and ND⁻ with the two tetraazamacrocycles. The formation energies were interpreted in terms of ΔΔE₃₋₁ values, which characterize the difference in stability for the triplet and singlet complexes. In the case of [Ni(cyclam)]²⁺ complexation, ΔΔE₃₋₁ values for both anions were negative, which means that triplet is always more stable than singlet state; the high-spin complex with GO⁻ is stronger than the one with ND⁻, though the difference is not significant, of 1.57 kcal mol⁻¹ only. While this result can be taken as ambiguous (that is, it does not rule out the possibility of forming high-spin [Ni(cyclam)]²⁺ carboxylate), one should remember about two circumstances which are virtually impossible to account for in the calculations:

(1) GO⁻ and ND⁻ are extremely simplified models for real GO and ND materials, in terms of both nanoparticle size and the presence of oxygenated functional groups adjacent to carboxyls subjected to coordination functionalization. In particular, steric hindrance resulting from the presence of other functionalities would have much lower degree on GO (only two groups at the sides) than on ND (several groups surrounding the target COOH group).

(2) The real reaction medium includes water and alcohol solvent molecules, as well as a high concentration of ions including NH₄⁺, OH⁻ and perchlorates (counterions of both Ni(II) tetraazamacrocyclic complexes). Taken as a whole, they create shielding and/or competing effects for the interacting species. Apparently, these effects manifest stronger in the case of ND, making the formation of high-spin complexes with [Ni(cyclam)]²⁺ negligible or impossible at all.

On the other hand, in the case of [Ni(tet b)]²⁺, even without considering the above circumstances, comparison of the ΔΔE₃₋₁ values explicitly demonstrated that the formation of high-spin complex is highly unfavorable on ND⁻ contrary to GO⁻, where ΔΔE₃₋₁ values obtained are 13.22 and −4.64 kcal mol⁻¹, respectively. The factor which results in so drastic differences in the behavior of [Ni(cyclam)]²⁺ and [Ni(tet b)]²⁺, is the existence of six methyl substituents in the macrocyclic ring of tet b ligand, creating significant steric hindrance for carboxylate to approach Ni²⁺ ion.

Acknowledgements

Financial support from the National Autonomous University of Mexico (UNAM, grant DGAPA-IN200516) and from the National Council of Science and Technology of Mexico (CONACYT, grant 250655) is greatly appreciated. The authors acknowledge experimental attempts of ND functionalization with the tetraazamacrocyclic complexes undertaken by PhD students Natalia Alzate-Carvajal and Verónica Henao-Holguín at UNAM and Tufts University.

References

1. V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Functionalization of graphene: covalent and non-covalent approaches, derivatives and applications, Chem. Rev., 2012, 112, 6156–6214.
2. D. Chen, H. Feng and J. Li, Graphene oxide: preparation, functionalization, and electrochemical applications, Chem. Rev., 2012, 112, 6027–6053.
3. A. N. Khlobystov and A. Hirsch, Organometallic and coordination chemistry of carbon nanomaterials, Dalton Trans., 2014, 43, 7345.
4. M. R. Axet, O. Dechy-Cabaret, J. Durand, M. Gouygou and P. Serp, Coordination chemistry on carbon surfaces, Coord. Chem. Rev., 2016, 308, 236–345.
5. J. Malig, N. Jux and D. M. Guldi, Toward multifunctional wet chemically functionalized graphene—Integration of oligomeric, molecular, and particulate building blocks that reveal photoactivity and redox activity, Acc. Chem. Res., 2013, 46, 53–64.
6. I. V. Lightcap and P. V. Kamat, Graphitic design: prospects of graphene-based nanocomposites for solar energy conversion, storage, and sensing, Acc. Chem. Res., 2013, 46, 2235–2243.
7. S. Niyogi, E. Bekyarova, J. Hong, S. Khizroev, C. Berger, W. de Heer and R. C. Haddon, Covalent chemistry for graphene electronics, J. Phys. Chem. Lett., 2011, 2, 2487–2498.
8. A. Wojcik and P. V. Kamat, Reduced graphene oxide and porphyrin. An interactive affair in 2-D, ACS Nano, 2010, 4, 6697–6706.
9. V. D. Pham, J. Lagoute, O. Mouhoub, F. Joucken, V. Repain, C. Chacon, A. Bellec, Y. Girard and S. Rousset, Electronic interaction between nitrogen-doped graphene and porphyrin molecules, ACS Nano, 2014, 8, 9403–9409.
10. J. Tang, L. Niu, J. Liu, Y. Wang, Z. Huang, S. Xie, L. Huang, Q. Xu, Y. Wang and L. A. Belfiore, Effect of photocurrent enhancement in porphyrin–graphene covalent hybrids, Mater. Sci. Eng., C, 2014, 34, 186–192.
11. I. Kruusenberg, J. Mondal, L. Matisen, V. Sammelselg and K. Tammeveski, Oxygen reduction on graphene-supported MN₄ macrocycles in alkaline media, Electrochem. Commun., 2013, 33, 18–22.
12. C. F. Hermanns, K. Tarafder, M. Bernien, A. Krüger, Y. M. Chang, P. M. Oppeneer and W. Kuch, Magnetic coupling of porphyrin molecules through graphene, Adv. Mater., 2013, 25, 3473–3477.
13. M. Zhu, Z. Li, B. Xiao, Y. Lu, Y. Du, P. Yang and X. Wang, Surfactant assistance in improvement of photocatalytic hydrogen production with the porphyrin noncovalently functionalized graphene nanocomposite, ACS Appl. Mater. Interfaces, 2013, 5, 1732–1740.
14. P. Guo, P. Chen and M. Liu, One-dimensional porphyrin nanoassemblies assisted via graphene oxide: sheetlike functional surfactant and enhanced photocatalytic behaviors, ACS Appl. Mater. Interfaces, 2013, 5, 5336–5345.
15. J. Geng and H.-T. Jung, Porphyrin functionalized graphene sheets in aqueous suspensions: from the preparation of graphene sheets to highly conductive graphene films, J. Phys. Chem. C, 2010, 114, 8227–8234.
16. D. Huang, J. Lu, S. Li, Y. Luo, C. Zhao, B. Hu, M. Wang and Y. Shen, Fabrication of cobalt porphyrin – electrochemically reduced graphene oxide hybrid films for electrocatalytic hydrogen evolution in aqueous solution, Langmuir, 2014, 30, 6990–6998.
17. M. Jurow, V. Manichev, C. Pabon, B. Hageman, Y. Matolina and C. M. Drain, Self-organization of Zr(IV) porphyrinoids on graphene oxide surfaces by axial metal coordination, Inorg. Chem., 2013, 52, 10576–10582.
18. A. Wang, L. Long, W. Zhao, Y. Song, M. G. Humphrey, M. P. Cifuentes, X. Wu, Y. Fu, D. Zhang, X. Li and C. Zhang, Increased optical nonlinearities of graphene nanohybrids covalently functionalized by axially-coordinated porphyrins, Carbon, 2013, 533, 327–338.
19. S. Lisi, P. Gargiani, M. Scardamaglia, N. B. Brookes, V. Sessi, C. Mariani and M. G. Betti, Graphene-induced magnetic anisotropy of a two-dimensional iron phthalocyanine network, J. Phys. Chem. Lett., 2015, 6, 1690–1695.
20. M. Bernien, H. Naggert, L. M. Arruda, L. Kipgen, F. Nickel, J. Miguel, C. F. Hermanns, A. Krüger, D. Krüger, E. Schierle, E. Weschke, F. Tuczek and W. Kuch, Highly efficient thermal and light-induced spin-state switching of an Fe(II) complex in direct contact with a solid surface, ACS Nano, 2015, 9, 8960–8966.
21. Y. Murashima, M. R. Karim, N. Saigo, H. Takehira, R. Ohtani, M. Nakamura, M. Koinuma, L. F. Lindoy, K. Kuroiwad and S. Hayami, Graphene oxide and reduced graphene oxide hybrids with spin crossover iron(III) complexes, Inorg. Chem. Front., 2015, 2, 886–892.
22. C. F. Hermanns, K. Tarafder, M. Bernien, A. Krüger, Y.-M. Chang, P. M. Oppeneer and W. Kuch, Magnetic coupling of porphyrin molecules through graphene, Adv. Mater., 2013, 25, 3473–3477.
23. S. Bhandary, O. Eriksson and B. Sanyal, Defect controlled magnetism in FeP/graphene/Ni(111), Sci. Rep., 2013, 3, 3405.
24. D. Klar, S. Bhandary, A. Candini, L. Joly, P. Ohresser, S. Klyatskaya, M. Schleberger, M. Ruben, M. Affronte, O. Eriksson, B. Sanyal and H. Wende, Field-regulated switching of the magnetization of Co-porphyrin on graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144411.
25. J. Mao, H. Zhang, Y. Jiang, Y. Pan, M. Gao, W. Xiao and H.-J. Gao, Tunability of supramolecular kagome lattices of magnetic phthalocyanines using graphene-based moiré patterns as templates, J. Am. Chem. Soc., 2009, 131, 14136–14137.
26. A. Candini, V. Bellini, D. Klar, V. Corradini, R. Biagi, V. De Renzi, K. Kummer, N. B. Brookes, U. del Pennino, H. Wende and M. Affronte, Ferromagnetic exchange coupling between Fe phthalocyanine and Ni(111) surface mediated by the extended states of graphene, J. Phys. Chem. C, 2014, 118, 17670–17676.
27. A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Graphene spintronic devices with molecular nanomagnets, Nano Lett., 2011, 11, 2634–2639.
28. A. H. Hung, R. J. Holbrook, M. W. Rotz, C. J. Glasscock, N. D. Mansukhani, K. W. MacRenaris, L. M. Manus, M. C. Duch, K. T. Dam, M. C. Hersam and T. J. Meade, Graphene oxide enhances cellular delivery of hydrophilic small molecules by co-incubation, ACS Nano, 2014, 8, 10168–10177.
29. V. A. Basiuk, N. Alzate-Carvajal, L. V. Henao-Holguín, E. V. Rybak-Akimova and E. V. Basiuk, Coordination functionalization of graphene oxide with tetraazamacrocyclic complexes of nickel(II): generation of paramagnetic centers, Appl. Surf. Sci., 2016, 371, 16–27.
30. X. Liang and P. J. Sadler, Cyclam complexes and their applications in medicine, Chem. Soc. Rev., 2004, 33, 246–266.
31. P. O. Whimp, M. F. Bailey and N. F. Curtis, Some cyclic tetra-amines and their metal-ion complexes. Part VI. The crystal structure of acetato-C-rac-(5,7,7,12,14,14-hexamethyl-1,4,8,11-tetra-azacyclotetradecane)nickel(II) perchlorate, J. Chem. Soc. A, 1970, 1956–1963.
32. E. V. Basiuk, V. A. Basiuk, J. Gómez-Lara and R. A. Toscano, A bridged high-spin complex bis-[Ni(II)(rac-5,5,7,12,12,14-hexamethyl-1,4,8,11-tetraazacyclotetradecane)]-2,5-pyridinedicarboxylate diperchlorate monohydrate, J. Inclusion Phenom. Macrocyclic Chem., 2000, 38, 45–56.
33. E. V. Basiuk, V. A. Basiuk, S. Hernández-Ortega, M. Martínez-García and J.-M. Saniger-Blesa, (C-rac-5,5,7,12,12,14-Hexamethyl-1,4,8,11-tetraazacyclotetradecane-κ4N)(nicotinato-O,O′)nickel(II) perchlorate, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 553–555.
34. V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, The properties and applications of nanodiamonds, Nat. Nanotechnol., 2012, 7, 11–23.
35. A. Krueger, New carbon nanomaterials: biological appilcations of functionalized nanodiamond materials, Chem.–Eur. J., 2008, 14, 1382–1390.
36. A. Krueger and D. Lang, Functionality is key: recent progress in the surface modification of nanodiamond, Adv. Funct. Mater., 2012, 22, 890–906.
37. V. N. Mochalin and Y. Gogotsi, Wet chemistry route to hydrophobic blue fluorescent nanodiamond, J. Am. Chem. Soc., 2009, 131, 4594–4595.
38. E. V. Basiuk, A. Santamaría-Bonfil, V. Meza-Laguna, T. Y. Gromovoy, E. Alvares-Zauco, F. F. Contreras-Torres, J. Rizo, G. Zavala and V. A. Basiuk, Solvent-free covalent functionalization of nanodiamond with amines, Appl. Surf. Sci., 2013, 275, 324–334.
39. E. V. Basiuk, V. A. Basiuk, V. Meza-Laguna, F. F. Contreras-Torres, M. Martínez, A. Rojas-Aguilar, M. Salerno, G. Zavala, A. Falqui and R. Brescia, Solvent-free covalent functionalization of multi-walled carbon nanotubes and nanodiamond with diamines: looking for cross-linking effects, Appl. Surf. Sci., 2012, 259, 465–476.
40. N. Alzate-Carvajal, E. V. Basiuk, V. Meza-Laguna, I. Puente-Lee, M. H. Farías, N. Bogdanchikova and V. A. Basiuk, Solvent-free one-step covalent functionalization of graphene oxide and nanodiamond with amines, RSC Adv., 2016, 6, 113596–113610.
41. B. Delley, An all-electron numerical method for solving the local density functional for polyatomic molecules, J. Chem. Phys., 1990, 92, 508–517.
42. B. Delley, Fast calculations of electrostatics in crystals and large molecules, J. Phys. Chem., 1996, 100, 6107–6110.
43. B. Delley, From molecules to solids with the DMol3 approach, J. Chem. Phys., 2000, 113, 7756–7764.
44. B. Delley, D. E. Ellis, A. J. Freeman, E. J. Baerends and D. Post, Binding energy and electronic structure of small copper particles, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2132–2144.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
47. L. V. Henao-Holguín and V. A. Basiuk, Interaction of a Ni(II) tetraazaannulene complex with elongated fullerenes as simple models for carbon nanotubes, J. Mol. Model., 2015, 21, 146.
48. V. A. Basiuk and L. V. Henao-Holguín, Dispersion-corrected density functional theory calculations of meso-tetraphenylporphine-C₆₀ complex by using DMol3 module, J. Comput. Theor. Nanosci., 2014, 11, 1609–1615.
49. E. V. Basiuk, M. Martínez-Herrera, E. Álvarez-Zauco, L. V. Henao-Holguín, I. Puente-Lee and V. A. Basiuk, Noncovalent functionalization of graphene with a Ni(II) tetraaza[14]annulene complex, Dalton Trans., 2014, 43, 7413–7428.

---