Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New carbon allotropes with metallic conducting properties: a first-principles prediction†
Xinyu Fan,
Jiao Li and
Gang Chen *
*
Laboratory of Advanced Materials Physics and Nanodevices, School of Physics and Technology, University of Jinan, Jinan 250022, China. E-mail: phdgchen@hotmail.com
First published on 20th March 2017
Abstract
Combining density functional theory computation and the global minimum structural search, we have found new α-, β-, and δ-phographene carbon allotropes. The α-phographene is almost degenerate in energy with the previously reported phagraphene, which is energetically favorable as compared to the β- and δ-phographenes and the other known non-honeycomb two-dimensional carbon allotropes. Our careful studies of the α- and β-phographenes show good dynamic, thermal, and mechanical stabilities. The pristine α- and β-phographenes are metallic, which would be altered to wide-gap semiconductors by hydrogenation. Additionally, the α-phographene shows enhanced joint density of states at the energy of ∼1.6 eV, which may find applications in photoelectronics. The analyses on the growth of structural motifs and the effects of net charge suggest the possibilities for experimentally fabricating α-phographene. Interestingly, the α-phographene has a Young's modulus and Poisson's ratio close to those of graphene, showing remarkable mechanical properties. It may also find applications in supporting Au or Pt clusters as high-performance complex catalyst nanostructures, calling for further investigations on both theory and experiment.
1. Introduction
Due to the rich electronic hybridization configurations of sp, sp2, sp3, and their combinations, carbon is known as the most versatile element to form many allotropes ranging from zero-, one-, and two-dimensional nanostructures to three-dimensional bulk materials,1–47 such as fullerene, carbon nanotubes, graphene, graphite and diamond. The planar structures featuring the sp2 or sp2-based mixing hybridizations are the base materials for building many low-dimensional (2D) carbon nanostructures, which could be either wrapped to form fullerene or rolled into carbon nanotubes. The fullerene found in 1985 by Smalley et al.1 consists of 12 carbon pentagons separated from each other by 20 carbon hexagons, which gains high electronic stability as a molecular cluster due to the large gap (∼1.6 eV) between the highest occupied molecular orbital and the lowest unoccupied molecular orbital, stimulating extraordinary studies to form fullerene chemistry. In 1991, Iijima first reported the carbon nanotube,2 whose conducting properties are determined by the rolling curvature associated with the chiral vector of its base material – the honeycomb carbon sheet,3 triggering numerous investigations of both fundamental properties and potential applications. Though the sheet structure based low-dimensional carbon nanostructures had been extensively studied in both theory and experiment, the first two-dimensional carbon sheet was only successfully synthesized on experiment in 2004 by Novoselov et al.4 Preserved by both inversion symmetry and time reversal symmetry, the conjugate π and π* bands touch at Fermi energy to form Dirac cones at K and K′ points in reciprocal space with nearly linear dispersion, resulting in high mobility massless charge carriers. The success of graphene has motivated extensive researches for newer forms of 2D materials.The outstanding progress in the research field of graphene has also inspired the investigations of various 2D carbon allotropes. Besides the hexagonal graphene with ideal sp2 electronic configuration, the experimentalist has the methodologies to generate networks of combinations of sp, sp2 and sp3 hybridized carbons.5 Carbon that can form a variety of polygons ranging from linear chains to dodecagons attracts a lot of attentions in exploring new carbon planar nanostructures, which are, for example, the graphyne,10–20 graphdiyne,20–23 graphenylene,24,25 biphenylene,26,27 radialenes,28 pentagraphene,29 pentahexoctite,30 HOP-graphene,31 pentaheptities,32,33 haeckelites,34 squarographenes,35 planar C4 sheet,36–42 OP-graphene,43,44 circumcoro-graphyne,45 coro-graphene,45 W-sheet,42,46 and phagraphene.47,48 Very interesting it is the successful fabrication of graphdiyne on experiment,21,22 which shows the promise in experimentally producing new carbon sheet structures. Recently, Wang et al.47 proposed the phagraphene composed of 5–6–7 carbon polygons, which is lower in energy than most of the previously predicted 2D carbon allotropes. Also, considering the fact of the 5–7 polygons known as Stone–Wales defect49,50 is stable in the defected graphene, the phagraphene holds the promise for fabrication. In addition to the geometrical stability of the 5–7 polygons, the 5–8 polygons are actually also stable configuration as evidenced in the experimental studies of the 5–8 defect chain in graphene.51,52 By arranging the pentagons, hexagons, and octagons, Mandal et al.31 and Sharma et al.30 recently reported two different 2D carbon allotropes composed of the 5–6–8 carbon rings, which are referred in this paper as the γ- and ε-phographenes (accounting the pentagon–hexagon–octagon structural characteristics) to facilitate discussion. By carrying out the global minimum structure search with the efficient evolutionary algorithm, we have found three new structural isomers of the phographene, which would be discussed as the α-, β-, and δ-phographenes in this paper. Among the structural isomers of phographene, the α-phographene has the lowest energy. The previously reported γ- and ε-phographenes are ∼50 and ∼150 meV per atom higher in total energy, suppressing their experimental fabrications. Furthermore, the α-phographene is a little lower in energy than the recently reported 5–6–7 polygon characterized phagraphene,47 which may gain much lower total energy in the charged state. This in combination with our detailed studies of the dynamic, thermal, and mechanical stabilities suggest the priority of its experimental realization. Additionally, our studies on the electronic properties, the mechanical properties, the hydrogenation effects, and the usage in supporting precious metal clusters as complex catalyst nanostructures show attractive fundamental and application properties of the phographene, calling for further investigations on both theory and experiment.
2. Computational details
The first principles calculations were carried out with the density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP).53 Both the projector augmented-wave potential and the planewave basis set were used.54 The cutoff energy of the plane-wave basis set was set to 500 eV. The exchange and correlation energies were treated by using the generalized gradient approximation (GGA) with the Perdew, Burke, and Ernzerhof (PBE) parameterization.55 The phographene was placed in the xy plane, with a vacuum of 15 Å along z direction to minimize the effects from its neighboring images. The Monkhorst–Pack technique56 was used to sample the k points in Brillouin zone. According to the primitive unit cells for the planar α-, β-, γ-, δ- and ε-phases, the k-meshes of 7 × 7 × 1, 5 × 11 × 1, 9 × 11 × 1, 5 × 9 × 1, and 9 × 13 × 1 were carefully tested. The energies were converged to 10−5 eV and the calculated Hellmann–Feynman forces acting on each atom were converged to 20 meV Å−1. The phonon dispersion was calculated with the Phonopy code using the finite displacement method.57 In order to obtain reliable results, the density functional theory calculations with higher accuracy were performed, for which the criteria of 10−8 eV and 0.1 meV Å−1 were adopted for the convergences of the energies and the Hellmann–Feynman forces. Ab initio molecular dynamics simulations (AIMD) were carried out to estimate the thermal stability. Referring to the primitive unit cell, we used the 4 × 4 × 1 sized supercell to minimize the effects from the periodic boundary conditions to explore the possible structural reconstruction. During the simulation, the temperature was controlled via the Nosé–Hoover technique.58 The global minimum structural search was carried out by using an efficient evolutionary algorithm as implemented in the Universal Structure Predictor: Evolutionary Xtallography (USPEX),59–62 which is interfaced with VASP code to select the low-energy structural configurations. Among the 17 plane space groups, the randomly selected 2D symmetry groups were adopted in generating geometrical structures of the 2D carbon structures. The structural searches started with the input carbon atoms ranging from 6 to 24, using the randomly generated lattice parameters and atomic coordinates.3. Results and discussion
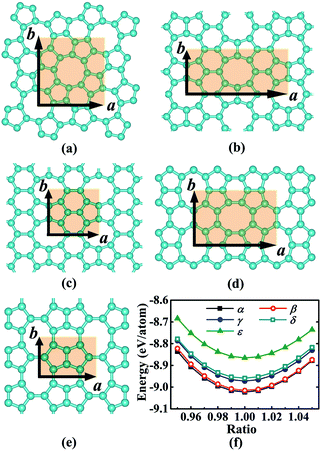
3.1 Geometrical configuration and stability
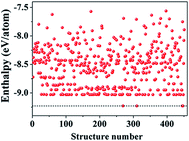
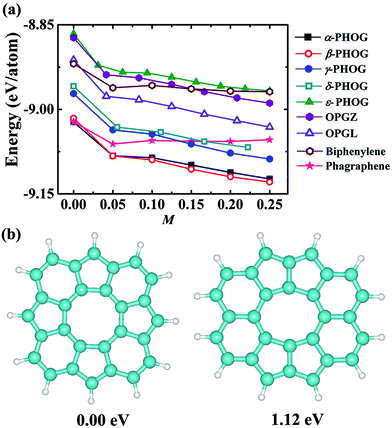
We began our study with a global minimum structural search using an efficient and systematic evolutionary structural search algorithm developed by Oganov and coworkers.59–62 In the evolutionary process of the structural search, the population of 30% of the structure candidates with low total energies were evolved over successive generations of random variation and selection. The structural evolutionary search with 20 carbon atoms in the unit cell is schematically shown in Fig. 1 for illustration. Besides the lowest energy honeycomb structure of graphene, both the previously reported phagraphene47 composed of 5–6–7 carbon rings and the carbon allotropes composed of 5–6–8 carbon rings were found as the low energy planar allotropes. In order to facilitate discussion, we would like to refer the 5–6–8 (penta–hexa–octa) carbon allotrope as phographene. In Fig. 2, we show the geometrical configurations of the phographenes and the corresponding phase diagram calculated on PBE-level. The corresponding lattice parameters are prvodied in Table 1. The α-, β-, and δ-phases are the first time proposed carbon allotropes while the γ- and ε-phases correspond to the previously reported ones by Mandal et al.31 and Sharma et al.,30 respectively. Referring to the lowest energy α-phographene, the β-, γ-, δ-, and ε-phases are calculated on PBE-level to be 7, 50, 64, and 157 meV per atom higher in total energy, respectively. Besides the relative energies calculated with PBE functional, the corresponding energies calculated with the local density approximation (LDA),63,64 Perdew–Wang 91 (PW91),65 Tao–Perdew–Staroverov–Scuseria (TPSS)66 and the revised TPSS meta-GGA (rev-TPSS)67 are also tabulated in Table 2. The newly proposed α-phographene is almost degenerate in energy with the previously reported phagraphene. The in-plane densities of the carbon atoms of the α- and β-phographenes and the phagraphene47 are 0.363, 0.366, and 0.371 atoms per Å2. The α-phographene with smaller atomic density is found to have the lowest energy, hinting the effects of the topological arrangement of the carbon polygons. The other new carbon allotropes β- and δ-phographenes are about 7 and 64 meV per atom higher in energy. The previously reported γ- and ε-phographenes have about 51 and 156 meV per atom higher energies. The other carbon allotropes as the biphenylene,26 OPG-L,43 OPG-Z,43 circumcoro-graphyne,45 coro-graphene,45 C4 sheet,36–42 graphenylene,24,25 graphyne,10–20 graphdiyne20–23 and penta-graphene29 are found to be about 103, 112, 148, 129, 231, 307, 427, 502, 555, and 708 meV per atom higher in energy, respectively. Based on the analyses on the calculated energies, we would like hereafter to concentrate on discussing the newly proposed α- and β-phographenes. At the end of the section of the discussion and results, we would also attempt to discuss the possibilities of their fabrications.| Parameter | α | β | γ | δ | ε |
|---|---|---|---|---|---|
| a | 7.42 | 11.14 | 5.61 | 8.66 | 5.79 |
| b | 7.42 | 4.91 | 4.89 | 5.71 | 3.83 |
| N | 20 | 20 | 10 | 18 | 8 |
| Allotrope | LDA | PW91 | PBE | TPSS | rev-TPSS |
|---|---|---|---|---|---|
| Phagraphene | 0.0 | 0.0 | 0.4 | 1.8 | 1.9 |
| α-Phographene | 5.9 | 0.4 | 0.0 | 0.0 | 0.0 |
| β-Phographene | 10.6 | 7.5 | 6.8 | 7.7 | 6.9 |
| γ-Phographene | 54.5 | 50.9 | 50.3 | 51.8 | 51.2 |
| δ-Phographene | 67.9 | 64.4 | 63.5 | 64.5 | 62.4 |
| ε-Phographene | 157.4 | 157.6 | 156.7 | 155.5 | 152.2 |
| Biphenylene | 112.4 | 104.4 | 103.3 | 102.8 | 102.4 |
| OPG-L | 122.9 | 114.0 | 112.3 | 112.3 | 110.7 |
| OPG-Z | 158.0 | 149.3 | 147.6 | 148.3 | 146.1 |
| CCG | 143.5 | 131.7 | 132.5 | 125.2 | 126.3 |
| CG | 251.4 | 235.9 | 234.1 | 226.7 | 226.3 |
| C4 sheet | 337.8 | 310.1 | 315.7 | 298.7 | 301.6 |
| Graphenylene | 461.6 | 429.9 | 426.5 | 426.4 | 424.4 |
| Graphdiyne | 676.5 | 557.2 | 564.6 | 538.4 | 558.5 |
| Graphyne | 594.2 | 502.3 | 508.6 | 489.7 | 505.5 |
| Penta-graphene | 691.0 | 709.0 | 704.0 | 718.8 | 698.4 |
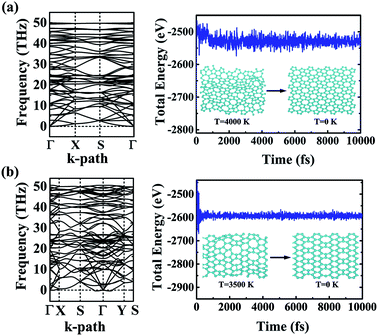
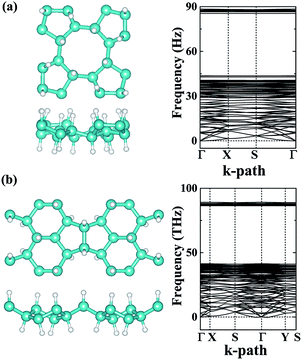
The dynamic and thermal stabilities of the α- and β-phographenes are studied in Fig. 3. The calculated phonon spectrum of α-phographene does not have any imaginary mode in the entire Brillouin zone, confirming its dynamic stability. However, the phonon spectrum shows the almost neglected imaginary modes round Γ point for the β-phographene. Considering the good stabilities judged from our later discussion of the AIMD simulations and the mechanical stability evaluation, the presence of the imaginary modes may be attributed to the uncertainties of our calculations. Also, these imaginary modes would be easily removed by applying a slight tensile strain on the β-phographene. In Fig. 3, we have carefully evaluated the melting temperature of the α- and β-phographenes to estimate their heat stabilities by using the AIMD simulations, which have been confirmed to be useful in evaluating the thermal stabilities of planar materials.68,69 In order to minimize the constraints of the periodic boundary conditions on the atomic movement, the carbon allotropes were simulated by using the 4 × 4 × 1 supercells for exploring possible structural reconstructions. The geometrical structures were monitored during the simulations. The stabilities of the coro-graphene and circumcoro-graphyne45 were previously estimated at 300 K, which are evaluated at 1000 K of the phagraphene47 and penta-graphene.29 In our studies, we have estimated the highest temperatures for the α- and β-phographenes to withstand against structural reconstructions, which are found to be 4000 and 3500 K, respectively. In Fig. 3, the evolutions of their total potential energies as a function of simulation time for the AIMD simulations at the corresponding highest temperatures are shown, respectively. Additionally, the structures obtained at the end of the simulations are presented as the insets in Fig. 3, which are 0.63 and 0.49 eV per atom higher in energy than the ideal planar structures of the corresponding ground states. Although structural distortions could be clearly seen, the structural skeletons are in fact preserved. Using them as the initial states, we have also carried out full structural optimizations at 0 K, which could quickly converge to the corresponding ground states, suggesting α- and β-phographenes to be protected by high energy barriers against structural transitions on the potential energy surface.
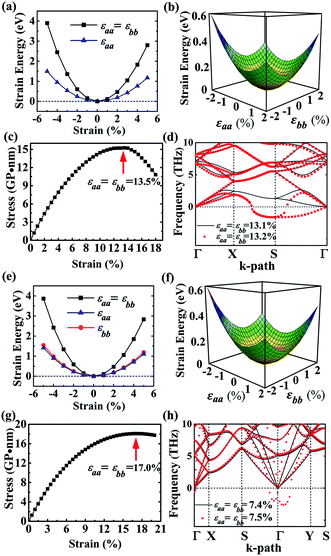
As to the application, the strain may also happen to the carbon allotrope, for example, which could be induced by the lattice mismatch between the planar sheet and the supporting substrate. Therefore, the mechanical stabilities of α- and β-phographenes are also worth of evaluating. In Fig. 4, we have studied the strain energy versus the applied strain, which is calculated by subtracting the total energy of the ground state structure from that of the strained structure. The Fig. 4a and e show the results of the α- and β-phographenes under the equi-biaxial and uniaxial strains, respectively. The corresponding energy surfaces versus the strains applied along the arbitrary in-plane directions are provided in Fig. 4b and f, respectively. The smooth evaluations of strain energies show that the deformation energies keep positive in the range of the studied strain loading in Fig. 4b and f, which suggest the mechanical stabilities according to the mechanical stability criteria.8 Additionally, we have calculated the corresponding linear elastic constants by using the finite distortion method. Following the standard Voigt notation, the elastic strain energy per unit can be written as:
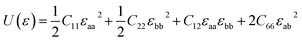 | (1) |
| Phographene | C11 | C22 | C12 | C66 |
|---|---|---|---|---|
| α | 310.41 | 310.41 | 79.65 | 130.63 |
| β | 320.41 | 293.58 | 141.86 | 95.64 |
Providing to use the new carbon allotrope in air conditions, the structural stability may bear effects from the oxygen. In our studies, we have carefully studied the adsorption of an O2 molecule on the phographenes. Same as to the hexagonal graphene, both the α-phographene and the β-phographene could not adsorb the O2, hinting the structural stability for the applications in air conditions. Additionally, hydrogenation is the often used technique for modifying the properties of 2D materials. We have also evaluated the stabilities of the hydrogenated α- and β-phographenes, whose lowest energy configurations are schematically shown in Fig. 5 along with the corresponding phonon spectra (the higher energy hydrogenation configurations are provided in the ESI Fig. S1 and S2†). In comparison with the phonon spectra for the pristine phographenes shown in Fig. 3, the presence of the high frequency modes comes from the covalent C–H bonding. Also, no imaginary mode in the simulated spectra suggests the structural stabilities.
3.2 Mechanical and electronic properties
Considering the applications, the mechanical properties of the carbon allotropes are also worth of evaluating on theory. Based on the tensor components calculated for the eqn (1), we studied the in-plane Young's modulus for the α- and β-phographenes, which are shown in Fig. 6. The 0°, 45°, and 90° angles correspond to the directions along with the lattice a, the diagonal axis, and the lattice b of the corresponding primitive unit cells, respectively. For the α-phographene, the lattices a and b are symmetrically equivalent resulting in the same Young's moduli along them, which are calculated to be 290.0 N m−1. As shown in Fig. 6, the modulus along with the directions corresponding to the angles between 0° and 90° would get larger. The largest Young's modulus is found to be in the diagonal direction (corresponds to the 45° angle), which is 312.9 N m−1. The β-phographene has different conditions, whose modulus along the lattices a and b are calculated to be 251.9 and 230.8 N m−1, respectively. The maximum is also found in the diagonal direction, which is 268 N m−1. Both of the primitive unit cells of them contain 20 C atoms, respectively. The areas of the 2D unit cells are 55.1 and 54.7 Å2 for the α- and β-phographenes, respectively. However, the calculated in-plane Young's moduli show that the β-phographene with slightly densely arranged C atoms is softer than the α-phographene, bearing the effects from the topological arrangements of the penta-, hexa-, and octa-carbon rings. Additionally, the Young's moduli of graphene,4 phagraphene,47 and penta-graphene29 are calculated to be 331.4, 292.9, 263.8 N m−1, respectively. The α-phographene shows comparable in-plane stiffness with graphene, suggesting good mechanical properties. In Fig. 6, the Poisson's ratio, ν, has also been theoretically estimated. The stiffer α-phographene shows overall smaller ratios as compared with the β-phographene. In comparison with the ν = 0.21 referring to the stretching in the lattice direction of graphene, the studied Poisson's ratios also show remarkable mechanical properties of the α-phographene. If the α-phographene was stretched, it would act similarly with its cousin part graphene which would only shrink slightly in the lateral direction. The maximum and minimum values happen to the situations of stretching the α-phographene along the lattice direction and the diagonal direction, which are ∼0.26 and 0.20, respectively. The maximum and minimum values of the β-phographene would be obtained by stretching it along the lattice b and a directions, which are calculated to be 0.44 and 0.38, respectively. Again, the α-phographene shows superior mechanical properties than the β-phographene.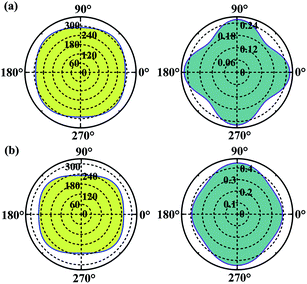 | ||
| Fig. 6 The orientation-dependences of the Young's modulus in N m−1 (left) and Poisson's ratio (right) of the α- and β-phographenes, respectively. | ||
The calculated energy bandstructures are presented in Fig. 7 for the α- and β-phographenes. Unlike graphene, no Dirac electronic characteristics are found. Both of them show metallic conducting properties. The effects of different topological arrangements of C atoms in the 2D carbon allotropes could also be seen in the corresponding conducting properties. Previous studies show that the graphene,4 OPG-Z,43 phagraphene,47 and circumcoro-graphyne45 have Dirac cones showing semimetal properties. The graphyne,10–20 graphdiyne,20–23 graphenylene,24 coro-graphene,45 and penta-graphene29 are semiconductors. And, the radialenes,28 pentahexoctite,30 HOP-graphene,31 pentaheptities,32,33 haeckelites,34 squarographene,35 C4 sheet,36–42 W-sheet,42,46 and OPG-L43,44 are reported to be metallic. It is well known that the DFT with GGA-PBE has the deficiency in describing bandgap in the calculated bandstructure. It reduces the original problem to an auxiliary problem involving fictitious noninteracting particles moving in a one-body effective potential, the familiar Hartree potential, and an exchange–correlation potential. The byproduct of the Kohn–Sham approach is a set of single-particle eigenvalues, which tends to underestimate the bandgap. In this study, we have also applied the more accurate Heyd–Scuseria–Ernzerhof (HSE) hybrid functional which includes a screened short-range Hartree–Fock exchange term.73,74 The HSE06 functional with the empirical parameter α = 0.25 was adopted, which is widely used for studying the semiconductor materials. Our calculations on HSE level confirm the conducting properties of the α- and β-phographenes. One can see that the bandstructures shown in Fig. 7 have distinct characteristics for the α- and β-phographenes. There are nearly parallel bands in the proximity of Fermi energy of the α-phographene to help increase the joint density of states at the energy of ∼1.6 eV, which may find applications in photoelectronics.
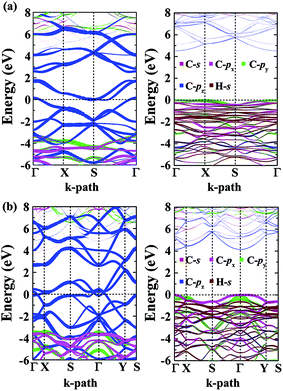 | ||
| Fig. 7 The orbital-resolved bandstructures of the phographenes (left) and the corresponding hydrogenated sheets (right). The α- and β-phographenes are studied in the (a) and (b), respectively. | ||
As shown in Fig. 7, both the valence and conducting bands around Fermi energy originate from the pz orbitals in the α- and β-phographenes, which would form the π-like bonds on both sides of the 2D carbon allotropes, agreeing with the sp2-like electronic hybridization configurations. In the fully hydrogenated allotropes, the pz orbital would be saturated with hydrogen atoms. All of the electrons would be bound in the strong σ-like covalent bonds, opening wide bandgaps in the calculated bandstructures of the hydrogenated α- and β-phographenes. Previously, Sun and coworkers reported that the remarkable ferromagnetic properties could be obtained in the semi-hydrogenated graphene.75 As to the semi-hydrogenated phographenes, our careful analyses of the phonon spectra support their structural stabilities. Unlike the semihydrogenated graphene, the ground states of the hydrogenated phographenes are antiferromagnetic with more than 19 meV per coupling than the corresponding ferromagnetic states, respectively. In the lowest energy configuration of the semihydrogenated phographene, the naked C–C dimer pair gains presence in the pentagonal carbon rings, which tends to form π-like bond paring the corresponding pz electrons. The unpaired pz electrons are distributed on 4 carbon atoms in the carbon octagon, which are separated with each other by the carbon atoms bonded with H atoms on the octagonal ring, preferring the antiferromagnetic couplings.
3.3 Discussion on the structural growth
As shown in Table 2, the newly proposed α- and β-phographenes are almost degenerate with the previously reported phagraphene in energy. From the point of view of the energy, the phagraphene and the low-lying phographenes gain almost the same possibilities in structural growing, challenging the experimental fabrications of α- or β-phographene single crystal materials. In experimental studies, the metal surfaces, such as the {111}-faceted surfaces of Cu, Ag, Au, and Pt, are usually used as substrates for growing 2D materials, which are rich of electrons in surface states. Furthermore, the methodology of near-surface alloy could be used to alter the reactive of metal surfaces,76,77 which could be used to enhance the charge transfer between the metal substrate and its supported 2D materials. Additionally, the injection of electrons was previously used to engineer the reactivity of 2D materials.78 Therefore, we would like to consider the effects of the electron injection on the structural growth of carbon allotropes, with the purpose to shed light on the corresponding experimental fabrications. In Fig. 8a, the energy evolutions of the low energy carbon allotropes are studied as a function of the quantity of the injected electrons. Among the examined allotropes, the α- and β-phographenes could be separated from the other ones, which would get much more favored for experimental fabrications according to the lower total energies in the charged states. For example, the phagraphene would be ∼60 meV per atom higher than the α- and β-phographenes in the −0.2 e per atom charged state, which are however almost degenerate in energy in the neutral state.From the point of view of the energy, we reach now that the α- and β-phographenes could be not separated with each other in both neutral and negatively charged states. Though the positively charged state may have difficulty to be realized on experiment, we also calculated the energies of the α- and β-phographenes after removing some electrons from the corresponding neutral states, which however could not bring obvious energy difference between them also. In order to shed light on the possibilities of which phase of phographene would gain priority for fabrication, we also studied the formation of the corresponding structural units. The pentagonal, hexagonal, heptagonal, and octagonal rings are the structural units which could be obtained on experiment for carbon nanostructures. We start our studies with an isolated carbon octagon, followed by introducing more carbon rings (see the ESI Fig. S3†). Based on the carbon octagon, the formation of an adjacent carbon hexagon is a little lower in energy than a carbon pentagon. Introducing one more carbon ring, the configuration of the hexagonal and pentagonal rings adhering on the adjacent C–C edges of the seed structural unit – the carbon octagon and sharing one C–C between them would be preferable. Again, adding one more carbon ring, the lowest energy structure shows the tendency for arranging the hexagonal and pentagonal rings alternatively on the adjacent C–C edge of the carbon octagon. Following this trend, the structural fragment of the α-phographene could be obtained (see the Fig. 8b). In comparison, the structural fragment of the β-phographene shown in Fig. 8b is also studied. While both the studied fragments contain 20 C atoms and 12 H atoms, the one for the α-phographene gains 1.12 eV lower total energy to gain priority for experimentally synthesis. This may facilitate the fabrication of the α-phographene, calling for experimental realization.
3.4 Catalytic properties as supporting noble metal catalysts
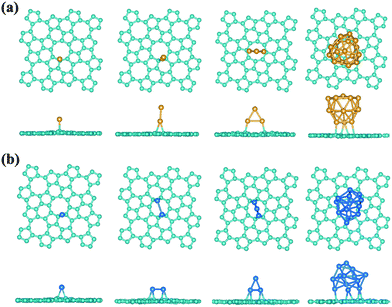
Interestingly, a most recent theory-experiment joint study shows the advances in achieving high-performance catalytic properties by using the nitrogen-doped graphene to support platinum atoms or particles, where the enhanced interaction between Pt and N-doped graphene plays an important role.79 In the ideal pristine graphene, the pz electrons would be bound in the conjugate π-bonds making the graphene to some sense inert, whose reactivity could be enhanced by the structural defect, chemical modification, bending curvature, and tensile strain, etc.80–84 Compared with the graphene, the sp2 hybridization in phographene is perturbed, which may in turn also affect the reactivity. Hereafter, with the purpose to facilitate discussion and considering the above discussion on the structural growth, we would like to take the α-phographene as the prototype structure for examining the topologically enhanced reactivity. In our studies, we have calculated the adsorption of the O2, H2, CO, and N2 gas molecules on the α-phographene, which would not be hold in chemisorption states. However, the difference in reactivity between graphene and phographene could be seen in the adsorption of Au atom. In our studies, we have calculated the adsorptions of Au and Pt clusters with the PBE functional. The relativistic effects were included by using the scalar relativistic approach. A single Au atom could not be adsorbed on graphene while it can adhere on phographene by developing chemical-like bonding between them. The best adsorption site is upon a carbon atom (see Fig. 9a). The bond length between Au and C atoms is 2.19 Å, being slightly longer than the corresponding atomic radius sum (2.05 Å). Additionally, the adsorption energy, Ead, is calculated to be 0.43 eV by the below definition.| Ead = Esheet + Emetal − Emetal/sheet | (2) |
| Structure | Au | Au2 | Au3 | Au16 | Pt | Pt2 | Pt3 | Pt12 |
|---|---|---|---|---|---|---|---|---|
| Graphene | — | — | — | — | 1.59 | 0.96 | 1.44 | 0.57 |
| Phographene | 0.43 | 0.73 | 1.18 | 0.31 | 2.16 | 1.68 | 2.67 | 1.72 |
4. Conclusions
Based on the density functional theory computation and the global minimum structural search, we have found the α-, β-, and δ-phographenes as new carbon allotropes. The α-phographene is almost degenerate in energy with the previously reported phagraphene. The β- and δ-phographenes are about 7 and 63 meV per atom higher in energy. The previously reported γ- and ε-phographenes have about 51 and 155 meV per atom higher energies. The other known non-honeycomb 2D carbon allotropes including the graphyne, graphdiyne, C4-sheet, penta-graphene, etc. are >100 meV per atom higher in energy. Both the α- and β-phographenes are found to have superior dynamic, thermal, and mechanical stabilities. In the charged state, the α- and β-phographenes would be significantly lowered in energy as compared to the phagraphene. Furthermore, our analysis on the growth of structural motifs shows the preference of the fabrication of α-phographene. Additionally, the α-phographene has close Young's modulus and Poisson's ratio to those of graphene, indicating remarkable mechanical properties. Both α- and β-phographenes are metallic. The α-phographene shows enhanced joint density of states at the energy of ∼1.6 eV, which may find applications in photoelectronics. Hydrogenation would alter them to wide-gap semiconductors. The enhanced adsorptions of the Pt and Au clusters on the α-phographene show the probabilities in supporting precious metal species to form high-performance complex catalyst nanostructures, being attractive to call for experimental investigations.Acknowledgements
The authors gratefully acknowledge the financial supports from the National Natural Science Foundation of China (NSFC) (Grant No. 11674129 and 11374128).References
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56 CrossRef CAS.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 2003 Search PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- A. T. Balaban, C. C. Rentia and E. Ciupitu, Rev. Roum. Chim., 1968, 13, 231 CAS.
- D. Li, F. Tian, D. Duan, Z. Zhao, Y. Liu, B. Chu, X. Sha, L. Wang, B. Liu and T. Cui, RSC Adv., 2014, 4, 17364 RSC.
- M. J. Xing, B. H. Li, Z. T. Yu and Q. Chen, RSC Adv., 2016, 6, 32740 RSC.
- X. Zhu and M. Wang, RSC Adv., 2016, 6, 112035 RSC.
- Z. G. Fthenakis, RSC Adv., 2016, 6, 78187 RSC.
- H. Lu and S.-D. Li, J. Mater. Chem. C, 2013, 1, 3677 RSC.
- R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687 CrossRef CAS.
- N. Narita, S. Nagai, S. Suzuki and K. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11009 CrossRef CAS.
- V. R. Coluci, S. F. Braga, S. B. Legoas and D. S. Galvão, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035430 CrossRef.
- A. N. Enyashin and A. L. Ivanovskii, Phys. Status Solidi B, 2011, 248, 1879 CrossRef CAS.
- Y. Yang and X. Xu, Comput. Mater. Sci., 2012, 61, 83 CrossRef CAS.
- J. Zhou, K. Lv, Q. Wang, X. S. Chen, Q. Sun and P. Jena, J. Chem. Phys., 2011, 134, 174701 CrossRef PubMed.
- S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111 CrossRef CAS.
- D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804 CrossRef PubMed.
- B. G. Kim and H. J. Choi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115435 CrossRef.
- S. Chopra, RSC Adv., 2016, 6, 89934 RSC.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256 RSC.
- X. Qian, H. Liu, C. Huang, S. Chen, L. Zhang, Y. Li, J. Wang and Y. Li, Sci. Rep., 2014, 5, 7756 CrossRef PubMed.
- M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593 CrossRef CAS PubMed.
- Q. Song, B. Wang, K. Deng, X. Feng, M. Wagner, J. D. Gale, K. Müllen and L. Zhi, J. Mater. Chem. C, 2013, 1, 38 RSC.
- W. Liu, M.-S. Miao and J.-Y. Liu, RSC Adv., 2015, 5, 70766 RSC.
- M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, ACS Nano, 2010, 4, 4565 CrossRef CAS PubMed.
- N. N. Karaush, S. V. Bondarchuk, G. V. Baryshnikov, V. A. Minaeva, W.-H. Sun and B. F. Minaev, RSC Adv., 2016, 6, 49505 RSC.
- E. Konstantinova, S. O. Dantas and P. M. V. B. Barone, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035417 CrossRef.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372 CrossRef CAS PubMed.
- B. R. Sharma, A. Manjanath and A. K. Singh, Sci. Rep., 2014, 4, 7164 CrossRef CAS PubMed.
- B. Mandal, S. Sarkar, A. Pramanik and P. Sarkar, Phys. Chem. Chem. Phys., 2013, 15, 21001 RSC.
- V. H. Crespi, L. X. Benedict, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13303 CrossRef.
- M. Deza, P. W. Fowler, M. Shtogrin and K. Vietze, J. Chem. Inf. Comput. Sci., 2000, 40, 1325 CrossRef CAS PubMed.
- H. Terrones, M. Terrones, E. Hernández, N. Grobert, J.-C. Charlier and P. M. Ajayan, Phys. Rev. Lett., 2000, 84, 1716 CrossRef CAS PubMed.
- M. J. Bucknum and E. A. Castro, Solid State Sci., 2008, 10, 1245 CrossRef CAS.
- H. Y. Zhu, A. T. Balaban, D. J. Klein and T. P. Zivkovic, J. Chem. Phys., 1994, 101, 5281 CrossRef CAS.
- X. Q. Wang, H. D. Li and J. T. Wang, Phys. Chem. Chem. Phys., 2012, 14, 11107 RSC.
- Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505 CrossRef PubMed.
- J. Nisar, X. Jiang, B. Pathak, J. Zhao, T. W. Kang and R. Ahuja, Nanotechnology, 2012, 23, 385704 CrossRef PubMed.
- X.-L. Sheng, H.-J. Cui, F. Ye, Q.-B. Yan, Q.-R. Zheng and G. Su, J. Appl. Phys., 2012, 112, 074315 CrossRef.
- G. Long, Y. Zhou, M. Jin, M. Jin, B. Kan, Y. Zhao, A. Gray-Weale, D. Jiang, Y. Chen and Q. Zhang, Carbon, 2015, 95, 1033 CrossRef CAS.
- L.-C. Xu, R.-Z. Wang, M.-S. Miao, X.-L. Wei, Y.-P. Chen, H. Yan, W.-M. Lau, L.-M. Liu and Y.-M. Ma, Nanoscale, 2014, 6, 113 CrossRef PubMed.
- C. Su, H. Jiang and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075453 CrossRef.
- C.-P. Tang and S.-J. Xiong, AIP Adv., 2012, 2, 042147 CrossRef.
- N. V. R. Nulakani, M. Kamaraj and V. Subramanian, RSC Adv., 2015, 5, 78910 RSC.
- X. Q. Wang, H. D. Li and J. T. Wang, Phys. Chem. Chem. Phys., 2013, 15, 2024 RSC.
- Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182 CrossRef CAS PubMed.
- L. F. C. Pereira, B. Mortazavi, M. Makaremi and T. Rabczuk, RSC Adv., 2016, 6, 57773 RSC.
- A. Stone and D. Wales, Chem. Phys. Lett., 1986, 128, 501 CrossRef CAS.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26 CrossRef CAS PubMed.
- J. Lahiri, Y. Lin, P. Bozkurt, I. I. Oleynik and M. Batzill, Nat. Nanotechnol., 2010, 5, 326 CrossRef CAS PubMed.
- J.-H. Chen, G. Autès, N. Alem, F. Gargiulo, A. Gautam, M. Linck, C. Kisielowski, O. V. Yazyev, S. G. Louie and A. Zettl, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121407 CrossRef.
- G. Kress and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef.
- G. Kress and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227 CrossRef CAS PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172 CrossRef CAS.
- X.-F. Zhou, X. Dong, A. R. Oganov, Q. Zhu, Y. Tian and H.-T. Wang, Phys. Rev. Lett., 2014, 112, 085502 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- J. P. Perdew and Z. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- J. Li, Y. Wei, X. Fan, H. Wang, Y. Song, G. Chen, Y. Liang, V. Wang and Y. Kawazoe, J. Mater. Chem. C, 2016, 4, 9613 RSC.
- J. Li, X. Fan, Y. Wei, J. Liu, J. Guo, X. Li, V. Wang, Y. Liang and G. Chen, J. Mater. Chem. C, 2016, 4, 10866 RSC.
- C. G. Lee, X. D. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385 CrossRef CAS PubMed.
- M. Born and H. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1998 Search PubMed.
- J. Li, X. Fan, Y. Wei and G. Chen, Sci. Rep., 2016, 6, 31840 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- J. T. Jiang, S. L. Xiu, M. M. Zheng, T. T. Jia, H. Y. Liu, Y. Zhang and G. Chen, Chem. Phys. Lett., 2014, 613, 74 CrossRef CAS.
- J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867 CrossRef CAS PubMed.
- M. M. Zheng, S. J. Li, Y. Su, G. Chen and Y. Kawazoe, J. Phys. Chem. C, 2013, 117, 25077 CAS.
- M. M. Zheng, T. Q. Ren, G. Chen and Y. Kawazoe, J. Phys. Chem. C, 2014, 118, 7442 CAS.
- Q. Sun, Z. Li, D. J. Searles, Y. Chen, G. Lu and A. Du, J. Am. Chem. Soc., 2013, 135, 8246 CrossRef CAS PubMed.
- N. Cheng, S. Stambula, D. Wang, M. N. Banis, J. Liu, A. Riese, B. Xiao, R. Li, T.-K. Sham, L.-M. Liu, G. A. Botton and X. Sun, Nat. Commun., 2016, 7, 13638 CrossRef CAS PubMed.
- M. Zhou, A. Zhang, Z. Dai, C. Zhang and Y. P. Feng, J. Chem. Phys., 2010, 132, 194704 CrossRef PubMed.
- S. L. Xiu, M. M. Zheng, P. Zhao, Y. Zhang, H. Y. Liu, S. J. Li, G. Chen and Y. Kawazoe, Carbon, 2014, 79, 646 CrossRef CAS.
- G. Chen, S. J. Li, Y. Su, V. Wang, H. Mizuseki and Y. Kawazoe, J. Phys. Chem. C, 2011, 115, 20168 CAS.
- M. Zhou, A. Zhang, Z. Dai, Y. P. Feng and C. Zhang, J. Phys. Chem. C, 2010, 114, 16541 CAS.
- G. Chen and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125410 CrossRef.
- S. Bulusu, X. Li, L. S. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326 CrossRef CAS PubMed.
- G. Chen, Q. Wang, Q. Sun, Y. Kawazoe and P. Jena, J. Chem. Phys., 2010, 132, 194306 CrossRef PubMed.
- I. Fampiou and A. Ramasubramaniam, J. Phys. Chem. C, 2012, 116, 6543 CAS.
- G. Chen, P. Jena and Y. Kawazoe, J. Chem. Phys., 2008, 129, 074305 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01762f |
| This journal is © The Royal Society of Chemistry 2017 |