Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A peculiar layered 12-fold cationic coordination compound LiInTi2O6: phase relations, crystal structure and color-tunable photoluminescence†
Liu-Mei Suab,
Xing Fanab,
Ge-Mei Cai *ab and
Zhan-Peng Jin*ab
*ab and
Zhan-Peng Jin*ab
aSchool of Materials Science and Engineering, Central South University, Changsha, 410083, Hunan, P. R. China. E-mail: caigemei@csu.edu.cn; jin@csu.edu.cn
bEducation Ministry Key Laboratory of Non-ferrous Materials Science and Engineering, Central South University, Changsha, 410083, Hunan, P. R. China
First published on 20th April 2017
Abstract
Developing new hosts is one of the significant and intriguing aspects in the field of luminescence materials. Herein, we report a novel LiInTi2O6 host for phosphors in solid state lighting. The sub-solidus phase relationships, thermal stability, crystal structure, as well as composition- and temperature-dependent luminescence were investigated and discussed by means of various analytical techniques, including powder X-ray diffraction (XRD), differential scanning calorimetry (DSC), structure solution, photoluminescence excitation (PLE) and emission (PL) spectra, decay lifetime, high-temperature luminescence and chromaticity coordinates. LiInTi2O6 crystallizes in a trigonal unit cell with lattice parameters of a = b = 5.1050(1) Å, c = 28.5622(4) Å, and Z = 6 in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 166), consisting of an unusual 12-fold coordination hexagonal prism structural framework. Taking LiInTi2O6 as the host, a series of Dy3+/Tm3+ singly-doped and co-doped phosphors was successfully synthesized. With increasing Dy3+ concentration, the emission colors of LiInTi2O6:Tm3+,Dy3+ phosphors can be appropriately tuned from blue to yellow, going through the white region, based on the principle of energy transfer. Energy transfer efficiencies were calculated and the mechanism was confirmed to follow a resonant-type electric dipole–dipole interaction. A configuration coordinate diagram was employed to explain the thermal quenching behaviour of the white lighting phosphor. Structural characteristics and evolution trends of representative titanates were summarized, providing available information for photo/electrical materials designing.
m (No. 166), consisting of an unusual 12-fold coordination hexagonal prism structural framework. Taking LiInTi2O6 as the host, a series of Dy3+/Tm3+ singly-doped and co-doped phosphors was successfully synthesized. With increasing Dy3+ concentration, the emission colors of LiInTi2O6:Tm3+,Dy3+ phosphors can be appropriately tuned from blue to yellow, going through the white region, based on the principle of energy transfer. Energy transfer efficiencies were calculated and the mechanism was confirmed to follow a resonant-type electric dipole–dipole interaction. A configuration coordinate diagram was employed to explain the thermal quenching behaviour of the white lighting phosphor. Structural characteristics and evolution trends of representative titanates were summarized, providing available information for photo/electrical materials designing.
1. Introduction
In recent years, in recognition of the importance of saving energy, the light-emitting diode (LED) solid-state lighting industry has gradually gained much attention and has motivated many governments around the world to put scientific R&D plans in place in consideration of either energy issues or economic growth.1–5 In particular, white LEDs, which exhibit remarkable properties that are superior to their conventional incandescent and fluorescent counterparts due to their merits of excellent reliability, high luminous efficiency, long lifetime, and low energy consumption, are accepted as the next-generation of solid-state lighting sources in the field of energy-saving technologies.6–8 As a key component in phosphor-converted WLEDs, inorganic luminescent materials undeniably play an important role in determining the performance of solid-state lighting devices;9 it is therefore required that they possess high conversion efficiency, appropriate emission colors as well as good stabilities. Given the high desirability for developing high-performance phosphors, abundant research efforts have been triggered to seek after novel phosphors through various strategies.10–12 Exploring a suitable host to accommodate diverse activators to generate different colored phosphors is essential, and has stimulated researchers to devote themselves to investigating a variety of material systems, including but not limited to silicates, borates, niobates, phosphates, oxynitrides, and fluorides, leading to the discovery of a large quantity of phosphors with distinct crystal structures and fascinating photoluminescence properties.13–17 As one of the research hotspots, exploring new compounds with special structures for phosphors is a long-standing development direction in the field of inorganic luminescent materials.Among the variety of inorganic structural compounds, perovskites score over others due to their structural versatility and physical properties. In either the non-doped form or as a doped system, they have been applied as thermoelectric materials, catalysts, dielectrics, ferroelectrics, solid-state electrolytes, and have recently sprung up in the luminescence field.18 A family of isomorphous layered perovskites, (ALn)0.5TiO3, where A represents an alkali-metal ion and Ln denotes a lanthanide, have been exploited as excellent candidates for phosphor hosts.19 They are proven to be have two-dimensional layered structures built by corner-shared TiO6 octahedra, with A and Ln ions located at the interstices of TiO6 groups. The band gap absorbing TiO6 octahedral groups give rise to their interesting photoluminescence properties.20 To our knowledge, on account of its similarity to lanthanide ions, in terms of ionic radius and physicochemical properties, the indium ion is found to be able to substitute for lanthanide ion in some types of compounds to form isomorphous or heteromorphic crystal structures, some of which even have outstanding luminescence properties.21,22 Therefore, the focus of this project was the search for potential layered compounds in the Li2O–In2O3–TiO2 ternary system.
From this point of view, in this contribution, we have systematically investigated the phase relationship of the Li2O–In2O3–TiO2 ternary system via solid-state reactions, leading to the discovery of a new ternary compound, LiInTi2O6. To determine the crystal structure of this compound, crystallographic analysis based on powder X-ray diffraction data was implemented. Considering the underlying optical functions of a novel layered phase, especially one in which the ligand properties and ionic radius of In3+ is similar to rare-earth ions, blue-emitting of Tm3+ and yellow-emitting of Dy3+ ions were chosen as the co-doped activators to prepare white-light emitting LiInTi2O6 phosphors, in view of effective energy transfer existing between them in some special crystal field environments. In this work, the structure-, composition- and temperature-dependent luminescence properties of Tm3+ and Dy3+ co-doped LiInTi2O6 phosphors are investigated by means of structural analysis, photoluminescence excitation (PLE) and emission (PL) spectra, decay lifetimes, high-temperature luminescence, and chromaticity coordinates. Integrating these results indicate that LiInTi2O6 is a promising candidate as a phosphor host in solid-state lighting.
2. Experimental procedures
All polycrystalline samples with different nominal compositions in the Li2O–In2O3–TiO2 system were synthesized by conventional solid-state reaction using stoichiometric amounts of analytical reagent Li2CO3 (99.99%, Sinopharm Chemical Reagent Co. Ltd., Shanghai, China), In2O3 (99.99%, Sinopharm Chemical Reagent Co. Ltd., Shanghai, China) and TiO2 (99.9%, Sinopharm Chemical Reagent Co. Ltd., Shanghai, China) as starting materials. Oxide powders were weighed according to different compositions in 2 ± 0.0005 g batches and mixed with an agate mortar. The mixtures were calcined in alumina crucibles at 800 °C for 12 h at a heating rate of 5 °C min−1, followed by cooling inside the furnace to room temperature. Calcined powders were reground and sintered at 1000 °C for 24 h at 5 °C min−1, then furnace cooled and ground for X-ray diffraction (XRD) investigation. The sintering procedure was repeated until no significant changes were observed in the XRD patterns. Rare-earth doped LiInTi2O6 phosphors were prepared via a solid-state reaction method as well, by adding rare-earth oxides Tm2O3 and Dy2O3 with purity of 99.99% (Alfa Aesar) into the starting material batches, according to stoichiometric ratios. Synthesis conditions were the same as that of the polycrystalline samples described above.Phase identification of products was conducted using powder XRD patterns collected on an X-ray diffractometer (Rigaku D/MAX-2500, Rigaku Co., Tokyo, Japan) with Cu Kα radiation and a graphite monochromator operating at 40 kV and 250 mA. Powder diffraction data used for crystal structure analysis of LiInTi2O6 were gathered on a powder X-ray diffractometer (PANalytical X'Pert Pro, PANalytical B.V., Almelo, Netherlands) with Cu Kα radiation in a step scanning mode over a 2θ range from 8° to 130°, with an interval of 2θ = 0.026°. Structure solution for LiInTi2O6 was performed by using the JANA2006 software package.23,24 The structure solution led to a reasonable rough structure model including all of the atomic sites, which was refined by the Rietveld method25 using the Fullprof_suite program26 on the basis of powder diffraction data. The thermal stability of LiInTi2O6 was investigated by the thermal analysis method using a differential scanning calorimeter (DSC) (SETSYS evolution, SETARAM INSTRUMENTATION, Caluire, France) in the temperature range of 25–1300 °C with a heating rate of 10 °C min−1 under an argon atmosphere.
Photoluminescence excitation (PLE) and photoluminescence emission (PL) spectra were recorded on a fluorescence spectrophotometer (Hitachi, F-7000) equipped with a 150 W xenon lamp as the excitation source. The temperature-dependent luminescence properties were measured on the same fluorescence spectrophotometer equipped with a computer-controlled heating attachment (Tianjin Orient KOJI Co. Ltd, TAP-02). Photoluminescence decay curves were obtained from a fluorescence spectrometer (Edinburgh, FLS-920) with a nF900 flash lamp as the excitation source. The CIE coordinates were calculated by using the PL data according to the CIE 1931 standard colorimetric systems. All the measurements were performed at room temperature.
3. Results and discussion
3.1. Phase relations in Li2O–In2O3–TiO2 ternary system
For the purpose of investigating phase relations in the Li2O–In2O3–TiO2 ternary system, many polycrystalline samples with certain compositions were synthesized. Phase assemblages of these products were analyzed by using powder XRD data collected at room temperature. Based on analysis of all the prepared samples, by means of retrieving phases according to ICCD-PDF (PDF-4+ 2012) and ICSD (version 2014) databases, the phases contained in mixtures were identified. Surprisingly, a new ternary compound with a set of unknown diffraction patterns detected in some TiO2-riched samples was discovered in this work and no isostructural phases in databases were matched with it. Its formula was determined as LiInTi2O6, based on nominal composition and contact rules for phase regions. Consequently, phase regions, i.e. sub-solidus phase relations in the Li2O–In2O3–TiO2 ternary system were determined under the present experimental conditions, according to the results of phase identification. The phase diagram for Li2O–In2O3–TiO2 is shown in Fig. 1. It is divided into seven determinate three-phase regions by two-phase join-lines. As for the Li2O-rich region, marked with dashed lines in Fig. 1, it could not be determined due to Li2O volatilizing and reacting with the corundum crucibles at high temperature.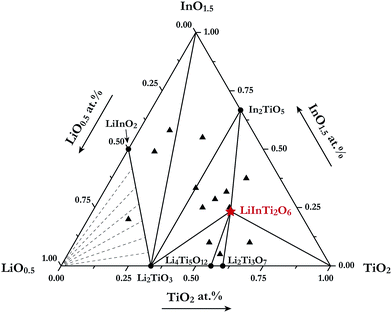 | ||
| Fig. 1 Sub-solidus phase relationships of the Li2O–In2O3–TiO2 ternary system at 1000 °C. The filled triangles stand for samples located at three-phase regions and the star denotes pure LiInTi2O6. | ||
In the In2O3–TiO2 subsystem, only one binary compound, In2TiO5 (PDF#82-0326) was ever reported, and is now confirmed in this work. It was found to be isostructural to In2VO5 with an orthorhombic unit cell (S.G. Pnma) of a = 7.2418 Å, b = 3.5018 Å, and c = 14.890 Å, and its crystal structure has been refined by the Rietveld method.27 As for the Li2O–In2O3 subsystem, two binary compounds, LiInO2 and Li3InO3, were reported.28,29 Li3InO3, containing the constituent of Li2O as high as 75 mol%, was not detected under the present experimental conditions. The Li2O–TiO2 binary phase diagram has been assessed by Izquierdo et al.30 Four stable lithium titanates, Li4TiO4, Li2TiO3, Li4Ti5O12, and Li2Ti3O7, form in this binary system. Except for the Li4TiO4 phase, all the others were confirmed in this work. Li2TiO3 undergoes an order-disordered phase transformation from monoclinic β-phase to cubic γ-phase at about 1155 °C.31 Herein, only the low-temperature monoclinic β-Li2TiO3 (PDF#33-0831) was observed. Referring to the spinel phase Li4Ti5O12 (PDF#49-0207) and the ramsdellite-like phase Li2Ti3O7 (PDF#34-0393), they decompose in the form of the peritectoid reaction above 1018 °C and eutectoid reaction below 940 °C, respectively.30,32 As a consequence, both of these phases were detected within the range of our experimental temperature. Extrapolated to the Li2O–In2O3–TiO2 ternary system, as aforementioned, only the formation of a new ternary compound LiInTi2O6 was confirmed, and its thermal stability as well as the crystal structure is elaborated in the following section.
3.2. Thermal stability and crystal structure of LiInTi2O6
Investigation of the phase thermal stability has a great significance for materials synthesis design; therefore, we aimed to clarify the thermal stability of the newly discovered ternary compound, LiInTi2O6. The thermal analysis curve collected by DSC is shown in Fig. 2a. An obvious endothermic peak centered at 1153.5 °C was detected. Accordingly, it can be speculated that LiInTi2O6 would endothermically decompose upon heating to about 1153.5 °C. In order to verify this conjecture, some heat treatment experiments for LiInTi2O6 were performed. XRD patterns for pure phase LiInTi2O6 and its products heated at different temperature are shown in Fig. 2b. It is obvious that when heated at 1050 °C for 24 h, its XRD pattern remains unchanged. This means that LiInTi2O6 does not decompose at the present temperature. Upon being heated at 1100 °C for 24 h, some tiny diffraction peaks assigned to In2TiO5 (PDF#82-0326) and TiO2 (PDF#77-0440) turned up, in addition to the content of LiInTi2O6 decreasing, thus indicating that LiInTi2O6 decomposition was initiated. When heated at higher the temperature of 1200 °C, this compound completely decomposed into In2TiO5, TiO2 and Li2Ti3O7 (PDF#34-0393). Consequently, a four-phase transformation reaction of LiInTi2O6 → TiO2 + In2TiO5 + Li2Ti3O7 is considered to take place in the range of 1100–1200 °C. According to the DSC curve, its temperature was determined to be about 1153.5 °C. Besides, the sharp endothermic peak with the minimum at 1292 °C corresponds to the incongruently melting point of Li2Ti3O7.30,32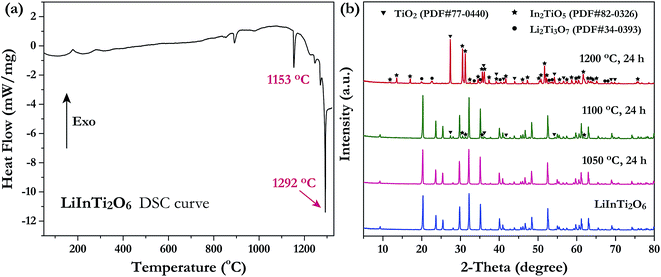 | ||
| Fig. 2 (a) The DSC curve of LiInTi2O6. (b) XRD patterns of LiInTi2O6 heated at 1050, 1100 and 1200 °C, respectively, compared to the pure phase pattern. | ||
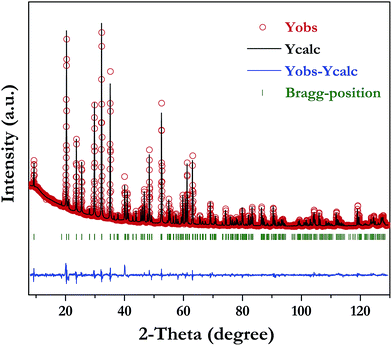
The XRD pattern of LiInTi2O6 can be indexed to a trigonal unit cell with lattice parameter of a = b = 5.1050(1) Å, c = 28.5622(4) Å, and Z = 6 in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 166) by using the WinCSD program package.33 The rough structural model of LiInTi2O6 solved by the charge-flipping method34 consists of 6 crystallographic sites for distinct atoms: one lithium site, one indium site, two titanium sites, and two sites for oxygen. Based on this unprocessed crystal structure, further structural modification via Rietveld refinement was performed. The final refined plot for LiInTi2O6 is depicted in Fig. 3 and the refined crystallographic parameters and reliability factors are listed in Table 1. Primary reliability factors were converged to RB = 5.66%, Rp = 2.88%, Rwp = 4.39%, and S = 2.31, indicating that this crystal structure for LiInTi2O6 is reasonably accepted. Structural parameters including atomic occupations and bond lengths for LiInTi2O6 are listed in Table 2 and 3, respectively. Refinement shows that titanium ions occupy two 6c sites; the other 6c site is co-occupied by lithium and titanium ions, and the remaining 6c site is a mixed In/Li/Ti site. It is worth mentioning that according to the atomic occupancies of refinement, the actual formula of this new ternary compound should be Li0.856In0.92Ti1.672O6, which deviated from stoichiometry; we approximately adopted LiInTi2O6 to denote this new ternary compound in this context.
m (No. 166) by using the WinCSD program package.33 The rough structural model of LiInTi2O6 solved by the charge-flipping method34 consists of 6 crystallographic sites for distinct atoms: one lithium site, one indium site, two titanium sites, and two sites for oxygen. Based on this unprocessed crystal structure, further structural modification via Rietveld refinement was performed. The final refined plot for LiInTi2O6 is depicted in Fig. 3 and the refined crystallographic parameters and reliability factors are listed in Table 1. Primary reliability factors were converged to RB = 5.66%, Rp = 2.88%, Rwp = 4.39%, and S = 2.31, indicating that this crystal structure for LiInTi2O6 is reasonably accepted. Structural parameters including atomic occupations and bond lengths for LiInTi2O6 are listed in Table 2 and 3, respectively. Refinement shows that titanium ions occupy two 6c sites; the other 6c site is co-occupied by lithium and titanium ions, and the remaining 6c site is a mixed In/Li/Ti site. It is worth mentioning that according to the atomic occupancies of refinement, the actual formula of this new ternary compound should be Li0.856In0.92Ti1.672O6, which deviated from stoichiometry; we approximately adopted LiInTi2O6 to denote this new ternary compound in this context.
a RB = ∑|IO,h − IC,h|/∑|IO,h|.b RP = ∑|yi − yC,i|/∑yi.c 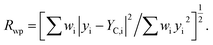 d S = Rwp/Rexp. d S = Rwp/Rexp. |
|
|---|---|
| Chemical Formula | LiInTi2O6 |
| Diffractometer | X'Pert Pro, PANalytical |
| Radiation type | Cu Kα, λ = 1.54060 Å |
| 2θ interval (°) | 8.021–129.987 |
| Step size of 2θ (°) | 0.026 |
| Space group | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 166) m (No. 166) |
| Z | 6 |
| a (Å) | 5.1050(1) |
| b (Å) | 5.1050(1) |
| c (Å) | 28.5622(4) |
| V (Å3) | 644.64(2) |
| Number of points | 4692 |
| Number of reflections | 350 |
| Number of structure parameters | 118 |
| Number of profile parameters | 12 |
| RBa (%) | 5.66 |
| Rpb (%) | 2.88 |
| Rwpc (%) | 4.39 |
| Sd | 2.31 |
| Atom | Site | x | y | z | Biso (Å2) | Occupancy |
|---|---|---|---|---|---|---|
| Li1 | 6c | 0 | 0 | 0.4190(4) | 1.1(3) | 0.814(1) |
| Ti1 | 6c | 0 | 0 | 0.4190(4) | 1.1(3) | 0.186(1) |
| In | 6c | 0 | 0 | 0.0741(1) | 0.6(4) | 0.916(1) |
| Li2 | 6c | 0 | 0 | 0.0741(1) | 0.6(4) | 0.042(1) |
| Ti2 | 6c | 0 | 0 | 0.0741(1) | 0.6(4) | 0.042(1) |
| Ti3 | 6c | 0 | 0 | 0.3255(2) | 0.5 | 0.743(1) |
| Ti4 | 6c | 0 | 0 | 0.1819(1) | 0.5 | 0.743(1) |
| O1 | 36i | −0.0320(14) | 0.3157(17) | 0.6998(3) | 1.1(2) | 0.5 |
| O2 | 36i | −0.0174(17) | 0.6837(15) | 0.1321(3) | 1.7(2) | 0.5 |
| Bond | Length (Å) | Bond | Length (Å) |
|---|---|---|---|
| Li1/Ti1–O1 (×6) | 2.1857 | In/Li2/Ti2–O1 (×6) | 2.1698 |
| Li1/Ti1–O2 (×6) | 2.2645 | In/Li2/Ti2–O2 (×6) | 2.2839 |
| Average | 2.2251 | Average | 2.2269 |
| Ti3–O1 (×6) | 1.8444 | Ti4–O2 (×6) | 1.7946 |
| Ti3–O1 (×6) | 1.9736 | Ti4–O2 (×6) | 2.1201 |
| Average | 1.9090 | Average | 1.9574 |
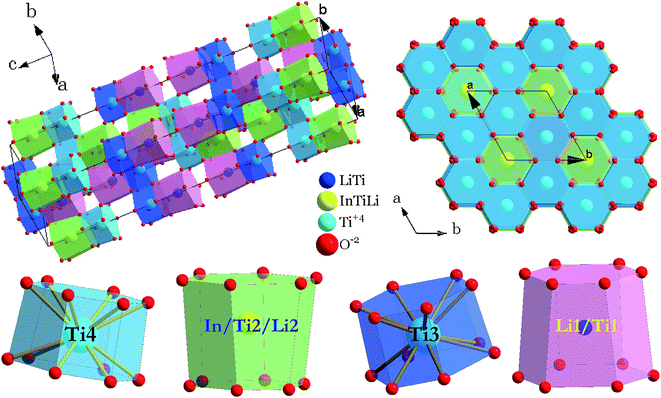
The crystal structure and coordination environments for cation sites of LiInTi2O6 are presented in Fig. 4. All the cations appear to have the same coordination environments, i.e. they are all coordinated with 12 oxygens to form distorted 12-fold coordination hexagonal prisms depending on the central cations. In three-dimensional structural framework, mixed hexagonal prisms stack layer by layer along the c axis in the form of edge-sharing and face-sharing. Titanium ions respectively occupying two distinct 6c sites, denoted as Ti3 and Ti4 in Fig. 4, alternately pile up along the c axis and are separated by (Li/Ti)O12 and (In/Li/Ti)O12 hexagonal prisms. In every TiO12 polyhedral layer, hexagonal prisms share three side-faces with each other at 120° angles to form hexagonal prismatic holes. By means of face-sharing, TiO12 polyhedra spread out towards the a and b axis to form two-dimensional sheets.
3.3. Color-tunable luminescence properties of LiInTi2O6:Tm3+,Dy3+ phosphors
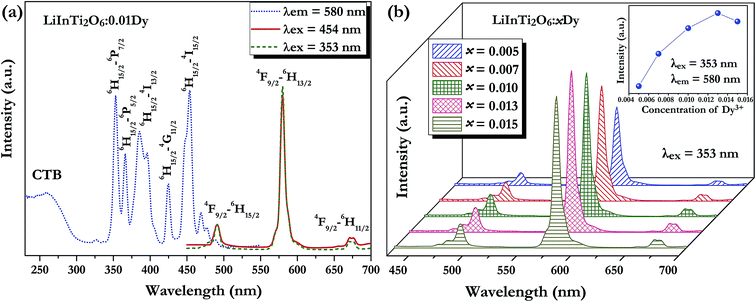
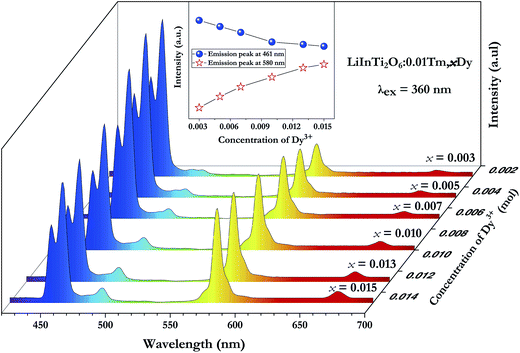
Fig. 5a shows the room temperature PLE and PL spectra for the Dy3+-activated LiInTi2O6 phosphor. When monitoring the characteristic emission of Dy3+ at 580 nm (4F9/2–6H13/2), the PLE spectrum of LiInTi2O6:0.01Dy3+ consists of a broad charge-transfer excitation band (CTB) and a series of sharp peaks in the range of 300–500 nm. Since Dy3+ in oxides does not have charge-transfer transition bands longer than 200 nm,35,36 the CTB in PLE spectrum of LiInTi2O6:0.01Dy3+ is mainly attributed to the absorption of Ti–O polyhedra in the host.37,38 The narrow excitation peaks are assigned to the f–f electronic transitions from the ground state 6H15/2 to distinct excited states (marked in Fig. 5a) of Dy3+ within its 4f9 electron configuration.38,39 Two excitation transitions at 353 nm (6H15/2–6P7/2) and 454 nm (H15/2–4I15/2) have comparable emission intensities, indicating that LiInTi2O6:Dy3+ phosphors are potential light-converting candidates for UV-LED and blue-LED applications in solid-state lighting. Upon excitation at 353 nm and 454 nm, the PL spectra of LiInTi2O6:0.01Dy3+ exhibit characteristic emissions of Dy3+. Evidently, the emission intensity of the electric dipole transition (4F9/2–6H13/2) located in the yellow region and centered at 580 nm is significantly higher than that of the blue emission peaking at 491 nm, which originated from a magnetic dipole transition of 4F9/2–6H15/2. Generally, the former transition is hypersensitive to the crystal-field environment of Dy3+.39,40 When Dy3+ occupies a lattice site that deviates from an inversion center, the 4F9/2–6H13/2 transition of yellow emission dominates and has a much higher intensity than the blue emission,41 therefore confirming that Dy3+ ions in LiInTi2O6:Dy3+ phosphors occupy the non-centrosymmetric 6c (C3v) sites, which are away from an inversion center in the centrosymmetric space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Fig. 5b presents the PL spectra of LiInTi2O6:xDy3+ phosphors with different Dy3+ doping concentrations under the excitation of 353 nm, as well as the dependence of emission intensities on Dy3+ concentrations (inset). As seen, the emission spectra profiles and the intensity ratio of yellow to blue emission (Y/B = 6.1–6.5) are almost unaltered over the full Dy3+-doped concentration range, indicating the surrounding environments for Dy3+ are not significantly changed as its concentration increased. As shown in the inset of Fig. 5b, the concentration quenching for LiInTi2O6:xDy3+ phosphors occur at x = 0.013, owing to cross relaxation between the energy levels of Dy3+, i.e. energy transfer from a transition of 4F9/2–6F3/2 in one Dy3+ to another Dy3+, with the transition of 6H15/2–6F11/2 of matching energy.
m. Fig. 5b presents the PL spectra of LiInTi2O6:xDy3+ phosphors with different Dy3+ doping concentrations under the excitation of 353 nm, as well as the dependence of emission intensities on Dy3+ concentrations (inset). As seen, the emission spectra profiles and the intensity ratio of yellow to blue emission (Y/B = 6.1–6.5) are almost unaltered over the full Dy3+-doped concentration range, indicating the surrounding environments for Dy3+ are not significantly changed as its concentration increased. As shown in the inset of Fig. 5b, the concentration quenching for LiInTi2O6:xDy3+ phosphors occur at x = 0.013, owing to cross relaxation between the energy levels of Dy3+, i.e. energy transfer from a transition of 4F9/2–6F3/2 in one Dy3+ to another Dy3+, with the transition of 6H15/2–6F11/2 of matching energy.
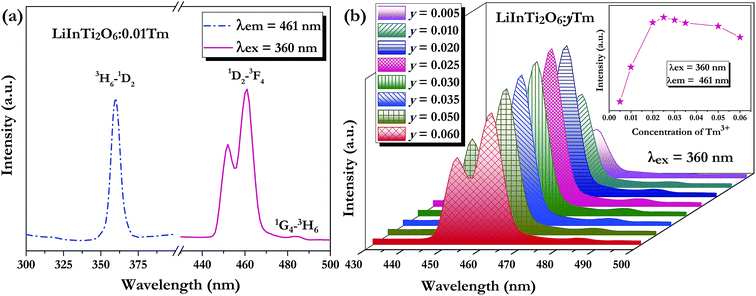
As for the Tm3+-activated LiInTi2O6 phosphors, their PLE and PL spectra are depicted in Fig. 6. The PLE spectrum of LiInTi2O6:0.01Tm3+ monitored at 461 nm simply exhibits a characteristic excitation peak of Tm3+ at 359 nm, which is generated from an f–f transition of 3H6–1D2 within the 4f12 configuration of Tm3+. Under the excitation of 360 nm, the PL spectrum shows an intense blue emission at 461 nm, attributed to the electronic dipole transition of 1D2–3F4, as well as a weak emission at 484 nm (1G4–3H6). With increased Tm3+ doping concentration, emission spectra profiles for LiInTi2O6:yTm3+ remained invariable and emission intensities of peaks at 459 nm gradually increased with the increasing concentration, and obviously decreased after reaching the maximum at y = 0.025, owing to the concentration quenching effect (inset in Fig. 6b).
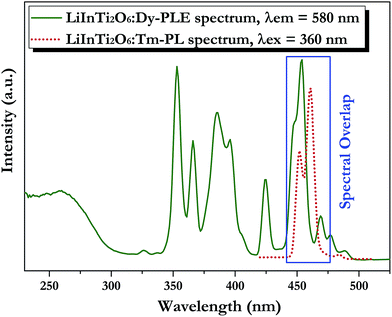 | ||
| Fig. 7 Spectral overlap between PL spectrum of LiInTi2O6:Tm3+ (red dotted line) and PLE spectrum of LiInTi2O6:Dy3+ (olive solid line). | ||
In order to achieve white-light emission in single-phase Tm3+/Dy3+ co-activated LiInTi2O6 phosphors, appropriate doping ratios of activators and excitation wavelengths are required. In this work, the more the Tm3+ is doped, the less the Dy3+ can be co-doped. Based on scores of trial and error experiments, the co-doping concentration of Tm3+ was determined to be 0.01 to obtain white-light emission under UV excitation, in spite of its optimal doping concentration being 0.025 in the LiInTi2O6 host. Consequently, a series of LiInTi2O6:0.01Tm3+,xDy3+ (x = 0, 0.003, 0.005, 0.007, 0.01, 0.013, and 0.015) phosphors with different Dy3+ concentrations were synthesized and their photoluminescence properties were investigated. As seen in Fig. S1 and S2,† Tm3+ and Dy3+ can be simultaneously incorporated into the LiInTi2O6 host, without causing any changes in the crystal lattice. Fig. 8 shows the PL spectra of as-prepared samples under 360 nm excitation. Obviously, all the PL spectra for Dy3+/Tm3+ co-doped LiInTi2O6 phosphors consist of characteristic emission bands for both Tm3+ and Dy3+. With the concentration of Dy3+ increasing, the emission intensities of Tm3+ centered at 461 nm monotonically decrease, whereas those of Dy3+ gradually increase. This observed variation in trend can also be seen from the dependence of emission intensities on Dy3+ doping concentrations in the inset of Fig. 8. This variation supports the occurrence of effective energy transfer from Tm3+ to Dy3+ in LiInTi2O6:Tm3+,Dy3+ phosphors. This kind of energy transfer between the sensitizer of Tm3+ and the activator of Dy3+ is mainly ascribed to the energy of the emission transition 1D2–3F4 for Tm3+ matching well with the excitation transition 6H15/2–4I15/2 for Dy3+. The energy transfer process between proposed energy levels of Dy3+ and Tm3+ are illustrated in Fig. 9. Upon 359 nm excitation, electrons in Tm3+ ions are excited from the 3H6 ground state to the 1D2 excited state. Some energy is then released on account of excited electrons jumping down to the 3F4 excitation state to emit blue light, while residual energy is absorbed by electrons of Dy3+ in the ground state 6H15/2, to jump up to the 4I15/2 excited state, due to energy matching. Subsequently, there is non-radiative relaxation to the 4F9/2 level and the generation of characteristic emission transitions of Dy3+ ions to emit colourful lights.
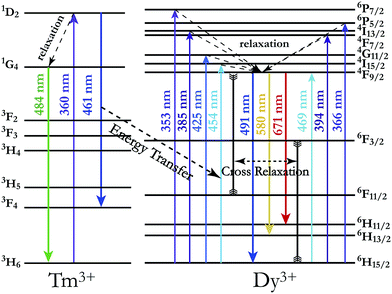 | ||
| Fig. 9 Schematic energy level diagram illustrating characteristic excitation and emission of Tm3+ and Dy3+, and energy transfer process from Tm3+ to Dy3+. | ||
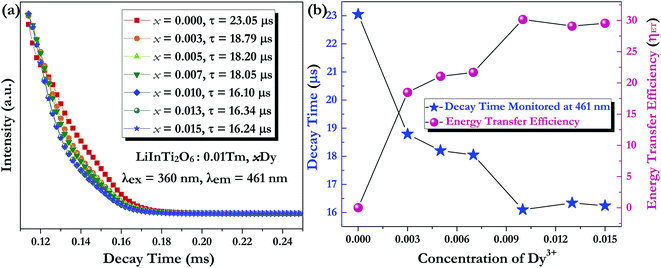
Generally speaking, the energy transfer process can be revealed by the photoluminescence decay behaviour of phosphors; therefore, in order to further confirm the presence of energy transfer from Tm3+ ions to Dy3+ ions in LiInTi2O6:Tm3+,Dy3+ phosphors, photoluminescence decay curves were investigated. Fig. 10a shows the decay curves of Tm3+ emission in LiInTi2O6:0.01Tm3+,xDy3+ phosphors recorded at 461 nm under the excitation of 360 nm. It was found that all the decay curves associated with the emission transition of 1D2–3F4 at 461 nm can be well fitted to a second-order exponential decay function:
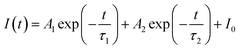 | (1) |
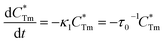 | (2) |
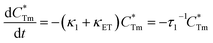 | (3) |
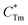 stands for energy state concentrations of Tm3+; κ1 and κET are rate constants for photoluminescence of Tm3+ and energy transfer from Tm3+ to Dy3+, respectively; τ0 and τ1 are decay lifetimes of sensitizer Tm3+ in the absence and presence of activator Dy3+, respectively. According to eqn (2) and (3), the rate constant κET and energy transfer efficiency ηET can be calculated as follows:
stands for energy state concentrations of Tm3+; κ1 and κET are rate constants for photoluminescence of Tm3+ and energy transfer from Tm3+ to Dy3+, respectively; τ0 and τ1 are decay lifetimes of sensitizer Tm3+ in the absence and presence of activator Dy3+, respectively. According to eqn (2) and (3), the rate constant κET and energy transfer efficiency ηET can be calculated as follows:| κET = τ1−1 − κ1 = τ1−1 − τ0−1 | (4) |
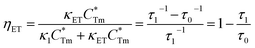 | (5) |
The dependence of lifetimes and energy transfer efficiencies on Dy3+ concentration is plotted in Fig. 10b, from which one can see that the average lifetimes decreased and energy transfer efficiencies generally increased with the increment of Dy3+ content, indicating energy transfer from Tm3+ to Dy3+.
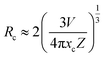 | (6) |
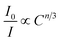 | (7) |
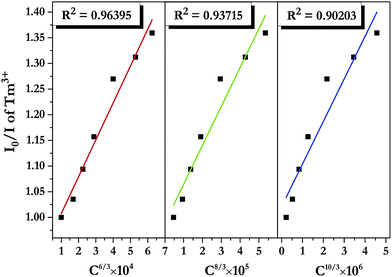 | ||
| Fig. 11 Dependence of I0/I of Tm3+ on the sum of Tm3+ and Dy3+ concentrations C6/3, C8/3, and C10/3 in LiInTi2O6:0.01Tm3+,xDy3+ phosphors. | ||
The energy transfer process is a feasible route to tuning the emission colors of light-conversion phosphors for practical applications. Consequently, a white light emission could be realized via energy transfer by adjusting the ratio of Tm3+ and Dy3+ to a suitable value in a single-component LiInTi2O6:Tm3+,Dy3+ phosphor. In order to demonstrate the practical application of LiInTi2O6:Tm3+,Dy3+ phosphors, a 366 nm UV lamp was used to irradiate the phosphors. As a consequence, a series of digital lighting photographs was obtained, as shown in Fig. 12. For comparison, correlated Commission International de I'Eclairage (CIE) chromaticity coordinates with different doping concentrations, determined on the basis of their corresponding PL spectra under excitation of 366 nm, are also listed. It was found that the Tm3+ singly-doped LiInTi2O6 phosphor (point 1 in Fig. 12) exhibits blue-light emission with CIE chromaticity coordinate (0.1606, 0.0864), while the Dy3+ singly-doped LiInTi2O6 phosphor (point 8) shows yellow light with CIE chromaticity coordinate (0.4483, 0.4312). As for Tm3+/Dy3+ co-doped LiInTi2O6 phosphors, the colour tone can be tuned from blue, with chromaticity coordinate of (0.2496, 0.2041), to white, with (0.3340, 0.3104), across the white lighting region with an increase in Dy3+ doping concentrations based on the principle of energy transfer from Tm3+ to Dy3+. These results suggest that LiInTi2O6:Tm3+,Dy3+ phosphors can be effectively excited with UV light and they are potential single-component blue-yellow tunable candidates for possible applications in white-light-emitting UV-LEDs for solid-state lighting.
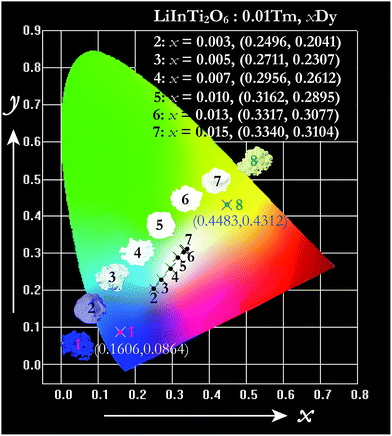 | ||
| Fig. 12 CIE chromaticity diagram of LiInTi2O6:0.01Tm3+ (point 1), LiInTi2O6:0.015Dy3+ (point 8), and LiInTi2O6:0.01Tm3+,xDy3+ phosphors (point 2–7) under 366 nm UV excitation. | ||
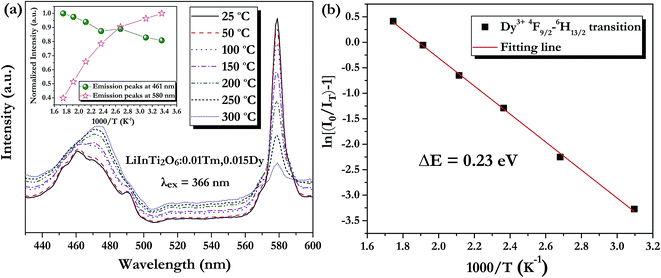
As is well known, lighting devices usually suffer from thermal invalidation with the increase in service time at high temperature, and some peculiar behaviour may be encountered. This phenomenon also applies to LEDs, which influences the photoluminescence of the light-conversion components, i.e. phosphors. Thus, temperature stability, i.e. thermal quenching behaviour of photoluminescence, is an important issue to be considered in evaluating the luminescence properties of phosphors. The temperature-dependent emission spectra for the as-prepared LiInTi2O6:0.01Tm3+,0.015Dy3+ phosphor under 366 nm excitation was carried out from 25 to 300 °C, and normalized emission intensities of Tm3+ and Dy3+ as a function of temperature are presented in Fig. 13a. As can be seen, the positions of the maximum peaks for Tm3+ originating from the 1D2–3F4 transition are red-shifted and the emission intensity abnormally increases with the increase in temperature to 300 °C; whereas, the PL intensity at 580 nm for Dy3+ significantly decreases as temperature increases, ascribed to thermal quenching. The red-shift occurs because with the increase in temperature, the host lattice expands due to the thermal expansion effect; thus, the bond lengths between activators and ligands increase, leading to a decrease in the crystal field, which decreases the transition energy.48,49 In general, at a high temperature, the population density of thermal active phonons increases, and the electron–phonon interaction is intense, causing an increase in the thermally activated nonradiative transition probability; as a consequence, emission intensity decreases.48,49 However, the abnormal dependence of emission intensity on temperature for Tm3+, which occurs in LiInTi2O6:Tm3+,Dy3+ phosphors results from a phenomenon known as negative thermal quenching (NTQ).50,51 Similar NTQ phenomena are also observed in other reported luminescent materials.49,52,53 Temperature-dependent electron numbers in eigenstates, which dominantly affect the PL intensity, are contributed by four components: electron relaxation, radiative transition, nonradiative transition and thermal excitation. When the energy separation between the initial excited state and some middle excited states is comparable to the temperature of the system, thermal excitation of electrons from the latter states to the former state is significant.54 Meanwhile, the energy eigenvalues for these middle excited states are smaller than that of the initial state. Therefore, thermal excitation of electrons in Tm3+ accounts for the NTQ phenomenon. As for Dy3+, as seen in Fig. 13a, the PL intensity at 580 nm significantly decreases as temperature is increased, representing positive thermal quenching. The thermal quenching temperature (T0.5), defined as the temperature at which the emission intensity is 50% of its original value, is approximately determined to be 255 °C.55 The temperature dependence of the PL intensity can be described by the Arrhenius equation, from which the activation energy can be accordingly calculated:17,55
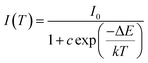 | (8) |
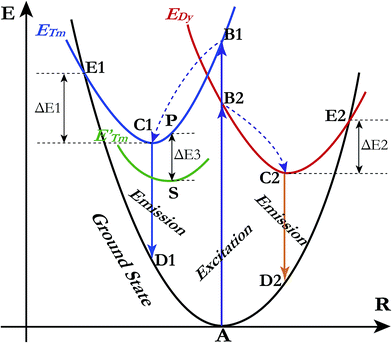
A qualitative explanation for the thermal quenching behaviour of phosphors can be obtained from the one-dimensional configuration coordinate model.42 Fig. 14 shows the configuration coordinate diagram of Tm3+ and Dy3+ in the LiInTi2O6 host. Ideally, under excitation, the 4f electrons of Tm3+ and Dy3+ are promoted from the ground states (point A in curve ground state) into the excited states (point B1 and B2 in curve ETm and EDy), then quickly relax to the lowest energy level of the excited states (point C1 and C2) by multi-phonon emission and return to the ground state, accompanied by radiative transition emissions corresponding to lines C1D1 and C2D2. However, nonradiative processes, e.g. thermal quenching, will always compete with radiative processes in luminescence materials. As seen in Fig. 14, as the temperature increases, the excited electrons are thermally activated via electron–phonon interactions to the intersection (point E1 and E2) between the ground state and excited state. By means of the crossing (point E1 and E2) it is possible to return to the ground state (point A) in a nonradiative manner by means of multiphonon relaxation. The excitation energy is then partially given up as heat to the lattice, giving rise to thermal quenching. The energy difference, ΔE, needed to be overcome in this process, between the relaxed excited state and the cross, is exactly the activation energy of thermal quenching for activators;46,58 the larger its value, the greater the thermal stability of the phosphors. For Tm3+, the NTQ means that with increasing temperature, thermal excitation of electrons from the sublevel excited state (curve E′Tm) to the initial excited state (curve ETm) cannot be ignored. The electrons excited from sublevels (line SP) will compensate for the loss of electrons by nonradiative transition via point E1. Certainly, the energy (ΔE3) required to overcome thermal excitation should be smaller than that for electron–phonon interaction to the intersection (ΔE1).
3.4. Comparison of crystal structures of representative titanates
A comprehensive understanding of the chemical bonding and coordination geometry of titanates is necessary to design and select the appropriate phosphor hosts. The initial aim of this work was to design material in the Li2O–In2O3–TiO2 system with crystal structure similar to the perovskite (ALn)0.5TiO3. In effect, in spite of the obtained compound LiInTi2O6 having a similar formula to (ALn)0.5TiO3, it presents absolutely different ionic coordination environments and structural symmetry, compared to that of (ALn)0.5TiO3. In most cases, crystal field environments for transition metal ions in crystal structures generally possess octahedral or tetrahedral symmetry. Nevertheless, the special case of the titanium ion with 12-fold coordinated hexagonal prismatic symmetry in LiInTi2O6 is noted in this work. Herein, we sketchily elucidate the structure distinction of several titanates, providing helpful information for photo/electrical material design.The well-known titanate compounds that are extensively applied in functional materials are the perovskite family. The ideal perovskite-type titanates generally crystallize in a cubic system with space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (S.G. No. 221, O1h), such as SrTiO3, having Ti4+ coordinated with 6 oxygens to form corner-sharing TiO6 regular octahedra and Sr2+ located at the 12-fold coordinated interstices of TiO6 groups.59 By full or partial substitution of suitable cations in Sr2+ sites, different types of modified perovskites can be obtained. They demonstrate deviations from ideal perovskite either by changes in constituents, or distortions and tilting of TiO6 octahedra, or a combination of both,60,61 giving rise to differences in coordination circumstances and bond connectivity. The detailed information for crystal structures of ATiO3 titanates are summarized in Table 4. Ideal perovskite-type SrTiO3 has a regular TiO6 group with equal Ti–O bond lengths, and Ti–O–Ti bond angle equal to 180°. With either Ca2+ or Ba3+, having a slightly smaller or larger ionic radius, being substituted for the Sr2+ ions in the cubic lattice, the electronic interaction between cations and ligands will change, so as to influence the crystal structure.62,63 As a result, regular TiO6 groups are distorted with one Ti–O bond stretched and the opposite one compressed, as well as Ti–O–Ti bond angles deviating from 180° linear connectivity. The family of (Li0.5Ln0.5)TiO3 perovskites, with Ln ionic radius smaller than 0.95 Å, are isomorphic to CaTiO3, with Li+ and Ln3+ co-occupying the same Ca2+ site.64 With the ionic radius of Ln3+ decreasing, the degree of distortion and tilting of TiO6 octahedra increases. Generally, the Ti–O–Ti bond angles decrease, accompanied by the decrease in covalence of chemical bonds between Ti and O, resulting in the decrease in band widths and the increase in band gap due to the increase in electron delocalisation;19,65,66 it is therefore necessary to obtain further deep theoretical and experimental insights into the structure–property relationship for this series of compounds. When In3+ with a smaller ionic radius replaces Ln3+, TiO6 octahedra do not exist and polyhedra connection changes from corner-sharing to face-sharing, presenting different bonding styles. Considering having a smaller ionic radius and the same ionic valence as Ln3+ and In3+, the imaginary compound (Li0.5Sc0.5)TiO3 with the same crystal structure of either (Li0.5Ln0.5)TiO3 or (Li0.5In0.5)TiO3 is expected to be synthesized. Furthermore, the compounds (Na0.5In0.5)TiO3 and (K0.5In0.5)TiO3, which are isomorphous to (Li0.5In0.5)TiO3, are also expected to exist in view of Na, K and Li being congener elements; however, in future work, their existence needs to be confirmed via experiment. It can therefore be concluded that chemical unit substitution has provided an effective means and many opportunities for designing and exploring novel functional materials.
m (S.G. No. 221, O1h), such as SrTiO3, having Ti4+ coordinated with 6 oxygens to form corner-sharing TiO6 regular octahedra and Sr2+ located at the 12-fold coordinated interstices of TiO6 groups.59 By full or partial substitution of suitable cations in Sr2+ sites, different types of modified perovskites can be obtained. They demonstrate deviations from ideal perovskite either by changes in constituents, or distortions and tilting of TiO6 octahedra, or a combination of both,60,61 giving rise to differences in coordination circumstances and bond connectivity. The detailed information for crystal structures of ATiO3 titanates are summarized in Table 4. Ideal perovskite-type SrTiO3 has a regular TiO6 group with equal Ti–O bond lengths, and Ti–O–Ti bond angle equal to 180°. With either Ca2+ or Ba3+, having a slightly smaller or larger ionic radius, being substituted for the Sr2+ ions in the cubic lattice, the electronic interaction between cations and ligands will change, so as to influence the crystal structure.62,63 As a result, regular TiO6 groups are distorted with one Ti–O bond stretched and the opposite one compressed, as well as Ti–O–Ti bond angles deviating from 180° linear connectivity. The family of (Li0.5Ln0.5)TiO3 perovskites, with Ln ionic radius smaller than 0.95 Å, are isomorphic to CaTiO3, with Li+ and Ln3+ co-occupying the same Ca2+ site.64 With the ionic radius of Ln3+ decreasing, the degree of distortion and tilting of TiO6 octahedra increases. Generally, the Ti–O–Ti bond angles decrease, accompanied by the decrease in covalence of chemical bonds between Ti and O, resulting in the decrease in band widths and the increase in band gap due to the increase in electron delocalisation;19,65,66 it is therefore necessary to obtain further deep theoretical and experimental insights into the structure–property relationship for this series of compounds. When In3+ with a smaller ionic radius replaces Ln3+, TiO6 octahedra do not exist and polyhedra connection changes from corner-sharing to face-sharing, presenting different bonding styles. Considering having a smaller ionic radius and the same ionic valence as Ln3+ and In3+, the imaginary compound (Li0.5Sc0.5)TiO3 with the same crystal structure of either (Li0.5Ln0.5)TiO3 or (Li0.5In0.5)TiO3 is expected to be synthesized. Furthermore, the compounds (Na0.5In0.5)TiO3 and (K0.5In0.5)TiO3, which are isomorphous to (Li0.5In0.5)TiO3, are also expected to exist in view of Na, K and Li being congener elements; however, in future work, their existence needs to be confirmed via experiment. It can therefore be concluded that chemical unit substitution has provided an effective means and many opportunities for designing and exploring novel functional materials.
| Compound | Structure | Space group | Coordination geometry | Site symmetry | Ti–O–Ti angle | Ti–O bond length (Å) | Ref. |
|---|---|---|---|---|---|---|---|
| SrTiO3 | Cubic | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221) m (221) |
Sr: 12-fold cuboctahedron | Sr: m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
180° | Ti–O: 1.9550 × 6 | 59 |
| Ti: 6-fold regular octahedron | Ti: m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
||||||
| BaTiO3 | Tetragonal | P4mmm (99) | Ba: 12-fold cuboctahedron | Ba: 4mmm | Ti–O1–Ti: 180° | Ti–O1: 1.8802 | 63 |
| Ti: 6-fold octahedron | Ti: 4mmm | Ti–O2–Ti: 171° | Ti–O2: 2.0043 × 4 | ||||
| Ti–O1: 2.1338 | |||||||
| CaTiO3 | Orthorhombic | Pnma (62) | Ca: 8-fold side-bicapped trigonal prism | Ca: m | Ti–O1–Ti: 147.3° | Ti–O1: 1.9845 × 2 | 62 |
| Ti: 6-fold octahedron | Ti: −1 | Ti–O2–Ti: 146.8° | Ti–O2: 1.9927 × 2 | ||||
| Ti–O1: 1.9969 × 2 | |||||||
| Li0.5Gd0.5TiO3 | Orthorhombic | Pnma (62) | Li/Gd: 8-fold side-bicapped trigonal prism | Li/Gd: m | Ti–O1–Ti: 148.0° | Ti–O1: 2.0238 × 2 | 64 |
| Ti: 6-fold octahedron | Ti: −1 | Ti–O2–Ti: 146.4° | Ti–O2: 1.9688 × 2 | ||||
| Ti–O1: 2.0695 × 2 | |||||||
| Li0.5Y0.5TiO3 | Orthorhombic | Pnma (62) | Li/Y: 8-fold side-bicapped trigonal prism | Li/Y: m | Ti–O1–Ti: 147.9° | Ti–O1: 2.0047 × 2 | 64 |
| Ti: 6-fold octahedron | Ti: −1 | Ti–O2–Ti: 146.7° | Ti–O2: 1.9625 × 2 | ||||
| Ti–O1: 2.0492 × 2 | |||||||
| Li0.5Lu0.5TiO3 | Orthorhombic | Pnma (62) | Li/Lu: 8-fold side-bicapped trigonal prism | Li/Lu: m | Ti–O1–Ti: 148.1° | Ti–O1: 2.0119 × 2 | 64 |
| Ti: 6-fold octahedron | Ti: −1 | Ti–O2–Ti: 146.3° | Ti–O2: 1.9491 × 2 | ||||
| Ti–O1: 2.0595 × 2 | |||||||
| LiInTi2O6 | Trigonal | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (166) m (166) |
Li/In/Ti: 12-fold hexagonal prism | Li/In/Ti: 3m | Ti3–O1–Ti3: 102.7° | Ti3–O1: 1.8444 × 6 | This work |
| Ti4–O2–Ti4: 103.1° | Ti3–O1: 1.9736 × 6 | ||||||
| Ti4–O2: 1.7946 × 6 | |||||||
| Ti4–O2: 2.1201 × 6 |
4. Conclusions
Sub-solidus phase relationships of the Li2O–In2O3–TiO2 ternary system were determined to be composed of seven three-phase regions separated by two-phase join-lines. A new ternary compound, LiInTi2O6, was discovered and synthesized. Its thermal stability was investigated and found to endothermically decompose in the range of 1100–1200 °C via a four-phase transformation reaction. The crystal structure of LiInTi2O6 was solved by the charge-flipping method and refined by the Rietveld method on the basis of powder XRD data. LiInTi2O6 crystallizes in a trigonal unit cell with lattice parameters of a = b = 5.1050(1) Å, c = 28.5622(4) Å, and Z = 6 in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 166), consisting of a three-dimensional structural framework constructed by distorted 12-fold coordination hexagonal prisms, which stack layer by layer along the c axis via edge-sharing and face-sharing. Taking LiInTi2O6 as the host, a series of Dy3+/Tm3+ singly-doped and co-doped phosphors were successfully synthesized. The energy transfer process from Tm3+ to Dy3+ in LiInTi2O6:0.01Tm3+,Dy3+ phosphors was systematically demonstrated by studying their photoluminescence emission spectra and decay curves. The energy transfer efficiency ηET was increased with the increment of Dy3+ contents. The interaction mechanism for energy transfer was determined to conform to a non-radiative electric dipole–dipole (d–d) interaction with critical distance of 20.17 Å between Tm3+ and Dy3+. By properly adjusting the concentration of activators, the color tone of LiInTi2O6:Tm3+,Dy3+ phosphors can be tuned from blue to white across the white lighting region. Moreover, the negative thermal quenching (NTQ) phenomenon is observed in this white lighting phosphor and results in excellent thermal stability against temperature quenching. The thermal quenching behaviour is qualitatively explained by the one-dimensional configuration coordinate model. The present results indicate that LiInTi2O6:Tm3+,Dy3+ phosphors may potentially be applied as single-component colour-tuneable candidates in UV-pumped white LEDs.
m (No. 166), consisting of a three-dimensional structural framework constructed by distorted 12-fold coordination hexagonal prisms, which stack layer by layer along the c axis via edge-sharing and face-sharing. Taking LiInTi2O6 as the host, a series of Dy3+/Tm3+ singly-doped and co-doped phosphors were successfully synthesized. The energy transfer process from Tm3+ to Dy3+ in LiInTi2O6:0.01Tm3+,Dy3+ phosphors was systematically demonstrated by studying their photoluminescence emission spectra and decay curves. The energy transfer efficiency ηET was increased with the increment of Dy3+ contents. The interaction mechanism for energy transfer was determined to conform to a non-radiative electric dipole–dipole (d–d) interaction with critical distance of 20.17 Å between Tm3+ and Dy3+. By properly adjusting the concentration of activators, the color tone of LiInTi2O6:Tm3+,Dy3+ phosphors can be tuned from blue to white across the white lighting region. Moreover, the negative thermal quenching (NTQ) phenomenon is observed in this white lighting phosphor and results in excellent thermal stability against temperature quenching. The thermal quenching behaviour is qualitatively explained by the one-dimensional configuration coordinate model. The present results indicate that LiInTi2O6:Tm3+,Dy3+ phosphors may potentially be applied as single-component colour-tuneable candidates in UV-pumped white LEDs.
Conflict of interest
The authors declare no competing financial interest.Acknowledgements
Financial supports by grants from the National Key Research and Development Plan (No. 2016YFB0701301), the National Natural Science Foundation of China (No. 51472273), the Major State Basic Research Development Program of China (No. 2014CB6644002), the outstanding graduate project of Advanced Non-ferrous Metal Structural Materials and Manufacturing Collaborative Innovation Center (No. 510070027), and the Project of Innovation-driven Plan in Central South University (No. 2015CX004) are gratefully acknowledged.References
- N. Bardsley, S. Bland, L. Pattison, M. Pattison, K. Stober, F. Welsh and M. Yamada, Solid-State Lighting Research and Development: Multi-Year Program Plan, Solid-State Lighting Program, Building Technologies Office, Office of Energy Efficiency and Renewable Energy, U.S. Department of Energy, Washington D.C, 2014 Search PubMed.
- N. Bardsley, S. Bland, M. Hansen, L. Pattison, M. Pattison, K. Stober and M. Yamada, Solid-State Lighting R&D Plan, Solid-State Lighting Program, Building Technologies Office, Office of Energy Efficiency and Renewable Energy, U.S. Department of Energy, Washington D.C, 2015 Search PubMed.
- J. Y. Tsao, H. D. Saunders, J. R. Creighton, M. E. Coltrin and J. A. Simmons, J. Phys. D: Appl. Phys., 2010, 43, 354001 CrossRef.
- M. H. Crawford, IEEE J. Sel. Top. Quantum Electron., 2009, 15, 1028–1040 CrossRef CAS.
- S. Pimputkar, J. S. Speck, S. P. DenBaars and S. Nakamura, Nat. Photonics, 2009, 3, 180–182 CrossRef CAS.
- M. Shang, C. Li and J. Lin, Chem. Soc. Rev., 2014, 43, 1372–1386 RSC.
- J. H. Oh, S. J. Yang and Y. R. Do, Light: Sci. Appl., 2014, 3, e141 CrossRef CAS.
- C. Branas, F. J. Azcondo and J. M. Alonso, IEEE Industrial Electronics Magazine, 2013, 7, 6–14 CrossRef.
- N. C. George, K. A. Denault and R. Seshadri, Annu. Rev. Mater. Res., 2013, 43, 481–501 CrossRef CAS.
- Z. Xia, C. Ma, M. S. Molokeev, Q. Liu, K. Rickert and K. R. Poeppelmeier, J. Am. Chem. Soc., 2015, 137, 12494–12497 CrossRef CAS PubMed.
- G. Li, C. C. Lin, W. T. Chen, M. S. Molokeev, V. V. Atuchin, C. Y. Chiang, W. Zhou, C. W. Wang, W. H. Li, H. S. Sheu, T. S. Chan, C. Ma and R. S. Liu, Chem. Mater., 2014, 26, 2991–3001 CrossRef CAS.
- X. J. Wang, L. Wang, T. Takeda, S. Funahashi, T. Suehiro, N. Hirosaki and R. J. Xie, Chem. Mater., 2015, 27, 7689–7697 CrossRef CAS.
- M. Chen, Z. Xia, M. S. Molokeev and Q. Liu, Inorg. Chem., 2015, 54, 11369–11376 CrossRef CAS PubMed.
- X. Zhang and M. Gong, Dalton Trans., 2014, 43, 2465–2472 RSC.
- N. Liu, J. Y. Si, G. M. Cai and Y. Tao, RSC Adv., 2016, 6, 50797–50807 RSC.
- Z. Leng, L. Li, X. Che and G. Li, Mater. Des., 2017, 118, 245–255 CrossRef CAS.
- Q. Q. Zhu, L. Wang, N. Hirosaki, L. Y. Hao, X. Xu and R. J. Xie, Chem. Mater., 2016, 28, 4829–4839 CrossRef CAS.
- S. K. Gupta, P. S. Ghosh, A. K. Yadav, N. Pathak, A. Arya, S. N. Jha, D. Bhattacharyya and R. M. Kadam, Inorg. Chem., 2016, 55, 1728–1740 CrossRef CAS PubMed.
- Y. Inaguma, T. Tsuchiya and T. Katsumata, J. Solid State Chem., 2007, 180, 1678–1685 CrossRef CAS.
- G. Blasse and A. Bril, J. Chem. Phys., 1968, 48, 3652–3656 CrossRef CAS.
- G. Cai, X. L. Chen, W. Y. Wang, Y. F. Lou, J. Liu, J. T. Zhao and H. H. Chen, J. Solid State Chem., 2008, 181, 646–651 CrossRef CAS.
- L. Su, X. Fan, G. Cai and Z. Jin, Ceram. Int., 2016, 42, 15994–16006 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352 Search PubMed.
- H. Rietveld, Acta Crystallogr., 1967, 22, 151–152 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- T. Gaewdang, J. P. Chaminade, P. Gravereau, A. Garcia, C. Fouassier, P. Hagenmuller and R. Mahiou, Mater. Res. Bull., 1993, 28, 1051–1060 CrossRef CAS.
- R. Hoppe and B. Schepers, Z. Anorg. Allg. Chem., 1958, 295, 233–240 CrossRef CAS.
- F. Stewner and R. Hoppe, Z. Anorg. Allg. Chem., 1970, 374, 239–258 CrossRef CAS.
- G. Izquierdo and A. R. West, Mater. Res. Bull., 1980, 15, 1655–1660 CrossRef CAS.
- H. Kleykamp, Fusion Eng. Des., 2002, 61–62, 361–366 CrossRef CAS.
- J. C. Mikkelsen, J. Am. Ceram. Soc., 1980, 63, 331–335 CrossRef CAS.
- L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805 CrossRef CAS.
- G. Oszlanyi and A. Suto, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 134–141 CrossRef PubMed.
- C. K. Jørgensen, Mol. Phys., 1962, 5, 271–277 CrossRef.
- J. L. Sommerdijk and A. Bril, J. Electrochem. Soc., 1975, 122, 952–954 CrossRef CAS.
- X. Liu, Y. Lü, C. Chen, S. Luo, Y. Zeng, X. Zhang, M. Shang, C. Li and J. Lin, J. Phys. Chem. C, 2014, 118, 27516–27524 CAS.
- Y. Lü, X. Tang, L. Yan, K. Li, X. Liu, M. Shang, C. Li and J. Lin, J. Phys. Chem. C, 2013, 117, 21972–21980 Search PubMed.
- X. Min, M. Fang, Z. Huang, Y. Liu, C. Tang and X. Wu, J. Am. Ceram. Soc., 2015, 98, 788–794 CrossRef CAS.
- Y. Shi, Y. Wang and Z. Yang, J. Alloys Compd., 2011, 509, 3128–3131 CrossRef CAS.
- Q. Su, Z. Pei, L. Chi, H. Zhang, Z. Zhang and F. Zou, J. Alloys Compd., 1993, 192, 25–27 CrossRef CAS.
- S. Shionoya, W. M. Yen and H. Yamamoto, Phosphor handbook, CRC press, 2006 Search PubMed.
- Y. Liu, Y. Yang, G. Qian, Z. Wang and M. Wang, Mater. Sci. Eng., B, 2007, 137, 74–79 CrossRef CAS.
- T. Grzyb, RSC Adv., 2014, 4, 2590–2595 RSC.
- G. Blasse, Phys. Lett. A, 1968, 28, 444–445 CrossRef CAS.
- J. Zhou and Z. Xia, J. Mater. Chem. C, 2015, 3, 7552–7560 RSC.
- D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070 CrossRef CAS.
- J. S. Kim, Y. H. Park, S. M. Kim, J. C. Choi and H. L. Park, Solid State Commun., 2005, 133, 445–448 CrossRef CAS.
- Z. Xia, X. Wang, Y. Wang, L. Liao and X. Jing, Inorg. Chem., 2011, 50, 10134–10142 CrossRef CAS PubMed.
- M. Watanabe, M. Sakai, H. Shibata, C. Satou, S. Satou, T. Shibayama, H. Tampo, A. Yamada, K. Matsubara, K. Sakurai, S. Ishizuka, S. Niki, K. Maeda and I. Niikura, Phys. B, 2006, 376–377, 711–714 CrossRef CAS.
- M. Hauser, A. Hepting, R. Hauschild, H. Zhou, J. Fallert, H. Kalt and C. Klingshirn, Appl. Phys. Lett., 2008, 92, 211105 CrossRef.
- X. H. Huang, C. Zhang, C. B. Tay, T. Venkatesan and S. J. Chua, Appl. Phys. Lett., 2013, 102, 111106 CrossRef.
- F. Kang, M. Peng, Q. Zhang and J. Qiu, Chem.–Eur. J., 2014, 20, 11522–11530 CrossRef CAS PubMed.
- S. Hajime, Jpn. J. Appl. Phys., 1998, 37, 550 CrossRef.
- S. Zhang, Y. Nakai, T. Tsuboi, Y. Huang and H. J. Seo, Chem. Mater., 2011, 23, 1216–1224 CrossRef CAS.
- X. Chen, Z. Xia and Q. Liu, Dalton Trans., 2014, 43, 13370–13376 RSC.
- N. Zhang, C. Guo, J. Zheng, X. Su and J. Zhao, J. Mater. Chem. C, 2014, 2, 3988–3994 RSC.
- G. H. Muñoz, C. L. de la Cruz, A. F. Muñoz and J. O. Rubio, J. Mater. Sci. Lett., 1988, 7, 1310–1312 CrossRef.
- M. A. Peña and J. L. G. Fierro, Chem. Rev., 2001, 101, 1981–2018 CrossRef.
- A. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- A. Glazer, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 756–762 CrossRef.
- M. L. Moreira, E. C. Paris, G. S. do Nascimento, V. M. Longo, J. R. Sambrano, V. R. Mastelaro, M. I. B. Bernardi, J. Andrés, J. A. Varela and E. Longo, Acta Mater., 2009, 57, 5174–5185 CrossRef CAS.
- K. C. Huang, T. C. Huang and W. F. Hsieh, Inorg. Chem., 2009, 48, 9180–9184 CrossRef CAS PubMed.
- A. G. Belous, G. N. Novitskaya and S. V. Polyanetskaya, Inorg. Mater., 1987, 23, 1177–1179 Search PubMed.
- M. Wiegel, M. Hamoumi and G. Blasse, Mater. Chem. Phys., 1994, 36, 289–293 CrossRef CAS.
- G. Blasse and L. G. J. De Haart, Mater. Chem. Phys., 1986, 14, 481–484 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01891f |
| This journal is © The Royal Society of Chemistry 2017 |