Open Access Article
Open Access ArticleLAPONITE®-pilocarpine hybrid material: experimental and theoretical evaluation of pilocarpine conformation†
Vanessa R. R. Cunha *a,
Filipe C. D. A. Lima
*a,
Filipe C. D. A. Lima bc,
Vanessa Y. Sakaia,
Leiz M. C. Vérasd,
José R. S. A. Leitede,
Helena M. Petrillib and
Vera R. L. Constantinoa
bc,
Vanessa Y. Sakaia,
Leiz M. C. Vérasd,
José R. S. A. Leitede,
Helena M. Petrillib and
Vera R. L. Constantinoa
aDepartamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, C. P. 26077, 05508000, São Paulo, SP, Brazil. E-mail: vrrc@iq.usp.br
bInstituto de Física, Universidade de São Paulo, C. P. 66318, 05508090, São Paulo, SP, Brazil
cInstituto Federal de Educação Ciência e Tecnologia de São Paulo, 15991502, Matão, SP, Brazil
dNúcleo de Pesquisa de Biodiversidade e Biotecnologia, BIOTEC, Universidade Federal do Piauí, Campus Ministro Reis Velloso, 64202020, Parnaíba, PI, Brazil
eArea de Morfologia, Faculdade de Medicina, FM, Universidade de Brasília, UnB, Campus Universitário Darcy Ribeiro, Distrito Federal, DF, 70910900, Brasília, Brazil
First published on 23rd May 2017
Abstract
The intercalation of protonated pilocarpine (Pilo+) into model LAPONITE® (Lap) is here investigated in order to address its conformational properties upon entrapment. Pilo is an alkaloid available as a drug for the treatment of glaucoma and xerostomia, and clays are potential candidates for drug delivery. Therefore, the physico-chemical characterization of the Pilo-Lap material is here studied through chemical elementary analysis, X-ray diffraction, mass spectrometry coupled to thermogravimetric analysis (TGA-MS), solid state 13C nuclear magnetic resonance (NMR) and Raman spectroscopy. The experimental spectroscopic data are confronted with performed calculations which confirmed the presence of pilocarpine, while the XRD data also show the immobilization of Pilo+ into the clay. TGA-MS analyses indicated a significant modification in the thermal decomposition profile of the organic species after intercalation. A DTG peak associated with the release of carbon dioxide and water molecules is observed at 315 °C for PiloHCl and at 378 °C for Pilo-Lap. Supported by the theoretical calculations, the experimental XRD, vibrational and NMR spectra suggest that pilocarpine may undergo geometrical changes upon the intercalation process. A characteristic fingerprint was observed as a vibrational change in the band at 768 cm−1 for PiloHCl (assigned mainly to the lactone ring breathing vibrational mode) and a band at 782 cm−1 for Pilo-Lap (assigned mainly to the imidazole ring bending in the plane) in the Raman spectra.
Introduction
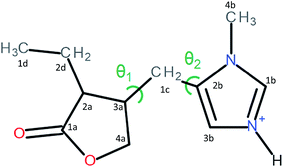
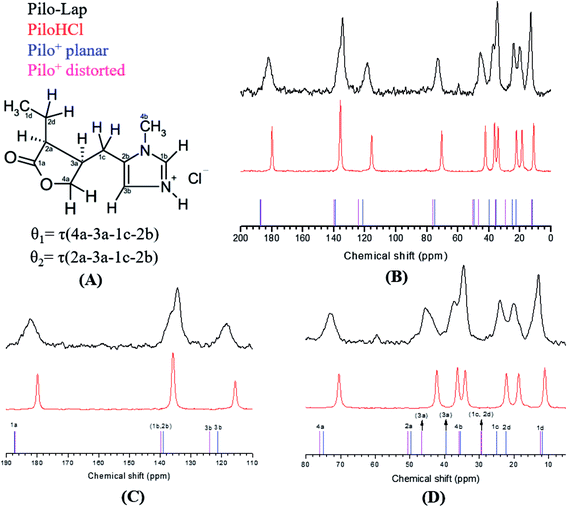
Pilocarpine (Pilo) is a well-known alkaloid produced by the pharmaceutical industry for the control of intraocular pressure associated with glaucoma.1 In order to reduce the symptom, the drug increases the contraction of smooth muscle and relaxes the iris sphincter muscle of animal organisms.2 Furthermore, the alkaloid can stimulate cholinergic receptors, as for example in the induction of salivary glands. Oral administration of pilocarpine can stimulate the production of saliva after 15 minutes and it is maintained for up to three hours.3,4 These experimental findings suggest the possibility of treating xerostomia disease (dry mouth) through administration of the alkaloid.5 Pilocarpine stability in solution relies on the environment since it is chemically stable at pH values between 4 and 6;6 in alkaline medium, it can change to isopilocarpine, and below pH 4 the ester group can be hydrolyzed, forming pilocarpic acid.6,7 Since cellular receptors have a high biological and chemical specificity, these structural changes affect the pharmaceutical effects.8According to single crystal X-ray diffraction (XRD) studies, pilocarpine can adopt different geometrical arrangements if associated with trichlorogermanate(II) or chloride anions in the protonated form (Pilo+)9,10 or if coordinated to copper(II), PiloCuCl2, or cobalt(II), PiloCoCl2.11 Hence, it is possible to distinguish the two most common geometrical arrangements: planar, for copper and cobalt complexes; distorted, for trichlorogermanate(II) and chloride salts. Fig. 1 shows the 2D structure of the cationic pilocarpine (Pilo+), where θ1 and θ2 indicate the geometrical differences between the two forms. Bento et al.12 characterized the vibrational properties of the distorted pilocarpine hydrochloride (PiloHCl) using both the Fourier transformed infrared (FT-IR) technique and Density Functional Theoretical (DFT) simulations of the distorted form of the cationic species in vacuum conditions (Pilo+ distorted). To the best of our knowledge, the spectroscopic properties of cationic pilocarpine in the planar form (Pilo+ planar) have not yet been investigated, or an inspection made of the possible characteristics caused by the different conformers.
Recently, geometrical changes caused by the complexation of epiisopiloturine, a similar alkaloid, with metal ions have been reported.13 Epiisopiloturine has the same structure as pilocarpine, aside from an extra phenyl radical attached in the carboxylate acid group, resulting in a sequence of three rings: imidazole, carboxylate and phenyl. Leite et al.14 characterized the epiisopiloturine structure, showing a π–π stacking between the imidazole and the phenyl group. On the other hand, in 2016 Ferreira et al.13 showed the XRD results for epiisopiloturine complexed with Cu2+ and Zn2+, indicating geometric distortions and the absence of the π–π stacking.
A promising way of preserving the chemical properties of drugs such as pilocarpine can be achieved by using drug carriers. Clay minerals have low cost purification and are well accepted in the human body, which makes them good candidates for controlled administration.15–17 Recently, successful biomedical applications of pharmaceutical species intercalated into clays, e.g., anti-microbial activity, wound treatment, regenerative medicine, biosensors and medical devices,16,18 have been reported. LAPONITE® (Lap) has shown high potential use in health care due to its chemical controlled composition since it is a synthetic clay.19 There are several applications using Lap as, for example, functionalization with fluorophore amines for the design of biosensors,20 as part of a hydrogel with polyacrylamide for potential biomedical applications21 and as a model for delivery systems based on nanocomposites.22–24 LAPONITE® has also been used in the regenerative medicine field, since the dissociation products are non-toxic and it has an important role in tissue engineering. The biocompatibility of Lap has been observed and also incorporation of the layered material did not alter the adhesion properties of human mesenchymal stem cells, hMSCs.25 Since Lap does not have paramagnetic or luminescence impurities that affect the NMR precision or Raman description, it can be inspected by these techniques.
Nevertheless, inorganic layered material like clays, or layered double hydroxides, may induce conformational changes on the guest species during the intercalation process, affecting the conformation as, for example, in the case of polymers,26,27 tetracyclines,28 proteins29 and DNA.30
The investigation of the intercalation of pilocarpine into the synthetic LAPONITE® clay mineral is addressed in this work. Thermogravimetric analysis coupled to mass spectrometry (TGA-MS), XRD patterns, elementary analysis, FT-Raman spectroscopy and solid state NMR data were combined with theoretical simulations in the framework of the DFT to inspect possible geometrical modifications after the intercalation.
Materials and methods
LAPONITE® RD (abbreviated Na-Lap), Na0.7+[(Si8Mg5.5Li0.3)O20(OH)4]0.7−, with a cation-exchange capacity (CEC) of 5 × 10−6 eq. g−1, was obtained from Laporte Inorg. Pilocarpine was extracted from the leaves of Jaborandi (Pilocarpus jaborandi) and purified by Vegeflora Extração do Nordeste LTDA (Fig. S1, ESI†). Pilocarpine hydrochloride 99% (molar mass = 243.76 g mol−1), C11H16N2O2·HCl, was provided by Biotec-UFPI, and the high performance liquid chromatography technique (HPLC) was used to confirm the purity. The details of these results are shown in the ESI (Fig. S2).† These two reagents were used as received.Preparation of Pilo-Lap material
A dispersion containing 200 mL of deionized water and 2 g of LAPONITE® was stirred for 2 hours at room temperature. After this period, the mixture was kept without stirring for 1 hour. The agitation was restarted and 2 mmol of dissolved pilocarpine hydrochloride was added into the dispersion, i.e., twice the CEC of Lap. The final pH value was 5.9. The system was stirred for 4 days, and then left to rest for 2 days. The hybrid material was separated by lyophilization and maintained in a desiccator at reduced pressure with silica gel. The obtained material presents 5.1% of C, 2.3% of H, 1.1% of N and 4.0% of H2O.Physical measurements
X-ray diffraction (XRD) patterns of powdered samples were recorded on a Rigaku diffractometer, model Miniflex, using CuKα radiation (1.541 Å, 30 kV, 15 mA, scan step of 0.03°) and a Ni filter. Elemental chemical analysis (C, H, and N) was performed in a PerkinElmer model 2400 analyzer at the Instituto de Química (Universidade de São Paulo – USP). Mass coupled thermal analyses (thermogravimetric analysis and mass spectrometry, TGA-MS) were recorded on a Netzsch thermoanalyser model TGA/DSC (Differential Scanning Calorimetry) 490 PC Luxx coupled to an Aëolos 403 C mass spectrometer, using an aluminum crucible, under synthetic air flow of 50 mL min−1 and a heating rate of 10 °C min−1. Solid State Nuclear Magnetic Resonance (NMR) data was obtained in a Bruker Advance II+ NMR spectrometer 300 MHz for 1H and 75 MHz for 13C. The signals were acquired at room temperature using (CP/MAS) 4 ms of contact time for cross-polarization (CP), ppm sequence for 1H decoupling and 1 s of recycle delay and magic angle spinning (MAS) at 10 kHz in a 4 mm diameter zirconia rotor. The FIDs were processed using an exponential window function with 30 Hz of line broadening. The 13C chemical shifts were calibrated using adamantine and TMS (tetramethylsilane) as references.Fourier transform Raman (FT-Raman) spectra were recorded in an FT-Raman Bruker FRS-100/S spectrometer using 1064 nm excitation radiation (Nd:YAG laser Coherent Compass 1064-500 N) and a Ge detector. Spectral range of 3500–50 cm−1, resolution of 4 cm−1, 1024 scans and intensity of 80 mW. Fourier transform infrared (FT-IR) spectra of samples diluted in KBr were recorded in an FT-IR ABB Bomem – MB Series, MB 102, model SZM4400G, with a coupled diffuse reflectance accessory (Pike Technologies, Inc.). Spectral range of 4000–400 cm−1, resolution of 4 cm−1 and same intensity of 80 mW.
Computational methods
The cationic pilocarpine (Pilo+) structures were extracted from X-ray crystallographic data.10,11 Two possible conformations were adopted to carry out the simulation: the planar (Pilo+ planar) and distorted (Pilo+ distorted) forms. The systems were investigated using the Kohn–Sham31 scheme for the Density Functional Theory (DFT)32 as implemented in the computational Gaussian 09 code.33 In order to investigate the environmental effects, the Pilo+ structures were simulated in aqueous medium. The Polarizable Continuum Model (PCM) was employed to describe the solvent34 using a dielectric constant of 78.35. This method creates the solute cavity via a set of overlapping spheres, being one of the most frequently used continuum solvation methods. This setup considering a positive charge and a continuum solvent is a tentative way to model the interaction with the clay that can be understood as electrostatic due to the absence of chemical modifications of the molecule in the current intercalation process. The basis set 6-311G(d,p) and the exchange correlation functional B3LYP35 were used to obtain the electronic structure, the vibrational spectra and the geometrical properties of the Pilo+ forms. In order to simulate the 13C NMR chemical shifts, the aug-cc-PVDZ basis set was employed instead, in vacuum, including two diffuse functions for the description of heavy atoms. Moreover, the TMS reference was also calculated using the same improved basis set; the Gauge Including Atomic Orbitals (GIAO) method36 was used for the NMR analysis. This theoretical setup was successfully applied to the investigation of similar systems composed primarily of carbon, oxygen, nitrogen and hydrogen.37–41 In all cases, the geometry of the Pilo+ was relaxed until the forces reached a local stationary minimum in the potential energy surface. This assures the correct description of the vibrational properties, which are related to the second derivative of the energy with respect to the Cartesian nuclear coordinates.Results and discussion
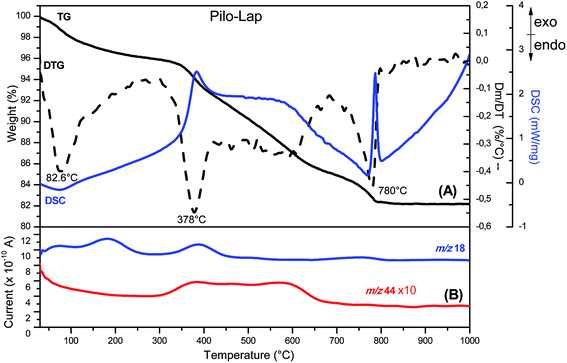
According to the chemical analysis and the water content, obtained by thermal analysis, the chemical formula of Pilo-Lap is (C11H17N2O2)0.13Na0.57[(Mg5.5Li0.3)Si8O20(OH)4]·1.8H2O. The amount of pilocarpine is 3.44 wt% or 16.5 mmol/100 g, and this alkaloid is neutralizing 33% of the clay negative charge.The TG and DSC curves of Lap, Fig. S3 (ESI),† reveal that the synthetic clay presents two thermal events. The first one concerns the release of water molecules (6.7% of mass loss) and occurs in the 30 to 230 °C temperature range while the second event (620 to 830 °C) is the collapse of the layer structure by the layer dehydroxylation process.42 As can be seen by the endothermic event (DSC curve) in Fig. S4 (ESI),† pilocarpine hydrochloride melts at 207 °C. A DTG peak is observed at 315 °C and the MS curve shows that it is decomposed, releasing CO2 (m/z = 44) and H2O (m/z = 18). When intercalated into Lap, Fig. 2, the decomposition of the alkaloid into the volatile products is initiated at about 250 °C and the DTG curve shows a peak at 378 °C. The modifications observed in the thermal profile of Pilo after intercalation are significant compared to the pilocarpine hydrochloride results, reinforcing the influence of the confinement between clay layers on the guest properties.
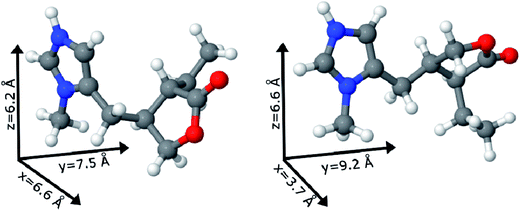
The two possible geometric conformations of Pilo+, shown in Fig. 3, were investigated within the DFT framework. The main geometric parameters obtained from XRD and the optimized DFT results are summarized in Table 1. The Pilo+ distorted calculation started from the XRD results of PiloHCl10 and the Pilo+ planar calculation started from the XRD results of PiloCoCl2.11 The geometric changes between PiloHCl and PiloCoCl2 are mostly related to the torsion angles. The other calculated distances are in general in very good agreement (less than 5% average difference) with the experimental results. The total energy results show that the Pilo+ planar structure is the most stable, with 10.50 kJ mol−1 difference to the Pilo+ distorted conformation. This is a typical energy barrier for torsion angles.43,44 Although PiloHCl displays the distorted form in the crystal,10 it is known that the role of the chemical environment is crucial in establishing its conformation.10,11
| PiloHCl | Pilo+ distorted | PiloCoCl2 | Pilo+ planar | |
|---|---|---|---|---|
| Bond length | ||||
| 1a–2a | 1.51 | 1.53 | 1.50 | 1.53 |
1a![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.21 | 1.19 | 1.21 | 1.19 |
| 1a–O | 1.35 | 1.37 | 1.35 | 1.37 |
| 2a–2d | 1.54 | 1.55 | 1.51 | 1.55 |
| 3a–1c | 1.52 | 1.55 | 1.54 | 1.53 |
| 3a–4a | 1.53 | 1.54 | 1.53 | 1.54 |
| 4a–O | 1.45 | 1.44 | 1.46 | 1.43 |
| 1b–N | 1.33 | 1.33 | 1.34 | 1.33 |
| 1b–N+ | 1.33 | 1.33 | 1.32 | 1.33 |
| 2b–N | 1.38 | 1.40 | 1.39 | 1.40 |
2b![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 3b 3b |
1.36 | 1.37 | 1.35 | 1.37 |
| 3b–N+ | 1.38 | 1.38 | 1.38 | 1.38 |
| 4b–N | 1.46 | 1.47 | 1.46 | 1.47 |
| 1c–2b | 1.49 | 1.49 | 1.49 | 1.50 |
| 1d–2d | 1.53 | 1.53 | 1.54 | 1.53 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Bond angle | ||||
| 3a–1c–2b | 113.37 | 115.90 | 111.73 | 114.02 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Torsion angle | ||||
| θ1 = τ(4a–3a–1c–2b) | 168.46 | 171.95 | 74.46 | 70.18 |
| θ2 = τ(2a–3a–1c–2b) | 74.53 | 59.93 | 186.82 | 188.75 |
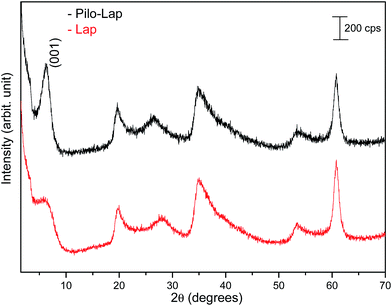
Under the synthesis condition (pH = 5.9) pilocarpine is in the cationic form (Pilo+), which makes the intercalation into the cationic clay favorable and can preserve its structure, since the synthesis prevents the transformation of the alkaloid. However, clays are well known to induce conformational changes in intercalated species.26–30 Therefore, the conformation of protonated pilocarpine was evaluated after the entrapment between the LAPONITE® layers. The X-ray diffraction pattern of Pilo-Lap, Fig. 4, shows the typical42 XRD profile of LAPONITE®, Table 2. Nevertheless, the 001 reflection in the low-angle 2θ region, assigned to the interlayer space of the layered material, shows a dependence on the interlayer content. This reflection reveals a discrete increase from 14.0 Å in Na-Lap to 14.6 Å in Pilo-Lap. Subtracting the 9.6 Å value of the thickness of the clay layer, the interlayer space occupied by the organic cation is ca. 5 Å. Considering the dimensions of the Pilo+ conformers shown in Fig. 3, the Pilo+ distorted conformation (6.6 Å, 5.5 Å and 6.2 Å) can be ruled out, since it cannot fit into the Lap interlayer space. On the other hand, the Pilo+ planar conformation has one of its dimensions smaller than 5 Å, which fits in the interlayer region. Therefore, from only the XRD analysis, an arrangement matching the planar conformation is suggested.
| Lap | Pilo-Lap | hkl | ||
|---|---|---|---|---|
| 2θ | d (Å) | 2θ | d (Å) | |
| 3.15 | 14.0 | 3.02 | 14.6 | (001) |
| 19.95 | 4.45 | 19.65 | 4.51 | (110, 020) |
| 27.93 | 3.19 | 26.55 | 3.35 | (004) |
| 35.01 | 2.56 | 34.68 | 2.58 | (130, 200) |
| 53.37 | 1.71 | 53.40 | 1.71 | (150, 240, 310) |
| 60.81 | 1.52 | 60.81 | 1.52 | (060, 330) |
Since PiloCoCl2 was not measured in the present study and only XRD results are available in the literature, no analysis of this system will be performed in the following.
13C CPMAS NMR spectra of PiloHCl and Pilo-Lap, Fig. 5, were performed in order to examine intermolecular and guest–host interactions. The experimental data is also shown in Table 3, and the chemical shifts were assigned according to the theoretical DFT values. The data are in an overall very good agreement with the literature,45 which is reproduced in the second column of Table 3 for easy reference, where a difference between the 1b/3b carbons can be noticed and it seems that they were interchanged in Gaggelli et al.’s45 tentative attribution.
| Carbon atom | Pilo from Gaggelli et al.45 | PiloHCl | Pilo-Lap | Pilo+ distorted | Pilo+ planar |
|---|---|---|---|---|---|
| a Results. | |||||
| 1d | 11.40 | 11.14 | 12.94 | 12.19 | 13.19 |
| 2d | 17.90 | 18.65 | 20.16 | 24.81 | 29.45 |
| 1c | 20.70 | 22.18 | 24.06 | 28.15 | 29.79 |
| 4b | 33.30 | 34.10 | 34.53 | 35.91 | 34.56 |
| 3a | 36.20 | 36.34 | 37.28 | 40.58 | 45.77 |
| 2a | 44.60 | 42.26 | 45.58 | 46.25 | 50.29 |
| 4a | 71.30 | 70.43 | 73.10 | 68.37 | 71.53 |
| 3b | 135.40 | 115.64 | 118.38 | 117.97 | 121.26 |
| 1b | 132.70 | 135.40 | 134.48 | 132.62 | 133.41 |
| 2b | 116.90 | 135.40 | 136.3 | 141.68 | 140.86 |
| 1a | 182.40 | 179.84 | 182.15 | 173.94 | 174.05 |
The overall agreement between the PiloHCl and Pilo-Lap 13C NMR results confirms the presence and integrity of pilocarpine after the intercalation, which is the main concern regarding its pharmacological activity. Moreover, a systematic tendency to increasing values can be noticed when comparing the PiloHCl and Pilo-Lap results shown in Table 3, with the only exception being the almost degenerated carbon 1b. The same tendency to increasing values can also be noticed when comparing the Pilo+ distorted and Pilo+ planar results, with the exception of the signals 4b and 2b. Nevertheless, these differences are beyond the expected precision of the chemical shifts presented in Table 3.
The chemical shifts of the 1d/4b and 1c/2d atoms are in accordance with the expected CH3 and CH2 in the literature.45,46 On the other hand, a region strained by the entrapment of Pilo+ into the clay is the one involving the 1a, 2a and 4a carbons of the lactone ring: for example, atom 1a presents 179.84 ppm in PiloHCl and 182.15 ppm in Pilo-Lap. This deshielding is probably due to the fact that the lactone and the negatively charged Lap layers induce the electron delocalization of this group in order to maximize the interaction between the drug and the Lap layers. The intercalation process also affects the carbons of the imidazole ring. Carbon 3b was shifted from 115.64 ppm (PiloHCl) to 118.38 ppm (Pilo-Lap), which indicates the electron delocalization of the positively charged N on the aromatic ring being influenced by the negatively charged host layers. Since the species is in a charged state, the DFT results may not precisely match all chemical shifts.
In summary, the 13C NMR data indicate a systematic trend of increasing values going from one to the other conformer here analyzed (Pilo+ distorted and Pilo+ planar) as well as in the experimental results (PiloHCl and Pilo-Lap).
The detailed vibrational assignments from 400 to 3200 cm−1 of the Pilo+ distorted in the framework of DFT, but in vacuum conditions, have already been performed by Bento et al.,12 as well as FT-IR and Raman measurements. Although different basis sets and environmental conditions (vacuum vs. water) have been used, a general good agreement between the presently obtained and Bento et al. results was observed. In order to evaluate the influence of the chemical environment on the vibrational spectra, the theoretical cationic pilocarpine dispositions were simulated in different situations, as discussed in the ESI (Fig. S5).† Therefore, in the following discussion only the analysis of the spectra in the 600 to 1300 cm−1 region for the Pilo+ distorted and Pilo+ planar in water (PCM), which has been shown to be relevant for the present conformational comparison (PiloHCl and Pilo-Lap), will be addressed.
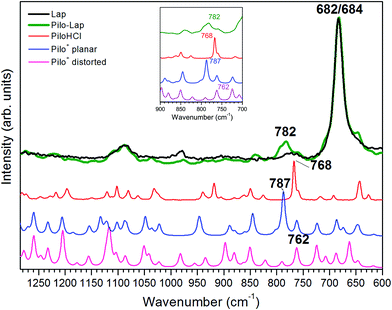
Table 4 and Fig. 6 present the vibrational FT-Raman data of PiloHCl and Pilo-Lap, as well the calculated Pilo+ planar and Pilo+ distorted with the corresponding theoretical band attributions. No scaling factor was applied to the calculated wavenumbers, since the correction of the anharmonic contribution is usually relevant only at high values (above 1300 cm−1).38 The Lap FT-Raman spectrum is also shown in Fig. 6 and the FT-IR spectra are shown in Fig. S6 (ESI).† The 950–1150 cm−1 region in the Pilo-Lap spectrum is dominated by silicate Lap which masks the Pilo bands; the strong signals at 684 (Lap) and 682 (Pilo-Lap) cm−1 are characteristic of the distorted tetrahedral SiO4 unit in C3V symmetry of the clay structure.47 Hence, our discussion will focus on the bands in the region 700–950 cm−1.
| PiloHCl (cm−1) | Pilo+ distorteda (cm−1) | Tentative attribution distortedb | Pilo-Lap (cm−1) | Pilo+ planar (cm−1) | Tentative attributionb planar |
|---|---|---|---|---|---|
| a Selected values obtained through DFT using functional/basis set B3LYP/6-311G(d,p).b Main groups involved in the vibration.c ν = stretching, νs = symmetric stretching, νas = antisymmetric stretching, w = wagging, r = rocking, t = twisting. | |||||
| 768 | 762 | w(1d), r(2d), breathing (lactone)c | 782 | 787 | In-plane bending (imidazole), sc(1c, 2b, 3a) |
| 850 | 851 | w(1d), t(2d), r(1c), C–H in-plane bending (imidazole and lactone) | 840 | 845 | In-plane bending (lactone), t(2d), r(1c) |
| 862 | 863 | C–H and N–H in-plane bending (imidazole) | 870 | 860 | C–H and N–H in-plane bending (imidazole) |
| 918 | 897 | t(2d), C–H in-plane bending (lactone) | 896 | 889 | r(1c), w(1d, 2d), breathing (lactone) |
| 940w | 935 | Out-of-plane bending (imidazole), w(1d, 2d, 4b), r(1c) | 940 | 947 | r(1c), w(1d), C–H in-plane bending (lactone) |
| 1032 | 1041 | νas(O–4a–3a), ν(1d![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 2d) 2d) |
1037 | 1036 | ν(O–4a), C–H in-plane bending (lactone) |
| 1081 | 1086 | Out-of-plane bending (imidazole), w(4b) | 1087 | 1084 | w(4b), t(2d), r(1c), ν(2a–3a; 1a–O; 1b–N) |
| 1102 | 1103 | ν(2a–2d; 1a–O) + w(1d) | 1106 | 1102 | w(1d, 4b); ν(1c–2b), t(2d) |
| 1120 | 1123 | w(1d, 4b), t(1c), νs(1b–N–3b) | 1148 | 1121 | w(1d, 4b), t(2d), C–H in-plane bending (lactone), νs(1b–N–3b), t(1c) |
| 1281 | 1278 | w(1c, 1d), t(2d), C–H in-plane bending (lactone) | 1274 | 1271 | t(1c, 1d, 2d), C–H in-plane bending (lactone) |
As can be noticed from Table 4, a fingerprint difference between both calculated pilocarpine conformations is in the band located at 762 (Pilo+ distorted) and 787 cm−1 (Pilo+ planar). The band at 762 cm−1, that corresponds to 768 cm−1 for PiloHCl, is assigned mainly to the breathing mode of the lactone group, whereas the band at 787 cm−1, related to 782 cm−1 for Pilo-Lap, involves the out-of-plane and in-plane bending of the imidazole and lactone groups. These modes are illustrated in Fig. 7. Another difference between the calculated forms is that the band at 935 cm−1 (Pilo+ distorted) corresponds to the out-of-plane bending of the imidazole group, whereas that at 947 cm−1 (Pilo+ planar) is the in-plane bending of the lactone. Nevertheless, both frequencies correspond to the same 940 cm−1 value in the experimental spectra (PiloHCl and Pilo-Lap) and therefore are not suitable for fingerprinting the theoretical and experimental relation.
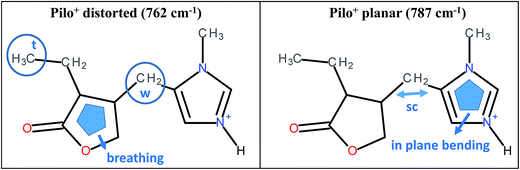 | ||
| Fig. 7 Schematic representation of the vibrational modes of Pilo+ distorted at 762 cm−1 and Pilo+ planar at 787 cm−1. | ||
In summary, the main target of the present study is the conformational changes upon intercalation in protonated pilocarpine and, to accomplish this task, the Raman spectra of Pilo+ in distorted and planar conformations, starting from crystallography data, were simulated. The theoretical results have shown that not only did some characteristic vibrational frequencies change but also their vibrational assignments: on the one hand, Pilo+ distorted shows lactone ring activity and on the other hand, Pilo+ planar shows imidazole ring activity. The band used as a marker to differentiate both conformers and to correlate them with the experimental ones is the band at 762 cm−1 for Pilo+ distorted and 787 cm−1 for Pilo+ planar. These bands were associated with PiloHCl at 768 cm−1 and with Pilo-Lap at 782 cm−1. In order to further inspect the correlation between the two theoretical conformers and the experimental results, presented in Table 4, they are plotted in Fig. S7 (ESI).† Good linear correlations between the experimental and the calculated frequencies were obtained in all cases (Fig. S7A–D†). The differences between theoretical and experimental frequencies are in accordance with this type of correlation in the literature.40,48,49 Although the coefficients of determination (R2) are similar, differing by 10−3, the best linear correlations between experimental and calculated frequencies were obtained by associating PiloHCl with Pilo+ distorted (Fig. S7A†) and Pilo-Lap with Pilo+ planar (Fig. S7D†). Most important is the fact that the characteristic first point of the curves in Fig. S7B† (768 cm−1 pilocarpine with 787 cm−1 Pilo+ planar) and Fig. S7C† (782 cm−1 Pilo-Lap with 762 cm−1 Pilo+ distorted) are slightly outside the straight correlation, whereas these points match very well in Fig. S7A and D.† However, it should be noticed that discrepancies in the experimental Pilo-Lap and theoretical frequency correlations can also be addressed by the fact that the simulations are performed only for the organic species, i.e., the clay framework is not considered. The results presented here also suggest that Pilo+ changes to the planar form during the intercalation process.
Assuming this correspondence, the influence of the intercalation process on the vibrational modes can be further inspected as shifts: (a) from 850 in PiloHCl to 840 cm−1 in Pilo-Lap that correspond respectively to 851 cm−1 (Pilo+ distorted), assigned mainly to the C–H in-plane bending of the imidazole and lactone groups, and 845 cm−1 (Pilo+ planar), assigned to the in-plane bending of the lactone group; (b) from 862 in PiloHCl to 870 cm−1 in Pilo-Lap that corresponds to 863 cm−1 (Pilo+ distorted) and 860 cm−1 (Pilo+ planar), having the same vibrational mode assigned to the C–H and N–H in-plane bending of the imidazole group; (c) although with a weak signal, from 918 cm−1 in PiloHCl to 896 cm−1 in Pilo-Lap, corresponding to 897 cm−1 (Pilo+ distorted), attributed to the C–H in-plane bending (lactone) and 889 cm−1 (Pilo+ planar), attributed to the breathing of the lactone ring. Although, as was mentioned above, the 950–1150 cm−1 region is dominated by the Lap bands, a shift from 1120 in PiloHCl to 1148 cm−1 in Pilo-Lap could also be due to the intercalation process, corresponding respectively to: 1123 cm−1 (Pilo+ distorted) and 1121 cm−1 (Pilo+ planar), attributed to the 1c twisting, 1d and 4b wagging and the symmetric stretching of the 1b–N–3b bonds; additionally, Pilo+ planar displays the torsion of 2d and in-plane bending of the lactone group.
Conclusions
Structural and spectroscopic properties of pilocarpine intercalated into LAPONITE®, presented as a model carrier, were examined and confronted with theoretical simulations performed in the framework of the Density Functional Theory. The results indicated that the chemical structure of the molecule is maintained, while some interesting aspects regarding conformations were observed, as addressed below. To the best of our knowledge, we did not find any results regarding drug release and we also did not perform these tests, while we agree that this is a very interesting topic.The XRD data have shown a successful Pilo+ intercalation process, by ion exchange, into the synthetic Lap. In addition, TGA-MS results demonstrated a modification in the thermal profile after intercalation between the layers due to changes in the Pilo environment.
13C NMR results confirm the integrity of the organic species after intercalation into Lap. Although no significant signature chemical shift change was detected, a clear tendency towards larger values could be observed upon intercalation (from PiloHCl to Pilo-Lap) which could also be related to the two theoretical conformational models, Pilo+ distorted and Pilo+ planar, studied here.
The theoretical fingerprints that demonstrated the distinction between the conformations related to the Raman activity are the band modifications 762/787 cm−1 for Pilo+ distorted and planar, respectively; these bands were associated with 768/782 cm−1 for PiloHCl and Pilo-Lap.
These results suggest that Pilo+ may assume a conformation between the LAPONITE® layers (Pilo+ planar) different from that observed in the precursor PiloHCl (Pilo+ distorted). Nevertheless, since many vibrational modes are superposed, it cannot be ruled out that a mixture of both forms is present after the intercalation. Given the theoretical energy barrier of 10.50 kJ mol−1 between the two conformers investigated here, it is possible to further infer that further conformations may also be present.
As shown here, imposed by the entrapment, Pilo+ can have at least two different conformations; attention to this aspect should be given in the development of drug delivery applications using clays as carriers.
Acknowledgements
The authors acknowledge the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP Projects: 2012/12209-9, 2012/02326-8), Fundação de Amparo à Pesquisa do Estado do Piauí (FAPEPI), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq: 140674/2013-6), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), and Nanobiomed (Nanomedicine Network/CAPES) for financial support and scholarships. This work has used the USP-HPC, USP-Rice agreement and CENAPAD/SP computational facilities. Phytobios LTDA, Anidro do Brasil Extrações S.A. (Centro flora Group) for the study grant awarded. We are also thankful to the Laboratório de Espectroscopia Molecular (LEM, Instituto de Química – USP) for the Raman spectra recording.References
- S. S. Anumolu, Y. Singh, D. Gao, S. Stein and P. J. Sinko, J. Controlled Release, 2009, 137, 152–159 CrossRef CAS PubMed.
- G. Li, S. Farsiu, S. J. Chiu, P. Gonzalez, E. Lütjen-Drecoll, D. R. Overby and W. D. Stamer, Invest. Ophthalmol. Visual Sci., 2014, 55, 3737 CAS.
- L. R. Wiseman and D. Faulds, Drugs, 1995, 49, 143–155 CrossRef CAS PubMed.
- R. G. Hendrickson, A. P. Morocco and M. I. Greenberg, J. Emerg. Med., 2004, 26, 429–432 CrossRef PubMed.
- R. Bernardi, C. Perin, F. L. Becker, G. Z. Ramos, G. Z. Gheno, L. R. Lopes, M. Pires and H. M. T. Barros, Braz. J. Med. Biol. Res., 2002, 35, 105–110 CrossRef CAS PubMed.
- W. N. Charman, L. E. McCrossin, N. L. Pochopin and S. L. A. Munro, Int. J. Pharm., 1992, 88, 397–404 CrossRef CAS.
- K. Persson and O. Åström, J. Chromatogr. B: Biomed. Sci. Appl., 1997, 697, 207–215 CrossRef CAS.
- T. P. Kenakin, R. A. Bond and T. I. Bonner, Pharmacol. Rev., 1992, 44, 351–362 CAS.
- S. Fregerslev, S. E. Rasmussen, B. Olofsson and P. H. Nielsen, Acta Chem. Scand., 1968, 22, 2541–2556 CrossRef CAS.
- P. W. Codding and M. N. G. James, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 429–434 CrossRef.
- B. Wisser and C. Janiak, Z. Anorg. Allg. Chem, 2007, 633, 1796–1800 CrossRef CAS.
- R. R. F. Bento, P. T. C. Freire, A. M. R. Teixeira, J. H. Silva, N. R. Romero and F. M. Pontes, Braz. J. Phys., 2009, 55, 62–68 Search PubMed.
- M. C. Portes, J. De Moraes, L. M. C. Véras, J. R. Leite, A. C. Mafud, Y. P. Mascarenhas, A. E. V. Luz, F. C. D. A. De Lima, R. R. Do Nascimento, H. M. Petrilli, P. L. S. Pinto, G. Althoff and A. M. D. C. Ferreira, J. Coord. Chem., 2016, 1–39 Search PubMed.
- L. M. C. Véras, V. R. R. Cunha, F. C. D. A. Lima, M. A. Guimarães, M. M. Vieira, Y. D. M. Campelo, V. Y. Sakai, D. F. Lima, P. S. Carvalho Jr, J. A. Ellena, P. R. P. Silva, L. C. Vasconcelos, M. Godejohann, H. M. Petrilli, V. R. L. Constantino, Y. P. Mascarenhas and J. R. de Souza de Almeida Leite, PLoS One, 2013, 8, e66702 Search PubMed.
- S. Mintova, M. Jaber and V. Valtchev, Chem. Soc. Rev., 2015, 44, 7207–7233 RSC.
- M. Ghadiri, W. Chrzanowski and R. Rohanizadeh, RSC Adv., 2015, 5, 29467–29481 RSC.
- B. P. Nair and C. P. Sharma, Langmuir, 2012, 28, 4559–4564 CrossRef CAS PubMed.
- E. E. Gaskell and A. R. Hamilton, Future Med. Chem., 2014, 6, 641–655 CrossRef CAS PubMed.
- C. Aguzzi, P. Cerezo, C. Viseras and C. Caramella, Appl. Clay Sci., 2007, 36, 22–36 CrossRef CAS.
- T. Felbeck, K. Hoffmann, M. M. Lezhnina, U. H. Kynast and U. Resch-Genger, J. Phys. Chem. C, 2015, 119, 12978–12987 CAS.
- C. Li, C. Mu, W. Lin and T. Ngai, ACS Appl. Mater. Interfaces, 2015, 7, 18732–18741 CAS.
- K. J. Sorauf, D. E. Connors, T. A. Wells and K. E. Miller, Appl. Clay Sci., 2014, 87, 197–204 CrossRef CAS.
- K. Li, S. Wang, S. Wen, Y. Tang, J. Li, X. Shi and Q. Zhao, ACS Appl. Mater. Interfaces, 2014, 6, 12328–12334 CAS.
- S. Wang, Y. Wu, R. Guo, Y. Huang, S. Wen, M. Shen, J. Wang and X. Shi, Langmuir, 2013, 29, 5030–5036 CrossRef CAS PubMed.
- A. K. Gaharwar, S. M. Mihaila, A. Swami, A. Patel, S. Sant, R. L. Reis, A. P. Marques, M. E. Gomes and A. Khademhosseini, Adv. Mater., 2013, 25, 3329–3336 CrossRef CAS PubMed.
- S. Kim, M. A. Motyka, A. M. Palomino and N. J. Podraza, Clays Clay Miner., 2012, 60, 363–373 CrossRef CAS.
- S. Kim, A. M. Palomino and C. M. Colina, Mol. Simul., 2012, 38, 723–734 CrossRef CAS.
- M. E. Parolo, M. J. Avena, M. C. Savini, M. T. Baschini and V. Nicotra, Colloids Surf., A, 2013, 417, 57–64 CrossRef CAS.
- M. Revault, H. Quiquampoix, M. H. Baron and S. Noinville, Biochim. Biophys. Acta, Gen. Subj., 2005, 1724, 367–374 CrossRef CAS PubMed.
- P. Cai, Q.-Y. Huang and X.-W. Zhang, Environ. Sci. Technol., 2006, 40, 2971–2976 CrossRef CAS PubMed.
- W. Kohn and L. J. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Rev A.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- V. R. R. Cunha, P. A. D. Petersen, M. B. Gonçalves, H. M. Petrilli, C. Taviot-gueho, F. Leroux, M. L. A. Temperini and V. R. L. Constantino, Chem. Mater., 2012, 24, 1415–1425 CrossRef CAS.
- M. D. Halls and H. B. Schlegel, J. Chem. Phys., 1999, 111, 8819 CrossRef CAS.
- V. R. R. Cunha, C. M. S. Izumi, P. A. D. Petersen, A. Magalhães, M. L. A. Temperini, H. M. Petrilli and V. R. L. Constantino, J. Phys. Chem. B, 2014, 118, 4333–4344 CrossRef CAS PubMed.
- M. A. Rocha, P. A. D. Petersen, E. Teixeira-Neto, H. M. Petrilli, F. Leroux, C. Taviot-Gueho and V. R. L. Constantino, RSC Adv., 2016, 6, 16419–16436 RSC.
- V. R. R. Cunha, V. A. Guilherme, E. de Paula, D. R. de Araujo, R. O. Silva, J. V. R. Medeiros, J. R. S. A. Leite, P. A. D. Petersen, M. Foldvari, H. M. Petrilli and V. R. L. Constantino, Mater. Sci. Eng., C, 2016, 58, 629–638 CrossRef CAS PubMed.
- G. F. Perotti, H. S. Barud, Y. Messaddeq, S. J. L. Ribeiro and V. R. L. Constantino, Polymer, 2011, 52, 157–163 CrossRef CAS.
- M. Alves-Santos, L. Y. A. Dávila, H. M. Petrilli, R. B. Capaz and M. J. Caldas, J. Comput. Chem., 2006, 27, 217–227 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, Phys. Rev. Lett., 2014, 113, 55701 CrossRef PubMed.
- E. Gaggelli, N. Gaggelli, G. Valensin and A. Vivi, Can. J. Chem., 1993, 71, 738–741 CrossRef CAS.
- R. M. Silverstein, F. X. Webster, D. J. Kiemle and D. L. Bryce, Spectrometric Identification of Organic Compounds, Wiley, 8th edn, 2014 Search PubMed.
- R. L. Frost and L. Rintoul, Appl. Clay Sci., 1996, 11, 171–183 CrossRef CAS.
- I. M. Nangoi, V. S. Vaiss, W. F. Souza, S. S. X. Chiaro and A. A. Leitão, Appl. Clay Sci., 2015, 107, 131–137 CrossRef CAS.
- A. Gryff-Keller and P. Szczeciński, RSC Adv., 2014, 4, 27290 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02017a |
| This journal is © The Royal Society of Chemistry 2017 |