Experimental and ab initio studies of two UV nonlinear optical materials

Abstract

Two new acentric polyborates, Ba₃(OH)(B₉O₁₆)[B(OH)₃] and Ba_2.16Pb_0.84(OH)(B₉O₁₆)[B(OH)₃] have been synthesized hydrothermally and their structures have been determined by single-crystal X-ray diffraction. Both crystals are isostructural and crystallize in the trigonal space group P31c (no. 159). Their structures feature a three-dimensional (3D) B₉O₁₉ framework with 6-membered-ring tunnels, in which the Ba or Pb/Ba cations and [B(OH)₃] groups reside. Powder second-harmonic-generation (SHG) measurements reveal that Ba₃(OH)(B₉O₁₆)[B(OH)₃] and Ba_2.16Pb_0.84(OH)(B₉O₁₆)[B(OH)₃] are type-I phase-matchable, with SHG responses of 1.1× and 1.2× KH₂PO₄, respectively. UV-Vis-NIR diffuse reflectance analysis indicates that Ba₃(OH)(B₉O₁₆)[B(OH)₃] and Pb_0.29Ba_2.71(OH)(B₉O₁₆)[B(OH)₃] have band gaps of 5.11 and 4.65 eV, respectively. In addition, first-principles calculations were employed to elucidate the origin of the NLO properties and the relationship of structure–properties.

---

Introduction

Nonlinear optical (NLO) materials have numerous important applications in semiconductor photolithography, laser micromachining, photochemical synthesis, and material processing due to their abilities to expand the frequency range of solid-state lasers from UV to IR.^1,2 Over the past decades, extensive efforts have been made to search for new NLO materials with excellent properties, including a large second harmonic generation (SHG) response and wide transparency window,³ etc. To enhance the SHG response of the materials, “distortable” metal cations containing the d⁰ or d¹⁰ transition metals (e.g., Ti⁴⁺, V⁵⁺, Zn²⁺, Cd²⁺, etc.) and stereochemically active lone pair (SCALP) cations (Bi³⁺, Pb²⁺, Te⁴⁺, etc.) are introduced into the crystal structures.^4–7 Unfortunately, the introduction of these cations always causes red shifts of the ultraviolet (UV) absorption edge. Compared with the d⁰ or d¹⁰ transition metal, alkaline-earth metal cations have wide transmittances in UV region. In addition, borate is transparent in UV range as well. And it has a twice probability (in average) to be non-centrosymmetric than that of other inorganic compounds,^1a which becomes a good candidate for NLO materials.

With this in minds, we combine the alkaline-earth metal cation with the borate system and successfully synthesize a new barium borate, Ba₃(OH)(B₉O₁₆)[B(OH)₃] (I), through the hydrothermal method. It has a large band gap of 5.11 eV and is type-I phase matchable with SHG responses of about 1.1× K₂HPO₄ (KDP). Through our investigation, barium atoms can be replaced by lead atoms to generate larger SHG response in many non-centrosymmetric structures.^8,9 For instance, Pb₂Ba₃(BO₃)₃Cl exhibit a large SHG response 6× higher than its isomorphic compound Ba₅(BO₃)₃Cl. Thus, we tried to substitute lead for barium in compound I and obtained another new compound, Ba_2.16Pb_0.84(OH)(B₉O₁₆)[B(OH)₃] (II). To systematically study the substitution influence of the Pb cations on optical properties, we synthesize the polycrystalline samples of Pb₃(OH)(B₉O₁₆)[B(OH)₃] (III),¹⁰ which is isomorphic with I and II. In this paper, we combine experimental characterization and theoretical calculations to study the optical properties among these three compounds. In addition, the thermal behavior and infrared (IR) spectra on these three compounds are also reported.

Experimental

Synthesis

All reagents were of analytical grade. Three compounds were synthesized under hydrothermal condition. The mixtures were mixed homogeneously and transferred to heat-sealed FEP Teflon pouches. The pouches were placed in 23 mL Teflon-lined stainless steel vessels and each vessel was added with about 8 mL distilled water. Then the vessels were heated to 210 °C for 12 days and cooled to room temperature at a rate of 2 °C h⁻¹. The resulting colorless columnar crystals were obtained, washed with distilled water, and finally dried in air at ambient temperature.

Compound I. A mixture of Ba(OH)₂·8H₂O (0.210 g, 0.67 mmol), H₃BO₃ (0.227 g, 3.67 mmol) and 0.1 mL of anhydrous ethylenediamine was mixed homogeneously. The yield of the product was just about 10% based on Ba(OH)₂·8H₂O. To increase the yield of compound I, we adjusted the proportion of raw material with a mixture of Ba(NO₃)₂ (0.090 g, 0.34 mmol), H₃BO₃ (0.106 g, 1.71 mmol), Li(OH)·H₂O (0.024 g, 0.57 mmol) and NH₄NO₃ (0.024 g, 0.15 mmol) in deionized water. Thus the yield of the product increases to 95% based on Ba(NO₃)₂.

Compound II. A mixture of BaCO₃ (0.099 g, 0.50 mmol), H₃BO₃ (0.247 g, 3.99 mmol), Pb(CH₃COO)₂·3H₂O (0.095 g, 0.25 mmol), PbF₂ (0.015 g, 0.06 mmol) and 0.2 mL NaOH solution (0.8 M) was mixed homogeneously. Colorless crystals of compound II were obtained in a yield of 85% based on BaCO₃.

Compound III. A mixture of PbO (0.186 g, 0.83 mmol), B₂O₃ (0.296 g, 4.25 mmol), and 0.2 mL of glacial acetic acid was mixed homogeneously. Colorless crystals of compound III were obtained in a yield of about 90% based on PbO.

Structural determination

Single crystals of compounds I and II were collected at room temperature on a Bruker SMART APEX II CCD diffractometer with graphite monochromatic Mo Kα radiation (λ = 0.71073 Å) at 296(2) K and integrated with the SAINT program.¹¹ The numerical absorption corrections were carried out using the SCALE program for area detector. All calculations were performed with programs from the SHELXTL crystallographic software package,¹² and all of the atoms were refined using full-matrix least-squares techniques with anisotropic thermal parameters and finally converged for F₀² ≥ 2σ(F₀²). During the refinement, we found that in the structure of compound I, the Ba(1) atom has a large thermal factor and a large Q peak is around the Ba(1) atom. Refined with the split model, a Ba(1) site with 88.9% occupancy and a Ba(2) site with 11.1% occupancy converge with better R values and reasonable temperature factors. The structures were checked for missing symmetry elements by the program PLATON.¹³ There was no higher symmetry to be found. Details of crystal parameters, data collection and structure refinements were shown in Table 1. The atomic coordinates, equivalent isotropic displacement coefficients and important bond lengths and angels were listed in Tables S1 and S2 in the ESI,† respectively. For comparison, the structure of compound III was reexamined and the data was also listed in Table 1.

Table 1 Crystal data and structure refinement results for compounds I, II and III

a R1 = ∑||F0| − |Fc||/∑|F0| and wR2 = [∑w(F0^2 − Fc^2)^2/∑wF0^4]^1/2 for F0^2 > 2σ(F0^2).
Empirical formula	I	II	III
Formula weight	844.15	902.78	1053.70
Crystal system	Trigonal	Trigonal	Trigonal
Space group, Z	P31c, 2	P31c, 2	P31c, 2
Unit cell dimensions	a = 10.252(9) Å	a = 10.218(8) Å	a = 10.080(9) Å
	c = 8.623(3) Å	c = 8.587(1) Å	c = 8.533(1) Å
Volume (Å^3)	785.0(3)	776.3(1)	751.0(1)
Density (calculated) (mg m^−3)	3.571	3.910	4.642
Theta range for data collection (deg)	2.29 to 27.41	2.30 to 27.26	2.33 to 27.66
Limiting indices	−13 ≤ h ≤ 11, −13 ≤k ≤ 11, −9 ≤ l ≤ 11	−12 ≤h ≤13, 12 ≤k ≤13, −9 ≤ l ≤ 11	−13 ≤ h ≤ 13, −11 ≤ k ≤ 13, −8 ≤ l ≤ 11
Reflections collected/unique	4561/1139 [R(int) = 0.0539]	4331/1109 [R(int) = 0.0787]	4458/1044 [R(int) = 0.0440]
Completeness to theta	100.0%	100.0%	100.0%
Goodness-of-fit on F^2	1.150	1.071	1.004
Final R indices [F0^2 > 2σ(F0^2)]^a	R1 = 0.0457, wR2 = 0.0919	R1 = 0.0527, wR2 = 0.1155	R1 = 0.0239, wR2 = 0.0403
R indices (all data)^a	R1 = 0.0489, wR2 = 0.0931	R1 = 0.0595, wR2 = 0.1186	R1 = 0.0264, wR2 = 0.0412
Extinction coefficient	0.0018(3)	0.0071(1)	0.0029(2)
Largest diff. peak and hole (e Å^−3)	1.574 and −1.404	1.673 and −2.123	1.294 and −0.759

---

Powder X-ray diffraction (XRD). Powder XRD patterns of polycrystalline sample of compounds I, II and III were obtained on a Bruker D2 PHASER diffractometer with Cu Kα radiation (λ = 1.5418 Å) at room temperature (Fig. S1 in the ESI†). The 2θ range was 10–70° with a step size of 0.02° and a fixed counting time of 1 s per step.

Infrared and UV-vis-NIR spectrum measurements. The IR spectrum was recorded with a Shimadzu IR Affinity-1 Fourier transform IR spectrometer in the 400–4000 cm⁻¹ wave number range. The samples were mixed thoroughly with dried KBr (5 mg of each sample and 500 mg of KBr). UV-Vis-NIR diffuse reflectance spectrum was measured at room temperature on a Shimadzu SolidSpec-3700DUV spectrophotometer with a range from 190 to 2600 nm.

Thermal analysis

The thermal gravity-differential scanning calorimetric (TG-DSC) analyses were carried out on NETZSCH STA 449 °C instrument at a temperature range of 30–1000 °C with a heating rate of 10 °C min⁻¹ under a constant flow of nitrogen gas.

Second-order NLO measurement

Powder SHG measurements were performed on a modified Kurtz-NLO system using a pulsed Nd:YAG laser (1064 nm, 10 kHz, 10 ns). A detailed description of the methodology has been published.¹⁴ As the powder SHG efficiency has been shown to strongly depend on particle size. The crystals of three compounds were ground and sieved into distinct particle size ranges: <20, 20–38, 38–55, 55–88, 88–105, 105–150, and 150–200 μm, respectively. The microcrystalline samples of KDP served as the standard and were also sieved into the same particle size ranges.

Theoretical calculation details

The band structure of compounds I and III have been calculated by the first principles method. For compound I, we only think that the Ba(1) atoms are 100% occupancy used for the calculation, while for compound II calculations were not performed since the site disorder existed in the structure. The plane-wave pseudopotential method implemented in the CASTEP package¹⁵ was used to calculate the electronic structure and NLO properties. We adopted GGA-PBE as the exchange correlation function and norm-conserving pseudopotential to treat electron–core interactions.^16,17 The kinetic energy cutoff was set as 800 and 870 eV for compounds I and III, respectively. The outmost electrons of H, B, and O, as well as Ba-5s² 5p⁶ 6s² and Pb-5s² 5p⁶ 5d¹⁰ 6s² 6p², were considered to be valence electrons. The k-point was set as 2 × 2 × 2 for compounds I and III.

At a zero frequency, the SHG coefficients were calculated using the length-gauge formalism method derived by Aversa et al. and developed by Lin and Zhang et al.^18–20 The static second-order nonlinear coefficients can be ascribed to virtual-electron (VE) and virtual-hole (VH) processes,

x⁽²⁾_αβγ = x⁽²⁾_αβγ(VE) + x⁽²⁾_αβγ(VH). (1)

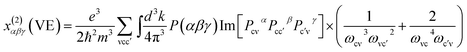Where x⁽²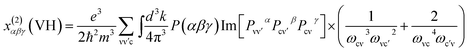⁾_αβγ(VE) and x⁽²⁾_αβγ(VH) can be computed by the following eqn (2) and (3), respectively.here, α, β, γ are Cartesian components, while ν and ν′ donate valence bands (VBs), c and c′ donate conduction bands (CBs). And then P(αβγ), ℏω_ij and P_ij^α refer to full permutation, the band energy difference and momentum matrix elements, respectively.

Results and discussion

Crystal structure

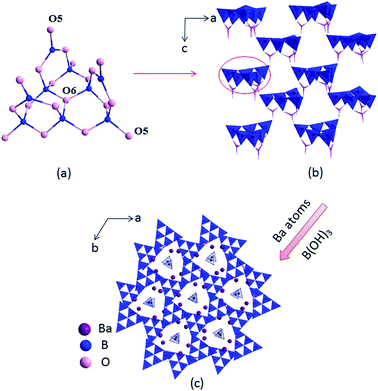
The compounds I, II and III are isostructural, hence, only the structure of compound I is discussed as the representative. Compound I crystallizes in a trigonal crystal system with an acentric space group of P31c (no. 159). In the asymmetric unit, the Ba, B and O atoms occupy one, four and eight crystallographically unique positions, respectively (Table S1 in the ESI†). The B atoms are bonded to three or four O atoms to form two kinds of coordination models BO₃ triangles and BO₄ tetrahedra. Six BO₄ tetrahedra connected with three BO₃ triangles to construct B₉O₁₉ group (Fig. 1a), which further connected by sharing oxygen atoms to build a 3D framework with tunnels along c axis (Fig. 1b), where the Ba atoms and B(OH)₃ reside in (Fig. 1c).

Fig. 1 Structure of compound I (the Ba–O bonds and H atoms are omitted for clarity).

In the structure of compound I, the Ba atoms are connected with nine O atoms to form the Ba(1)O₉ polyhedra, with the Ba–O bond lengths ranging in 2.496(3)–3.192(1) Å (average = 2.811(0) Å). Three Ba(1)O₉ polyhedra connect with each other by sharing edges to form the 3D Ba–O framework (Fig. S2 in the ESI†). The B–O distances vary from 1.347(1)–1.441(1) Å (average = 1.376(5) Å) in the BO₃ triangles and 1.442(1)–1.534(1) Å (average = 1.472(3) Å) in the BO₄ tetrahedra, respectively, which are also similar to reported values in other borates, such as Ba₄B₁₁O₂₀F,^5d M₂Ca₃B₁₆O₂₈ (M = Rb, Cs)²¹ and Sr₄B₁₀O₁₈(OH)₂·2H₂O.²² In addition, the bond valences of the Ba, Pb, B and O atoms have been calculated according to the Brown parameters for compounds I, II and III and are listed in Table S1 in the ESI,† which are in agreement with their ideal oxidation state (Ba, +2; Pb, +2; B, +3; O, −2).

Compounds I, II and III are isostructural and their fundamental structure units are all B₉O₁₉ group, which further connected with each other to build the 3D framework. While the coordination of the cations are not the same. In compound II, one site is occupied by constitutionally disordered Pb and Ba atoms, which is different from the total occupation of atoms on each site for compound III. In addition, in compounds I and II, the Ba atoms and Pb/Ba atoms are both located in nine coordination environments to form the Ba(1)O₉ and Ba/PbO₉ polyhedra, respectively. While in compound III, the Pb atoms are located in four coordination environments to form the PbO₄ tetrahedra. Then three PbO₄ tetrahedra are linked by sharing O₇ atoms to form isolated Pb₃O₁₀ unit (Fig. S1c†).

Thermal analysis

The TG-DSC curves of three compounds are shown (Fig. S3†). Hydroxyl groups exist in three compounds, but at a relatively high temperature, it will be removed in the form of water molecule. Evident weight loss has been observed for compounds I, II and III in the temperature range 400–700, 400–600 and 200–300 °C, respectively. For compound I, the weight loss is 7.3%, which is due to the release of 3.5 molecules H₂O per formula unit (calculated value 7.5%). For compound II, the weight loss of 3.9% is due to the releases of the two molecules H₂O (calculated 4.0%). While for compound III, the weight loss is 1.8% due to the release of one molecule H₂O (calculated 1.7%).

IR spectrum

The IR spectra of compounds I, II and III are shown in Fig. S4.† Accordingly the absorption peaks are listed in Table 2. The spectra are similar on these three compounds. We can see that the absorption peaks locate at 3000–3450 cm⁻¹ assigning to the vibrations of the OH groups. The strong absorption peaks between 1259 and 1433 cm⁻¹ can be attributed to the asymmetric stretching of the BO₃ groups, whereas the absorption peaks at about 925–950 cm⁻¹ can be attributed to the symmetric stretching of the BO₃ groups. The peaks located at ∼1120 and ∼810 cm⁻¹ are the asymmetric and symmetric stretching of the BO₄ groups, respectively. The bending vibrations of the BO₃ and BO₄ groups can be observed in the range 510–756 cm⁻¹. The results show that the BO₃ and BO₄ groups exist in the three compounds.^23,24

Table 2 Assignments of the infrared absorption peaks for compounds I, II and III

Mode description	I (cm^−1)	II (cm^−1)	III (cm^−1)
Characteristic peak of OH	3007	3455	3441
Asymmetric stretching of B3–O	1433, 1284	1424, 1318, 1267	1432, 1347, 1259
Asymmetric stretching of B4–O	1130, 1060	1122, 1056	1120, 1056
Symmetric stretching of B3–O	925	939	950
Symmetric stretching of B4–O	803	815	810
Out-of-plane bending of B3–O	756, 658, 614	747, 664	743, 663, 601
Bending of B4–O and B3–O	523	510	518

---

UV-Vis-NIR diffuse reflectance spectroscopy

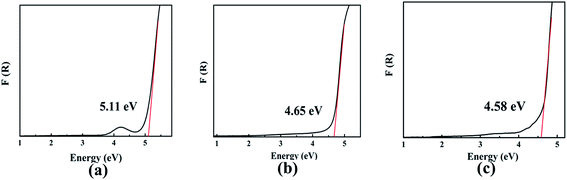
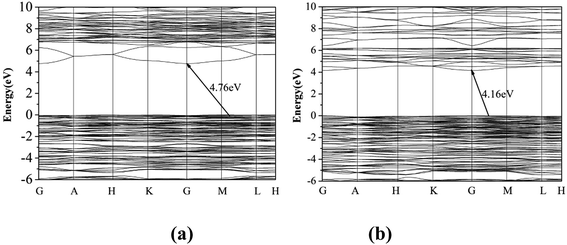
The optical diffuse reflectance spectra of compounds I, II and III in the region 190–2600 nm were measured (Fig. S5†). Reflectance spectra were converted to absorbance using the function, F(R) = (1 − R)²/2R, where R is the reflectance and F(R) is the Kubelka–Munk remission function.^25,26 It is obtained that the experimental energy gaps of compounds I, II and III are 5.11, 4.65 and 4.58 eV, respectively (Fig. 2). Obviously, there is a red shift of the absorption edges from compound I to III due to the substitution of Pb for Ba atom.

Fig. 2 The optical absorption spectra of compounds I (a), II (b) and III (c).

The first principle calculation results show that compounds I and III are indirect band gap compounds with calculated band gap 4.76 eV for compound I and 4.16 eV for compound III (Fig. 3). The calculated band gaps are smaller than the experimental ones, which is mainly caused by the inaccuracy of the exchange correlation energy.^27,28

Fig. 3 The band gap of compounds I (a) and III (b).

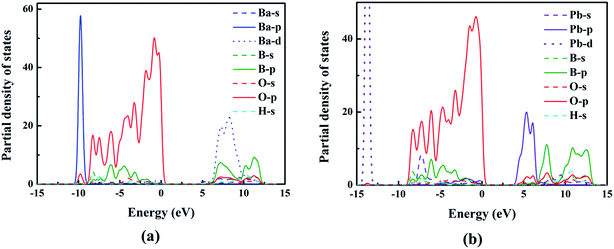
To better understand the relationship between electronic structures and optical properties, the density of states (DOS) of compounds I and III were compared and shown in Fig. 4. At the valence band, the two compounds have similar electronic structures: the inner valence orbitals for the constituent ions (i.e., O-2s orbitals, B-sp mixed orbitals, Ba-4s orbitals, and H-s orbitals), respectively. The valence bands from −10 to 0 eV for both compounds are mainly composed of the O-2p orbitals, B-2p orbitals, Ba-4p orbitals and H-s orbitals, respectively, and the O-2p orbitals have dominant contribution to the maximum of the valence bands. The conduction bands are mainly composed of B-2p orbitals, O-2p orbitals and Ba-5d for compound I, and B-2p orbitals, O-2p orbitals and Pb-6p for compound III. We can see that Pb-6p orbitals of compound III locate nearer to the Fermi level than Ba-5d orbitals of compound I, which cause the small red shift of the band gaps from compound I to compound III.

Fig. 4 The PDOS of compounds I (a) and III (b).

Second-harmonic generation effects

We have also investigated their SHG responses since the title compounds belong to a NCS space group (P31c). Compounds I, II and III exhibit a SHG response of 1.1, 1.2 and 2.7 times that of KDP, respectively (Fig. 5), which indicates that the Pb substitution can enhance the SHG response in the three compounds. In addition, compounds I, II and III are all type-I phase matchable because the second-harmonic intensities increase with the increase of particle size and go to saturation values.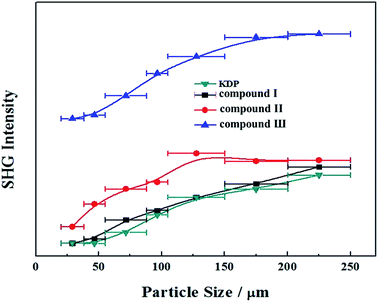

Fig. 5 Powder SHG of compounds I, II and III at 1064 nm. Curves are drawn to guide the eye and are not a fit to the data.

To visualize the SHG response of electronic states of compounds I and III, the SHG-density method²⁹ was used to analyze the relationship between optical properties and electronic states. Since the VE and VH have the important effect on the SHG coefficient, both processes were analyzed. For compounds I and III, it crystallizes 3m point group, there are three non-zero NLO coefficients. For d₂₂ of compound I, the contribution from the VE is 64.1% and VH is 35.9% (Fig. 6). In the occupied states, the O(8)-2p orbitals are dominant in both VE and VH processes. While in unoccupied states, the O(6)-2p and O(8)-2p orbitals are main contributors in the VE process. The B(2)-2p and B(4)-2p orbitals play major roles in the VH process. Thus, the B–O groups have the important contribution on the SHG. For compound III, VE processes are the main contributions to the d₂₂ SHG coefficients (Fig. 7). The analysis shows that the main contributions are BO₃ groups and lead cations with stereochemically active lone pair.

Fig. 6 SHG-weighted electron densities of the occupied and unoccupied orbitals in the VE and VH processes of compound I. (a) Occupied orbitals of VE process; (b) unoccupied orbitals of VE process; (c) occupied orbitals of VH process; (d) unoccupied orbitals of VH process.

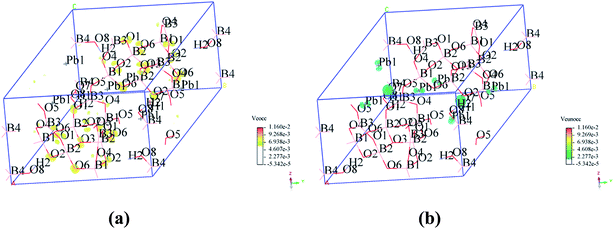Fig. 7 SHG-weighted electron densities of the occupied and unoccupied orbitals in the VE processes of compound III. (a) Occupied orbitals of VE process; (b) unoccupied orbitals of VE process.

Conclusion

Combining alkaline earth metal with borate, new compounds, Ba₃(OH)(B₉O₁₆)[B(OH)₃] and Pb_0.29Ba_2.71(OH)(B₉O₁₆)[B(OH)₃] have been synthesized by the hydrothermal method for the first time. Their structures feature a three-dimensional (3D) B₉O₁₉ framework with tunnels along c-direction, in which the Ba or Pb/Ba cations and [B(OH)₃] groups dwell. Ba₃(OH)(B₉O₁₆)[B(OH)₃], Pb_0.29Ba_2.71(OH)(B₉O₁₆)[B(OH)₃] and Pb₃(OH)(B₉O₁₆)[B(OH)₃] are type-I phase-matchable, with SHG responses 1.1, 1.2 and 2.7× KDP, respectively. The band gap of Ba₃(OH)(B₉O₁₆)[B(OH)₃] (5.11 eV) is larger than that of Pb₃(OH)(B₉O₁₆)[B(OH)₃] (4.65 eV). First-principle calculations reveal that the bottom of conduction band of Ba₃(OH)(B₉O₁₆)[B(OH)₃] is dominated by Ba-5d orbital, while, in Pb₃(OH)(B₉O₁₆)[B(OH)₃], the bottom of conduction band is dominated by Pb-6p orbital. The SHG response density shows that the B–O groups have the important contribution to SHG response in Ba₃(OH)(B₉O₁₆)[B(OH)₃]. While the BO₃ groups and lead cations with stereochemically active lone pair have main contribution in Pb₃(OH)(B₉O₁₆)[B(OH)₃].

Acknowledgements

This work is supported by the Western Light Foundation of CAS (Grant 2016-QNXZ-A-2), 973 Program of China (Grant No. 2014CB648400), the National Natural Science Foundation of China (Grant No. U1303392, 51425206), the Youth Innovation Promotion Association CAS (Grant 2015353).

References

1. (a) P. Becker, Adv. Mater., 1998, 10, 979; (b) C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. Sin., Ser. B, 1985, 28, 235; (c) M. E. Hagerman and K. R. Poeppelmeier, Chem. Mater., 1995, 7, 602.
2. (a) P. G. Schunemann, P. A. Budni and K. L. Schepler, Mater. Res. Bull., 1998, 23, 45; (b) D. F. Eaton, Science, 1991, 253, 281.
3. (a) Y. C. Wu, T. Sasaki, S. Nakai, A. Yokotani, H. Tang and C. T. Chen, Appl. Phys. Lett., 1993, 62, 2614; (b) Y. Mori, I. Kuroda, S. Nakajima, T. Sasaki and S. Nakai, Appl. Phys. Lett., 1995, 67, 1818; (c) L. Cheng, J. Cryst. Growth, 1991, 110, 697; (d) A. O. Okorogu, S. B. Mirov, W. Lee, D. I. Crouthamel, N. Jenkins, A. Y. Dergachev, K. L. Vodopyanov and V. V. Badikov, Opt. Commun., 1998, 155, 307; (e) G. D. Boyd, T. J. Bridges and C. K. N. Patel, Appl. Phys. Lett., 1972, 21, 553; (f) H. S. Ra, K. M. Ok and P. S. Halasyamani, J. Am. Chem. Soc., 2003, 125, 7764.
4. (a) G. H. Zhou, Z. J. Ma, K. C. Wu and N. Ye, J. Mater. Chem., 2012, 22, 19911; (b) G. H. Zou, G. Nam, H. G. Kim, H. Jo, T. S. You and K. M. Ok, RSC Adv., 2015, 5, 84754; (c) H. W. Huang, J. Y. Yao, Z. S. Lin, X. Y. Wang, R. He, W. J. Yao, N. X. Zhai and C. T. Chen, Angew. Chem., 2011, 123, 10456; (d) Y. Z. Huang, L. M. Wu, X. T. Wu, L. H. Li, L. Chen and Y. F. Zhang, J. Am. Chem. Soc., 2010, 132, 12788; (e) S. C. Wang, N. Ye, W. Li and D. Zhao, J. Am. Chem. Soc., 2010, 132, 8779.
5. (a) G. H. Zou, C. S. Lin, H. Jo, G. Nam, T. S. You and K. M. Ok, Angew. Chem., Int. Ed., 2016, 128, 12257; (b) K. Wu, Z. H. Yang and S. L. Pan, Angew. Chem., Int. Ed., 2016, 55, 6713; (c) J. L. Song, C. L. Hu, X. Xu, F. Kong and J. G. Mao, Angew. Chem., Int. Ed., 2015, 54, 3679; (d) Y. Wang and S. L. Pan, Coord. Chem. Rev., 2016, 323, 15; (e) H. P. Wu, H. W. Yu, Z. H. Yang, X. L. Hou, S. L. Pan, X. Su, K. R. Poeppelmeier and J. M. Rondinelli, J. Am. Chem. Soc., 2013, 135, 4215.
6. (a) W. L. Zhang, W. D. Cheng, H. Zhang, L. Geng, C. S. Lin and Z. Z. He, J. Am. Chem. Soc., 2010, 132, 1508; (b) H. W. Yu, S. L. Pan, H. P. Wu, W. W. Zhao, F. F. Zhang, H. Y. Li and Z. H. Yang, J. Mater. Chem., 2012, 22, 2105; (c) L. Wang, S. L. Pan, L. Chang, J. Hu and H. Yu, Inorg. Chem., 2012, 51, 1852.
7. (a) M. Wen, X. Su, H. P. Wu, J. J. Lu, Z. H. Yang and S. L. Pan, J. Phys. Chem. C, 2016, 120, 6190; (b) F. F. Zhang, F. Y. Zhang, B. H. Lei, Z. H. Yang and S. L. Pan, J. Phys. Chem. C, 2016, 120, 12757; (c) M. Wen, Z. P. Lian, H. P. Wu, X. Su, Q. F. Yan, J. J. Lu, Z. H. Yang and S. L. Pan, RSC Adv., 2015, 5, 53448.
8. (a) X. Y. Dong, Q. Jing, Y. J. Shi, Z. H. Yang, S. L. Pan, K. R. Poeppelmeier, J. Young and J. M. Rondinelli, J. Am. Chem. Soc., 2015, 137, 9417; (b) H. Y. Li, H. P. Wu, X. Su, H. W. Yu, S. L. Pan, Z. H. Yang, Y. Lu, J. Han and K. R. Poeppelmeier, J. Mater. Chem. C, 2014, 2, 1704.
9. Z. H. Chen, S. L. Pan, Z. H. Yang, X. Y. Dong, X. Su and Y. Yang, J. Mater. Sci., 2013, 48, 2590.
10. E. L. Belokoneva, S. Y. Stefanovich, T. A. Borisova and O. V. Dimitrova, Russ. J. Inorg. Chem., 2001, 46, 1621.
11. SAINT, Version 7.60A, Bruker Analytical X-ray instruments, Inc., Madison, WI, 2008.
12. G. M. Sheldrick, SHELXTL-97 Sheldrick: Program for Crystal Structure Refinement, University of Gottingen, Germany, 1997.
13. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7.
14. L. Bohaty, Z. Kristallogr. Cryst. Mater., 1983, 164, 279.
15. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Rrfson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
16. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
17. I. Varga, J. Pipek and B. Vasvári, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4978.
18. C. Aversa and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636.
19. J. Lin, M. H. Lee, Z. P. Liu, C. Chen and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13380.
20. B. B. Zhang, Z. H. Yang, Y. Yang, M.-H. Lee, S. L. Pan, Q. Jing and X. Su, J. Mater. Chem. C, 2014, 2, 4133.
21. X. Y. Zhang, D. N. Li, H. P. Wu, Z. H. Yang and S. L. Pan, RSC Adv., 2016, 6, 14205.
22. F. Y. Zhang, Q. Jing, F. F. Zhang, S. L. Pan, Z. H. Yang, J. Han, M. Zhang and S. J. Han, J. Mater. Chem. C, 2014, 2, 667.
23. (a) X. F. Wang, F. F. Zhang, B. H. Lei, Z. H. Yang and S. L. Pan, RSC Adv., 2016, 6, 100849; (b) G. Q. Shi, F. F. Zhang, B. B. Zhang, D. W. Hou, X. L. Chen, Z. H. Yang and S. L. Pan, Inorg. Chem., 2017, 56, 344; (c) H. P. Wu, X. Su, S. J. Han, Z. H. Yang and S. L. Pan, Inorg. Chem., 2016, 55, 4806.
24. (a) Y. Yang, X. Su, S. L. Pan, M. Zhang, Y. Wang, J. Han and Z. H. Yang, CrystEngComm, 2014, 16, 1978; (b) E. L. Belokoneva, E. A. Ruchkina and O. V. Dimitrova, Russ. J. Inorg. Chem., 2001, 46, 20.
25. P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593.
26. J. Tauc, Mater. Res. Bull., 1970, 5, 721.
27. M. K. Y. Chan and G. Ceder, Phys. Rev. Lett., 2010, 105, 196403.
28. J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 188.
29. C. H. Lo, Master Degree Thesis, Tamkang University, 2005.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1540435–1540437. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra02027a

‡ JJ and GQ contributed equally.

---