Open Access Article
Open Access ArticleNew 10H perovskites Ba5Ln1−xMn4+yO15−δ with spin glass behaviour†
Congling Yin *a,
Genfang Tianb,
Guobao Lic,
Fuhui Liaoc and
Jianhua Linc
*a,
Genfang Tianb,
Guobao Lic,
Fuhui Liaoc and
Jianhua Linc
aCollege of Material Science and Engineering, Jiangxi University of Science and Engineering, Ganzhou, Jiangxi Province 341000, P. R. China. E-mail: congling.yin@gmail.com
bNeutron Scattering Lab, Department of Nuclear Physics, China Institute of Atomic Energy, Beijing 102413, P. R. China
cBeijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, P. R. China
First published on 5th July 2017
Abstract
New 10H perovskite phases of composition Ba5Ln1−xMn4+yO15−δ (Ln = Sm–Lu) have been synthesised by solid-state reactions at 1300 °C. Their crystal structures have been investigated using X-ray and neutron diffraction. The 10H perovskite structure has an ordered arrangement of Ln and Mn ions on the corner-sharing octahedral centres and the face-sharing octahedral centres respectively. MnO6 octahedral distortions and short Mn–Mn distances have been identified in these structures, and oxygen vacancies are found in the c-BaO3 layers. Additionally, magnetic measurements and neutron diffraction identify spin glass transitions in these new materials. These transitions are related to the Mn ions on the corner sharing octahedral sites, which mediate magnetic interactions between tetramers of MnO6 octahedra.
Introduction
Interest in the physics of manganites has motivated investigation of the hexagonal perovskite BaMnO3−δ system, which shows a variety of crystal structures and magnetic properties.1–5 A series of polytypes (2H → 15R → 8H → 6H → 10H → 4H) have been identified in the BaMnO3−δ system as the oxygen vacancy δ increases.4,5 Further perovskite polytypes may be generated when Mn is replaced by other cations.Many doped BaMxMn1−xO3 systems have been explored, for example, with M = Ca,6,7 Ti,8,9 Fe,10,11 Co,12,13 Ru,14,15 Ir,16 In,17,18 and rare earths Ln.19–23 This led to the discovery of a range of M-cation ordered 10H perovskites Ba5In0.93Mn4O14.40,17 Ba5Sn1.1Mn3.9O15,24 Ba5Ce0.83Mn4.17O15,25 and Ba5Sb1−xMn4+xO15−δ.26 The Ba5MMn4O15 10H perovskite structure consists of close packed BaO3 layers in a (cchhh)2 sequence. The large M ions occupy the corner-sharing octahedral centre M1, and the Mn ions sit on the face-sharing octahedral centres M2 and M3, as shown in Fig. 1. Polymorphs of BaMnO3−δ have long range antiferromagnetic (AFM) order of all the Mn spins, with TN = 220–270 K.4,5 However, the long-range magnetic order is suppressed in the 10H perovskites with low-level doping, and the metal occupying the corner-sharing M1 site plays a key role in the magnetic behaviour of these materials. Ba5In0.93Mn4O14.40 has diamagnetic In3+ ions on the M1 site and weak AFM interactions between the tetramers of face-sharing MnO6 octahedra, and no magnetic order is observed down to 2 K. Ba5Sn1.1Mn3.9O15 (ref. 24) and Ba5Ce0.83Mn4.17O15 (ref. 25) have Mn4+ ions occupying 10–20% of the M1 sites and undergo spin glass transitions below 10 K. Ba5Sb1−xMn4+xO15−δ26 phases have 24–36% M1 site occupancy by Mn3+ ions, and long range AFM order of partial Mn spins (moment ≈ 0.5 μB) below 129–167 K. The presence of Mn3+ ions on the M1 site causes ferro- or ferri-magnetic clusters to freeze below a second magnetic transition, in the temperature range 13–22 K.
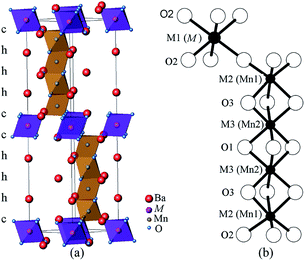 | ||
| Fig. 1 10H Ba5MMn4O15−δ perovskite structure (a) the unit cell and (b) the octahedral centres. The M ion is on the M1 site, and Mn ions sit on the M2 and M3 sites. | ||
The BaLnxMn1−xO3 system contains several cation-ordered perovskites: 6H Ba3LnMn2O9 and 12R Ba4LnMn3O12 (Ln = Er, Ce, Pr, and Nd).20–23,27 The 6H and 12R polytypes feature dimers and trimers of face-sharing MnO6 octahedra respectively,23,27 alternating with LnO6 octahedra. The 6H and 12R perovskites are closely related to the 10H perovskite. Considering the similarity of Ln elements, we predicted the existence of 10H BaLnxMn1−xO3 series and started an experimental exploration. Herein we report the syntheses, crystal structures and magnetic properties of 10H Ba5Ln1−xMn4+yO15−δ (Ln = Sm–Lu) perovskites.
Experimental
Polycrystalline Ba5Ln1−xMn4+yO15−δ samples were synthesised from BaCO3, MnCO3, and Ln2O3 (Ln = Sm–Gd and Dy–Lu) or Tb4O7. For each sample, the starting materials were thoroughly mixed in an agate mortar and pestle and heated in an alumina crucible at 1000 °C for 10 h to decompose the carbonates. Then the material was reground, pressed into pellets (20 ton per cm2), and heated at 1300 °C for a total of 30–50 h with slow cooling to room temperature. At several intermediate steps the material was re-ground and re-pressed, and X-ray powder diffraction (XRPD) measurements were made at each step to track the reaction to completion.The phase purity of the samples was checked by XRPD using a Rigaku D/Max-2000 diffractometer with graphite monochromator. This generated Cu Kα radiation at 40 kV and 100 mA. Data were collected over the 2θ range 6–120° in step scanning mode. Neutron powder diffraction data were collected using the BT-1 32 detector neutron powder diffractometer at the NIST Center for Neutron Research reactor, NBSR. A Cu (311) monochromator with a 90° take-off angle gave incident neutrons with λ = 1.5403(2) Å, and in-pile collimation of 15 minutes of arc was used. Data were collected over the 2θ range 3–168° with a step size of 0.05°. The diffraction data were analysed with the GSAS program.28 The Rietveld refinement was carried out assuming a pseudo-Voigt function for the peak shape and a calculated background using linear interpolation between a set of fixed points. Selected-area electron diffraction (SAED) were carried out on Tecnai G2 F30 with an accelerating voltage of 300 kV. The magnetic properties were investigated using a Quantum Design MPMS-SS superconducting quantum interference device (SQUID) magnetometer. Data were recorded in a 20 Oe or 1000 Oe applied field while warming the sample from 2–300 K, following both zero-field cooling (ZFC) and field cooling (FC).
Results and discussion
Chemical composition and 10H phase formation
The initial Ba5LnMn4O15−δ samples consisted of mixed 10H and 12R phases. To eliminate the 12R phase, we first varied and found the Ln content that gave the lowest amount of a 12R phase. Then we fixed the Ln content at these values, and varied and optimised the Mn fractions. By repeating these optimisation steps for several cycles, 10H phase-pure samples were obtained with the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln
Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratios listed in Table 1. Their general chemical formula is Ba5Ln1−xMn4+yO15−δ (Ln = Sm–Lu).
Mn ratios listed in Table 1. Their general chemical formula is Ba5Ln1−xMn4+yO15−δ (Ln = Sm–Lu).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln
Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratios of the 10H Ba5LnMn4O15−δ samples
Mn ratios of the 10H Ba5LnMn4O15−δ samples
| Ln | Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn Mn |
Ln | Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn Mn |
|---|---|---|---|
| Sm | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.98 0.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.01 4.01 |
Ho | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.86 0.86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.12 4.12 |
| Eu | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.87 0.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.02 4.02 |
Er | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.82 0.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.17 4.17 |
| Gd | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.82 0.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.17 4.17 |
Tm | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.80 0.80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.14 4.14 |
| Tb | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.15 4.15 |
Yb | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.83 0.83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.17 4.17 |
| Dy | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.86 0.86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.12 4.12 |
Lu | 5.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.78 0.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.21 4.21 |
Fig. 2 shows the XRPD patterns of the pure Ba5Ln1−xMn4+yO15−δ samples, which are similar to that of Ba5Sb1−xMn4+xO15. The XRPD patterns of all our materials can be indexed using a hexagonal unit cell, with lattice parameters a = 5.76–5.80 Å and c = 23.75–24.04 Å. The Selected-Area Electron Diffraction (SAED) patterns collected on the Ba5Sm0.98Mn4.01O15−δ sample along [010], [0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1] and [1
1] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] zone axes are shown in Fig. 3. No superstructure reflections are seen, and all the observation reflections agree with the indexing results. The systematic absence of the reflections hh
0] zone axes are shown in Fig. 3. No superstructure reflections are seen, and all the observation reflections agree with the indexing results. The systematic absence of the reflections hh l: l = 2n + 1 is consistent with the space group P63/mmc.
l: l = 2n + 1 is consistent with the space group P63/mmc.
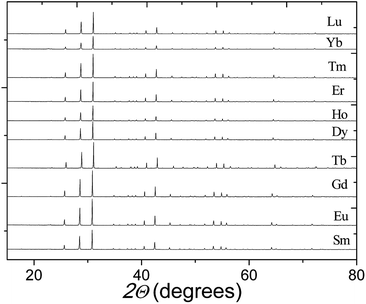 | ||
| Fig. 2 X-ray diffraction patterns of our Ba5Ln1−xMn4+yO15−δ samples, each showing a pure 10H perovskite phase. | ||
 | ||
Fig. 3 SAED patterns of Ba5Sm0.98Mn4.01O15−δ along (a) [010], (b) [0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1], and (c) [1 1], and (c) [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]. No superstructure is observed. 0]. No superstructure is observed. | ||
The X-ray structures of Ba5Ln1−xMn4+yO15−δ
Rietveld refinement against the XRPD data was performed using the 10H Ba5Sb1−xMn4+xO15 structural model. Ln ions and Mn ions occupy the M1 site, whilst the M2 and M3 sites are solely occupied by Mn. The ratio of Ln and Mn on the M1 site was fixed according to the ratio of reagents used. The refinements were insensitive to occupancies and isotropic thermal parameters of the oxygen sites, which were held at unity and 0.025 Å2 respectively. Good fits were obtained with Rwp (weighted-profile residual) factors of 4.1–6.5% and χ2 (goodness-of-fit) values in the range 1.7–3.0. The refined plots for all the sample are shown in ESI (Fig. S1–S10†). The refined crystallographic parameters and selected bond lengths are shown for all samples in Table S1.†Across the Ba5Ln1−xMn4+yO15−δ series, the lattice parameters and cell volume increase monotonically, in line with the increasing ionic radius of the Ln3+ cation used. The sole exception is the Tb compound, which has considerably smaller lattice parameters and cell volume, as shown in Fig. 4. The refined Tb–O bond length (2.10 Å) is close to the calculated Tb4+–O2− length, indicating that the Tb ion is tetravalent. Tb4+ ions have also been found in the 12R perovskite series Ba4LnIr3O12 and Ba4LnRu3O12.29,30
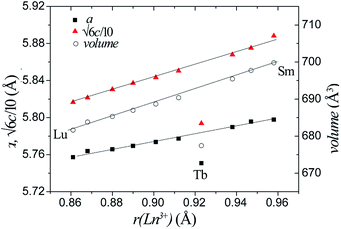 | ||
| Fig. 4 The lattice parameters and unit cell volumes of all our Ba5Ln1−xMn4+yO15−δ phases vary according to the radius of the Ln ion in each. | ||
All of our 10H perovskites have an ordered arrangement of Ln and Mn cations. Like the M = In3+ and Sb5+ 10H analogues, Mn ions alone occupy the octahedral centres that form face-sharing tetramers. These MnO6 octahedra are distorted, with two sets of three Mn–O distances. For all our samples the Mn1 and Mn2 sites have very similar average Mn–O bond distances, of about 1.93 Å as shown in Fig. 5. This is the same as the Mn4+–O2− distance calculated from Shannon's radii,31 indicating that the Mn ions in the sites forming tetramers of MnO6 octahedra in the Ba5Ln1−xMn4+yO15−δ phases is tetravalent. The Mn–Mn distances inside each tetramer range from 2.35 Å to 2.52 Å, close to the Mn–Mn distance in elemental α-Mn.32 This observation may suggest a degree of d-orbital overlap between neighbouring Mn ions within each tetramer. The distortion of the MnO6 octahedra forming the tetramers is evidenced by the fact that the Mn1–Mn2 distance is around 0.1 Å longer than the Mn2–Mn2 distance in all of our Ba5Ln1−xMn4+yO15−δ samples.
The corner-sharing octahedral centre has mixed occupancy, with Ln ions in majority (more than 78%) and a minority of secondary Mn ions (less than 21%). Notably, the Ba5Ln1−xMn4+yO15−δ samples are non-stoichiometric, with (Ln + Mn)/Ba values of 0.98–1. This non-stoichiometric associated with the vacancies at the M1 site (less than 10%), which has also been observed in Ba5In0.94Mn4O14.40.17 As expected, the Ln–O distances increase with the size of Ln3+ except for the Tb-containing sample. The values are 10% smaller than the calculated Ln3+–O2− distances for all the samples, due to the partial occupation the M1 site by Mn.
Combined X-ray and neutron diffraction studies on Ba5Lu0.78Mn4.21O15−δ
Due to their weak X-ray scattering, oxygen sites are not well described with PXRD. To find the exact oxygen positions and explore possible oxygen vacancies, we studied our sample of Ba5Lu0.78Mn4.21O15−δ using powder neutron diffraction. Rietveld refinements using X-ray and neutron diffraction data simultaneously were performed, starting from the refined X-ray structure. The oxygen occupancies were refined, and oxygen vacancies were found on the O2 site. The final refinement gave a good fit, with overall Rwp and χ2 parameters of 6.4% and 2.3 respectively. The neutron refinement is shown in Fig. 6.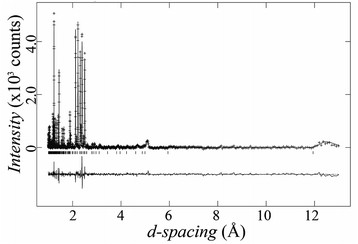 | ||
| Fig. 6 Experimental and calculated neutron diffraction pattern of Ba5Lu0.78Mn4.21O15−δ, with the difference plot offset below. | ||
The refined atomic parameters are listed in Table 2. The O2 site in the c-BaO3 layers is 6% vacant. Due to this oxygen deficiency, the O2 site has a larger thermal displacement factor than the O1 and O3 sites. The nearby sites Ba2 and M1 sites also have relatively large thermal factors.
| Atom | x, y, z | Occup. | 100× U Å−2 |
|---|---|---|---|
| a Lattice parameters: a = 5.7580(1) Å and c = 23.7445(3) Å. | |||
| Ba1 | 2/3, 1/3, 0.25 | 1 | 0.93(9) |
| Ba2 | 2/3, 1/3, 0.4422(1) | 1 | 1.09(6) |
| Ba3 | 1, 0, 0.3437(1) | 1 | 0.82(6) |
| M1 (Lu/Mn) | 1, 0, 0.5 | 0.78/0/21 | 1.10(9) |
| M2 (Mn1) | 1/3, 2/3, 0.4065(2) | 1 | 0.83(11) |
| M3 (Mn2) | 1/3, 2/3, 0.3010(2) | 1 | 0.67(10) |
| O1 | 0.1836(4), 0.8164(4), 0.25 | 1 | 0.88(8) |
| O2 | 0.1765(3), 0.3530(6), 0.4486(1) | 0.940(9) | 1.36(8) |
| O3 | 0.4818(2), 0.9636(4), 0.3516(1) | 1 | 0.80(6) |
From the refined occupancies, this material has the composition Ba5Lu0.78Mn4.21O14.64. The average valence state of Mn ions is found to be 4.0, and the Mn ions on the M1 site must also be Mn4+ ions in order to maintain electroneutrality. Our other Ba5Ln1−xMn4+yO15−δ samples probably have Mn4+ ions on the M1 site as well, similar to the Ce4+ and Sn4+ analogues.24,27 However, the Ba5Sb1−xMn4+xO15−δ analogue is different with Mn3+ ions on the M1 site.26 For the BaMxMn1−xO3 10H perovskites, the average valence of the cations occupying the M1 site approaches +4 in keeping with Pauling's principle.
The Ba5Lu0.78Mn4.21O14.64 sample has oxygen vacancy in the c-BaO3 layers, which is similar to that in the In-doped analogue.17 The M1 site in both compounds has a high occupancy of M3+ ions, which requires neighbouring oxygen vacancies to compensate the charge imbalance. When M4+ or M5+ ions dominate on the M1 site, oxygen vacancies in the c-BaO3 layers are no longer present, as seen in the Ce4+, Sn4+, and Sb5+ analogues.24–27
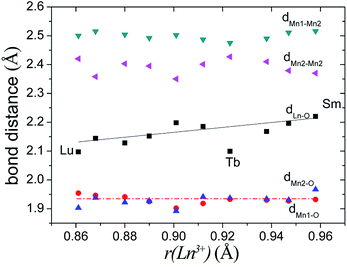
In Ba5Lu0.78Mn4.21O14.64, the MnM2–O2 distance is 0.12 Å less than the MnM2–O3 distance, which indicates considerable distortion of the MnM2O6 octahedron. In analogous materials with a small M ion, such as Sb5+, the two MnM2–O distances are nearly equal and the MnM2O6 octahedron is undistorted.26 This indicates that the degree of MnM2O6 distortion in the Ba5MMn4O15−δ 10H perovskites is related to the size of M ion, rM. The Mn–O distances are plotted against rM in Fig. 7. The most noticeable trend is that MM2–O2 distance shows a significant, linear decrease as rM increases. The MM2–O3 distance increases slightly with rM.
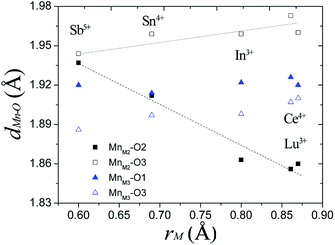 | ||
| Fig. 7 The Mn–O distances of the face-sharing octahedra for several Ba5MMn4O15−δ 10H perovskites vary with the radius of the M ion. | ||
For Ba5Lu0.78Mn4.21O14.64, the MnM3O6 octahedron is almost undistorted, as evidenced by similarity of the two MnM3–O distances. This is similar to other 10H perovskites.
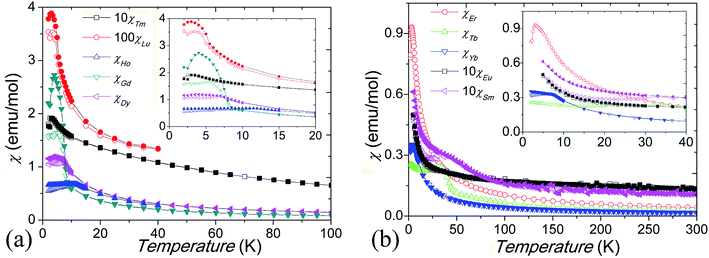
Magnetic properties
Low-temperature magnetic susceptibility data for our Ba5Ln1−xMn4+yO15−δ materials are shown in Fig. 8. All are paramagnetic at high temperatures and show linear M–H variation, without hysteresis, at 300 K. The susceptibilities of the materials with Ln = Sm3+ and Eu3+ do not follow the Curie–Weiss law, due to the temperature dependent magnetic moments of these ions. The samples with Ln = Gd–Lu have susceptibility maxima at their spin freezing temperatures TF = 3–34 K, and divergent ZFC and FC magnetic susceptibilities below TF. In comparison to the samples containing an Ln3+ cation, which have around 15% Mn occupancy of the M1 site, the sample containing Tb4+ has a higher TF = 34 K, which is due to anti-site dislocation of Mn4+ and Tb4+ ions on the M2 sites increasing the fraction of Mn on the M1 site. Mn4+/M4+ site mixing has been observed in the other 10H BaMx4+Mn1−xO3 perovskites.24,25 Curie–Weiss fits to the susceptibility above TF give an effective paramagnetic moment μeff = 1.5–2.9 μB per Mn ion for the Ln = Gd–Lu samples (Table 3), which is smaller than that expected for localized Mn4+ spins (3.87 μB). Negative Weiss temperatures (θ = −2.5 K to −65 K) indicate that AFM interactions are dominant. Similarly small paramagnetic moments of 0.88–1.44 μB per Mn4+ ion, and large negative θ ≈ −2000 K, have reported in the 10H perovskite analogue Ba5Ce1−xMn4+xO15.25,27 This is probably due to the formation of AFM Mn clusters inside the tetramers, consistent with the observation of very short Mn–Mn distances and the significantly reduced magnetic moments of the Mn4+ ions.| Ln | Gd3+ | Tb4+ | Dy3+ | Ho3+ | Er3+ | Tm3+ | Yb3+ | Lu3+ |
|---|---|---|---|---|---|---|---|---|
| TF/K | 8.5 | 34.0 | 7.0 | 11.5 | 3.0 | 3.0 | 5.5 | 3.5 |
| θ/K | −2.5 | −39 | −13 | −7.2 | −28 | −52 | −15.5 | −65 |
| μeff (f.u.)/μB | 8.2 | 8.5 | 11.4 | 10.3 | 10.4 | 9.0 | 6.3 | 3.3 |
| μeff (Ln)/μB | 7.9 | 7.9 | 10.6 | 10.6 | 9.6 | 7.6 | 4.5 | 0 |
| μeff (Mn)/μB | 1.9 | 2.2 | 2.8 | 1.5 | 2.8 | 2.9 | 2.4 | 1.6 |
| Ms (f.u.)/μB | 0.3 | 0.05 | 1 | 0.8 | 0.5 | 0.06 | 0.05 | 0.05 |
Magnetic hysteresis and saturation occur at 2 K for the Ln = Gd–Lu samples, and the Gd3+, Dy3+, and Er3+ samples show history dependent magnetisation, as shown in Fig. 9. The Tb4+ and Yb3+ samples show small magnetic anisotropy with coercive fields of 20 mT at 2 K, and the other samples have isotropic magnetization, as shown in Fig. 9 inset. Due to the Mn ions in the tetramers forming AFM clusters, their total moments are almost zero at 2 K. The saturated moment Ms is therefore determined by the moments of the magnetic ions on the M1 site. The early Ln3+ samples have large Ms = 0.3–1 μB, close to that of ferromagnetic spin freezing Mn4+ cations on M1 site. The later Ln3+, and Tb4+, samples have a much smaller Ms ≈ 0.05 μB, similar to that of the Sn4+ and In3+ analogue materials.17,24 This probably indicates AFM spin freezing of the Mn4+ ions on the M1 site. The different behaviours of the samples with early and late Ln cations reflects the changing difference in size between the Ln and Mn ions. A large size difference, as is found for the early Ln materials, tends to introduce oxygen vacancies and thus Mn3+ ions in the c-BaO3 layers, resulting in a Mn3+–O2−–Mn4+ local ferromagnetic network and ferromagnetic spin freezing clusters.
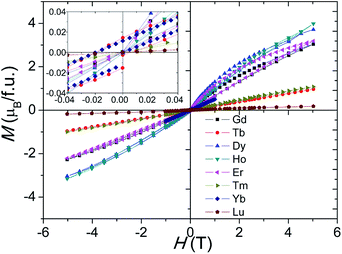 | ||
| Fig. 9 Isothermal M–H curves at 2 K for the Ba5Ln1−xMn4+yO15−δ (Ln = Gd–Lu) samples. The inset expands the low field region of the plot. | ||
Neutron diffraction data were collected for Ba5Er0.82Mn4.17O15−δ at 1.5 K, 10 K and 60 K, as shown in Fig. 10. No magnetic scattering is observed below the TF = 3.0 K transition observed in the susceptibility, suggesting that this transition is due to short-range spin freezing, though further neutron studies, AC magnetic susceptibility measurements and μSR experiments will be useful in characterising this state more fully.
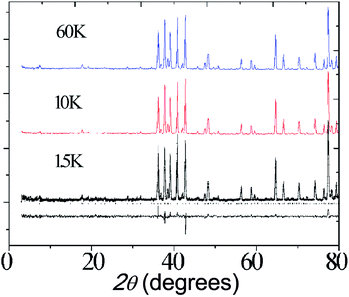 | ||
| Fig. 10 Neutron diffraction profiles of Ba5Lu0.78Mn4.21O15−δ at different temperature. Fitting to the 1.5 K pattern is shown. | ||
Conclusions
The new 10H perovskites Ba5Ln1−xMn4+yO15−δ (Ln = Sm–Lu) have been synthesised by high temperature solid-state reactions. These materials have an ordered arrangement of Ln and Mn cations. The face-sharing octahedral centres are occupied by Mn4+ ions, whilst the corner-sharing octahedra are occupied by Ln and Mn cations. Oxygen vacancies are found in the c-BaO3 layers. Within tetramers of MnO6 octahedra, the two MnM2O6 octahedra are distorted but the two MnM3O6 octahedra are almost undistorted. The MnM2O6 distortion is related to the size of the M ion in the Ba5MMn4O15−δ 10H perovskite structure.The Ba5Ln1−xMn4+yO15−δ perovskites (Ln = Sm–Lu) are paramagnetic at high temperatures. The Ln = Gd–Lu samples have spin freezing transitions at TF = 3.0–34 K, which have been characterised from their magnetic hysteresis at 2 K and low-temperature neutron diffraction. The spin freezing transition is related to the partial occupation of Mn4+ ions on the M1 sites of the 10H structure. The saturated moment is also related to the magnetic ions on the M1 site.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant 21271014, Grant 21301077 and Grant 51662013), and Scientific Research Key Program of Beijing Municipal Commission of Education (KM201010005019). We thank J. P. Attfield for the advice and encouragement and Alexander Browne for English modification. We acknowledge the support of the National Institute of Standards and Technology, U. S. Department of Commerce, in providing the neutron research facilities used in this work.Notes and references
- J. M. Gonzalez-Calbet, M. Parras, J. M. Alonso and M. Vallet-Regi, J. Solid State Chem., 1993, 106, 99 CrossRef CAS.
- T. Negas and R. S. Roth, J. Solid State Chem., 1971, 3, 323 CrossRef CAS.
- E. J. Cussen and P. D. Battle, Chem. Mater., 2000, 12, 831 CrossRef CAS.
- J. J. Adkin and M. A. Hayward, Chem. Mater., 2007, 19, 755 CrossRef CAS.
- J. J. Adkin and M. A. Hayward, J. Solid State Chem., 2006, 179, 70 CrossRef CAS.
- N. Floros, C. Michel, M. Hervieu and B. Raveau, J. Solid State Chem., 2002, 168, 11 CrossRef CAS.
- N. Floros, C. Michel, M. Hervieu and B. Raveau, Chem. Mater., 2000, 12, 3197 CrossRef CAS.
- G. M. Keith, C. A. Kirk, K. Sarma, N. M. Alford, E. J. Cussen, M. J. Rosseinsky and D. C. Sinclair, Chem. Mater., 2004, 16, 2007 CrossRef CAS.
- L. Miranda, A. Feteira, D. C. Sinclair, K. Boulahya, M. Hernando, J. Ramírez, A. Varela, J. M. González-Calbet and M. Parras, Chem. Mater., 2009, 21, 1731 CrossRef CAS.
- L. Miranda, J. Ramirez-Castellanos, M. Hernando, A. Varela, J. M. Gonzalez-Calbet and M. Parras, Eur. J. Inorg. Chem., 2007, 15, 2129 CrossRef.
- L. Miranda, D. C. Sinclair, M. Hernando, A. Varela, A. Wattiaux, K. Boulahya, J. M. Gonzalez-Calbet and M. Parras, Chem. Mater., 2009, 21, 5272 CrossRef CAS.
- L. Miranda, A. Feteira, D. C. Sinclair, M. G. Hernandez, K. Boulahya, M. Hernando, A. Varela, J. M. Gonzalez-Calbet and M. Parras, Chem. Mater., 2008, 20, 2818 CrossRef CAS.
- L. Miranda, J. Ramirez-Castellanos, A. Varela, J. M. Gonzalez-Calbet, M. Parras, M. Hernando, M. T. Fernandez-Diaz and M. G. Hernandez, Chem. Mater., 2007, 19, 1503 CrossRef CAS.
- J. G. Zhao, L. X. Yang, Y. Yu, F. Y. Li, R. C. Yu and C. Q. Jin, J. Solid State Chem., 2008, 181, 1767 CrossRef CAS.
- C. L. Yin, G. B. Li, W. A. Kockelmann, J. H. Lin and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 094420 CrossRef.
- N. A. Jordan and P. D. Battle, J. Mater. Chem., 2003, 13, 2220 RSC.
- C. L. Yin, G. B. Li, T. N. Jin, L. P. You, J. L. Tao, J. W. Richardson, C. K. Loong, J. L. Sun, F. H. Liao and J. H. Lin, Chem. Mater., 2008, 20, 2110 CrossRef CAS.
- N. Creon, C. Michel, A. Hervieu, A. Maignan and B. Raveau, Solid State Sci., 2003, 5, 243 CrossRef CAS.
- X. J. Kuang, C. Bridges, M. Allix, J. B. Claridge, H. Hughes and M. J. Rosseinsky, Chem. Mater., 2006, 18, 5130 CrossRef CAS.
- H. Yang, Y. K. Tang, L. D. Yao, W. Zhang, Q. A. Li, F. Y. Li, C. Q. Jin and R. C. Yu, J. Alloys Compd., 2007, 432, 283 CrossRef CAS.
- H. Yang, Z. E. Cao, X. Shen, W. J. Feng, J. L. Jiang, J. F. Dai and R. C. Yu, J. Mater. Sci., 2008, 43, 5679 CrossRef CAS.
- A. F. Fuentes, K. Boulahya and U. Amador, J. Solid State Chem., 2004, 177, 714 CrossRef CAS.
- C. Rabbow and H. Mullerbuschbaum, Z. Naturforsch., B: J. Chem. Sci., 1994, 49, 1277 CAS.
- C. L. Yin, G. B. Li, T. N. Jin, J. L. Tao, J. W. Richardson, C. K. Loong, F. H. Liao and J. H. Lin, J. Alloys Compd., 2010, 489, 152 CrossRef CAS.
- A. M. Mario, M. Olivier, C. Silviu, J. C. Gabriel and H. G. Gilles, J. Solid State Chem., 2013, 198, 186 CrossRef.
- C. L. Yin, G. B. Li, W. A. Kockelmann, F. H. Liao, J. P. Attfield and J. H. Lin, Chem. Mater., 2010, 22, 3269 CrossRef CAS.
- A. M. Mario, M. Olivier, P. Caroline, R. Pascal, C. Silviu and H. G. Gilles, New J. Chem., 2015, 39, 829 RSC.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report, LAUR, 2004, pp. 86–748, unpublished.
- Y. Shimoda, Y. Doi, Y. Hinatsu and K. Ohoyama, Chem. Mater., 2008, 20, 4512 CrossRef CAS.
- Y. Shimoda, Y. Doi, M. Wakeshima and Y. Hinatsu, J. Solid State Chem., 2009, 182, 2873 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- J. A. Oberteuffer and J. A. Ibers, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1499 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02183f |
| This journal is © The Royal Society of Chemistry 2017 |