Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of the aggregation state of amorphous calcium phosphate on hydroxyapatite nucleation kinetics†
Shuqin Jiang ab,
Wenjing Jinc,
Ya-Nan Wangc,
Haihua Pan
ab,
Wenjing Jinc,
Ya-Nan Wangc,
Haihua Pan *c,
Zhiwei Sun*a and
Ruikang Tang
*c,
Zhiwei Sun*a and
Ruikang Tang b
b
aSchool of Public Health, Department of Toxicology, Capital Medical University, Beijing 100069, China. E-mail: zwsun@ccmu.edu.cn
bCenter for Biomaterials & Biopathways, Department of Chemistry, Zhejiang University, Hangzhou 310027, China
cQiushi Academy for Advanced Studies, Zhejiang University, Hangzhou 310027, China. E-mail: panhh@zju.edu.cn
First published on 12th May 2017
Abstract
Calcium phosphates are one of the most important biogenic minerals found in living organisms. Recent studies have suggested a non-classical mineralization pathway, which emphasizes the amorphous calcium phosphate (ACP) as a precursor phase during biomineral crystallization. However, its precise mechanism in mineralization is still poorly understood. Here, we found the aggregation state of ACP affected the nucleation of hydroxyapatite (HAP), which was controlled by collagen-I fibrils in simulated body fluids (SBFs). Our experiment reveals that at low supersaturation, collagen-I fibrils can prevent the self-aggregation of ACP precursor nanoparticles, thus promoting HAP heterogeneous nucleation by increasing the effective surface area of ACP. However, at high supersaturation, the aggregation state of ACP didn't change, and the nucleation rate of HAP kept almost the same. This finding suggests that the aggregation of ACP plays an important role in controlling HAP nucleation kinetics, which follows a new strategy to promote the biomineralization process.
1. Introduction
Biomineralization is a biological process to form hard tissues such as teeth, bone, and shells in mammals.1 Study of biomineralization not only facilitates the synthesis of biomimetic materials more effectively, but also helps to understand fundamental theories of biology. Nucleation is the first step in crystallization, thus it determines the size distribution, polymorphism and crystallization pathway of crystallites.2 In the scenario of the classical nucleation theory (CNT), the nucleation processes are understood as chain reactions of monomers in solution.3 However, the actual nucleation pathways are more complicated than CNT in some crystallization systems.4–6 Take the crystallization of hydroxyapatite (HAP, Ca5(PO4)3OH), a model crystal for bone and dentin mineral phases,7,8 increasing evidence supported that the mineralization of HAP is via a transient amorphous calcium phosphate (ACP, Ca3(PO4)2) phase both in vitro9,10 and in vivo.11,12 So the key issue to understand the nucleation of HAP is to know how ACP transforms into HAP and how to control HAP nucleation rate.However, the mechanism of how ACP transforms into HAP is still challenged from several points of view,13 such as the dissolution–reprecipitation mechanism, reorganization of Posner's clusters, and the surface-mediated transformation mechanism. Therefore, studying on the ACP mediated HAP nucleation pathway and mechanism is very necessary and has a profound significance in biomineralization. In previous work, primary nucleation of HAP on ACP-solution interface has been confirmed both by TEM observations14,15 and nucleation kinetics data.16,17 So, in principle, increasing the surface area of ACP nanoparticles will promote HAP nucleation. However, this hypothesis has never been proven directly. To corroborate this, one needs to change the surface area of ACPs while keeping other conditions almost the same (the solution pH and the composition of solution, i.e. the soluble species), and compare the nucleation rate with the surface area. Whereas, it's hard to control the aggregation state of ACPs unless introducing strong additives. Polyelectrolytes are known to be used to obtain well dispersed ACPs,18,19 but water-soluble polyelectrolytes have a strong effect on the precipitation and dissolution of calcium phosphate.20,21 In previous work, we found that the soluble polymers (non-collagenous) inhibit HAP nucleation by absorbed on ACP surface, thus decrease the surface area of ACP reacting with Ca2+.17 However, in this work, we used assembled collagen-I fibrils (insoluble in our system) to control the aggregation of ACPs, thus increase the surface area of ACP directly. Furthermore, the effect of soluble additives can be avoided in this system. Whereas, it's well documented that collagen-I fibrils play a dominant role in intra-fibrillar mineralization of HAP in synergy with non-collagenous proteins (NCPs) or NCP-mimetic polyelectrolytes.9 In our system collagen fibrils have no effect on intra-fibrillar mineralization without NCP. We found that HAP nucleation rate was promoted by increasing the surface area of ACPs in simulated body fluids (SBFs),22,23 which corroborated the hypothesis of surface nucleation model directly.
2. Experimental
Chemicals
All chemicals were analytical grade and were purchased from Aladdin Reagent (Shanghai, China) unless specifically mentioned. Double distilled water was used and all solutions were filtered through 0.22 μm Millipore films prior to use.HAP crystallization
Calcium (Ca) solutions contained CaCl2 and MgCl2, and phosphate (P) solutions contained Na2HPO4, Na2SO4, NaCl, KCl, N-2-hydroxyethylpiperazine-N′-2-ethane sulfonic acid (HEPES, GenomBioMed Technology Inc., Hangzhou, China). SBF solutions that mimicking physiological fluids was obtained by rapidly mixing of equal volumes of designated Ca and P solutions, and the concentrations of each species were listed in Table S1 in ESI.† The solution pH curves were monitored by a PHSJ-3F pH meter with E-201-C composite electrode (Leici Instrument, Shanghai, China). The composite electrode was calibrated by 25 mM NaH2PO4/Na2HPO4 standard buffer solution (pH = 6.86, 25 °C) and 10 mM Na2B4O7·10H2O standard buffer solution (pH = 9.18, 25 °C) with an average error less than 0.02 pH units before use. Each experiment was repeated at least 4 times.Aggregation control of ACPs
ACPs aggregation state can be controlled by collagen-I adding protocols. There were two protocols for the introduction of collagen-I (stock solution: 5 mg mL−1, Gibco, Invitrogen, US) into the mineralization reaction: (i) pre-mixing: 100 μL collagen-I stock solution was added into 5 mL of P solution prior to mixing with 5 mL Ca solution. (ii) Post-mixing: 100 μL collagen-I was added into the ACP suspension (after the mixing of 5 mL P and 5 mL Ca solutions). The final concentration of collagen-I fibril in both protocols was 50 μg mL−1.Characterization
At designated time, the reaction suspensions were removed and centrifuged at 5400 rpm for 3 min (Sigma 1-6P, Germany).The precipitations were washed with ethanol for twice, and dried in vacuum for 24 h at 40 °C. They were characterized by Fourier Transformed Infrared spectroscopy (FTIR, IRAffinity-1, Shimadzu) and X-ray diffraction (XRD, Ultima IV with D/teX Ultra, Cu Kα radiation λ = 1.54 Å, Rigaku). For Transmission Electron Microscopy (TEM/SAED, HT-7700, Hitachi) examination, the specimens were obtained by paddling copper grid in suspension, and washing with water and ethanol, and dried by lamp-light.
Concentrations of calcium and phosphate in solution were measured by inductive coupled plasma atomic emission spectrometry (ICP-AES, iCAP 6300, Thermo Fisher). For this purpose, aliquots were taken from the supernatant solutions at designated reaction times, filtered with a syringe filter with a pore size of 25 nm to remove any trace of ACP precipitates, and then the filtrate was immediately diluted with 5 per cent hydrochloric acid.
Solution chemistry calculation
The supersaturation of the solutions was calculated by VMINTEQ 3.0 (available from: http://www.lwr.kth.se/-English/OurSoftware/vminteq), which was given by,
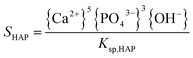 | (1) |
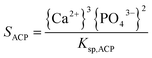 | (2) |
3. Results and discussion
HAP crystallization stages and nucleation kinetics
The nucleation rate of HAP was hard to measure but the induction time (ti) was easy to detect. Considering the nucleation rate can be estimated by J = 1/(Vti),25 where V is the volume of the solution. In our system, since HAP formation is accompanied by a continuous drop of solution pH (see eqn (3)), the crystallization kinetics can be precisely monitored by a pH meter,16,17,19,26 which provides a convenient and effective in situ method to follow the crystallization process and give valuable information on the changes in induction time (ti).| 3Ca3(PO4)2(s) + Ca2+ + 2H2O → 2Ca5(PO4)3(OH)(s) + 2H+ | (3) |
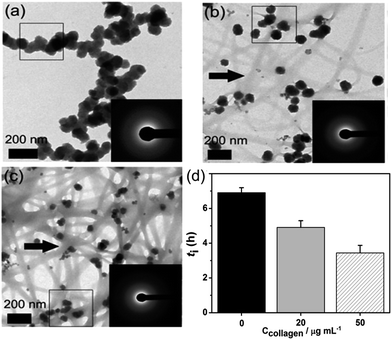
In a typical pH curve (Fig. 1a), the whole process could be divided into three stages. At stage I, pH value kept relatively stable and it had been generally agreed that ACP was precipitated. Rather, this metastable stage was regarded as the induction period for HAP nucleation. At stage II, the fast drop of pH suggested the occurrence of HAP crystallization. At stage III, it was the period for post-crystallization (HAP ripening). The induction time was determined by the intersection of tangents on the pH curve for stages I and II as shown in Fig. 1a. At designated time (marked by black arrows in Fig. 1a), the mineral phases were confirmed by ex situ characterizations (Fig. 1b–h, S1 and S2†). From Fig. 1b, ACPs were formed at stage I (t = 10 min) and confirmed by electron diffraction patterns (Fig. 1c). In addition, at phase transition period (t = 45 min, 50 min; measure method sees Fig. 1a), the newly formed sheet-like crystallites were mainly on ACP precursors surface (Fig. 1d and e) and ACPs completely transformed into HAP finally (t = 100 min, Fig. 1g). This process was identified by SAED patterns and the diffusive diffractions became bright diffraction rings which is the (002) and (211) diffractions of HAP (Fig. 1c, f and h). However, the transformation process has been proposed to occur, either via an intermediate phase which mostly is octacalcium phosphate (Ca8(HPO4)2(PO4)4·5H2O, OCP), or directly from ACP to HAP.27 Through chemistry calculation (Table S1†), after the precipitation of ACP, the solution is still supersaturated with respect to OCP and HAP. So, in principle, ACP could also be transformed into OCP. From FTIR analysis (Fig. S1†), the lack of absorption band at 917 cm−1 which is assigned to P–(OH) stretch and OH inplane bend of HPO4,28 meaning the absence of OCP. In addition, XRD patterns showed that the crystallites were HAP (Fig. S2†). Moreover, if the intermediate phase OCP is existed, the concentration of calcium should be increased and so do the solution pH (eqn (4)).29 However, the concentration of calcium was decreased (Fig. S3†). Furthermore, the in situ pH curves showed that the solution pH did not increase in the whole stages (Fig. 1a). Therefore, through TEM observations, FTIR, XRD characterizations and concentration change of calcium and pH curve, we can see that HAP is the primary crystal phase in our systems. Meanwhile, this transformation of HAP at ACP-solution interface was also frequently observed and reported in previous work.15–18,27,30,31
| 3Ca3(PO4)2(s) + 7H2O → Ca8(HPO4)2(PO4)4·5H2O(s) + Ca2+ + 2OH− | (4) |
When adding collagen-I into SBF (solution composition see Table S1 in ESI†), TEM observations showed the different aggregation states of the precursor phase in the presence and absence of collagen-I fibrils. In control group without collagen-I, the initially formed ACP nanoparticles were in aggregated state (Fig. 2a). However, the involvement of collagen-I fibrils could prevent the aggregation of ACP particles and the formed particles were adsorbed and dispersed individually on the fibrils (Fig. 2b and c). Moreover, from Fig. S4 and S5,† we can see the kinetic growth of ACP particles during induction time, and they were still in separated state. Thus the aggregation state of ACP particles could be altered by collagen-I fibrils. For ACP-mediated HAP nucleation, the effective supersaturation will be dropped to the level of ACP-saturated solution due to ACP is formed before HAP nucleation. In our calculation, the effective supersaturations (Seff) are actually close to each other no matter how much calcium and phosphate are introduced into solutions (see Table S1 in ESI†). So the effective supersaturation can be treated as a constant, and so do the heterogeneous nucleation barrier (eqn (5)). As corroborated in our previous work,16,17 the nucleation rate (J) of ACP mediated HAP nucleation can be expressed as:
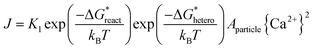 | (5) |
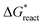 is the chemical reaction barrier for HAP nucleation;
is the chemical reaction barrier for HAP nucleation; 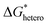 is the heterogeneous nucleation barrier; Aparticle is the total surface area of ACP particles; {Ca2+} is the activity of residue Ca2+ after the precipitation of ACP.
is the heterogeneous nucleation barrier; Aparticle is the total surface area of ACP particles; {Ca2+} is the activity of residue Ca2+ after the precipitation of ACP.
Here we can see that the nucleation rate is correlated with the nucleation barriers, the surface area of ACP, and the free calcium in solution. As the chelation capacity of collagen-I molecule with calcium is quite small (about 0.1 mol Ca kg−1 of collagen-I,32 the chelated calcium is just 5 μM for 50 μg mL−1 collagen-I solutions, which can be neglected for nearly 900 μM of free calcium after the precipitation of ACP (see Table S1 in ESI†). To confirm this theoretical analysis, we used ICP-AES to measure the calcium concentration with or without collagen-I. The results showed that the chelated calcium is 10 μM for 50 μg mL−1 collagen-I in our system. So, the concentration of free calcium ions in solution is almost the same for systems with and without collagen-I. Then the prevention of ACPs from self-aggregation certainly increases the effective surface area of ACP particles, which can promote HAP nucleation kinetics according to ACP-mediated nucleation theory. Therefore, in the presence of collagen-I fibrils, the induction time (ti) was decreased, which means the nucleation rate of HAP was promoted (Fig. 2d). However, this promotion effect might also be caused by the difference of formed ACP or collagen-I fibrils act as templates for HAP heterogeneous nucleation. This will be discussed as follows.
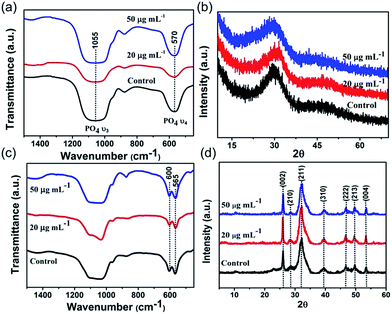
To confirm the crystallization is still the ACP-mediated HAP nucleation pathway in the presence of collagen-I fibrils, the phases of early formed minerals and the final minerals were examined by ex situ characterizations. At early period (t = 10 min), FTIR showed the broad absorption bands at about 1055 cm−1 (phosphate ν3 vibrations) and 570 cm−1 (phosphate ν4 bending), which could be assigned to the ACP signals33 (Fig. 3a). Moreover, the broad and diffusive patterns of XRD at about 30° (Fig. 3b) supported the presence of ACP precursors in the solids.13 From results of TEM, sphere-like particles were observed and the selected area electron diffraction (Fig. 2b and c) also indicated the mineral phase was amorphous. The phase of final mineral (at 24 h) was also examined. FTIR spectra (Fig. 3c) showed the splitting of the absorption peaks for phosphate ν4 bending (600 cm−1, 565 cm−1), indicating the transformation of ACP to HAP.33 In XRD patterns (Fig. 3d), the diffractions from (002) and (211) faces (2θ = 25°, 32° respectively) of HAP was observed, which further confirming the solid phase transition.34 These results indicated the ACP-mediated HAP crystallization pathway in the absence and presence of collagen-I fibrils. Moreover, the Ca/P ratios of ACP particles (formed at induction time, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65) were 1.50 ± 0.04 (mean ± s.d., without collagen-I) and 1.52 ± 0.06 (with 50 μg mL−1 collagen-I) which were all closed to 1.5.34 In addition, the Ca/P ratios of final crystals (t = 24 h) were 1.69 ± 0.02 (without collagen-I) and 1.69 ± 0.01 (with 50 μg mL−1 collagen-I), respectively (Table S2 in ESI†). These results further confirmed the final crystals were HAP (Ca/P = 1.67).34 Therefore, with or without collagen-I fibrils the Ca/P ratios of formed ACPs and HAPs are almost the same. Moreover, the particles size and the zeta potentials of these ACPs with or without collagen-I were also characterized (Fig. S6†). Due to ACP particles are in aggregated state, the measured hydrodynamic size is much larger than TEM observations. Considering Mg2+ plays an important role in controlling ACP mediated HAP transformation, the concentration of Mg2+ in formed ACP and HAP were measured. In Table S2,† we can see that the amount of incorporated Mg2+ into ACP is few at induction time (about 0.15 mM at ln
S = 26.65) were 1.50 ± 0.04 (mean ± s.d., without collagen-I) and 1.52 ± 0.06 (with 50 μg mL−1 collagen-I) which were all closed to 1.5.34 In addition, the Ca/P ratios of final crystals (t = 24 h) were 1.69 ± 0.02 (without collagen-I) and 1.69 ± 0.01 (with 50 μg mL−1 collagen-I), respectively (Table S2 in ESI†). These results further confirmed the final crystals were HAP (Ca/P = 1.67).34 Therefore, with or without collagen-I fibrils the Ca/P ratios of formed ACPs and HAPs are almost the same. Moreover, the particles size and the zeta potentials of these ACPs with or without collagen-I were also characterized (Fig. S6†). Due to ACP particles are in aggregated state, the measured hydrodynamic size is much larger than TEM observations. Considering Mg2+ plays an important role in controlling ACP mediated HAP transformation, the concentration of Mg2+ in formed ACP and HAP were measured. In Table S2,† we can see that the amount of incorporated Mg2+ into ACP is few at induction time (about 0.15 mM at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65). Besides, with or without collagen-I, the amount of incorporated Mg2+ into ACP is almost the same at given system. Thus, the decrease of induction time (ti) in the presence of collagen-I at ln
S = 26.65). Besides, with or without collagen-I, the amount of incorporated Mg2+ into ACP is almost the same at given system. Thus, the decrease of induction time (ti) in the presence of collagen-I at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65 (Fig. 2d) can't be caused by the different amount of Mg2+ into ACP.
S = 26.65 (Fig. 2d) can't be caused by the different amount of Mg2+ into ACP.
Effect of collagen-I fibrils on HAP nucleation
Distincting from other soluble additives, collagen-I molecules can be self-assembled into triple helical polypeptides and further be assembled into fibrils with 67 nm D-period bands along the long axis35 in physiological fluids (with neutral pH). In such a case, collagen-I is more like a substrate rather than a free molecule. A heterogeneous nucleation should be taken into account in such a situation. For heterogeneous nucleation, the nucleation barrier will be reduced to,25
 | (6) |
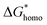 , the homogeneous nucleation barrier; f is the interfacial correlation factor. The homogeneous nucleation rate (Jhomo) and heterogeneous nucleation rate (Jhetero) is respectively expressed as:25
, the homogeneous nucleation barrier; f is the interfacial correlation factor. The homogeneous nucleation rate (Jhomo) and heterogeneous nucleation rate (Jhetero) is respectively expressed as:25
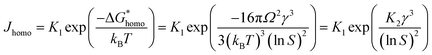 | (7) |
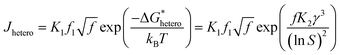 | (8) |
Combining eqn (7) and (8), we can get:
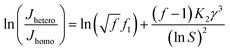 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S can be expected and obtain an eye guide line.
S can be expected and obtain an eye guide line.
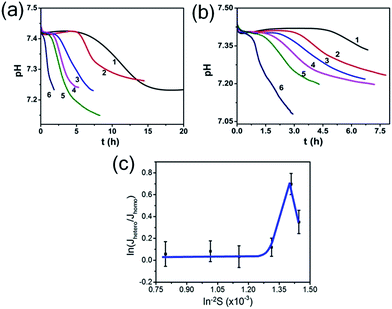
So, to evaluate the effect of collagen-I fibrils on HAP nucleation kinetics by CNT, we performed a series of experiments at different supersaturations in the absence (as control) (Fig. 4a) and presence (Fig. 4b) of collagen-I (50 μg mL−1). Clearly, in the presence of collagen-I, HAP nucleation was promoted at relatively lower supersaturation (Fig. S7†). The promotion effect might be caused by the reduction of nucleation barrier by heterogeneous nucleation that taking collagen-I fibril as a substrate in the view of CNT (eqn (6)). But the systematic nucleation kinetics data cannot be well explained by CNT. In CNT, the plot of ln(Jhetero/Jhomo) vs. ln−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S should give a linear relationship (eqn (9)). In contrast, here we found it was a non-linear plot (Fig. 4c). In eqn (9), the signs of slopes of the curve determine the sign of f − 1 (note K2 < 0). At lower supersaturation (ln
S should give a linear relationship (eqn (9)). In contrast, here we found it was a non-linear plot (Fig. 4c). In eqn (9), the signs of slopes of the curve determine the sign of f − 1 (note K2 < 0). At lower supersaturation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S: 26.30 to 26.65, i.e. ln−2
S: 26.30 to 26.65, i.e. ln−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S: 1.45 to 1.41 × 10−3), f was larger than 1 (i.e. f − 1 > 0); but for moderate supersaturation (ln
S: 1.45 to 1.41 × 10−3), f was larger than 1 (i.e. f − 1 > 0); but for moderate supersaturation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65 to 27.60), f became less than 1; at higher supersaturation (ln
S = 26.65 to 27.60), f became less than 1; at higher supersaturation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 27.60 to 35.44), f was approximate to 1, i.e. close to that of homogeneous nucleation. So, this complicated change of interfacial correlation factor (f, cf. eqn (6)) with respect to supersaturation could not be answered by CNT satisfactorily, that meaning collagen-I fibrils played as a passive nucleation template for ACP-mediated HAP nucleation kinetics, which has been mentioned by previous works and these researches indicated that crystal nucleation is directed by non-collagenous proteins (NCPs).38,39
S = 27.60 to 35.44), f was approximate to 1, i.e. close to that of homogeneous nucleation. So, this complicated change of interfacial correlation factor (f, cf. eqn (6)) with respect to supersaturation could not be answered by CNT satisfactorily, that meaning collagen-I fibrils played as a passive nucleation template for ACP-mediated HAP nucleation kinetics, which has been mentioned by previous works and these researches indicated that crystal nucleation is directed by non-collagenous proteins (NCPs).38,39
However, Wang et al.40 indicated that collagen can initiate and orientate the apatite nucleation without any other NCPs. But this results were achieved at high collagen concentration (250 mg L−1), so the collagen solutions are no longer fluids. Therefore, in our system, collagen-I fibrils have no effect on HAP heterogeneous nucleation without NCPs. Furthermore, to confirm this conclusion, we quantitatively analyze the amount of initial formed ACP nanoparticles in the absence or presence of collagen-I fibrils (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65). The concentration of calcium and phosphate in solution were measured by ICP-AES. The results showed that the consumed calcium and phosphate concentration are 0.4235 ± 0.017 mM (mean ± s.d.) and 0.2884 ± 0.1087 mM in control group, respectively. In collagen group (50 μg mL−1), the consumed calcium and phosphate concentration are 0.4017 ± 0.067 mM and 0.2725 ± 0.092 mM. So the amount of initial formed ACPs have no difference in control and collagen group. In addition, we used FTIR to determine the percentage of crystallinity in apatite calcium phosphate and the splitting function (SF) was obtained to evaluate the crystallinity.33 FTIR spectrums were obtained in each period (Fig. S8a and b†) and through splitting function (SF) we can see that there is no significant crystallinity difference between control and collagen group (Fig. S8d†), which means the amount change of ACP and HAP was almost the same at each period. More importantly, the initially formed ACP is about 80–100 nm and can't infiltrate into collagen fibril (Fig. S9a and b†). So the final apatite crystal randomly formed in solution (Fig. S9c†) instead of intra-fibrillar mineralization. In brief, our above analysis supported the notion that the promotion effect of HAP nucleation (Fig. 2d, S7†) can not be caused by HAP nucleate on collagen-I fibrils.
S = 26.65). The concentration of calcium and phosphate in solution were measured by ICP-AES. The results showed that the consumed calcium and phosphate concentration are 0.4235 ± 0.017 mM (mean ± s.d.) and 0.2884 ± 0.1087 mM in control group, respectively. In collagen group (50 μg mL−1), the consumed calcium and phosphate concentration are 0.4017 ± 0.067 mM and 0.2725 ± 0.092 mM. So the amount of initial formed ACPs have no difference in control and collagen group. In addition, we used FTIR to determine the percentage of crystallinity in apatite calcium phosphate and the splitting function (SF) was obtained to evaluate the crystallinity.33 FTIR spectrums were obtained in each period (Fig. S8a and b†) and through splitting function (SF) we can see that there is no significant crystallinity difference between control and collagen group (Fig. S8d†), which means the amount change of ACP and HAP was almost the same at each period. More importantly, the initially formed ACP is about 80–100 nm and can't infiltrate into collagen fibril (Fig. S9a and b†). So the final apatite crystal randomly formed in solution (Fig. S9c†) instead of intra-fibrillar mineralization. In brief, our above analysis supported the notion that the promotion effect of HAP nucleation (Fig. 2d, S7†) can not be caused by HAP nucleate on collagen-I fibrils.
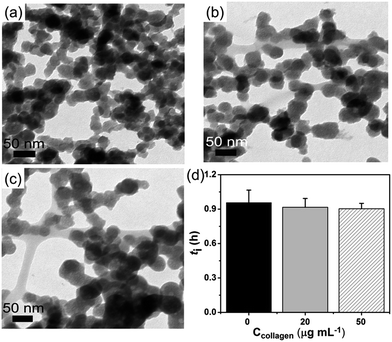
Besides, at high supersaturation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 35.44), compared to control (Fig. 5a) the precipitated ACP particles were still intensively aggregated (Fig. 5b and c). It might be that a large amount of ACPs (with higher number density) formed instantly at high supersaturation, so that they got rapidly aggregated before being separated by collagen-I fibrils. This aggregation behavior was not influenced even by increasing collagen-I concentrations (80 and 160 μg mL−1, cf. Fig. S10 in ESI†). As a result, the induction time (ti) was not affected by the involvement of the collagen-I fibrils (Fig. 5d, S10e†) at high supersaturation. That is to say, if the aggregation state of ACPs is not changed, HAP nucleation rate will not be promoted. In addition, above analysis indicating that the collagen-I fibrils, as substrates, have no obvious effect on reducing HAP nucleation barriers was further confirmed.
S = 35.44), compared to control (Fig. 5a) the precipitated ACP particles were still intensively aggregated (Fig. 5b and c). It might be that a large amount of ACPs (with higher number density) formed instantly at high supersaturation, so that they got rapidly aggregated before being separated by collagen-I fibrils. This aggregation behavior was not influenced even by increasing collagen-I concentrations (80 and 160 μg mL−1, cf. Fig. S10 in ESI†). As a result, the induction time (ti) was not affected by the involvement of the collagen-I fibrils (Fig. 5d, S10e†) at high supersaturation. That is to say, if the aggregation state of ACPs is not changed, HAP nucleation rate will not be promoted. In addition, above analysis indicating that the collagen-I fibrils, as substrates, have no obvious effect on reducing HAP nucleation barriers was further confirmed.
ACPs aggregation state affect HAP nucleation
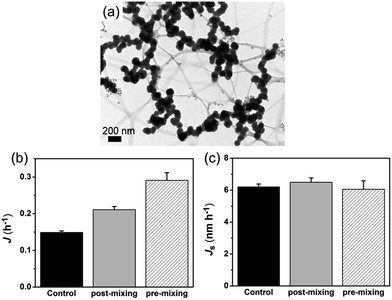
In order to confirm the nucleation rate of HAP is affected by the aggregation state of ACP particles, we used a “post-mixing” protocol in which collagen-I was introduced into the system after the formation and aggregation of ACPs (for details see Experimental section). Under TEM observation, it revealed that ACP particles were in aggregated state by using the post-mixing protocol (Fig. 6a). In this way, we had three systems with the same amount of calcium and phosphate in solutions, i.e. the control group (without collagen-I), pre-mixing group and post-mixing group (both with collagen-I). For these systems, the free Ca2+ and the amount of ACP (VACP, ACP volume; or mACP, ACP mass) were of the same. In prediction of eqn (5), the change of the aggregation state and the size of ACP spherules would alter the specific surface area (SACP = AACP/VACP) of ACP. Due to the amount of formed mineral was few at low supersaturation (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 26.65) and considering in samples preparation, the centrifugation and drying process might also affect the aggregation state of ACPs. However, these disadvantages can be avoided by direct TEM observations.31 Herein, we used TEM (see ESI for details†) to determine the specific surface area of ACP. As a results (Fig. S14–S16 and Table S3 in ESI†), when preventing ACP from aggregation, the specific surface area of ACP was increased from 0.024 ± 0.004 nm−1 (control group) to 0.053 ± 0.013 nm−1 (pre-mixing group). In comparison, the post-mixing protocol had less effect on ACP surface area (SACP = 0.032 ± 0.004 nm−1). Thereby, Fig. 6b shows that increasing the total surface area of ACP (pre-mixing > post-mixing > control) will promotes HAP nucleation. If the nucleation rate was furthermore normalized by ACP surface area by using specific surface area, i.e., Js = 1/(tiSa), we found that the values of Js for the three different cases were actually similar (Fig. 6c). This analysis followed that the HAP nucleation from ACP was primarily determined by the interface area and thereby, the aggregation state of ACP (i.e. the specific surface area) was the most important influence factor in phase-transformation based mineralization. On the other hand, collagen-I fibrils themselves have no impact on ACP mediated HAP nucleation was further confirmed.
S = 26.65) and considering in samples preparation, the centrifugation and drying process might also affect the aggregation state of ACPs. However, these disadvantages can be avoided by direct TEM observations.31 Herein, we used TEM (see ESI for details†) to determine the specific surface area of ACP. As a results (Fig. S14–S16 and Table S3 in ESI†), when preventing ACP from aggregation, the specific surface area of ACP was increased from 0.024 ± 0.004 nm−1 (control group) to 0.053 ± 0.013 nm−1 (pre-mixing group). In comparison, the post-mixing protocol had less effect on ACP surface area (SACP = 0.032 ± 0.004 nm−1). Thereby, Fig. 6b shows that increasing the total surface area of ACP (pre-mixing > post-mixing > control) will promotes HAP nucleation. If the nucleation rate was furthermore normalized by ACP surface area by using specific surface area, i.e., Js = 1/(tiSa), we found that the values of Js for the three different cases were actually similar (Fig. 6c). This analysis followed that the HAP nucleation from ACP was primarily determined by the interface area and thereby, the aggregation state of ACP (i.e. the specific surface area) was the most important influence factor in phase-transformation based mineralization. On the other hand, collagen-I fibrils themselves have no impact on ACP mediated HAP nucleation was further confirmed.
4. Conclusions
This study reveals the aggregation state of ACP can affect HAP nucleation kinetics. Our results directly confirmed that preventing ACP precursor from self-aggregation in solution, will increase the specific surface area of ACP, and then promote HAP nucleation. In biomineralization, well dispersed ACP particles have been observed in the growth zones of forming fin bones,11 which is distinct from the aggregated ACP in biomimetic mineralization systems.41–43 In this regard, controlling the aggregation state of ACP plays a critical role in controlling the nucleation of HAP. This finding would enrich our understanding on the regulation of HAP crystallization in biomineralization.Acknowledgements
This work was supported by the Fundamental Research Funds for the Central Universities (2012XZZX005), National Natural Science Foundation of China (21571155, 21601129).References
- S. Weiner and P. M. Dover, Rev. Mineral. Geochem., 2003, 54, 1–29 CrossRef CAS.
- P. G. Vekilov, Nanoscale, 2010, 2, 2346–2357 RSC.
- D. Kashchiev and A. Firoozabadi, J. Cryst. Growth, 2003, 250, 499–515 CrossRef CAS.
- D. Gebauer, A. Volkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- H. Cölfen and S. Mann, Angew. Chem., Int. Ed., 2003, 42, 2350–2365 CrossRef PubMed.
- E. Beniash, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2011, 3, 47–69 CrossRef CAS PubMed.
- R. Z. Legeros, Adv. Dent. Res., 1988, 2, 164–180 CrossRef CAS PubMed.
- F. Nudelman, K. Pieterse, A. George, P. H. H. Bomans, H. Friedrich, L. J. Brylka, P. A. J. Hilbers, G. De With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1004–1009 CrossRef CAS PubMed.
- A. S. Deshpande and E. Beniash, Cryst. Growth Des., 2008, 8, 3084–3090 CAS.
- J. Mahamid, B. Aichmayer, E. Shimoni, R. Ziblat, C. Li, S. Siegel, O. Paris, P. Fratzl, S. Weiner and L. Addadi, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6316–6321 CrossRef CAS PubMed.
- J. Mahamid, A. Sharir, L. Addadi and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12748–12753 CrossRef CAS PubMed.
- S. V. Dorozhkin, Acta Biomater., 2010, 6, 4457–4475 CrossRef CAS PubMed.
- J. Tao, H. Pan, J. Wang, J. Wu, B. Wang, X. Xu and R. Tang, J. Phys. Chem. C, 2008, 112, 14929–14933 CAS.
- H. Pan, X. Liu, R. Tang and H. Xu, Chem. Commun., 2010, 46, 7415–7417 RSC.
- S. Jiang, Y. Chen, H. Pan, Y. Zhang and R. Tang, Phys. Chem. Chem. Phys., 2013, 15, 12530–12533 RSC.
- S. Jiang, H. Pan, Y. Chen, X. Xu and R. Tang, Faraday Discuss., 2015, 179, 451–461 RSC.
- J. Tao, H. Pan, Y. Zeng, X. Xu and R. Tang, J. Phys. Chem. B, 2007, 111, 13410–13418 CrossRef CAS PubMed.
- P. B. Y. Ofir, R. G. Lippman, N. Garti and H. Füredi-Milhofer, Cryst. Growth Des., 2004, 4, 177–183 CAS.
- R. A. Perez, H. W. Kim and M. P. Ginebra, J. Tissue Eng., 2012, 3, 2041731412439555 Search PubMed.
- T. Mai, S. Boye, J. Yuan, A. Völkel, M. Gräwert, C. Günter, A. Lederer and A. Taubert, RSC Adv., 2015, 5, 103494–103505 RSC.
- A. Oyane, H. M. Kim, T. Furuya, T. Kokubo, T. Miyazaki and T. J. Nakamura, J. Biomed. Mater. Res., Part A, 2003, 65, 188–195 CrossRef PubMed.
- T. Kokubo and H. Takadama, Biomaterials, 2006, 27, 2907–2915 CrossRef CAS PubMed.
- J. Christoffersen, M. R. Christoffersen, W. Kibalczyc and F. A. Andersen, J. Cryst. Growth, 1989, 94, 767–777 CrossRef CAS.
- X. Y. Liu, in Advances in Crystal Growth Research, Elsevier, Amsterdam, 2001 Search PubMed.
- X. Yang, B. Xie, L. Wang, Y. Qin, Z. J. Henneman and G. H. Nancollas, CrystEngComm, 2011, 13, 1153–1158 RSC.
- K. Chatzipanagis, M. Iafisco, T. R. Herrero, M. Bilton, A. Tampieri, R. Kröger and J. M. Delgado-López, CrystEngComm, 2016, 18, 3170–3173 RSC.
- B. O. Fowler, M. Markovic and W. E. Brown, Chem. Mater., 1993, 5, 1417–1423 CrossRef CAS.
- M. S. A. Johnsson and G. H. Nancollas, Crit. Rev. Oral Biol. Med., 1992, 3, 61–82 CAS.
- Y. Chen, W. Gu, H. Pan, S. Jiang and R. Tang, CrystEngComm, 2014, 16, 1864–1867 RSC.
- Y. Wang, S. Jiang, H. Pan and R. Tang, CrystEngComm, 2016, 18, 379–383 RSC.
- C. Zhu, Y. Sun, Y. Wang, Y. Luo and D. Fan, Mater. Sci. Eng., C, 2013, 33, 2611–2619 CrossRef CAS PubMed.
- J. D. Termine and A. S. Posner, Nature, 1966, 211, 268–270 CrossRef CAS PubMed.
- S. Koutsopoulos, J. Biomed. Mater. Res., 2002, 62, 600–612 CrossRef CAS PubMed.
- J. P. R. O. Orgel, T. C. Irving, A. Miller and T. J. Wess, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9001–9005 CrossRef CAS PubMed.
- X. Y. Liu and S. M. Lim, J. Am. Chem. Soc., 2003, 125, 888–895 CrossRef CAS PubMed.
- H. Jiang, X. Y. Liu, G. Zhang and Y. Li, J. Biol. Chem., 2005, 280, 42061–42066 CrossRef CAS PubMed.
- W. G. S. Stevenson and A. Veis, Calcif. Tissue Int., 1986, 38, 135–141 CrossRef.
- A. George and A. Veis, Chem. Rev., 2008, 108, 4670–4693 CrossRef CAS PubMed.
- Y. Wang, T. Azaïs, M. Robin, A. Vallée, C. Catania, P. Legriel, G. P. Arnaudet, F. Babonneau, M. M. G. Guille and N. Nassif, Nat. Mater., 2012, 11, 724–733 CrossRef CAS PubMed.
- W. Kibalczyc, Cryst. Res. Technol., 1989, 24, 773–778 CrossRef CAS.
- E. D. Eanes, J. D. Termine and M. U. Nylen, Calcif. Tissue Res., 1973, 12, 143–158 CrossRef CAS PubMed.
- N. Ikawa, T. Kimura, Y. Oumi and T. Sano, J. Mater. Chem., 2009, 19, 4906–4913 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Solution compositions, figures and tables. See DOI: 10.1039/c7ra02208e |
| This journal is © The Royal Society of Chemistry 2017 |