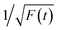Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electron transition pathways of graphene oxide quantum dots unraveled by emission wavelength dependent photoluminescence lifetime
Rongyan Guo *a,
Tao Lib and
Shuie Shic
*a,
Tao Lib and
Shuie Shic
aSchool of Physics and Telecommunication Engineering, Zhoukou Normal University, Zhoukou, Henan 466001, China. E-mail: guorongyan2016@163.com
bDepartment of Technology and Physics, Zhengzhou University of Light Industry, Zhengzhou 450002, People's Republic of China
cCollege of Electronic and Electrical Engineering, Henan Normal University, Xinxiang, Henan 453007, China
First published on 3rd April 2017
Abstract
The excitation wavelength dependent photoluminescence (PL) of graphene oxide quantum dots (GOQDs), which is frequently explained by size effects and radiative surface states, has drawn broad interest. In this work, the size of sp2 carbon clusters embedded in the GOQDs are found to be 2.8–4.8 nm by transmission electron microscopy. The energy gap estimated by the effective-mass method matches approximately with the observed emission wavelength. It clearly shows that the photogenerated carriers are quantum confined in the sp2 clusters. Moreover, the dependence of the PL lifetime on emission wavelength is close to a steady-state PL spectrum, which is different to that of semiconductor quantum dots, and suggests that the surface states significantly contribute to the long-wavelength emission.
1. Introduction
Carbon based nanostructures, including graphene oxide (GO), reduced graphene oxide (RGO), graphene oxide quantum dots (GOQDs), and carbon nanoparticles have attracted much attention due to their excitation-dependent photoluminescence (PL).1–5 It implies that the fluorescence colour could be tuned simply by changing the excitation wavelength, without modifying the chemical composition, shapes, sizes or structures. However, the intrinsic mechanism for the excitation dependent PL is still highly debated currently. As revealed by Kasha's rule,6 the fluorescence should be independent of the excitation wavelength, since all the excited electrons, regardless of the initial excitation photon energy, would relax to the lowest unoccupied molecular orbital (LUMO) or the bottom of conduction band before radiative recombination. Thence the excitation-dependent PL is rather an anomalous effect.Presently a variety of PL mechanisms are proposed to explain the excitation dependent emission, such as the size effect, surface traps model, giant red-edge effect, edge states model.7–14 But to date still no completely convincing mechanism that can unambiguously elucidate the excitation dependent emission. Size effect, which is intrinsically caused by quantum confinement effect, is a widely accepted model.11–14 To be detailed, the radiative recombination of electron–hole localized in the sp2 clusters is responsible for the emission. And energy gaps of GOQDs are determined by their sizes and shapes. According to the effective-mass approximation model, smaller sizes lead to wider energy gaps. It hints that the movement of PL excited at different wavelengths intrinsically derive from size distribution of the nanosheets. The size effect has been widely adopted to explain excitation dependent emission of carbon based nanostructures so far.11–14 However, Dai et al. reported that the GO nanosheets of different sizes showed optical absorbance, PL and PLE spectra locating at same position. It looks quite contradictory to the quantum confinement effect.11 But the rGO nanosheet contains graphene islands, also known as conjugated aromatic domains or isolated sp2 hybridised carbon clusters, separated by disordered regions. And they proposed that the PL should originate from the size effect of the isolated sp2 clusters instead of the nanosheets. Thence even if the sizes of GO nanosheets are quite different, the sizes of the sp2 clusters are very close, leading to the similar optical properties. It is also believed that the PL is strongly related with the surface trap states, such as functional groups, oxygen related disorder-induced localized states and other surface defects.15,16 However, to our knowledge, there is still a requirement of direct experimental evidence to support the relevant PL mechanism.2
In this work, GOQDs are obtained by hydrothermally cutting of graphene oxide sheets. The GOQDs solution shows excitation-dependent emission ranging from 420 to 570 nm. High-resolution transmission electron microscopy (HRTEM) and Raman spectra are used to study the size distribution of sp2 carbon clusters embedded in the GOQDs. The emission wavelengths are in agreement with the size distribution of sp2 carbon clusters according to the model of effective-mass approximation. Moreover, the PL decay curves of different emissions (400 to 600 nm) excited at the fixed wavelength (375 nm) and PL decay curves of the same emission (460 nm) excited at different wavelengths (375 and 405 nm) are substantially measured. And energy relaxation time τ and radiative recombination time β are obtained by numerical fitting of the time-resolved PL curves. The β increases firstly and then decreases with the emission wavelengths and shows a maximum at emission of ca. 500 nm. The results indicate that the emission from 420 to 500 is dominated by the size effect while the emission at wavelength longer than 500 nm may partially origin from radiative surface states.
2. Experimental
Graphene oxide was prepared by the modified Hummers method using natural graphite power.13 Aqueous solution of the GOQDs was fabricated by a hydrothermal process. A 1 mg L−1 GO suspension was prepared by dispersing the 80 mg GO in 80 mL deionized water. Then the GO suspension was treated by ultrasonic vibration for 1 h and its pH was adjusted to neutral by 1 M NaOH. The suspension was then transferred to a Teflon lined autoclave (100 mL) and heated to 180 °C for 5 h. Afterwards, the suspension was under ultrasonic vibration for 1 h. Finally, the GOQD-1 solution was obtained by centrifugation at 9000 rpm for 20 min. GOQD-2 and GOQD-3 were fabricated by hydrothermal reactions for 12 and 24 hours, respectively.HRTEM images were captured by an aberration corrected TEM (FEI Titan 80-300) at 80 kV, which is below the knock-on damage threshold of graphene. Raman spectrum was measured on a T64000 Raman spectrometer by using a 514.5 nm laser as the excitation source. Both steady-state and time-resolved PL (TRPL) measurements were performed on an Edinburgh FLS-920 fluorescence spectrometer.
3. Results and discussion
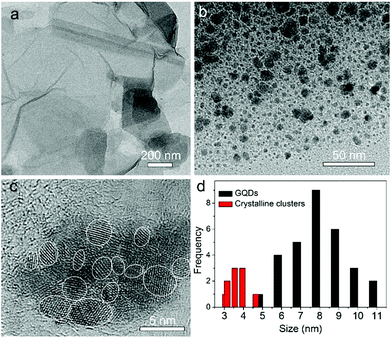
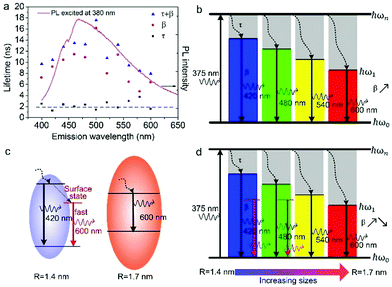
Fig. 1a shows the TEM image of the GO sheets. They are thin film with microscale sizes. And the large GO sheets were cut to ultrasmall GOQDs by hydrothermal treatments. The TEM of the obtained GOQDs is shown in Fig. 1b. They are 2–11 nm with random shapes. Furthermore, HRTEM image of an individual GOQD was recorded (Fig. 1c). As highlighted by the white circles, there are many crystalline clusters embed in a single GOQD, which experimentally confirmed the presence of isolated sp2 clusters directly. Since the shapes of the crystalline regions are arbitrary, to estimate the size distribution, the clusters are approximated as ellipses. The size is defined as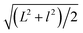 , in which L and l are elliptical long axis and short axis, respectively. Both the size distributions of GOQDs and isolated sp2 clusters are calculated from the TEM images (Fig. 1d). The sp2 clusters are about 2.8–4.8 nm with the most probable size at about 3.3 nm.
, in which L and l are elliptical long axis and short axis, respectively. Both the size distributions of GOQDs and isolated sp2 clusters are calculated from the TEM images (Fig. 1d). The sp2 clusters are about 2.8–4.8 nm with the most probable size at about 3.3 nm.
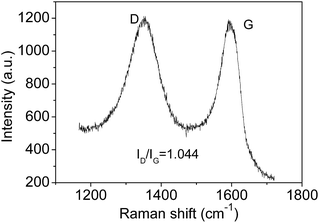
The Raman spectrum also can be used to estimate the crystallite sizes in carbon materials.17 The Raman spectra of a single graphite crystal shows only one mode at 1575 cm−l (G band) which is assigned to the E2g mode of the infinite crystal due to the in-plane motions of the hexagonal “honeycomb” network. Other carbon materials with “boundary”, such as polycrystalline graphite, graphene oxide, carbon nanospheres, activated carbon and carbon nanotubes always exhibit another band at 1355 cm−l (D band), attributing to a change in the selection rules for Raman activity of certain phonons which are inactive in the infinite lattice.13 Therefore, the D band is caused by a breakdown of the k-selection rule. The intensity of the D band is inversely proportional to the effective crystallite size in the graphite plane.17,18 The intensity of this band allows an estimate of the crystallite size. The intensity ratio of D band to G band (ID/IG) shows a linear relationship with 1/d, in which d is the crystallite size.17 The size of crystallites is estimated to be ca. 4.0 nm according to the obtained Raman spectrum (Fig. 2), which is very close to the size from HRTEM images. However, note only approximate sizes are acquired by the Raman method. It is reasonable that they are not equal completely. Obviously, the TEM results are more accurate. The Raman results further confirmed the presence of nano-sized sp2 clusters, and the results verify that Raman is useful tool to analysis the sizes of sp2 clusters qualitatively. Furthermore, the notable D band suggests there are substantial surface states (Fig. 2).
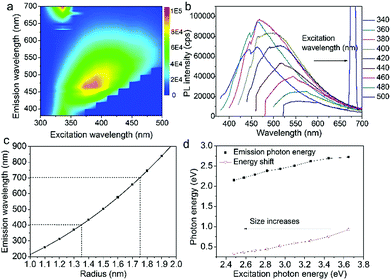
Fig. 3a shows the excitation-emission contour mapping of GOQDs solution. The PL peak position moves as the excitation wavelength changes. It is a typical excitation dependent emission, similar to previous works.13,19–23 PL spectra excited at 340 to 500 nm with an interval of 20 nm are depicted in Fig. 3b. As the excitation wavelength increases from 340 to 500 nm, the emission wavelength shifts from 440 to 550 nm. The strongest emission appears at 480 nm. The PL spectra are normally quite broad with a FWHM typically about 125 nm.
Supposing the size effect, the energy gaps rely on the sizes and shapes of localized sp2 clusters. Bigger the size, the narrower is the energy gap resulting in longer wavelength emission. When the excitation wavelength increases, sp2 clusters with bigger sizes would be excited, so that the emission wavelength increases. Thus, the emission moves as the excitation wavelength changes. As shown in Fig. 1d, due to the size distribution of the sp2 carbon clusters, the strongest emission should originate from the clusters of the most probable size. The dependence of energy gap on size can be estimated by the following equation:22
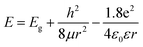 | (1) |
in which Eg = 0.04 eV is the band gap of bulk graphite,24,25 μ is the reduced mass of the exciton, which is determined by the effective mass of electron (me) and hole (mh), μ = memh/(me + mh). Herein, me = 0.42m0 and mh = 0.069m0, where m0 is the free-electron mass. Hence, μ = 0.05926m0.26 ε is the dielectric constant of carbon, it is about 15.22 r is the radius of the sp2 clusters. Accordingly, the function of energy gap on sizes is plotted in Fig. 3c. The emission of 400–700 nm corresponds to sizes of 2.7–3.5. Moreover, the location of the strongest emission (480 nm) observed in Fig. 3b corresponds to r of 1.47 nm, which is in very close to the most probable size acquired by TEM. In the effective-mass approximation model (eqn (1)), the particle is supposed to be spherical. However here the sp2 clusters are 2D sheets of random shapes. Thus, eqn (1) only estimate the bandgaps roughly. In principle, the distribution of the energy gaps given by the size distribution matches with the emission wavelengths in the range of 400–700 nm. Additionally, emission photon energy and energy shift (Stokes shift, the energy difference between luminescence and excitation) versus the excitation photon energy is plotted in Fig. 3d. The energy shift could be well represented by an equation of ΔE = E0/r2, which is in good agreement with the size effect observed in silicon quantum dots.27 As excitation wavelength increases from 340 (3.65) to 500 nm (2.48 eV), the energy shift (ΔE) decreases from 928 to 331 meV, clearly show that the carriers at excited states are quantum confined in the sp2 clusters.27
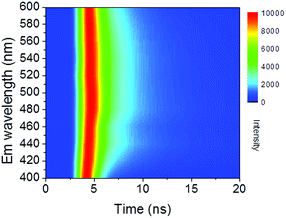
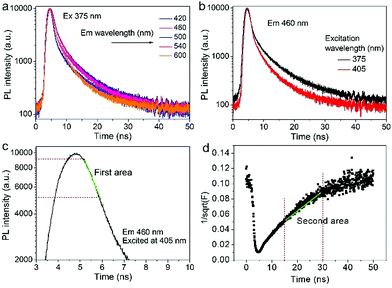
Time-resolved PL decay curves were acquired by using a time-correlated single-photon counting system. A 5 MHz pulsed laser is used as the excitation light (375 or 405 nm). The decay curves of different emissions (420 to 620 nm) excited at 375 nm (Fig. 4 and 5a) and the decay curves of the same emission (460 nm) excited at 375 and 405 nm (Fig. 5b) were substantially measured. A quite conspicuous tendency that the PL decay rate slows down and then speeds up as the monitored wavelength increases from 400 to 600 nm (Fig. 4). A numerical analysis is performed based on a reported model.28,29 Specifically, fluorescence process could be described by relaxation time τ and recombination time β. And these two values could be extracted by fitting the time-resolved fluorescence curves. In this fluorescence scheme, regarding electron transitions of a quantum dot, only the high excited state ℏωn is largely occupied but the bottom of the conduction band ℏω1 and the ground state ℏω0 is basically empty at the initial PL decay stage. Therefore, the PL decay is predominantly determined by the occupation of ℏω1 relaxed from ℏωn, thus the a nonradiative relaxation time τ (relax from ℏωn to ℏω1) can be fitted at this initial PL decay stage. In the following PL decay stages, all three energy levels are partially occupied and the PL decay spectrum becomes quite complicated. However, a certain time window (e.g. 15–30 ns) can be resolved that 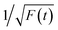 is linearly related with t. During this time interval ℏωn is almost unoccupied, while the variations of ℏω1 and ℏω0 occupations are similar.28,29 Thence in this time window, radiative recombination time β (relax from ℏω1 to ℏω0) can be acquired.
is linearly related with t. During this time interval ℏωn is almost unoccupied, while the variations of ℏω1 and ℏω0 occupations are similar.28,29 Thence in this time window, radiative recombination time β (relax from ℏω1 to ℏω0) can be acquired.
As shown in Fig. 5c and d, the fluorescence decay contains two distinct areas, with a first area could be described by a single exponential decay:
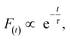 | (2) |
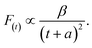 | (3) |
Thereafter, by fitting these two different parts in time-resolved fluorescence curves respectively, we could further to acquire the values for τ and β. The fitting process is as following: the instrumental response is treated by a reconvolution firstly. The relaxation value τ is fitted by single exponential formula from the first window of the PL decay function F(t) in the photon count range between 9 × 103 and 4 × 103, (shown in Fig. 5c). Then the recombination value β is acquired by fitting the transformed time-resolved fluorescence curve (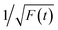 ) in the late-stage time window, i.e., between 15 and 30 ns, since
) in the late-stage time window, i.e., between 15 and 30 ns, since 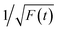 is well approximated as linear related to time t (Fig. 5d).
is well approximated as linear related to time t (Fig. 5d).
According to the above model, τ and β values corresponding to emissions at different wavelengths are obtained and plotted in Fig. 5a. It shows that the PL lifetime (τ + β) increases firstly and then decreases with the emission wavelengths and shows a maximum at emission of ca. 500 nm. The tendency is consistent with the PL spectrum excited at 380 nm. Similar emission wavelength dependent PL lifetime was also observed by Deng et al.30 Their lifetime values were fitted by a biexponential function y(t) = A1e−t/τ1 + A2e−t/τ2 and τave was acquired by τave = A1τ1 + A2τ2. However, the τave does not point to a defined electronic transition. In our model, τ and β values are clearly assigned to relaxation time from ℏωn to ℏω1 and radiative recombination time from ℏω1 to ℏω0 respectively, which enables a more comprehensive insight into the electron transition pathways.
The τ mainly represents the electron–phonon interactions. In a quantum dot, the excitonic states are discrete, the electron–phonon interaction rate in a semiconductor nanostructure can be very low when ℏωn − ℏωs1 ≠ ℏωp, which is known as the phonon bottleneck.28 Here τ is about 2 ns. Therefore, the τ changes little when the detection wavelength increases. The same principle also can be concluded from decay curves of the same emission (460 nm) excited at different wavelengths (375 and 405 nm) shown in Fig. 5b. When the excitation wavelength changes from 375 to 405 nm, the energy difference between ℏωn and ℏω1 decreases from 0.611 to 0.366 eV, the decay curves in the initial 5 ns are almost superposition, corresponding τ slightly shortens from 1.698 to 1.44 ns.
As reported in many semiconductor quantum dots, faster recombination in smaller clusters due to larger overlap of the electron–hole wave functions.31,32 Thereby, as supposed in Fig. 6b, β is expected to monotonically increases with the emission wavelength. However, the GOQDs are different to traditional semiconductor quantum dots, the surface states play essential roles other than mere size effect. As illustrated in Fig. 6c, in addition to emission of blue photon (e.g. 420 nm), the excited state of a smaller sp2 carbon cluster may relax to a surface state before emission of 600 nm. And the surface state possesses a shorter lifetime due to the nature of localized state.13 Besides, the long-wavelength photons (e.g. 600 nm) also may emit directly from a bigger sp2 carbon cluster due to quantum confinement effect.
Consequently, the dependence of β values, as well as PL lifetime on emission wavelength is explained in Fig. 6d. The β values exhibit noticeable increment at longer detection wavelength in the range of 400–500 nm, which is a direct reflection of the size effect and in good agreement with aforementioned discussion. Whereas, with regard to the emission of 500 to 600 nm, they may originate from bigger sp2 carbon clusters or radiative surface states. Thus, the β values may decreases as emission wavelength increases due to the shorter lifetime of surface states.
In order the gain more insight into the influence of size effect and surface states on PL properties, GOQDs were fabricated by hydrothermal reactions for 5, 12, and 24 hours, respectively. They are designated as GOQD-1, GOQD-2 and GOQD-3, correspondingly. Raman spectra show that ID/IG decreases as reaction time increases, suggesting that sp2 clusters grow up and number of surface groups decreases. It is understandable that longer reaction time lead to more thorough reduction. The steady-state PL spectra of all the GOQDs are quite similar regardless of the reaction time. Fig. 7b shows the 440 nm TRPL of GOQD-1 decays the fastest and the decay rate slightly slows down from GOQD-1 to GOQD-3. According to our model proposed above, the 440 nm mainly stems from the size effect. When the monitored wavelength is fixed at 440 nm, the corresponding sizes of sp2 clusters are the same for different GOQDs. Although, from GOQD-1 to GOQD-3, the collective size of sp2 cluster increases, recombination rate only declines a little. Whereas, the lifetime of 540 nm emission evidently increases with reaction time (Fig. 7c). In our model, the 540 nm emission is strongly affected by surface state with very short lifetime. When the reaction time is prolonged, the surface states are further removed, thus the PL lifetime extends. Therefore, the TRPL spectra of different GOQDs are well explained.
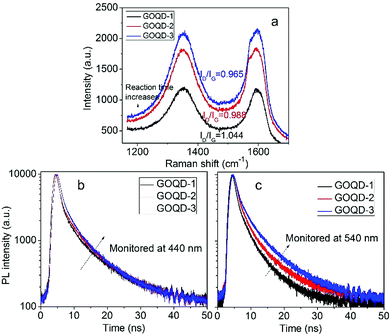 | ||
| Fig. 7 (a) Raman spectra of GOQDs fabricated by hydrothermal reactions of different time. (b, c) Time-resolved PL spectra of different GOQDs monitored 440 (b) and 540 nm (c). | ||
4. Conclusions
In summary, we have gained a comprehensive insight into the electron transition pathway of PL from GOQDs. Firstly, the HRTEM images and Raman spectrum are used to confirm the presence of sp2 hybridised carbon clusters embedded in the GOQDs and determine their size distribution. The energy gap estimated by the effective-mass approximation nearly matches with the observed emission wavelength. These evidences suggest that size effect significantly contribute to the excitation dependent emission of GOQDs. Secondly, the strong dependence of PL lifetime on detection wavelength reveals that the emissions of 400 to 500 nm are predominately caused by size effect of smaller sp2 carbon clusters while the 500 to 600 nm PL may stem from bigger sp2 carbon clusters or radiative surface states.Acknowledgements
The research of this paper has been sponsored by Henan Provincial Research Foundation for Science and Technological Breakthroughs, China (Grant No. 142102210599, 132102210577).References
- H. J. Sun, L. Wu, W. L. Wei and X. G. Qu, Mater. Today, 2013, 16, 433 CrossRef CAS.
- Z. X. Gan, H. Xu and Y. L. Hao, Nanoscale, 2016, 8, 7794 RSC.
- L. P. Lin, M. C. Rong, F. Luo, D. M. Chen, Y. R. Wang and X. Chen, TrAC, Trends Anal. Chem., 2014, 54, 83 CrossRef CAS.
- J. H. Shen, Y. H. Zhu, X. L. Yang and C. Z. Li, Chem. Commun., 2012, 48, 3686 RSC.
- Z. X. Gan, S. J. Xiong, X. L. Wu, C. Y. He, J. C. Shen and P. K. Chu, Nano Lett., 2011, 11, 3951 CrossRef CAS PubMed.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14 RSC.
- Y. H. Deng, X. Chen, F. Wang, X. A. Zhang, D. X. Zhao and D. Z. Shen, Nanoscale, 2014, 6, 10388 RSC.
- J. Lee, K. Kim, W. I. Park, B. H. Kim, J. H. Park, T. H. Kim, S. Bong, C. H. Kim, G. S. Chae, M. Jun, Y. Hwang, Y. S. Jung and S. Jeon, Nano Lett., 2012, 12, 6078 CrossRef CAS PubMed.
- S. K. Cushing, M. Li, F. Q. Huang and N. Q. Wu, ACS Nano, 2014, 8, 1002 CrossRef CAS PubMed.
- D. Kozawa, X. Zhu, Y. Miyauchi, S. Mouri, M. Ichida, H. B. Su and K. Matsuda, J. Phys. Chem. Lett., 2014, 5, 1754 CrossRef CAS PubMed.
- X. M. Sun, Z. Liu, K. Welsher, J. T. Robinson, A. Goodwin, S. Zaric and H. J. Dai, Nano Res., 2008, 1, 203 CrossRef CAS PubMed.
- G. Eda, Y. Y. Lin, C. Mattevi, H. Yamaguchi, H. A. Chen, I. S. Chen, C. W. Chen and M. Chhowalla, Adv. Mater., 2010, 22, 505 CrossRef CAS PubMed.
- Z. X. Gan, S. J. Xiong, X. L. Wu, T. Xu, X. B. Zhu, X. Gan, J. H. Guo, J. C. Shen, L. T. Sun and P. K. Chu, Adv. Opt. Mater., 2013, 1, 926 CrossRef.
- S. H. Jin, D. H. Kim, G. H. Jun, S. H. Hong and S. Jeon, ACS Nano, 2013, 7, 1239 CrossRef CAS PubMed.
- Y. Q. Dong, H. C. Pang, H. B. Yang, C. X. Guo, J. W. Shao, Y. W. Chi, C. M. Li and T. Yu, Angew. Chem., Int. Ed., 2013, 52, 7800 CrossRef CAS PubMed.
- H. Nie, M. J. Li, Q. S. Li, S. J. Liang, Y. Y. Tan, L. Sheng, W. Shi and S. X. A. Zhang, Chem. Mater., 2014, 26, 3104 CrossRef CAS.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126 CrossRef CAS.
- Y. Zhou, Q. L. Bao, L. A. L. Tang, Y. L. Zhong and K. P. Loh, Chem. Mater., 2009, 21, 2950 CrossRef CAS.
- W. Sun, Y. X. Du and Y. Q. Wang, J. Lumin., 2010, 130, 1463 CrossRef CAS.
- J. Liu, X. L. Liu, H. J. Luo and Y. F. Gao, RSC Adv., 2014, 4, 7648 RSC.
- S. N. Qu, X. Y. Liu, X. Y. Guo, M. H. Chu, L. G. Zhang and D. Z. Shen, Adv. Funct. Mater., 2014, 24, 2689 CrossRef CAS.
- Y. L. Hao, Z. X. Gan, J. Q. Xu, X. L. Wu and P. K. Chu, Appl. Surf. Sci., 2014, 311, 490 CrossRef CAS.
- Y. Li, Y. Zhao, H. H. Cheng, Y. Hu, G. Q. Shi, L. M. Dai and L. T. Qu, J. Am. Chem. Soc., 2012, 134, 15 CrossRef CAS PubMed.
- J. W. McClure, IBM J. Res. Dev., 1964, 8, 255 CrossRef CAS.
- N. García, P. Esquinazi, J. Barzola-Quiquia and S. Dusari, New J. Phys., 2012, 14, 053015 CrossRef.
- S. Y. Zhou, G. H. Gweon, J. Graf, A. V. Fedorov, C. D. Spataru and R. D. Diehl, Nat. Phys., 2006, 2, 595 CrossRef CAS.
- N. M. Park, C. J. Choi, T. Y. Seong and S. J. Park, Phys. Rev. Lett., 2001, 86, 1355 CrossRef CAS PubMed.
- H. Xu, V. Chmyrov, J. Widengren, H. Brismar and Y. Fu, Phys. Chem. Chem. Phys., 2015, 17, 27588 RSC.
- Z. X. Gan, X. L. Wu, H. Xu, N. Zhang, S. P. Nie and Y. Fu, J. Phys. D: Appl. Phys., 2016, 49, 275107 CrossRef.
- X. X. Deng, J. Sun, S. W. Yang, H. Shen, W. Zhou, J. Lu, G. Q. Ding and Z. Y. Wang, Appl. Phys. Lett., 2015, 107, 241905 CrossRef.
- Y. C. Zhang, A. Pancholi and V. G. Stoleru, Appl. Phys. Lett., 2007, 90, 183104 CrossRef.
- Y. I. Mazur, J. W. Tomm and V. Petrov, Appl. Phys. Lett., 2001, 78, 3214 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |