Computational investigation on the large energy gap between the triplet excited-states in acenes

Abstract

The large energy gap between the two triplet excited-states in acenes has a huge impact on their optical and electronic properties. Accurate calculation and full use of this gap have always been a major challenge in the field of organic semiconductor materials. In the present study, we focus on the precise description of the large gap between the T₁ and T₂ states, and taking a series of acenes (benzene, naphthalene, anthracene, tetracene, and pentacene) as examples, investigate their excited state behavior to verify the energy gap structure. The results show that the symmetry of the transition molecular orbital and the excited state properties have a great influence on the transition energy, and may be the main cause of the large energy gap.

---

1. Introduction

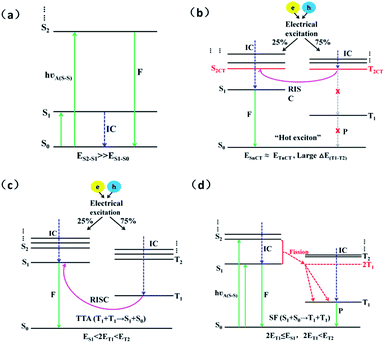
In an electroluminescent device, electrons and holes driven by the electric field generate excitons. Generally, initially formed excitons tend to relax to the lowest singlet (S₁) and triplet (T₁) states before radiative decay in accordance with Kasha's rule, as a result of the much faster internal conversion (IC) rate than the intersystem crossing (ISC) rate.¹ Of course, there are some rare exceptions that do not obey this rule. For instance, azulene emits from the S₂ state instead of the S₁ state as a result of the large energy gap between the S₁ and S₂ states which leads to the IC (S₂ → S₁) process becoming too slow to compete with the fluorescent radiation process of S₂ → S₀, as shown in Fig. 1(a).^2,3 Similarly, a large energy gap between the triplet states can also lead to changes in the exciton radiation path. The TPA-NZP molecule displays the typical hot exciton mechanism. Its huge triplet state energy gap (ΔE_T1–T2) between the first (T₁) and the second (T₂) excited-state causes the IC (T₂ → T₁) rate to be so slow that it cannot compete with the RISC (T₂ → S₂) rate, thus ensuring the smooth channel of the high exciton and near 100% yield of singlet excitons harvested in the EL device, as shown in Fig. 1(b).^4–10 In addition, P-type delayed fluorescence (triplet–triplet annihilation TTA) molecules annihilate the two triplets to form an excited singlet and a ground-state singlet to improve exciton utilization; however to completely ensure this mechanism, the energy of the T₁ state is greater than the S₁ but less than T₂ (E_S1 < 2E_T1 < E_T2), that is, there are energy gaps between the S₁, T₁ and T₂, as shown in Fig. 1(c).¹¹ The third example is singlet fission (SF) in which two triplet excitations are produced from an excited singlet. Suitable candidates for SF should have S₁ state energy more than twice the T₁ energy and for the efficient formation of triplets by singlet fission, it is important to ensure that neither 2E_T1 − E_S1 nor 2E_T1 − E_T2 are distinctly positive, as shown in Fig. 1(d).^12–14 The above three examples show that the energy gap between the triplet states can slow down the IC rate which is comparable with the ISC rate. This will give rise to a change in the resultant ratio of excitons generated between the singlet and triplet state in the EL device, which further causes a change in fluorescent efficiency.

Fig. 1 Simple schematic of the exciton decay and the electroluminescence process of (a) azulene molecules; (b) hot exciton mechanism; (c) TTA mechanism; and (d) SF mechanism. Where, S: singlet state; T: triplet state; F: fluorescence; P: phosphorescence; K_IC: internal conversion rate; K_RISC: reverse intersystem crossing rate; CT: charge-transfer state; and ΔE_ST: singlet–triplet energy splitting.

Among the many electroluminescent materials, due to their simple structure, easy synthesis and high luminous efficiency, acenes have received extensive attention as potential candidate materials for TTA, hot exciton and singlet fission; thus the study of acenes triplet excited-state has also gradually increased.^15–21 For instance, Lewis and Kasha,²² McClure,²³ Hunziker,^24,25 and Meyer et al.²⁶ have probed experimentally the triplet states of naphthalene and the lowest triplet state in longer stable oligomers has also been determined experimentally.^27–31 However, the energy of the higher triplet states and the energy gap between them have not been given any attention both experimentally and theoretically.

In the present study, we first aim to ascertain the accuracy of the method applied to describe the energy level of the triplet state, and on this basis, we further focus on the large transition energy gap between the T₁ and T₂ state taking a series of acenes (benzene, naphthalene, anthracene, tetracene, and pentacene) (as shown in Scheme 1) as examples to investigate the transition properties of their triplet excited states to explore the huge resulting ΔE_T1–T2. The study of the excited state behaviour of these molecules to verify their high level triplet excited state energy gap structure is very helpful for a rational molecular design to adjust and control the gap between the excited states with the aim of developing new ideas on the adjustable energy gap of high performance organic photoelectric functional materials.

Scheme 1 Representation of the acenes investigated herein.

2. Methodology and computational details

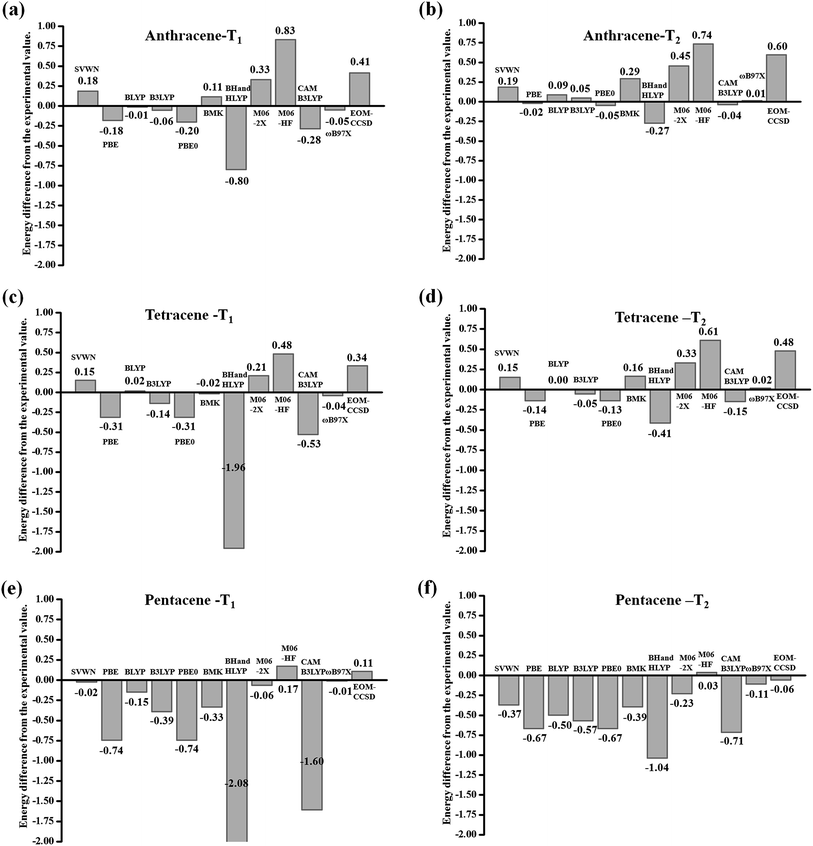
As is known, the ground-state electronic structures for most chromophores can be conveniently obtained using various quantum chemistry computational methods. However, it is difficult to calculate the electronic structures of the electronic excited state for molecular systems, especially the triplet state. Nowadays, the equation of motion coupled cluster with single and double excitation model³² (EOM-CCSD) methods and time-dependent density functional theory^33–38 (TD-DFT) are very popular computational methods to determine excited-state electronic structures. TD-DFT is the most widely-used method to describe the excited-state properties of medium to large molecular systems. The EOM-CCSD method takes into account both single and double substitutions and can give relatively accurate results, but the calculation cost is very high; whereas TD-DFT is a more cost-effective method to calculate the excited-state. In the present study, in order to explore the energy gap between the triplet excited states of acenes, the excited state energy needs to be calculated accurately first. To assess the performances of the TD-DFT approaches, we tried to cover a broad and diverse selection of functionals. We use the typical acenes molecule anthracene, tetracene and pentacene (Scheme 1) as examples to investigate the most suitable functionals. The performance of 2 local functionals (SVWN³⁹ and PBE⁴⁰), 7 hybrid functionals (BLYP (0%HF),⁴¹ B3LYP (20%HF),⁴² PBE0 (25%HF),⁴³ BMK (42%HF),⁴⁴ BH and HLYP (50%HF),⁴⁵ M06-2X (56%HF),⁴⁶ and M06HF (100%HF),⁴⁷) and 2 long-range-corrected functionals CAM-B3LYP⁴⁸ and ωB97X⁴⁹ in combination with 6-31+G(d,p) basis sets⁵⁰ is explored. The EOM-CCSD method is also included for comparison purposes.

In this part, we focus on describing the transition energy level of the triplet states (T₁ and T₂) accurately. As shown in Fig. 2, we used different methods and functionals as abscissa, and the difference between the experimental value as the ordinate for mapping histograms.⁵¹ On the whole, each functional of the DFT method shows a tendency to gradually underestimate the transition energy as the conjugate length increases. When the conjugate length is small (anthracene), the difference between the calculated values of T₁ and T₂ and the experimental values is not as large as the whole, where the maximum value is 0.83 eV and the minimum value is only 0.01 eV, among which the BLYP, B3LYP and ωB97X functionals are controlled within the range of 0.1 eV. When the conjugate length increases to tetracene, the difference increases and the maximum value reaches −1.96 eV, where the BLYP and ωB97X functionals remain within the range of 0.1. When the conjugate length continues to increase to pentacene, the difference is further increased, where the maximum value is −2.08 eV, as calculated by the BH and HLYP functional. As can be seen in Fig. 2(e) and (f), the difference values are systematically negative, which indicates that the TD-DFT functional tends to underestimate the transition energies in the relatively long conjugate systems. Only the ωB97X functional continues to maintain a difference of less than 0.1. This situation may be due to the conjugate length growth, where the distance of the electron transition increases, and similar to the charge transfer process, the traditional local functionals and most hybrid functionals underestimate the transition energy with an increase in conjugate length. However, the ωB97X functional optimizes the range separation parameter ω through the self-consistent restriction system, which aims at physically motivated correction for the long-range Coulomb interaction. This functional can be established to enable the accurate and quantitative description of the intramolecular charge-transfer (CT) state. At the same time, the EOM-CCSD method also exhibits the trend that with conjugate length growth the transition energy gradually goes from being overvalued to underestimated. Considering the computational accuracy and cost, the TD-DFT/ωB97X method was finally chosen to describe the excited-state properties of acenes. Earlier benchmarks have shown that different functionals have almost no effect on the geometries of the ground states and the minimum structures are similar in accuracy to the structures obtained from experiment.⁵² Herein, all ground state structures were optimized using the B3LYP functional combined with the 6-31+G(d,p) basis set. The optimized structures were confirmed to be local energy minima by calculating vibrational frequencies. All DFT/TD-DFT and EOM-CCSD calculations were performed with Gaussian09.D.01 Revision.⁵³

Fig. 2 Histograms of the difference from the experimental value for the triplet vertical excitation energies (eV) calculated using TD-DFT and the EOM-CCSD method with respect to the acene: (a) T₁ for anthracene; (b) T₂ for anthracene; (c) T₁ for tetracene; (d) T₂ for tetracene; (e) T₁ for pentacene and (f) T₂ for pentacene.

3. Results and discussion

3.1 Transition energy gap between T₁ and T₂ (ΔE_T1–T2)

We take the conjugate length (number of benzene ring) as the abscissa and triplet excitation energy as the ordinate in drawing presented in Fig. 3. Overall, with the growth of the conjugated length and the excitation energies of T₁ and T₂ show a downward trend, which can be explained by the fact that the excitation energy of the triplet states is associated with the conjugate length, and the longer the length the lower the transition energy. However, there is a special phenomenon that from benzene to anthracene T₁ decreases by about 1.0 eV for each benzene added and it decreases by only about 0.2 eV from tetracene to pentacene. At the same time, the excitation energy of T₂ reduces by a similar value of about 0.8 eV from benzene to anthracene, until from tetracene to pentacene the gap between T₂ is reduced to 0.2 eV. Thus, the trend of the gap between T₁ and T₂ (ΔE_T1–T2) first increases (from 1.10 eV to 1.44 eV) then decreases (from 1.44 eV to 1.33 eV) and finally stabilizes (from 1.33 eV to 1.37 eV).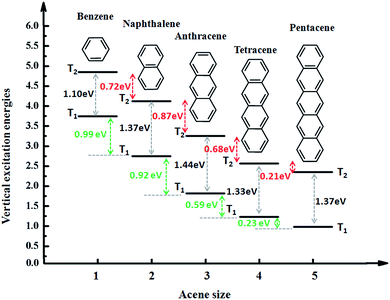

Fig. 3 Energy diagrams of the acenes (benzene, naphthalene, anthracene (An), tetracene, and pentacene).

Anthracene has the largest ΔE_T1–T2 and benzene has the smallest ΔE_T1–T2. Is the large ΔE_T1–T2 related to its structural characteristics? To facilitate a comparison, we chose a series of common anthracene derivatives, for which their triplet excitation energy was calculated using the TD-DFT/ωB97X method, as presented in Fig. 4. The results show that due to the introduction of heteroatoms, the energy changes a lot, where ΔE_T1–T2 both increases and decreases, which indicates that the cause of the large ΔE_T1–T2 is the structure and other reasons. In the next section we will discuss the cause of the large more ΔE_T1–T2 by analyzing the nature of the transitional or excited states.

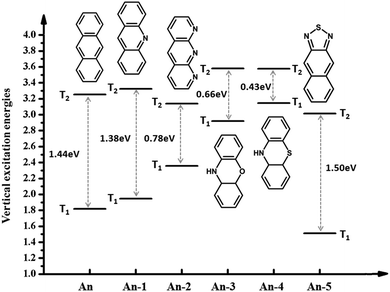Fig. 4 Energy diagrams of anthracene derivatives of the first two triplet excited-states from calculation.

3.2 The molecular orbitals (MOs)

We analyzed the transition configurations of the T₁ and T₂ excited-state of the acenes. As shown in Table 1, the T₁ transition is mainly contributed from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO), and the coefficient increases with the conjugate length. It is implied that the longer the conjugate length, the more intense the transition from the HOMO to LUMO. On the contrary, the transition of the T₂ state presents other modes, since it is a transition from the inner MOs of the HOMO to the LUMO. For example the transition of the T₂ state in anthracene is HOMO−2 → LUMO, tetracene is HOMO−2 → LUMO and pentacene is HOMO−1 → LUMO and molecules with such transitions are accompanied by a large ΔE_T1–T2 in energy levels. Upon further analysis of the orbital energy, it was noted that the energy differences between HOMO−1 and HOMO in anthracene, tetracene and pentacene are very large, which are 1.28 eV, 1.62 eV and 1.44 eV, respectively. Therefore, the electron transition energies from these inner occupied orbitals to the LUMO are much larger than from the HOMO to LUMO. We also analyzed the symmetry of the molecular orbital, as listed in Table 1. As is known, the electronic transition is in accordance with the rules of parity, which requires that the molecules must change their symmetry after the transition. In other words, the transition is allowed if the symmetry of the orbital is changed after the electron transition, for example u → g and g → u, whereas the transition is prohibited for u → u and g → g. As shown in Table 1, from naphthalene to pentacene, the T₂ all show the transition between the same parity MO, which means that these transitions are parity-forbidden. This feature may lead to the emergence of a large energy difference between T₁ and T₂.

Table 1 MOs character and symmetry of the acenes (benzene, naphthalene, anthracene (An), tetracene, and pentacene)

	MOs character and coefficient	Orbital symmetry	Transition probability (YES or NO)	ΔET1–T2 (eV)
Benzene	T1 HOMO → LUMO 0.48	e1g → e2u	YES	1.10
	T2 HOMO → LUMO + 1 0.47	e1g → e2u	YES
	T3 HOMO−1 → LUMO + 1 0.47	e1g → e2u	YES
Naphthalene	T1 HOMO → LUMO 0.66	au → b1g	YES	1.37
	T2 HOMO−1 → LUMO 0.50	b2g → b1g	NO
	T3 HOMO−2 → LUMO 0.49	b3u → b1g	YES
Anthracene	T1 HOMO → LUMO 0.69	b2g → b3u	YES	1.44
	T2 HOMO−2 → LUMO 0.50	au → b3u	NO
	T3 HOMO−1 → LUMO 0.61	b1g → b3u	YES
Tetracene	T1 HOMO → LUMO 0.71	au → b1g	YES	1.33
	T2 HOMO−2 → LUMO 0.50	b2g → b1g	NO
	T3 HOMO−1 → LUMO 0.67	b3u → b1g	YES
Pentacene	T1 HOMO → LUMO 0.77	b2g → b3u	YES	1.37
	T2 HOMO−1 → LUMO 0.51	au → b3u	NO
	T3 HOMO−3 → LUMO 0.43	b2g → b3u	YES

---

3.3 Excited state properties

Excited-state configurations from the stationary points of the ground-state energy surfaces were then obtained at the TD-DFT/ωB97X/6-31+G(d,p) level. We analyzed the natural transition orbital (NTOs)⁵⁴ of the T₁ and T₂ excited-states of acenes. From Fig. 5, the nature of the two excited states, T₁ and T₂, deserves some other comments. In the transition process, the “particles” are very similar but the “holes” are different for T₁ and T₂. From benzene to pentacene the T₁ state is largely represented by singly excited configurations, and among them, the HOMO → LUMO has the largest weight. The π → π* density is mostly centered between the C atoms so that the T₁ transition may be classified as a covalent state. On the contrary, the contributions to the T₂ state from all singly excited configurations are smaller and more balanced, which correspond to the promotion of an electron from HOMO−1 or HOMO−2 to LUMO, where the location of the electron density distribution changes in different repeat units, such as the charge-transfer state. On the other hand, the NTOs of the T₁ and T₂ transition have extremely similar electron cloud distributions with the frontier molecular orbitals (FMOs). The NTOs of the T₁ state indicate the character of the local excited state, and the T₂ state shows some characteristics of the charge-transfer state. The two excited states show different characteristics of the excited state and the orbital symmetry, thus there is a big difference in energy.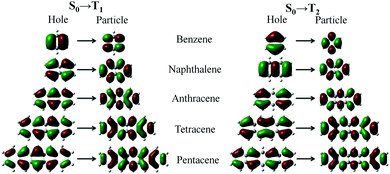

Fig. 5 Natural transition orbital (NTOs) of T1 and T2 for the acenes (benzene, naphthalene, anthracene, tetracene, and pentacene).

Since the transition of the triplet state is forbidden, we could not calculate the transition matrix, which cannot be intuitive to determine whether the transition properties will affect its energy difference. Hence, for further verification, we selected a few molecules that have large singlet energy differences, ΔE_S1–S2, and quantified the composition of these excited states.

We calculated the wave functions of the electron–hole pairs from the transition density matrix and plotted them in a two-dimensional (2D) color-filled map, which is related to the probability of finding the electron and hole in the atomic orbitals localized on each non-hydrogen atom, using the Multiwfn software 3.3.9 Revision.⁵⁵ From this map we can understand which atoms are mainly affected by the electron transition and which atom pairs are strongly coherent when the electron transits. If the effect is stronger during the transition the value is brighter in the map. The diagonal part of the map represents the LE component localized on the main backbone, whereas the off-diagonal region denotes the CT component. The map in Fig. 6 shows that the values of the S₁ and the S₂ transition have a great difference, for example, the values of the S₁ state of azulene (ΔE_S1–S2 = 1.48 eV) are only concentrated in the lower left quarter of the map in the diagonal, but the values of the S₂ state transition are distributed throughout the graph. Both the diagonal and the off-diagonal are included, which indicates that the transition of the S₁ state are LE and localized on one of the group of the azulene molecule. On the contrary, the S₂ state exhibit both CT and LE properties. The same trend is displayed for the other molecules in Fig. 6. This means that the transition properties of the S₁ state and the S₂ state are different in mechanism. It is also seen from the distribution of electron clouds of NTOs that the S₁ and S₂ states of pentacene and An-5 are the same as that of the T₁ and T₂ states, which indicates that the transitions of the T₁ and T₂ states also have different transition properties. This may also be one of the reasons that lead to the energy difference.

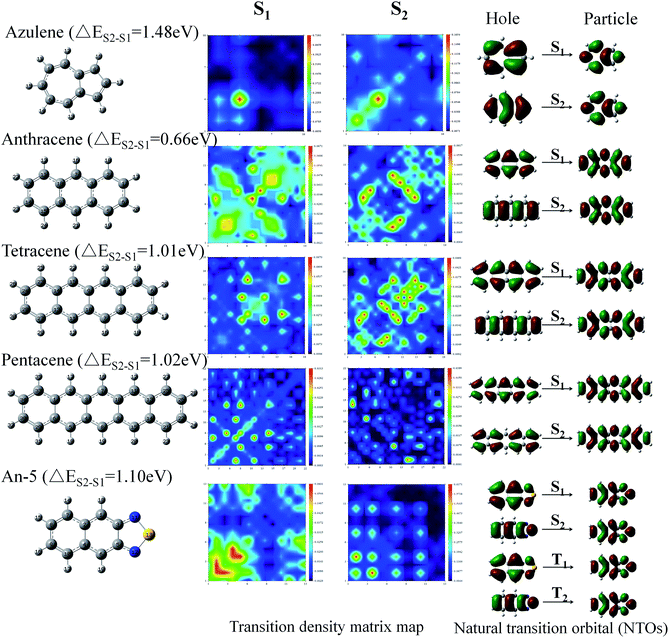Fig. 6 Transition density matrix map and the natural transition orbital (NTO) of S₁ and S₂ for some molecules (azulene, anthracene, tetracene, pentacene and An-5), that have a large ΔE_S1–S2.

4. Conclusions

The description of the triplet excited state is highly challenging for standard density functionals. Using the typical acenes molecules anthracene, tetracene and pentacene, we benchmarked the EOM-CCSD method and 2 local functionals (SVWN and PBE), 7 hybrid functionals (BLYP, B3LYP, PBE0, BMK, BHHLYP, M06-2X and M06HF), and two long-range-corrected functional CAM-B3LYP and ωB97X of the DFT method in combination with the 6-31+G(d,p) basis sets in the framework of the simulation of the triplet excited state properties. The overall results suggest that the ωB97X functional is the closest to the experimental values. On the basis of calculating the transition energy of the excited state accurately, we find that the ΔE_T1–T2 of the acenes molecules has a certain trend and anthracene has the largest. We further studied the triplet transition molecular orbital and excited state properties of the acene molecules. The results show that the symmetry of the transition molecular orbital and the excited state properties are very different in the molecule with a relatively large energy gap. This finding will provide an approach for the design of adjustable energy molecules and provide a reference for the application of energy levels of triplet excited states in the future.

Acknowledgements

We are grateful for financial support from National Science Foundation of China (grant number 51603127, 91233113, 51273078, 51473063, 51203091) and National Basic Research Program of China (973 Program grant number 2013CB834705, 2013CB834801, 2015CB655003).

References

1. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14.
2. M. Damm, F. Deckert, H. Hippler and J. Troe, J. Phys. Chem., 1991, 95, 2005.
3. P. Foggi, F. V. R. Neuwahl, L. Moroni and P. R. Salvi, J. Phys. Chem. A, 2003, 107, 1689.
4. W. J. Li, D. D. Liu, F. Z. Shen, D. G. Ma, Z. M. Wang, Y. Xu, B. Yang, Y. G. Ma and T. Feng, Adv. Funct. Mater., 2012, 22, 2797.
5. W. J. Li, Y. Y. Pan, R. Xiao, Q. M. Peng, S. T. Zhang, D. G. Ma, F. Li, F. Z. Shen, Y. H. Wang, B. Yang and Y. G. Ma, Adv. Funct. Mater., 2014, 24, 1609.
6. S. Tang, W. J. Li, F. Z. Shen, D. D. Liu, B. Yang and Y. G. Ma, J. Mater. Chem., 2012, 22, 4401.
7. S. T. Zhang, W. J. Li, L. Yao, Y. Y. Pan, B. Yang, Y. G. Ma, F. Shen and R. Xiao, Chem. Commun., 2013, 49, 11302.
8. L. Yao, S. T. Zhang, R. Wang, W. J. Li, F. Z. Shen, B. Yang and Y. G. Ma, Angew. Chem., 2014, 126, 2151.
9. Y. Y. Pan, W. J. Li, S. T. Zhang, L. Yao, C. Gu, H. Xu, B. Yang and Y. G. Ma, Adv. Opt. Mater., 2014, 2, 510.
10. W. J. Li, Y. Y. Pan, L. Yao, H. C. Liu, S. T. Zhang, C. Wang, F. Z. Shen, B. Yang, Y. G. Ma and P. Lu, Adv. Opt. Mater., 2014, 2, 892–901.
11. Y. C. Luo and H. Aziz, Adv. Funct. Mater., 2010, 20, 1285.
12. C. E. Swenberg and N. E. Geacintov, Org. Mol. Photophys., 1973, 18, 489.
13. M. Pope and C. E. Swenberg, Electronic Processes in Organic Crystals and Polymers, Oxford University Press, Oxford, U.K., 2nd edn, 1999, p. 134.
14. M. Smith and J. Michl, Chem. Rev., 2010, 110, 6891.
15. T. Zeng, R. Hoffmann and N. Ananth, J. Am. Chem. Soc., 2014, 136, 5755.
16. S. F. Nelson, Y. Y. Lin, D. J. Gundlach and T. N. Jackson, Appl. Phys. Lett., 1998, 72, 1854.
17. A. Skotheim and J. E. Reynolds, Conjugated Polymers: Theory, Synthesis, Properties, and Characterization, CRC Press, 2006.
18. K. Müllen and G. Wegner, Electronic Materials: The Oligomer Approach, Wiley-VCH, 1998.
19. J. H. Burroughes, D. D. C. Bradeley, A. R. Brown, R. N. Marks, K. Machay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539.
20. M. Berggren, O. Inganas, J. Rasmusson, G. Gustafsson, M. R. Andersson, O. Wennerstrom and T. Hjertberg, Nature, 1994, 372, 444.
21. T. Dobbertin, M. Kroeger, D. Heithecker, D. Schneider, D. Metzdorf, H. Neuner, E. Becker, H.-H. Johannes and W. Kowalsky, Appl. Phys. Lett., 2003, 82, 284.
22. G. N. Lewis and M. Kasha, J. Am. Chem. Soc., 1994, 66, 2100.
23. D. S. McClure, J. Chem. Phys., 1949, 17, 905.
24. H. Hunziker, Chem. Phys. Lett., 1969, 3, 504.
25. H. E. Hunziker, J. Chem. Phys., 1972, 56, 400.
26. Y. H. Meyer, R. Astier and J. M. Leclercq, J. Chem. Phys., 1972, 56, 801.
27. S. P. McGlynn, T. Azumi and M. Kasha, J. Chem. Phys., 1964, 40, 507.
28. T. G. Pavlopoulos, J. Chem. Phys., 1972, 56, 227.
29. J. Burgos, M. Pope, C. E. Swenberg and R. R. Alfano, Phys. Status Solidi B, 1977, 83, 249.
30. C. Hellner, L. Lindqvist and P. C. Roberge, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 1928.
31. H. Angliker, E. Rommel and J. Wirz, Chem. Phys. Lett., 1982, 87, 208.
32. G. E. Scuseria and H. F. Schaefer III, J. Chem. Phys., 1989, 90, 3700.
33. Y. Y. Pan, J. Huang, S. T. Zhang, D. W. Yu, B. Yang and Y. G. Ma, RSC Adv., 2016, 6, 108404.
34. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439.
35. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218.
36. C. Van Caillie and R. D. Amos, Chem. Phys. Lett., 1999, 308, 249.
37. C. Van Caillie and R. D. Amos, Chem. Phys. Lett., 2000, 317, 159.
38. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433.
39. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
41. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
42. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
43. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
44. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405.
45. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
46. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
47. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126.
48. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51.
49. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
50. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223.
51. H. Chakraborty and A. Shuklab, J. Chem. Phys., 2014, 141, 164301.
52. Y. Y. Pan, J. Huang, Z. M. Wang, D. W. Yu, B. Yang and Y. G. Ma, RSC Adv., 2017, 7, 19576.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.1, Gaussian, Inc., Wallingford CT, 2009.
54. R. L. Martin, J. Chem. Phys., 2003, 118, 477.
55. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.

---