Open Access Article
Open Access ArticleCarbonic acid monoethyl ester as a pure solid and its conformational isomerism in the gas-phase
Jürgen Bernardab,
Eva-Maria Köck ab,
Roland G. Huber†
c,
Klaus R. Liedlc,
Ludwig Calld,
Robert Schlöglb,
Hinrich Grothe
ab,
Roland G. Huber†
c,
Klaus R. Liedlc,
Ludwig Calld,
Robert Schlöglb,
Hinrich Grothe e and
Thomas Loerting
e and
Thomas Loerting *a
*a
aInstitute of Physical Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria. E-mail: thomas.loerting@uibk.ac.at
bMax-Planck-Institut für chemische Energiekonversion, D-45470 Mülheim an der Ruhr, Germany
cInstitute of General, Inorganic and Theoretical Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria
dInstitute of Organic Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria
eInstitute of Materials Chemistry, TU Wien, A-1060 Vienna, Austria
First published on 21st April 2017
Abstract
The monoesters of carbonic acid are deemed to be unstable and decompose to alcohol and carbon dioxide. In spite of this, we here report the isolation of the elusive carbonic acid monoethyl ester (CAEE) as a pure solid from ethanolic solutions of potassium bicarbonate. The hemiester is surprisingly stable in acidic solution and does not experience hydrolysis to carbonic acid. Furthermore, it is also stable in the gas phase, which we demonstrate by subliming the hemiester without decomposition. This could not be achieved in the past for any hemiester of carbonic acid. In the gas phase the hemiester experiences conformational isomerism at 210 K. Interestingly, the thermodynamically favored conformation is only reached for the torsional movement of the terminal ethyl group, but not the terminal hydrogen atom on the millisecond time scale. Accordingly, IR spectra of the gas phase trapped in an argon matrix are best explained on the basis of a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of monomeric conformers. Our findings necessitate reevaluation of claims of the formation of a carbonic acid polymorph in methanolic solution, which is the subject of a forthcoming publication.
1 mixture of monomeric conformers. Our findings necessitate reevaluation of claims of the formation of a carbonic acid polymorph in methanolic solution, which is the subject of a forthcoming publication.
Introduction
Carbonic acid monoalkyl esters are elusive molecules. The organic chemistry textbook Houben–Weyl reads as “The monoesters of carbonic acid, known as hemicarbonic acids, are formed by the reaction of alcohols with carbon dioxide. They are unstable and undergo decomposition to alcohols and carbon dioxide. Hemicarbonic acids can be isolated as salts, or mixed anhydrides with carboxylic acids. Upon esterification with another molecule of a hydroxyl compound, hemicarbonic acids form stable organic carbonates”.1 In solution, carbonic acid monoalkyl esters represent important intermediates in the reactions of carbon dioxide with alcohols finally resulting in dialkyl carbonates,2–6 e.g., the simplest organic carbonate dimethyl carbonate. Rossi et al. recently showed evidence that carbonated alcoholic beverages such as beer, sparkling wine, whisky soda or rum cola contain carbonic acid monoethyl ester (CAEE) in millimolar concentration.7 Dibenedetto et al. have shown that carbonic acid monomethyl ester (CAME) is stable at 300 K in solution long enough so that its 1H and 13C NMR spectra can be recorded.8 Reisenauer et al. were able to produce CAME together with isobutene in the gas phase by pyrolysis of tert-butyl methyl carbonate and characterized it by IR spectroscopy after trapping in noble gas matrices at 8 K.9 Furthermore, carbonic acid monoalkyl esters might also serve as intermediates in attempts of utilizing carbon dioxide as a synthetic building block, removing it in this way from the atmosphere in the context of greenhouse warming.While the occurrence in solution as intermediates seems to be established now, isolation of carbonic acid monoalkyl esters in pure solid form has remained a challenge. In their review Shaikh and Sivaram specify that “Hemicarbonic acid can only be isolated as salts (with inorganic metal such as sodium and potassium), simple anhydrides, or mixed anhydrides with carboxylic acids.”.10 We want to emphasize that the term “hemicarbonic acid” is a short, but incorrect form of what should be named more precisely “hemiesters of carbonic acid”. Furthermore we want to emphasize that there is in fact one single report of a successful isolation of a pure hemiester of carbonic acid, namely CAME (HO2COCH3) by Behrendt et al. in the 1970s.11,12 This was achieved via synthesis of alkali metal monoalkyl carbonates M[O2COR],13 following the protocol of Dumas and Peligot established in 1840.14 The protonated form could then be formed by interaction between a suspension of the salt Na[O2COCH3] in dimethyl ether and a solution of HCl in dimethyl ether under cryoconditions, namely at 223 K.11,12 After distilling off dimethyl ether at 193 K, CAME could be isolated as a pure, colourless solid of melting point 237 K. Its IR spectrum and acid dissociation constant pKa were also determined by Behrendt et al.11,12 The IR spectrum led them to conclude that CAME exists as a monomer. Furthermore it is instable in contact with water, so the technique for its formation requires protonation in non-aqueous solution.
To the best of our knowledge, no hemiesters of carbonic acids other than CAME could be isolated so far, neither in the gas phase nor as a pure solid. In this study we demonstrate that CAEE (HO2COC2H5) can be prepared as a pure solid using a cryotechnique and characterized by FT-IR spectroscopy, and furthermore that this solid evaporates without decomposition at 210 K by trapping the vapor above the solid in an argon matrix at 6 K.
Experimental
Isolation of the ethyl hemiester as a solid
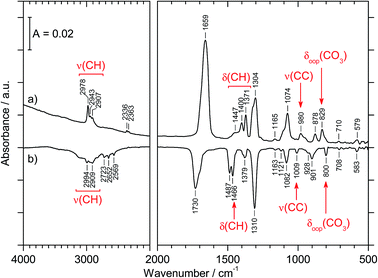
The preparation of CAEE was done from an ethanolic solution of potassium bicarbonate (KHCO3, Sigma Aldrich, >99.5%). Alkali bicarbonates and carbonates are barely soluble in ethanol. 0.25 g KHCO3 were suspended in 10 ml C2H5OH (AustrAlco; ethanol absolute for analysis 99.8%). The solution was stirred and heated to 321 K for several hours, but still only a small fraction of the salt dissolves in ethanol. The suspended particles were sedimented and about 3 ml of the solution were nebulized in N2 carrier gas by means of an air brush pistol (Harder & Steenbeck; model grafo or infinity). The droplets of diameter ø ≈ 10 μm produced in this way were precooled to 0 °C and introduced into a vacuum chamber through an aperture (ø = 500 μm).15,16 Behind the aperture the pressure difference between ambient and the vacuum chamber causes the droplets to form a cone and to travel at ultrasonic speed. These droplets are then splat-cooled at a cryoplate kept at 78 K, producing a layer of a few hundred micrometers in thickness after a few minutes. Upon impact of the aerosol on a cryoplate at liquid nitrogen temperature (T = 78 K) layers of glassy solution are formed. There is no significant evaporation of the droplets under such conditions.15,16 IR transparent windows (cesium iodide, CsI, or silicon, Si) serve as the cryoplate.15,16 The solution droplets are immobilized almost instantaneously at cooling rates up to 107 K s−1, which is known as hyperquenching.17,18 The hyperquenching chamber was pumped to a base pressure of 10−6 mbar, using an oil-free scroll pump (Varian Triscroll) and a turbomolecular pump (Leybold Turbovac 361). To keep the pressure after the injection of the solutions in nitrogen as carrier gas low, a cryopump (Leybold RW 6000 compressor unit and RGD 1245 cold head) is located inside the vacuum chamber and kept at 11 K. At this temperature the carrier gas condenses as a solid on the cryopump.After deposition of the glassy bicarbonate solution layers the cryoplate was heated in vacuo to 290 K, which results in evaporation of the solvent and a solid precipitate remaining on the cryoplate. This step of evaporating the solvent from the dissolved salt was not part of the technique employed by Hage, Hallbrucker and Mayer for preparing carbonic acid polymorphs from either aqueous or methanolic solution.15,16 Thus, comparison of our results with the results obtained by them is only possible to a limited extent. Upon dissolving in ethanol the bicarbonate may transform to the monoethyl carbonate, and upon evaporating ethanol the reaction may be reversed to form the bicarbonate again. The IR spectrum of the precipitate shown in Fig. 1a provides evidence for the precipitate to be the monoethyl carbonate. Bands indicating presence of the ethyl group are marked in red. That is, by evaporating the solvent at cryoconditions the back-reaction to bicarbonate is much slower than the evaporation of the solvent, i.e., the reaction product is kinetically controlled. This precipitate was treated with 1.5 M aqueous HCl at 180 K to afford CAEE, first in solution and after heating and removal of water as a pure solid. The reaction progress was monitored in situ by FT-IR spectroscopy using a Varian Excalibur 3100, in which the beam of light passes through optical discs (KBr) into the vacuum chamber, through the thin film sample and out of the vacuum chamber to the detector. FT-IR spectra were recorded with a resolution of 4 cm−1 and by accumulating 100 scans. Fig. 1b shows the IR spectrum of the solid assigned to be CAEE.
Sublimation and matrix isolation of the ethyl hemiester
After preparation of the pure solid in the laboratory in Innsbruck we removed it from the vacuum chamber, immersed the sample on the cryoplate in liquid nitrogen and carried it to Vienna for matrix isolation. Matrix isolation spectroscopy is a technique aimed to obtain pure vibrational spectra at low temperatures isolating non-rotating single molecules by trapping them in an IR transparent and inert solid matrix, namely argon. Our matrix isolation study was done in the ultrahigh-vacuum chamber in Vienna, which was previously employed for successfully isolating reactive species such as halogen oxides19 or carbonic acid.20 FT-IR spectra were recorded using a Bruker Vertex 80v which offers an evacuated optical path (2 mbar) and a resolution of 0.2 cm−1 at which 1024 scans were accumulated. The details of the matrix isolation procedure can be found in ref. 21. The ratio of isolated molecules to argon atoms is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000. This ratio of the isolated species has been roughly estimated by measuring the partial pressure above the solid sample (which is on the order of 10−8 mbar at 210 K) and the partial pressure of argon entering the vacuum system through a capillary (which is about 1–2 10−5 mbar). For comparison, the partial pressure of pure carbonic acid at higher temperature (250 K) was estimated to be 10−7 mbar.20 At 210 K and at such low pressure the mean free path between gas–gas collisions is on the order of meters, i.e., much longer than the distance between the thin film and the mirror, i.e., there is a molecular flow from the surface to the mirror. We use matrix isolation spectroscopy (rather than mass-spectrometry) to identify the species we have obtained and to assess purity, especially to assess whether or not carbonic acid is present. Just like for mass-spectrometric techniques evaporation of the solid is required for matrix isolation spectroscopy. However, ionization and ionization-induced fragmentation are not an issue in the matrix isolation technique since the neutral molecules are landed in the matrix, by contrast to mass-spectrometric techniques. In other words, since carbonic acid and carbonic acid esters very readily fragment in mass-spectrometric experiments unfragmented parent ions can barely be observed. Thus, both of them show fragments at the same m/z ratio, and this technique is not suitable for discriminating between CAEE and carbonic acid. Also the presence or absence of the ethyl group cannot be reliably used to discriminate between the two since traces of ethanol may be present in carbonic acid, e.g., as inclusion. By contrast, the vibrational bands are shifted between the two molecules, and so matrix isolation spectroscopy is the better analytic technique to assess the purity of the sample. X-ray diffraction would in principle be suitable as well. However, the thin film nature of the samples and their in situ formation in a vacuum chamber do not allow for a ready investigation by diffraction.
1000. This ratio of the isolated species has been roughly estimated by measuring the partial pressure above the solid sample (which is on the order of 10−8 mbar at 210 K) and the partial pressure of argon entering the vacuum system through a capillary (which is about 1–2 10−5 mbar). For comparison, the partial pressure of pure carbonic acid at higher temperature (250 K) was estimated to be 10−7 mbar.20 At 210 K and at such low pressure the mean free path between gas–gas collisions is on the order of meters, i.e., much longer than the distance between the thin film and the mirror, i.e., there is a molecular flow from the surface to the mirror. We use matrix isolation spectroscopy (rather than mass-spectrometry) to identify the species we have obtained and to assess purity, especially to assess whether or not carbonic acid is present. Just like for mass-spectrometric techniques evaporation of the solid is required for matrix isolation spectroscopy. However, ionization and ionization-induced fragmentation are not an issue in the matrix isolation technique since the neutral molecules are landed in the matrix, by contrast to mass-spectrometric techniques. In other words, since carbonic acid and carbonic acid esters very readily fragment in mass-spectrometric experiments unfragmented parent ions can barely be observed. Thus, both of them show fragments at the same m/z ratio, and this technique is not suitable for discriminating between CAEE and carbonic acid. Also the presence or absence of the ethyl group cannot be reliably used to discriminate between the two since traces of ethanol may be present in carbonic acid, e.g., as inclusion. By contrast, the vibrational bands are shifted between the two molecules, and so matrix isolation spectroscopy is the better analytic technique to assess the purity of the sample. X-ray diffraction would in principle be suitable as well. However, the thin film nature of the samples and their in situ formation in a vacuum chamber do not allow for a ready investigation by diffraction.
Calculations: isomer stability, frequencies and isomerization barriers
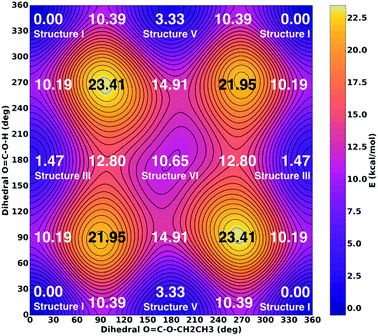
Ab initio quantum mechanical calculations of six different conformers of CAEE were performed to obtain reference frequencies for annotating measured spectra. Relaxed potential energy surfaces (PES) and vibrational frequencies and zero-point energies for conformational isomerism were calculated using the Gaussian 09 package.22 All calculations were performed using second-order Møller–Plesset perturbation theory (MP2) with the augmented correlation consistent basis sets of Dunning and co-workers.23–25 Initial optimization was done at the MP2/aug-cc-pVDZ level of theory requiring ‘verytight’ convergence on displacement and forces. Starting from the resulting geometry, further optimization at the MP2/aug-cc-pVTZ level of theory using ‘verytight’ convergence criteria yielded an energy minimum for frequency calculations. Subsequently, normal modes and IR intensities were determined at this minimum geometry using MP2/aug-cc-pVTZ and used to identify the various signals observed in the experimentally obtained spectra. Vibrational spectra were scaled by the factor of 0.98 to obtain the best match. According to the “Computational Chemistry Comparison and Benchmark DataBase” the best scaling factor to be used for vibrations calculated using MP2/aug-cc-pVTZ is 0.953 ± 0.033 as determined from a comparison of 358 vibrations in 117 molecules.26A two-dimensional relaxed PES scan was performed around the torsions A:4-3-2-1 and B:4-3-5-6 simultaneously (see Fig. 5). Torsion A was sampled for 345 degrees in 15 degree intervals and torsion B was sampled from 0 to 180 degrees in 15 degree intervals for a total of 312 points. Torsions A and B were frozen at each point and a geometry optimization at the MP2/aug-cc-pVTZ level was performed. The resulting energies were plotted as a two-dimensional map and the key minima, maxima and saddle points were labeled with their respective energies (Fig. 6). In contrast with Fig. 5, PES energies do not include zero-point corrections as this would require a frequency calculation at each point. The ethyl torsion 3-5-6-9 was unrestrained for the PES scan.
Zero-point energies were calculated, but did not significantly alter the energy landscape without entertaining a zero-point energy correction. Specifically, the zero-point energy correction does not change the stabilities by more than ±0.1 kcal mol−1.
Results
Our approach of preparing CAEE starts from KHCO3 in ethanolic solution and involves evaporation of the solvent at cryo-conditions followed by treatment with a protonating agent. Our initial aim for this study was to try whether or not protonation of bicarbonates and formation of carbonic acid (H2CO3) is possible in ethanolic solution by using a technique that is similar to the one employed by Hage, Hallbrucker and Mayer for isolation of carbonic acid in aqueous solution.15,16 Thus, one key question associated with the present work is whether or not carbonic acid (H2CO3) is the product of our cryo-reaction. Whether or not carbonic acid is indeed produced hinges on the question about the reactivity of carbonic acid hemiesters at cryoconditions. Most notably, do they experience acid-catalyzed hydrolysis to form carbonic acid or are they stable against hydrolysis? We do find they are much more stable than expected against hydrolysis. In fact, we do not find any traces of carbonic acid in our product, but pure CAEE, both in the solid and the gaseous state. That is, the surprising stability of the hemiester has prevented our initial aim of preparing another carbonic acid polymorph.The formation of CAEE was effected from an ethanolic solution of potassium bicarbonate (KHCO3, Sigma Aldrich, >99.5%). Subsequent sample preparation/isolation was performed with a hyperquenching method directly in the cryo-FT-IR vacuum chamber (more details see in the Experimental section). Residual solvent was evaporated and pumped off inside the chamber, which results in the pure solid of first the salt of CAEE and second – after protonation – the hemiester itself. With the cryo-FT-IR setup we can directly control this preparation procedure. In addition the resulting solid can be transferred to another laboratory, which we did to gather high resolution IR-spectra of single molecules trapped in an inert matrix.
We obtain CAEE purely in both the solid and the gaseous state since we are able to sublime the solid without appreciable decomposition at cryoconditions in the vacuum. CAEE was previously neither known in crystalline form nor as gas phase species. For CAME either the solid state11,12 or the gaseous state (in a mixture with isobutene)9 were accessible. Thus, no inferences about their stability and phase transitions could be made, which we now establish in our manuscript. This provides us with the unique opportunity to investigate the conformational isomerism of this molecule at low temperatures, close to the ground state. So far, the knowledge about conformational isomerism in carbonic acid hemiesters is solely based on the high-temperature pyrolysis experiment by Reisenauer et al., who have established two conformational isomers for CAME in the gas-phase at a pyrolysis temperature of about 1000 K.9
Isolation of the ethyl hemiester as a solid
| Lit.13 | Expt., Fig. 1a | Assign.13 |
|---|---|---|
| a vw, very weak; w, weak; m, medium, s, strong; vs, very strong; sh, shoulder, νs and νas, symmetric and asymmetric stretching mode; δs and δas, symmetric and asymmetric bending in-plane; δoop, out of plane bending mode; ω, wagging mode. | ||
| 2967 (s); 2907 (m) | 2978 (m); 2943 (w); 2907 (w) | ν(CH) |
| 1689 (s) | 1659 (vs) | νas(CO2) |
| 1484 (w); 1445 (w); 1389 (m); 1370 (s) | 1447 (sh); 1400 (m); 1371 (m) | δ(CH) |
| 1295 (s) | 1304 (s) | νs(CO2) |
| 1274 (m) | δs(CH3) | |
| 1172 (w); 1114 (m); 1075 (sh) | 1165 (vw) | ν(CO) |
| 1059 (s) | 1074 (s) | ν(CO) |
| 966 (s) | 980 (m) | ν(CC) |
| 876 (s) | 878 (m) | ω(CH2) |
| 821 (s); 812 (w) | 829 (m) | δoop(CO3) |
| 701 (w) | 710 (vw) | δas(CO2) |
| 584 (w) | 579 (w) | δs(CO2) |
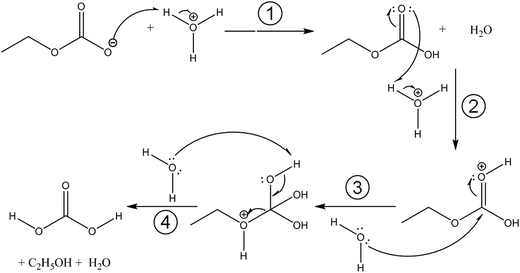
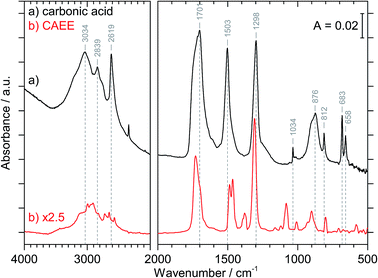
Fig. 3 compares the spectra of the new species (bottom red trace, rescaled from Fig. 1b) obtained here with β-H2CO3 (top black trace) as taken from literature,27 and Table 2 presents assignments to CAEE. Apparently, the new species obtained in the present work shows more IR active bands than β-H2CO3. Thus, some bands cannot satisfactorily be explained on the basis of a pure solid of carbonic acid H2CO3. In particular, there is no explanation for the bands at 1466, 1310, 1163, 1121 and 1009 cm−1 if one assumed the new solid species to be a polymorph of carbonic acid, in analogy to the assignments done earlier by Hage, Hallbrucker and Mayer.16,28 However, assuming the new species to be CAEE (HO2COC2H5), these frequencies can easily be explained on the basis of stretching and deformation modes of the ethyl group. On this basis, the band at 1466 cm−1 is assigned to δ(CH), at 1310 cm−1 to δs(CH3) and at 1009 cm−1 to ν(CC), cf. Table 2. The band at 1163 cm−1 and 1121 cm−1 can be assigned as ν(CO) modes of the ethyl ester. Also the bands at 2994 and 2909 cm−1 can be explained as CH-stretching modes rather than as combination bands. This implies that only the protonation (step 1 in Fig. 2), but not the hydrolysis of the hemiester (steps 2–4 in Fig. 2) take place at cryoconditions in acidic solution.
| β-H2CO3 | CAEE | CAEE |
|---|---|---|
| Lit.28 | Expt., Fig. 1b | Assign. |
| a νs and νas, symmetric and asymmetric stretching mode; δip and δoop, in-plane and out-of-plane bending mode. | ||
| 3030 | 2994 | ν(CH) |
| 2969 | 2909 | ν(CH) or 2 × νas[EtOCOH] |
| 2830 | 2723 | νas[EtOCOH] + δip(COH) or 2 × νas[EtOCOH] + 2 × δip(CO3) |
| 2652 | ||
| 2613 | 2569 | 2 × δip(COH) |
| 1698 | 1730 | ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
| 1504 | 1487 | νas[EtOCOH] |
| 1466 | δ(CH) | |
| 1302 | 1379 | δip(COH) |
| 1310 | δs(CH3) | |
| 1163; 1121 | ν(CO) | |
| 1038 | 1082 | νs[EtOCOH] |
| 1009 | ν(CC) | |
| 910; 881 | 928; 901 | δoop(COH) |
| 813 | 800 | δoop(CO3) |
| 686; 664 | 583 | δip(CO3) |
The crystal structure of the new species CAEE is not known, and could also not be determined in this work because the thin film geometry did not allow for a good quality X-ray diffractogram to be recorded. Hence, the intermolecular coupling between individual molecules is not entirely clear, and unexpected shifts of bands could occur, e.g., if CAEE formed dimers in the solid state. For this reason the assignment of the unexplained bands in Table 2 to the vibrational modes of the ethoxy-group does not represent a rigorous proof of the isolated solid to be CAEE. The comparison merely shows that the assignment is more complete and better than based on solid carbonic acid. One way of improving the reliability of assignments would be isotope substitution, e.g., repeating the experiment using deuterated or 13C reagents. However, the low solubility of bicarbonates in ethanol and the rather large amount of solvent required to form a thin film solid did not allow us to successfully repeat the experiment using ethanol isotopically labeled at the ethyl group (e.g., ethanol-d2) as the solvent.
In order to sort out the question of the nature of the new solid species we rely on matrix isolation, i.e., we evaporated the solid and investigated the gas phase above by trapping it in a frozen noble gas matrix. Since IR spectroscopy of this matrix is a highly sensitive technique it allows us to carefully assess the nature, including conformational isomerism, and purity of our products.
Matrix isolation of the vapor above the solid
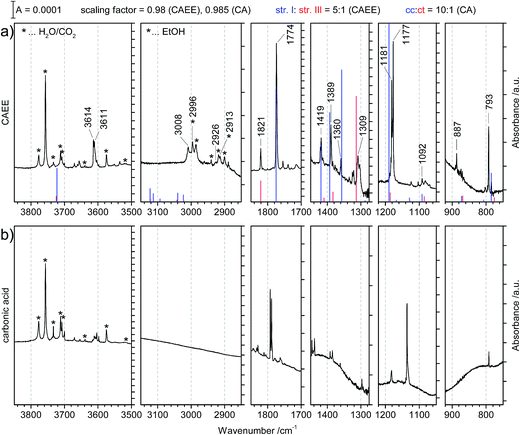 | ||
Fig. 4 (a) Matrix isolation spectrum of the new species CAEE in argon matrix. The calculated line spectrum assuming a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of structures I and III from Fig. 5 is indicated in color. Labelled bands are assigned to CAEE. Bands marked with stars correspond to decomposition products, namely water, carbon dioxide and ethanol. These match literature data of individual molecules isolated in argon matrix to better than ±0.5 cm−1 (see ref. 20 and 29). (b) Matrix isolation spectrum of carbonic acid in argon matrix as taken from our published data, augmented with spectral ranges previously not shown.20 1 mixture of structures I and III from Fig. 5 is indicated in color. Labelled bands are assigned to CAEE. Bands marked with stars correspond to decomposition products, namely water, carbon dioxide and ethanol. These match literature data of individual molecules isolated in argon matrix to better than ±0.5 cm−1 (see ref. 20 and 29). (b) Matrix isolation spectrum of carbonic acid in argon matrix as taken from our published data, augmented with spectral ranges previously not shown.20 | ||
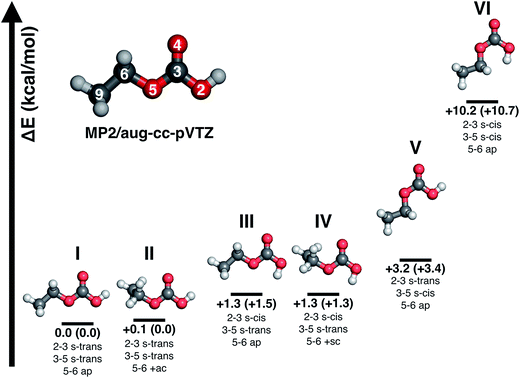
Major differences between the two sets of spectra are found for the C–H stretching region, which is featureless for carbonic acid, but which contains several bands for CAEE. This region is complicated by the presence of anti- and gauche-ethanol in the matrix,29 which reflects either unreacted ethanol or ethanol as decomposition product from CAEE. Ethanol bands are marked by stars, and some of them overlap with the bands assigned to the ethoxy group of CAEE. However, the four most intense bands of the most stable isomer (structure I in Fig. 5) can be identified, and are labelled in Fig. 4a. Even though the scaled calculated frequencies do not match the experimental observations, the calculated shifts between the four individual bands are exactly reproduced in the experiment, i.e., the pattern matches. It is also clear that the labelled bands for the other spectral regions (Fig. 4a) do not coincide with carbonic acid bands (Fig. 4b) observed in the matrix isolation experiment, e.g., the most intense band is shifted by about +50 cm−1 to 1177 cm−1, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band by −18 cm−1 to 1774 cm−1. These shifts are so large that carbonic acid monomers cannot account for the observations. Similarly, the carbonic acid dimer20 is not suitable at all to explain the bands. Our suggestion of CAEE to explain the observations is based on a comparison with calculated bands for the six isomers shown in Fig. 5, which are energy minima in gas phase calculations at MP2/aug-cc-pVTZ level of theory.
O stretching band by −18 cm−1 to 1774 cm−1. These shifts are so large that carbonic acid monomers cannot account for the observations. Similarly, the carbonic acid dimer20 is not suitable at all to explain the bands. Our suggestion of CAEE to explain the observations is based on a comparison with calculated bands for the six isomers shown in Fig. 5, which are energy minima in gas phase calculations at MP2/aug-cc-pVTZ level of theory.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety as a substitutent are named in analogy to the nomenclature of 1,3-butadiene using the descriptors s-cis and s-trans,30,31 whereas the conformation around the single bond 5–6 is named in accordance with Klyne-Prelog stereo-nomenclature, where ap indicates antiperiplanar, +sc clockwise synclinal and +ac clockwise anticlinal.32 Five conformational isomers are within only 4 kcal mol−1 so that they are realistic candidates to be found in the gas phase. The most stable one is characterized by a weak internal hydrogen bond between the terminal OH and C
O moiety as a substitutent are named in analogy to the nomenclature of 1,3-butadiene using the descriptors s-cis and s-trans,30,31 whereas the conformation around the single bond 5–6 is named in accordance with Klyne-Prelog stereo-nomenclature, where ap indicates antiperiplanar, +sc clockwise synclinal and +ac clockwise anticlinal.32 Five conformational isomers are within only 4 kcal mol−1 so that they are realistic candidates to be found in the gas phase. The most stable one is characterized by a weak internal hydrogen bond between the terminal OH and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, as well as a weak interaction between the CH2 group and the C
O bonds, as well as a weak interaction between the CH2 group and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, i.e., the conformation 2–3 s-trans, 3–5 s-trans and 5–6 ap. We note that all six structures do not show any symmetry elements other than the identity, i.e., all point groups are C1. Some of the structures are close to having a mirror plane (equivalent to the paper plane), but in the end the CS structures are less stable than the C1 structures.
O bond, i.e., the conformation 2–3 s-trans, 3–5 s-trans and 5–6 ap. We note that all six structures do not show any symmetry elements other than the identity, i.e., all point groups are C1. Some of the structures are close to having a mirror plane (equivalent to the paper plane), but in the end the CS structures are less stable than the C1 structures.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 mixture of isomers I and III. Table 3 presents a comparison of the observed bands in argon matrix with calculated gas phase spectra for the most stable carbonic acid monomer20 and for the six conformational isomers of CAEE shown in Fig. 5. A scaling factor of 0.98 was applied to the harmonic frequencies reported in Table 3. Applying a scaling factor of 0.96 to the unscaled frequencies reported by Reisenauer et al. on the CCSD(T)/cc-pVTZ level of theory (Table S7 in ref. 9) yields an excellent agreement between calculated spectra. Fig. 5 also contains energies relative to the most stable conformer. Numbers in brackets indicate relative energies with inclusion of zero-point energies. As expected, zero-point energies are very similar for different conformers, and so the relative energies are not significantly affected by zero-point effects.
1 mixture of isomers I and III. Table 3 presents a comparison of the observed bands in argon matrix with calculated gas phase spectra for the most stable carbonic acid monomer20 and for the six conformational isomers of CAEE shown in Fig. 5. A scaling factor of 0.98 was applied to the harmonic frequencies reported in Table 3. Applying a scaling factor of 0.96 to the unscaled frequencies reported by Reisenauer et al. on the CCSD(T)/cc-pVTZ level of theory (Table S7 in ref. 9) yields an excellent agreement between calculated spectra. Fig. 5 also contains energies relative to the most stable conformer. Numbers in brackets indicate relative energies with inclusion of zero-point energies. As expected, zero-point energies are very similar for different conformers, and so the relative energies are not significantly affected by zero-point effects.
| Cis–cis H2CO3 | HOCO2C2H5 | ||||
|---|---|---|---|---|---|
| Theo. | Assign. | Expt., Fig. 4a | Structure I | Structure II | Assign. |
| Theory | Theory | ||||
| 3726 (15) | νs(OH) | ||||
| 3725 (206) | νas(OH) | 3611 | 3722 (111) | 3722 (110) | ν(OH) |
| 1797 (516) | ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
1774 | 1775 (410) | 1773 (377) | ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
| 1438 (144) | νas(C(OH)2) | 1419 | 1419 (68) | 1413 (93) | ω(CH2), δip(COH), δs(CH3) |
| 1389 | 1394 (108) | 1389 (85) | δs(CH3), δip(COH) | ||
| 1263 (28) | δip(COH) | 1360 | 1357 (160) | 1359 (125) | ω(CH2), δip(COH) |
| 1143 (434) | ν(O–C–O) | 1181 | 1190 (537) | 1190 (514) | δip(COH) |
| 963 (19) | δ(CO3) | 887 | 872 (5) | 865 (5) | δas(CH3), δip(COC) |
| 786 (41) | δoop(COH) | 793 | 785 (26) | 785 (25) | δoop(CO3), r(CH2) |
| HOCO2C2H5 | |||||
|---|---|---|---|---|---|
| Expt., Fig. 4a | Structure III | Structure IV | Structure V | Structure VI | Assign. |
| Theory | Theory | Theory | Theory | ||
| 3614 | 3724 (88) | 3722 (93) | 3722 (107) | 3752 (69) | ν(OH) |
| 1821 | 1821 (376) | 1819 (343) | 1800 (626) | 1831 (567) | ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
| 1414 | 1410 (22) | 1402 (21) | 1409 (8) | 1404 (11) | ω(CH2), δip(COH), δs(CH3) |
| 1384 | 1383 (57) | 1381 (53) | 1388 (52) | 1382 (11) | δs(CH3), δip(COH) |
| 1309 | 1312 (639) | 1320 (281); 1311 (334) | 1346 (204) | 1297 (532) | ω(CH2), δip(COH) |
| 1177 | 1185 (121) | 1185 (114) | 1172 (317) | 1171 (56) | δip(COH) |
| 868 (26) | 862 (29) | 848 (1) | 845 (7) | δas(CH3), δip(COC) | |
| 784 | 775 (18) | 775 (8) | 774 (30) | 762 (15) | δoop(CO3), r(CH2) |
Comparison of the new spectrum (Fig. 4a) with calculated frequencies and intensities yields the same result as the comparison between the two experimental spectra in Fig. 4 does. It becomes immediately clear that carbonic acid does not satisfactorily explain the observed matrix spectrum. The matrix isolation spectrum of a mixture of carbonic acid monomers and the cyclic dimer was reported in ref. 20. None of the carbonic acid monomeric conformers nor the dimer explain the spectrum in Fig. 4a. Most notably, the rather strong band at 1389 cm−1 cannot be explained, the band at 1360 cm−1 can only be matched if a shift of about 100 cm−1 is accepted. Similarly, the weak band at 887 cm−1 cannot be explained unless a shift of 75 cm−1 is accepted. The calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration is also shifted by about 25 cm−1, whereas in earlier work we found agreement between calculated gas phase and measured matrix bands of better than 5 cm−1.20
O stretching vibration is also shifted by about 25 cm−1, whereas in earlier work we found agreement between calculated gas phase and measured matrix bands of better than 5 cm−1.20
By contrast to carbonic acid, there is an excellent match for the CAEE conformers shown in Fig. 5. In terms of calculated IR spectra structures I and II are very similar (see Table 3) so that it seems out of practical reach to distinguish them experimentally. Furthermore, also structures III and IV show practically identical IR spectra, so that they also cannot be distinguished in experiments. We do not find evidence for structures V and VI in the matrix spectrum (see Fig. 4a). This is expected for structure VI because it is disfavored by 10.2 kcal mol−1. The best match between observed and calculated spectrum is found by assuming a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of structures I/II and III/IV. The matching is demonstrated in Fig. 4a by showing the calculated line spectrum of such a mixture. In the frequency range up to 1800 cm−1 the calculated band positions and intensities match in an excellent way with the observed bands. Above 2900 cm−1 the frequency scaling does not reproduce exact band positions especially since hydrogen bonding is involved, as known from many previous studies about frequency scaling. However, the calculated patterns still show a good match. In particular there is an excellent match between calculated band splitting and experimentally observed splitting. However, this region is also affected by water and ethanol in the matrix.
1 mixture of structures I/II and III/IV. The matching is demonstrated in Fig. 4a by showing the calculated line spectrum of such a mixture. In the frequency range up to 1800 cm−1 the calculated band positions and intensities match in an excellent way with the observed bands. Above 2900 cm−1 the frequency scaling does not reproduce exact band positions especially since hydrogen bonding is involved, as known from many previous studies about frequency scaling. However, the calculated patterns still show a good match. In particular there is an excellent match between calculated band splitting and experimentally observed splitting. However, this region is also affected by water and ethanol in the matrix.
To make the case for the 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, Table 3 is split in two parts, where the top part lists the matrix bands assigned to structure I/II and the bottom part lists the bands assigned to structures III/IV. As explained below, this reproduces the measured spectrum in an excellent way.
1 mixture, Table 3 is split in two parts, where the top part lists the matrix bands assigned to structure I/II and the bottom part lists the bands assigned to structures III/IV. As explained below, this reproduces the measured spectrum in an excellent way.
All calculated bands (see Fig. 4, lines) are actually observed in the spectrum, and all of them agree to better than 10 cm−1. The location of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band is even matched to an accuracy of 1 cm−1. The only exception is the OH-stretching band, which is well known to be overestimated.20 Furthermore, the calculated intensity pattern also matches the experimentally observed pattern well. The bands at 1774 and 1181/1177 cm−1 are the most intense ones both in calculation and in experiment, and the bands at 3614/3611, 1419 and 1389 cm−1 are about 3–7 times less intense than the former two ones. Structure I and II match the experimental spectrum well. Both of them show a weak interaction between the OH-group as well as the OC2H5-group with the C
O stretching band is even matched to an accuracy of 1 cm−1. The only exception is the OH-stretching band, which is well known to be overestimated.20 Furthermore, the calculated intensity pattern also matches the experimentally observed pattern well. The bands at 1774 and 1181/1177 cm−1 are the most intense ones both in calculation and in experiment, and the bands at 3614/3611, 1419 and 1389 cm−1 are about 3–7 times less intense than the former two ones. Structure I and II match the experimental spectrum well. Both of them show a weak interaction between the OH-group as well as the OC2H5-group with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Whereas in structure I the stabilization arises from interaction of the methylene group with the C
O bond. Whereas in structure I the stabilization arises from interaction of the methylene group with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, it is from the methyl group in structure II. The former is calculated to be imperceptibly more stable, namely by 0.1 kcal mol−1 according to MP2/aug-cc-pVTZ.
O group, it is from the methyl group in structure II. The former is calculated to be imperceptibly more stable, namely by 0.1 kcal mol−1 according to MP2/aug-cc-pVTZ.
Structures III–VI in Fig. 5 are characterized by the fact that there is only one weak intramolecular bond to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, either from the OH-terminus (structure V) or from the OC2H5-terminus (structures III and IV) or none at all (structure VI). Therefore, the latter is the least stable one, compared to structure I disfavored by 10.2 kcal mol−1. The other candidates are disfavored by only about 1.3–3.2 kcal mol−1, and therefore also likely to be observed in the vapor trapped at 210 K. Inspection of Table 3 reveals that the best marker band to discriminate the conformational isomers is the C
O group, either from the OH-terminus (structure V) or from the OC2H5-terminus (structures III and IV) or none at all (structure VI). Therefore, the latter is the least stable one, compared to structure I disfavored by 10.2 kcal mol−1. The other candidates are disfavored by only about 1.3–3.2 kcal mol−1, and therefore also likely to be observed in the vapor trapped at 210 K. Inspection of Table 3 reveals that the best marker band to discriminate the conformational isomers is the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band, which is shifted by +30 to 50 cm−1 in structures III–VI compared to structures I and II. Indeed we find a band at 1821 cm−1 of about 15–20% of the intensity of the band at 1774 cm−1. This exactly and hence best matches the position calculated for the very similar structures III and IV. In these structures there is also a shift of about −10 cm−1 compared to the band at 792 cm−1 observed in experiment and assigned here to structures I/II. Indeed a band of about 15–20% of the intensity is found at 782 cm−1, thereby suggesting that the matrix spectrum can be rationalized on the basis of a 5
O stretching band, which is shifted by +30 to 50 cm−1 in structures III–VI compared to structures I and II. Indeed we find a band at 1821 cm−1 of about 15–20% of the intensity of the band at 1774 cm−1. This exactly and hence best matches the position calculated for the very similar structures III and IV. In these structures there is also a shift of about −10 cm−1 compared to the band at 792 cm−1 observed in experiment and assigned here to structures I/II. Indeed a band of about 15–20% of the intensity is found at 782 cm−1, thereby suggesting that the matrix spectrum can be rationalized on the basis of a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of structures I/II and structures III/IV. Structure VI can be ruled out due to the absence of a band near 762 cm−1 or 1292 cm−1, structure V can be ruled out based on the absence of the relatively strong band predicted at 1346 cm−1. By contrast there are bands in the experimental spectrum near 1312 cm−1, in accordance with the idea of 15–20% of structures III/IV present in the gas phase mixture. Assuming this type of a mixture of monomeric conformers we are able to explain extremely well all bands observed experimentally both in terms of intensity and in terms of position. The only bands we do not explain are the very weak band at 1710–1760 cm−1 and the bands at 1090–1120 cm−1, which are less than 10% of the intensity of the most intense bands. Fig. 4a shows the calculated line spectrum assuming a 5
1 mixture of structures I/II and structures III/IV. Structure VI can be ruled out due to the absence of a band near 762 cm−1 or 1292 cm−1, structure V can be ruled out based on the absence of the relatively strong band predicted at 1346 cm−1. By contrast there are bands in the experimental spectrum near 1312 cm−1, in accordance with the idea of 15–20% of structures III/IV present in the gas phase mixture. Assuming this type of a mixture of monomeric conformers we are able to explain extremely well all bands observed experimentally both in terms of intensity and in terms of position. The only bands we do not explain are the very weak band at 1710–1760 cm−1 and the bands at 1090–1120 cm−1, which are less than 10% of the intensity of the most intense bands. Fig. 4a shows the calculated line spectrum assuming a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of structures I and III in the gas phase (see Fig. 5), and can be directly compared to the experimental spectrum in argon matrix. The very good agreement between the two demonstrates that we have isolated CAEE both in its pure solid form and after sublimation in Ar matrix at a purity of >99%. In the gas-phase we see evidence for a 5
1 mixture of structures I and III in the gas phase (see Fig. 5), and can be directly compared to the experimental spectrum in argon matrix. The very good agreement between the two demonstrates that we have isolated CAEE both in its pure solid form and after sublimation in Ar matrix at a purity of >99%. In the gas-phase we see evidence for a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of two conformers, but no evidence for dimers, by contrast to the case of carbonic acid.20 There is no evidence for the formation of a carbonic acid polymorph after dissolving bicarbonate in ethanolic solution, evaporating the solvent at cryo-conditions in the vacuum and protonation.
1 ratio of two conformers, but no evidence for dimers, by contrast to the case of carbonic acid.20 There is no evidence for the formation of a carbonic acid polymorph after dissolving bicarbonate in ethanolic solution, evaporating the solvent at cryo-conditions in the vacuum and protonation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. This results in a ratio of approximately 22
K. This results in a ratio of approximately 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at the sublimation temperature of 210 K. This is significantly different from the experimentally found ratio of 5
1 at the sublimation temperature of 210 K. This is significantly different from the experimentally found ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This raises the question why thermodynamic equilibrium is not attained.
1. This raises the question why thermodynamic equilibrium is not attained.In order to shed light on this question we have studied the kinetics of the isomerization process and compare the time scales for switching between isomers with the time scale the CAEE molecules spend in the gas phase. At the temperature of 210 K the velocity v of CAEE molecules can be calculated from kinetic gas theory. Using v = (2 × RT/M)1/2 and the molecular weight for CAEE (M = 90 × 10−3 kg mol−1) the most likely velocity in the Boltzmann distribution of velocities is v = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm s−1. The distance between the surface of the thin film and the mirror, on which the matrix freezes, is a few centimeters. Thus, the CAEE molecules take about 0.5 ms between desorption and landing in the matrix.
600 cm s−1. The distance between the surface of the thin film and the mirror, on which the matrix freezes, is a few centimeters. Thus, the CAEE molecules take about 0.5 ms between desorption and landing in the matrix.
The time scale for isomerization can be estimated from the potential energy landscape shown in Fig. 6. In this 2D landscape the stable structures I, III, V and VI are indicated based on two dihedral angles. Please note that structures II and IV are very close to structures I and III, respectively, but not found on this landscape because these structures are not encountered in the scans.
If a molecule desorbs from the surface it may be in an unfavorable conformational state because the crystal field might force molecules into such orientations. Thus, it is necessary to know how long it takes for them to convert to the most stable isomer. For structure V a barrier of 7.06 kcal mol−1 (see Fig. 6, 10.39–3.33 kcal mol−1) needs to be overcome in order to convert to structure I. This represents the torsional movement of the ethyl group, specifically from 3–5 s-cis to 3–5 s-trans conformation. Based on Eyring theory and the quasi-equilibrium assumption of transition state theory this barrier can be converted to a reaction rate constant k using the equation k = kBT/h × exp(−ΔG′/RT), using Planck's constant h, the Boltzmann constant kB and the barrier ΔG′. This equation assumes the absence of quantum tunneling and corner cutting effects on the rate constant. This seems plausible for a gas-phase temperature of 210 K, whereas in the matrix itself at much lower temperatures of 10 K tunneling may play an important role.33 The half-life against isomerization τ can then be calculated from τ = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/k. Approximating ΔG′ with the energy difference, an energy barrier of 7.06 kcal mol−1 results in the half-life of isomer V, τ(V → I) = 9 μs. This time is shorter than the residence time in the gas-phase by about a factor of 50. In other words, 50 half-lives have passed before the molecule lands in the matrix. Accordingly, all of the isomer V molecules initially sublimed to the gas phase have already converted to isomer I before landing. For comparison, the half-life of isomer III towards isomer I is much longer, τ(III → I) = 600 μs based on the higher barrier of 8.72 kcal mol−1. In this case the residence time in the gas-phase is similar to the half-life. That is, only half of the isomer III molecules transform to isomer I. Isomer VI very rapidly transforms to isomer III, since the barrier only amounts to 2.15 kcal mol−1: its half-life is about 0.1 μs, and so this isomer cannot persist long enough in the gas-phase to be detectable in the matrix.
2/k. Approximating ΔG′ with the energy difference, an energy barrier of 7.06 kcal mol−1 results in the half-life of isomer V, τ(V → I) = 9 μs. This time is shorter than the residence time in the gas-phase by about a factor of 50. In other words, 50 half-lives have passed before the molecule lands in the matrix. Accordingly, all of the isomer V molecules initially sublimed to the gas phase have already converted to isomer I before landing. For comparison, the half-life of isomer III towards isomer I is much longer, τ(III → I) = 600 μs based on the higher barrier of 8.72 kcal mol−1. In this case the residence time in the gas-phase is similar to the half-life. That is, only half of the isomer III molecules transform to isomer I. Isomer VI very rapidly transforms to isomer III, since the barrier only amounts to 2.15 kcal mol−1: its half-life is about 0.1 μs, and so this isomer cannot persist long enough in the gas-phase to be detectable in the matrix.
As a result of these considerations, half of the isomer III that has sublimed from the thin film or that has emerged from the isomer VI → isomer III conversion will persist and enter the matrix. By contrast, isomer V and isomer VI do not survive for 0.5 milliseconds, which would be required to reach the matrix. In other words, the flipping of the terminal H-atom is too slow for the conformer population to reach thermodynamic equilibrium in 0.5 milliseconds, whereas the flipping of the terminal ethyl-group is fast enough. As a result, the matrix contains only molecules, for which the ethyl group is on the same side as the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, whereas the terminal H-atom can be on either side of the C
O group, whereas the terminal H-atom can be on either side of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. That is, only the ester group of CAEE is under thermodynamic control, whereas the acid group of CAEE is not fully equilibrated. For this reason, much more of structure III, about 15% of the mixture, is observed experimentally, as compared to complete thermodynamic control, which would result in only about 4.4% of isomer III in the matrix.
O group. That is, only the ester group of CAEE is under thermodynamic control, whereas the acid group of CAEE is not fully equilibrated. For this reason, much more of structure III, about 15% of the mixture, is observed experimentally, as compared to complete thermodynamic control, which would result in only about 4.4% of isomer III in the matrix.
Discussion and conclusions
Isolation of solid CAEE, no traces of carbonic acid
With the textbook knowledge in mind that carbonic acid monoethyl ester (CAEE) cannot be isolated in its pure form and with the goal to learn more about carbonic acid polymorphism we have undertaken a study of the protonation of bicarbonate at low-temperature conditions in absolute ethanol as a solvent. About 20 years ago, Hage et al. had developed a cryotechnique for isolation of two distinct carbonic acid polymorphs using methanol and water as solvents.15,16,28,34,35 In the present study we investigate the cryoreactions of potassium bicarbonate dissolved in ethanol after removal of the solvent and treatment with aqueous acid. Unlike the original technique employed by Hage et al., we first dissolve KHCO3 and then deposit a glassy layer of dissolved KHCO3 on a cryoplate at 78 K. Instead of depositing a glassy layer of HCl dissolved in the same solvent, we first heat the glassy layer of KHCO3 in vacuo without the presence of a strong acid. This results in evaporation of the solvent and a solid residue, which we identify to be pure monoethyl carbonate K[O2COCH2CH3] from the agreement of the IR spectra reported by Behrendt et al. and Fig. 1a. This claim is also backed from the analysis of the matrix spectrum in Fig. 4a. That is, ethylation has taken place after evaporation from ethanolic solution, but the thermodynamically favorable back-reaction to bicarbonate is inhibited at the low temperatures used for evaporation of the solvent. To the best of our knowledge, this is the first time this compound was obtained from KHCO3. We note that other synthesis routes are available to prepare K[O2COCH2CH3]. However, these routes do not use KHCO3 as starting point, and are hence not suitable in the context of our question whether an unknown polymorph of carbonic acid might be accessible from ethanolic solution.The spectrum obtained after treatment of potassium monoethyl carbonate with acid is shown in Fig. 1b. This spectrum is not identical to either the spectrum of crystalline β-H2CO3 (see Fig. 3), or to the spectrum of its amorphous precursor.27 Therefore, the alkyl group remains covalently linked after protonation at cryoconditions rather than being cleaved by hydrolysis. In other words, steps 2–4 in Fig. 2 are too slow to be of practical importance at cryoconditions. That is, the hydrolysis step does not take place, which would transform the ester into H2CO3. In this case, CAEE (HOCOOC2H5) rather than H2CO3 is the final product obtained after treatment with HCl and removal of solvent at ∼210 K. From the much better qualitative match of the assignments we conclude that the observed solid state spectrum indicates that in fact we were able to isolate pure CAEE.
Sublimation and matrix isolation of CAEE
Unfortunately, polymorph identification solely on the basis of vibrational spectra is a difficult task. Isotope substitution studies or single crystal X-ray diffraction could provide a more definitive answer, but this is not feasible at the moment using the thin solid films produced here and given the extremely low solubility of bicarbonate in ethanol. Also mass-spectrometry could provide an answer: after sublimation of the solid we expect to observe a signal at a m/z ratio of 62.03 in case of carbonic acid, but at m/z = 90.07 in case of CAEE. Unfortunately, all these molecules fragment easily upon ionization before entering the mass-filter. So far, our attempts to detect the unfragmented parent ions using electron-impact ionization were unsuccessful. However, earlier work by Terlouw et al.36 has shown that at least a very weak parent carbonic acid ion signal at m/z = 62 can be detected. Future studies on attempts to detect the unfragmented ions in mass-spectrometry experiments might be based on soft ionization using vacuum ultraviolet light.In order to answer the question whether we have indeed isolated pure solid CAEE with high confidence we have here undertaken a matrix isolation study of the thin solid film, which avoids the ionization step and instead lands the neutral gas phase molecules in an inert matrix. The IR-spectrum of the vapor collected in vacuum at 210 K and deposited together with solid argon can be explained in an excellent manner assuming the presence of conformers of CAEE, whereas there is no match with carbonic acid matrix spectra reported earlier.20 If carbonic acid is present at all, it is an impurity of <1%. We suggest a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of the conformers I/II and III/IV to be present in the gas phase above the solid compound from the comparison with spectra calculated at MP2/aug-cc-pVTZ level of theory. Again, isotope substitution would be desirable to back up the interpretation, but is very hard to be realized in practice.
1 mixture of the conformers I/II and III/IV to be present in the gas phase above the solid compound from the comparison with spectra calculated at MP2/aug-cc-pVTZ level of theory. Again, isotope substitution would be desirable to back up the interpretation, but is very hard to be realized in practice.
One interesting aspect of the conformational isomerism in CAEE is that according to the thermodynamic stabilities we would expect a matrix that is much more depleted of conformer III, namely at a ratio of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rather than the experimental observation of 5
1 rather than the experimental observation of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. We explain the difference based on the energy barriers for conformational isomerism depicted in Fig. 6. These barriers are low enough for isomer VI to convert to isomer III and for isomer V to convert to the most stable isomer I within 0.5 ms, which is the time each CAEE molecule resides in the gas phase before entering the matrix. However, the barrier for the conversion of isomer III to isomer I is high enough so that only part of the isomer III molecules transform to isomer I, thereby avoiding thermodynamic equilibrium. In turn, this implies that a significant fraction of the molecules subliming from the thin solid CAEE film are initially in the unfavorable structure III (or structure VI, which rapidly transforms to structure III).
1. We explain the difference based on the energy barriers for conformational isomerism depicted in Fig. 6. These barriers are low enough for isomer VI to convert to isomer III and for isomer V to convert to the most stable isomer I within 0.5 ms, which is the time each CAEE molecule resides in the gas phase before entering the matrix. However, the barrier for the conversion of isomer III to isomer I is high enough so that only part of the isomer III molecules transform to isomer I, thereby avoiding thermodynamic equilibrium. In turn, this implies that a significant fraction of the molecules subliming from the thin solid CAEE film are initially in the unfavorable structure III (or structure VI, which rapidly transforms to structure III).
We conclude that the evidence we provide here is compelling and clearly proves that we have isolated CAEE in its pure form and evaporated it without significant decomposition in the vacuum, in spite of the lack of further desirable experiments. This defies claims of the impossibility to isolate the pure solid and demonstrates how powerful cryotechniques can be in isolating compounds, which are deemed to be instable.1,10
Implications for carbonic acid polymorphism
Recently, the nature of the α-polymorph of carbonic acid was questioned by Bernard based on the study of the crystalline solid and its isotopologues37 and later by Reisenauer et al. based on a study of gas phase pyrolysis products trapped in matrix.9 Both suggest it to be the methyl hemiester of carbonic acid instead of carbonic acid itself. For this reason we do not include a comparison with “α-H2CO3” in Fig. 3, which was synthesized first in the 1990s by Hage, Hallbrucker and Mayer.15,16,35 The present study raises the question whether the methyl hemiester was formed in the work by Hage, Hallbrucker and Mayer, and whether this hemiester is also resistant against hydrolysis under cryo-conditions. This question is not straightforward to answer since they used a cryo-technique different from the one used by Bernard,37 and hence a more elaborate discussion is required. A detailed discussion on the nature of solid “α-H2CO3” and a reinvestigation of the interpretation of the matrix spectra above “α-H2CO3”21 will, thus, be the topic of a subsequent publication. By contrast, the nature of β-H2CO3 (ref. 28) and the matrix spectrum of carbonic acid isolated from sublimed β-H2CO3 (ref. 20) remains undoubted and was confirmed in the work by Reisenauer et al.9 Hence, we restrict ourselves here to a comparison with β-H2CO3 in Fig. 3.Author contributions
J. B. carried out the experimental work, R. G. H. carried out the computational work. T. L., R. S. and H. G. designed the experimental study, K. R. L. designed the computational study. L. C. worked on the stereo-nomenclature of the title compound and its conformers. J. B., E.-M. K., L. C., H. G. and T. L. wrote the manuscript.Conflict of interests
The authors declare no competing financial interests.Acknowledgements
We gratefully acknowledge financial support by the Austrian Science Fund FWF (projects P18187 and I1392). H. G. is grateful for the purchase of the Bruker Vertex 80v FT-IR spectrometer from infrastructure funds of TU Wien.References
- J. G. Knight, in Science of Synthesis: Houben-Weyl Methods of Molecular Transformations, Thieme, 2005, ch. 18.2.1.1.3, p. 67 Search PubMed.
- S. Sakai, T. Fujinami, T. Yamada and S. Furusawa, Nippon Kagaku Kaishi, 1975, 1789–1794 CrossRef CAS.
- N. Yamazaki, S. Nakahama and F. Higashi, Ind. Eng. Chem. Prod. Res. Dev., 1979, 18, 249–252 CrossRef CAS.
- W. A. Hoffman, J. Org. Chem, 1982, 47, 5209–5210 CrossRef CAS.
- C. Bruneau and P. H. Dixneuf, J. Mol. Catal., 1992, 74, 97–107 CrossRef CAS.
- S. Oi, Y. Kuroda, S. Matsuno and Y. Inoue, Nippon Kagaku Kaishi, 1993, 985–987 CrossRef CAS.
- M. R. Rossi, D. T. R. Vidal and C. L. do Lago, Food Chem., 2012, 133, 352–357 CrossRef CAS PubMed.
- A. Dibenedetto, M. Aresta, P. Giannoccaro, C. Pastore, I. Papai and G. Schubert, Eur. J. Inorg. Chem., 2006, 908–913 CrossRef CAS.
- H. P. Reisenauer, J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2014, 53, 11766–11771 CrossRef CAS PubMed.
- A. A. G. Shaikh and S. Sivaram, Chem. Rev., 1996, 96, 951–976 CrossRef CAS PubMed.
- G. Gattow and W. Behrendt, Angew. Chem., Int. Ed., 1972, 11, 534–535 CrossRef CAS.
- W. Behrendt, G. Gattow and Z. Anorg, Z. Anorg. Allg. Chem., 1973, 398, 198–206 CrossRef CAS.
- W. Behrendt, G. Gattow and M. Drager, Z. Anorg. Allg. Chem., 1973, 397, 237–246 CrossRef CAS.
- J. Dumas and E. Peligot, Liebigs Ann. Chem., 1840, 35, 281 CrossRef.
- W. Hage, A. Hallbrucker and E. Mayer, J. Am. Chem. Soc., 1993, 115, 8427–8431 CrossRef CAS.
- W. Hage, A. Hallbrucker and E. Mayer, J. Mol. Struct., 1997, 408, 527–531 CrossRef.
- E. Mayer, J. Appl. Phys., 1985, 58, 663–667 CrossRef CAS.
- E. Mayer, CryoLetters, 1988, 9, 66–77 CAS.
- O. Galvez, A. Zoermer, A. Loewenschuss and H. Grothe, J. Phys. Chem. A, 2006, 110, 6472–6481 CrossRef CAS PubMed.
- J. Bernard, R. G. Huber, K. R. Liedl, H. Grothe and T. Loerting, J. Am. Chem. Soc., 2013, 135, 7732–7737 CrossRef CAS PubMed.
- J. Bernard, M. Seidl, I. Kohl, E. Mayer, K. R. Liedl, O. Galvez, H. Grothe and T. Loerting, Angew. Chem., Int. Ed., 2011, 50, 1939–1943 CrossRef CAS PubMed.
- M. J. Frisch, et al., GAUSSIAN09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- CCCBDB, National Institute of Standards and Technology, Standard Reference Database, 2015, Vol. 101, http://cccbdb.nist.gov/vibscale2.asp?method=3%26basis=18.
- K. Winkel, W. Hage, T. Loerting, S. L. Price and E. Mayer, J. Am. Chem. Soc., 2007, 129, 13863–13871 CrossRef CAS PubMed.
- W. Hage, A. Hallbrucker and E. Mayer, J. Chem. Soc., Faraday Trans., 1996, 92, 3197–3209 RSC.
- S. Coussan, Y. Bouteiller, J. P. Perchard and W. Q. Zheng, J. Phys. Chem. A, 1998, 102, 5789–5793 CrossRef CAS.
- G. P. Moss, Pure Appl. Chem., 1996, 68, 2193–2222 CrossRef CAS.
- E. L. Eliel and S. H. Wilen, Stereochemistry of Organic Compounds, John Wiley & Sons, Inc., 1994 Search PubMed.
- W. Klyne and V. Prelog, Experientia, 1960, 16, 521–523 CrossRef CAS.
- J. P. Wagner, H. P. Reisenauer, V. Hirvonen, C. H. Wu, J. L. Tyberg, W. D. Allen and P. R. Schreiner, Chem. Commun., 2016, 52, 7858–7861 RSC.
- W. Hage, A. Hallbrucker and E. Mayer, J. Chem. Soc., Faraday Trans., 1995, 91, 2823–2826 RSC.
- W. Hage, A. Hallbrucker and E. Mayer, J. Chem. Soc., Faraday Trans., 1996, 92, 3183–3195 RSC.
- J. K. Terlouw, C. B. Lebrilla and H. Schwarz, Angew. Chem., Int. Ed., 1987, 26, 354–555 CrossRef.
- J. Bernard, Ph.D. thesis, University of Innsbruck, 2014.
Footnote |
| † Present address: Bioinformatics Institute (BII), Agency for Science, Technology and Research (A*STAR), Matrix 07-01, 30 Biopolis Street, 138671 Singapore. |
| This journal is © The Royal Society of Chemistry 2017 |