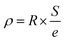Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of organic additives on the intergranular conductivity of Al-doped ZnO†
J. Gamon *ab,
D. Giaume
*ab,
D. Giaume a,
G. Lefèvrea,
T. Le Mercierb and
P. Barbouxa
a,
G. Lefèvrea,
T. Le Mercierb and
P. Barbouxa
aChimie ParisTech, PSL Research University, CNRS, Institut de Recherche de Chimie Paris (IRCP), 75005 Paris, France. E-mail: jacinthe.gamon@chimie-paristech.fr
bSolvay, Research and Innovation Center of Paris (RIC Paris), 52 rue de la Haie-Coq, 93306 Aubervilliers, France
First published on 2nd August 2017
Abstract
The development of ink-based solutions as alternative routes to vacuum-based deposition techniques requires methods to improve their intergranular conductivity without thermal sintering. The effect of organic additives on the interparticle electron transfer between grains of an Al-doped ZnO powder was studied. The resistivity of the modified powders was measured as a function of compression to reach a reproducible state. The surface adsorption of selected molecules strongly enhances intergranular electron transfer, up to a factor of 20. This improvement has been linked to the decrease of the intergranular potential barrier height, associated with the energy distance between the Fermi level of the oxide and the LUMO of the molecules.
I. Introduction
Deposition of colloidal inks have attracted much attention over the past decades as an alternative to vacuum-based thin films deposition technics.1–5 The method relies on the coating of an ink – the active material mixed in a solvent with additives to be subsequently removed – on a substrate using processes such as roll to roll, doctor blade, serigraphy, inkjet printing.6 The major advantage being the reduced investment cost and large scalability, this deposition route is also well suited for materials requiring soft chemical treatment, deposition onto plastic substrates or integration into hybrid organic/inorganic systems. However, a disadvantage of these solution techniques is that the resulting films are poorly densified and may contain residual organic impurities used during the ink formulation. This is the case of oleylamine, a very good particle stabilizer in most solvents that limits the conductivity in semiconductor films.3,5 Most of the time, an annealing treatment is required to densify the film and remove the insulating impurities.7–9 However, this sintering step often induces cracks as well as carbon-based impurities at the grain boundaries, and is again not suited for materials with low degradation temperatures (the active material itself, the substrate or other sensitive films composing the device).An example of this drawback is related to the case of transparent conducting oxides (TCOs) which are used as front contacts in photovoltaic devices or connectors in many display applications. Their conductivity is crucial for the efficiency of the device. Many solution-based processes have been described in the literature4 (sol gel,16 chemical bath deposition,17 spray pyrolysis18), for which the resistivity reaches down to 2 × 10−3 Ω cm for ITO thin films.19 However vacuum-based deposition routes (typically sputtering20 or pulsed laser deposition21) still offer the best performances with a resistivity still lower by one order of magnitude and reaching down to 10−4 Ω cm (sputtered ITO20,22). Therefore, solutions to obtain highly conducting liquid-based and low temperature processed thin films need to be further developed. For that purpose, a large effort must be put on improving the intergranular electrical transfer in these materials.
Most efforts focus on the ink formulation, using conducting ligands which stabilize the suspension prior to the deposition but also act as sintering agents after deposition.10,11 Ligand removal12,13 or ligand exchange14,15 with more conducting ones can also be performed.
Among TCO materials ZnO:Al has the additional advantages to be non-toxic and earth-abundant, which is one of the reason for its interest in the industry, especially in photovoltaics. Optimization of dye-sensitized solar cells already focused on the improvement of the electrical transfer between adsorbed molecules and this semiconductor. Previous works demonstrated that the grain-to-grain electronic transfer in a ZnO compact depends on the nature of the molecules sandwiched between the grains.10,32 The best results are bound to the position of the lowest unoccupied molecular orbitals (LUMO) of these molecules above the conduction band of the n-type semiconductor.23,24
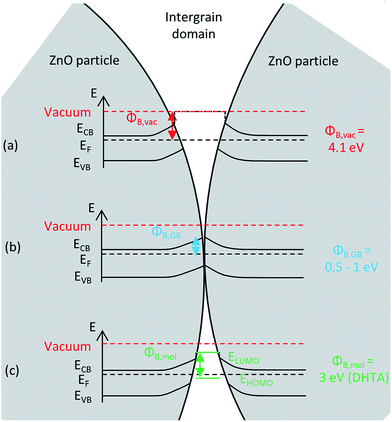
When considering the case of an n-type semiconductor, such as ZnO:Al, the main charge carriers are electrons that diffuse through the conduction band. Their energy can therefore be estimated as the energy at the minimum of the conduction band, ECB. In polycrystalline semiconductor assemblies, the energy levels at the particles surface differ from the bulk, as the surface gathers carrier traps coming either from dangling bonds, from a change in chemical composition compared to the bulk, or from adsorbed surface species (such as water, oxygen…).25 Segregation of impurities at grain boundaries also occurs due to a size mismatch, or coulombic interactions.26–28 These defects trap electrons or holes and an energy band bending occurs on both sides of the grain boundary to establish electronic equilibrium.29–31 This phenomenon is at the origin of the so-called double Schottky barrier, the height of which depends on the intergranular domain. In areas where particles are not in contact, the intergranular domain may be considered as vacuum, and the barrier height is equal to the difference between the vacuum level and the conduction band level (Fig. 1a).32 When particles are in contact, the height of the potential barrier, ΦB,GB, depends on the excess charge of main carriers trapped at the interface (the grain boundary) (Fig. 1b), it can be determined for example by the energy position of the surface states.30 If an organic molecule is introduced in the intergranular domain (Fig. 1c), the barrier height becomes equal to the difference between the LUMO of the molecule and the electron energy since for an n-type semiconductor, charge carriers transfer through the LUMO. Respectively, in the case of p-type semiconductors, they would transfer through the HOMO of the molecules.
This energy barrier affects intergranular electronic transport. There are three ways for an electron in the conduction band to overcome the barrier and therefore contribute to the conductivity: (i) thermionic emission, if the thermal energy is higher than the barrier height, and (ii) tunneling across the barrier and (iii) transfer through surface states. Tunneling is described by quantum mechanics and the probability for the electron to cross the barrier, T, can be described by eqn (1):10,32
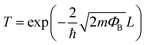 | (1) |
To summarize, the intergranular electron transfer will be favored, when particles will be in close contact or when an organic molecule with a suitable LUMO will separate the two grains.
In this work, we discuss the grain-to-grain electronic transfer in a ZnO:Al powder as a function of the nature of the molecules sandwiched between the grains.10,32 We examined the influence of the LUMO energy levels of different organic additives on ZnO:Al intergranular conductivity. Our goal is to establish a direct link between (i) the improvement of the intergranular electronic conductivity of a semiconductor and (ii) the energy position of an organic molecule adsorbed at its surface.
We chose to study the conductivity of a compressed powder at relatively low pressure (between 1 and 70 MPa of uniaxial pressure) in order to obtain reproducible results. This is also an artificial manner to reproduce experimental conditions of wet deposited thin films where a high porosity is maintained and the contact pressure results from capillary effects.
II. Experimental
A. DFT calculations
The Frontier orbitals energy levels of the organic molecules were calculated thanks to ground state geometry optimization and frequency calculations using DFT method with the global hybrid functional PBE1PBE, using Gaussian basis sets 6-31G(d). The wave function type is unspecified and water is used as implicit solvent.B. Materials
An aluminum-doped zinc oxide powder (3 wt%) was purchased from Umicore (Zano® Al-10 Powder). It consists of nanosized particles (Fig. S0†). The surface area of the as-purchased powder is 30 m2 g−1. All experiments with organic additives were performed with a batch of powder produced by heating the commercial powder in a tubular furnace under an H2/Ar (4%) atmosphere at 900 °C for 1 hour with heating and cooling ramps of 5 °C min−1. After annealing, the surface area of the powder decreased down to 2 m2 g−1. A sintered pellet was obtained by pressing this annealed ZnO:Al powder under an uniaxial press at 100 MPa, after which the same thermal treatment under H2 was performed a second time. The compactness of the pellet before sintering is 63%, and 70% after sintering.Succinic acid (SA), 99%; terephtalic acid (TA), 98%; 2-nitroterephthalic acid (NTA), 99%; 3,5-dinitrobenzoic acid (DNBA), 99%; 2,5-diaminoterephthalic acid (DATA), 95%, 2,5-dihydroxyterephthalic acid (DHTA), 98% and poly(thiophene-3-[2-(2-methoxyethoxy)ethoxy]-2,5-diyl), sulfonated solution (PTS) 2% in 1,2-propanediol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopropanol
isopropanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water, 3
water, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, were all purchased from Sigma Aldrich.
1, were all purchased from Sigma Aldrich.
C. Techniques and equipment
A Flash 2000 analyzer (ThermoFisherScientific) was used for the quantitative determination of carbon in the Al-doped ZnO powder grafted with terephtalic acid derivatives and succinic acid. Measurements were performed and repeated 3 times on 10 mg of sample. Quantitative mass determination of the grafted polymer in the PTS-functionalized Al-doped ZnO powder was performed by thermogravimetric analysis under oxygen, thanks to a Netzsch STA 449F3 TGA-TDA apparatus.Resistivity measurements as a function of temperature were obtained with the four probes method. Contacts were made with a silver paste (purchased from SPI supplies). This was used to compare the effect of H2 annealing and sintering.
The specific surface area of the powders were measured thanks to the method Brunauer, Emmett and Teller (BET) with a Belsorp apparatus.
D. Functionalization procedure
The organic additives studies were performed on the H2/Ar annealed ZnO:Al powder, which presented the most reproducible conductivity.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopropanol
isopropanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water, 3
water, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used for the functionalization of ZnO:Al with the polythiophene. 1 mL of this solution was diluted in 200 mL of water, which corresponds to a polymer concentration of approximately 10−4 M. 2 g of annealed ZnO:Al powder was dispersed in the solution thanks to vigorous stirring, yielding a weight ratio PTS/ZnO
1 was used for the functionalization of ZnO:Al with the polythiophene. 1 mL of this solution was diluted in 200 mL of water, which corresponds to a polymer concentration of approximately 10−4 M. 2 g of annealed ZnO:Al powder was dispersed in the solution thanks to vigorous stirring, yielding a weight ratio PTS/ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al of 1 wt%. The suspension was kept under agitation overnight and filtered through a Büchner funnel without further washing. The powder was then dried at 150 °C in order to thoroughly remove the organic solvents present in the commercial solution of PTS.
Al of 1 wt%. The suspension was kept under agitation overnight and filtered through a Büchner funnel without further washing. The powder was then dried at 150 °C in order to thoroughly remove the organic solvents present in the commercial solution of PTS.In order to determine the quantity of molecules present at the surface of the grafted ZnO:Al particles, carbon and nitrogen were quantified thanks to CHNS analysis for carboxylate molecules, whereas TGA was performed for the PTS functionalization. Indeed, the amount of carbon is not exactly known in the polymer, and CHNS analysis would not enable to determine the exact amount of molecules adsorbed. This analysis reveals a weight percentage between 0.15% and 0.35% for the carboxylate molecules, and 0.81% for the sulfonated polythiophene.
Taking into account the specific surface of the powder, 2 m2 g−1, this corresponds to 2.5 to 3.8 molecules adsorbed per nm2. This value is high and probably indicates some residual ungrafted molecules. The effect of the amount of adsorbed molecules was therefore considered. For this experiment, the powder was immersed in aqueous solutions of different concentration of molecules, then only dried (and not filtered) to control the exact amount of molecule intimately dispersed with the ZnO:Al powder.
E. Experimental set-up for resistivity measurements under pressure
The set-up used for the resistivity measurements is similar to that of Celzard et al.33 and has already been presented by our group.34 A 13 mm-diameter stainless steel cylindrical swagelock cell equipped with two plungers and internally covered by a Mylar sheet to provide electrical insulation was filled with the appropriate mass of powder. The powder surface was first flattened thanks to taps on the bench, before delicately placing the whole cell between two compression moving platens of a numerically monitored Instron 5966 testing system (Fig. 2a). The displacement rate of the upper compression plate was imposed, and the resultant force applied on the cell was recorded. The full profile of compression cycle is described in Fig. 2b.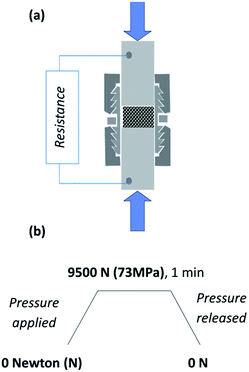 | ||
| Fig. 2 (a) Set-up for resistivity measurements of the ZnO:Al powder under pressure. (b) Profile of the compression cycle. | ||
The powder thickness was directly related to the platens displacement, setting first the zero displacement on the empty cell pressed under 73 MPa (maximum pressure), and for each pressure, systematically subtracting afterwards the displacement due to the cell deformation from the displacement recorded with powder.
The two plungers were connected to a Keithley 2400 ohmmeter, which recorded the two probe resistance R, between the plungers during the compression cycle. Because two probe resistance measurements may include junction resistance contribution, a preliminary calibration was performed with different amounts of powder to validate that the resistance was linearly linked to the calculated thickness. The extrapolation of the resistance at zero mass accounts for the junction resistance and stays below 0.4 Ω. This negligible junction resistance was not taken into account in our results, and only comparisons between samples were made.
The resistivity was obtained by the formula:
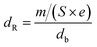 | (2) |
III. Results and discussion
A. Improving bulk electrical conductivity
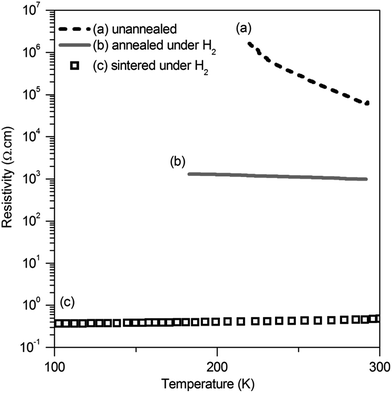
The resistivity of the as-purchased Al-doped ZnO was measured with the four probe method on a pellet pressed at 100 MPa. Its compactness is 63%, and its resistivity is 5 × 104 Ω cm (300 K) with a thermally activated behavior as for a semiconductor (Ea = 0.24 eV) (Fig. 3a). This result was obtained on a pellet previously dried at 100 °C for 12 h in an oven. We observed a strong irreproducibility during this measurement and realized that the water vapor pressure (relative humidity) had a strong effect on the conductivity. This effect is attributed to surface proton diffusion. The conducting properties of the semiconductor zinc oxide are known to be very sensitive to adsorbed species such as oxygen, carbon monoxide. To avoid non-reproducible measurements due to surface effects,35,36 doping of zinc oxide is required so that its intrinsic electronic conductivity becomes higher than proton surface conductivity and remains weakly altered by surface states.Thus, the powder was annealed in a tube furnace under H2/Ar at 900 °C before pelletizing. This considerably decreased the resistivity of the pellet down to 1 kΩ cm (300 K) with an activation energy of 0.1 eV (Fig. 3b), while slightly increasing its compactness to 68%. An annealing treatment under a reducing atmosphere (5% H2/Ar) at 900 °C is well known to be very beneficial as suggested in the literature.37–39
This increased conductivity after thermal treatment is probably due to a better aluminum insertion into the zinc oxide structure. Indeed, the annealing should shifts the equilibria of the following reaction (eqn (3)) towards the right, therefore increasing the doping by aluminum and the amount of charge carriers:
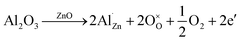 | (3) |
Moreover, the desorption of negatively charged oxygen species at the grain boundaries during annealing may result in a higher carrier mobility and also contributes to the increase in conductivity.38,39
This annealing procedure is important to obtain a reproducible intrinsic conductivity in the grains.
A similar pellet was also sintered (i.e. as a ceramic) at 900 °C – for 12 h under H2/Ar. The compactness of the resulting ceramic was 70%. But its resistivity falls down to 4 × 10−1 Ω cm at 300 K and is nearly independent of the temperature, characteristic of a metallic behavior (Fig. 3c). This demonstrates that by improving intergranular contacts in the pellet, the resistivity can decrease at least by 3 orders of magnitude lower than the simply pressed powder. This high conductivity value may be considered as an upper limit for the intergranular conductivity of the grains and, as a matter of fact, the goal of the following studies with organic additives would be to reach a similar value by improving intergranular electronic transfers, with room temperature particle surface functionalization instead of high temperature sintering.
B. Choice of organic molecule and energy diagram
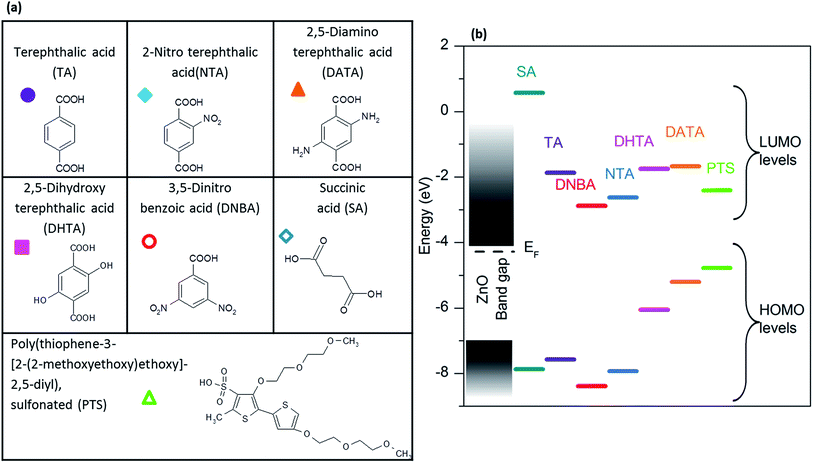
A range of small molecules, presented in Fig. 4a, was selected to study the influence of functionalization on ZnO:Al intergranular conductivity, and more specifically, the influence of an anchoring group, or a conjugated pi system on the molecules. Terephthalic acid and its analogues revealed to be appropriate for this study due to their carboxylate function, known to be a good anchoring group at the surface of zinc oxide,24 as well as for their conjugated pi systems favoring electronic transfer. The substituting groups were selected in order to obtain different LUMO levels. Succinic acid, an aliphatic molecule possessing the same carboxylate function, was added to the study. Its LUMO level is higher. A substituted polythiophene (PTS) was also selected as it is known to be a good electronic mediator, as well as possessing a low LUMO level.40,41 Energy levels of the isolated molecules were calculated thanks to DFT calculations, and positioned relatively to the conduction and valence band levels of ZnO (Fig. 4b).C. Effect of organic molecules on the intergranular conductivity
The resistivity of the ZnO:Al powder functionalized with the different molecules has been studied at room temperature as a function of the applied pressure. The relative density of the powder under compression is plotted on Fig. S4,† and shows that the powder compaction is not affected by molecule grafting.The change of the resistivity versus the applied pressure is presented on a log–log plot on Fig. 5. For the sake of clarity, it is only shown for a selection of most representative molecules. Below 106 Pa, the powders are only weakly densified and remain very loose, so their measurements are very irreproducible. Under higher pressure, a strong decrease of the resistivity is observed, during which elastic and plastic deformations take place. The elastic phenomena can be estimated by the increase of resistivity upon the pressure release. The plastic contribution is indicated by the resulting hard pellet, which only returns to powder if ground in a mortar. If the pressure is increased – typically to 109 Pa – a flat stage is obtained, corresponding to the end of the deformation.42
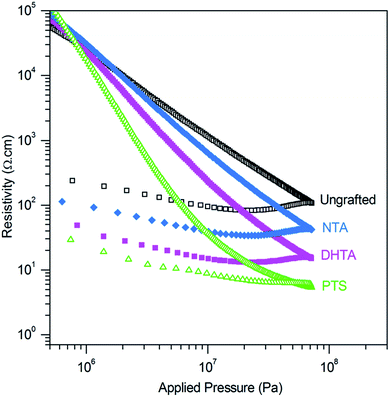 | ||
| Fig. 5 Resistivity in function of the applied pressure on ungrafted and grafted ZnO:Al powder (H2/Ar annealed powder) (anchoring molecules in legend). | ||
In Fig. 5, the resistivity and the pressure are represented in a logarithmic scale. A linear plot is observed for the ungrafted material, which is typically obtained for powders under compression. This indicates that the resistivity follows a power-type law: ρ = q × Pγ, where P is the pressure in Pa, q is a constant which contains contributions from the elastic modulus of the grain core and surface, the conductivity, the grain diameter and the surface layer thickness. γ is a dimensionless exponent, the value of which reflects the surface layer properties. For an ideal powder of spherical particles with no surface layer, the Hertz model, describing the surface contact area between particles as a function of the applied pressure, predicts that in the elastic regime γ = −2/3.42,43
The values of γ obtained on our experimental curves is 1.2 for ungrafted ZnO:Al. The deviation from Hertz law for the grafted powders indicates the non-uniformity of the surface layer as well as the contribution of plastic deformations.43 All the resistivity measurements show an excellent reproducibility above 2 × 106 Pa. All the molecules used in this study present a positive effect on the conductivity, except for the non-conjugated succinic acid, SA, which does not show any effect at all (the resistivity versus applied pressure exactly superposes with the ungrafted material in Fig. 6) Thus, a conjugated pi-system is necessary to improve the intergranular conductivity. The resistivity of the grafted powders becomes lower than the ungrafted material beyond 1 or 10 MPa, depending on the organic species. DATA and DHTA for instance decrease the resistivity by a factor of 5. The sulfonated polythiophene polymer (PTS) has the largest effect: the resistivity drops dramatically and becomes 20 times lower (at 73 MPa) than for the ungrafted powder.
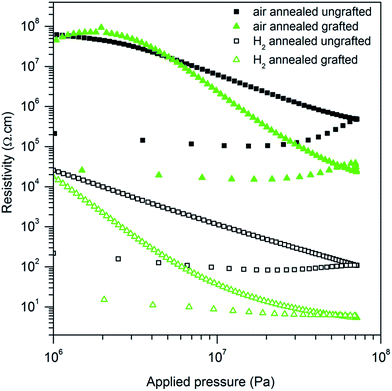 | ||
| Fig. 6 Resistivity versus applied pressure of ungrafted (black squares) and PTS-grafted (green triangles) ZnO:Al powder annealed at 900 °C under air (full symbols), or under H2/Ar (empty symbols). | ||
The conductivity increase is independent on the amount of molecules added to the surface. This was confirmed by additional experiments performed on powders immersed in aqueous solutions with different concentrations of molecules, then only dried (and not filtered) to control the exact amount of molecule intimately dispersed with the ZnO:Al powder. The PTS-grafted ZnO:Al had to be dried at higher temperature (150 °C) to remove solvent residues. As the drying temperature could be responsible for the conductivity enhancement, through the creation of carbon species for instance, the same drying process was performed on the ungrafted and NTA-grafted powders. In both cases, the conductivity of the powder dried at 150 °C was lower than that of the powder dried at 70 °C, invalidating the role of temperature drying on the high conductivity of the PTS-grafted sample.
Moreover, this polymer is known to be a good conductor44–46 and is used as a p-type semiconductor in photovoltaic devices.47–49 Our goal here is to enable grain to grain electron transfer, but avoid polymer percolation, so that the bulk electrical properties of the material are still those of ZnO. In order to verify that no percolation of the polymer alone causes the electron transport, the resistivity of a poorly conducting ZnO:Al powder (i.e. annealed under air in order to obtain the same specific surface as the powder annealed under H2) was measured before and after PTS-functionalization (Fig. 6).
The resistivity of the air-annealed powder is 3 orders of magnitude higher than that of the hydrogen-annealed powder, as discussed in part A. The PTS addition enables to increase the overall conductivity by one order of magnitude as compared to the raw powder. For the air-annealed and H2-annealed samples as well. If PTS percolation was responsible for the conductivity enhancement, the resistivity value of both functionalized samples would be equal and as low. As this is not the case, one can conclude that the resistivity enhancement is only due to improved intergranular contacts.
In Fig. 7, the resistivity observed at 70 MPa has been plotted as a function of the difference between the energy levels of the LUMO and the HOMO of the grafted molecules. It is difficult to compare the results obtained for the functionalization with the carboxylate molecules with those obtained for the PTS functionalization as the chain length as well as the anchoring group is different. However, the positive effect of surface functionalization on the conductivity can be linked to the molecule HOMO–LUMO gap: ΔH–L = ELUMO − EHOMO. The smaller ΔH–L, the more conducting the compressed powder. This dependence will be explained in terms of energy level alignment in the next section.
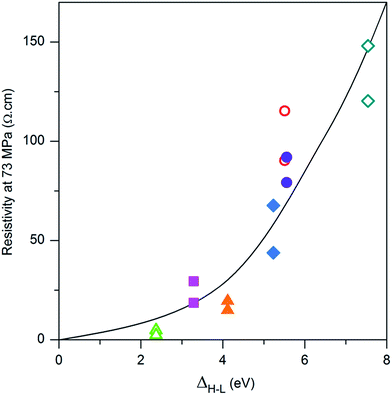 | ||
| Fig. 7 Resistivity of grafted ZnO:Al powder (H2/Ar annealed powder) under 73 MPa in function of the energy difference ΔH–L. The color and sign represent the value (repeated twice) for a specific molecule (correspondences are given in Fig. 4). | ||
D. Discussion on energy level alignment and electron transfer
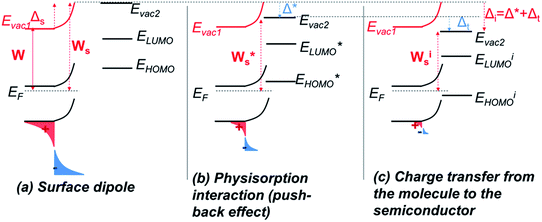
The energy level alignment at the interface between a semiconductor or a metal and an organic molecule is difficult to estimate and has been a controversial issue.50,51 With the advances in the field of hybrid electronic devices such as sensors or DSSC, a growing interest towards this understanding has recently showed up to control charge transfer and performances.First, before considering aligning the energy levels of the molecules with those of the solid, we must assess how the conduction and valence bands of the solid as well as the vacuum level are affected at the surface. Indeed, for a metal or a semiconductor, the potential well imposed by the work function is not infinitely deep. Therefore, there is a slight probability to find electrons outside this well: electrons are said to be leaking out of the surface.52,53 This results in the creation of a surface dipole, noted Δs, which means a change of the work function, Ws, at the surface compared to that of the bulk, W (Fig. 8a). Surface effects in n-type semiconductor tend to increase this dipole, because of acceptor states located at the surface which trap electrons.
When a molecule approaches the surface of a solid, electronic distribution rearrangement occurs upon interaction (charge transfer, mirror force, interface states, surface rearrangement…53), which contributes to a new change in the work function. Its amplitude strongly depends on the type of interaction electrostatic or chemical bonding for instance.50,52–55 Many different effects have been described, mostly for metal/organic interfaces, but these can be ascribed to semiconductors as well.
Recent studies aiming at developing a universal law for the alignment of energy levels between metals (or metal oxides) on one side and organic molecules converge towards the distinction of two regimes.56–58 First, for low interacting interfaces, no charge exchange occurs, and a common vacuum level is set between the molecule and the solid. This regime is said to follow the Schottky–Mott rule, which states that the energy levels are those of the solid and of the molecule taken separately, within a constant, noted Δ*, which depends on the physisorption mechanism, which itself introduces a dipole of amplitude Δ* at the interface.
A main contribution to this dipole is called the push-back effect. It stipulates that the electronic cloud leaking out of the solid's surface is pushed back inside upon adsorption, and therefore the surface dipole and the work function are reduced.52 As a consequence, the energy levels of the molecules (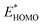 and
and 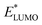 ) are lowered with respect to the Fermi level, EF, of the solid.
) are lowered with respect to the Fermi level, EF, of the solid.
This push-back dipole is always negative (Fig. 8b), and therefore lowers the surface work function 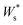 .52,56 The amplitude of Δ* has been proved to be similar for many different low interacting interfaces.56,57
.52,56 The amplitude of Δ* has been proved to be similar for many different low interacting interfaces.56,57
The second regime occurs when a charge is transferred through the interface. According to Greiner et al. this charge transfer may take place when the ionization energy (or the electronic affinity) is smaller (or bigger) than the solid's work function.56 In this case, the energy levels of the molecule are shifted regarding those of the solid: the HOMO (or LUMO) becomes pinned to the solid's Fermi level (not directly at the Fermi level, but separated by an energy ε, explained by Braun et al. by the electron polaronic binding energy57). The origin of this phenomenon is attributed by the authors to an electron transfer from the HOMO of the molecule to the solid (or from the solid to the LUMO), because the ionized molecules are thermodynamically more stable than their neutral form. This induces a new change in the surface dipole and a new surface work function, noted Δt and Wis respectively. Fig. 8c depicts this case. For any molecule such that EI < Ws, the HOMO pinning regime occurs, the amplitude of Δt is strongly dependent on the molecule, on the contrary to Δ* established in the first regime.
In our system, before adsorption, the zinc oxide surface benefits from an upwards band bending. This situation is typical in n-type semiconductor, where electrons, coming from the conduction band, transfer to acceptor states at the surface (originating from dangling bonds, variation in chemical composition…).26–28,31 This leads to the enhancement of the work function at the interface as shown on Fig. 8a. As molecules draw near the surface, if the work function at the surface becomes bigger than the ionization energy of the molecule, a charge transfer is favorable from the molecule to the solid, which itself results in the downward shift of the energy levels (negative Δt) down to the pinning of the HOMO to the Fermi level. This situation is the one described in Fig. 8.
Considering this hypothesis, the energy levels of the molecules have been repositioned assuming this hypothesis of Fermi level pinning (Fig. S5†). In this case, the energy barrier height, ΦB,mol, for electron transfer can be directly linked to ΔH–L. This conclusion would explain why the lower ΔH–L induces a low potential barrier at the grain boundary through the introduction of a vacant energy level when the LUMO of the molecule is closest to the conduction band of the semiconductor. Concerning PTS functionalization, due to its long chain length (around 10 units), it is likely that a combined effect of the low potential barrier height as well as a higher amount of intergranular volume filled with the organic species takes place, enhancing even more the powder conductivity.
IV. Conclusion
We have studied the influence of organic additives on the interparticle conductivity of ZnO:Al powders. The resistivity evolution of the powder under compression reveals that the surface adsorption of molecules strongly enhances intergranular electron transfer under pressures as low as 1 MPa. The effect is dominated by the position of the LUMO of the molecule as compared to the energy levels of the ZnO material. The most efficient organic additive, a sulfonated polythiophene, could even decrease the resistivity by a factor 20 at 73 MPa. This improvement is linked to a decrease of the intergranular potential barrier height, as well as to an increased contact area between particles. Further work should address the electron distribution and the electron transfer between the molecules and the solid surface. This study opens the way for a better conductivity control of thin films deposited by liquid-based processes, in which particles are not sintered and often show high intergranular resistivity. Functionalization using simple conjugated organics could therefore be an alternative to high temperature annealing steps, non-feasible for deposition on polymeric flexible substrates or for sensitive materials decomposing under high temperatures.Acknowledgements
We thank Dr T. Le Bahers (Laboratoire de Chimie, ENS de Lyon, France) for performing DFT calculations and for sharing his knowledge about electron transfer in organic molecules, The Structural Metallurgy team at the Institut de Recherche de Chimie de Paris (IRCP, Chimie ParisTech, PSL Research University, France) for giving us access and time to their Ingstrom Press used for the conductivity measurements, Dr F. Decampo (Solvay, Bollate Research Center, Italy) and Dr J. Wilson (Solvay, Research and Innovation Center of Paris, France) for giving their advice and expertise on choosing and anchoring polythiophenes onto zinc oxide. We also thank T. Barbier, S. Goyard, S. Croyeau and W. Win (Solvay, Research and Innovation Center of Paris, France) for performing ICP and CHNS analysis.Notes and references
- H. W. Choi, T. Zhou, M. Singh and G. E. Jabbour, Nanoscale, 2015, 7, 3338–3355 RSC.
- M. M. Ling and Z. Bao, Chem. Mater., 2004, 16, 4824–4840 CrossRef CAS.
- S. E. Habas, H. A. S. Platt, M. F. A. M. van Hest and D. S. Ginley, Chem. Rev., 2010, 110, 6571–6594 CrossRef CAS PubMed.
- R. M. Pasquarelli, D. S. Ginley and R. O'Hayre, Chem. Soc. Rev., 2011, 40, 5406 RSC.
- D. V. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2010, 110, 389–458 CrossRef CAS PubMed.
- J. Alex, der Vater des Computers, ed. K. Zuse, Parzeller, Fulda, 2000 Search PubMed.
- M. N. Kamalasanan and S. Chandra, Thin Solid Films, 1996, 288, 112–115 CrossRef CAS.
- M. Law, J. M. Luther, Q. Song, B. K. Hughes, C. L. Perkins and A. J. Nozik, J. Am. Chem. Soc., 2008, 130, 5974–5985 CrossRef CAS PubMed.
- J. W. Cho, A. Ismail, S. J. Park, W. Kim, S. Yoon and B. K. Min, ACS Appl. Mater. Interfaces, 2013, 5, 4162–4165 CAS.
- M. V. Kovalenko, M. Scheele and D. V. Talapin, Science, 2009, 324, 1417–1420 CrossRef CAS PubMed.
- C. Murray, E. Shevchenko and D. Talapin, International Business Machines Corporation, Columbia University, US Pat., US20070057255 A1, 2007.
- M. V. Jarosz, V. J. Porter, B. R. Fisher, M. A. Kastner and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195327 CrossRef.
- M. Grouchko, A. Kamyshny, C. F. Mihailescu, D. F. Anghel and S. Magdassi, ACS Nano, 2011, 5, 3354–3359 CrossRef CAS PubMed.
- D. C. Oertel, M. G. Bawendi, A. C. Arango and V. Bulović, Appl. Phys. Lett., 2005, 87, 213505 CrossRef.
- J. M. Luther, M. Law, Q. Song, C. L. Perkins, M. C. Beard and A. J. Nozik, ACS Nano, 2008, 2, 271–280 CrossRef CAS PubMed.
- L. Znaidi, Mater. Sci. Eng., B, 2010, 174, 18–30 CrossRef CAS.
- K. Govender, D. S. Boyle, P. B. Kenway and P. O'Brien, J. Mater. Chem., 2004, 14, 2575–2591 RSC.
- T. Theresa John, M. Mathew, C. Sudha Kartha, K. P. Vijayakumar, T. Abe and Y. Kashiwaba, Sol. Energy Mater. Sol. Cells, 2005, 89, 27–36 CrossRef.
- S. Seki, Y. Sawada, M. Ogawa, M. Yamamoto, Y. Kagota, A. Shida and M. Ide, Surf. Coat. Technol., 2003, 169–170, 525–527 CrossRef CAS.
- U. Betz, M. Kharrazi Olsson, J. Marthy, M. F. Escolá and F. Atamny, Surf. Coat. Technol., 2006, 200, 5751–5759 CrossRef CAS.
- H. Agura, A. Suzuki, T. Matsushita, T. Aoki and M. Okuda, Thin Solid Films, 2003, 445, 263–267 CrossRef CAS.
- K. Ellmer, Nat. Photonics, 2012, 6, 809–817 CrossRef CAS.
- W. Cai, J. R. Peck, D. W. van der Weide and R. J. Hamers, Biosens. Bioelectron., 2004, 19, 1013–1019 CrossRef CAS PubMed.
- E. Galoppini, Coord. Chem. Rev., 2004, 248, 1283–1297 CrossRef CAS.
- J. Goldberger, D. J. Sirbuly, M. Law and P. Yang, J. Phys. Chem. B, 2005, 109, 9–14 CrossRef CAS PubMed.
- Y. Kajikawa, J. Appl. Phys., 2013, 114, 043719 CrossRef.
- A. Tschöpe and R. Birringer, J. Electroceram., 2001, 7, 169–177 CrossRef.
- C. H. Ling, J. H. Fisher and J. C. Anderson, Thin Solid Films, 1972, 14, 267–288 CrossRef CAS.
- C. R. M. Grovenor, J. Phys. C: Solid State Phys., 1985, 18, 4079 CrossRef CAS.
- F. Greuter and G. Blatter, Semicond. Sci. Technol., 1990, 5, 111 CrossRef CAS.
- V. Šnejdar and J. Jerhot, Thin Solid Films, 1976, 37, 303–316 CrossRef.
- A. Zabet-Khosousi and A.-A. Dhirani, Chem. Rev., 2008, 108, 4072–4124 CrossRef CAS PubMed.
- A. Celzard, J. F. Marêché, F. Payot and G. Furdin, Carbon, 2002, 40, 2801–2815 CrossRef CAS.
- D. Giaume, X. Pétrissans and P. Barboux, J. Power Sources, 2014, 272, 100–106 CrossRef CAS.
- Q. Qi, T. Zhang, Q. Yu, R. Wang, Y. Zeng, L. Liu and H. Yang, Sens. Actuators, B, 2008, 133, 638–643 CrossRef CAS.
- B. M. Kulwicki, J. Am. Ceram. Soc., 1991, 74, 697–708 CrossRef CAS.
- Z. Lu, J. Zhou, A. Wang, N. Wang and X. Yang, J. Mater. Chem., 2011, 21, 4161 RSC.
- J. F. Chang, W. C. Lin and M. H. Hon, Appl. Surf. Sci., 2001, 183, 18–25 CrossRef CAS.
- B.-Y. Oh, M.-C. Jeong and J.-M. Myoung, Appl. Surf. Sci., 2007, 253, 7157–7161 CrossRef CAS.
- P. Lubis and M. Saito, Jpn. J. Appl. Phys., 2014, 53, 071602 CrossRef.
- P. I. Djurovich, E. I. Mayo, S. R. Forrest and M. E. Thompson, Org. Electron., 2009, 10, 515–520 CrossRef CAS.
- K.-J. Euler, J. Power Sources, 1978, 3, 117–136 CrossRef CAS.
- M. Creyssels, E. Falcon and B. Castaing, Powders Grains 2009 Proc. 6th Int. Conf. Micromechanics Granul. Media, 2009, pp. 123–126 Search PubMed.
- J. Roncali, Chem. Rev., 1992, 92, 711–738 CrossRef CAS.
- N. Toshima and S. Hara, Prog. Polym. Sci., 1995, 20, 155–183 CrossRef CAS.
- E. E. Sheina, S. M. Khersonsky, E. G. Jones and R. D. McCullough, Chem. Mater., 2005, 17, 3317–3319 CrossRef CAS.
- K. Yao, L. Chen, Y. Chen, F. Li and P. Wang, J. Phys. Chem. C, 2012, 116, 3486–3491 CAS.
- Y. Kim, S. Cook, S. M. Tuladhar, S. A. Choulis, J. Nelson, J. R. Durrant, D. D. C. Bradley, M. Giles, I. McCulloch, C.-S. Ha and M. Ree, Nat. Mater., 2006, 5, 197–203 CrossRef CAS.
- M. Reyes-Reyes, K. Kim and D. L. Carroll, Appl. Phys. Lett., 2005, 87, 083506 CrossRef.
- T. M. Brenner, G. Chen, E. P. Meinig, D. J. Baker, D. C. Olson, R. T. Collins and T. E. Furtak, J. Mater. Chem. C, 2013, 1, 5935 RSC.
- A. Dominguez, M. Lorke, A. L. Schoenhalz, A. L. Rosa, T. Frauenheim, A. R. Rocha and G. M. Dalpian, J. Appl. Phys., 2014, 115, 203720 CrossRef.
- G. Heimel, L. Romaner, E. Zojer and J.-L. Bredas, Acc. Chem. Res., 2008, 41, 721–729 CrossRef CAS PubMed.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- A. Natan, L. Kronik, H. Haick and R. T. Tung, Adv. Mater., 2007, 19, 4103–4117 CrossRef CAS.
- A. Junay, Direct synthesis of conducting polymers from simple monomers, Université Rennes 1, 2015 Search PubMed.
- M. T. Greiner, M. G. Helander, W.-M. Tang, Z.-B. Wang, J. Qiu and Z.-H. Lu, Nat. Mater., 2011, 11, 76–81 CrossRef PubMed.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- L. Ley, Y. Smets, C. I. Pakes and J. Ristein, Adv. Funct. Mater., 2013, 23, 794–805 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02975f |
| This journal is © The Royal Society of Chemistry 2017 |