First-principles investigation of the orientation influenced He dissolution and diffusion behaviors on W surfaces

Abstract

The dissolution and diffusion behaviors of helium (He) for four low-Miller-index tungsten (W) surfaces [(110), (100), (112), and (111)] are systematically studied using the density functional theory to understand the surface-orientation-dependent He bubble formation. The results show that He accumulation on the surfaces is mainly affected by self-trapping and the formation of He-induced vacancies. He-induced vacancies tend to form on the surfaces of W(111), W(100), and W(112) than in the bulk. Specifically, for the W(111) surface, He accumulation is facilitated by the high activation barrier arising from He-induced vacancy trapping, whereas the W(110) surface is resistant to the formation of He bubbles because of the higher vacancy and He formation energies. Our results are helpful for understanding the orientation dependence of surface damage on the W surface under low-energy high flux He ion irradiation and designing irradiation-resistant plasma-facing materials.

---

1. Introduction

Tungsten (W) is considered a main candidate material for divertors in future fusion reactors [such as the International Thermonuclear Experimental Reactor (ITER)]^1,2 because of its low tritium retention, low sputtering, high heat conductivity and high melting point (3690 K). Under an extreme fusion environment, such as in divertors, W is exposed to the irradiation of low energy (1–100 eV) high flux (∼10²⁴ m⁻² s⁻¹) helium (He) plasma, which can induce surface damage such as voids, bubbles, nanostructures, and sputtering erosion. He plasma irradiation causes He accumulation, and bubble formation causes major surface damage to W-based divertors, which leads to the degradation of the thermal and mechanical properties of divertors, thus resulting in the instability of the plasma performance. Therefore, it is urgent to investigate He bubble formation and growth on W surfaces with the aim of decreasing He bubbles.

Many investigations have been conducted on the behavior of He on W surfaces. Significant morphology changes (such as He bubbles^3,4 or nanofuzz formations^5–7) are found on the W surface regions under low energy, high flux He ion irradiation. Moreover, studies have indicated that bubble formation and surface morphology are affected by the surface orientation under low energy He irradiation.^8,9 Ohno et al. observed by scanning electron microscopy (SEM) and transmission electron microscopy (TEM) that the effects of surface orientation on the surface morphology change when W is exposed to low energy, high flux He plasmas and they also discussed the He-induced morphology determined by the angle between a slip face and surface.⁸ The results of Parish et al. also showed some morphology changes on a previously smooth surface due to low energy He ion plasma.⁹ For example, the (001) surface formed pyramids, the (114) and (112) surfaces formed wavy and stepped structures, and the (103) surface remained smooth, where such phenomenon was related to crystal texture, structure growth and loop punching.⁹ The exact formation mechanisms and process of He bubble formation on W surfaces are still not fully understood, thus further theoretical studies are required to clarify the surface orientation effects.

In general, He accumulation and bubble formation depend on He dissolution and diffusion. Previous studies based on density functional theory (DFT) calculations for He behaviors in W bulk have been reported, which showed a strong attraction between He–He and a low diffusion barrier in the bulk.^2,10,11 The interactions between He projectiles and pre-existing He bubbles on W surfaces were reported using molecular dynamics (MD) simulation under low energy He ion irradiation, which indicated that He projectiles can be trapped by pre-existing bubbles.¹² Moreover, many theoretical studies at different scales found surface orientation effects on He diffusion and depth distribution on W surfaces.^13–17 Wirth et al. reported higher He retention in W(111) and W(211) than that in W(100) and W(011) under He plasma derived from MD simulation.¹³ Furthermore, surface morphology determined by surface orientation was also reported using MD simulation.¹⁴ In addition, studies found that smaller He clusters migrate toward W surfaces and cause stacking W atom formations using MD^16,18 and self-evolving atomistic kinetic Monte Carlo (SEAKMC)¹⁹ methods, which cause He accumulation on W surfaces. Wang et al. employed DFT to study the He dissolution behavior on W surfaces and found that He atoms are easier to form He clusters by self-trapping on surfaces, where only the W(110) surface was considered.²⁰

Herein, we systematically explore the dissolution and diffusion behaviors of He on W surfaces with different orientations using the first-principles method. The vacancy and He formation energy, He–He binding energy and He diffusion barrier are calculated for four low-Miller-index surfaces [(110), (112), (111), and (100)]. The surface-orientation-influenced He bubble formation is explained by considering the surface stability, He dissolution, and He diffusion on the different surfaces. Our results concerning the surface orientation effects on He bubble formation are certainly helpful for designing irradiation resistant plasma-facing materials (PFMs).

2. Computational details

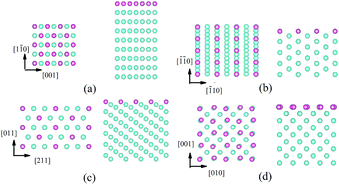
All calculations were performed using the DFT-based Vienna ab initio simulation package (VASP).²¹ The interactions between ionic cores and valence electrons were described by projector-augmented wave (PAW)²² potentials. The exchange correlation functional was considered as the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE).²³ The kinetic energy cutoff for the plane-wave basis set was as 400 eV. The first-order Methfessel–Paxton method²⁴ was applied for the Fermi surface smearing with a width of 0.1 eV.

A slab was used to model W surfaces (Fig. 1), which consist of W atom layers [9 layers for W(110), W(112) and W(100), and 17 layers for W(111)] and a vacuum layer with the thickness of 12 Å. The structure models of the W(110), W(112) and W(111) and W(100) surfaces contain 108, 108 and 136, and 144 W atoms, respectively. We used k-meshes of 3 × 3 × 1, 4 × 4 × 1 and 3 × 5 × 1, and 3 × 4 × 1 for sampling the Brillouin zones of the W(100), W(110) and W(111) and W(112) slabs, respectively, in which the k-point spacing for the surface supercell was <0.026 (2π/Å). Only He and the outmost 5 layers of the W [9 layers for W(111)] slab were allowed to relax and the rest of the W atoms were fixed at their bulk positions. The convergence criteria for the electronic self-consistent iteration and the ionic relaxation were set as 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively. The climbing image nudged elastic band (CI-NEB) method^25,26 was used to determine the He diffusion barrier.

Fig. 1 Slab model (left: top view and right: side view) of the W surfaces for (a) (110), (b) (112), (c) (111), and (d) (100). To guide the view, the first-layer W atoms are highlighted by lilac spheres.

The W(100) surface undergoes reconstruction at low temperatures;^27,28 therefore, a reconstruction model was employed, in which the top layer atoms shift 0.27 Å and the second layer atoms shift 0.05 Å to form zigzag chains.²⁹ The tetrahedral interstitial site (TIS) is considered in the current work since He prefers to occupy the TIS with a lower formation energy compared to the octahedral site (OIS), according to previous investigations.^30–32 Zero-point energy (ZPE) corrections might be taken into account for light elements, such as H and He. Based on previous literature, with the consideration of ZPE corrections, He formation energy would undergo a slight change (0.03 eV for the OIS, and 0.07 eV for the TIS),^2,31 then the tetrahedral-octahedral relative stability remains unchanged. Moreover, herein, we mainly focus on the differences in the He formation energies at different surfaces. Therefore, we do not take into account the ZPE effect since our conclusions will not be impacted by ZPE.

3. Results and discussion

The W surface damage is related to the following three main factors: (1) surface stability, (2) He dissolution behavior and (3) He diffusion behavior on the surface. For surface stability, we have demonstrated that the W(110) surface is the most stable surface, whereas the W(111) surface is the most unstable.³³ For the W(111) surface, He atoms dissolving would cause more significant modification of the surface morphology and defect formation because the atoms on the surface are easier to reconstruct due to the larger interlayer relaxation and surface energy.^34–37 However, it is difficult for the atoms of the W(110) surface to displace and form surface defects with a smaller interlayer distance relaxation.^34–37 Vacancy formation energy, He formation energy, and He–He binding energy are related to He dissolution behavior, for which small formation energies and large binding energies result in He accumulating and bubbles forming on the surface. On the other hand, He diffusion behavior is determined by its diffusion barrier, and high barriers can hinder He moving away from the surface, thus leading to He accumulation. Therefore, herein, we discuss He dissolution and diffusion on W surfaces.

3.1 Dissolution of He atoms on W surfaces

He bubbles will form with He accumulation on W surfaces by He dissolution, thus the different dissolution behaviors of He on W surfaces can cause heterogeneity in the bubble formations. The formation energies of vacancies and He are discussed to explore the He dissolution behavior on W surfaces. Previous studies showed that vacancies could trap He at interstitial sites, which results in initial bubble nucleation.^2,38 A smaller vacancy formation energy means that surface vacancies are easier to form near the surface, which aggravates He accumulation. The smaller He formation energy means that He can remain stable and easily accumulate at the surface region. In addition, the He atoms can trap the neighboring He atoms, forming He clusters,³⁹ thus the He–He binding energy is the key to understanding He bubble and growth formation caused by self-trapping on surfaces.

3.1.1 Formation energy of vacancies. Vacancies as He trapping sites play an important role in the formation of He bubbles.^2,38 The vacancy formation ability is probed by the vacancy formation energy, which is defined as

E^f_V = E_S+V − E_S + E_b, (1)

where, E_S+V and E_S are the total energies of the W surface with and without a vacancy, respectively, and E_b is the total energy of a W atom in the bulk. The obtained formation energy of vacancies in the bulk is 3.19 eV, which is in agreement with previous studies (3.11 eV (ref. 38) and 3.19 eV (ref. 40)). As shown in Table 1, the formation energy of vacancy in the surface is much smaller than that in the bulk, which indicates that the vacancy density is higher near the surface. The formation energy of vacancy in the W(110) surface is the largest among the four low-Miller-index surfaces studied, which implies that the W(110) surface is more difficult to form vacancies, whereas the W(111) surface is prone to form vacancies due to its smaller vacancy formation energy.

Table 1 Vacancy formation energy E^f_V (eV) at different layers of W surfaces with different orientations. The asterisks represent the cases of the vacancy moving toward the first layer after structure relaxation

Vacancy location	1st layer	2nd layer	3rd layer	4th layer
W(110)	1.88	2.82	3.18	3.28
W(112)	1.04	2.28	3.28	3.38
W(100)	0.33	*	3.09	3.44
W(111)	0.67	1.76	2.70	3.27

---

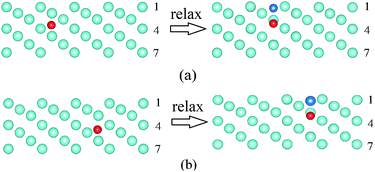
In addition, the vacancy at the second layer of the W(100) surface is very unstable and would move to the first layer after structure relaxation (the corresponding process is demonstrated in Fig. S1 of the ESI†), which means that vacancies mainly form at the first layer of the W(100) surface. Consequently, the He accumulation on the W(110) and W(100) surfaces is less than that on the W(111) and W(112) surfaces due to the surface vacancies trapping the He atoms and the formation of He–vacancy complexes.

3.1.2 Dissolution of a single He atom on W surfaces. To understand the dissolution behavior of He atoms on W surfaces, the He formation energies of different TISs with depths in different W orientation surfaces are explored and are defined as:

E^f_He = E_S+He − E_S − E(He), (2)

where, E_S+He is the total energy of the W surface with an interstitial He atom and E(He) is the energy of an isolated He atom.

The formation energy of He at different TISs (corresponding structures are demonstrated in Fig. S2 of the ESI†) is shown in Fig. 2, which converges to the bulk value of 6.18 eV (6.16 eV in a previous work³⁹) with the depth of 4 Å. We found that He would escape and move 3 Å further away from the surface when He dissolves in the subsurface after relaxation (schematically represented in Fig. S3 of the ESI†), which means that He cannot stably remain at the subsurface. Moreover, the interaction between the He atoms and W surfaces is a weak physical binding because the adsorption energy is only 0.009 eV.

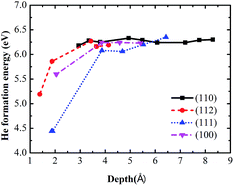Fig. 2 Formation energy of He as a function of the depth in the W surfaces with different orientations.

As shown in Fig. 2, the He formation energy in different surfaces exhibits the order of W(110) > W(112) > W(100) > W(111). The dissolved He atom prefers to stay at the W(111), W(112) and W(100) surfaces because of the lower formation energy. As for the W(111) surface (Fig. 3), the He dissolution induces a reduction in the vacancy formation energy of the surrounding W atoms, which results in the formation of vacancies and interstitial W atoms on the surface. Similar phenomena are also found on the W(112) and W(100) surfaces (corresponding process is shown in Fig. S4 and S5 of the ESI†). With an increase in He_n clusters in W bulk, the vacancy formation energies significantly decrease the near clusters.⁴¹ It was claimed in previous studies that He clusters could cause the formation of a vacancy and interstitial W atom when n > 5.⁴² Whereas, this phenomenon is more obvious on the surface than that in the bulk according to our results. For example, on the W(111) surface, a single He atom dissolving on the surface regions can cause the formation of vacancies and interstitial W atoms. Based on MD simulation, Li et al. also found that interstitial W atoms are mostly formed along the (111) orientation during the formation and growth of He clusters.^14,43 These occurrences imply that surface damage is very severe under He ion irradiation because He can induce vacancy formation on W surfaces. He atoms combine with the He-induced vacancies, which further reduces the He formation energies and leads to the formation of He–vacancy complexes on the surface. The formed complexes will trap more interstitial He atoms and cause He accumulation. This process explains the experimental phenomenon^3,4,6 of bubble formation under low energy (no displacement damage) He ion irradiation.

Fig. 3 Side view (upper part only) of the W(111) surface with a dissolved single He atom before and after relaxation. (a) He dissolved between the 3rd and 4th layer and (b) He dissolved between the 4th and 5th layer. The number represents the corresponding layer. Light blue: W atoms, blue: interstitial W atoms and red: He atoms.

3.1.3 He–He interaction and self-trapping on W surfaces. For H atoms, the interaction between H–H shows a strong repulsion within the short-range in W bulk, which means that H atoms are difficult to accumulate with each other to form H blisters.⁴⁴ Whereas, He atoms are different and easily form clusters in perfect W crystals (without defects such as vacancies) due to the strong attraction between He–He.³⁹ Previous studies showed that strong binding exists between two He atoms with the value of 1.0 eV.³⁹ The formation of He clusters caused by self-trapping can produce displacement and defects in surrounding W atoms, which aggravate He accumulation on the surfaces. With the He clusters growing and moving, the surface will blister and its morphology will change. The He–He binding energy is obtained by

E^b = 2 E_S+He − E_S+2He − E_S, (3)

where, E_S+2He is the total energy of the W surface with two interstitial He atoms. Table 2 shows the distance dependence of the binding energies of two He atoms at the interstitial sites between the 4th and 5th layer of the surfaces, where Confs. 1–8 denote structures with different initial He–He distances (corresponding structures are shown in Fig. S6–S9 of the ESI†), such as, Conf. 1 of the W(110) surface represents the structure with an initial He–He distance of 1.59 Å. The positive and negative values indicate attraction and repulsion, respectively. As shown in this table, the interaction of two He atoms becomes very weak as the He–He distance increases over 3 Å, which is similar to that in W bulk.

Table 2 He–He binding energy E^b (eV) at the interstitial site between the 4th and 5th layer of the W surfaces with different orientations; d_i (Å) and d_j (Å) are the initial and relaxed He–He distances, respectively. The positive and negative binding energies indicate attraction and repulsion, respectively. Confs. 1–8 represent structures of the W surface with different initial He–He distances (corresponding structures are shown in Fig. S6–S9 of the ESI)

Configuration	W(110)			W(112)			W(111)			W(100)
	di	dj	E^b	di	dj	E^b	di	dj	E^b	di	dj	E^b
Conf. 1	1.59	1.50	1.05	1.46	1.46	3.62	1.03	1.46	0.71	2.24	2.29	0.21
Conf. 2	2.24	2.55	0.30	2.76	1.51	0.96	1.51	1.47	0.71	3.08	3.08	−0.01
Conf. 3	2.75	1.52	0.97	3.12	1.47	3.52	2.17	1.46	0.71	3.23	3.16	−0.04
Conf. 4	3.17	2.96	0.14	4.10	4.43	0.02	2.83	4.49	−0.23	4.48	4.48	0.03
Conf. 5	3.88	3.70	0.12	4.50	4.54	0.03	2.96	4.49	−0.23	5.01	4.87	0.05
Conf. 6	4.48	4.48	0.10	5.28	5.22	0.03	3.46	4.48	−0.61	6.34	6.34	0.10
Conf. 7	4.76	4.72	−0.02	5.51	5.51	−0.04	4.15	4.49	0.23	6.73	6.69	0.02
Conf. 8	5.49	5.53	0.02	5.70	5.62	−0.04	6.47	7.79	0.03	7.12	7.09	−0.02

---

In most cases, two He atoms combine through attraction to each other with initial He–He distances smaller than 3 Å below the W(110), W(112), and W(111) surfaces. On the W(110) and W(112) surfaces, the He–He binding energy is about 1.0 eV when two He atoms form He₂. However, the He–He binding energy (∼0.7 eV) and self-trapping distance (capture radius) are smaller when two He atoms combine on the W(111) surface than on the other surfaces. For example, for Conf. 1 of the W(111) surface, two He atoms form an He₂-vacancy complex after structure relaxation, as shown in Fig. 4(b). Also, the behaviors of Confs. 2 and 3 are similar to that of Conf. 1 after relaxation, which implies that the interaction between two He atoms is weaker than that on the W(110) and W(112) surfaces. In addition, when the He–He distance is larger than 2.83 Å on the W(111) surface, these two atoms will respectively form two He–vacancy complexes after relaxation, which further increases the He–He distances, such as Conf. 4 shown in Fig. 4(c). The formed He₂-vacancy or He–vacancy complex moves to the surface after structure relaxation, which provides support to previous simulation results that there is an interaction between He clusters and W surfaces.^18,45

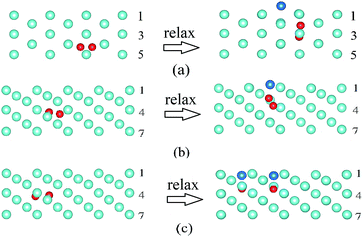Fig. 4 Side view (upper part only) of two He atoms at the depth between the 4th and 5th layer (some cases in Table 2) before and after relaxation. (a) Conf. 1 of the W(112) surface; (b) Conf. 1 of the W(111) surface and (c) Conf. 4 of the W(111) surface. The number represents the corresponding layer. Light blue: W atoms, blue: interstitial W atoms and red: He atoms.

Furthermore, there are some specialty cases in Table 2, such as Conf. 2 of the W(110) surface, Conf. 1 of the W(100) surface, and Confs. 1 and 3 of the W(112) surface. For Conf. 2 of the W(110) surface, it does not form He₂ when the He–He distance is 2.24 Å. These two He atoms do not combine because the force direction is closely packed and another W atom exits when the structures relax, as explained by Wang et al.²⁰ Similarly, the He atoms do not form He₂ for Conf. 1 of the W(100) surface; meanwhile, the He–He binding energies are larger than 3.50 eV for Confs. 1 and 3 of the W(112) surface, which leads to the two He atoms forming an He₂-vacancy complex and an interstitial W atom, such as Conf. 1, as shown in Fig. 4(a).

Moreover, as shown in Fig. 3 and 4, the dissolved He atoms would induce the formation of W vacancies, interstitial atoms, and complexes (He-vacancies or He₂-vacancies) below the W surfaces. Hammond et al. found an analogous phenomenon based on MD simulation.¹³ The formed defects (such as vacancies and clusters) will trap surrounding interstitial He atoms and cause He accumulation near the defects. These small clusters may be considered the formation of initial He bubbles. He cluster growth will cause more displacement of W atoms and the formation of interstitial W atoms. The formed interstitial W atoms move out of the surface layer, which causes the formation of adatoms and the W surface morphology changes. With the amount of interstitial W atoms and He bubbles increasing, incipient nanofuzz will form at the surface regions. This process provides a good explanation for the nanofuzz formation under low energy He ion irradiation.^6–8

We further explored self-trapping He at different depths on W surfaces with different orientations to understand the effects of surface dependence on He–He interactions (corresponding configuration structures are shown in Fig. S10–S13 of the ESI†). The He–He formation energy is defined as

E^f_2He = E_S+2He − E_S − 2E(He). (4)

Here, all the symbols take the same definitions as above. The obtained value in the bulk is 11.34 eV, which is in agreement with previous value of 11.42 eV obtained by Zhang et al.¹⁰ As seen from Table 3, for the W(100), W(111), and W(112) surfaces, the formation energies of two He atoms are smaller than that in the bulk, which results in these surfaces being prone to He accumulation. For the W(100) surface, the larger binding energy means stronger He self-trapping near the surface, which may result in the formation of isolated large bubbles. For the W(111) surface, the He–He binding energy is smaller than that in the bulk (1.0 eV (ref. 39)), which means weaker self-trapping and the formation of small bubbles. Based on the discussion above, He may be prone to form He–vacancy complexes by combining with He-induced vacancies rather than He clusters by self-trapping on the W(111) surface. Considering the large formation energy, the W(110) surface does not easily generate the initial He bubble.

Table 3 Binging energy E^b (eV) and formation energy E^f_2He (eV) of two He atoms on W surfaces with different orientations as the He distribution depth increases. The asterisks represent the cases of no obtain binding energy due to that He escaping from the W surfaces or not forming He₂

Layer	W(110)		W(112)		W(111)		W(100)
	E^b	E^f2He	E^b	E^f2He	E^b	E^f2He	E^b	E^f2He
2–3	1.49	11.07	*	*	*	*	1.52	9.88
3–4	1.05	11.53	0.93	9.43	0.68	8.21	1.27	11.21
4–5	1.05	11.53	0.96	11.48	0.71	9.17	*	*
5–6					1.12	11.04
6–7					1.15	11.01
7–8					1.39	11.01

---

In summary, the orientation influenced He dissolution on W surfaces was found by calculating the vacancy and He formation energies as well as the He–He binding energy on the different W surfaces. The formed vacancies can trap interstitial He atoms resulting in He accumulation near the surface. One or two He atoms can cause displacement of the surrounding W atoms and form vacancies, which lead to He inducing much more severe surface damage than H. The dissolved He atom is easier to induce vacancy formation on the W(111), W(100), and W(112) surfaces than in the bulk, which will cause He accumulation on the surfaces due to He-induced vacancy trapping. The He atoms remain unstable at the W(110) surface due to the larger He formation energy as well as difficulties forming vacancies. Our results clearly show the heterogeneity of the He dissolution behavior.

3.2 Diffusion of He toward the surface

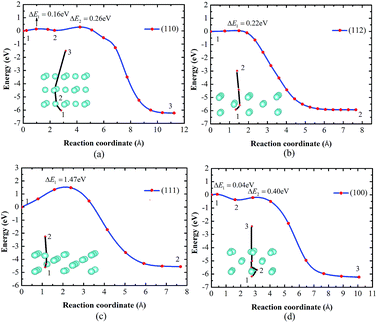
He diffusion behavior influences the He distribution on the surface, which is determined by the He diffusion energy barriers. Due to the fact that the He diffusion along the TIS–TIS path is the optimal path suggested in recent studies,^2,39 the same path was set in our studies on the diffusion behaviors on the W surface. The TIS below the third layer surface is set as the initial state, in which the position in the vacuum away from the surface (>3 Å) is set as the final state. It should be noted that the initial states of He in the W(111) and W(112) surfaces change after structure relaxation. The He atom in the W(111) and W(112) surfaces moves from the TIS to the He-induced vacancy site and the interstitial site between the 2nd and 3rd layer, respectively [Fig. 5(b) and (c)].

Fig. 5 He diffusion towards the surfaces of (a) W(110), (b) W(112), (c) W(111), and (d) W(100). Insets represent the diffusion paths (TIS–TIS) of the He atom toward the surface. Light blue: W atoms and red: He sites.

As seen in Fig. 5, the He diffusion energy barriers are 1.47 eV, 0.40 eV, 0.26 eV and 0.05 eV for the W(111), W(100), W(110), and W(112) surfaces, respectively. There are much larger He diffusion barriers in the surfaces [such as the W(111) surface] than that in the bulk (0.06 eV given by Becquart et al.³⁹). Previous studies have found that trap mutation reactions easily occur on the W(111) surface.^14,15 In our studies on the behaviors of He diffusion toward the surface, the He escaping behavior is affected by the trap mutation on the W(111) surface. As shown in Fig. 5(c), the change in the He diffusion initial state can be expressed as:

W + He → He–V + W_s, (5)

where, He–V and W_s are an He–vacancy complex and interstitial W atom, respectively. He dissolves between the 3rd and 4th layer of the W surfaces, which causes the displacement of the surrounding W atoms, and forms a W vacancy and an interstitial W atom. The dissolved He atom combines with a vacancy and the interstitial W atom moves near the surface. In this case, He must overcome the vacancy-binding barrier to escape from the surface, which causes a higher activation barrier and aggravates the He accumulation on the surface. For the W(100) surface, He diffusion induces W vacancy formation in the second layer. The vacancy trapping hinders He moving to the surface. As for the W(110) surface, the situations seem more complicated and needs further investigation. The barrier is lower on the W(112) surface, which is caused by surface texture. As shown in Fig. 5(b), the W(112) surface is a step surface with a low area density. The He atom easily diffuses along the channels when He moves to the step edge. The discussions above exhibit evidence that shows a vacancy-trapping mechanism hinders He escaping from the surface. Taking into consideration temperature effects, He can easily escape and desorb from the surfaces of W(100), W(110), and W(112) due to their relatively smaller barriers than W(111). The activation barrier of He on the W(111) surface is as high as 1.47 eV, and He can only escape from the W(111) surface by overcoming the vacancy-binding barrier at very high temperatures, which results in He accumulating easier on the W(111) surface.

In summary, the above results imply that He accumulation and bubble formation are influenced by the surface orientation. The He dissolution behavior shows that the W(111) surface forms He accumulation easier because of its smaller formation energy for vacancies and He, as well as the formation of He-induced vacancies. The high He activation barrier aggravates He accumulation on the W(111) surface. The formation of He-induced vacancies cause He accumulation on the W(111), W(100), and W(112) surfaces. Therefore, the W(111) surface is more prone to He bubble formation than the other surfaces, whereas the W(110) surface is resistant to He bubble formation.

4. Conclusions

By exploring the dissolution and diffusion behaviors of He on different W surfaces using the first-principles method, surface orientation influenced surface damage is discussed. The results show that the vacancy formation energy, He self-trapping, and He-induced vacancy formation all affect He accumulation on the W surface, among which He self-trapping and He-induced vacancy formation play an important role in He bubble formation. He prefers to induce vacancies and the formation of interstitial W atoms near the surfaces of W(111), W(100), and W(112) than in the bulk, which causes He accumulation on these surfaces. When the W surface faces H and He ion irradiation, such as in the ITER, H accumulation is severe on the W(111), W(112), and W(100) surfaces due to the fact that He-induced vacancies provide trapping sites for H atoms and aggravates H retention. In addition, it is difficult for He to escape from the surface due to He-induced vacancy trapping, which causes a higher activation barrier and aggravates the He accumulation on the W(111) surface, whereas the W(110) surface is resistant to He bubbles due to its large vacancy and He formation energies. These results are helpful for understanding He bubble formation on W surfaces and explaining the orientation-influenced He bubble and surface morphologies under low energy He ion irradiation.

Acknowledgements

This work was supported by the National Science Foundation of China under Grant No. 11474283, 11475215, and 11605231; the key project of National Science Foundation of China under Grant No. 11534012; the Youth Innovation Promotion Association of CAS under Grant No. 2016386; the One Hundred Person Project of the Chinese Academy of Sciences No. Y54N251241; and Director Grants of CASHIPS. The calculations were partly performed in the Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center and Computer Network Information Center of Chinese Academy of Science, and partly using the Tianhe-2JK computing time award at the Beijing Computational Science Research Center (CSRC).

References

1. G. Federici, C. H. Skinner and J. N. Brooks, et al., Nucl. Fusion, 2001, 41, 1967.
2. G. H. Lu, H. B. Zhou and C. S. Becquart, Nucl. Fusion, 2014, 54, 086001.
3. D. Nishijima, M. Y. Ye and N. Ohno, et al., J. Nucl. Mater., 2003, 97, 313.
4. D. Nishijima, M. Y. Ye and N. Ohno, et al., J. Nucl. Mater., 2004, 1029, 329.
5. M. J. Baldwin and R. P. Doerner, Nucl. Fusion, 2008, 48, 035001.
6. S. Kajita, W. Sakaguchi and N. Ohno, et al., Nucl. Fusion, 2009, 49, 095005.
7. M. J. Baldwin and R. P. Doerner, J. Nucl. Mater., 2010, 404, 165.
8. N. Ohno, Y. Hirahata and M. Yamagiwa, et al., J. Nucl. Mater., 2013, 438, S879.
9. C. M. Parish, H. H. Harry and M. Meyer, et al., Acta Mater., 2014, 62, 173.
10. P. B. Zhang, T. T. Zou and J. J. Zhao, J. Nucl. Mater., 2015, 467, 465.
11. H. B. Zhou, Y. L. Liu and G. H. Liu, Comput. Mater. Sci., 2016, 112, 487.
12. Y. Ding, C. Q. Ma, M. Li and Q. Hou, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 368, 50.
13. K. D. Hammond and B. D. Wirth, J. Appl. Phys., 2014, 116, 143301.
14. M. Li, J. C. Cui and J. Wang, et al., Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 352, 92.
15. X. S. Wang, Z. W. Wu and Q. Hou, J. Nucl. Mater., 2015, 465, 455.
16. F. Sefta, N. Juslin and B. D. Wirth, J. Appl. Phys., 2013, 114, 243518.
17. D. Maroudas, S. Blondel and L. Hu, et al., J. Phys.: Condens. Matter, 2016, 28, 064004.
18. L. Hu, K. D. Hammond and B. D. Wirth, et al., Surf. Sci., 2014, 626, L21.
19. A. V. Barashev, H. Xu and R. E. Stoller, J. Nucl. Mater., 2014, 454, 421.
20. J. Wang, Y. Zhang and H. B. Zhou, et al., J. Nucl. Mater., 2015, 461, 230.
21. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
22. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
24. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
25. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901.
26. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978.
27. K. Yonehara and L. D. Schmidt, Surf. Sci., 1971, 25, 238.
28. M. K. Debe and D. A. King, Phys. Rev. Lett., 1977, 39, 708.
29. D. Spišák and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195426.
30. T. Seletskaia, Y. Osetsky and R. E. Stoller, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134103.
31. H. B. Zhou, Y. L. Liu and S. Jin, et al., Nucl. Fusion, 2010, 50, 115010.
32. B. Jiang, F. R. Wan and W. T. Geng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 134112.
33. G. Y. Pan, Y. S. Zhang, Y. G. Li, et al., Int. J. Mod. Phys. C, submitted.
34. A. Nojima and K. Yamashita, Surf. Sci., 2007, 601, 3003.
35. X. Wei and J. B. Adams, Surf. Sci., 1994, 319, 45.
36. S. G. Wang, E. K. Tian and C. W. Lung, J. Phys. Chem. Solids, 2000, 61, 1295.
37. B. Q. Fu, W. Liu and Z. L. Li, Appl. Surf. Sci., 2009, 255, 8511.
38. C. S. Becquart and C. Domain, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 255, 23.
39. C. S. Becquart and C. Domain, Phys. Rev. Lett., 2006, 97, 196402.
40. G. Y. Huang, N. Juslin and B. D. Wirth, Comput. Mater. Sci., 2016, 123, 121.
41. Y. W. You, X. S. Kong and X. B. Wu, et al., Nucl. Fusion, 2016, 57, 016006.
42. Y. W. You, D. D. Li and X. S. Kong, et al., Nucl. Fusion, 2014, 54, 103007.
43. M. Li, J. C. Cui and J. Wang, et al., J. Nucl. Mater., 2013, 433, 17.
44. J. C. Xu and J. J. Zhao, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 3170.
45. L. Hu, K. D. Hammond and B. D. Wirth, et al., J. Appl. Phys., 2014, 115, 173512.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03281a

---