Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring ion migration in Li2MnSiO4 for Li-ion batteries through strain effects†
Mingzhen Jia a,
Hongyan Wang*a,
Zhandong Sunb,
Yuanzheng Chena,
Chunsheng Guo
a,
Hongyan Wang*a,
Zhandong Sunb,
Yuanzheng Chena,
Chunsheng Guo c and
Liyong Gan
c and
Liyong Gan c
c
aSchool of Physical Science and Technology, Southwest Jiaotong University, Key Laboratory of Advanced Technology of Materials, Ministry of Education, Chengdu 610031, China. E-mail: hongyanw@home.swjtu.edu.cn
bDepartment of Physics, University of Debrecen, Debrecen 4026, Hungary
cSuperconductivity and New Energy R&D Center, Southwest Jiaotong University, Mail Stop 165#, Chengdu 610031, China
First published on 16th May 2017
Abstract
The orthorhombic crystal Li2MnSiO4 is widely studied as a potential high specific energy cathode material for rechargeable batteries. However, low ion diffusion hinders its development. In this paper, first principles calculations were performed to investigate the effect of lattice strain on the ionic diffusion and the defect formation in Li2MnSiO4, which are directly related to the rate performance. The computational results show that the Li2MnSiO4 material has a two dimensional pathway for effective lithium ion transport, and the Li ion migration barrier is sensitive to the strain applied on the lattice. When strain is applied in bc plane, the migration energy increases/decreases with compressive/tensile strain (from −5% to +5%) for both channels. Furthermore, strain applied in ab and ac planes can also affect Li migration, but the effect is not as obvious as when strain is applied in the bc plane. The Li/Mn anti-site defect cannot be produced spontaneously, and the defect formation energy slightly decreases when strain works on the lattice. In fact, an appropriate strain value can improve the rate performance of Li2MnSiO4 effectively for applications.
1. Introduction
The high energy and power density of Li-ion rechargeable batteries have been focused on since the development of electric vehicles, portable electronics and large-scale grid storage.1,2 However, most batteries deliver capacities far below their theoretical values in practical use. One important reason is the low ionic diffusion or electronic conductivity of the electrode materials.3,4 Research into electrode materials plays a major role in the development of lithium ion batteries. Much attention has been concentrated on the development of electrode technology, in particular for the cathode material, which is the most expensive and capacity limiting component in battery systems.5In search of various cathode materials, Nytén et al.6 first successfully synthesized the Li2FeSiO4 material in 2005. The family of Li2MSiO4 (M = Mn, Fe, Co, Ni) silicate materials has attracted much attention as potential materials for Li-ion batteries,7 because these compounds’ elements are abundant, low cost and environmentally friendly, and two lithium ions could be extracted per formula unit (f.u.) in theoretical work. Li2CoSiO4 exhibits a large irreversible capacity in the cycle process, about 170 mA h g−1 capacity (1.1 Li per f.u.) at the first charge and only 60 mA h g−1 irreversible capacity in the first discharge.8 The Ni-based silicate material has not been synthesized experimentally, and theoretical calculations pointed out prohibitively high voltages when lithium is extracted from Li2NiSiO4.5,9 In 2012, Rangappa et al.10 prepared Li2FeSiO4 and Li2MnSiO4 by a rapid one pot supercritical fluid synthesis method. It is found that the two cathode materials provide a high reversible capacity (about 340 mA h g−1 at 45 ± 5 °C) and two lithium ions could be completely extracted/inserted into the structure. Some research also suggests that the second lithium ion is removed more easily from Li2MnSiO4 than from Li2FeSiO4, because the high oxidation state Mn4+ is more accessible than the unusual Fe4+ state.11 Therefore, Li2MnSiO4 is one of the most promising cathode materials for lithium ion batteries.
For the pure Li2MnSiO4 material, the intrinsic electronic and ionic conductivity is poor, and the capacity has a serious loss upon cycling. So far, there are many methods to improve the performance of the material, such as carbon coating, chemical doping and particle nanosizing. Research suggests that carbon–Li2MnSiO4 exhibited a stable discharge behavior and improved electrochemical performance.12,13 Al, Ga, Fe, Cr, V, etc. have been doped to the Li2MnSiO4 material,14–17 and these dopants play an active role in improving the electrochemical properties in some cases. It should be noted that many problems still remain. Recently, some researchers reported that changing the lattice strain could be considered as a useful method to improve the kinetic properties of various cathode materials, as the activation barrier energy is sensitive to the lattice strain. The layered LiCoO2 has a one-dimensional pathway for Li migration, and first principles calculations show that activation barrier decreases/increases depend on tensile/compressive stress along the c-axis direction between −5% and +5%.18 For the olivine compounds LiFePO4 and NaFePO4, Tealdi et al.19 suggested that the strain of the lattice has a remarkable effect on the material, with a major increase of the Li+ and Na+ conductivity and a decrease of the blocking defect. Moreover, changing the lattice strain is regarded as an effective method to modulate the properties of materials, such as optics,20 superconductivity21 and conductivity.22 With the development of technology, some experiments have shown an improvement in the performance of oxide materials for solid oxide fuel cells (SOFCs) by tuning the lattice strain. The lattice strain plays a positive role in ionic migration, oxygen vacancy formation, and oxygen molecule adsorption.23 For example, the ionic conductivity has been greatly improved, increasing by about five to eight orders of magnitude.24,25 Thus, researching the lattice strain in the Li2MnSiO4 material is necessary.
Controlling the ion dynamics of the electrode material is critical for the Li ion battery. In this paper, we present a density functional theory investigation of a silicate type of Li2MnSiO4 material. The influence of the crystal structure under biaxial strain on the ab, ac and bc planes is considered in detail. Then the strain effects on the Li ion migration and defect formation are discussed. So far, there have been no experiments about improving the properties of Li2MnSiO4 by controlling the strain. We hope our results could play a guiding role for further practical applications in the future.
2. Computational details
First principles calculations were performed using the Vienna Ab Initio Simulation Package (VASP) code,26,27 and core ion and valence electron interactions based on the projector augmented wave (PAW) potentials.28 The Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) was used for the exchange–correlation energy.29 In order to accurately simulate the strong interaction character of the d electrons for the transition-metal ions, the Hubbard-type correction is included.30The lattice parameters, cell volumes and the atomic positions are fully optimized and relaxed until the energy is less than 1.0 × 10−5 eV and the force on each atom is less than 0.02 eV Å−1. We used the conjugate gradient minimization method for geometry optimization. A Monkhorst–Pack grid with 2 × 2 × 2 (for a 2 × 2 × 2 supercell) meshes was employed in the irreducible Brillouin zone.31 A kinetic energy cutoff of 500 eV was used for the plane-wave. Following previous reports, the effective Ueff (U–J) is fixed at 5 eV for the Mn-3d state.32,33 According to the above calculation method, biaxial lattice strain is applied in the ab, ac and bc planes. For the strained systems, in the range of −5% to +5%, the strain value is compared with the relaxed lattice parameters and is applied simultaneously in two crystal axes. The lattice strain, ε, is expressed by the following equation:
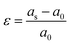 | (1) |
The minimum energy pathways and activation barriers of Li ion migration were calculated using the climbing image nudged elastic band (CI-NEB) method,38,39 in which a number of images are optimized between the starting point and the end point along the reaction path. The CI-NEB method is a modification of the NEB method. The image is made to climb up along the elastic band to converge rigorously on the highest saddle point.
3. Results and discussion
3.1 Strain effects on the crystal structure
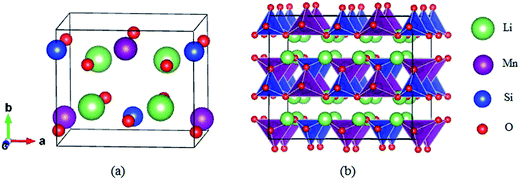
The structure of Li2MnSiO4 was first reported by Dominko et al.40 in 2006, and it is analogous to that of the Li2FeSiO4 (ref. 41) crystal, with the space group pmn21 accompanied by a slightly distorted orthorhombic lattice. The lattice parameters are a = 6.3109(9) Å, b = 5.3800(9) Å, c = 4.9662(8) Å, and α = β = γ = 90°. The Li2MnSiO4 compound has a rich polymorphism with a series of [MnO4], [SiO4] and [LiO4] tetrahedral units. As seen in Fig. 1, the [MnO4] and [SiO4] tetrahedral structures are in the same direction parallel to the c axis and form an interaction arrangement in the ab plane. All tetrahedra are corner-sharing at the red oxygen atoms, and the Mn and Si ions are located at the centers of the oxygen tetrahedra. The Li ions are located between the layers of [MnO4] and [SiO4]. The optimized crystal parameters of Li2MnSiO4 are listed in Table S1 in the ESI.† Our results are in excellent agreement with experiments and other theoretical work.40,42,43 The good reproduction of the experimental structure provides a good starting point for our calculations.The Li2MnSiO4 supercell was first optimized with zero strain applied. Subsequently, plane biaxial compressive and tensile strains were applied in the ab, ac and bc planes. By providing a strain value, the atomic position is able to be optimized satisfactorily. Using this procedure, for example, when strain is applied in the ab plane, the lattice parameter c becomes the only lattice parameter of the crystal structure for scaling behavior. Fig. 2 shows the total energy of the Li2MnSiO4 supercell as a function of the lattice parameter c for both compressive and tensile strain in the ab plane. The optimized total energy is obtained by employing parabolic curves. Here we use twice optimization (with two different accuracy values: 1% and 0.1%) for energy minimization to obtain the accurate lattice parameters. We can easily get the result that the introduction of positive tensile strain is more favorable than compressive strain from the total energy. When no strain is applied, optimized c equals 10.065 Å, and this value is between +1% and −1% strain. With strain applied in the ac and bc planes (see Fig. S1, ESI†), we can get the same results. The strained structures of minimized energy were used as the initial configurations for ion migration and defect calculations.
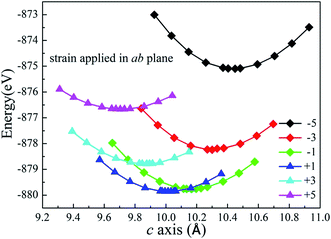 | ||
| Fig. 2 Total energy for the supercell (2 × 2 × 2) of Li2MnSiO4 as a function of the lattice parameter c for different strain applied in the ab plane. | ||
In general, as a positive strain is applied in the biaxial plane, a decrease in the third parameter is observed whereas the volume slightly increases. When the strain is applied negatively, the third parameter increases and the volume decreases slightly.36 Fig. 3 shows the calculated volumes with compressive and tensile strain applied. Comparing Fig. 2 and S1 (ESI†), we notice an excellent agreement of the lattice parameters and volumes with our computational results. The computed structural parameters and volumes of Li2MnSiO4 under six strains are summarized in Fig. S2, ESI.† All of this supports the rationality of our models and the stability of the structure under the strain applied.
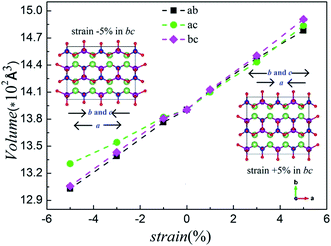 | ||
| Fig. 3 The calculated volumes for the Li2MnSiO4 (corresponding to unit cell) structure under various strains applied in the ab, ac and bc planes. | ||
3.2 Lithium ion migration in the Li2MnSiO4 structure
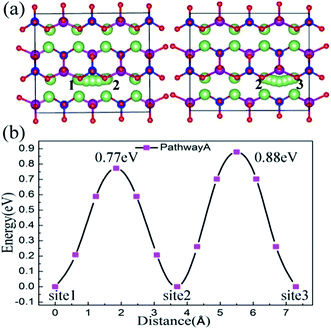
To investigate the influence of lattice strain on the Li ion diffusion behavior, first we studied the migration properties in the unstrained Li2MnSiO4 structure. The CI-NEB method, combined with a DFT+U approach, was used to calculate the saddle points. The lithium diffusion process uses a vacancy mechanism in the 2a × 2b × 2c supercell, which contains 31 lithium ions and one lithium vacancy. The essence of diffusion is the position exchange of a lithium vacancy and the neighboring lithium ions. For the Li2MnSiO4 structure, three possible migration pathways are identified: (a) pathway A – along the [100] direction, (b) pathway B – zigzag trajectory in the bc (011) crystal plane, and (c) pathway C – also in the bc plane and across the [MnSiO4] layer.In the [100] direction, the migration steps are schematically shown in Fig. 4(a). There are two kinds of pathways according to the different surrounding environments, which are labeled from site 1 to site 2 and site 2 to site 3. The calculated activation energy for pathway A is given in Fig. 4(b). Actually, there are different twice hopping situations for different activation energies. When lithium jumps from site 1 to site 2, the activation barrier is about 0.77 eV, the jumping distance is 3.70 Å, and the neighbor of the migrating ion is a [SiO4] tetrahedron. For another removal of a Li ion from site 2 to site 3, the neighbor is a [MnO4] tetrahedron, the activation barrier is about 0.88 eV and the jumping distance is 3.60 Å. From the above results, pathway A characterizes a linear channel in the Li layer. The activation barrier energy is 0.88 eV when a lithium ion migrates by pathway A.
For the bc plane, Li ion migration along pathway B is characterized by a zigzag trajectory between the Mn–Si–O layers. The migration steps and activation barriers are schematically shown in Fig. 5(a) and (b), respectively. Pathway B also consists of twice hopping, i.e. jumping from site 3 to site 4 and then from site 4 to site 5. From the migration structure (Fig. 5(a)), the twice hopping exhibits the same migration performance. The calculated activation barrier is about 0.78 eV and the jumping distance is 3.62 Å. For pathway C, the Li ion migrates across the [MnSiO4] layer, which induces a large electrostatic repulsive interaction between Li+ and the [MnSiO4] layer.44 This migration leads to a large activation barrier of 1.90 eV and the jumping distance is 4.95 Å (Fig. S3, ESI†), which are both substantially larger than the values for pathway A and pathway B. Therefore, it can be regarded as impossible that the Li ion migration follows pathway C.
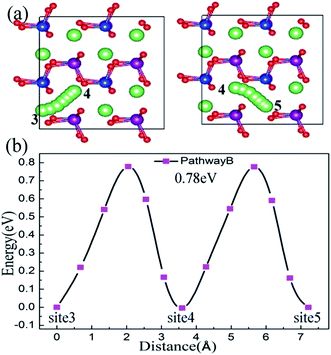 | ||
| Fig. 5 Pathway B is in the bc plane, not across the [MnSiO4] layer. The Li ion migration steps are shown in (a) and activation barriers are shown in (b). | ||
In the Li2MnSiO4 structure, all the Li ions occupy the same Wyckoff (4b) positions. So in each migration process, jumping into or out of different Li sites, the total energy remains the same. This can be seen clearly in the activation energy curves (Fig. 4(b), 5(b) and S3, ESI†); i.e. in pathway A, the energy of the system is almost the same whether the Li vacancy is at site 1, site 2 or site 3, likewise in pathway B and pathway C. From the lithium migration result, we can infer that the Li2MnSiO4 compound has a two dimensional pathway for Li ion migration. This is in good agreement with other theoretical work.11,44 Moreover, the other orthosilicate materials, Li2FeSiO4 and Li2CoSiO4, also have a 2D migration of lithium ions.45,46
3.3 Strain effects on Li ion migration
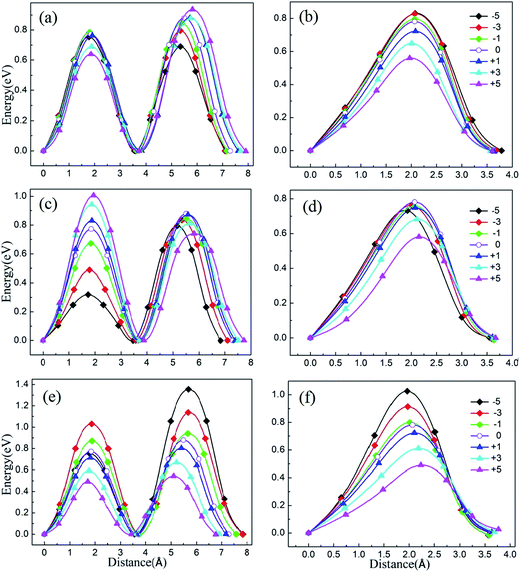
To illustrate the relationship between lattice strain and the Li ion migration barrier energy, the activation barrier of Li2MnSiO4 under different strains was calculated for two pathways. The lithium migrations were subjected to biaxial compressive and tensile strains between −5% and +5% in the ab, ac and bc planes. According to the migration of lithium ions in the unstrained Li2MnSiO4 material, here twice hopping mechanisms were calculated for pathway A and once hopping mechanisms were calculated for pathway B. The migration energy curves are shown in Fig. 6(a) and (b), (c) and (d), and (e) and (f), representing the energy when strain is applied in ab, ac and bc planes, respectively. For pathway A, the twice migration exhibits different energy barriers. We use the higher one as the lithium ion diffusion energy. Moreover, due to the crystal anisotropy, the mechanism of lithium migration shows different properties when biaxial strain is applied on different planes for Li2MnSiO4.Fig. 7 shows the migration barrier along the two channels as a function of applied strain. The activation barrier increases slightly with the strain applied in the ab and ac planes for Li diffusion in pathway A ([100] direction, Fig. 7(a)). Interestingly, the activation barrier shows an obvious decrease in the bc plane. As the strain changes from −5% to 5%, the activation barrier drops from about 1.36 eV to 0.54 eV. The energy value decreases gradually with the increase of strain from negative (ε < 0) to positive (ε > 0), and by almost forty percent for the unstrained system when +5% tensile strain is applied. That is to say, the Li ion diffusion coefficient becomes larger/smaller when the a axis lattice is elongated/compressed. The mechanism of the change in lithium migration under strain is very complicated.47 In general, the Li ion migration barrier is determined by the potential energy surface along the migration pathway, which is related to both the migration space and structural modifications.18,19,48 From the energy minimized structures, we can obtain the result that lattice parameter a gradually decreases when strain is applied in the bc plane. Therefore, the Li–Li hopping distance for migration along the [100] direction decreases, while it increases for the other planes (Fig. S2, ESI†). Additionally, the available polyhedron volumes at the saddle points also influence the activation barrier. Shorter Li–Li hopping distances and larger polyhedron volumes can decrease the Li ion activation energy. This rule is also useful in olivine systems; Tealdi et al.19 reported that LiFePO4 and NaFePO4 both have a one dimensional pathway for alkali-ion migration (along with the [010] direction). When strain is applied in LiFePO4 and NaFePO4, the migration energy decreases along with strain for the ac plane, while it increases slightly along with strain for the ab and bc planes.
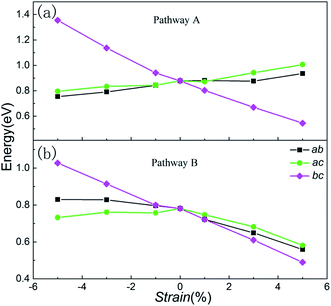 | ||
| Fig. 7 Change in the lithium ion activation barriers as a function of strain for (a) pathway A and (b) pathway B. | ||
Then, we start to consider Li ion migration in the bc plane for pathway B. We plot the activation barrier as a function of applied strain in Fig. 7(b). The activation barrier is different to that for pathway A. When strain is applied in the ab and bc planes, the lithium ion activation energy barriers decrease as a function of strain. In other words, the barriers are increased with compressive strain and reduced with tensile strain, compared to the unstrained condition. For the ac plane, the activation barrier has a slight change when compressive strain is applied. When tensile strain is applied it shows an obvious decrease. From our calculations, the strain-induced change of the activation barrier in the bc plane is more sensitive than that imposed in the ab and ac planes. During migration of lithium ions with a zigzag trajectory in the bc plane (pathway B), the tensile strain applied in the bc plane enlarged the lattice parameters b and c. Even though this increased the Li–Li hopping distances, the available polyhedron volumes at the saddle points were increased. Finally, under both different effects for Li migration, the barrier energy decreased. As the strain changes from −5% to 5%, the activation barrier drops from 1.03 eV to 0.50 eV. For the strain applied in the ab and ac planes, the change of the activation barrier for Li migration is less sensitive than the strain in the bc plane.
Therefore, the above results show that lithium ion migration can be enhanced substantially for both diffusion pathways through applying tensile strain in the bc plane. This suggests that applying strain in the bc plane is an effective method for increasing the ionic conductivity, which improves the rate performance of Li2MnSiO4 as a cathode material. This provides a good direction for future investigations into controlling the lattice parameters. In fact, this is a great challenge for the experimental technology associated with lattice mismatch, defect effects, the Jahn–Teller effect and so on. In order to find a more accurate explanation for the correlation between Li ion migration and lattice strain, further studies are necessary.
3.4 Strain effects on defects
The inherent defect of the silicate cathode materials Li2MSiO4 (M = Mn, Fe, Co, Ni), which involves the exchange of Li for an M atom, can be detrimental to the ion intercalation properties:
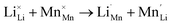 | (2) |
It was reported that anti-site disorder occurred when Li2MnSiO4 was first experimentally synthesized,40 with partial occupancies of Li and Mn at the 4b and 2a sites. The rearrangement of atoms in site-exchange materials influences the overall electrochemical performance.49
In order to determine whether the biaxial strain affects the intrinsic site-exchange defect, models with one pair of Li/Mn site-exchange (SE structure) based on the strained structures were built, and then the total energies of the defect structures were calculated. Comparing these energies with the energy of the undefective structure, we get the formation energy of one pair of Li/Mn site-exchange. Fig. 8 shows the total energy of two types of structure and the formation energy as a function of the biaxial strain in the bc plane for Li2MnSiO4. The formation of undefective Li2MnSiO4 is more favorable than that of the SE structure, no matter how much strain (−5% to +5%) is applied in the material. The result agrees well with other theoretical work when no strain is applied in Li2MnSiO4.11 This suggests that the SE defective structure cannot be produced spontaneously in theory. Besides, from the two curves of the total energy, both the Li2MnSiO4 and SE structures have the highest stability without strain.
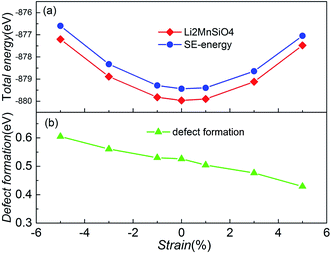 | ||
| Fig. 8 (a) The total energy for the Li2MnSiO4 and SE structures as a function of the applied biaxial/compressive strain in the bc plane. (b) Formation energy of one pair of Li/Mn site-exchange, based on eqn (2). | ||
In particular, as the imposed strain increases from compressive to tensile strain, the Li/Mn site-exchange formation energy slightly decreases. From Fig. 8(b), the formation of this defect ranges from 0.60 eV to 0.43 eV when the strain is applied from compressive −5% to tensile +5%. These values indicate that the defect is more pronounced for tensile strain. Changes in defect formation energy can be interpreted from structural modifications. Notice that the volume of the system increases gradually when the strain value increases. The increase of structural space makes the Li ion migration barrier decrease, and exchange of the defect Li and Mn sites is easier. In the LiFePO4 olivine system, the exchange of a Li ion with a neighboring Fe atom is involved, but the strain effects on defect formation are different from those in Li2MnSiO4.19 This suggests that the strain in LiFePO4 is not a crucial parameter to modulate the Li/Fe anti-site defect population, and the anti-site formation energy does not change dramatically when the applied strain is changed from compressive −3% to tensile +3%.
Therefore, from this section the key conclusion is that the defect of Li/Mn site-exchange cannot be produced spontaneously when strain is applied in the bc plane for Li2MnSiO4. Unfortunately, the calculation of one pair Li/Mn site-exchange formation energy found that the defect is more pronounced for tensile strain. Although the strain is applied in the bc plane, the ionic conductivity can be greatly improved. In summary, when trying to improve the performance of Li2MnSiO4 by using lattice strain, both types of strain should be taken into account and an appropriate value of strain chosen.
4. Conclusions
Changing lattice strain is considered to be a promising method to modulate the structural properties of materials. In this work, we use first principles and a CI-NEB method to investigate the ionic diffusion properties of Li2MnSiO4 when strain is applied in the ab, ac and bc planes. The result from the total energy shows that the introduction of tensile strain is more favorable than that of compressive strain. More importantly, the strain applied in the bc plane has a remarkable effect on Li migration, and the activation energy increases/decreases upon application of compressive/tensile strain for both pathways. For the Li2MnSiO4 material, the migration barriers are about 0.88 eV and 0.78 eV. These are reduced to 0.54 eV and 0.49 eV when the tensile strain is +5%. Besides, the Li/Mn anti-site defect of Li2MnSiO4 is also calculated, and the structure without defects has more stability than the SE system. But the formation energy of the defect decreases slightly when strain is applied. This is a slightly unfavorable modification to improve the rate performance of the material. These results suggest that an appropriate strain applied in the bc plane could improve the Li ion conductivity.Acknowledgements
We are grateful to the China National Science Foundation (Grants No. 11174237, 11404268), the Sichuan Province Applied Basic Research Plan (2017JY0056) and Fundamental Research Funds (Grant No. 2682015QM04) for the Central Universities for support of this work.References
- Y. K. Sun, Z. Chen and H. J. Noh, et al. Nanostructured high-energy cathode materials for advanced lithium batteries, Nat. Mater., 2012, 11(11), 942–947 CrossRef CAS PubMed.
- D. Larcher and J. M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7(1), 19–29 CrossRef CAS PubMed.
- M. D. Bhatt and C. O’Dwyer, Recent progress in theoretical and computational investigations of Li-ion battery materials and electrolytes, Phys. Chem. Chem. Phys., 2015, 17(7), 4799–4844 RSC.
- H. Yu, Y. G. So and A. Kuwabara, et al. Crystalline grain interior configuration affects lithium migration kinetics in Li-rich layered oxide, Nano Lett., 2016, 16(5), 2907–2915 CrossRef CAS PubMed.
- R. J. Gummow and Y. He, Recent progress in the development of Li2MnSiO4 cathode materials, J. Power Sources, 2014, 253, 315–331 CrossRef CAS.
- A. Nytén, A. Abouimrane and M. Armand, et al. Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material, Electrochem. Commun., 2005, 7(2), 156–160 CrossRef.
- M. E. Arroyo-de Dompablo, M. Armand and J. M. Tarascon, et al. On-demand design of polyoxianionic cathode materials based on electronegativity correlations: an exploration of the Li2MSiO4 system (M = Fe, Mn, Co, Ni), Electrochem. Commun., 2006, 8(8), 1292–1298 CrossRef CAS.
- C. Lyness, B. Delobel and A. R. Armstrong, et al. The lithium intercalation compound Li2CoSiO4 and its behaviour as a positive electrode for lithium batteries, Chem. Commun., 2007, 46, 4890–4892 RSC.
- S. Q. Wu, Z. Z. Zhu and Y. Yang, et al. Structural stabilities, electronic structures and lithium deintercalation in LixMSiO4 (M = Mn, Fe, Co, Ni): A GGA and GGA+U study, Comput. Mater. Sci., 2009, 44(4), 1243–1251 CrossRef CAS.
- D. Rangappa, K. D. Murukanahally and T. Tomai, et al. Ultrathin nanosheets of Li2MSiO4 (M = Fe, Mn) as high-capacity Li-ion battery electrode, Nano Lett., 2012, 12(3), 1146–1151 CrossRef CAS PubMed.
- C. A. J. Fisher, N. Kuganathan and M. S. Islam, Defect chemistry and lithium-ion migration in polymorphs of the cathode material Li2MnSiO4, J. Mater. Chem. A, 2013, 1(13), 4207–4214 CAS.
- V. Aravindan, K. Karthikeyan and K. S. Kang, et al. Influence of carbon towards improved lithium storage properties of Li2MnSiO4 cathodes, J. Mater. Chem., 2011, 21(8), 2470–2475 RSC.
- M. Zhang, S. Zhao and Q. Chen, et al. Li2+xMnSi1−xAlxO4/C nanoparticles for high capacity lithium-ion battery cathode applications, RSC Adv., 2014, 4(58), 30876–30880 RSC.
- N. Kuganathan and M. S. Islam, Li2MnSiO4 lithium battery material: atomic-scale study of defects, lithium mobility, and trivalent dopants, Chem. Mater., 2009, 21(21), 5196–5202 CrossRef CAS.
- S. Zhang, Z. Lin and L. Ji, et al. Cr-doped Li2MnSiO4/carbon composite nanofibers as high-energy cathodes for Li-ion batteries, J. Mater. Chem., 2012, 22(29), 14661–14666 RSC.
- Z. L. Gong, Y. X. Li and Y. Yang, Synthesis and Characterization of Li2MnxFe1−xSiO4 as a Cathode Material for Lithium-Ion Batteries, Electrochem. Solid-State Lett., 2006, 9(12), A542–A544 CrossRef CAS.
- C. Deng, S. Zhang and Y. X. Wu, et al. Partial substitution of Mn/Si with V, Cr or Al in Li2MnSiO4 nanoparticle: dependence of the physical and electrochemical properties on the substitution strategy, J. Electroanal. Chem., 2014, 719, 150–157 CrossRef CAS.
- F. Ning, S. Li and B. Xu, et al. Strain tuned Li diffusion in LiCoO2 material for Li ion batteries: a first principles study, Solid State Ionics, 2014, 263, 46–48 CrossRef CAS.
- C. Tealdi, J. Heath and M. S. Islam, Feeling the strain: enhancing ionic transport in olivine phosphate cathodes for Li- and Na-ion batteries through strain effects, J. Mater. Chem. A, 2016, 4(18), 6998–7004 CAS.
- A. M. Smith, A. M. Mohs and S. Nie, Tuning the optical and electronic properties of colloidal nanocrystals by lattice strain, Nat. Nanotechnol., 2009, 4(1), 56–63 CrossRef CAS PubMed.
- C. W. Hicks, D. O. Brodsky and E. A. Yelland, et al. Strong increase of Tc of Sr2RuO4 under both tensile and compressive strain, Science, 2014, 344(6181), 283–285 CrossRef CAS PubMed.
- X. Li, K. Maute and M. L. Dunn, et al. Strain effects on the thermal conductivity of nanostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(24), 245318 CrossRef.
- K. Wen, W. Lv and W. He, Interfacial lattice-strain effects on improving the overall performance of micro-solid oxide fuel cells, J. Mater. Chem. A, 2015, 3(40), 20031–20050 CAS.
- J. Lee, S. J. Pennycook and S. T. Pantelides, Simultaneous enhancement of electronic and Li+ ion conductivity in LiFePO4, Appl. Phys. Lett., 2012, 101(3), 033901 CrossRef.
- R. A. De Souza, A. Ramadan and S. Hörner, Modifying the barriers for oxygen-vacancy migration in fluorite-structured CeO2 electrolytes through strain: a computer simulation study, Energy Environ. Sci., 2012, 5(1), 5445–5453 CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- M. E. Arroyo-de Dompablo, M. Armand and J. M. Tarascon, et al. On-demand design of polyoxianionic cathode materials based on electronegativity correlations: an exploration of the Li2MSiO4 system (M = Fe, Mn, Co, Ni), Electrochem. Commun., 2006, 8(8), 1292–1298 CrossRef CAS.
- G. Zhong, Y. Li and P. Yan, et al. Structural, Electronic, and Electrochemical Properties of Cathode Materials Li2MSiO4 (M = Mn, Fe, and Co): Density Functional Calculations, J. Phys. Chem. C, 2010, 114(8), 3693–3700 CAS.
- K. Wen, K. H. L. Zhang and W. Wang, et al. Physical justification for ionic conductivity enhancement at strained coherent interfaces, J. Power Sources, 2015, 285, 37–42 CrossRef CAS.
- P. Strasser, S. Koh and T. Anniyev, et al. Lattice-strain control of the activity in dealloyed core–shell fuel cell catalysts, Nat. Chem., 2010, 2(6), 454–460 CrossRef CAS PubMed.
- C. Ferrara, C. Eames and M. S. Islam, et al. Lattice strain effects on doping, hydration and proton transport in scheelite-type electrolytes for solid oxide fuel cells, Phys. Chem. Chem. Phys., 2016, 18(42), 29330–29336 RSC.
- C. Tealdi and P. Mustarelli, Improving oxygen transport in perovskite-type LaGaO3 solid electrolyte through strain, J. Phys. Chem. C, 2014, 118(51), 29574–29582 CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113(22), 9978–9985 CrossRef CAS.
- R. Dominko, M. Bele and M. Gaberšček, etal. Structure and electrochemical performance of Li2MnSiO4 and Li2FeSiO4 as potential Li-battery cathode materials, Electrochem. Commun., 2006, 8(2), 217–222 CrossRef CAS.
- A. Nytén, A. Abouimrane and M. Armand, et al. Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material, Electrochem. Commun., 2005, 7(2), 156–160 CrossRef.
- H. Lee, S. D. Park and J. Moon, et al. Origin of poor cyclability in Li2MnSiO4 from first-principles calculations: layer exfoliation and unstable cycled structure, Chem. Mater., 2014, 26(13), 3896–3899 CrossRef CAS.
- M. E. Arroyo-deDompablo, R. Dominko and J. M. Gallardo-Amores, et al. On the energetic stability and electrochemistry of Li2MnSiO4 polymorphs, Chem. Mater., 2008, 20(17), 5574–5584 CrossRef CAS.
- N. Kuganathan and M. S. Islam, Li2MnSiO4 lithium battery material: atomic-scale study of defects, lithium mobility, and trivalent dopants, Chem. Mater., 2009, 21(21), 5196–5202 CrossRef CAS.
- A. Liivat and J. O. Thomas, Li-ion migration in Li2FeSiO4-related cathode materials: a DFT study, Solid State Ionics, 2011, 192(1), 58–64 CrossRef CAS.
- P. Zhang, X. D. Li and S. Yu, et al. Effects of Na Substitution on Li Ion Migration in Li2CoSiO4 Cathode Material, J. Electrochem. Soc., 2013, 160(4), A658–A661 CrossRef CAS.
- H. J. Yan, Z. Q. Wang and B. O. Xu, et al. Strain induced enhanced migration of polaron and lithium ion in λ-MnO2, Funct. Mater. Lett., 2012, 5(04), 1250037 CrossRef.
- Y. Shin, H. Ding and K. A. Persson, Revealing the Intrinsic Li Mobility in the Li2MnO3 Lithium-Excess Material, Chem. Mater., 2016, 28(7), 2081–2088 CrossRef CAS.
- L. Li, L. Zhu and L. H. Xu, et al. Site-exchange of Li and M ions in silicate cathode materials Li2MSiO4 (M = Mn, Fe, Co and Ni): DFT calculations, J. Mater. Chem. A, 2014, 2(12), 4251–4255 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03528d |
| This journal is © The Royal Society of Chemistry 2017 |