Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A statistical analytical model for hydrophilic electropore characterization: a comparison study†
P. Marracinoa,
M. Libertia,
P. T. Vernierb and
F. Apollonio *a
*a
aDepartment of Information Engineering, Electronics, and Telecommunications, Sapienza University of Rome, Rome, Italy. E-mail: apollonio@diet.uniroma1.it
bFrank Reidy Research Center for Bioelectrics, Old Dominion University, Norfolk, VA 23508, USA
First published on 22nd June 2017
Abstract
Molecular dynamics (MD) simulations have proved to be a useful tool for unveiling many aspects of pore formation in lipid membranes under the influence of external electric fields. In order to compare the size-related properties of pores in bilayers of various compositions, generated and maintained under different physical and chemical conditions, reference metrics are needed for characterizing pore geometry and its evolution over time. In the present paper three different methodologies for evaluating electropore geometrical behavior will be compared: (i) the first allows analysis of the dimensions of the pore through an algorithm that uses a Monte Carlo simulated annealing procedure to find the best route for a sphere with variable radius to squeeze through the pore channel; (ii) a more recent procedure extracts pore volume from an integration of a three-dimensional model of the irregular shape of the pore; (iii) a new method based on a statistical approach (following essential dynamics principles) describes pore geometrical fluctuations in a robust and reproducible way. For the same pore height of 2 nm the three methods give rise to mean electropore radii up to 3-fold different. The three approaches described here are not system-specific, i.e. the methods can be generalized for any kind of pore for which appropriate structural information is available.
Introduction
Membrane electroporation or electropermeabilization is recognized to cause a considerable increase in the electrical conductivity and permeability of the plasma membrane by the use of an externally applied electrical field.1,2Although this physical phenomenon is described in terms of transition of semi-permeable membranes from closed states to porated ones as the transmembrane potential exceeds a critical threshold,3,4 the complex mechanisms underlying electroporation processes in living cells are still not definitely established. In particular, several measurement techniques (i.e. electrical measurements,5 flow cytometry,6 and fluorescence microscopy7) indicate that permeabilization can occur in a few ns, implying a direct rearrangement of membrane components; however, even if optical recording of isolated electropores in planar droplet interface bilayers have been proposed,8 real-time analysis of membrane poration is still something that has never been completely experimentally proven. In this context, molecular dynamics (MD) simulations can provide an important perspective to elucidate nanoscale and nanosecond processes as the ones related to phospholipid double layer electropermeabilization.
MD simulations provide atomic-scale information on energetics and dynamics of complex biomolecular structures,9 on interactions of proteins with electric fields10–18 and on the behavior of membranes in electric fields, where it has been shown that application of a sufficiently strong electric field across lipid bilayers leads to the intrusion of water defects and the formation of aqueous, conductive pores.19–23 For the case of lipid bilayers in permeabilizing electric fields, thanks to MD simulations, the molecular mechanism has been unveiled,19,20,24 and the different stages of pore formation have been characterized.25
The diffusion of electropores, along with their rapid fluctuation in conductance, confirms that their structure is highly dynamic; this unique feature is well captured by MD simulations, in fact lipid electropores formed through molecular simulations are changing progressively and dynamically in time.26
Recently it has been shown that the lipid electropores can be stabilized by reducing the applied electric field from a higher value used for pore formation value to a lower sustaining value, enabling the characterization of the properties of these permeabilizing structures under controlled, steady-state conditions.27–29 The pores can be sustained for long periods (hundreds of nanoseconds or longer) by applying an external electric field of the appropriate magnitude along the axis of the pore. The diameter of the pore can be tuned by varying the external field, enabling a systematic examination of the ion conductance of lipid electropores.30 In this way an electropore can be maintained in a quasi-stable equilibrium condition, enabling a systematic analysis of its geometric and other properties.
Several methods have been used for the geometric characterization of membrane pores. One of these was developed for determining the size of the cavities in protein channels, which provide a solvent-filled pathway for solute translocation (Hole program, http://www.holeprogram.org/).31 The method developed by Smart and colleagues uses the van der Waals surface of molecules to infer the minimum cavity radius in a mechanistic fashion, i.e., a probe sphere with radius equal to the cavity radius should pass through the cavity without any direct obstruction. This method has been used to characterize lipid electropores.24
Another method extracts radius in a different way to define a pore size metric.22 Here the length of the pore in the z-direction (normal to the bilayer plane) is determined by the mean (xy) plane of the nitrogen (N) and phosphorus (P) atoms for each leaflet of the bilayer. The region between the two P–N planes (the bilayer interior) is divided into bins 1.5 nm thick in the z-direction, with each bin overlapping its neighbor by 0.5 nm. For each bin, the minimum and maximum x- and y-positions of the nitrogen and phosphorus atoms (in the pore walls) are calculated, and the center of the bin is taken to be the average of the maximum and minimum values. The radius for each bin is defined as the average distance between the positions of all phosphorus and nitrogen atom in that bin and the center. The overall pore radius is then selected as the smallest of the bin radii for each time point. The electropore boundaries may be determined from water density profiles32,33 rather than from phosphorus and nitrogen spatial locations.
Fernández and co-authors34 extracted pore volume in a three-step procedure. First, the porated section of the membrane is divided into three regions: an upper head group (polar) region, a lower head group (polar) region, and an intermediate (nonpolar) region (the bilayer interior). The nonpolar region is divided along the pore axis (z-axis) into cylindrical slices (cylindroids) whose radii are approximated from the coordinates of the water molecules at the greatest distance from the pore axis in the plane of the bilayer (x-axis and y-axis). The volume is then the sum of the volumes of all the cylindroids.
Finally, Marracino and co-authors recently introduced a new procedure for lipid pore characterization, based on the covariance matrix method.35 This approach, which extracts the pore geometry from a statistical analysis of the tridimensional surface of the pore, has been used to characterize a complex biomolecular system in physiological conditions36 and in external electric fields.37–40
As more and more complex and heterogeneous membrane systems are simulated, robust, reliable, and reproducible metrics are needed for comparisons of size and structure of stable pores, to facilitate the development of physics-based expressions for pore dynamics as a function of system components and conditions.
Here we compare three methods for defining electropore geometry,31,34,35 focusing on the differences among them and their strong and weak points, with the goal of capturing the essential geometric features of the electropore, so that the pore's surface area and volume can be quantitatively characterized.
Materials and methods
Simulation conditions
All molecular dynamics (MD) simulations were performed using the GROMACS set of programs, version 4.6.6.41 Lipid topologies were derived from OPLS united-atom parameters42 obtained from Peter Tieleman of the University of Calgary (http://moose.bio.ucalgary.ca). The Simple Point Charge (SPC) water model was used.43 Systems were coupled to a temperature bath at 310 K with a relaxation time of 0.1 ps and a pressure bath at 1 bar with a relaxation time of 1 ps, each using the v-rescale coupling algorithm,44 and the Berendsen algorithm,45 respectively. Pressure was coupled semi-isotropically (using a compressibility of 4.5 × 10−5 bar−1) normal to and in the plane of the membrane. Bond lengths were constrained using the LINCS algorithm46 for lipids and SETTLE47 for water. Short-range electrostatic and Lennard-Jones interactions were cut off at 1.0 nm. Long-range electrostatics were calculated by the PME algorithm48 using fast Fourier transforms and conductive boundary conditions. Reciprocal-space interactions were evaluated on a 0.12 nm grid with fourth-order B-spline interpolation. The parameter ewald_rtol, which controls the relative error for the Ewald sum in the direct and reciprocal space, was set to 10−5. Periodic boundary conditions were employed to mitigate system size effects.Systems and structures
All systems contained 512 lipid molecules—1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC)—and an ionic solution made of 88 potassium ions, 88 chloride ions, and approximately 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules, resulting in an initial potassium chloride concentration of about 91 mM in the bulk water. The initial box size was approximately 13 nm × 13 nm × 13 nm. After the equilibrated configuration was reached, the methodology described in ref. 34 to produce a trajectory with a stable electropore was used. An electric field of 400 megavolt per meter (MV m−1) was initially applied along the z-axis (normal to the bilayer plane). After electropore formation, the electric field intensity was lowered to 30 MV m−1 for a 50 ns productive run in order to stabilize the pore. No constraints have been applied to the system's roto-translational degrees of freedom, hence the pore has not been artificially immobilized. By visual inspection via VMD program,49 the lower-field trajectory exhibits a rather stable electropore for about 40 ns, while for the last 10 ns the electropore starts to expand, eventually becoming divergent. This is well represented in Fig. 1, where the axes of the ellipse representative of the central section of the pore are reported as a function of time as obtained with the statistical/analytical method fully described in the following (see section The statistical/analytical method).
000 water molecules, resulting in an initial potassium chloride concentration of about 91 mM in the bulk water. The initial box size was approximately 13 nm × 13 nm × 13 nm. After the equilibrated configuration was reached, the methodology described in ref. 34 to produce a trajectory with a stable electropore was used. An electric field of 400 megavolt per meter (MV m−1) was initially applied along the z-axis (normal to the bilayer plane). After electropore formation, the electric field intensity was lowered to 30 MV m−1 for a 50 ns productive run in order to stabilize the pore. No constraints have been applied to the system's roto-translational degrees of freedom, hence the pore has not been artificially immobilized. By visual inspection via VMD program,49 the lower-field trajectory exhibits a rather stable electropore for about 40 ns, while for the last 10 ns the electropore starts to expand, eventually becoming divergent. This is well represented in Fig. 1, where the axes of the ellipse representative of the central section of the pore are reported as a function of time as obtained with the statistical/analytical method fully described in the following (see section The statistical/analytical method).
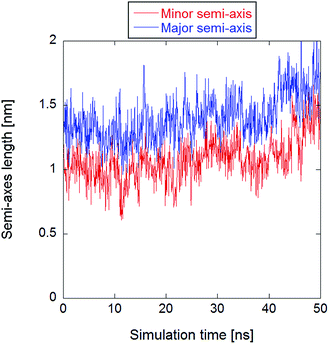 | ||
| Fig. 1 Time course of the minor and major axes of the central section of the electropore, clearly showing a divergent trend after the first 40 ns. | ||
For the purpose of the present work, although the three presented methodologies are able to describe the electropore morphology for any pore dynamics, the initial 40 ns have been considered in order to better compare the output of the three methodologies. As a matter of fact, the reason for the choice of a stable pore is essentially computational: one is able to study a possible electropore equilibrium condition, and hence to confine the analysis on a well selected region of the phase-space. This allowed the calculation of some statistical properties (see the standard errors and the standard deviations provided in the following) of the output data.
In order to minimize the electropore translational motion during the simulation it is convenient to apply a centering algorithm. The re-centering group is here chosen by taking into account, in the very central region of the pore (defined by lipid heads spatial distribution, see the Results section for the details), only those lipids whose translation along the z-axis do not exceed 0.2 nm (absolute value) from the membrane center of mass. The resulting re-centering group consisted in six lipids uniformly distributed around the inner pore region.
In the following sections, the three specified methodologies for determining electropore geometry will be applied to the molecular simulation described above, and the results for pore volume and shape will then be compared. As discussed in the following sections, the results are strongly dependent on the specific approach adopted. Even after the method is selected one must decide, for example, on what will constitute the limits of the pore walls. Shall they be more sharply defined by atoms of the phospholipid head groups or more loosely defined by water molecules, those in the pore channel and those hydrating the head groups? Fig. 2 points out these two ways.
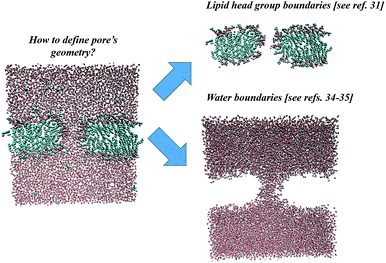 | ||
| Fig. 2 Two possible approaches for electropore definition. Molecular graphics images were generated with visual VMD 1.8.7.49 | ||
The HOLE method
Fig. 3 presents the methodological approach for obtaining the complete profile of electropore radii along the z direction. The procedure requires the user to specify an initial point p that lies anywhere within the pore. A probe sphere with radius R(p) can be centered at p without overlapping any atom:| R(p) = miniNatom[|xi − p| − vdWi] | (1) |
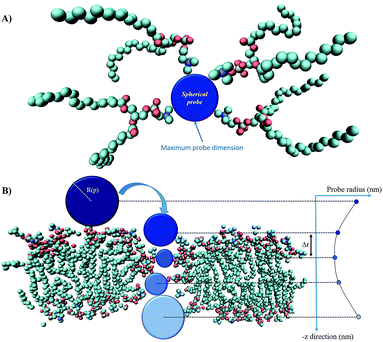 | ||
| Fig. 3 The main steps of the ‘hole’ method: panel (A) shows a top view of the spherical probe (blue) tangent to the van der Waals surfaces of lipid head group atoms; panel (B) is the side view of the spherical probe entering the pore (water molecules are not shown); as the probe enters more deeply into the electropore the maximum sphere radius may change, depending on the local constriction determined by lipid heads. Molecular graphics images were generated with visual VMD 1.8.7.49 | ||
The maximum probe dimension is essentially determined by the vdWi radii of the lipid heads atoms. For the sake of simplicity, in panel (A) of Fig. 3 only four representative lipids have been represented, hence the maximum probe sphere is just tangent to the nearest van der Waals surface. As the probe enters more deeply into the electropore, the maximum sphere radius may change, according to the local constriction. The net result can be thought of as producing the locus of a flexible sphere “squeezing” through the center of the ion channel. The use of Monte Carlo simulated annealing reduces the possibility of the routine becoming stuck in a local minimum. Panel (B) of Fig. 3 gives a graphical representation of different probe spheres at different pore heights: the complete probe radii profile is indicative of the electropore shape. In this work scripts available from HOLE 2.2 were used (http://www.holeprogram.org/). Following this methodological approach, the direct evaluation of electropore volume is obtained via the summation of several circular cylindroids:
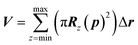 | (2) |
The water cylindrical slabs method
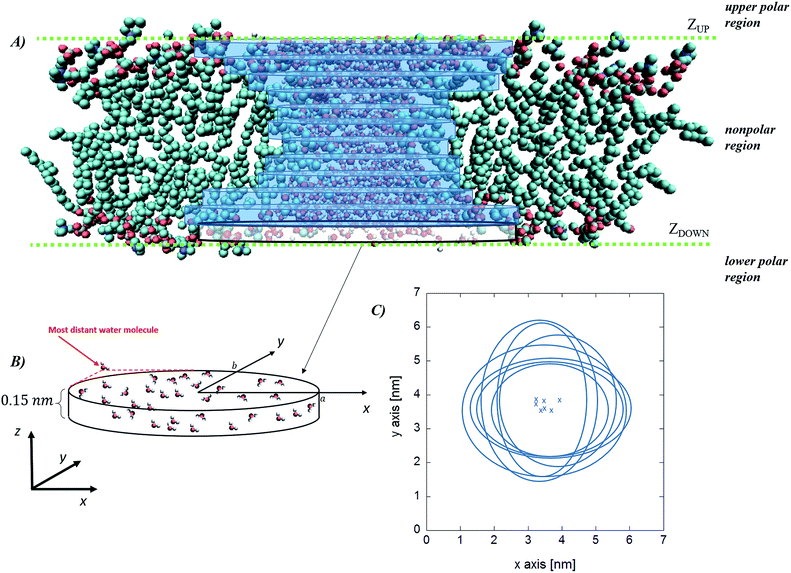
While the previous approach allows the geometrical characterization of the electropore starting from lipid head group atoms' spatial occupancy, different strategies can be adopted in order to reconstruct the pore shape, for example by taking into account water density profiles through the pore. One of the first methods proposing this approach is the one introduced by Fernández and coworkers34 and here presented as the “water cylindrical slabs” approach as the electropore sections have cylindrical shapes. This method, after establishing electropore upper and lower terminations, represents the lipid pore shape as a stack of elliptical slices with a fixed height Δz. The overall procedure is depicted in Fig. 4. To accurately characterize the pore geometry at a given time, a three-step algorithm is applied. First, the pore is centered inside the simulation box as explained in the Systems and structures section. Second, once the pore has been centered, the membrane is partitioned in three different parts: the upper polar region, the internal nonpolar region, and the lower polar region (Fig. 4 panel A). In order to detect the boundaries of the internal nonpolar region in the z direction, the average position of the z coordinate is computed for a specific atom (depending on the specific lipid model used within the simulation; P or N for POPC) belonging to lipid head groups. In Fig. 4 (panel A) these average z positions ZUP and ZDOWN are shown for the upper and the lower leaflets, respectively. The nonpolar region is then considered to be confined between [ZDOWN and ZUP]. Third, the system volume occupied by water molecules in the pore is sliced in cylindroids (cylinder with elliptical base in the x, y plane) with proper height in the z direction. The radii of the cylindroids are defined by the distances between the most distant water molecules in x and y directions (Fig. 4 panel B), as far as a certain cut-off distance. The volume of the pore, V, is finally geometrically defined and computed as the volume of the geometric figure combining all the cylindroids inside the nonpolar region of the membrane. Panel (C) of Fig. 4 points out the extremely different shapes of the stacked elliptical sections of the pore. As with the HOLE method, a direct evaluation of electropore volume can be obtained via:
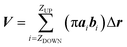 | (3) |
 | ||
| Fig. 4 Water cylindrical slabs method. Schematic representation of the simulation box, indicating the water region, the upper and the lower polar regions of the bilayer and the internal nonpolar region of the bilayer (panel A) together with the stack of cylindroids building up the pore. In panel (B) a magnification of the lower cylindroid is given, with the indication of the water molecules considered to define each elliptical slice (panel C, crosses correspond to the center of the cylindroids). Note that the latter definition implies that the cylindroids axes are aligned along the x–y Cartesian reference frame. Molecular graphics images were generated with visual VMD 1.8.7.49 | ||
The statistical/analytical method
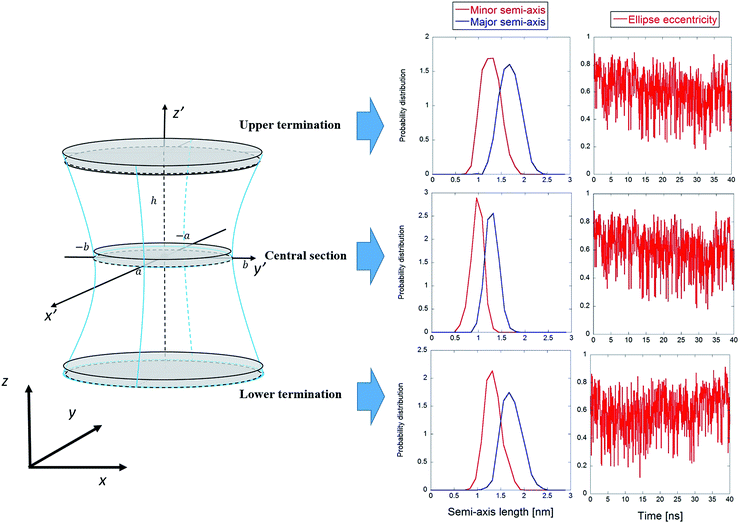
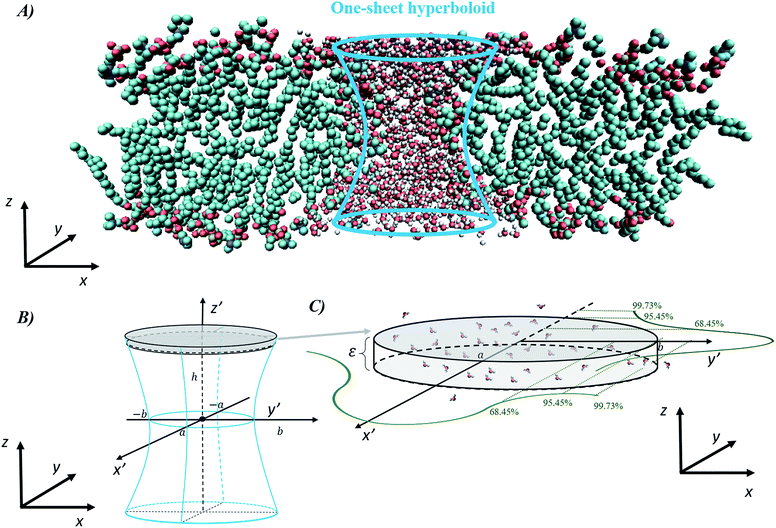
The final method, proposed by Marracino et al.,35 extracts the pore radius from an analysis of the tridimensional surface of the pore. Pore geometry is irregular and variable on the nanosecond time scale, but at the same time there is a significant and discernible structure from which a tridimensional surface can be extracted. This yields a rigorous characterization of the whole pore volume, and also some biophysical variables of interest such as water polarizability, water diffusivity, and ion and small molecule transport. The electropore geometry is constructed from the positional fluctuations of water molecules, i.e. via a purely statistical approach. In particular, this procedure aims to go beyond the method implemented by Fernández et al.,34 where, although similar outcomes are produced, the cylindrical slices forming the electropore are obtained via a mechanical approach. Fig. 5 shows the overall approach to describing the geometry of the lipid electropore by extracting the geometrical parameters needed to fully describe the pore as a one-sheet hyperboloid, the quadric surface that well approximates the electropore 3D region (see Fig. 5, panel A). The one-sheet hyperboloid is a quadric with equation
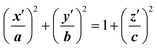 | (4) |
 | ||
| Fig. 5 General procedure for approximating an electropore as a three-dimensional, one-sheet hyperboloid, with a graphical representation of the electropore (panel A) and the theoretical methods used to extract the geometrical parameters from a molecular dynamics trajectory (panels B and C). Molecular graphics images were generated with visual VMD 1.8.7.49 | ||
From panel (B) of Fig. 5 it is evident that the central section of the hyperboloid and its termination are defined by the ellipses in z′ = 0, z′ = ZUP and z′ = ZDOWN, each with two semi-axes. The parameters a, b and c in eqn (4) can be found following the procedure given in ref. 35.
In order to extract from MD simulations the correct values for the hyperboloid parameters, i.e. to calculate the geometric fluctuations of the water molecules present in a certain region, we use the covariance matrix method.36,39 This method was previously employed to characterize the geometry of complex biomolecular systems (e.g. proteins) by approximating its overall structure to the ellipsoid given by the eigenvectors of the covariance matrix as obtained by the distribution of the x, y, and z coordinates of the protein atoms (the geometrical matrix ![[C with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0043_0303.gif) ). This is a direct extension of the most general essential dynamics (ED) analysis, which focuses on seeking those collective degrees of freedom that best approximate the total amount of fluctuations of a dynamical system. ED is based on a principal component analysis (PCA) of MD-generated structures.51 In the present case (a lipid bilayer) one can define bi-dimensional elliptical sections obtained by the distribution of the x, y coordinates of the atoms of the water molecules. Since water molecules occupy a volume, one can consider cylindroids (cylinder with elliptical base in the x, y plane) with a height approximating the radius of a water molecule (0.15 nm) in the z direction.34 Note that the slight variation along the z coordinate of water atoms does not significantly modify the distributions along the x, y coordinates. Therefore, for a cylindrical slab defined by water atoms, the elements of the 2 × 2 geometrical matrix at each time frame are given by
). This is a direct extension of the most general essential dynamics (ED) analysis, which focuses on seeking those collective degrees of freedom that best approximate the total amount of fluctuations of a dynamical system. ED is based on a principal component analysis (PCA) of MD-generated structures.51 In the present case (a lipid bilayer) one can define bi-dimensional elliptical sections obtained by the distribution of the x, y coordinates of the atoms of the water molecules. Since water molecules occupy a volume, one can consider cylindroids (cylinder with elliptical base in the x, y plane) with a height approximating the radius of a water molecule (0.15 nm) in the z direction.34 Note that the slight variation along the z coordinate of water atoms does not significantly modify the distributions along the x, y coordinates. Therefore, for a cylindrical slab defined by water atoms, the elements of the 2 × 2 geometrical matrix at each time frame are given by
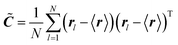 | (5) |
In panel (C) of Fig. 4 the Gaussian atomic positional distribution along each eigenvector is shown, with three possible measures for each semi-axis length. Hereafter 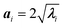 (i = 1, 2); i.e., the value for the geometrical semi-axes are taken as two times (95%) the value of the mean square fluctuations of the water atomic positions along each eigenvector. By knowing the magnitudes of the semi-axes (a1, a2) and directions (c1, c2) at each MD frame, one can quantitatively describe each elliptical section given in eqn (5) in its internal reference system (i.e., a = a1; b = a2 and the x′ and y′ axes are directed along c1 and c2). Finally, by applying the same procedure for different slices spanning from one end of the pore to the other, one can obtain the instantaneous three-dimensional surface that defines the pore.
(i = 1, 2); i.e., the value for the geometrical semi-axes are taken as two times (95%) the value of the mean square fluctuations of the water atomic positions along each eigenvector. By knowing the magnitudes of the semi-axes (a1, a2) and directions (c1, c2) at each MD frame, one can quantitatively describe each elliptical section given in eqn (5) in its internal reference system (i.e., a = a1; b = a2 and the x′ and y′ axes are directed along c1 and c2). Finally, by applying the same procedure for different slices spanning from one end of the pore to the other, one can obtain the instantaneous three-dimensional surface that defines the pore.
The volume calculation is straightforward, using Cavalieri's principle, from which one can find the volume of a solid as a “stack of slices” between the electropore terminations ±k:
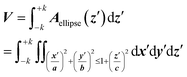 | (6) |
Moving to the more convenient elliptical coordinate system, it follows:
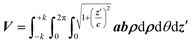 | (7) |
Results
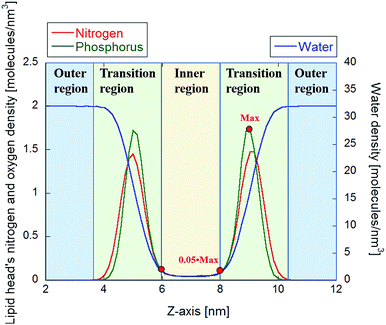
To determine electropore geometry with these three proposed methodologies it is crucial to identify the boundaries of the pore along the pore axis. The proper termination positions, and hence the length of the pore, can be identified by considering the density distributions of nitrogen and phosphorus atoms on the lipid head groups along the z-axis of the Cartesian reference frame. In Fig. 6 it is apparent that the two Gaussian-like density profiles (centered around 5 and 9 nm along the z-axis for both the nitrogen and phosphorus atoms) correspond to the two interface regions of the bilayer, as also apparent from the water density profile within the same region. The null nitrogen/phosphorus densities at 3.5 nm and 10.6 nm (corresponding to the transition between the regions depicted in green and blue in Fig. 6) identify the furthest head groups forming the pore walls. In the HOLE method these points can be used to determine the initial spherical probe radius (see dark blue sphere in Fig. 3), which will decrease while entering in the electropore (see spheres in progressing lighter blue in Fig. 3). The inner region shown in Fig. 6 is, conversely, the basis for identifying the electropore terminations (ends) for the latter two methods. This inner region, i.e. where the N (or P) density is steady and non-zero, indicates the electropore channel, where POPC molecules are rotated out of the plane of the bilayer and water molecules can pass. While the HOLE method extracts electropore geometry from lipid head group atom positions, the other two approaches define pore shape from water density profiles. Termination values to be inserted into eqn (3) and (7) have been chosen as close as possible to the transition between green and yellow regions of Fig. 6 (here we use ±5% of the phosphorus density).HOLE method outcomes
The HOLE program was used to capture the instantaneous pore geometry at different frames of the overall equilibrated trajectory. A spherical probe, with a maximum radius of 5 nm, is translated along the z-axis direction, with fixed steps of 0.025 nm. At the electropore upper termination the probe radius starts to decrease, finally reaching lower values according to the local pore constriction. Fig. 7 shows the link between the lipid head group N and P densities (a structural reference) and the spherical probe radius. In the figure two profiles are presented, representing the mean values taken from nine consecutive frames of the trajectory (one each 5 ns in order to cover the entire 40 ns equilibrium trajectory), for the largest spherical probe which can fit the channel without overlapping with van der Waals radii of two different sets: one considering all lipid atoms, the other taking into account only P and N atoms of the lipids. The green curve represents the spherical probe as constrained by all atoms of lipid headgroups, while the black one represents the same probe just constrained by the phosphorous and nitrogen atoms of the lipid headgroups.In both cases, as soon as the probe reaches the electropore entrance, the radius begins to decrease monotonically, reaching the lower sphere radius at about z = 7 nm, corresponding to the center of symmetry of the density profile. The radius profile calculated via the HOLE program exhibits a sharp transition from the initial 2 nm radius at the boundary between the outer and transition regions (as defined in the previous section) to the 0.5 nm radius at the midpoint of the pore, for the first set of atoms, and about 0.7 nm radius for the latter set of atoms. In both cases the profiles indicate a peculiar hourglass shape. It is interesting to compare the latter data with the ones obtained by Casciola et al.,25 where the charge imbalance protocol is used to obtain a stable electropore and the HOLE method is used to evaluate the pore radius/charge imbalances relationship. Our results match well (within the error bars) the one reported in ref. 25 for the lowest value of charge imbalance (nonetheless the different simulated system could play a key role in the latter comparison).
Water cylindrical slabs method outcomes
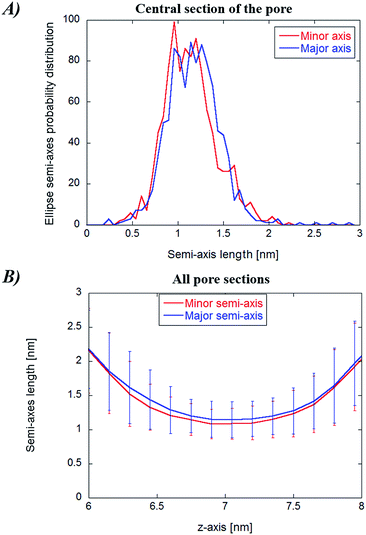
In Fig. 8, panel (A), the probability distribution of the central cylindroid axes (corresponding to the electropore middle section) is presented. The complete mean radius profiles along the pore channel are presented in panel (B) of the figure. The radii of the cylindroids spanning from the upper to the lower boundaries (ZUP and ZDOWN) are determined from the distances between the most distant water molecules in x and y directions as far as a distance of 3 nm. The values of the axes ai and bi for each slice i (see eqn (3)) do not significantly differ from each other, indicative of roughly circular electropore sections. Again, the electropore shape is hourglass-like.Statistical/analytical method outcomes
The main results from the application of the statistical analytical method are reported in Fig. 9, which highlights the three cylindroids needed to unambiguously define the 3D one sheet hyperboloid, i.e., the upper (z′ = ZUP in eqn (4)) and lower terminations (z′ = ZDOWN), as well as the central section (z′ = 0). It can be seen in Fig. 9 that the lengths of the semi-axes are stable over the time of the trajectory, with mean values indicative of proper ellipses. The eccentricity values confirm this behavior, also indicating sharp transitions of the elliptic sections, probably combined with rapid rotations of the ellipse semi-axes. In order to verify this, in Table 1 the mean square x, y-components of the elliptic sections geometrical eigenvectors are computed. The reported values indicate the absence of favored rotational orientations due to presence of the exogenous electric field aligned along the z-axis (for a freely tumbling elliptic section, these mean values should be 1/2).| Section | 〈c1,x2〉 | 〈c1,y2〉 |
|---|---|---|
| Upper termination | 0.57 ± 0.05 | 0.43 ± 0.05 |
| Central | 0.56 ± 0.04 | 0.44 ± 0.04 |
| Lower termination | 0.59 ± 0.06 | 1.41 ± 0.06 |
As expected, the central section semi-axes are smaller than those for the two termination ellipses, confirming the general properties of the one-sheet hyperboloid. Following the general hyperboloid equations given in ref. 35 one can easily obtain the parameters a, b, and c in eqn (4), viz., a =1.03 nm, b = 1.35 nm, and c = 1.22 nm, respectively (obtained from the mean values of the semi-axes time series; for the calculation details and the geometrical representation of the electropore see the ESI†).
Electropore volume by the three methods
Eqn (2), (3), and (7) allow the explicit calculation of pore volume. For a direct comparison among the three methods the pore height is set to same value h = 2 nm, confined between the terminations ZUP and ZDOWN, as previously defined. In Table 2 the calculated volumes are reported for all three methods. Moreover, for the HOLE method, two further volume calculations have been carried out by modifying the electropore terminations (see discussion of Fig. 5).| a Terminations as in the water cylindrical slabs and the statistical/analytical methods, h = 2 nm.b Terminations at nitrogen atom distribution peaks, h = 4 nm.c Terminations at the boundaries between transition and outer regions, h = 7 nm. | |||
|---|---|---|---|
| Methods | Hole | Water cylindrical slabs | Statistical/analytical |
| Volume | 1.71a nm3 | 16.8 nm3 | 12.1 nm3 |
| (5.8b nm3) | |||
| (28.5c nm3) | |||
Discussion and conclusions
Characterization of the shape and size of lipid electropores is essential for understanding how pore dimensions affect intra- and extra-pore (proximal and distal) water diffusivity, water dipole behavior, ion and small molecule translocation, and membrane mechanical properties.The algorithm developed by Smart and coworkers, which extracts electropore geometry from pore atom positions,31 and two more recent approaches, which define pore shape from water density profiles,34,35 were analyzed. All three methodologies are able to provide the boundaries of the pore in three dimensions at any time point, so the volume of the pore, the radius anywhere along the z-axis (normal to the plane of the bilayer), and other geometric characteristics like the shape of pore sections can be determined.
Although quantitative examples of the results of applying these methods have been given for a stable electropore simulation, in principle any electropore can be followed in time and in response to changes in simulation parameters (temperature, pressure, bilayer composition, salt concentration). For example, the threshold for pore formation may significantly change depending on the different chemical species present in the simulation,24,30 with known effects on electroporation-induced currents in experimental approaches52–56 (in particular, Wu and coworkers,55 as corollary to their measurements, used a numerical approach for the pore diameter computation, finding a value around 3.4 nm, in line with similar estimations from chronopotentiometric measurements applied to planar lipid membranes by Kalinowski and colleagues56).
Nonetheless, the validity of the three methods is general and independent from the system; moreover, it is not necessary to have a stabilized or static permeabilized bilayer, as one can be interested in following the natural fluctuations of pores over time.
Apart the chemical species adopted to define the electropore, HOLE defines the shape of the electropore sections differently from the other two methods. HOLE uses a spherical probe large enough to avoid contact with the pore walls (defined by vdWi radii of the lipid head group atoms), repeating the procedure for the whole pore length, while the other two take into account more rigorously the actual position-dependent cross-section of the pore along its axis. The HOLE radii values are small relative to the radii obtained with the other two methods, possibly a result of underestimating the solvent-accessible area by ignoring the water molecules in the pore.
The main difference between the water cylindrical slabs34 and the statistical-analytical35 methods is the mechanical versus statistical definition of pore elliptical sections. In our previous work,35 the electropore geometry is defined by water positional fluctuations. This allows a quantitative description of electropore boundaries, where each elliptical slice includes 95% of the Gaussian atomic positional distribution of water molecules along each semi-axis. This method should provide more rigorous estimates of electropore dimensions than those given by the method of Fernández et al.,34 where pore radii are approximated from the coordinates of the water molecules at the greatest distance from the pore axis in the plane of the bilayer, which could lead to overestimation of pore radius, and by the method of Smart et al., where the pore walls are defined by lipid atoms, without taking into consideration the water molecules in the pore (free in the solvent-filled center or hydrating the pore wall head groups) and thus underestimating the lateral extent of the pore. Fig. 10 confirms these assumptions.
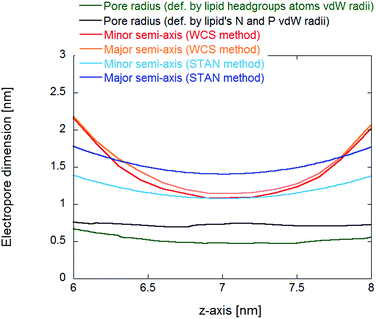 | ||
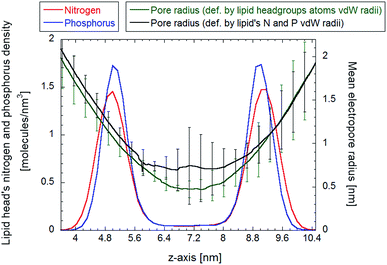
| Fig. 10 Comparison of pore dimensions along the electropore channel. In the inner region of the pore, as defined in Fig. 6, the HOLE method pore radius is much smaller than the radii from the water cylindrical slabs (WCS) and statistical/analytical (STAN) methods, resulting in a much smaller electropore volume. | ||
For reproducible volume calculations, a key point is the choice of electropore upper and lower terminations. For the water cylindrical slabs and the statistical/analytical methods the overall pore length is about 2 nm (see Fig. 6) and proper comparisons can be made. The statistical/analytical method produces slightly smaller volumes than the water cylindrical slabs method. The HOLE method yields smaller value estimations for the pore volume. Not only when we used a 2 nm height as for the other two methods, but also if we increase the height up to 4 nm (the distance between the two nitrogen density peaks of Fig. 6). The volume becomes comparable only if we consider as height the distance between the ends of the transition regions (h = 7 nm).
Finally, while the pore has an hourglass-like shape in all three methodologies, the pore elliptical sections are more easily reproduced with the statistical/analytical methodology (see Fig. 10). In fact, the use of eqn (5) guarantees the extraction of the correct shape, since it quantitatively describes each elliptical section in its internal reference system.
Acknowledgements
This project received support within the framework of the Joint IIT-Sapienza LAB on Life-NanoScience Project (81/13 16-04-2013) and from the Sapienza University of Rome, Research Projects, 2015 (C26A15T3T2). PTV was supported in part by the Air Force Office of Scientific Research (FA9550-15-1-0517, FA9550-14-1-0123) and by the Old Dominion University Frank Reidy Research Center for Bioelectrics.References
- K. Kinosita and T. Y. Tsong, Biochim. Biophys. Acta, 1977, 471, 227 CrossRef CAS.
- E. Neumann, M. Schaeferridder, Y. Wang and P. H. Hofschneider, EMBO J., 1982, 1, 841 CAS.
- P. T. Vernier, Z. A. Levine, Y. H. Wu, V. Joubert, M. J. Ziegler, L. M. Mir and D. P. Tieleman, PLoS One, 2009, 4(11), e7966 Search PubMed.
- E. C. So, K. L. Tsai, F. T. Wu, M. C. Hsu, K. C. Wu and S. N. Wu, Cell. Physiol. Biochem., 2013, 32, 402 CrossRef CAS PubMed.
- R. Benz and U. Zimmermann, Biochim. Biophys. Acta, 1980, 597, 637 CrossRef CAS.
- K. J. Muller, V. L. Sukhorukov and U. Zimmermann, J. Membr. Biol., 2001, 184, 161 CrossRef CAS PubMed.
- P. T. Vernier, Y. H. Sun and M. A. Gundersen, BMC Cell Biol., 2006, 7, 37 CrossRef PubMed.
- J. T. Sengel and M. I. Wallace, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(19), 5281 CrossRef CAS PubMed.
- L. Zanetti-Polzi, P. Marracino, M. Aschi, I. Daidone, A. Fontana, F. Apollonio, M. Liberti, G. D'Inzeo and A. Amadei, Theor. Chem. Acc., 2013, 132(11), 1 CrossRef CAS.
- P. Marracino, M. Liberti, E. Trapani, C. J. Burnham, M. Avena, J. A. Garate, F. Apollonio and N. J. English, Int. J. Mol. Sci., 2016, 17(7), 1133 CrossRef PubMed.
- S. J. Beebe, Bioelectrochemistry, 2015, 103, 52 CrossRef CAS PubMed.
- X. Wang, Y. Li, X. He, S. Chen and J. Z. H. Zhang, J. Phys. Chem. A, 2014, 118, 8942 CrossRef CAS PubMed.
- Y. Xie, C. Liao and J. Zhou, Biophys. Chem., 2013, 179, 26 CrossRef CAS PubMed.
- R. Reale, N. J. English, J. A. Garate, P. Marracino, M. Liberti and F. Apollonio, J. Chem. Phys., 2013, 139(20), 205101 CrossRef PubMed.
- L. Astrakas, C. Gousias and M. Tzaphlidou, J. Appl. Phys., 2011, 109, 094702 CrossRef.
- N. J. English, G. Y. Solomentsev and P. O'Brien, J. Chem. Phys., 2009, 131(3), 035106 CrossRef PubMed.
- F. Toschi, F. Lugli, F. Biscarini and F. Zerbetto, J. Phys. Chem. B, 2009, 113, 369 CrossRef CAS PubMed.
- Z. Kong, H. Wang, L. Liang, Z. Zhang, S. Ying, Q. Hu and J. W. Shen, J. Mol. Model., 2017, 23, 113 CrossRef PubMed.
- F. Apollonio, M. Liberti, A. Amadei, M. Aschi, M. Pellegrino, M. D'Alessandro, M. D'Abramo, A. Di Nola and G. D'Inzeo, IEEE Trans. Microwave Theory Tech., 2008, 56(11), 2511 CrossRef CAS.
- D. P. Tieleman, BMC Biochem., 2004, 5, 10 CrossRef PubMed.
- M. Tarek, Biophys. J., 2005, 88, 4045 CrossRef CAS PubMed.
- M. C. Ho, M. Casciola, Z. A. Levine and P. T. Vernier, J. Phys. Chem. B, 2013, 117, 11633 CrossRef CAS PubMed.
- M. J. Ziegler and P. T. Vernier, J. Phys. Chem. B, 2008, 112, 13588 CrossRef CAS PubMed.
- M. Casciola, D. Bonhenry, M. Liberti, F. Apollonio and M. Tarek, Bioelectrochemistry, 2014, 100, 11 CrossRef CAS PubMed.
- M. Casciola, M. A. Kasimova, L. Rems, S. Zullino, F. Apollonio and M. Tarek, Bioelectrochemistry, 2016, 109, 108 CrossRef CAS PubMed.
- M. Tokman, J. H. Lee, Z. A. Levine, M. C. Ho, M. E. Colvin and P. T. Vernier, PLoS One, 2013, 8(4), e61111 CAS.
- Z. A. Levine and P. T. Vernier, J. Membr. Biol., 2010, 236, 27 CrossRef CAS PubMed.
- R. A. Böckmann, B. L. de Groot, S. Kakorin, E. Neumann and H. Grubmüller, Biophys. J., 2008, 95, 1837 CrossRef PubMed.
- T. J. Piggot, D. A. Holdbrook and S. Khalid, J. Phys. Chem. B, 2011, 115, 13381 CrossRef CAS PubMed.
- M. L. Fernández, G. Marshall, F. Sagués and R. Reigada, J. Phys. Chem. B, 2010, 114, 6855 CrossRef PubMed.
- O. S. Smart, J. G. Neduvelil, X. Wang, B. A. Wallace and M. S. Sansom, J. Mol. Graphics, 1996, 14, 354 CrossRef CAS PubMed.
- H. Leontiadou, A. E. Mark and S. J. Marrink, Biophys. J., 2004, 86, 2156 CrossRef CAS PubMed.
- A. A. Gurtovenko and I. Vattulainen, Biophys. J., 2007, 92, 1878 CrossRef CAS PubMed.
- M. L. Fernández, M. Risk, R. Reigada and P. T. Vernier, Biochem. Biophys. Res. Commun., 2012, 423, 325 CrossRef PubMed.
- P. Marracino, F. Castellani, P. T. Vernier, M. Liberti and F. Apollonio, J. Membr. Biol., 2017, 250, 11 CrossRef CAS PubMed.
- S. Del Galdo, P. Marracino, M. D'Abramo and A. Amadei, Phys. Chem. Chem. Phys., 2015, 17(46), 31270 RSC.
- P. Marracino, A. Amadei, F. Apollonio, G. D Inzeo, M. Liberti, A. D. Crescenzo, A. Fontana, R. Zappacosta and M. Aschi, J. Phys. Chem. B, 2011, 115(25), 8102 CrossRef CAS PubMed.
- P. Marracino, M. Migliorati, A. Paffi, M. Liberti, A. Denzi, G. D'Inzeo and F. Apollonio, Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, USA, 2012, vol. 6347282, p. 5674 Search PubMed.
- P. Marracino, F. Apollonio, M. Liberti, G. d'Inzeo and A. Amadei, J. Phys. Chem. B, 2013, 117(8), 2273 CrossRef CAS PubMed.
- A. Amadei and P. Marracino, RSC Adv., 2015, 5(117), 96551 RSC.
- D. Van der Spoel, E. Lindahl, B. Hess and the GROMACS development team, GROMACS User Manual version 4.6.6, 2014, http://www.gromacs.org Search PubMed.
- O. Berger, O. Edholm and F. Jahnig, Biophys. J., 1997, 72(5), 2002 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces, ed. B. Pullman, Reidel, Dordrecht, The Netherlands, 1981, p. 331 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126(1), 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Di Nola and J. R. Haak, J. Chem. Phys., 1984, 81(8), 3684 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, Comput. Chem., 1997, 18(12), 1463 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13(8), 952 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. J. A. Pedersen, Chem. Phys., 1995, 103(19), 8577 CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087 CrossRef CAS.
- A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Protein. Struct. Funct. Genet., 1993, 17(4), 412 CrossRef CAS PubMed.
- Y. C. Liu, P. C. Wu, D. B. Shieh and S. N. Wu, Int. J. Nanomed., 2012, 7, 1687 CrossRef CAS PubMed.
- S. N. Wu, C. C. Yeh, H. C. Huang and W. H. Yang, Cell. Physiol. Biochem., 2011, 28(5), 959 CrossRef CAS PubMed.
- S. N. Wu, C. C. Yeh, P. Y. Wu, H. C. Huang and M. L. Tsai, Cell. Physiol. Biochem., 2012, 62(1), 211 CAS.
- S. N. Wu, H. C. Huang, C. C. Yeh, W. H. Yang and Y. C. Lo, Biochem. Biophys. Res. Commun., 2011, 405(3), 508 CrossRef CAS PubMed.
- S. Kalinowski, S. Koronkiewicz, M. Kotulska and K. Kubica, Bioelectrochemistry, 2007, 70, 83–90 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03812g |
| This journal is © The Royal Society of Chemistry 2017 |