Effects of oxygen-deficiency on crystal structure, dielectric and ferroelectric properties in Sr₅SmTi_3+2xNb_7−2xO_30−x with tungsten bronze structure

Abstract

Oxygen-deficient tungsten bronze ceramics with general formula Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1, 0.25) are prepared. The effects of oxygen deficiency on the crystal structure, dielectric and ferroelectric properties are investigated. With increasing oxygen deficiency, the crystal structure becomes less stable and the lattice shrinks, while the ferroelectricity is weakened, and the low temperature relaxation enhanced. Commensurate superlattices observed in Sr₅SmTi₃Nb₇O₃₀, corresponding to the onset of the ferroelectric transition as reported previously. In compositions with x = 0.1 and 0.25, two factors that A-site cross occupancies and disturbance of oxygen vacancies on the ferroelectric order are noticed and related to the change from ferroelectric behavior to diffuse one. Three orders of incommensurate superlattice reflections are observed in x = 0.1 and 0.25 compositions. The first-order incommensurate superlattice reflections appear at positions (h + 1/4 − δ, k + 1/4 − δ, l + 1/2), reflecting the common feature in tungsten bronzes with relaxor or diffuse ferroelectric nature. The second-order incommensurate superlattice reflections are observed on the (00l) (l = 0, 1, 2, 3, …) planes around the (h + 1/2, k + 1/2, l) positions, while the third-order incommensurate superlattice reflections are observed on the (00l) (l = 1/2, 3/2, …) planes, by the side of the first-order ones. The appearance of higher-order is believed to reduce the high structural energy induced by the oxygen deficiency.

---

1. Introduction

The tungsten bronze structure is composed of ten distorted octahedra sharing corners in such a way that three different interstices (2 tetragonal A1, 4 pentagonal A2, and 4 triangle C) are available for cation occupancy in the general formula (A1)₂(A2)₄(C)₄(B1)₂(B2)₈O₃₀, which can be obtained from the perovskite structure by rotation of the BO₆ octahedra.^1,2 The chemical composition of tungsten bronzes is very flexible and according to the occupation of the interstices, three types of tungsten bronzes can be defined, such as full-filled (all interstice sites full, exp. K₃Li₂Nb₅O₁₅), filled (C site empty, Ba₂NaNb₅O₁₅) and un-filled (A site partially occupied and C site empty, (Sr_xBa_1−x)Nb₂O₆) tungsten bronzes. The two kinds of octahedral B sites can by occupied by the same or different cations, like Ti, Fe, Nb, Ta, etc.

In recent years, a number of Pb-free ferroelectrics have been determined in tetragonal filled tungsten bronze family of M_6−pR_pTi_2+pNb_8−pO₃₀ (p = 1, 2; M = Ba or Sr; R = rare earth).^3–15 In these materials, a ferroelectric transition followed by up to three low-temperature dielectric relaxations are generally detected with decreasing temperature. Zhu et al. reported the ferroelectric transition changes from the normal one to relaxor through diffuse one with decreasing the radius difference between A1- and A2-site ions, Δr.³ A crystal-chemical model is proposed recently to explore the composition and local structure influence on the relaxor or ferroelectric behavior.⁴ The model considers two competing driving forces: large average A-site cation size extends the BO₆ octahedra which enhances polarizability, while low A1 tolerance factor favors modulated tilt pattern of commensurate superstructure and is always associated with normal ferroelectric behavior.

Besides the modulation of positive ions, creation of oxygen vacancies is also an effective way to manipulate the properties of oxides, and oxygen deficiency has been drawing considerable attention in many perovskite oxides.^16–24 Oxygen vacancies can be created by doping or atmospheric reduction.^23,24 According to the authors' experience, for tungsten bronzes M_6−pR_pTi_2+pNb_8−pO₃₀, O₂ or N₂ atmosphere annealing has no obvious effect on the dielectric and ferroelectric properties. This might be one possible reason why the effects of oxygen vacancies in tungsten bronzes have rarely been studied. Recently, effects of oxygen vacancies on the electrical properties in filled tungsten bronze Ba₄Nd₂Fe₂Nb₈O₃₀ have been reported.²⁵ The sensitivity of oxygen vacancies in Ba₄Nd₂Fe₂Nb₈O₃₀ to O₂ or N₂ atmosphere annealing is attributed to the B-site Fe cations with variable valance. For the titanium niobate systems, in order to create oxygen vacancies, a new family of tungsten bronze ceramics Ba₄Nd₂Ti_4+2xNb_6−2xO_30−x has been synthesized and investigated.²⁶ With increasing x, the dielectric properties shows a transition from classic ferroelectric behavior with x = 0 to a relaxor-like behavior with x = 1, reflecting the disturbance of oxygen vacancies on the ferroelectric order. These researches suggest the possibility and significance for studying the effects of oxygen vacancies in tungsten bronzes.

In the present work, chosen Sr-based filled tungsten bronze Sr₅SmTi₃Nb₇O₃₀ as the ferroelectric endpoint, oxygen deficient tungsten bronze ceramics Sr₅Sm₁Ti_3+2xNb_7−2xO_30−x (x = 0, 0.1, 0.25) has been prepared, and the crystal structure, dielectric and ferroelectric properties are studied.

2. Experimental procedure

Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1, 0.25) ceramics were prepared by a standard solid-state reaction, using reagent grade SrCO₃ (99.95%), Sm₂O₃ (99.99%), TiO₂ (99.9%), and Nb₂O₅ (99.99%) powders as the raw materials. The weighed raw materials were mixed by ball milling with zirconia media in deionized water for 24 h. Because of the hydration of Sm₂O₃, it was additionally preheated at 900 °C for 30 minutes before weighing. The three mixtures were calcined in high-purity alumina crucibles at 1300 °C in air for 3 h followed by a second grinding to reach a homogeneous granulometric distribution. Adding with organic binders (8 wt% polyvinyl alcohol), the reground powders were pressed into cylindrical compacts of around 12 mm in diameter and around 1.2 mm in thickness under the pressure of about 98 MPa. The disks were sintered at 1250–1350 °C in air for 3 h to find the best sintering condition for the present ceramics. After sintering, the disks were cooled to 1000 °C at a rate of 2 °C min and further cooled inside the furnace.

The crystalline phase constitution was identified using powder X-ray diffraction (XRD, LabX XRD-6000, SHIMADZU Co., Japan) analysis with Cu Kα radiation. The bulk density of the ceramics was calculated by measuring its mass and diameter. The microstructure of the polished and thermally etched surfaces of the sintered disks was characterized using scanning electron microscopy (SEM, SIRION-100, FEI, Netherlands). Thermal etching was conducted at 1100 °C for 20 min. The XRD data for Rietveld analysis was collected over the 2θ range of 8° to 130° with steps of 0.02° and a count time of 2 s (D/max 3B, Rigaku Co., Tokyo, Japan). The Rietveld structure calculation was carried out using the FULLPROF program. The bulks were thinned around several micrometers mechanically and then polished by ion beam for transmission electron microscopy (TEM) observation. Selected area electron diffractions (SAED) were carried out using a TEM (Tecnai G2 F20 S-TWIN, FEI Co., Hillsboro, USA). Dielectric properties in the range of 173 K to 573 K were measured with a broadband dielectric spectrometer (Turnkey Concept 50, Novocontrol Technologies., Hundsangen, Germany) over a frequency range of 1 Hz to 5 MHz. P–E hysteresis loops are evaluated at room temperature 1 Hz by a Precision Materials Analyzer (RT Premier II, Radiant Technologies, Inc., NM, USA). The applied electric field increased from 10 kV cm⁻¹ to 100 kV cm⁻¹.

3. Results and discussion

Dense Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1 and 0.25) ceramics with relative density above 95% are obtained. The relative density of the present ceramics decreases with increasing x value, which is due to more oxygen vacancies. The SEM images are shown in Fig. 1, indicating columnar grains for all compositions.

Fig. 1 SEM micrograph of thermal etching surface for Sr₅SmTi_3+2xNb_7−2xO_30−x ceramics: (a) x = 0; (b) x = 0.1; (c) x = 0.25.

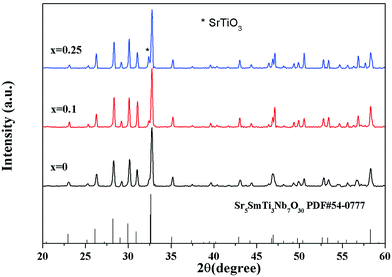
Fig. 2 shows the X-ray diffraction patterns for Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1 and 0.25) ceramics. Tetragonal tungsten bronze structure with space group P4bm is determined by indexing the XRD peaks according to the JCPDS (Joint Committee for Powder Diffraction Standards) card no. 54-0777. Very small amount of secondary phase (cubic SrTiO₃ with space group of Pm3̄m) is detected in the compositions of x = 0.1(4.33%) and x = 0.25(8.01%), which is due to the structure instability induced by the oxygen deficiency. The structure parameters of Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1 and 0.25) are listed in Table 1. The unit cell of the three compositions shrinks with increasing x, reflecting the increasing oxygen vacancies.

Fig. 2 XRD patterns of Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1, 0.25) ceramics.

Table 1 Unit cell parameters and effective tolerance factors for Sr₅SmTi_3+2xNb_7−2xO_30−x

	x = 0	x = 0.1	x = 0.25
a (Å)	12.3830(7)	12.2920(1)	12.2905(1)
c (Å)	3.8834(2)	3.8686(2)	3.8677(7)
Vunit (Å^3)	585.91	584.54	584.26
	0.9998	0.9952	0.9951

---

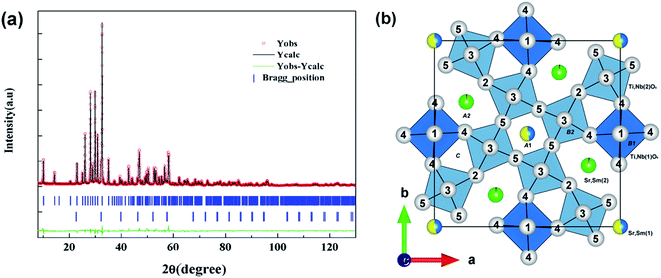
However, the situation is quite different in Sr₅SmTi_3.2Nb_6.8O_29.9, where a small amount of A2-site Sr cations entered into the smaller A1 site by exchanging equal A1-site Sm cations into A2 site. [001] projection of the unit cell of Sr₅SmTi_3.2Nb_6.8O_29.9 shows that O₅ and O₃ are the nearest and next nearest oxygen ions around A1 sites (see Fig. 3(b)). According to ref. 26, in the oxygen-deficient tungsten bronzes Ba₄Nd₂Ti_4+2xNb_6−2xO_30−x, oxygen vacancies locate preferentially in the coordination sphere of Nd and Ti/Nb(2) atoms, which correspond to the areas around A1 sites. It could be suggested that in Sr₅SmTi_3.2Nb_6.8O_29.9, oxygen vacancies also prefer to locate at O₃ and O₅ sites, and more Sr cations occupying the A1 sites probably aims to stablize the tetragonal tungsten bronze crystal structure.

Fig. 3 Crystal structure of Sr₅SmTi_3.2Nb_6.8O_29.9 (x = 0.1) (a) Rietveld analysis results of XRD patterns (experimental data: circles; calculated data: upper lines, and difference: bottom lines). (b) [001] Projection of the unit cell. Ti,Nb(1)O₆ and Ti,Nb(2)O₆ octahedra are shown in blue and gray blue, respectively. Oxygen sites 1 to 5 and cation sites A1, A2, B1, B2, and C are indicated.

The Rietveld refinement using FULLPROF program is performed for the XRD data of composition with x = 0.1 (Sr₅SmTi_3.2Nb_6.8O_29.9) to get more structure information. The final difference between the experimental data and the calculated data is shown in Fig. 3(a) and final atomic positions and thermal parameters are summarized in Table 2. Relatively higher residuals are obtained (R_p = 5.77, R_wp = 7.72, R_exp = 2.58 andχ² = 8.93), compared with that for Sr₅SmTi₃Nb₇O₃₀ (R_p = 0.0571, R_wp = 0.0796, and χ² = 1.95).¹¹ Moreover, other anomalies are found in the atomic distribution of Sr and Sm cations in the A sites and the ultra high thermal parameters (B_iso value) obtained for O₁, O₃ and O₅, as shown in Table 2. In Sr₅SmTi₃Nb₇O₃₀, 4 Sr cations occupy larger pentagonal A2 sites and extra Sr occupies tetragonal A1 sites together with Sm, as reported in ref. 11. According to Ba₄Nd₂Ti_4+2xNb_6−2xO_30−x, the oxygen vacancies are likely to present associated with O₃ and O₅, which will induce instability in these O sites with higher B_iso values. Thus, high B_iso values for O₁, O₃ and O₅ here obtained in the x = 0.1 composition may also suggest the location of oxygen vacancies.

Table 2 Final atomic positions and thermal parameter of Sr₅SmTi_3.2Nb_6.8O_29.9

Atom	Wyckoff position	x/a	y/b	z/c	Biso (Å^2)	Occupancy
Sm1	2a	0.00000	0.00000	1.0(4)	1.77(5)	0.1133
Sr1	2a	0.00000	0.00000	1.0(4)	1.77(5)	0.1367
Sm2	4c	0.17083(1)	0.67083(1)	1.0(4)	4.03(7)	0.0117
Sr2	4c	0.17083(1)	0.67083(1)	1.0(4)	4.03(7)	0.4883
Ti1/Nb1	2b	0.00000	0.50000	0.5(4)	2.11(9)	0.0786/0.1714
Ti2/Nb2	8d	0.07570(1)	0.21475(1)	0.5(4)	1.44(3)	0.3216/0.6784
O1	2b	0.00000	0.50000	1.1(4)	5.0(2)	1.0
O2	4c	0.2771(5)	0.7771(5)	0.6(4)	0.2(2)	1.0
O3	8d	0.0739(8)	0.1998(6)	1.0(4)	5.0(2)	1.0
O4	8d	0.3370(6)	0.0080(5)	0.6(4)	0.57(2)	1.0
O5	8d	0.1314(7)	0.0627(8)	0.6(4)	5.0(2)	1.0

---

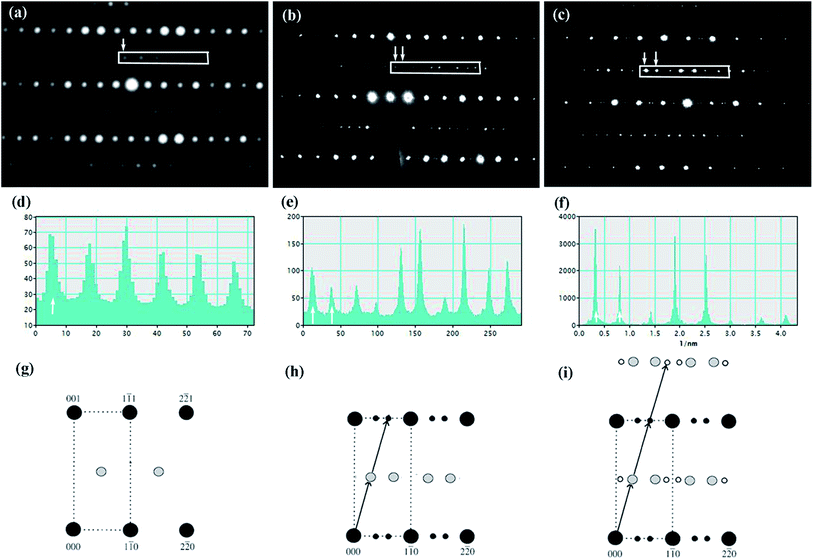
Fig. 4(a)–(c) is the selected area electron diffraction (SAED) patterns of Sr₅SmTi_3+2xNb_7−2xO_30−x(x = 0, 0.1 and 0.25) ceramics taken along [110] zone axis at ambient temperature. The fundamental reflections in all patterns of these compounds could be indexed on the tetragonal tungsten bronze (TTB) cell P4̄bm. For Sr₅SmTi₃Nb₇O₃₀ (x = 0), commensurate satellite reflections appears at h/2, k/2, l/2 positions (Fig. 4(a)), which is consistent with the previous report,¹⁴ and the pattern could be indexed using a unit cell with Ima2 symmetry 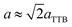, 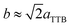and 2c ≈ 2c_TTB according to Levin et al.⁵ and Stennett et al.⁶ As shown in Fig. 4(b) and (c), up to three-order incommensurate superlattice (ICS) reflections are observed for compositions with x = 0.1 and 0.25. The first-order incommensurate superlattice reflections are observed at positions (h + 1/4 − δ, k + 1/4 − δ, l + 1/2). The incommensurability parameter δ is the measure of the deviation from commensurate periodicity that is defined as δ = (x − y)/(x + y), where x and y is the distance of the neighboring incommensurate superstructure spot.²⁷ The value of δ here is determined as about 0.16 for x = 0.1, and 0.10 for x = 0.25, which are similar to the δ value determined in Sr₅LaTi₃Nb₇O₃₀ (δ = 0.12),⁴ but higher than δ = 0.04 reported for Ba₄La₂Ti₄Nb₆O₃₀.⁵ Actually, δ value of the incommensurate modulation in tungsten bronzes is found to vary in a considerable range. For example, δ value is determined to be 0.050 to 0.034 at 473 to 100 K for Ba₄La₂Ti₄Nb₆O₃₀,⁵ and 0.059 for Ba₅LaTi₃Nb₇O₃₀.¹⁵ For Sr_1−xBa_xNb₂O₆,²⁷ the δ value is decreased from 0.185 to 0.170 as the Ba content increases from 0.25 to 0.75. According to Glass,²⁸ in Sr_1−xBa_xNb₂O₆, the increase of Ba/Sr ratio lowers the structure entropy and the development of the incommensurate modulation is believed to reduce the structural energy.²⁹ Thus, the larger δ value reflects relatively instable structure and disordered cation distribution in tungsten bronze compounds. In the case of commensurate modulation, the δ value is 0. Based on the above analysis, it could be considered that the oxygen deficiency in the present tungsten bronze family induces structure instability and cation disorder, and then results in the incommensurate modulation with similar δ values to that in Sr₅LaTi₃Nb₇O₃₀.

Fig. 4 The SAED patterns taken along [110] zone axis from a single grain of Sr₅SmTi_3+2xNb_7−2xO_30−x, (a) x = 0; (b) x = 0.1; (c) x = 0.25. (d)–(f) Are the corresponding line profiles of the satellite reflections in the rectangular boxes. The arrows indicate the appearance of the satellite reflections for commensurate modulation in (a), and incommensurate modulation in (b) and (c). (g)–(i) Schematic diffraction patterns in [110] projection.

Besides, the high structural energy induced by the oxygen deficiency also generates higher-order incommensurate reflections. The commensurate and incommensurate reflections observed in Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1 and 0.25) are furthered verified with line profiles in Fig. 4(d)–(f), respectively, and corresponding schematic patterns are shown in Fig. 4(g)–(i)). The second-order incommensurate superlattice reflections are observed on the (00l) (l = 0, 1, 2, 3, …) planes around the (h + 1/2, k + 1/2, l) positions for both x = 0.1 and 0.25, while the third-order incommensurate superlattice reflections are observed on the (00l) (l = 1/2, 3/2, …) planes, only for x = 0.25. Similar high order incommensurate reflections are reported in Sr_0.6Ba_0.4Nb₂O₆ (SBN) with huge large grains and is believed to result from the orthorhombic distortion associated with a shortened c axis, which is originated from the unfavorable occupation of A1 site by some trapped Ba cations during the rapid cooling process, as in the quenched SBN single crystal,³⁰ and planar defects are detected and is suggested to localize the increase structural energy caused by the orthorhombic distortion and thus stablize the incommensurate phase.³¹ According to the results of X-ray diffraction, cross distribution of Sr and Sm cations in the A1 and A2 sites exists in the x = 0.1 and 0.25 compositions. The A1 and A2 sites on the c = 1 planes, connected directly with O₅, the sites where the oxygen vacancies are preferred, therefore result in a severe distortion of oxygen octahedra. The appearance of higher-order incommensurate reflections in x = 0.1 and 0.25 compositions reduces the high structure energy caused by the unusual A-site cation distribution, oxygen vacancies and consequently the distortion of oxygen octahedra.

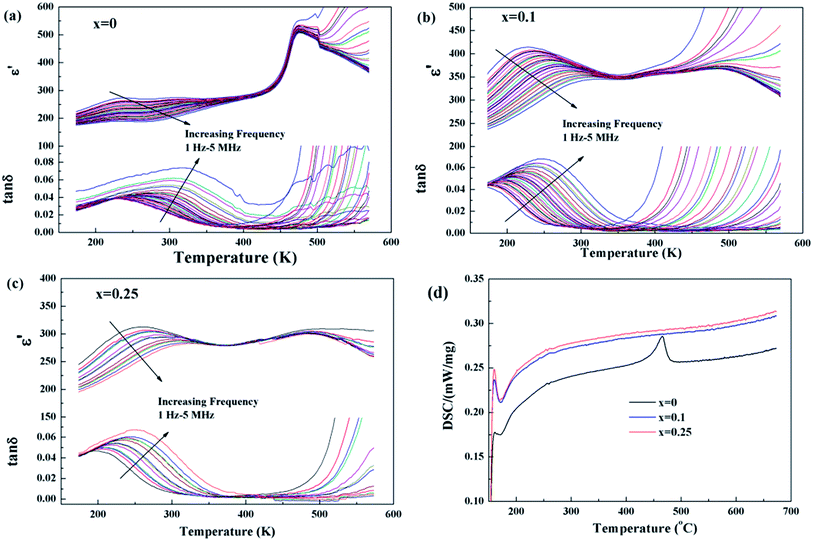
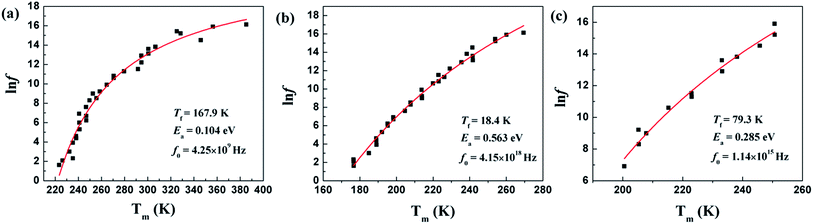
Temperature dependences of dielectric characteristics are collected for Sr₅SmTi_3+2xNb_7−2xO_30−xwith x = 0, 0.1 and 0.25, and shown in Fig. 5(a)–(c). For x = 0 composition (Fig. 5(a)), the dielectric permittivity exhibits a sharp peak at about 470 K and a weak relaxation at lower temperature around 250 K, which is consistent with the previous report,^12,13 and indicate a ferroelectric transition with an endothermic peak on heating in the DSC curve shown in Fig. 5(d). For both x = 0.1 and 0.25 compositions, a diffuse dielectric peak is observed around 500 K together with an enhanced low temperature relaxation around 200 K. Thus, a wide temperature range (200–500 K) with a stable dielectric constant (∼300) is formed and suggests these two compositions as potential temperature stable dielectrics. No DSC peak is observed for these two compositions (see Fig. 5(d)). The low temperature dielectric relaxation can also been observed in the dielectric loss curves with similar intense of tan δ ∼ 0.07 for all the three compositions, and shift to lower temperature with increasing x value. For the relaxation, the frequency dependency of T_m obtained from the dielectric loss (tan δ(T)) curves can be fitted to the Vogel–Fulcher relationship:

F = f₀ exp[−E_a/k(T_m − T_f)]

where f is the applied ac field frequency, f₀ is the Debye frequency, T_f is the static freezing temperature, E_a is the activation energy of the polar clusters and k is the Boltzmann's constant.³² The Vogel–Fulcher relationship is interpreted as a normal Debye relaxation with a temperature-dependent activation energy, and indicates the increasing interaction between local random dipolar regions.³² As shown in Fig. 6, the fitting parameters obtained for x = 0 suggesting a freezing process of some low temperature polarization, which is usually observed in tungsten bronze ferroelectrics.³ However, ultrahigh f₀ values are obtained for the oxygen deficient compositions with x = 0.1 and 0.25, which seem unreliable and without physical meanings. Therefore, the low temperature relaxations in compositions with x = 0.1 and 0.25 are not a Vogel–Fulcher type relaxation, reflecting the effect of the oxygen deficiency. The weakened ferroelectricity and enhanced relaxation in Sr₅SmTi_3+2xNb_7−2xO_30−x with x = 0.1 and 0.25 should be related to the random cross distribution in the A sites and the oxygen vacancies induced by the oxygen deficiency.

Fig. 5 Dielectric constant ε′ and dielectric loss tan δ of Sr₅SmTi_3+2xNb_7−2xO_30−x ceramics as functions of temperature and frequency: (a) x = 0; (b) x = 0.1; (c) x = 0.25, and (d) DSC curves of Sr₅SmTi_3+2xNb_7−2xO_30−x on heating.

Fig. 6 The frequency dependency of T_m obtained from the dielectric loss (tan δ(T)) curves for Sr₅SmTi_3+2xNb_7−2xO_30−x, (a) x = 0; (b) x = 0.1; (c) x = 0.25. The red lines indicate the fitting results to the Vogel–Fulcher relation. The fitting parameters are inserted.

P–E hysteresis loops for Sr₅SmTi_3+2xNb_7−2xO_30−x are shown in Fig. 7. Compared with the classic ferroelectric loop obtained for Sr₅SmTi₃Nb₇O₃₀ (Fig. 7(a)), almost linear P–E loops are obtained for both x = 0.1 and 0.25 when the applied electric field increases up to above 100 kV cm⁻¹ (Fig. 7(b) and (c)), reflecting the weakened ferroelectric nature.

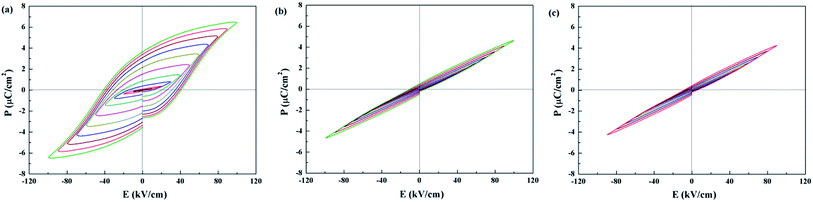Fig. 7 Polarization electric-field (P–E) curves measured at ambient temperature with a triangular wave form at 1 Hz of Sr₅SmTi_3+2xNb_7−2xO_30−x, (a) x = 0; (b) x = 0.1; (c) x = 0.25.

Generally, the relation between structure modulation and ferroelectricity in Sr₅SmTi_3+2xNb_7−2xO_30−x indicates that the normal ferroelectrics exhibit the commensurate modulation (x = 0), while the incommensurate modulation corresponds to the diffuse or relaxor behaviors (x = 0.1 and 0.25),as confirmed in many tungsten bronzes, where the structure modulation is dominated by radius difference between A1 and A2 sites.^3–6 In Sr₅SmTi_3+2xNb_7−2xO_30−x with x = 0.1, cross occupancy of Sr and Sm cations in the A1 and A2 sites makes more Sr cations in the A1 sites, leading to smaller radius difference between A1 and A2 sites and thus incommensurate modulation. This is quite different from the situation in Ba₄Nd₂Ti_4+2xNb_6−2xO_30−x, where the A site occupancies are unchanged.²⁶ Similar to Ba₄Nd₂Ti_4+2xNb_6−2xO_30−x, there appears to be a change in the non-statistical occupancy of B sites, and the oxygen vacancies are present primarily associated with O₃ and O₅, which are exclusive to B2 site coordination. Then the B2-site Ti cations only have coordination 5 instead of octahedral, and the 5-coordination Ti cannot forms the polar center,²⁶ thus disrupt the ferroelectric polar domains and dominating the diffuse and relaxor behaviors in Sr₅SmTi_3+2xNb_7−2xO_30−x with x = 0.1 and 0.25. The cross occupancy of Sr and Sm cations in the A1 and A2 sites is probably due to the less stable structure of Sr-based tungsten bronze than the Ba-based one.

4. Conclusions

Oxygen-deficient Sr₅SmTi_3+2xNb_7−2xO_30−x (x = 0, 0.1, 0.25) ceramics with tetragonal tungsten bronze structure have been synthesized and characterized. With increasing oxygen deficiency, the crystal structure become less stable and the lattice shrinks, while the ferroelectricity is weakened, and the low temperature relaxation enhanced. Commensurate modulation is observed in the ferroelectric Sr₅SmTi₃Nb₇O₃₀ (x = 0), while three orders of incommensurate satellite reflections are observed for compositions with x = 0.1, 0.25, and is believed to reduce the structural energy induced by the oxygen deficiency. Two factors are considered to understand the change from ferroelectric behavior to diffuse one. Firstly, the A site cross occupancy leads to smaller radius difference between A1 and A2 sites. Secondly, non-polar 5-coordination Ti cations caused by the O(3,5) vacancies interrupt the ferroelectric polar domains. Moreover, Sr₅SmTi_3+2xNb_7−2xO_30−x ceramics with x = 0.1 and 0.25 may be very good candidates for temperature-stable dielectrics with dielectric constant ∼300, and very low tan δ < 0.02 in a wide temperature range from 200 K to 500 K.

Acknowledgements

The present work was financially supported by the Chinese National Basic Research Program under Grant No. 2015CB654601, National Natural Science Foundation of China under Grant No. 51332006, and Fundamental Research Funds for the Central Universities under Grant No.2015QNA4008.

References

1. Y. Xu, Ferroelectric Materials and their Applications, Elsevier, North-Holland, Amsterdam, 1999, p. 247.
2. P. B. Jamieson, S. C. Abrahams and J. L. Bernstein, J. Chem. Phys., 1969, 48, 5048.
3. X. L. Zhu, K. Li and X. M. Chen, J. Am. Ceram. Soc., 2014, 97, 329.
4. X. L. Zhu, M. Fu, M. C. Stennett, P. M. Vilarinho, I. Levin, C. A. Randall, J. Gardner, F. D. Morrison and I. M. Reaney, Chem. Mater., 2015, 27, 3250.
5. I. Levin, M. C. Stennett, G. C. Miles, D. I. Woodward, A. R. West and I. M. Reaney, Appl. Phys. Lett., 2006, 89, 122908.
6. M. C. Stennett, I. M. Reaney, G. C. Miles, D. I. Woodward, A. R. West, C. A. Kirk and I. Levin, J. Appl. Phys., 2007, 101, 104114.
7. Y. H. Sun, X. M. Chen and X. H. Zheng, J. Appl. Phys., 2004, 96, 7435.
8. V. Bovtun, S. Kamba, S. Veljko, D. Nuzhnyy, K. Knizek, M. Savinov and J. Petzelt, J. Appl. Phys., 2007, 101, 054115.
9. X. L. Zhu, S. Y. Wu and X. M. Chen, Appl. Phys. Lett., 2007, 91, 162906.
10. E. Castel, M. Josse, D. Michau and M. Maglione, J. Phys.: Condens. Matter, 2009, 21, 452201.
11. X. L. Zhu and X. M. Chen, Appl. Phys. Lett., 2010, 96, 032901.
12. X. L. Zhu, X. Q. Liu and X. M. Chen, J. Am. Ceram. Soc., 2011, 94, 1829.
13. X. L. Zhu and X. M. Chen, J. Am. Ceram. Soc., 2012, 95, 3185.
14. X. L. Zhu and X. M. Chen, Appl. Phys. Lett., 2016, 108, 152903.
15. M. M. Mao, K. Li, X. L. Zhu and X. M. Chen, J. Appl. Phys., 2015, 117, 134108.
16. C. A. Paz de Araujo, J. D. Cuchiaro, L. D. McMillan, M. C. Scott and J. F. Scott, Nature, 1995, 374, 627.
17. J. F. Scott and M. Dawber, Appl. Phys. Lett., 2000, 76, 3801.
18. T. Rojac, M. Kosec, B. Budic, N. Setter and D. Damjanovic, J. Appl. Phys., 2010, 108, 074107.
19. R. Maier, J. L. Cohn, J. J. Neumeier and L. A. Bendersky, Appl. Phys. Lett., 2001, 78, 2536.
20. M. M. Kumar, V. R. Palkar, K. Srinivas and S. V. Suryanarayana, IBID, 2000, 76, 2764.
21. J. F. Schooley, W. R. Hosler and M. L. Cohen, Phys. Rev. Lett., 1964, 12, 474.
22. R. Ramesh, W. K. Chan, B. Wilkens, H. Gilchrist, T. Sands, J. M. Tarascon, V. G. Keramidas, D. K. Fork, J. Lee and A. Safari, Appl. Phys. Lett., 1992, 61, 1537.
23. P. Jakes, E. Erdem, R.-A. Eichel, L. Jin and D. Damjanovic, Appl. Phys. Lett., 2011, 98, 072907.
24. Z. Zhou, Y. Li, L. Yang and X. Dong, Appl. Phys. Lett., 2007, 90, 212908.
25. S. F. Liu, Y. J. Wu, J. Li and X. M. Chen, Appl. Phys. Lett., 2014, 104, 082912.
26. M. Prades, N. Masó, H. Beltrán, E. Cordoncillo and A. R. West, Inorg. Chem., 2013, 52, 1729.
27. L. A. Bursill and P. J. Lin, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 49.
28. A. M. Glass, J. Appl. Phys., 1969, 40, 4699.
29. P. J. Lin and L. A. Bursill, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 504.
30. R. Guo, A. S. Bhalla, G. Burns and F. H. Dacol, Ferroelectrics, 1989, 93, 397.
31. H.-Y. Lee and R. Freer, J. Appl. Cryst., 1998, 31, 683.
32. D. Viehland, S. J. Jang, L. E. Cross and M. Wuttig, J. Appl. Phys., 1990, 68, 2916.

---