Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Luminescence properties and site occupancy of Ce3+ in Ba2SiO4: a combined experimental and ab initio study†
Litian Lina,
Xiaoxiao Huangb,
Rui Shia,
Weijie Zhou a,
Yan Huangc,
Jiuping Zhonga,
Ye Taoc,
Jun Chend,
Lixin Ning
a,
Yan Huangc,
Jiuping Zhonga,
Ye Taoc,
Jun Chend,
Lixin Ning *b and
Hongbin Liang*a
*b and
Hongbin Liang*a
aMOE Key Laboratory of Bioinorganic and Synthetic Chemistry, KLGHEI of Environment and Energy Chemistry, School of Chemistry, Sun Yat-sen University, Guangzhou 510275, China
bAnhui Province Key Laboratory of Optoelectric Materials Science and Technology, Department of Physics, Anhui Normal University, Wuhu, Anhui 241000, China
cBeijing Synchrotron Radiation Facility, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100039, China
dSchool of Electronics and Information Technology, Sun Yat-sen University, Guangzhou 510275, China
First published on 12th May 2017
Abstract
Photoluminescence properties of Ba2−2xCexNaxSiO4 (x = 0.0005) prepared by a solid-state reaction method are first studied with excitation energies in the vacuum-ultraviolet (VUV) to ultraviolet (UV) range at low temperature. Five bands are observed in the excitation spectrum of Ce3+ 5d → 4f emission at 26.5 K. The highest energy band is attributed to the host excitonic absorption, from which the band gap energy of the host is estimated to be around 7.36 eV. The four lower energy bands are assigned to the 4f → 5d transitions of Ce3+ located at one of the two types of Ba sites in Ba2SiO4, based on a comparison of excitation spectra at different monitoring wavelengths. Under UV excitation, the material exhibits bright luminescence at 350–450 nm, with a fast decay time (∼26 ns at 4 K) and a high thermal quenching temperature (>500 K). In view of this, X-ray excited luminescence measurements are then conducted, and the results suggest a potential application of Ba2SiO4:Ce3+ as scintillation phosphors. Hybrid density functional theory (DFT) calculations within the supercell model are carried out to optimize the local structures of Ce3+ at the two Ba sites in Ba2SiO4, on which wave function-based ab initio embedded cluster calculations are performed to derive the 4f1 and 5d1 energy levels of Ce3+. On the basis of the calculated DFT total energies and the comparison between experimental and calculated 4f → 5d transition energies, we find that the luminescence originates predominantly from Ce3+ occupying nine-coordinated Ba2 sites. Furthermore, electronic properties of Ce3+ in Ba2SiO4 are evaluated to provide an understanding of the high thermal stability of the 5d luminescence at the level of electronic structures.
1. Introduction
Silicate compounds have been considered as suitable hosts of lanthanide ions for applications as luminescent materials due to their good chemical stability, low manufacturing cost, and environment-friendly characteristics.1 Recently, alkaline earth orthosilicate phosphors, M2SiO4:Ce3+, Eu2+ (M = Ca, Sr, Ba) have received renewed interest due to their potential use as phosphors in white light-emitting diodes (LEDs),2–5 although they were first reported more than four decades ago.6,7 A significant feature of this class of phosphors is the ease of tuning the emission wavelength by changing the composition of M cations or by manipulating the crystalline polymorphism. For instance, the emission color of SrxBa2−xSiO4:Eu2+ can be varied from green for Ba2SiO4:Eu2+ to yellow for Sr2SiO4:Eu2+,8 and Ca2SiO4:Ce3+ exhibited yellow emission in the γ-phase and light-blue emission in the β-phase.9 The light emission originates from spin- and parity-allowed 5d → 4f transition of Eu2+ or Ce3+, and the transition energy depends strongly on the geometric structure of the local environment due to the large crystal-field interaction of the 5d electron with its surroundings.10Among the alkaline earth orthosilicates, Ba2SiO4 stabilizes only in an orthorhombic structure with the space group Pmcn (no. 62), having two crystallographically distinct Ba sites (Ba1 and Ba2 sites) of Cs symmetry (Fig. 1a).11 Within a distance of 3.3 angstrom, the Ba1 and Ba2 sites are coordinated by ten and nine oxygen atoms, respectively. Activated by Ce3+, the material displays intense emission at around 384 nm under UV excitations,7 but the location of Ce3+ on the Ba1 or Ba2 site is not yet clear. When Ca2SiO4 was added to Ba2SiO4 via solid solution, the emission band shifted to longer wavelengths, at around 400 nm for Ba1.2Ca0.8SiO4:Ce3+ with a high thermal quenching temperature of 225 °C.12 It is noted that, although photoluminescence properties of Ca2SiO4:Ce3+ have been investigated in relation with the local structure of Ce3+,13 similar studies on the end member Ba2SiO4:Ce3+ are still lack. Such basic information is important in tailoring Ba2SiO4:Ce3+-containing phosphors with desired properties.
In the present work, we extend previous measurements of emission and excitation spectra of Ce-doped Ba2SiO4 by using VUV-UV excitations with synchrotron radiation at low temperatures, and then investigate luminescence properties of the compound under X-ray excitation. Hybrid DFT calculations within the supercell model are performed to optimize the local structures of Ce3+ located on the Ba1 and Ba2 sites, based on which wave function-based ab initio calculations within the embedded cluster model are carried out to derive the 4f1 and 5d1 energy levels of Ce3+. By comparing the DFT total energies for the CeBa1- and CeBa2-doped supercells and the calculated and experimental 4f → 5d transition energies, the site occupancy of Ce3+ in Ba2SiO4 is discussed in association with the local coordination structure. Moreover, electronic properties of Ce3+ in Ba2SiO4 are also evaluated to understand the thermal stability of the 5d luminescence. The paper is organized as follows. The experimental and computational methods are described in Section 2. The results of luminescence measurements and ab initio calculations are presented and discussed in Section 3, with the final conclusions collected in Section 4.
2. Methodology
2.1. Experimental details
Powder samples of Ba2−2xCexNaxSiO4 (x = 0.0005–0.06) were synthesized by the solid-state reaction at high temperature. The starting materials included analytical grade BaCO3, Na2CO3, and 99.99% purity SiO2 and CeO2, where Na2CO3 was used to introduce NaBa point defects to compensate for the excess charge of Ce3+ on the Ba2+ site. After being thoroughly mixed in an agate mortar using alcohol as the mixing medium, stoichiometric amounts of the materials were calcined in 10% H2/90% N2 reducing atmosphere at 1350 °C for 5 h. The phase purity and crystal structures of the samples were examined by powder X-ray diffraction patterns on a Rigaku D-MAX 2200 VPC X-ray diffractometer with a wavelength of 1.54056 Å Cu Kα radiation at 40 kV and 26 mA. High quality diffraction data of the Ba2SiO4 host for the Rietveld refinement were collected over a 2θ range from 10° to 110° at Bruker D8 advanced X-ray diffractometer also with Cu Kα radiation (40 kV and 40 mA), and the refinement was performed using TOPAS-Academic program. The UV-vis excitation and emission spectra as well as the luminescence decay curves were recorded at an Edinburgh FLS-920 combined with a steady-state and fluorescence lifetime spectrometer. The excitation and emission spectra in the VUV-UV range were measured on the beam line 4B8 of the Beijing Synchrotron Radiation Facility (BSRF) under normal operating conditions by using the spectrum of sodium salicylate (o-C6H4OHCOONa) as a reference.14 The spectra of X-ray excited luminescence were recorded via Ocean Optics QE65000 spectrometer combined with an X-ray tube with tungsten anode as excitation source operating at 90 kV and 5 mA.2.2. Computational details
The Ce-doped Ba2SiO4 crystal was modeled by a 2 × 1 × 2 supercell containing 112 atoms, in which one of the 32 Ba2+ ions was replaced by a Ce3+ and another by Na+ for charge compensation, corresponding to the chemical formula Ba2−2xCexNaxSiO4 (x ≈ 0.0625). Four different CeBa–NaBa double substitutions were considered, with Ce3+ located at a Ba1 or Ba2 site and Na+ at a nearest-neighbor or distant Ba site within the supercell. The nearest distance between Ce3+ ions in the supercell systems is around 10.2 Å, which is large enough to avoid their mutual influence in the computational study of localized electronic states of an individual Ce3+. The lattice parameters and atomic coordinates of the supercells were first optimized by periodic DFT with a hybrid functional in the PBE0 scheme,15 as implemented in the VASP package.16,17 The Ba(5s25p66s2), Si(3s23p2), O(2s22p4), and Ce(5s25p64f15d16s2) were treated as valence electrons, and their interactions with the cores were described by the projected augmented wave method.18 The convergence criteria for total energies and atomic forces were set to 10−4 eV and 0.02 eV Å−1, respectively, with a cutoff energy of 530 eV for the plane wave basis. One k-point Г was used to sample the Brillouin zone.The 4f → 5d transition energies of Ce3+ were calculated with a wave function-based embedded cluster approach. The Ce-centered cluster was first constructed on the basis of the DFT-optimized crystal structure, each comprising the central Ce3+ and the oxygen ions in the first coordination shell. Its immediate surrounding within a sphere of radius 10.0 Å was represented by several hundreds of ab initio model potentials (AIMPs),19 and the remainder of the surroundings were simulated by tens of thousands of point charges at lattice sites, which were generated with Lepetit's method.20 Wave function-based CASSCF/CASPT2 calculations with the spin–orbit effect were then carried out to obtain the 4f1 and 5d1 energy levels of Ce3+ by using the program MOLCAS.21 In the CASSCF calculations, a [4f, 5d, 6s] complete active space was adopted, and in the CASPT2 calculations, the dynamic correlation effects of the Ce3+(5s, 5p, 4f, 5d) electrons and the O2−(2s, 2p) electrons were taken into account. Further details of the calculations can be found in ref. 22 and 23.
3. Results and discussion
3.1. Structural characterization
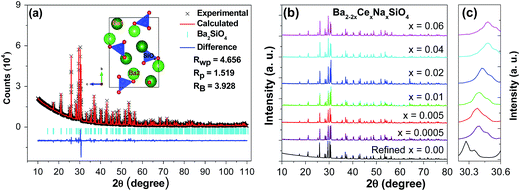
Rietveld refinement of the XRD pattern of Ba2SiO4 was performed, for which the orthorhombic structure (ICSD no. 6246)11 was employed as the initial model. A comparison of the experimental and calculated results (Fig. 1a) shows that the sample is of single phase without detectable impurities or a second phase. The sample crystallizes in an orthorhombic structure with the space group Pmcn, and the lattice parameters were determined to be a = 5.807 Å, b = 10.213 Å, c = 7.504 Å, V = 445.057 Å3. The atomic positions and occupancy factors are listed in Table 1. The average Ba–O bond lengths of the Ba1O10 and Ba2O9 coordination polyhedra are 2.985 and 2.826 Å, respectively. The present results for the structure of Ba2SiO4 are in good agreement with those reported in ref. 11. For Ce-doped samples, Ba2−2xCexNaxSiO4 (x = 0.0005–0.06), the XRD patterns are shown in Fig. 1b. No significant impurities peaks can be observed, indicating the Ce3+ and Na+ are completely dissolved into the host. The diffraction peak of (130) crystallographic plane shifts to larger angles as the doping concentration increases (Fig. 1c), which is due to a decrease in the size of the unit cell with increasing dopant content, in light of the smaller ionic sizes of Ce3+ and Na+ than that of Ba2+.24| Atom | Site | x | y | z | Occupancy |
|---|---|---|---|---|---|
| a a = 5.80737(3) Å, b = 10.21296(5) Å, c = 7.50385(4) Å, V = 445.057(4) Å3; space group, Pmcn; Z = 4; d = 5.47 g cm−3. | |||||
| Ba1 | 4c | 0.2500 | 0.0870 | 0.1608 | 1 |
| Ba2 | 4c | 0.2500 | 0.6955 | −0.0084 | 1 |
| Si | 4c | 0.2500 | 0.4200 | 0.2282 | 1 |
| O1 | 4c | 0.2500 | 0.5705 | 0.3097 | 1 |
| O2 | 8d | 0.0195 | 0.3479 | 0.3051 | 1 |
| O3 | 4c | 0.0250 | 0.4159 | 0.0130 | 1 |
3.2. Photoluminescence properties
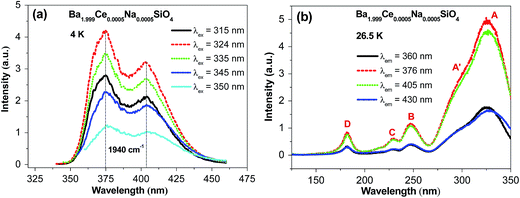
Fig. 2 shows the emission and excitation spectra of Ba1.999Ce0.0005Na0.0005SiO4 recorded at low temperatures. In Fig. 2a, the emission spectra were measured at 4 K under excitation at different wavelengths from 315 to 350 nm. All the spectra exhibit two-band profiles with the peak wavelengths almost overlapped with each other. The separations of the two bands are around 1940 cm−1, which is typical of 5d emission from a given kind of Ce3+ centers, and can be attributed to the transitions from the lowest excited 5d level to the spin–orbit split 2F5/2 and 2F7/2 multiplet terms of 4f1 configuration. The relative intensities of the emission spectra are in line with those at the excitation wavelengths within the lowest-energy excitation band profile (Fig. 2b). Since the doping concentration is low in the sample under investigation, the energy transfer between Ce3+ activators is expected to be inefficient. Thus, the above observations imply that the emissions come predominantly from one kind of Ce3+ centers with similar coordination environments. Considering the smaller ionic size of Ce3+ than Ba2+, we suppose that the emissions originate from Ce3+ centers located at nine-coordinated Ba2 sites rather than ten-coordinated Ba1 sites, as will be confirmed by ab initio calculations (see Section 3.3).Fig. 2b shows four representative VUV-UV excitation spectra of Ba1.999Ce0.0005Na0.0005SiO4 measured at 26.5 K, by monitoring the emission at different wavelengths. The relative intensities of the excitation spectra are consistent with those at the monitoring wavelengths within the emission spectral profile. Each of the spectra consists of four distinct bands at around 327 (band A), 248 (band B), 229 (band C) and 182 nm (band D), and a clear shoulder (A′) on the shorter-wavelength side of the band A. In light of the similarity of the spectral shapes, we assign the band A, B, C and the shoulder A′ to transitions from the ground 4f level to excited 5d levels of a given type of Ce3+ centers, presumably located at Ba2 sites. From the maximum energies of the lowest-energy excitation band (A) and the higher-energy emission band, the Stokes shift of the 5d → 4f emission is estimated to be 3843 cm−1 (0.48 eV), within the range of those for Ce-doped silicate compounds.25 The excitation band D at 182 nm (6.81 eV) is attributed to the host excitonic absorption, corresponding to the excitation of an electron from the top of the host valence band to the energetically lowest bound excitonic state. By taking into account the electron–hole binding energy of the exciton,26 the band gap of the host is estimated to be ∼1.08 × 6.81 = 7.36 eV.
Fig. 3 shows the decay curves of Ce3+ 5d → 4f emission at different wavelengths within the emission profile (Fig. 2a) upon 325 nm excitation of Ba1.999Ce0.0005Na0.0005SiO4 at 4 K. All the curves are overlapped with each other, and can be well fitted by the monoexponential function with lifetimes of about 26 ns, as indicated in the figure. These luminescence decay behaviors at different wavelengths are consistent with the presence of a single type of Ce3+ centers in the studied sample.
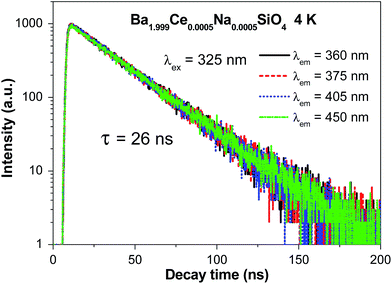 | ||
| Fig. 3 Luminescence decay curves (λex = 325 nm; λem = 360, 375, 405, and 450 nm) of Ba1.999Ce0.0005Na0.0005SiO4 at 4 K. | ||
In addition, we have also measured low-temperature emission and excitation spectra and luminescence decay curves of Ba1.9995Ce0.0005SiO4 without the presence of Na+ as charge compensators (see Fig. S1 and S2 in ESI†). Comparison of the results with those for Ba1.999Ce0.0005Na0.0005SiO4 indicates that the presence of Na+ has no obvious influence on spectral properties of Ce3+, and thus does not affect the occupation of Ce3+ at a given type of Ba2+ sites. Nevertheless, the addition of Na+ for charge compensation can lead to a lower concentration of point defects when compared to samples without Na+. These defects could act as electron–hole recombination centers and hence deteriorate the emission properties of the material.
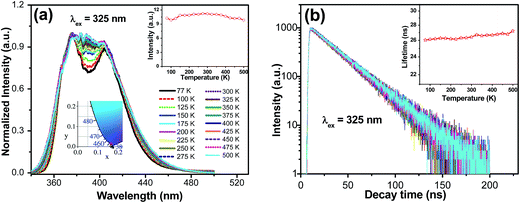
Fig. 4a displays the emission spectra of Ba1.999Ce0.0005Na0.0005SiO4 upon 325 nm excitation at temperatures from 77 to 500 K. The emission profile becomes more featureless with increasing temperature, which can be ascribed to thermally induced band broadening. The inset shows the CIE chromaticity coordinate of Ba1.999Ce0.0005Na0.0005SiO4, the emission colors at various temperatures all showing the same purple-blue (0.164, 0.013 ± 0.001). In addition, the temperature dependence of the integrated emission intensity is displayed in the right inset of the figure. It shows that from 77 to 500 K only ∼4% of the initial intensity is lost, indicating an excellent thermal stability of the phosphor. Fig. 4b gives the decay curves of 376 nm emission under excitation at 325 nm at different temperatures. All the curves exhibit similar monoexponential behaviors, and the derived lifetimes are plotted in the inset of the figure, which shows no luminescence quenching at up to 500 K. Instead, a slight increase in lifetime can be observed, probably due to an enhanced reabsorption at raised temperatures.27
3.3. X-ray excited luminescence properties
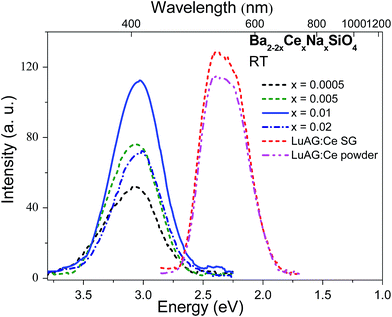
Considering the fast decay time (∼26 ns under UV excitation at 4 K) and excellent thermal stability (T0.5 > 500 K) of luminescence in Ba1.999Ce0.0005Na0.0005SiO4, as well as the large density (5.47 g cm−3) and effective atomic number (49.9) of Ba2SiO4, we have further evaluated the potential application of Ba2SiO4:Ce3+ as a scintillation phosphor. Fig. 5 shows a comparison of X-ray excited luminescence spectra of Ba2SiO4:Ce3+ and the commercial scintillators Lu3Al5O12:Ce3+ in single-crystal and powder forms measured at the same experimental conditions. Under X-ray excitation, Ba2SiO4:Ce3+ samples give broad and featureless emission bands at ∼408 nm due to 5d → 4f transitions of Ce3+. This is in line with the room temperature emission spectrum in Fig. 4, with slight difference in emission peaks as a result of detector and instrument responses. By using that of the commercial Lu3Al5O12:Ce3+ powder (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photon per MeV)28 as a reference, the absolute light yields for the x = 0.0005, 0.005, 0.01, and 0.02 samples were estimated to be 10
000 photon per MeV)28 as a reference, the absolute light yields for the x = 0.0005, 0.005, 0.01, and 0.02 samples were estimated to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300, 13
300, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 19
500, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 and 12
600 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 photon per MeV respectively. The large light yield of the x = 0.01 sample implies that Ba2SiO4:Ce3+ could be a promising scintillation material worth further optimization.
600 photon per MeV respectively. The large light yield of the x = 0.01 sample implies that Ba2SiO4:Ce3+ could be a promising scintillation material worth further optimization.
3.4. Ab initio calculations
| a (Å) | b (Å) | c (Å) | Eg (eV) | |
|---|---|---|---|---|
| PBE | 5.890 | 10.407 | 7.593 | 4.62 |
| PBE0 (25% HF) | 5.833 | 10.294 | 7.533 | 7.09 |
| PBE0 (28% HF) | 5.829 | 10.284 | 7.524 | 7.38 |
| Expt | 5.807 | 10.213 | 7.504 | 7.36 |
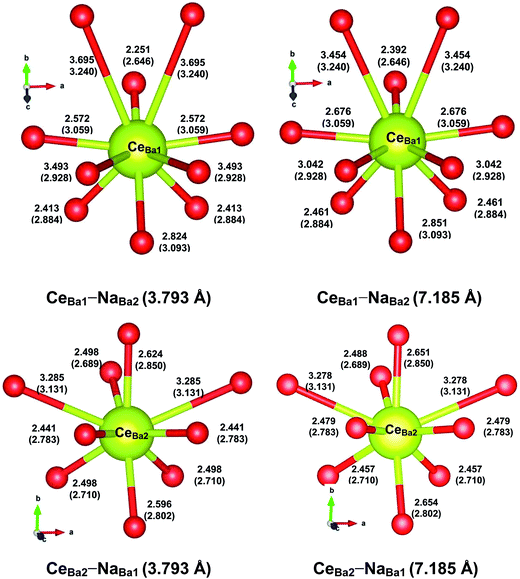
For Ce,Na-codoped Ba2SiO4 supercells, four different CeBa–NaBa double substitutions have been considered, which are distinguished by the shortest (3.793 Å) and longest (7.185 Å) Ba–Ba distances in the undoped supercell. Compared with the undoped supercell, the structural relaxation suggests that the incorporation of CeBa–NaBa causes small decreases (by 0.716–0.944%) in the supercell volume, and slightly distorts the orthorhombic structure of the undoped supercell into monoclinic structures, with the deviations of angles to within ±0.185°. Thus, the calculations predict a negligible deformation of the crystallographic phase when a small amount of Ce and Na are substituted into the Ba sites, in consistence with XRD measurements (Fig. 1b).
Table 3 presents the calculated DFT total energies for the four Ce,Na-codoped supercells. It shows that the two CeBa2–NaBa1 substitutions are much more stable than the two CeBa1–NaBa2 (by at least 670 meV), irrespective of the Ce–Na distance. For a given CeBa–NaBa combination, the two single substitutions prefer to be close to each other, as is expected from their opposite effective charges. The relative stabilities may be qualitatively understood by the valences of Ce3+ and Na+ calculated from their optimized local structures using the bond valence sum (BVS) method.29 The results are listed in the last two columns of Table 3. It shows that the BVS values of Ce3+ at the Ba2 site are much closer to the formal value (+3) than those of Ce3+ at the Ba1 site; the same is true for Na+. This suggests that the greater stability of CeBa2–NaBa1 than CeBa1–NaBa2 is due to the preference of Ce3+ at the Ba2 site over the Ba1 site. This point is further supported by the calculated DFT total energies for the optimized supercells with a single Ce3+ (Na+) substituted at the Ba1 or Ba2 site, with the net defect charge compensated by a uniform charge density. The results show that the CeBa2 (NaBa2) substitution is energetically more favorable by 979 meV (118 meV) than the CeBa1 (NaBa1) substitution, consistent with the above BVS analysis.
| d (Å) | Total energy (eV) | Relative total energy (meV) | Valence by BVS | |||
|---|---|---|---|---|---|---|
| Unrelaxed | Optimized | Ce | Na | |||
| CeBa2–NaBa1 | 3.793 | 3.333 | −1029.4551 | 0 | 2.759 | 0.698 |
| CeBa2–NaBa1 | 7.185 | 6.972 | −1029.3598 | 95 | 2.711 | 0.605 |
| CeBa1–NaBa2 | 3.793 | 3.642 | −1028.6900 | 765 | 2.636 | 0.916 |
| CeBa1–NaBa2 | 7.185 | 6.977 | −1028.1342 | 1321 | 2.259 | 0.882 |
The local structures of Ce3+ in the optimized supercells are depicted in Fig. 6, with the values of selected relaxed (unrelaxed) bond lengths indicated. All the CeBa substitutions cause decreases in the average bond length by 0.054–0.158 Å, consistent with the smaller ionic size of Ce3+ than Ba2+. The local structural distortion around CeBa1 is more severe than that around CeBa2. Specifically, the bond distances from CeBa1 (CeBa2) to the six (seven) nearest O atoms are decreased by 0.242–0.487 Å (0.148–0.342 Å), whereas to the four (two) farthest O atoms, the distances are increased by 0.114–0.565 Å (0.147–0.154 Å), presumably due to steric repulsion. It also shows that the nearby Na+ has a more pronounced effect on the local structures of CeBa1 than that of CeBa2, when compared with their respective local structures with a distant Na+ present. This indicates that the local structure of CeBa2 is more rigid than that of CeBa1, which could be correlated with greater stability of the former substitution than the later.
| CeBa1–NaBa2 (3.793 Å) | CeBa1–NaBa2 (7.185 Å) | CeBa2–NaBa1 (3.793 Å) | CeBa2–NaBa1 (7.185) | |
|---|---|---|---|---|
| 4f1 | 0 | 0 | 0 | 0 |
| 4f2 | 679 | 398 | 472 | 411 |
| 4f3 | 1066 | 496 | 863 | 671 |
| 4f4 | 2259 | 2230 | 2325 | 2343 |
| 4f5 | 2948 | 2585 | 2647 | 2572 |
| 4f6 | 3034 | 2710 | 3172 | 2892 |
| 4f7 | 3599 | 2941 | 3340 | 3223 |
| 5d1 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 391 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856 856 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 445 445 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 886 |
| 5d2 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 968 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069 069 |
| 5d3 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 571 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534 534 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937 937 |
| 5d4 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 380 |
46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304 304 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
| 5d5 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 830 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
To facilitate comparison with experimental excitation spectra, the calculated 4f1 → 5di (i = 1–5) transitions are schematically presented in Fig. 7, where the relative transition intensities within each cluster were calculated using the wave functions and energies at the spin–orbit level. It is apparent from the figure that the experimental excitation spectrum can be assigned to the 4f1 → 5di transitions of Ce3+ located at Ba2 sites. The lowest excitation band (band A, Fig. 7a) can be clearly ascribed to 4f1 → 5d1 transitions of CeBa23+, and the shoulder (A′) on the shorter wavelength side to 4f1 → 5d2 transitions. The two higher excitation bands, i.e., bands B and C, can be attributed to 4f1 → 5d3,4 transitions, respectively, but with an average underestimation of about 2140 cm−1. Thus, the above comparison provides direct evidence for the predominant preference of the dopant Ce3+ for the nine-coordinated Ba2 site over the ten-coordinated Ba1 site, which is also in consistence with the results of DFT total energy calculations.
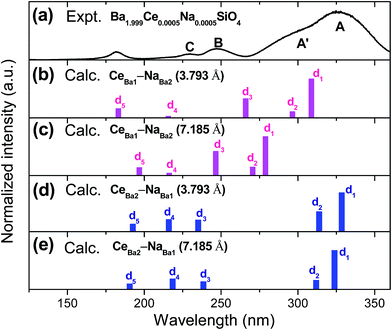 | ||
| Fig. 7 Schematic representation of the calculated energies and relative intensities of the 4f1 → 5di (i = 1–5) transitions of Ce3+ on the Ba2+ sites of Ba2SiO4. The VUV-UV excitation spectrum of Ba1.999Ce0.0005Na0.0005SiO4 (λem = 376 nm) at 26.5 K (see also Fig. 2b) is also shown for comparison. | ||
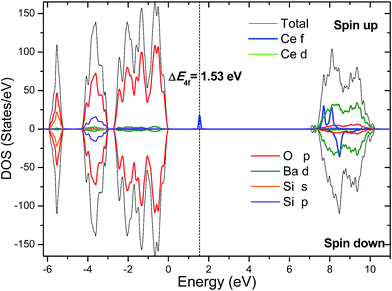
It is worth stressing that ΔE4f was derived in the single particle approximation of DFT (Kohn–Sham eigenvalues), and a more rigorous determination of the energy position of the occupied Ce3+ 4f state requires to calculate the charge transition level.30 The Ce-induced charge transition level ε(Ce3+/4+) with reference to the host VBM is defined as the Fermi level at which the defect formation energies of Ce3+ and Ce4+ are equal to each other, and can be computed using
| ε(Ce3+/4+) = Etot(Ce3+) − Etot(Ce4+) − εVBM |
Given the value of ε(Ce3+/4+), the energy difference (ΔE5d1) between the lowest Ce3+ 5d1 level and the conduction band minimum (CBM) of the host can also be estimated by
| ΔE5d1 = Egap − [ε(Ce3+/4+) + ΔE(4f1 → 5d1) − (1/2)ΔESS] |
4. Conclusions
We have investigated photoluminescence properties of Ce-doped Ba2SiO4 from a combination of experimental and theoretical methods. Under UV excitation, the compound Ba1.999Ce0.0005Na0.0005SiO4 exhibits bright luminescence at 350–450 nm, with a fast decay time (∼26 ns) and a high thermal quenching temperature (>500 K). The X-ray excited luminescence measurements were then conducted, and a comparison of the results with those of the commercial LuAG:Ce3+ suggests a potential application of Ba2SiO4:Ce3+ as scintillation phosphors. The VUV-UV excitation spectra obtained for Ba1.999Ce0.0005Na0.0005SiO4 by monitoring emission at different wavelengths at low temperature revealed that the emission originates predominantly from Ce3+ located at one type of Ba sites. This was found to be the nine-coordinated Ba2 site, on the basis of computations using hybrid DFT and wave function-based ab initio methods. In addition, the energy location of Ce3+ 4f and 5d1 states within the host band gap was derived theoretically, and the large energy separation (∼1.37 eV) between the 5d1 state and the host CBM is consistent with the high thermal stability of the 5d luminescence as observed experimentally. The present work also demonstrate that low-temperature excitation spectral measurements in combination with elaborate ab initio calculations are able to offer microscopic insight into the structure–property relationship of Ce3+ in a local environment of low symmetry, which is common in Ce-activated phosphors for practical applications.Acknowledgements
The work is financially supported by the National Natural Science Foundation of China (21671201, 11574003, U1432249, and U1632101). Technical assistance of the X-ray excited luminescence measurement Yihong Qi, Yangbing Xu, and Prof. Kai Wang from SYSU-CMU Joint Institute of Engineering is gratefully acknowledged.Notes and references
- W. M. Yen, A. Shionoya and H. Yamamoto, Phosphor Handbook, CRC Press, Boca Raton, FL, 2007 Search PubMed.
- Y. Li, J. Wang, X.-M. Wang, F. Pan, T. Zhou and R.-J. Xie, J. Mater. Chem. C, 2017, 5, 1022 RSC.
- D. Wen, H. Kuwahara, H. Kato, M. Kobayashi, Y. Sato, T. Masaki and M. Kakihana, ACS Appl. Mater. Interfaces, 2016, 8, 11615 CAS.
- Z. Xia, S. Miao, M. Chen, M. S. Molokeev and Q. Liu, Inorg. Chem., 2015, 54, 7684 CrossRef CAS PubMed.
- Z. Hao, J. Zhang, X. Zhang, Y. Luo, L. Zhang and H. Zhao, J. Lumin., 2014, 152, 40 CrossRef CAS.
- T. L. Barry, J. Electrochem. Soc., 1968, 115, 1181 CrossRef CAS.
- P. V. Kelsey and J. J. Brown, J. Electrochem. Soc., 1976, 123, 1384 CrossRef CAS.
- K. A. Denault, J. Brgoch, M. W. Gaultois, A. Mikhailovsky, R. Petry, H. Winkler, S. P. DenBaars and R. Seshadri, Chem. Mater., 2014, 26, 2275 CrossRef CAS.
- A. Kalaji, M. Mikami and A. K. Cheetham, Chem. Mater., 2014, 26, 3966 CrossRef CAS.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125117 CrossRef.
- H. Grosse and E. Tillmanns, Cryst. Struct. Commun., 1974, 3, 599 CAS.
- K. Park, J. Kim, P. Kung and S. M. Kim, J. Lumin., 2010, 130, 1292 CrossRef CAS.
- Y. Liu, Q. Fang, L. Ning, Y. Huang, S. Huang and H. Liang, Opt. Mater., 2015, 44, 67 CrossRef CAS.
- Y. Tao, Y. Huang, Z. Gao, H. Zhuang, A. Zhou, Y. Tan, D. Li and S. Sun, J. Synchrotron Radiat., 2009, 16, 857 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- Z. Barandiarán and L. Seijo, J. Chem. Phys., 1988, 89, 5739 CrossRef.
- A. Gellé and M. B. Lepetit, J. Chem. Phys., 2008, 128, 244716 CrossRef PubMed.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig and P. Neogrady, Comput. Mater. Sci., 2003, 28, 222 CrossRef.
- A. B. Muñoz-García and L. Seijo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 184118 CrossRef.
- L. Ning, X. Huang, J. Sun, S. Huang, M. Chen, Z. Xia and Y. Huang, J. Phys. Chem. C, 2016, 120, 3999 CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- P. Dorenbos, J. Lumin., 2005, 111, 89 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2000, 91, 155 CrossRef CAS.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077 CrossRef CAS.
- M. Nikl, A. Yoshikawa, K. Kamada, K. Nejezchleb, C. Stanek, J. Mares and K. Blazek, Prog. Cryst. Growth Charact. Mater., 2013, 59, 47 CrossRef CAS.
- N. Brese and M. O'keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192 CrossRef.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef.
- C. Pédrini, Phys. Status Solidi A, 2005, 202, 185 CrossRef.
- P. Dorenbos, J. Phys.: Condens. Matter, 2005, 17, 8103 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04145d |
| This journal is © The Royal Society of Chemistry 2017 |