Open Access Article
Open Access ArticlePrediction of magnetoresistance using a magnetic field and correlation between the magnetic and electrical properties of La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 (0 ≤ x ≤ 0.3) manganite†
Arwa Belkahlaa,
K. Cherifa,
J. Dhahri *a,
K. Taibib and
E. K. Hlilc
*a,
K. Taibib and
E. K. Hlilc
aLaboratoire de la Matière Condensée et des Nanosciences, Département de Physique, Faculté des Sciences de Monastir, 5019, Tunisia. E-mail: jemai_3000@yahoo.com
bLaboratoire de Science et Génie des Matériaux, Faculté de Génie Mécanique et Génie des Procédés, Université des Sciences et de la Technologie Houari Boumediene BP32 El Alia, Bab Ezzouar, 16111, Algiers, Algeria
cInstitut Neel, CNRS et Université Joseph Fourier, B, P, 166, 38042 Grenoble, France
First published on 14th June 2017
Abstract
In this paper, we have systematically investigated the effect of In doping on the magnetic and magnetocaloric effect (MCE) in La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 (0 ≤ x ≤ 0.3) manganite. All of the samples exhibit a second-order magnetic phase transition from the ferromagnetic to the paramagnetic state at the Curie temperature (TC). From the measurements of isothermal magnetization around (TC), we have determined the magnetic entropy change (ΔSM). It has been found that there was a large (ΔSM), i.e. a large (MCE), in all samples. Among them, a maximum (ΔSM) and the highest relative cooling power (RCP) under the magnetic field of 5 T are found to be 6.14 J kg−1 K−1 and 281 J kg−1, respectively for x = 0. This investigation suggests that our samples would be suitable candidates for magnetic refrigeration technology. The relationship between resistivity and magnetization was performed as ρ = ρ0 exp(−M/α). The (MCE) was investigated based on the resistivity measurements. The obtained results were discussed. A typical numerical method (Gauss function) was used for fitting the experimental data of resistivity. The simulation values such as metal–semiconductor transition temperature (TM–Sc) and maximum resistivity (ρmax), calculated from this function, showed promising agreement with the experimental data. The shifts of these values as a function of magnetic field for all samples have been interpreted.
1. Introduction
Since the discovery of the magnetocaloric effect (MCE) and colossal magnetoresistance (CMR) in perovskite-type oxide materials, the correlation between structure, magnetic, electrical, and transport properties has become a hotspot in today's research.1–6The MCE is the tendency of certain materials, to heat up or cool down during the application or removal of an external magnetic field. This phenomenon is an intrinsic property of magnetic materials and occurs due to the change in the alignment of the magnetic moments under an applied magnetic field. Commonly, the MCE is considered as the entropy change of the system in an isothermal process on applying field. Traditionally, the double-exchange (DE) model7 was suggested to understand the CMR behavior observed in these materials. In this model, a ferromagnetic (FM) interaction between the localized t2g spins resulted from the hopping of itinerant eg spins between adjacent Mn atoms subject to strong intra-site Hund's rule coupling. However, it has been found that the (DE) and the super-exchange (SE) mechanism are known to be sensitive to variation in the Mn–O–Mn bond angle and Mn–O bond length, both controlled by the average size of the A- or the B-site ions whereas the density of charge carriers is controlled by the Mn3+/Mn4+ ratio.8–10
Most of these materials with general formula R1−xAxMnO3 (where R is the rare-earth element, A is the divalent metal element and x is the doping level) have recently attracted considerable research interest in view of their fascinating fundamental properties such as magneto-resistance, magnetocaloric, charge ordering, phase separation, spin ordering, etc., leading to potential application in magnetic, magneto-electronic, photonic devices, infrared detector, as well as spintronics technology.11
Experimentally, manganese oxides, especially, the La–Sr based manganite (La0.7Sr0.3MnO3) are very familiar system. It exhibits a metal–semiconductor transition accompanied by a ferromagnetic–paramagnetic transition near the Curie temperature TC. There are several reports on the magnetocaloric properties of that compound where the large magnetic entropy change with a narrow range of working temperatures was reported at the vicinity of the transition temperature.12–14 The range of working temperature, as well as the transition temperature were modified by suitable substitutions of Sr and/or Mn ions by other ions.15,16 In addition, low-level substitution of Mn by Ni (2%) in La0.7Sr0.3MnO3 was found to enhance the magnetic entropy change (6.52 J kg−1 K−1 at an applied field of 5 T) and shift the transition temperature to above room temperature (350 K).17
More recently, a close interplay between magnetic structure and transport properties of these compounds has been explained by means of the (SE) and (DE) interactions, which are accompanied by the strong Jahn–Teller (JT) distortion and electron–phonon interaction arising from the deformation of the Mn3+O6 octahedral.18 According to (JT) distortion, the structure will distort by removing the degeneracy of the eg orbitals, to stabilize in the 3d3Z2−r2 with respect to the 3dx2−y2 orbitals.19 In this context, Xiong et al. also found a strong correlation between resistivity and magnetic-entropy change (ΔSM).20 So, we can calculate ΔSM based on the electrical measurement.
In a recent publication,21–23 there have been few models that can explain the conductive mechanism in our materials. Among those models, we point out the Mott's variable range hopping (VRH) and small polaron hopping (SPH) model in the semiconducting region and electron–electron, electron–phonon processes in the metallic region. To the best of our knowledge, no studies have been done on the mathematical model which can describe the carrier transport behavior of manganite as a function of temperature around the electrical phase transition and the relation between electrical and magnetic properties is a subject which is not much treated.
In this contribution, the first objective of this work is to determine the correlation between electrical and magnetic properties. The second objective is to develop a mathematical model to quantitatively analyze the temperature-dependent resistivity.
2. Experimental details
La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 (0 ≤ x ≤ 0.3) compounds were synthesized by Pechini sol–gel method24 using stoichiometric amounts of La(NO3)3–6H2O, Bi(NO3)3–5H2O, In(NO3)3·xH2O, Sr(NO3)2, Ca(NO3)2, Mn(NO3)2–4H2O (having a purity of more than 99.9% for each of them). Firstly, the reagents were dissolved in distilled water to obtain a mixed solution. Subsequently, when the nitrates were completely dissolved in the solution, citric acid (CA) and ethylene glycol (EG) were added in the required stoichiometric ratio. The process was heated first at 340–380 K with a vigorous stirring to evaporate water, increase viscosity and accelerate the poly-esterification reaction between CA and EG. Then the temperature was raised up to 450 K forming a dark viscous gel which slowly turned into a dark resin at 500 K. This resin was easily powdered in an agate mortar and was calcined at 870 K for 6 h in oxygen atmosphere to eliminate the carbons gases and the other organic compounds. Finally, at 1075 K for 10 h in following air synthesis the resulting powders were uniaxial pressed at 105 Pa into circular pellets with a thickness of 2 mm and diameter of 8 mm. The obtained black pellets were then sintered in an oxygen atmosphere at 1273 K for 48 h.The structure, the crystallinity and phase purity of the sample were checked by powder X-ray diffraction (XRD) measurements made at room temperature using “PANalytical X'Pert Pro” diffractometer with CuKα radiation (λ = 1.5406 Å). Data acquisition was done in the range of 2θ from 10 to 100° with a step size of 0.017° and a counting time of 18 s per step.
Structural analysis was carried out by the standard Rietveld method25 using the FULLPROF program.26
Magnetization vs. temperature (5–450 K) was measured in an applied magnetic field of 0.05 T, using BS1 and BS2 magnetometers developed in Louis Neel Laboratory of Grenoble. The resistivity of these samples was carried out by using the standard four probe method in the temperature range 5–600 K.
3. Results and discussion
3.1. XRD analysis
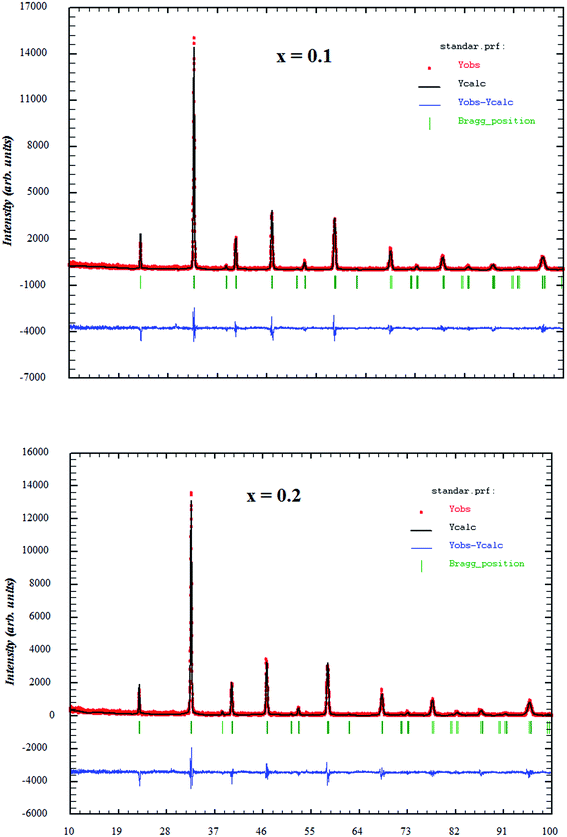
Fig. 1 shows the X-ray diffraction patterns for the La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 (x = 0.1, 0.2) compounds. No impurity peaks are observed in the pattern, indicating a single-phase formation of all samples. For all the samples, all peaks are satisfactorily indexed in the rhombohedra structure with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, hexagonal setting (Z = 6), in which the La/Bi/Sr/Ca atoms are at 6a (0, 0, ¼), Mn/In at 6b (0, 0, 0) and O at 18e (x, 0, ¼) positions. This profile has reasonable R-factors and excellent fits between calculated and observed patterns. We have listed the lattice parameters, unit cell volume, and fitting parameters in Table 1. It is seen that the lattice parameters and unit cell volume gradually increase with increasing In concentration. This can be attributed to the average ionic radius of the B-site 〈rB〉 which increases systematically as smaller Mn3+ ions (0.645) are replaced by larger In3+ ions (0.8).27
c, hexagonal setting (Z = 6), in which the La/Bi/Sr/Ca atoms are at 6a (0, 0, ¼), Mn/In at 6b (0, 0, 0) and O at 18e (x, 0, ¼) positions. This profile has reasonable R-factors and excellent fits between calculated and observed patterns. We have listed the lattice parameters, unit cell volume, and fitting parameters in Table 1. It is seen that the lattice parameters and unit cell volume gradually increase with increasing In concentration. This can be attributed to the average ionic radius of the B-site 〈rB〉 which increases systematically as smaller Mn3+ ions (0.645) are replaced by larger In3+ ions (0.8).27
| x = 0 | x = 0.1 | x = 0.15 | x = 0.2 | x = 0.3 | |
|---|---|---|---|---|---|
| Space group | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cell parameters | |||||
| a (Å) | 5.6318 (2) | 5.6434 (1) | 5.6536 (4) | 5.6576 (2) | 5.6621 (1) |
| c (Å) | 13.7733 (5) | 13.7866 (2) | 13.7954 (3) | 13.8239 (2) | 13.8704 (1) |
| V (Å3) | 378.33 (3) | 380.25 (4) | 381.87 (1) | 383.20 (2) | 385.10 (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Atoms | |||||
| La/Sr/Ca/Bi | |||||
| X | 0 | 0 | 0 | 0 | 0 |
| Y | 0 | 0 | 0 | 0 | 0 |
| Z | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| Biso (La/Sr/Ca/Bi) (Å2) | 0.439 (3) | 0.452 (5) | 0.351 (5) | 0.541 (2) | 0.245 (2) |
| Mn/In | |||||
| X | 0 | 0 | 0 | 0 | 0 |
| Y | 0 | 0 | 0 | 0 | 0 |
| Z | 0 | 0 | 0 | 0 | 0 |
| Biso (Mn/In) (Å2) | 0.379 (4) | 0.384 (3) | 0.248 (5) | 0.423 (1) | 0.265 (2) |
| O | |||||
| X | 0.442 (2) | 0.453 (1) | 0.459 (3) | 0.462 (1) | 0.470 (6) |
| Y | 0 | 0 | 0 | 0 | 0 |
| Z | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| Biso (O) (Å2) | 1.485 (5) | 1.340 (3) | 1.725 (5) | 1.254 (2) | 1.574 (4) |
| t | 0.968 | 0.961 | 0.958 | 0.954 | 0.947 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Bond lengths and bond angles | |||||
| dMn–O (Å) | 1.955 (7) | 1.967 (9) | 1.971 (9) | 1.973 (4) | 1.984 (7) |
| θMn–O–Mn (°) | 173.20 (3) | 166.08 (7) | 165.14 (6) | 164.49 (5) | 161.45 (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Discrepancy factors | |||||
| RP (%) | 2.2 | 2.3 | 2.4 | 2.4 | 2.3 |
| RWP (%) | 2.9 | 3.3 | 3.2 | 3.2 | 3.1 |
| χ2 | 1.26 | 1.63 | 1.37 | 1.55 | 1.44 |
The stability of perovskite sample is usually described in terms of Goldschmidt's tolerance factor (t), which can be calculated using the expression28
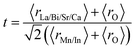 | (1) |
Most materials that are stable in the perovskite structure have (t) between 0.75 and 1.05. For all samples, (t) is well below 1 and implies a tendency toward tilting or rotation of distorted MnO6 octahedral framework of AMnO3 (A = La, Sr, Ca, Bi). With increasing In concentration, (t) decreases (from 0.968 to 0.947) due to the increase in the average ionic radius of the B-site cation, which compresses the Mn–O–Mn bond angle and increases the Mn–O bond length29 (Table 1).
3.2. Magnetic properties
Fig. 2 shows the temperature dependence of magnetization with field-cooled (FC) and zero field-cooled (ZFC) under a magnetic applied field of 0.05 T from x = 0 to x = 0.3.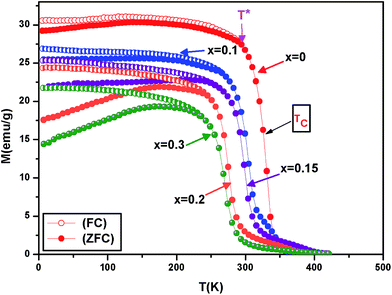 | ||
| Fig. 2 Temperature dependence of magnetization under ZFC and FC curves at a field of 0.05 T for La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3. | ||
All these samples exhibit a paramagnetic to ferromagnetic transition at the Curie temperature TC. This temperature has been determined by differentiating the M–T curves and is defined as the inflection point of the function dM/dT. With increases of In doping, the Curie temperature TC decreases from 330 K for x = 0 to 268 K for x = 0.3. This temperature reveals the long-range ferromagnetic ordering, indicating strong ferromagnetic exchange coupling between Mn and In sublattice.30 In the low temperature region, FC and ZFC curves diverge significantly in all samples at the so-called irreversibility temperature (T*). This temperature is defined as the temperature below which MZFC departs from MFC and large bifurcation starts to occur. We observe here that T* shifts to a lower temperature with an increase in In substitution and it is found to be 294 K, 266 K, 255 K, 245 K and 236 K for x = 0, x = 0.1, x = 0.15, x = 0.2 and x = 0.3, respectively. This splitting has been attributed to the magnetic frustration arising from a coexistence of insulating antiferromagnetic and metallic ferromagnetic phases, or from the competition between antiferromagnetic and ferromagnetic interactions. Moreover, the irreversibility for these samples demonstrates the signature of strong anisotropy field31 generated from ferromagnetic (FM) clusters in the system. The magnetic moment gradually diminishes and prominent bifurcation between ZFC and FC curves become more and more obvious with increasing In concentration.32 This phenomenon is observed in many magnetic materials.33–36
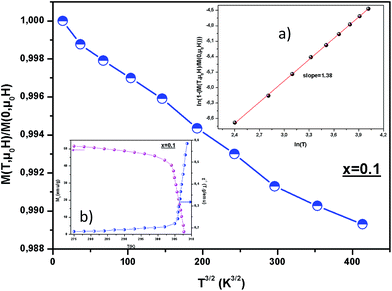
Furthermore, it is interesting to see which theoretical expression describes the temperature dependence of magnetization. According to Bloch's T3/2 law, at a low temperature, the zero field magnetization M(T,μ0H) should have a temperature dependence.37
| M(T,μ0H)/M(0,μ0H) = 1 − BT3/2 | (2) |
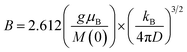 | (3) |
| E(q) = Δ + Dq2 | (4) |
| x = 0 | x = 0.1 | x = 0.15 | x = 0.2 | x = 0.3 | |
|---|---|---|---|---|---|
| Slope | 1.43 | 1.38 | 1.46 | 1.40 | 1.51 |
| B (10−5 K−2/3) | 2.91 | 2.70 | 2.03 | 1.85 | 1.69 |
| D (meV Å2) | 97.76 | 112.56 | 143.38 | 156.83 | 181.75 |
We assume that the magnetic moment at temperature T and magnetic field μ0H is given by
| M(T,μ0H) = MSp(T) + χμ0H | (5) |
The spontaneous magnetic moment of the sample can be obtained by fitting the linear part of magnetization at high magnetic field. The evolution of the spontaneous magnetization MSp and the susceptibility as a function of temperature, deduced from M(μ0H) measurements, can be shown in the inset (b) of Fig. 3 for x = 0.1 for example. The MSp(T) curve drops rapidly near TC = 310 K, TC = 298 K, TC = 275 K and TC = 268 K for x = 0, x = 0.15, x = 0.2 and x = 0.3, respectively showing a well-defined Curie temperature.
3.3. Magnetocaloric effect
The scope of this paper concerns the study of magnetocaloric effect (MCE), which is an intrinsic property of magnetic materials. It is the heating or cooling of materials when subjected to magnetic field variation, which is maximized when the material is near its magnetic ordering temperature.Fig. 4 shows the magnetic-field dependences of the magnetization measured at different temperatures around TC for x = 0 and x = 0.15 compounds for example. The magnetization was found to increase with decreasing temperature, where thermal fluctuations of spins decrease with decreasing temperature. Therefore, in order to understand the nature of the magnetic phase transition, we can use the Banerjee criterion.44 According to this law, the sign of slopes of the M2 vs. μ0H/M curves (Arrott plots) indicates the nature of the PM–FM transition; meaning that if a slope is negative, the transition is of first order (FOMT) while when it is positive, the transition is of second order (SOMT). The Arrott plots shown in inset of Fig. 4 clearly indicate a positive slope in the complete M2 range, confirming the SOMT.
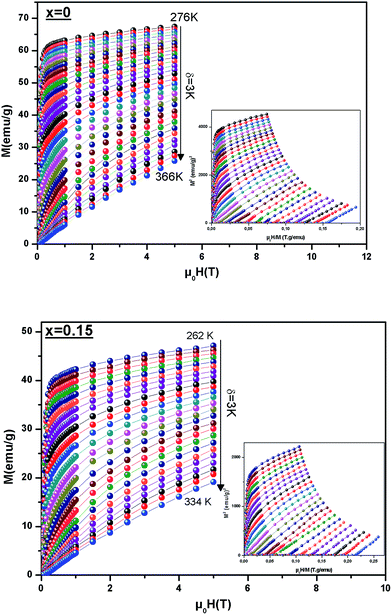 | ||
| Fig. 4 Isothermal magnetization measured at different temperatures around TC. The inset shows the Arrott plots for x = 0 and x = 0.15. | ||
The MCE properties have been evaluated by calculating two factors:
(i) Magnetic entropy change (ΔSM), which can be determined from the magnetization curves with the help of the Maxwell's relation given as:
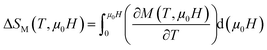 | (6) |
(ii) and Relative Cooling Power (RCP), which is the most meaningful parameter that provides a measure of the amount of heat transfer between hot and cold sinks during one ideal refrigeration cycle. It is defined as:
| RCP = −ΔSmaxM × δTFWHM | (7) |
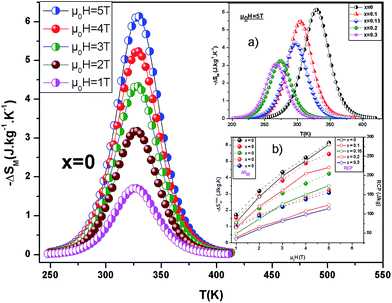
In Fig. 5, we represent the temperature dependence of (ΔSM) curve at different magnetic fields ranging from 1 to 5 T of x = 0 for example.
It is clear from this figure that the sign of the (ΔSM) is negative, which means that heat is liberated when (μ0H) is changed adiabatically. The value of (ΔSM) grows up to a maximum value (ΔSmaxM) where the temperature approaches TC and then decreases with increasing temperature. The obtained value of x = 0 for 5 T is about 62% of that presented by gadolinium metal (Gd). Gd, the reference for magnetocaloric materials, exhibits an isothermal entropy change of 5 J kg−1 K−1 and 9.8 J kg−1 K−1 for field changes of 2 T and 5 T, respectively.45
The evolution of (ΔSmaxM) with In3+ concentration is shown more clearly in the inset (a) of Fig. 5 We observed that (ΔSmaxM) drops with increasing substitution x, and exhibits values equal to 6.14 to 3.06 J kg−1 K−1 for x = 0 to 0.3 for 5 T.
An μ0H increase enhances (ΔSmaxM) and shifts the (ΔSmaxM) point gradually towards higher temperatures, which is indicative of a much larger entropy change being expected at higher magnetic fields (the inset (b) of Fig. 5).
The obtained RCP values of all samples are reported in Table 3, from which it can be clearly deduced that the substitution x decreases the value of the (RCP) factor from 281 J kg−1 for x = 0 to 114 J kg−1 for x = 0.3 at 5 T. These values are comparable with those reported in literature.45–49 From the inset (b) of Fig. 5, we observe that the RCP values exhibit a nearly linear dependence on the applied magnetic field.
| Material | TC (K) | μ0H (T) | ΔSmaxM (J kg−1 K−1) | RCP (J kg−1) | Ref. |
|---|---|---|---|---|---|
| La0.7Bi0.05Sr0.15Ca0.1MnO3 | 330 | 5 | 6.14 | 281 | This work |
| La0.7Bi0.05Sr0.15Ca0.1Mn0.9In0.1O3 | 305 | 5 | 5.46 | 221 | This work |
| La0.7Bi0.05Sr0.15Ca0.1Mn0.85In0.15O3 | 298 | 5 | 4.26 | 173 | This work |
| La0.7Bi0.05Sr0.15Ca0.1Mn0.8In0.2O3 | 275 | 5 | 3.24 | 123 | This work |
| La0.7Bi0.05Sr0.15Ca0.1Mn0.7In0.3O3 | 268 | 5 | 3.06 | 114 | This work |
| Gd | 293 | 5 | 9.5 | 410 | 45 |
| Gd5(Si2Ge2) | 275 | 5 | 18.5 | 535 | 46 |
| La0.75Sr0.1Ca0.15MnO3 | 310 | 5 | 5.8 | 195 | 47 |
| La0.7Sr0.25Na0.05MnO3 | 363 | 5 | 4.34 | 298 | 48 |
| La0.8Ba0.1Ca0.1Mn0.85Co0.15O3 | 212 | 5 | 2.27 | 123 | 49 |
3.4. Correlation between electrical and magnetic properties
It is well known that a strong correlation between the magnetic and electrical properties has been observed earlier.50,51 In manganites, the CMR and MCE are usually observed around ferromagnetic–paramagnetic (FM)–(PM) transition temperature and we have tried to find a relationship between the change in magnetic entropy and resistivity for all samples. Using resistivity data, we can evaluate the magnetic entropy change by the relation as follows:52
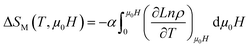 | (8) |
| ρ = ρ0 exp(−M/α) | (9) |
After that, O'Donnell et al.50 studied this type of correlation and it was found that the exact relation should be:
| ρ = ρ0 exp(−M2/α) | (10) |
While Chen et al.53 indicated that the resistivity is related to magnetization by the relation:
| ρ = ρ0 exp(−M2/αT) | (11) |
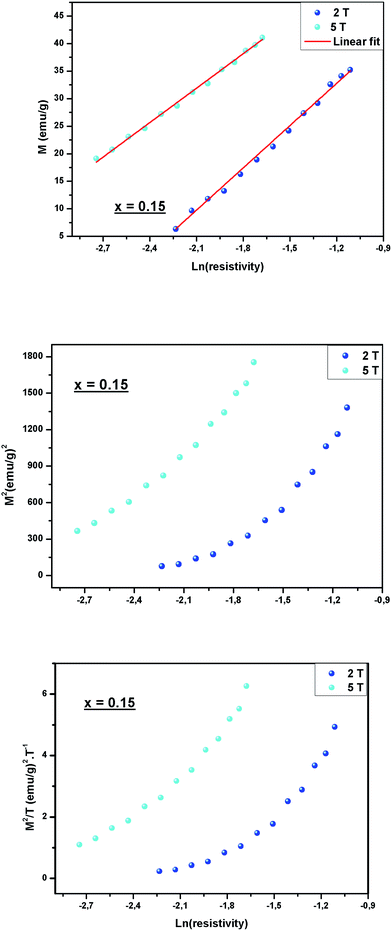
In Fig. 6, we can observe the variation of M, M2 and M2/T versus ln(resistivity) around TC for sample x = 0.15 under a magnetic field of 2 and 5 T for example.
On the one hand, Fig. 6 shows that the resistivity strongly depends on M which indicates that the relation (9) is very suitable to describe the relationship between electrical and magnetic properties for all samples. On the other hand, we have found that the slope of the fitting data remains practically the same α (= 22.56 emu g−1) even in different magnetic applied field for x = 0.15. Similar behavior was observed in all our samples.
Once the value of α was determined, we calculated magnetic entropy change around FM–PM transition for all samples, using the resistivity measurements as a function of magnetic applied field at several temperatures (Fig. 6).
Fig. 7 represents the variation of entropy change found from electrical and magnetic data as a function of temperatures at 5 T for sample x = 0.15. We can notice that the estimated values determined from ρ are found to agree with the experimental ones.
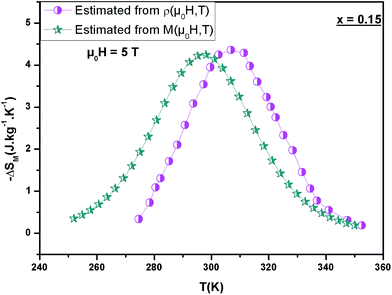 | ||
| Fig. 7 Temperature dependence of the (−ΔSM) measured from M(μ0H,T) and determined from ρ(μ0H,T) under μ0H = 5 T for La0.7Bi0.05Sr0.15Ca0.1Mn0.85In0.15O3. | ||
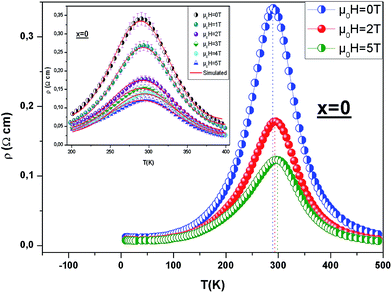
3.5. Prediction of electrical resistivity
The resistivity of manganite is determined by several parameters such as temperature, composition, the applied magnetic field, and so on. The effects of both applied magnetic field and temperature on the resistivity of our sample (x = 0) are shown in Fig. 8. All the samples display a clear metal–semiconducting (M–Sc) transition at a temperature TM–Sc, which is obtained from the inflection point of dρ/dT plots. The tactful way to understand these properties of the samples based on the mathematical relationship between the resistivity and the temperature or the magnetic field is to fit these curves. This prediction of the electrical resistivity was reported by changshi.54 According to their suggestion, the Gauss function which is a typical numerical method with a nonlinear curve fitting for the quantitative analysis, offers such an opportunity. The Gauss function is given by
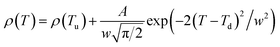 | (12) |
If the Gauss function is available for predicting electrical resistivity (ρ) in all the temperature ranges for LBSCMO, the minimum value of ρ is given by ρ(T|T→∞). Therefore, the physical signification of parameter ρ(Tu) is the electrical resistivity of manganite materials at high temperatures. The maximum value for ρ is given in the following equation
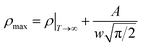 | (13) |
So, eqn (12) will be rewrite as:
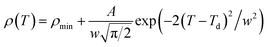 | (14) |
Then, the experimental data, have been simulated using eqn (14) which, are shown in the inset of Fig. 8 for x = 0 for example and the results are presented in table in ESI.†
To verify the accuracy of this simulation, the correlation coefficient (R2) of the simulated with experimental data is given in table in ESI.† The correlation coefficient, which was close to 1, showed a satisfactory agreement between experimental and the modeled data. The comparison between the peaks of the experimental data and the best-fitted value of Td, calculated from Gauss function, demonstrated that parameter Td corresponds to the metal–semiconducting transition temperature, TM–Sc.
Therefore, TM–Sc can be confirmed more precisely by the appropriate Gauss function simulation for other magnetic fields.
Fig. 9 shows the dependency of ρmax on the applied magnetic field for x = 0 for example. The best fitted results demonstrate that the logistic equation could properly give a quantitative relationship between ρmax and (μ0H) using the non-linear curve fitting, and the logistic relation is defined as
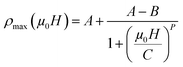 | (15) |
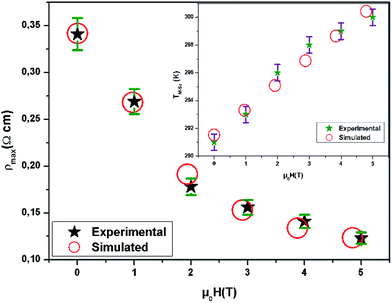 | ||
| Fig. 9 Experimental and simulated ρmax as a function of magnetic field. The inset: TM–Sc vs. μ0H for La0.7Bi0.05Sr0.15Ca0.1MnO3 compound. | ||
| x = 0 | x = 0.1 | x = 0.15 | x = 0.2 | x = 0.3 | |
|---|---|---|---|---|---|
| A | 0.101 | 0.161 | 0.121 | 0.202 | 0.196 |
| B | −0.141 | −0.212 | −0.495 | −0.698 | −1.237 |
| C | 1.489 | 1.230 | 1.578 | 1.112 | 1.134 |
| P | 1.912 | 2.241 | 1.594 | 1.878 | 1.845 |
| S | 1.857 | 2.086 | 1.771 | 1.771 | 3.210 |
| I | 291.524 | 278.285 | 263.904 | 257.904 | 247.333 |
This logistic function successfully describes the experimental behavior of the maximum electrical resistivity of all samples. According to this model, it can be observed that the maximum resistivity decreases with an increasing magnetic field. This phenomenon implies that the density of charge carriers increases with the increasing of the applied magnetic field. Therefore, it is important to use this model for predicting the maximum electrical resistivity, before applying the magnetic field.
From Fig. 8, it has been seen that when μ0H increases, TM–Sc of all samples shifts toward higher temperatures, which can confirm that TM–Sc is related to the applied magnetic field.
The TM–Sc as a function of magnetic field is shown in the inset of Fig. 9 for x = 0 for example.
From this figure, we can see, that there is a simple linear relationship between these two parameters. The equation that describes this relationship is written as:
| TM−Sc(μ0H) = S × (μ0H) + I | (16) |
The obtained constants are illustrated in Table 4.
Impressively, it seems that the theoretical results for TM–Sc derived by eqn (16) were proportional to the experimental results. Therefore, it can be concluded that μ0H is correlative with TM–Sc. Also, it is feasible that eqn (16) is used to investigate the potential shifts of TM–Sc by applying magnetic field. The shifts of the TM–Sc to the high-temperature range with the application of the magnetic field may occur because of the reduction in the charge carriers delocalization caused by applied magnetic field, which could result in reducing the resistivity. This field also uniformly caused a local spin ordering and due to this ordering, the ferromagnetic metallic state could overcome the semiconducting regime. Consequently, the conduction electrons (e1g) are completely polarized within the magnetic domains and could easily be transferred between the pairs of Mn3+ (t32ge1g: S = 2) and Mn4+ (t32ge0g: S = 3/2) via oxygen. So, TM–Sc shift to higher temperatures.
4. Conclusion
In conclusion, we have mainly studied the magnetic and magnetocaloric properties of La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 with x = 0–0.3. The magnetization vs. temperature curve is explained by the presence of the spin glass state in all samples in low temperature arising in the ZFC process and showing a sharp transition from paramagnetic to ferromagnetic phase at TC. According to the Arrott plots, we have found that all our samples have a second order magnetic phase transition. The (MCE) can be determined by direct and indirect methods. First, based on the magnetic measurement at applied field of μ0H = 5 T, La0.7Bi0.05Sr0.15Ca0.1Mn1−xInxO3 samples exhibit a maximum value of (ΔSM) which decreases from 6.14 J kg−1 K−1 for x = 0 to 3.06 J kg−1 K−1 for x = 0.3 with increasing In content and thus the RCP values also decrease. The large MCE, found in these samples, suggests that its can be considered as a promising potential candidate for magnetic refrigeration application. Second, from the temperature dependence of resistivity, we have succeeded to evaluate the (ΔSM). On the other hand, the resistivity was fitted using the mathematical model (Gauss function). The perfect agreement between the theoretical and the experimental values of TM–Sc and ρmax is obtained.References
- R. N. Mahato, K. Sethupathi, V. Sankaranarayanan and R. Nirmala, J. Appl. Phys., 2010, 107, 09A943 CrossRef.
- H. Choi, E. Y. Kim and C. M. Whang, Electron. Mater. Lett., 2011, 7, 231 CrossRef CAS.
- M. S. Anwar, S. Kumar, F. Ahmed, S. N. Heo, G. W. Kim and B. H. Koo, J. Electroceram., 2013, 30, 46 CrossRef CAS.
- R. P. Pawar, R. N. Jadhav and V. Puri, Electron. Mater. Lett., 2012, 8, 321 CrossRef CAS.
- M. S. Anwar, S. Kumar, F. Ahmed, N. Arshi and B. H. Koo, Mater. Res. Bull., 2012, 47, 2977 CrossRef CAS.
- H. E. Kim, K. H. Choi, M. W. Park and J. S. Lee, Electron. Mater. Lett., 2011, 7, 319 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 82, 403 CrossRef CAS.
- S. Jin, T. H. Tiefel, M. McCormack, R. A. Fastnacht, R. Ramesh and C. H. Chen, Science, 1994, 264, 413 CAS.
- R. V. Holmolt, J. Wocker, B. Holzapfel, L. Schultz and K. Samwer, Phys. Rev. Lett., 1993, 71, 2331 CrossRef PubMed.
- A. P. Ramirez, J. Phys.: Condens. Matter, 1997, 9, 8171 CrossRef CAS.
- Y. Tokura, Rep. Prog. Phys., 2006, 69, 797 CrossRef CAS.
- A. Dinesen and J. Tejada, J. Phys.: Condens. Matter, 2005, 17, 6257–6269 CrossRef CAS.
- D. N. H. Nam, N. V. Dai, L. V. Hong, N. X. Phuc, S. C. Yu, M. Tachibana and E. Takayama-Muromachi, J. Appl. Phys., 2008, 103, 043905 CrossRef.
- N. Chau, P. Q. Niem, H. N. Nhat, N. H. Luong and N. D. Tho, Phys. B, 2003, 327, 214 CrossRef CAS.
- M. Phan, S. Tian, D. Hoang, S. Yu, C. Nguyen and A. Ulyanov, J. Magn. Magn. Mater., 2003, 258, 309–311 CrossRef.
- M.-H. Phan and S.-C. Yu, J. Magn. Magn. Mater., 2007, 308, 325–340 CrossRef CAS.
- M.-H. Phan, N. D. Tho, N. Chau, S.-C. yu and M. Kurisu, J. Appl. Phys., 2005, 97, 103901 CrossRef.
- A. P. Ramirez, J. Phys.: Condens. Matter, 1997, 9, 8171 CrossRef CAS.
- D. Louca, T. Egami, E. L. Brosha, H. Röder and A. R. Bishop, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R8475(R) CrossRef.
- C. M. Xiong, J. R. Sun, Y. F. Chen, B. G. Shen, J. Du and Y. X. Li, IEEE Trans. Magn., 2005, 41, 122–124 CrossRef CAS.
- N. Zaidi, S. Mnefgui, J. Dhahri and E. K. Hlil, Ceram. Int., 2016, 42, 17687–17692 CrossRef CAS.
- A. Zaidi, T. Alharbi, J. Dhahri, S. Alzobaidi, M. A. Zaidi and E. K. Hlil, Appl. Phys. A, 2017, 123, 94 CrossRef.
- V. Punith Kumar, R. L. Hadimani, D. Paladhi, T. K. Nath, D. C. Jiles and V. Dayal, Mater. Sci. Eng., B, 2016, 209, 75–86 CrossRef CAS.
- M. Pechini, US Pat. no. 3330697, 1967.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- T. Roisnel and J. Rodriguez-Carvajal, Computer Program FULLPROF, LLB-LCSIM, May, 2003.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- V. M. Goldschmidt, Geochemistry, Oxford University Press, Oxford, 1958, p. 730 Search PubMed.
- N. Moutis, I. Panagiotopoulos, M. Pissas and D. Niarchos, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1129 CrossRef CAS.
- V. Markovich, I. Fita, R. Puzniak, A. Wisniewski, K. Suzuki, J. W. Cochrane, Y. Yuzhelevskii, Y. M. Mukovskii and G. Gorodetsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224409 CrossRef.
- J. Kuo and G. Sheng-Kai, Chin. Phys. B, 2009, 18, 3035 CrossRef.
- A. K. Pramanik and A. Banerjee, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214426 CrossRef.
- J. Mira, J. Rivsa, F. Rivadulla, C. V. Vazquez and M. A. L. Quintela, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2998 CrossRef CAS.
- D. N. H. Nam, K. Jonason, P. Nordblad, N. V. Khiem and N. X. Phuc, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 4189 CrossRef CAS.
- D. N. H. Nam, R. Mathieu, P. Nordblad, N. V. Khiem and N. X. Phuc, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1027 CrossRef CAS.
- M. Itoh, I. Natori, S. Kubota and K. Motoya, J. Phys. Soc. Jpn., 1994, 63, 1486 CrossRef CAS.
- B. Padmanabhan, S. Elizabeth, H. L. Bhat, S. RoBler, K. Dorr and K. H. Muller, J. Magn. Magn. Mater., 2006, 307, 288–294 CrossRef CAS.
- F. E. Luborsky, Ferromagnetic Materials, Elsevier, Amsterdam, 1979 Search PubMed.
- C. Kittel, Quantum Theory Solids, Wiley, New York, 1993 Search PubMed.
- V. N. Smolyaninova, J. J. Hamilton, R. L. Greene, Y. M. Mukovskii, S. G. Karabashev and A. M. Balbashov, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 5640 CrossRef CAS.
- P. Dai, J. A. Fernandez-Baca, E. W. Plummer, Y. Tomioka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 224429–224434 CrossRef.
- B. Padmanabhan, S. Elizabeth, H. L. Bhat, S. Rossler, K. Dorr and K. H. Muller, J. Magn. Magn. Mater., 2006, 307, 288–294 CrossRef CAS.
- A. Tozri, E. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2010, 322, 2516–2524 CrossRef CAS.
- B. K. Banerjee, et al., Phys. Lett., 1964, 12, 16–17 CrossRef.
- V. K. Pecharsky and K. A. Gshneidner Jr, J. Magn. Magn. Mater., 1997, 167, L179 CrossRef CAS.
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef.
- A. Dhahri, M. Jemmali, E. Dhahri and M. A. Valente, J. Alloys Compd., 2015, 638, 221–227 CrossRef CAS.
- S. E. Kossi, S. Ghodhbane, S. Mnefgui, J. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2015, 395, 134–142 CrossRef CAS.
- M. A. Gdaiem, A. Dhahri, J. Dhahri and E. K. Hlil, Mater. Res. Bull., 2017, 88, 91–97 CrossRef CAS.
- J. O'Donnell, M. Onellion, M. S. Rzchowski, J. N. Eckstein and I. Bozovic, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 6841 CrossRef.
- B. Chen, C. Uher, D. T. Orelli, J. V. Mantese, A. M. Mance and A. L. Micheli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 53, 5094 CrossRef.
- C. M. Xiong, J. R. Sun, Y. F. Chen, B. G. Shen, J. Du and Y. X. Li, IEEE Trans. Magn., 2005, 41, 122 CrossRef CAS.
- B. Chen, C. Uher, D. T. Orelli, J. V. Mantese, A. M. Mance and A. L. Micheli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 53, 5094 CrossRef.
- L. Changshi, J. Chem. Eng. Data, 2011, 56, 2 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04256f |
| This journal is © The Royal Society of Chemistry 2017 |