Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assessing the interaction between surfactant-like peptides and lipid membranes†
Thaciana Malaspinab,
Guilherme Colherinhasa,
Felipe de Oliveira Outib and
Eudes E. Fileti *b
*b
aDepartamento de Física, CEPAE, Universidade Federal de Goiás, CP. 131, 74001-970, Goiânia, GO, Brazil
bInstituto de Ciência e Tecnologia, Universidade Federal de São Paulo, 12231-280, São José dos Campos, SP, Brazil. E-mail: fileti@gmail.com; Fax: +55 12 3924 9500
First published on 19th July 2017
Abstract
Atomistic molecular dynamics simulations were used to study the interaction of AnK peptides (with n = 3, 6 and 9) in contact with two different types of lipid membranes, DPPC and DPPG. PMF calculations and their decomposition into enthalpic and entropic components allowed a detailed thermodynamic analysis of the energy profile associated with the adsorption and penetration of the peptides through the lipid membranes. Our simulations indicated a drastic difference between the interactions of the peptides with both membranes. For the peptide A6K the interaction with the DPPG and DPPC membranes were −222 kJ mol−1 and −16 kJ mol−1, respectively. PMF for the DPPC membrane did not show any minimum in the interface region, that is, no favorable interaction with its surface. On the other hand, the interaction with the DPPG membrane showed a clear minimum near the surface. This minimum, although shallow, −10 kJ mol−1, indicates that the adhesion of the AnK peptides on the surface of the DPPG membranes is a favorable process.
Introduction
Peptide-based nanomaterials have been the focus of research in recent years because of their excellent properties, such as versatility, biocompatibility and medicinal properties.1–5 An important class of peptides, which may exhibit a wide range of possibilities for biomedical applications is the amphiphilic peptides.1–3,5–13 Despite the various characteristics in common with lipids and detergents, such peptides, called surfactant-like peptides (SLPs), present an intrinsic difference that can lead to different physical consequences: the composition and structure of their tail. Unlike conventional surfactants whose hydrophobic tails interact in all directions through hydrophobic interactions, the amphiphilic peptide tail contains not only hydrophobic groups but also hydrophilic sites.14,15 This feature allows the SLPs to stabilize nanostructures in one direction through hydrophobic interactions and in the orthogonal direction by hydrogen bonds.14,15 Hydrogen bonds associated with hydrophobic interactions can stabilize even more complex secondary structures such as helices and sheets, whereas conventional lipids/surfactants are basically organized into micelles, vesicles and nanotubes.14,15In addition to the remarkable characteristics related to self-assembly, amphiphilic peptides also have desirable antibacterial properties.13,16–18 The relationship between the antibacterial activity of surfactant-type peptides and their propensity to form nanostructures has been investigated experimentally.13,19,20 Zhao et al. examined this relationship for the AnK peptide class (a sequence of n alanine residues and one cationic hydrophilic lysine head).13 They synthesized three different polypeptide structures with n = 3, 6 and 9, observed the formation of nanostructures and tested the antibacterial activity of each species. The A3K, A6K and A9K polypeptides were self-organized in bilayer, nanotubes and nanorods, respectively.13 The first showed very low antibacterial activity, while the intermediate showed moderate activity. The A9K peptide, in turn, proved to be the most efficient and additional biological assays confirmed the death of the bacteria through the rupture of the cell membrane induced by the contact with this peptide.13
Experimental studies indicate that exposure of A9K to a DPPC lipid membrane causes practically no perturbation to the membrane structure, whereas the same treatment for the DPPG membrane leads to substantial destabilization of the membrane structure. This is a trend entirely consistent with the high selectivity observed from hemolytic activity studies in membranes. In addition, interactions between the peptides and membranes can be expected to play a significant role in the membrane destabilization process. Although it is recognized that alanine tail size notably affects the self-organizing process of AnK peptides, it is not clear whether there is a size dependence on the direct interaction between these isolated peptides and lipid membranes. In this work, we carried out to a computational study evaluate the effect of polyalanine chain length on its interaction with lipid membranes. A detailed analysis of the thermodynamics of intermolecular interaction between AnK peptides and DPPC and DPPG lipid membrane models has been performed at the limit of infinite dilution (i.e. a single peptide at membrane system). In this way, we can describe with atomistic precision which factors are most relevant to the peptide–membrane interaction.
Simulation details
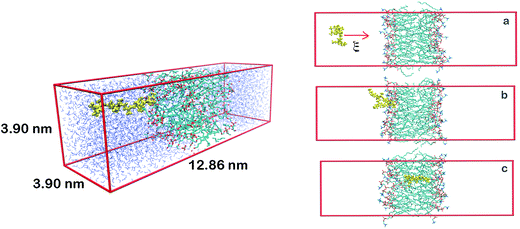
Here we are interested in analyzing the interactions of three different AnK peptides with two different biological membranes models, DPPC (dipalmitoyl-phosphatidyl-choline) and DPPG (dipalmitoyl-phosphatidyl-glycerol). These membranes present very different physicochemical characteristics. At physiological pH, DPPC membrane is in zwitterionic form, having no net charge, while DPPG membrane is in anionic form, carrying a negative charge per DPPG molecule. This difference is interesting because it allows us to analyze the effect of the charge on the interactions with the peptides. Additionally, from the biological point of view, we can consider the DPPC as a membrane model of mammalian cells and the DPPG as a bacterial membrane model.21,22Two different simulation series were performed to determine the structure, energetic and thermodynamics of the interaction between AnK polypeptides and the lipid membranes. At the first series of simulations, the peptides were immersed in a periodic computational cell containing 128 lipids and about 6000 water molecules, totaling about 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. Both pre-equilibrated membranes were obtained from Peter Tieleman database.23 In the computational cell for the DPPG membrane, 128 Na+ ions were also added to neutralize the lipid charges, making neutral the net charge on the membrane. The positive charge on lysine residue was neutralized using the chloride anion, keeping the peptides also electrostatically neutral. This resulted in six different investigated systems (see Fig. 1). The simulations were performed in the isobaric–isothermal ensemble (constant pressure and temperature, NpT) under conditions T = 323 K and p = 1 atm, with no additional applied surface tension. In these conditions, with a higher temperature, the surface tension is about 10% less than at room temperature.24 Thus, although the expected effects of the surface tension on our results are only slightly quantitative (not altering the analyzes as a qualitative way) we reduced them to the processes studied here, namely: adsorption and penetration of the peptide in the membranes. Water molecules were described using the TIP3P25 model while the lipids were modeled by the CHARMM36 (ref. 26) force field. The simulation cells were initially subjected to energy minimization aimed at the removal of high-energy contacts. Then, the equilibration process was conducted in both boxes for 5 ns, where the all unconstrained system was allowed to relax so that lipids and water interacted with each other. Finally, a trajectory of 40 ns, using a time step of 2 fs, was obtained for each of the systems. Configurations of the systems were saved every 10 ps totaling 4000 frames for statistical analysis. The molecular representation of each peptide and a representative configuration of a simulation cell are shown in Fig. 1.
000 atoms. Both pre-equilibrated membranes were obtained from Peter Tieleman database.23 In the computational cell for the DPPG membrane, 128 Na+ ions were also added to neutralize the lipid charges, making neutral the net charge on the membrane. The positive charge on lysine residue was neutralized using the chloride anion, keeping the peptides also electrostatically neutral. This resulted in six different investigated systems (see Fig. 1). The simulations were performed in the isobaric–isothermal ensemble (constant pressure and temperature, NpT) under conditions T = 323 K and p = 1 atm, with no additional applied surface tension. In these conditions, with a higher temperature, the surface tension is about 10% less than at room temperature.24 Thus, although the expected effects of the surface tension on our results are only slightly quantitative (not altering the analyzes as a qualitative way) we reduced them to the processes studied here, namely: adsorption and penetration of the peptide in the membranes. Water molecules were described using the TIP3P25 model while the lipids were modeled by the CHARMM36 (ref. 26) force field. The simulation cells were initially subjected to energy minimization aimed at the removal of high-energy contacts. Then, the equilibration process was conducted in both boxes for 5 ns, where the all unconstrained system was allowed to relax so that lipids and water interacted with each other. Finally, a trajectory of 40 ns, using a time step of 2 fs, was obtained for each of the systems. Configurations of the systems were saved every 10 ps totaling 4000 frames for statistical analysis. The molecular representation of each peptide and a representative configuration of a simulation cell are shown in Fig. 1.
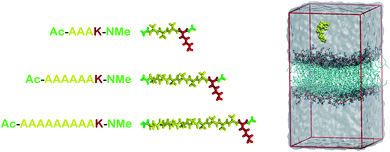 | ||
| Fig. 1 At left, molecular representations of the AnK peptides: A3K, A6K and A9K, with 3, 6, and 9 alanine groups in its tail. In red the lysine residue, in yellow the alanine chain and in green the acetyl and N-methyl amide ends. At right, a representative configuration of the simulation cell used to calculate the interaction between the peptides and the membranes. At the Table S1 from the ESI† we present the thickness and area per lipid for all systems investigated. | ||
The electrostatic interactions beyond 1.2 nm were accounted for by Particle-Mesh-Ewald (PME) method.27 The Lennard-Jones interactions were smoothly brought down to zero from 1.1 to 1.2 nm using the classical shifted force technique. The constant temperature, 323 K, was maintained by the velocity rescaling thermostat28 (with a time constant of 0.5 ps), which provides a correct velocity distribution for a statistical mechanical ensemble. The constant pressure of 1 atm was maintained by Parrinello–Rahman barostat29 with a time constant of 2.0 ps and a compressibility constant of 4.5 × 10−5 bar−1.
A second series of simulations was performed to determine the potential of mean force (PMF), the free energy curve that characterizes the process of insertion of the peptides inside the membranes in function of a reaction coordinate, in this case, the center of mass distances between membranes and peptides. This time we use simulation cells of different dimensions from previous ones since the protocol used in PMF calculations requires a larger z-dimension cell so that the peptide can be forced into the membrane starting from a sufficiently long distance. This initial long distance is important, so that at the beginning of the process peptide–membrane interaction be negligible. A representation of one of the PMF simulated cells is shown at Fig. 2.
Steered molecular dynamics simulations (SMD) were performed in order to force the insertion of the peptides into the membranes within 1 ns, according to the scheme shown at right of Fig. 3, using a harmonic force constant of 2000 kJ mol−1 nm−2 applied to the center of mass of the AnK peptide. The rate at which the peptide was pulled against the center of mass of the membrane was 0.01 nm ps−1. From the SMD trajectory 100 structures were separated by regular intervals of 0.05 nm of the reaction coordinate. These configurations were used at the umbrella sampling calculation, each consisting of a simulation window.30 This large number of configurations was necessary to ensure adequate overlap of the histograms along the entire distance of 5 nm, mainly in internal and superficial regions of the lipid membrane. For each of these configurations the peptide was held fixed by its center of mass to its position by a harmonic force constant of 2000 kJ mol−1 nm−2. For each window simulation the systems were sampled for 30 ns, preceded by an equilibration phase of 5 ns. To take into account information from all intermediate states we use the WHAM method.31 Both the SMD simulations and the PMF windows were performed under the same conditions of temperature and pressure and with the same models as those presented for the first series of simulations. All trajectories were propagated using the GROMACS 5.1 simulation engine.32
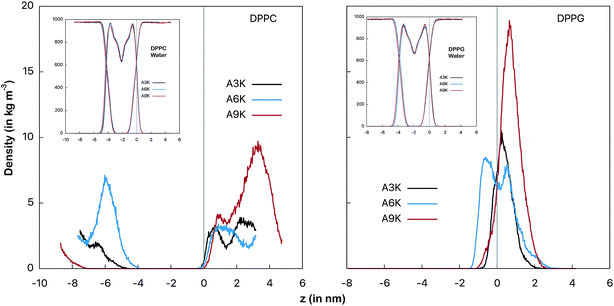 | ||
| Fig. 3 Mass density profiles of the peptides as an indicator of the relative position between the peptide and the membrane surface. At left the AnK peptides in interaction with the DPPC membrane and at right with the DPPG membrane. The vertical line indicates the position of the interface between the water and the membrane. This position is defined by crossing the density profiles of the water and the membrane and is placed at the origin for simplicity. The graphs on the inset show the profiles for the water and the membranes for each of the systems. The conformational changes at peptide, determined by the RMSD temporal evolution, are shown at Fig. S1 from ESI.† | ||
Results
Fig. 3 shows the mass distribution profiles of the peptides in relation to the membrane surface. Note that for the DPPC system the peptides are far from the surface of the membrane (indicated by the vertical gray line), that is, throughout the simulation they remain almost always solvated in the aqueous environment bulk. This is evident by observing mass distributions between 1 nm and 4 nm and also between −8 nm and −4 nm. We see that despite the zwitterionic character of the membrane and the cationic character of the peptides, the most favorable interaction for the peptides in the DPPC system is still with the aqueous environment.For the peptides in the DPPG system we observed different behavior. All three peptides spend most of the simulation time adsorbed onto the membrane surface. In particular, A6K peptide slightly permeates the surface, favoring the interaction with the membrane to the detriment of the interactions with the aqueous medium. On the other side, we observed that A9K peptide, although remains relatively close to the membrane surface, presents a significant probability of remaining solvated into the bulk water. Here it is interesting to note that, contrary to what has been suggested in the recent literature, AnK peptides do not have a hydrophobic tail.14,15 It has been shown that although alanine tails have hydrophobic side groups, when immersed in water, their hydrophilic sites form hydrogen bonds with the aqueous environment, favoring the hydration process.33 For A9K, which present the longer alanine chain, this behavior is more pronounced since this polypeptide forms a greater number of hydrogen bonds, as we will see further. At the same time the adhesion of the lower AnK peptides to the charged surface of the DPPG membrane is consistent with the electrostatic character of the system constituents, for which a strong Coulomb attraction is expected.
A clear confirmation of this strong interaction can be obtained by analyzing the lateral diffusion coefficient of the peptide. This coefficient is numerically equal to the slope of the lateral mean squared displacement (MSD) plotted as a function of time, given by the Einstein relation:34
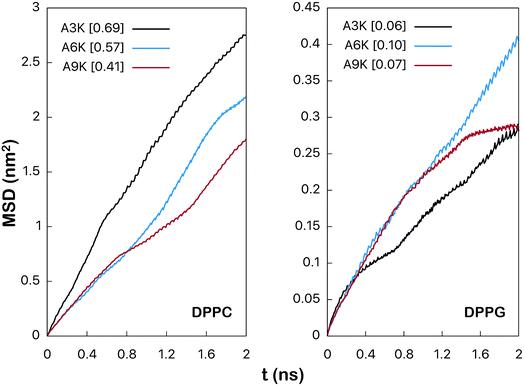 | ||
| Fig. 4 Mean square root displacement (MSD) (in nm2) of the peptides parallel to the membrane plane. The numerical value between brackets is the lateral diffusion coefficient (in 10−5 cm2 s−1) obtained by linear adjustment between 1 ns and 2 ns as shown at the Fig. S5 from the ESI.† | ||
Although the values obtained by the linear fitting of the curves of the Fig. 4 are not quantitatively accurate, the qualitative comparison is relevant and remains valid. As we can observe the values of diffusion coefficient for the peptides in the DPPG system are much smaller than the corresponding values in DPPC. For the A3K system, for example, the value of this coefficient is 0.69 × 10−5 cm2 s−1 in DPPC, whereas it is only 0.06 × 10−5 cm2 s−1 in DPPG. This reduction in the diffusion coefficient is related to the great loss of lateral mobility of the peptide and this loss is due precisely to the interactions between the peptide and the surface of the DPPG membrane. Note that in all cases the mobility of the peptides in the DPPC system is much greater since the expected interaction between peptides with its surface is rather low.
Energy analysis also confirms and quantifies the larger interaction between the peptides and the DPPG membrane. Fig. 5 shows the total interaction energy between the peptides and the membranes.
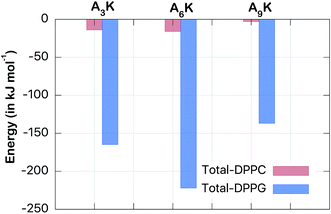 | ||
| Fig. 5 Total interaction energy (Coulomb + van der Waals) (in kJ mol−1). Note that the interaction between the peptides and the DPPG membrane is an order of magnitude greater than the corresponding interaction with the DPPC membrane. The convergence of this averages is described at the Fig. S4 from the ESI.† | ||
The drastic difference of around one order of magnitude between the interactions with both membranes reveals the preference of the peptides for the DPPG membrane. This finding certainly has consequences on the antibacterial character of the peptides. However, this interaction has its maximum not for the A9K peptide (which is considered the deadliest for bacteria) but for the A6K peptide. While the interaction of this with the DPPG membrane is −222 kJ mol−1 the interaction of A9K is only −137 kJ mol−1. Analogous behavior can be observed for AnK–DPPC interaction, but on a smaller scale. Thus, the interaction between disperse AnK peptides and lipid membranes not present a simple direct relationship to tail size, at least for these small peptides investigated herein. Therefore, the intensity of the membrane–peptide interaction is expected to be due to collective factors and not only to the size of the peptide.
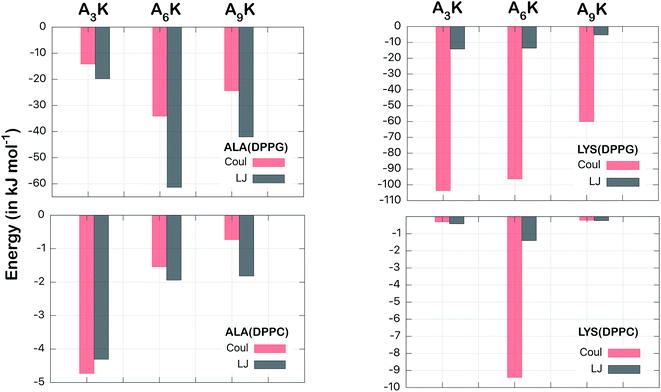
To get a better understanding of the energetics of this interaction, we decomposed the total interaction energy into their electrostatic (Coulomb) and van der Waals contributions. In addition, we also decomposed the energy in terms of the components by residues. In this way we can calculate the contributions of the polyalanine chain (ALA, An) separately from the contributions of the polar head (LYS, K).
Fig. 6 shows this decomposition of the interaction energy. Again, through the difference of the scales, the much greater intensity for the interaction of the peptides with the DPPG membrane is evident. This is confirmed in both aspects analyzed; the nature of the interactions (Coulomb or van der Waals) and the residue types (ALA or LYS). For alanine residues we observed that highest contribution came from the van der Waals interactions, of −61 kJ mol−1 to A6K, in relation to the corresponding electrostatic, of −34 kJ mol−1, in DPPG membrane. The only exception is for the A3K in DPPC, where the electrostatic energy (−4.7 kJ mol−1) is slightly higher than the van der Waals correspondent (−4.3 kJ mol−1). Here it is important to note that it is not intuitive that the van der Waals energy corresponding to the ALA groups of the A9K peptide is lower than those of the A6K peptide, since the polyalanine chain is larger for A9K peptide. For this case, as we have seen, the distance between the peptide A9K and the DPPG membrane is larger, implying a lower interaction energy. For the lysine residue, on the other hand, the electrostatic interactions are drastically greater than the corresponding van der Waals interactions, as expected. From Fig. 3 and from visual inspection it is possible to observe that, unlike for the other peptides, the polar head of the A6K peptide spends most of the time near the DPPC membrane surface while its alanine tail remains more distant. This, although not leading to peptide alignment with the normal membrane surface, significantly contributes to the interaction of the LYS group with the membrane, both reducing LJ interaction and considerably increasing Coulomb interaction, explain the much larger value for Coulomb interaction of the LYS group. The combined contribution of the van der Waals interactions from the ALA chain to the electrostatic interactions from the LYS group consists of most of the total energy, shown in Fig. 5. For the peptide A6K for example, we have a sum of −61–96 = −157 kJ mol−1 which is equivalent to about 70% of the total energy of interaction in DPPG membrane. It is important to note that although van der Waals contribution is expressive for membrane–peptide interaction, its dependence on polyalanine length has no relevant role.
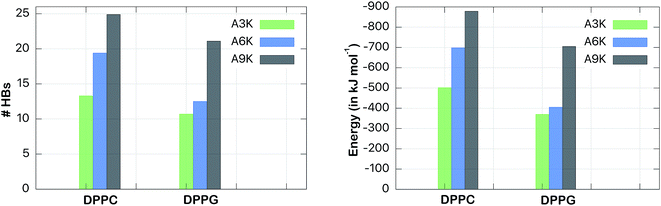
We also considered the interaction between the peptides and the aqueous medium, which allowed us to evaluate the impact of the hydrogen bonds on the interaction of peptides with the membrane. Fig. 7 shows the number of hydrogen bonds and the total interaction energies between the peptides and the water molecules in both DPPC and DPPG systems. For peptide A9K, for example, 25 hydrogen bonds were found with water in the DPPC system against only 21 in the DPPG system. However, the decrease in the number of hydrogen bonds, although relevant, is not the most important fact to note here, but rather the fact that both systems follow different trends. While the DPPC systems show a linear correlation between the polyalanine chain size with number of hydrogen bonds (n = 3, 6 and 9 against #HB = 13, 19 and 25), that is, the number of hydrogen bonds increases linearly with n, the same does not occur for the DPPG system.
There is a small increase in the number of hydrogen bonds when we compare A3K with A6K (a single hydrogen bond only), but a large increase when we compare A6K with A9K (9 hydrogen bonds). This is a direct reflection that A9K, among three peptides, is the one that most interacts with water. This behavior is consistent with the more hydrophilic character of the A9K.33 There is preferential interaction between the AnK peptides with the DPPG membrane, which decreases the area of the peptide accessible to the solvent, causing a decrease in the average number of hydrogen bonds between the peptides and water. As expected, the number of hydrogen bonds formed correlates with the interaction energy between the peptides and water. For the peptide A9K, which forms the largest amount of hydrogen bonds the interaction energy with water is −700 kJ mol−1.
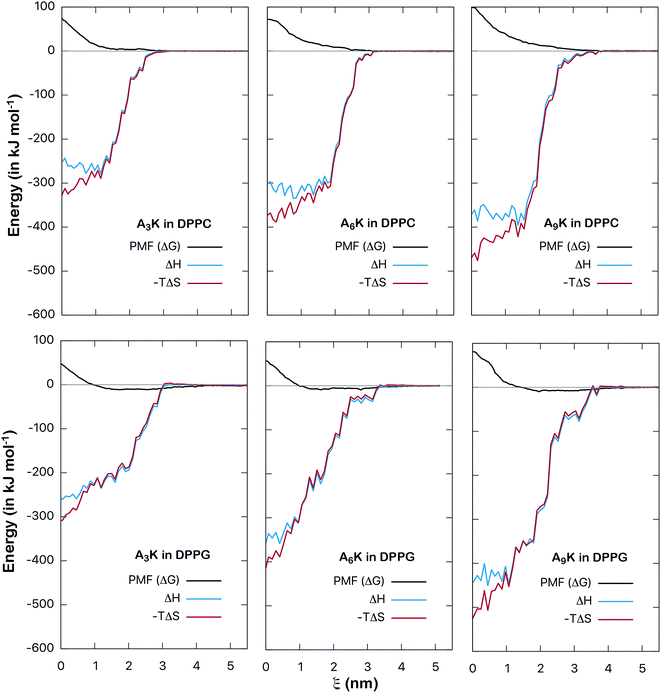
The energy analysis performed in the previous section provides a good basis for understanding the interactions between AnK peptides and lipid membranes. However, such an analysis is still superficial and takes into account only the pairwise potential energies. A more rigorous thermodynamic analysis must take into account not only enthalpic aspects, related to interaction energy itself, but also entropic aspects. In this way we can analyze the consequences of the degrees of freedom and the structural changes of peptides as they interact with the membranes. To obtain the related information about these thermodynamic potentials we perform the calculation of the PMF, which describes how the free energy between peptide and membrane varies along a chosen reaction coordinate. By calculating the enthalpy of the interaction, obtained point by point, we can also determine the entropy variation along the process directly through the expression: ΔG = ΔH − TΔS. In this way we can decompose the PMF and its enthalpic and entropic contributions thus obtaining a complete thermodynamic description for the interaction between the peptides and the membranes. The calculated here (Fig. 8) allow us to analyze in detail the thermodynamic aspects of these interactions.
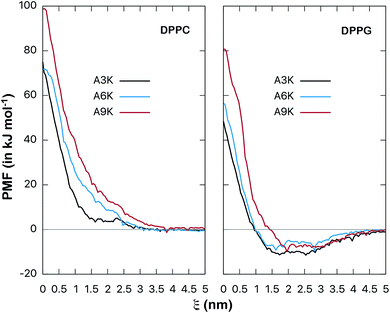 | ||
| Fig. 8 Potential of mean force (free energy as a function of distance ξ, in kJ mol−1) between AnK peptides and the center of lipid membranes. Comparison between DPPC and DPPG membranes. The energy is shifted so that it is zero at long distances. Bootstrap profiles, average values and standard deviations for the PMF calculation are given at Fig. S2 and S3 from ESI.† | ||
The potentials of mean force clearly show a strong repulsive behavior around the center of the membrane (ξ = 0) for both DPPC and DPPG systems. This repulsion to the permeation of the peptide is higher in the DPPC membrane and significantly higher for the A9K peptide in both cases. On the other hand, the behavior at the membrane/water interface is different for the two membranes. We see that the interaction between the AnK peptides and the DPPC membrane does not show any minimum in the interface region, which is at approximately 2 nm, and therefore, no favorable interaction with its surface. For the DPPG membrane, the interaction curve presents a minimum on its surface, which is favorable and responsible for the adhesion of the peptides on the surface of the membranes. For the three peptides, the intensity of this binding was about 10 kJ mol−1. Again, we observed that the intensity of the membrane–peptide interaction not present a simple direct dependence to tail size.
Of all works found at the literature involving the interaction between peptides and lipid membranes, most of them deal with zwitterionic membranes, such as DPPC, DMPC and POPC. Virtually nothing was found about the interaction between peptides and the DPPG membrane. One of the few examples found determines the adsorption energy between indolicin, a known antimicrobial peptide, with a DPPC/PG mixed membrane as being −14.6 kJ mol−1 which is a value close to that found above for the AnK peptides in DPPG.35
Finally, to characterize the energetic changes as the peptide approaches the lipid bilayer, we calculate the potential enthalpy as a function of the distance of center of mass between the peptide and the membrane. Fig. 9 shows the results for both types of systems, DPPC and DPPG. We can observe that as the peptide approaches the membrane its enthalpy decreases, that is, it contributes favorably to the free energy of adsorption. This is observed for both types of systems. We also see that the entropic contribution to the PMF increases, that is, as the peptide penetrates the membrane, an entropic penalty arises. The detailed balance between these forces shows that although the insertion of the peptide is favorable from the enthalpic point of view, it is not from the entropic point of view. For example, for the A9K system in DPPC, the enthalpy at the center of the membrane (at ξ = 0) is about −370 kJ mol−1 while the variation of the entropic component is approximately −470 kJ mol−1, which results in a positive free energy of 100 kJ mol−1, characterizing the insertion process as non-spontaneous. The same behavior is observed for all systems investigated. Although subtle, it can be observed in the curves for the DPPG system that in the interface region the enthalpy curves are slightly lower than those of the entropy, resulting in the favorable interaction discussed in the previous paragraph.
Conclusion
This work aimed to investigate, using atomistic molecular dynamics techniques, simplified models for the interaction between AnK peptides and DPPC and DPPG lipid membranes. Our simulations confirmed that positively charged peptides have a higher preference for interacting with the DPPG membrane than remaining hydrated in the bulk of water. The same did not occur for the zwitterionic membrane, a system in which the peptides remained hydrated for most of the simulation time. In this sense, a drastic difference of more than one order of magnitude between the interactions with both membranes was observed, with adhesion on DPPG surface being preferred by the peptides. For A6K peptide, for example, the interaction with the DPPG membrane is −222 kJ mol−1 while the interaction with the DPPC is only −16 kJ mol−1. The detailed analysis done through the decomposition of the total interaction energy in terms of the electrostatic and van der Waals components confirms that the van der Waals component is significant for the total interaction. On the other hand, this interaction seems not present a direct dependence on the size of the polyalanine tail of the peptide for the peptides investigated herein. Therefore, the intensity of the membrane–peptide interaction is expected to be due to collective factors and not only to the size of the peptide.The PMF calculations in the reaction coordinate that inserts the peptide into the lipid membrane allowed us to rigorously quantify the interaction between the peptides and the membranes. For the DPPC membrane the PMF did not present any minimum in the interface region and, therefore, none favorable interaction with its surface. On the other hand, the interaction with the DPPG membrane showed a clear minimum in its surface, which despite its moderate intensity, is favorable and responsible for the adhesion of the peptides on the surface of the membranes. For the three peptides, the intensity of this binding was about 10 kJ mol−1. There were few results for comparison, but the values mentioned in the text suggest that this energy of interaction with the surface of the membrane is reasonable and is consistent with the electrostatic character of the systems involved.
The simplified infinite dilution model, where a single peptide interacts with the biological membrane, was not sufficient to describe the process of membrane destabilization as observed experimentally. For this, considerations involving the concentration of peptides, morphology of peptide nanostructures, pH of solutions, among other physicochemical factors, must be taken into account in the model.
Acknowledgements
This work was supported by research grants from CAPES, FAPESP and FAPEG.References
- A. Dehsorkhi, V. Castelletto and I. W. Hamley, J. Pept. Sci., 2014, 20, 453–467 CrossRef CAS PubMed.
- A. W. Du and M. H. Stenzel, Biomacromolecules, 2014, 15, 1097–1114 CrossRef CAS PubMed.
- H. Hosseinkhani, P.-D. Hong and D.-S. Yu, Chem. Rev., 2013, 113, 4837–4861 CrossRef CAS PubMed.
- I. W. Hamley, Soft Matter, 2011, 7, 4122–4138 RSC.
- H. Cui, M. J. Webber and S. I. Stupp, Biopolymers, 2010, 94, 1–18 CrossRef CAS PubMed.
- A. Brandelli, Mini-Rev. Med. Chem., 2012, 12, 731–741 CrossRef CAS PubMed.
- S. Koutsopoulos, L. Kaiser, H. Eriksson and S. Zhang, Chem. Soc. Rev., 2012, 41, 1721–1728 RSC.
- F. Sgolastra, B. Deronde, J. Sarapas, A. Som and G. Tew, Acc. Chem. Res., 2013, 46, 2977–2987 CrossRef CAS PubMed.
- A. Sorrenti, O. Illa and R. Ortuño, Chem. Soc. Rev., 2013, 42, 8200–8219 RSC.
- D. Mandal, R. K. Tiwari, A. Shirazi, D. Oh, G. Ye, A. Banerjee, A. Yadav and K. Parang, Soft Matter, 2013, 9, 9465–9475 RSC.
- H. Xia, G. Gu, Q. Hu, Z. Liu, M. Jiang, T. Kang, D. Miao, Q. Song, L. Yao, Y. Tu, H. Chen, X. Gao and J. Chen, Bioconjugate Chem., 2013, 24, 419–430 CrossRef CAS PubMed.
- G. Cinar, H. Ceylan, M. Urel, T. S. Erkal, D. E. Tekin, A. B. Tekinay, A. Dâna and M. O. Guler, Biomacromolecules, 2012, 13, 3377–3387 CrossRef CAS PubMed.
- C. Cuixia, P. Fang, Z. Shengzhong, H. Jing, C. Meiwen, W. Jing, X. Hai, Z. Xiubo and R. L. Jian, Biomacromolecules, 2010, 11, 402–411 CrossRef PubMed.
- G. Colherinhas and E. E. Fileti, J. Phys. Chem. C, 2014, 118, 9598–9603 CAS.
- G. Colherinhas and E. E. Fileti, J. Phys. Chem. B, 2014, 118, 12215–12222 CrossRef CAS PubMed.
- C. Chena, J. Hua, S. Zhanga, P. Zhoua, X. Zhaob, H. Xua, X. Zhaoc, M. Yaseenc and J. R. Luc, Biomaterials, 2012, 33, 592–603 CrossRef PubMed.
- D. Gaspar, A. S. Veiga and M. A. R. B. Castanho, Front. Microbiol., 2013, 4, 294 Search PubMed.
- H. B. Albada, P. Prochnow, S. Bobersky, S. Langklotz, J. P. Schriek, J. E. Bandow and N. Metzler-Nolt, ACS Med. Chem. Lett., 2012, 3, 980–984 CrossRef CAS PubMed.
- X. Zhao, F. Pan, H. Xu, M. Yaseen, H. Shan, C. A. E. Hauser, S. Zhang and J. R. Lu, Chem. Soc. Rev., 2010, 39, 3480–3498 RSC.
- X. Zhao, Curr. Opin. Colloid Interface Sci., 2009, 14, 340–348 CrossRef CAS.
- A. Oszlánczi, A. Bóta, S. Berényi and E. Klumpp, Colloids Surf., B, 2010, 76, 519–528 CrossRef PubMed.
- K. Lohner, A. Latal, G. Degovics and P. Garidel, Chem. Phys. Lipids, 2001, 111, 177–192 CrossRef CAS PubMed.
- P. Tieleman, http://wcm.ucalgary.ca/tieleman/downloads.
- W. M. Haynes and D. R. Lide, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, Boca Raton, Fla, 92nd edn, 2011 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. Mackerell Jr, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10099 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101–014108 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7192 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187 CrossRef.
- M. Souaille and R. Roux, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435 CrossRef CAS PubMed.
- G. Colherinhas, F. Outi, T. Malaspina and E. E. Fileti, J. Mol. Liq., 2017 Search PubMed , submitted.
- Lateral Diffusion in Membranes, ed. P. F. F. Almeida and W. L. C. Vaz, Elsevier Science, New York, 1995 Search PubMed.
- I. C. Yeh, D. R. Ripoll and A. Wallqvist, J. Phys. Chem. B, 2012, 116, 3387–3396 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04537a |
| This journal is © The Royal Society of Chemistry 2017 |