 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular dynamics simulation of low-energy recoil events in titanate pyrochlores
Liyuan Donga,
Wahyu Setyawanb,
Yuhong Li*a,
Ram Devanathan*b and
Fei Gao *c
*c
aSchool of Nuclear Science and Technology, Lanzhou University, Lanzhou, Gansu 730000, China. E-mail: liyuhong@lzu.edu.cn
bEnergy and Environment Directorate, Pacific Northwest National Laboratory, Richland, WA 99352, USA. E-mail: ram.devanathan@pnnl.gov
cDepartment of Nuclear Engineering & Radiological Sciences, University of Michigan, Ann Arbor, MI 48109, USA. E-mail: gaofeium@umich.edu
First published on 14th July 2017
Abstract
Molecular dynamics simulations of low-energy displacement events in titanate pyrochlores A2Ti2O7 (A = Lu, Er, Gd, Eu, Ce, La) have been carried out along three main crystallographic directions, [100], [110] and [111], to determine threshold displacement energies (Ed) for A, Ti and O, corresponding defect configurations, and defect formation dynamics. The A-site cation size was found to have an important effect on the value of Ed for each type of ion in titanate pyrochlores. Ed depended on the knock-on direction, ion type, and Wyckoff position (48f vs. 8b site for O). The influence of A-site cation size on Ed for Ti and O48f was significantly larger than on Ed for A and O8b in titanate pyrochlores. Besides, the value of Ed for each type of atom in titanate pyrochlores was highly anisotropic. The largest change of Ed was for Ti, while the smallest change of Ed was for O8b. The energy required to displace the A cation was less than that to displace Ti. The lowest displacement energy was for the anion in titanate pyrochlores. The easiest displacement direction for Ti4+ and O48f was along [100], while the easiest directions for A3+ and O8b in titanate pyrochlores varied with the choice of A-site cation. Among the surviving defects, Frenkel pairs were dominant at the end of low-energy recoils. Cation displacements produced both cation and anion defects, while anion displacements produced only anion defects. Thus, cation displacement, which occurs at higher recoil energies, holds the key to amorphization. With increasing A-site cation radius in titanate pyrochlores A2Ti2O7 (A = Lu, Er, Gd, Eu), the variation of the Ed of Ti along [110] was similar to the variation of the experimental critical amorphization temperature (Tc). The displacement of Ti along [110] may play an important role in the amorphization of titanate pyrochlores.
1. Introduction
Titanate pyrochlores have been identified as primary host phases for the immobilization of actinides in durable waste forms and for the disposition of excess plutonium from nuclear weapons1–7 due to their radiation resistance. Consequently, the radiation response of titanate pyrochlores has been the subject of considerable research in the last few decades.8–15 Radiation damage during α-decay can cause microstructural changes, volumetric swelling, and decrease of structural durability that will eventually lead to leaching of actinides. Thus, it is very important to understand the effects of radiation damage and the defect production mechanisms in these pyrochlores.Previously, many studies have been performed to investigate the effects of chemical composition, especially the cation size, on the radiation damage resistance of pyrochlores.3,5,13,14,16–18 Based on experimental studies, Sickafus et al.3 suggested that the antisite defect formation energy is high in compounds containing large A-site cations and smaller B-site cations, and the ratio of radii of A-site and B-site cations can play a key role in the order–disorder (O–D) transformation, amorphization tolerance, and radiation resistance. Lian et al.14,19 investigated the amorphization resistance of titanate pyrochlores A2Ti2O7 (A = Sm, Eu, Gd, Dy, Lu, Y) irradiated by 1.0 MeV Kr+. The results indicated that Gd2Ti2O7 is more sensitive to radiation damage than other titanate pyrochlores, suggesting that A-site cations have an effect on the resistance of amorphization. Wang et al.20 studied the critical amorphization temperatures (Tc) in titanate pyrochlores (A2Ti2O7, A = Gd, Sm, Eu, Y) by using 1 MeV Kr+ irradiation. Tc is the temperature above which radiation by energetic particles cannot amorphize the material. The results indicated that Gd2Ti2O7 had the highest Tc ≈ 1100 K and that the critical dose for irradiation-induced amorphization varied with different lanthanides occupying the A-site. Meanwhile, Begg et al.21 investigated Tc for A2Ti2O7 (A = Y, Sm, Gd, Lu) by using 600 keV Bi+, and suggested that there are no significant effects of A-site cations on the resistance of titanate pyrochlores to ion-beam induced amorphization. Molecular statics studies by Minervini et al.18 revealed that the cation disorder increases with the increasing cation radius ratio: rB/rA. Molecular dynamics (MD) simulations by Devanathan et al.17,22 showed that cation choice in pyrochlores can affect the radiation tolerance, amorphization resistance, O–D transformation, and volume swelling. A modeling study by Xiao et al.23 indicated that the A-site cation has an important effect on the defect production mechanism, and that oxygen migration from O48f and O8b sites to O8a sites is dominant under low-energy irradiation. It is evident that chemical composition especially the choice of cations can affect the radiation response of pyrochlores. However, there are still considerable gaps in our understanding of the influence of A-site cation size on defect production by low-energy recoil events that occur near the end of range of energetic recoils in titanate pyrochlores. The present work addresses this need.
The threshold displacement energy (Ed) is a fundamental parameter needed to quantify displacements and defect production under energetic particle irradiation. Ed represents the energy needed to displace an atom to produce a stable defect on its own sublattice. Ed can be measured in experiments by using optical and thermally stimulated spectroscopies, electron paramagnetic resonance, positron annihilation, and electron microscopy.24–27 However, measuring Ed experimentally is still a challenging task. Furthermore, it is very difficult to study experimentally the details of displacement processes that occur in very short time and small length scales, or to distinguish the dynamic defect formation processes for each sublattice. Consequently, the experimental determination for Ed in ceramics is more difficult than in metals since ceramics usually consist of multiple sublattices. For pyrochlore compounds, only the threshold displacement energies for O sublattice in La2Zr2O7 are available in the literature.28 Theoretically, Ed can be calculated by the sudden approximation (SA) method24,29 or by the MD method. However, the SA method only relaxes the system by energy minimization, and does not consider the dynamic effect of the primary knock-on atom (PKA) or the mass ratio effect (heavier vs. lighter ions) during collision cascades. On the other hand, MD is ideal to simulate the dynamic collision process and the mass effect is inherently included. MD has been successfully used to determine the Ed in a variety of materials, such as α-Fe,30,31 FeCr,32 TiO2,33 and ZrSiO4.34 Devanathan et al.22 calculated Ed in Gd2Zr2O7 and Gd2Ti2O7 along 9 crystallographic directions with MD and suggested that greater ease of anion disorder, lower energy penalty for cation disorder, and faster ionic diffusion result in greater amorphization resistance. Xiao et al.35 and Gao et al.36 calculated Ed in Y2Ti2O7 using ab initio MD (AIMD), and indicated that the relative stability of cation interstitials may provide a pathway for driving irradiation-induced amorphization. Wang et al.37 calculated Ed in Gd2Zr2O7 and Gd2Ti2O7 by AIMD method, and revealed that anion order–disorder is more likely to be involved in the displacement than cation disordering. Although previous work has shed light on understanding the low-energy recoils and defect production process of certain pyrochlores, there have been few studies on the effects of cation choice on defect production in titanate pyrochlores. Therefore, the main purpose of this work is to investigate Ed and the defects produced during low energy displacement events in titanate pyrochlores.
In the current work, MD simulations have been employed to investigate the low-energy displacement events for each type of atom for 6 different chemical compositions of titanate pyrochlores A2Ti2O7 (A3+ = Lu3+, Er3+, Gd3+, Eu3+, Ce3+, La3+) along three crystallographic directions, namely [100], [110] and [111]. Since [100], [110] and [111] directions are major crystallographic orientations in the pyrochlore structure, these directions are the most studied in the previous studies. The aims are (1) to determine threshold displacement energies for all three sublattices in titanate pyrochlores along specific knock-on directions, (2) to obtain a fundamental insight into the defect formation process, and (3) to compare the response of the lattice to low-energy displacement events for each pyrochlore composition. The minimum value of Ed for each type of ion in titanate pyrochlore and corresponding directions have been determined. The values of Ed obtained in the current work can be used as input for binary collision Monte Carlo codes, such as TRIM38 and SRIM,39 to estimate displacement damage accumulation caused by electron, ion, or neutron irradiation, and provide a means to determine the damage dose in displacements per atom for ion-beam irradiation experiments. Since the system considered by TRIM/SRIM is anisotropic, the average value of Ed for all the directions simulated can be used as input for TRIM and SRIM. The simulations also provide details on the type of defects produced and the mechanism of defect production by low energy recoils.
2. Computational details
Titanate pyrochlore, with a general formula of A2Ti2O7 (A = rare earth elements), has a cubic structure as illustrated in Fig. 1. The unit cell (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m/227 space group)40 includes 8 formula units (Z = 8), containing 88 ions: 16A3+ cations, 16Ti4+ cations and 56O2− anions. The A3+ cations occupy the Wyckoff position 16d (1/2, 1/2, 1/2), the Ti4+ cations are at the 16c (0, 0, 0) position, and the O2− anions are at the 8b (3/8, 3/8, 3/8) and 48f (x, 1/8, 1/8) positions. Geometrically, A-site cations (with atomic radius of ∼100 pm) are eight-coordinated surrounded by six O48f and two O8b, while Ti cations (atomic radius of 60.5 pm) are six-coordinated and surrounded by six O48f anions.
m/227 space group)40 includes 8 formula units (Z = 8), containing 88 ions: 16A3+ cations, 16Ti4+ cations and 56O2− anions. The A3+ cations occupy the Wyckoff position 16d (1/2, 1/2, 1/2), the Ti4+ cations are at the 16c (0, 0, 0) position, and the O2− anions are at the 8b (3/8, 3/8, 3/8) and 48f (x, 1/8, 1/8) positions. Geometrically, A-site cations (with atomic radius of ∼100 pm) are eight-coordinated surrounded by six O48f and two O8b, while Ti cations (atomic radius of 60.5 pm) are six-coordinated and surrounded by six O48f anions.
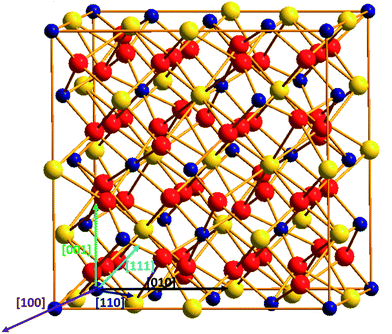 | ||
| Fig. 1 Titanate pyrochlores A2Ti2O7 structure: yellow sphere represents the A-site cations; blue sphere represents Ti cations; red sphere stands for O anions. | ||
A combination of long-range columbic potential with formal charges (+3 for A cation, +4 for Ti, and −2 for O) and modified short-range Buckingham potential was employed to describe the ionic interactions. The smooth particle mesh Ewald summation41 was used to calculate the electrostatic interactions with a cut off radius of 10 Å and tolerance of 10−8. To provide effective short-range potentials, the repulsive Ziegler–Biersack–Littmark (ZBL) potentials were used in the very short range and were smoothly joined to the Buckingham potentials by using exponential functions. The potential parameters have been described in detail elsewhere.18,42 According to the previous studies,18,42 these potentials can provide reasonable matches between the defect formation energies and static properties (such as lattice parameter, bulk modulus, and thermal properties) and the corresponding experimental measurements over a wide composition range, which validates these potentials for simulation of the effects of A-site cation and the dynamics of low-energy recoils in titanate pyrochlores.
The MD simulations were performed using the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code,43 which was developed at Sandia National Laboratory, USA. The simulation cell contained 3 × 3 × 3 unit cells and 2376 atoms with the side length of the cube being ∼30 Å. Periodic boundary conditions were employed. All simulations were performed with a time step of 0.5 fs. Before the low-energy cascade was simulated, the system was equilibrated at zero external pressure with constant number of atoms, pressure and temperature (NPT ensemble) for 15 ps at a temperature of 10 K. Using the equilibrated configuration, displacements were simulated with constant number of atoms, volume and energy (NVE ensemble) and the evolution of the system was followed for 4 ps. Three simulations were performed to determine Ed for A, Ti, O48f and O8b along each direction to evaluate the statistical effects, and only the smallest value is reported here.
Ed corresponds to the minimum energy to form stable defects, which were identified after 4 ps. For each simulation, the defects were detected by the Wigner–Seitz defect analysis44 method. This method has been shown to be ideal for determining defects in crystalline materials45,46 including α-Fe, SiC, semiconductors and oxides. For each type of atom in titanate pyrochlores, Ed was determined by running a series of simulations, with different kinetic energies imparted to a single primary knock-on atom (PKA) along a specific crystal direction. The initial PKA kinetic energy was 10 eV and this energy was increased in steps of 10 eV in subsequent simulations until a stable defect was created. Afterwards, the energy was decreased with a decrement of 1 eV until no stable defect was created. The lowest energy at which a stable defect was created was taken as the Ed for the corresponding sublattice.
3. Results and discussion
3.1 Ed in A2Ti2O7 pyrochlore along the [100] direction
Fig. 2 shows the variation of Ed for A, Ti, O48f and O8b in titanate pyrochlores A2Ti2O7 (A3+ = Lu3+, Er3+, Gd3+, Eu3+, Ce3+, La3+) with increasing A-site cation radius along the crystallographic direction [100]. Ed for Ti decreased significantly from 172 eV in Lu2Ti2O7 to 136 eV in La2Ti2O7. In contrast, Ed for A-site cation, O48f and O8b remained almost unchanged with values of 69.5 ± 1.5 eV, 52.5 ± 0.5 eV and 55 ± 2 eV, respectively. It should be mentioned that the value of Ed for Ce in Ce2Ti2O7 was 59 eV along the [100] direction, which was much lower than ∼70 eV for the A-site cation in the other titanate pyrochlores. This finding suggests that Ce2Ti2O7 may be more susceptible to displace along [100] direction than other titanate pyrochlores which may lead to differences in amorphization resistance of Ce2Ti2O7 compared to the other titanate pyrochlores. In addition, it's easier to displace the A-site cation than the Ti cation, and it requires less energy to displace anions than cations, which is consistent with the previous studies22,35–37 of titanate pyrochlores.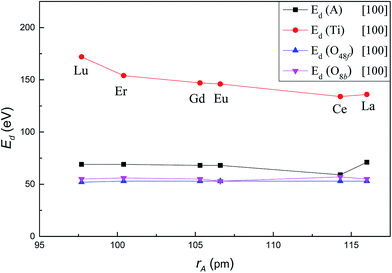 | ||
| Fig. 2 Variation of Ed value for A, Ti, O48f and O8b in A2Ti2O7 as a function of A-site cation ionic radii along [100] crystallographic direction. | ||
Table 1 lists defect end states for A, Ti, O48f and O8b in titanate pyrochlores after low-energy displacements along the knock-on direction [100]. The Kröger–Vink notation was used to describe defects created after displacement. Namely, VA represents an A-site vacancy, Bi represents a B-cation interstitial, and AB represents an antisite defect formed by an A-site cation on a B (Ti) site. When an A-site cation was displaced along [100], it encountered an adjacent Ti atom and occupied that site by displacing the Ti into an interstitial position. Therefore, the defects consisted of a VA, an ATi, and a Tii. The displacement process of a Ti PKA was more complex than that of an A-site cation. With Ti PKA, the formation of the expected TiA antisite did not occur in most of the titanate pyrochlores (A2Ti2O7; A = Lu, Er, Gd, Eu). Instead, the Ti PKA returned to its lattice site, while the secondary knock-on atom (SKA) (A-site cation) underwent a characteristic A-site cation [100] displacement leading to an ATi antisite defect. The A-site cation SKA recoil collided with a neighboring Ti and occupied its site, eventually pushing it to an interstitial position. The defect configurations after Ti recoils in A2Ti2O7 along [100] direction consisted of A-site cation vacancy, Ti interstitial and ATi antisite. However, there were different types of defects in Ce2Ti2O7 and La2Ti2O7. For Ti recoils along the [100] direction in Ce2Ti2O7, the Ti PKA collided with its neighboring Ce and occupied its site, eventually pushing the Ce into an interstitial position. Therefore, Ti vacancy, TiCe antisite and Ce interstitial were observed after Ti displacement in Ce2Ti2O7. In La2Ti2O7, when the Ti PKA was displaced along the [100] direction, the Ti moved far away from its initial site to form a stable interstitial, while a secondary knock-on atom (SKA) La collided with an adjacent Ti and occupied its site displacing the Ti into an interstitial position. Thus, Ti Frenkel pairs, La vacancy, LaTi antisite and Ti interstitial were produced after Ti displacement along the [100] direction. For O48f and O8b displacement along [100], the O-anion PKA moved far away from its original site and occupied an interstitial position, i.e. O Frenkel pairs were observed. Compared with the defect end states of Gd2Ti2O7 in previous studies, our results show excellent agreement with Devanathan's22 MD simulation and similarities of defect configuration with Wang's37 AIMD simulation. Along [100], cation displacements produced vacancies, interstitials and antisite defects on the cation sublattice, and anion displacements produced anion Frenkel pairs. These results are in excellent agreement with the type of defects observed after low-energy recoils by Chartier29 and Devanathan22 in pyrochlores.
| Name | A | Ti | O48f | O8b |
|---|---|---|---|---|
| Defects | Defects | Defects | Defects | |
| Lu2Ti2O7 | VLuTiiLuTi | VLuTiiLuTi | VOOi | VOOi |
| Er2Ti2O7 | VErTiiErTi | VErTiiErTi | VOOi | VOOi |
| Gd2Ti2O7 | VGdTiiGdTi | VGdTiiGdTi | VOOi | VOOi |
| Eu2Ti2O7 | VEuTiiEuTi | VEuTiiEuTi | VOOi | VOOi |
| Ce2Ti2O7 | VCeTiiCeTi | VTiCeiTiCe | VOOi | VOOi |
| La2Ti2O7 | VLaTiiLaTi | VTi2TiiVLaLaTi | VOOi | VOOi |
3.2 Ed in A2Ti2O7 pyrochlores along the [110] direction
Fig. 3 shows the variation of Ed for each type of atom in titanate pyrochlores with increasing A-site cation radius along the crystallographic direction [110]. The values of Ed for each type of ion in titanate pyrochlores show much more variation with increasing cation radius for recoils along [110] direction than along [100]. The Ed of the A-site cation increased from 103 eV in Lu2Ti2O7 to 147 eV in Eu2Ti2O7, then decreased slightly to 129 eV in La2Ti2O7. These values are much higher than the corresponding values for the [100] direction. The Ed of Ti increased considerably from 187 eV in Lu2Ti2O7 to 349 eV in La2Ti2O7. The Ed of O48f showed fluctuations with increasing A-site cation size, i.e. the Ed of O48f decreased from 184 eV in Lu2Ti2O7 to 116 eV in Gd2Ti2O7, then increased to 164 eV in Eu2Ti2O7, dropped abruptly to 94 eV in Ce2Ti2O7, and finally increased to 167 eV in La2Ti2O7. The Ed of O8b was almost steady with a slight increase from 28 eV in Lu2Ti2O7 to 35 eV in La2Ti2O7, except for an increase to 80 eV in Ce2Ti2O7. For displacements along the [110] direction, the Ed value for O48f was the smallest while the value for O8b was the largest in Ce2Ti2O7 among these titanate pyrochlores. Along [110], the value of Ed for the A cation was the highest and the value for Ti was the lowest in Eu2Ti2O7 among these titanate pyrochlores, which suggests that placing Eu in the A-site may cause an unusual radiation response compared to other A2Ti2O7 pyrochlores. In addition, the influence of A-site cation size on the variation of Ed for Ti and O48f was larger than that for A-site cation and O8b in titanate pyrochlores along the [110] direction. With increasing A-site cation size, the variation trends of Ed along [110] for Ti in some titanate pyrochlores A2Ti2O7 (A = Lu3+, Er3+, Gd3+, Eu3+) was similar to the variation of the critical amorphization temperature (Tc), in Lian's13 and Wang's20 experiments, while it is exactly the opposite of the trend in the critical amorphization dose (Dc)13 and structure parameter (x).13 Therefore, the lower the Ed value of Ti in the titanate pyrochlore, the lower is the value of the Tc, the higher is the Dc and x, the greater is the amorphization resistance, and the easier it is for the order–disorder transition. However, the variation of Ed for O48f was just the opposite. The displacement of Ti and O48f may play an important role in the amorphization resistance of certain titanate pyrochlores following low energy recoils.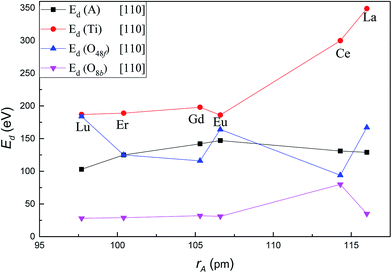 | ||
| Fig. 3 Variation of Ed value for A, Ti, O48f and O8b in A2Ti2O7 as a function of A-site cation ionic radii along [110] crystallographic direction. | ||
Table 2 presents a summary of defects for each type of atom in titanate pyrochlores after low-energy recoils along [110] direction. For A-site cation displacements along [110] in titanate pyrochlores, the A-site cation PKA initially collided with a Ti atom nearby and replaced it, then the replaced Ti kept moving and occupied a neighboring A-site cation (denoted as the third knock-on atom, TKA). Eventually the A-site cation TKA occupied an adjacent Ti and displaced it into an interstitial position. This displacement process resulted in the production of a complex defect cluster consisting of A-site cation vacancy, ATi antisite, TiA antisite, and Ti interstitial. Otherwise, the type of defects after A-site cation recoils in Lu2Ti2O7 was different from that in other titanate pyrochlores, i.e. the Lu PKA left its original site and occupied the Ti-site forming LuTi antisite; the replaced Ti occupied a nearby Lu site and eventually pushed the Lu into an interstitial position. Such a displacement along the [110] resulted in the production of defects consisting of Lu vacancy, antisites of LuTi and TiLu, and Lu interstitial. Because of the longer distance of the displacement collision process and the larger number of created defects, the Ed for A-site cation along [110] direction was higher compared to that along [100] direction. For Ti PKA along [110], Ti moved far away from its lattice site and occupied an interstitial position forming Ti Frenkel pairs, and one or more adjacent O-anions were also displaced off site forming anion Frenkel pairs. The number of anion Frenkel pairs depended heavily on the species of A-site cation. For example, there were three anion Frenkel pairs in Er2Ti2O7, while there was only one in Gd2Ti2O7. However, for Ti displacement along [110] direction in Ce2Ti2O7, only cation antisites of CeTi and TiCe are produced when the knock-on kinetic energy reached up to 300 eV. If Ce is substituted on the A-site of titanate pyrochlore, the amorphization susceptibility may be decreased, because the incident energy is dissipated by formation of cation anti-site defects, which are high energy defects in Ce2Ti2O7. Similar to the case of the [100] direction, only anion Frenkel pairs were created by anion displacement along the [110] direction in all the titanate pyrochlores studied. Compared with the defect configurations of titanate pyrochlores after low-energies recoils events in previous studies22,35–37 along [110], our results are consistent with classical MD simulation of Devanathan et al.22 The Ti-bridge and Ti-dumbbell which are considered as the stable configuration in the AIMD calculations of Wang et al.37 and Xiao et al.35 were not found in this work, which may be an indication of the limitation of empirical potentials.
| Name | A | Ti | O48f | O8b |
|---|---|---|---|---|
| Defects | Defects | Defects | Defects | |
| Lu2Ti2O7 | VLuLuiLuTiTiiLu | VTiTii2VO2Oi | VOOi | VOOi |
| Er2Ti2O7 | VErTii2ErTiTiEr | VTiTii3VO3Oi | VOOi | VOOi |
| Gd2Ti2O7 | VGdTii2GdTiTiGd | VTiTiiVOOi | VOOi | VOOi |
| Eu2Ti2O7 | VEuTii2EuTiTiEu | VTiTii2VO2Oi | VOOi | VOOi |
| Ce2Ti2O7 | VCeTii2CeTiTiCe | CeTiTiCe | VOOi | VOOi |
| La2Ti2O7 | VLaTii2LaTiTiLa | VTiTii2VO2Oi | VOOi | VOOi |
3.3 Ed in A2Ti2O7 pyrochlores along [111] direction
Fig. 4 presents the variation of Ed for each atom type as a function of A-site cation radius along the crystallographic direction [111]. With increasing A-site cation radius, the Ed of A-site cation increased from 52 eV in Lu2Ti2O7 to 91 eV in La2Ti2O7, the Ed of Ti increased significantly from 242 eV in Lu2Ti2O7 to 283 eV in La2Ti2O7. However, the value for O48f decreased from 162 eV in Lu2Ti2O7 to 130 eV in La2Ti2O7. The Ed of O8b increased slightly from 31 eV in Lu2Ti2O7 to 42 eV in Lu2Ti2O7. It is important to note that among six different titanate pyrochlores, Ed for A-site cation was the largest (100 eV) and Ed for Ti was the smallest (216 eV) when Ce is used as the A-site cation. That is to say, among these compounds, Ti was the most easily displaced in Ce2Ti2O7, while A-site cation was the least easily displaced, for PKA recoil along [111]. The result suggests that Ce2Ti2O7 may exhibit a different radiation resistance compared to other titanate pyrochlores. Compared with the previous studies, the Ed value of each atom in Gd2Ti2O7 is in good agreement with previous MD results,22 while significantly higher than Wang's37 AIMD results. The reason is that the charge transfer is ignored in the MD calculation as explained by Wang et al.37 Similar to the zirconate pyrochlores,23 A-site cation also has an important effect on the Ed of all atom types in titanate pyrochlores. Besides, it is easier to displace A-site cation than Ti4+, thus it requires less energy to displace A-site cation than Ti4+ in titanate pyrochlore which is consistent with the previous studies.22,35–37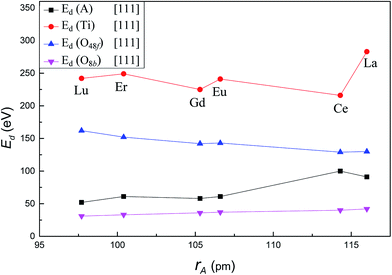 | ||
| Fig. 4 Variation of Ed value for A, Ti, O48f and O8b in A2Ti2O7 as a function of A-site cation ionic radii along [111] crystallographic direction. | ||
Table 3 summarizes the defects produced by displacement events for each type of atom in titanate pyrochlores along the crystal direction [111]. In most of the titanate pyrochlores (A2Ti2O7, A = Lu3+, Er3+, Gd3+, Eu3+), the A-site cation PKA moved far away from its initial site along this direction and occupied an interstitial position, forming an A-site cation Frenkel pair defect. It is worth noting that, after Ce displacements in Ce2Ti2O7 along [111], the Ce PKA moved far away from its equilibrium site and collided with a Ti atom to replace this atom, finally pushing the Ti into an interstitial position. Meantime, the nearby O was displaced from its original site resulting in an anion Frenkel pair. Therefore, A-site cation vacancy, ATi antisite, Ti interstitial and anion Frenkel pairs were produced. The value of Ed for Ce is the highest among these titanate pyrochlores because Ce PKA produced the largest number of defects, including defects on both cation and anion sublattices. Similarly, the defects after La displacements in La2Ti2O7 consisted of A-site cation vacancy, ATi antisite and Ti interstitial. For Ti displacement along [111], Ti Frenkel pairs were produced in Lu2Ti2O7 and Er2Ti2O7, while antisites of TiA and ATi were observed in Gd2Ti2O7, Eu2Ti2O7 and Ce2Ti2O7, and anion Frenkel pairs were also generated in Ce2Ti2O7. However, when Ti was displaced along [111] in La2Ti2O7, the Ti PKA returned to its site, after displacing an adjacent La off its site. The SKA La collided with a neighboring Ti and replaced the Ti atom, finally pushing the Ti into an interstitial position. Simultaneously, a neighboring O was pushed far away from its site, forming an anion Frenkel pair. Thus, A-site cation vacancies, LaTi antisite, Ti interstitials, and O Frenkel pairs were produced after Ti low-energy recoils along [111] direction. The highest Ed for Ti was observed in La2Ti2O7 among the titanate pyrochlores and the largest number of defects was produced after Ti displacement in the material. For the O-anion displacements along [111], we only observed anion Frenkel pairs, which is the same result as in the case of PKA directions [100] and [110]. For the anion low-energy displacement recoils, our results show excellent agreement with the previous studies.23,37 However, the defect end states of Gd and Ti along [111] are in good agreement with MD results of Devanathan et al.22 and AIMD results of Wang et al.37
| Name | A | Ti | O48f | O8b |
|---|---|---|---|---|
| Defects | Defects | Defects | Defects | |
| Lu2Ti2O7 | VLuLui | VTiTii | VOOi | VOOi |
| Er2Ti2O7 | VErEri | VTiTii | VOOi | VOOi |
| Gd2Ti2O7 | VGdGdi | TiGdGdTi | VOOi | VOOi |
| Eu2Ti2O7 | VEuEui | EuTiTiEu | VOOi | VOOi |
| Ce2Ti2O7 | VCeTiiCeTiVOOi | CeTiTiCeVOOi | VOOi | VOOi |
| La2Ti2O7 | VLaTiiLaTi | VLaTiiLaTiVOOi | VOOi | VOOi |
3.4 The minimum and average value of Ed in A2Ti2O7 pyrochlores
Table 4 lists the minimum value of Ed and corresponding directions for each type of ions in titanate pyrochlores. Among these three directions, the easiest displacement directions for Ti4+ and O48f is along [100], however, the corresponding directions for A3+ and O8b in titanate pyrochlores depended on the A-site cation size. The A3+ can be displaced at energies from 52 eV to 71 eV, while Ti can be displaced at energies ranged from 134 to 172 eV. Based on the minimum value of value of Ed, to displace A3+ required less energy than to displace Ti4+ cation, which is in good agreement with previous studies.22,35–37 The minimum value of Ed for O48f and O8b in titanate pyrochlore is around 53 eV and 35 eV, respectively, which is in excellent agreement with the results of (47 ± 5) eV for O in La2Zr2O7 pyrochlore examined experimentally by Smith et al.28 The smallest value of Ed for each type of ion in titanate pyrochlores varies considerably with A-site cation.| Name | A3+ | Ti4+ | O48f | O8b | ||||
|---|---|---|---|---|---|---|---|---|
| Ed (eV) | Direction | Ed (eV) | Direction | Ed (eV) | Direction | Ed (eV) | Direction | |
| Lu2Ti2O7 | 52 | [111] | 172 | [100] | 52 | [100] | 28 | [110] |
| Er2Ti2O7 | 61 | [111] | 154 | [100] | 53 | [100] | 29 | [110] |
| Gd2Ti2O7 | 58 | [111] | 147 | [100] | 53 | [100] | 32 | [110] |
| Eu2Ti2O7 | 61 | [111] | 146 | [100] | 53 | [100] | 31 | [110] |
| Ce2Ti2O7 | 59 | [100] | 134 | [100] | 53 | [100] | 40 | [111] |
| La2Ti2O7 | 71 | [100] | 136 | [100] | 53 | [100] | 35 | [110] |
In addition, the average value of Ed for each sublattice in titanate pyrochlores is listed in Table 5, which can be used as input for TRIM and SRIM.
| Name | A3+ | Ti4+ | O2− |
|---|---|---|---|
| Ed (eV) | Ed (eV) | Ed (eV) | |
| Lu2Ti2O7 | 75 | 200 | 85 |
| Er2Ti2O7 | 85 | 197 | 75 |
| Gd2Ti2O7 | 89 | 190 | 72 |
| Eu2Ti2O7 | 92 | 191 | 80 |
| Ce2Ti2O7 | 97 | 217 | 76 |
| La2Ti2O7 | 97 | 256 | 80 |
4. Conclusions
The Ed value and defect configurations after low-energy displacements for each type of atom in titanate pyrochlores A2Ti2O7 (A = Lu3+, Er3+, Gd3+, Eu3+, Ce3+, La3+) along [100], [110] and [111] crystallographic direction have been investigated by the classical molecular dynamics method. The main conclusions are as follows.(i) The value of Ed for each type of ion in titanate pyrochlores varies with the A-site cation composition. The influence of A-site cation radius on the value of Ed for Ti and O48f was much larger than that for A and O8b in titanate pyrochlore. Ed depended on knock-on direction, ion type, and Wyckoff position (48f and 8b for O). Besides, the value of Ed for each type of atom in titanate pyrochlore was highly anisotropic. The largest change of Ed was for Ti, while the smallest change of Ed was for O8b. With increasing A-site cation radius, the Ed value for Ti4+ cations in titanate pyrochlores along the [100] direction decreased steadily, while it generally increased along [110]. The Ed value for O48f decreased considerably with increasing A-site cation radius along [111]. Ed for O8b was almost stable at about (55 ± 2) eV, (31 ± 4) eV, and (37 ± 6) eV along [100], [110] and [111], respectively. Other Ed values did not show clear monotonic trends.
(ii) Along the [110] direction, in some A2Ti2O7 pyrochlores (A = Lu3+, Er3+, Gd3+, Eu3+), the Ed variation of Ti as a function of A-site cation radius followed a similar trend as the critical amorphization temperature (Tc) in previous experiments. It was found that the higher the value of Ed, the higher the critical amorphization temperature (Tc), and the weaker the amorphization resistance. Ti displacements along [110] may play a key role in the amorphization tolerance of titanate pyrochlores. Among these four materials, Gd2Ti2O7 exhibited the highest Ed for Ti along [110] of about 200 eV, which is correlated with Gd2Ti2O7 being the most susceptible to amorphization.
(iii) Based on the minimum value of Ed, it required less energy to displace the A3+ cation than the Ti4+ cation. The former had displacement energies from 52 to 71 eV, while the corresponding values for the latter ranged from 134 to 171 eV. Anions could be displaced at energies around 30 eV. Although our displacement energies from MD are significantly higher than Wang's AIMD results,37 both the methods exhibit some similar behavior in the mechanisms of defect creation and defect configuration.
(iv) The smallest Ed for each type of atom in every titanate pyrochlore occurred along different crystallographic directions. The easiest displacement direction for Ti4+ and O48f was along [100], while the corresponding directions for A3+ and O8b in titanate pyrochlores depended on the A-site cation size.
(v) The defects created after low-energy displacements consisted of cation interstitials and vacancies, cation antisite defects, and anion Frenkel-pairs. Among them, cation Frenkel pairs were dominant at the end of the low energy recoils. Both cation and anion defects were observed after cation displacements, while only anion defects were produced after anion displacements. Therefore, cation displacement, which occurs at higher energies, holds the key to amorphization resistance. For Ti recoils along [110], Ce and Ti ions exchanged sites to produce two antisite defects in Ce2Ti2O7 in contrast to the production of cation Frenkel pairs in other titanate pyrochlores. The formation of this high energy defect pair in Ce2Ti2O7 may make this particular titanate highly susceptible to amorphization.
Acknowledgements
L. Y. Dong wants to thank China Scholarship Council for supporting her study at the Pacific Northwest National Laboratory and University of Michigan. This work was supported by the National Natural Science Foundation of China (No. 11475076 and 11175076). F. Gao is supported by the award NRCHQ-13-G-38-0007 from the US Nuclear Regulatory Commission. The statements, findings, conclusions, and recommendations are those of the authors and do not necessarily reflect the view of the US Nuclear Regulatory Commission.References
- R. Ewing, W. Weber and F. Clinard, Prog. Nucl. Energy, 1995, 29, 63–127 CrossRef CAS.
- R. C. Ewing, J. Appl. Phys., 2004, 95, 5949 CrossRef CAS.
- K. E. Sickafus, R. W. Grimes, J. A. Valdez, A. Cleave, M. Tang, M. Ishimaru, S. M. Corish, C. R. Stanek and B. P. Uberuaga, Nat. Mater., 2007, 6, 217–223 CrossRef CAS PubMed.
- W. J. Weber, R. C. Ewing, C. Catlow, T. D. De La Rubia, L. Hobbs, C. Kinoshita, H. Matzke, A. Motta, M. Nastasi and E. Salje, J. Mater. Res., 1998, 13, 1434–1484 CrossRef CAS.
- K. E. Sickafus, Science, 2000, 289, 748–751 CrossRef CAS PubMed.
- W. J. Weber and R. C. Ewing, Science, 2000, 289, 2051–2052 CrossRef CAS PubMed.
- A. Ringwood, S. Kesson, N. Ware, W. Hibberson and A. Major, Nature, 1979, 278, 219–223 CrossRef CAS.
- J. Lian, X. Zu, K. Kutty, J. Chen, L. Wang and R. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 054108 CrossRef.
- J. Chen, J. Lian, L. M. Wang, R. C. Ewing and L. A. Boatner, Appl. Phys. Lett., 2001, 79, 1989 CrossRef CAS.
- K. B. Helean, S. V. Ushakov, C. E. Brown, A. Navrotsky, J. Lian, R. C. Ewing, J. M. Farmer and L. A. Boatner, J. Solid State Chem., 2004, 177, 1858–1866 CrossRef CAS.
- G. C. Lau, T. M. McQueen, Q. Huang, H. W. Zandbergen and R. J. Cava, J. Solid State Chem., 2008, 181, 45–50 CrossRef CAS.
- Y. H. Li, B. P. Uberuaga, C. Jiang, S. Choudhury, J. A. Valdez, M. K. Patel, J. Won, Y. Q. Wang, M. Tang and D. J. Safarik, Phys. Rev. Lett., 2012, 108, 195504 CrossRef CAS PubMed.
- J. Lian, J. Chen, L. M. Wang and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134107 CrossRef.
- J. Lian, L. M. Wang, R. C. Ewing and L. A. Boatner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 241, 365–371 CrossRef CAS.
- F. X. Zhang and S. K. Saxena, Chem. Phys. Lett., 2005, 413, 248–251 CrossRef CAS.
- S. X. Wang, B. D. Begg, L. M. Wang, R. C. Ewing, W. J. Weber and K. Kutty, J. Mater. Res., 1999, 14, 4470–4473 CrossRef CAS.
- R. Devanathan, F. Gao and C. J. Sundgren, RSC Adv., 2013, 3, 2901–2909 RSC.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873–1878 CrossRef CAS.
- J. Lian, R. C. Ewing, L. M. Wang and K. B. Helean, J. Mater. Res., 2011, 19, 1575–1580 CrossRef.
- S. Wang, L. Wang, R. Ewing and K. G. Kutty, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 169, 135–140 CrossRef CAS.
- B. D. Begg, N. J. Hess, W. J. Weber, R. Devanathan, J. P. Icenhower, S. Thevuthasan and B. P. McGrail, J. Nucl. Mater., 2001, 288, 208–216 CrossRef CAS.
- R. Devanathan and W. J. Weber, J. Appl. Phys., 2005, 98, 086110 CrossRef.
- H. Y. Xiao, W. J. Weber, Y. Zhang and X. T. Zu, Acta Mater., 2015, 87, 273–282 CrossRef CAS.
- R. Williford, R. Devanathan and W. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141, 94–98 CrossRef CAS.
- S. J. Zinkle and C. Kinoshita, J. Nucl. Mater., 1997, 251, 200–217 CrossRef CAS.
- P. Agnew, Philos. Mag. A, 1992, 65, 355–361 CrossRef CAS.
- D. R. Locker and J. M. Meese, IEEE Trans. Nucl. Sci., 1972, 19, 237–242 CrossRef CAS.
- K. L. Smith, M. Colella, R. Cooper and E. R. Vance, J. Nucl. Mater., 2003, 321, 19–28 CrossRef CAS.
- A. Chartier, C. Meis, J. P. Crocombette, L. R. Corrales and W. J. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 147102 CrossRef.
- C. Erginsoy, G. H. Vineyard and A. Englert, Phys. Rev., 1964, 133, A595–A606 CrossRef.
- K. Nordlund, J. Wallenius and L. Malerba, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 246, 322–332 CrossRef CAS.
- N. Juslin, K. Nordlund, J. Wallenius and L. Malerba, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 255, 75–77 CrossRef CAS.
- B. S. Thomas, N. A. Marks, L. R. Corrales and R. Devanathan, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 239, 191–201 CrossRef CAS.
- P. A. F. P. Moreira, R. Devanathan, J. Yu and W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 3431–3436 CrossRef CAS.
- H. Y. Xiao, F. Gao and W. J. Weber, J. Phys.: Condens. Matter, 2010, 22, 415801 CrossRef CAS PubMed.
- F. Gao, H. Y. Xiao and W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1693–1697 CrossRef CAS.
- X. J. Wang, H. Y. Xiao, X. T. Zu, Y. Zhang and W. J. Weber, J. Mater. Chem. C, 2013, 1, 1665–1673 RSC.
- W. Möller and W. Eckstein, Nucl. Instrum. Methods Phys. Res., Sect. B, 1984, 2, 814–818 CrossRef.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- M. Subramanian, G. Aravamudan and G. S. Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- L. Dong, Y. Li, R. Devanathan and F. Gao, RSC Adv., 2016, 6, 41410–41419 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- F. Gao and W. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 024106 CrossRef.
- L. Malerba, D. Terentyev, P. Olsson, R. Chakarova and J. Wallenius, J. Nucl. Mater., 2004, 329, 1156–1160 CrossRef.
- Y. Zhang, M. Ishimaru, T. Varga, T. Oda, C. Hardiman, H. Xue, Y. Katoh, S. Shannon and W. J. Weber, Phys. Chem. Chem. Phys., 2012, 14, 13429–13436 RSC.
| This journal is © The Royal Society of Chemistry 2017 |
