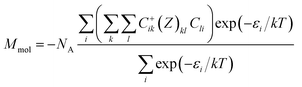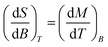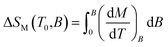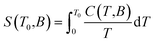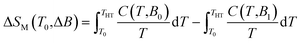DOI:
10.1039/C7RA04945E
(Paper)
RSC Adv., 2017,
7, 30763-30769
Magnetorefrigeration capability of a gadolinium(III) coordination polymer containing trimesic acid: a correlation between the isothermal magnetic entropy change and the gadolinium content
Received
2nd May 2017
, Accepted 1st June 2017
First published on 13th June 2017
Abstract
The Gd(III) coordination polymer [Gd(mes)(H2O)6]n (1), where H3mes stands for trimesic acid, was subjected to variable temperature/field magnetizations and heat capacity measurements. Analyses of the magnetic data revealed negligible magnetic interactions (zJ = −0.39 cm−1) and the isothermal magnetic entropy change −ΔSM = 36.0 J K−1 kg−1 at T = 2 K and B = 9 T. The evaluation of the heat capacity data resulted in a similar value of −ΔSM = 34.8 J K−1 kg−1. Thus, compound 1 shows a quite large magnetocaloric effect among Gd(III)-based molecular coolants. Furthermore, the correlation of the magnetocaloric effect based on the mass concentration of Gd atoms (cm(Gd)) was proposed as −ΔSM = 39.5cm(Gd)0.364 taking into account the experimental data for more than thirty Gd(III) compounds.
Introduction
The coordination compounds of lanthanides are of great interest due to their fascinating luminescent1 and magnetic properties.2 The gadolinium(III) compounds themselves are attention-grabbing from the application point of view due to the fact that they can be utilized as MRI agents3,4 and also as magnetic coolants. Indeed, the paramagnetic compounds with a large spin are prospective materials for magnetic refrigeration at low temperatures based on the magnetocaloric effect.5,6 The coordination compounds of Gd(III) began to be explored as magnetic coolants quite recently, and both polynuclear coordination compounds (molecular clusters)7 and polymeric coordination compounds8 were studied. Interestingly, a heptanuclear Gd(III) compound [Gd7(OH)6(thmeH2)5(thmeH)(tpa)6(CH3CN)2](NO3)2, where H3thme = tris(hydroxymethyl)ethane and Htpa = triphenylacetic acid, was shown to act as an efficient magnetic coolant, with T = 200 mK obtained using an adiabatic demagnetization experiment.9 The efficiency of such materials is usually determined by the isothermal magnetic entropy change ΔSM.10 Up to now, there are several reports on Gd(III) polymeric coordination compounds containing aromatic carboxylic acids as ligands and revealing the large magnetocaloric effect, e.g. [Gd(HCOO)(bdc)]n (bdc = 1,4-benzenedicarboxylic acid) with −ΔSM = 47.0 J K−1 kg−1,11 and [Gd2(N-BDC)3(dmf)4]n (N-BDC = 2-amino-1,4-benzenedicarboxylic acid) with −ΔSM = 29.0 J K−1 kg−1.12 This motivated us to investigate magnetic properties of the recently reported13 polymeric compound [Gd(mes)(H2O)6]n (1) comprising 1,3,5-benzenetricarboxylic acid (trimesic acid, H3mes) as a bridging ligand. Thus, we report on magnetic and magnetocaloric properties of this compound studied both experimentally and theoretically. Furthermore, a general correlation between the magnetorefrigeration capabilities and the gadolinium content of Gd(III) compounds is proposed.
Results and discussion
Synthesis and crystal structure of 1
As the synthesis and the crystal structure of 1 was already reported,13 herein we wish only briefly to summarize the key points relevant to the reported study. The crystal structure of 1 is composed of zig–zag chains, in which the Gd(III) atoms are bridged by carboxylic groups of the mes ligand, and coordination number 9 is achieved by coordination of six molecules of water (Fig. 1).13
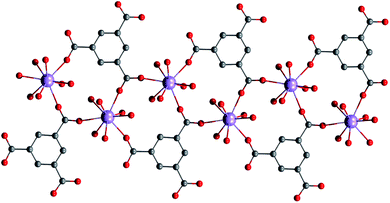 |
| | Fig. 1 Part of the crystal structure of 1 showing a zig–zag chain motif of the Gd(III) atoms.13 The hydrogen atoms were omitted for clarity. | |
The shortest distance between Gd⋯Gd is 5.810 Å and the shape of the coordination polyhedron {GdO9} is close to a spherical capped square antiprism according to the analysis done with the program SHAPE.14 Moreover, the hydrogen bonds play an important role in stabilizing the crystal structure.
Magnetic studies and DFT calculations for 1
The magnetic properties of 1 were determined in order to quantify the extent of magnetic interactions among the Gd(III) atoms (Fig. 2). The effective magnetic moment μeff is constant almost in the whole temperature range, there is only a small decrease of μeff when approaching T = 1.9 K, which suggests a very weak antiferromagnetic exchange or dipolar interactions. The reduced isothermal magnetization (Mmol/NAμB) data measured at T = 2, 5 and 10 K are overlapping and saturating at the maximum value of 6.9, thus magnetic anisotropy should be negligible. With the aim to fit magnetic behaviour of 1, a simple spin Hamiltonian model was used| | |
Ĥ = μBBgŜz − zJ〈Ŝz〉Ŝz
| (1) |
where apart from the Zeeman term the molecular-field correction parameter zJ was introduced, which quantifies intermolecular interactions.15 The 〈Ŝz〉 is a thermal average of the molecular spin projection. Then, the molar magnetization can be numerically calculated as| |
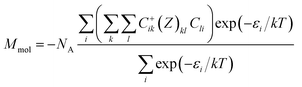 | (2) |
where Z is the matrix element of the Zeeman term and C are the eigenvectors resulting from the diagonalization of the complete spin Hamiltonian matrix. The inclusion of zJ means that iterative procedure must be applied.15 Both temperature and field dependent magnetic data were included in the fitting procedure, which resulted in the following set of magnetic parameters: zJ = −0.39 cm−1, g = 1.98. This means that there are almost negligible antiferromagnetic interactions among the paramagnetic Gd(III) atoms.
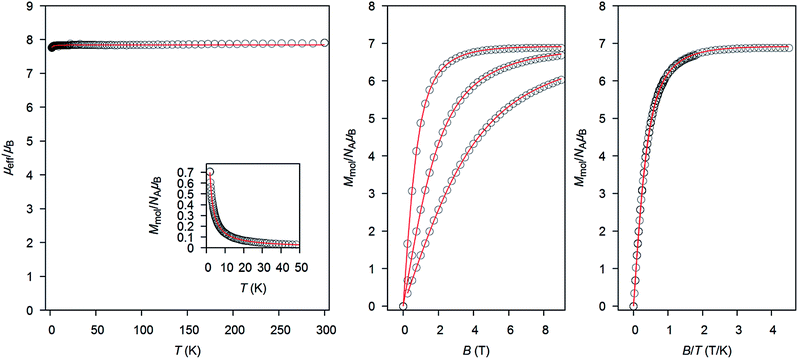 |
| | Fig. 2 The magnetic data for 1. (Left) The temperature dependence of the effective magnetic moment and molar magnetization measured at B = 0.1 T. (Middle) The isothermal magnetization data measured at T = 2, 5 and 10 K. (Right) The reduced magnetization data measured at T = 2, 5 and 10 K. Open circles: experimental data and red solid lines calculated data using the eqn (1), with zJ = −0.39 cm−1, g = 1.98. | |
The magnetic exchange between the Gd(III) atoms was also studied by density functional theory (DFT), where the geometry of the molecular fragment [Gd2(mes)4(H2O)12]6− was extracted from the experimental X-ray structure (Fig. 3). Herein, we utilized the well-known B3LYP functional and the J-values were evaluated from the energy difference Δ, between the high-spin (HS) and broken-symmetry (BS) spin states
by both Ruiz's approach
| | |
JRuiz = 2Δ/[(S1 + S2)(S1 + S2 + 1)]
| (4) |
and by Yamaguchi's approach
| | |
JYam = 2Δ/[〈S2〉HS − 〈S2〉BS]
| (5) |
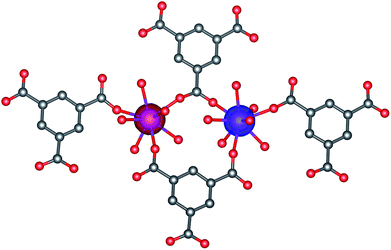 |
| | Fig. 3 The calculated isodensity surfaces of the broken symmetry spin states using B3LYP/def2-TZVPP for the molecular fragment [Gd2(mes)4(H2O)12]6− of 1. The positive and negative spin densities are represented by blue, and red surfaces, respectively, with the cut-off values of 0.01 e bohr−3. Hydrogen atoms are omitted for clarity. | |
Then, we obtained Δ = −0.227 cm−1, which resulted in JRuiz = −0.0081 cm−1 and JYam = −0.0093 cm−1. These minute values also supported the presence of a very weak antiferromagnetic exchange in 1.
Magnetocaloric properties of 1
In order to evaluate the magnetocaloric effect in 1, the magnetization data were measured densely between 1.9 and 10.1 K up to maximum magnetic field of 9 T, see Fig. 4. Subsequently, we used the Maxwell equation16| |
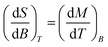 | (6) |
to evaluate ΔSM as| |
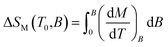 | (7) |
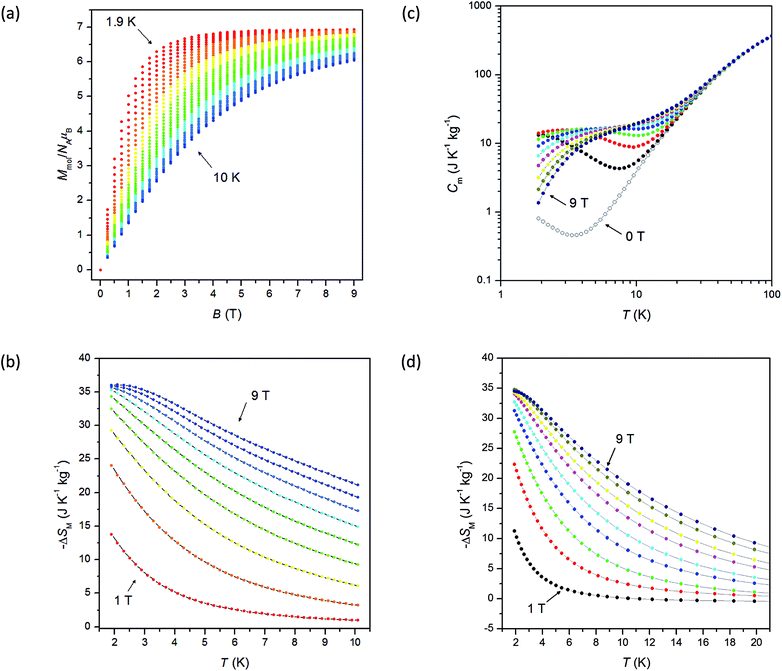 |
| | Fig. 4 (a) The densely-measured magnetization data of 1; (b) the isothermal magnetic entropy change ΔSM of 1 calculated from the magnetization data using the eqn (7); (c) the mass heat capacity of 1 measured at various magnetic fields up to 9 T; (d) the isothermal magnetic entropy change ΔSM of 1 calculated from the heat capacity data using the eqn (9). | |
The results are depicted in Fig. 4 and the maximum value of (−ΔSM) was found to be 36.0 J kg−1 K−1 at T = 1.9 K for highest magnetic field B = 9 T.
Next, the heat capacity of 1 was also measured at different magnetic fields in the temperature interval between 1.9 and 100 K in order to evaluate the magnetocaloric effect of this compound with a different technique, see Fig. 4. The entropy at given magnetic field is usually calculated as
| |
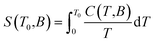 | (8) |
The right utilization of this equation ultimately requires knowledge of the temperature dependence of specific heat (C) down to absolute zero. This dependence is not known due to the limitation of our hardware (Tmin = 1.9 K), and thus the different approach was used, which was theoretically discussed in ref. 10 and applied e.g. in ref. 17 and 18. More specifically, every magnetic system at a given field B0 is characterized by a temperature THT above which total specific heats studied from 0 to B0 coincide. Thus, above THT the magnetic entropy is already saturated and temperature independent. Considering this fact, the eqn (8) can be modified and ΔSM can be calculated as follows
| |
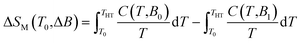 | (9) |
where
C(
T,
B0) and
C(
T,
B1) are experimental heat capacities for given temperature
T and zero magnetic field
B0, and non-zero magnetic field
B1, respectively. It is obvious that maximum −Δ
SM = 34.8 J kg
−1 K
−1 is achieved at
T = 1.9 K for highest magnetic field and this value is similar to that obtained from magnetization data.
To sum up, the value of −ΔSM = 36.0 J K−1 kg−1 at T = 2 K and B = 9 T for 1 is comparable with other gadolinium-based compounds containing either inorganic or organic acids as ligands, see Table 1.
Table 1 The isothermal magnetic entropy changes −ΔSM in Gd(III) compounds containing inorganic and/or organic acids as ligandsa
| Compoundb |
−ΔSM (J kg−1 K−1) |
T (K) |
ΔB (T) |
M/N(Gd) |
ρ (g cm−3) |
wGd (%) |
Ref. |
| Mr/N(Gd) is relative molecular mass divided by the number of Gd atoms; ρ – calculated density obtained from X-ray structural data; wGd – mass fraction. Abbreviations for ligands: Suc = succinate; Bdc = 1,4-benzenedicarboxylic acid; DMC = N,N-dimethylcarbamic acid; CAA = chloroacetic acid; nta = nitrilotriacetic acid; cit = citric acid; IDA = iminodiacetic acid; NA = nicotinic acid; Tacn = N,N′,N′′-trimethyl-1,4,7-triaza-cyclononane; Dhpimp = (E)-2-(2,3-dihydroxypropylimino)methyl)-phenol; H3mes = 1,3,5-benzenetricarboxylic acid; Tea = triethanolamine; TCA = thiophene-3-carboxylic acid; N-BDC = 2-amino-1,4-benzenedicarboxylic acid; Bbam = 3-bis((E)-(2-hydroxy-3-methoxybenzylidene)amino)maleonitrile; Abam = 2-amino-3-((E)-(2-hydroxy-3-methoxy benzylidene)amino)maleonitrile; Tttt = (1E,3Z,8Z,10E)-1,6,11-tris(2-hydroxy-3-methoxyphenyl)-2,5,7,10-tetraazaundeca-1,3,8,10-tetraene-3,4,8,9-tetracarbonitrile; Bipy = bipyridine; Thme = tris(hydroxymethyl)ethane; Tpa = triphenylacetic acid; Fum = fumarate; L = N,N′,N′′-trimethyl-N,N′′-bis(2-hydroxy-3-methoxy-5-methylbenzyl)-diethylenetriamine; Bmd = N,N′-bis(3-methoxysalicylidene)-1,3-diaminobenzene; Pmpm = phenol-2-methoxy-6-[(E)-(phenylimino)methyl]. |
| GdF3 |
74.8 |
3.2 |
9 |
214.24 |
7.062 |
73.39 |
19 |
| [Gd(OH)CO3]n |
66.4 |
1.8 |
7 |
234.27 |
5.349 |
67.12 |
20 |
| GdPO4 |
62.0 |
2.1 |
7 |
252.22 |
5.99 |
62.34 |
21 |
| Gd(OH)3 |
62.0 |
2 |
7 |
208.27 |
3.670 |
75.5 |
22 |
| [Gd(OH)2Cl]n |
61.8 |
3 |
7 |
226.72 |
5.161 |
69.36 |
23 |
| [Gd3(OH)8Cl]n |
59.8 |
3 |
7 |
214.42 |
5.181 |
73.34 |
23 |
| [Gd(HCOO)3]n |
55.9 |
1.8 |
7 |
292.30 |
3.856 |
53.80 |
24 |
| [Gd4(SO4)4(μ3-OH)4(H2O)]n |
51.3 |
2 |
7 |
274.82 |
3.877 |
57.22 |
25 |
| [Gd6(OH)6(suc)5(H2O)2]n·4nH2O |
48.0 |
1.8 |
7 |
317.35 |
2.99 |
53.37 |
26 |
| [Gd(OAc)3(H2O)0.5]n |
47.7 |
1.8 |
7 |
343.39 |
2.228 |
45.79 |
27 |
| [Gd(C4O4)(OH)(H2O)4]n |
47.3 |
3 |
9 |
358.36 |
2.383 |
43.88 |
28 |
| [Gd(HCOO)(bdc)]n |
47.0 |
2.25 |
9 |
366.38 |
2.662 |
42.92 |
11 |
| {[Gd6O(OH)8(ClO4)4(H2O)6](OH)4}n |
46.6 |
2.5 |
7 |
278.25 |
4.627 |
56.51 |
29 |
| [Gd24(DMC)36(CO3)18(H2O)2]·6H2O |
46.1 |
2.5 |
7 |
340.39 |
1.951 |
46.20 |
30 |
| [Gd(HCOO)(OAc)2(H2O)2]n |
45.9 |
1.8 |
7 |
356.39 |
2.397 |
44.12 |
12 |
| [Gd(OAc)3(MeOH)]n |
45.0 |
1.8 |
7 |
363.40 |
2.149 |
42.92 |
27 |
| [Gd48O6(OH)84(CAA)36(NO3)6(H2O)24(EtOH)12(NO3)Cl2]Cl3·6DMF·5EtOH·20H2O |
43.6 |
1.8 |
7 |
313.83 |
2.769 |
50.11 |
31 |
| [Gd2(OH)2(suc)2(H2O)]n·2nH2O |
42.8 |
2.6 |
7 |
317.35 |
2.815 |
49.55 |
26 |
| [Gd(nta)(H2O)2]n |
42.0 |
2 |
7 |
363.38 |
2.690 |
43.27 |
32 |
| [Gd(cit)(H2O)]n |
41.5 |
2 |
7 |
363.36 |
2.985 |
43.28 |
32 |
| [{Gd(OAc)3(H2O)2}2]·4H2O |
40.6 |
1.8 |
7 |
406.44 |
2.038 |
38.69 |
33 |
| {[Gd2(IDA)3]·2H2O}n |
40.6 |
2 |
7 |
371.90 |
2.480 |
42.28 |
34 |
| [Gd36O6(OH)49(NA)36(NO3)6(N3)3(H2O)20]nCl2n·28nH2O |
39.7 |
2.5 |
7 |
344.99 |
2.303 |
45.58 |
35 |
| [Gd38O(OH)42(ClO4)6(CAA)37(H2O)36(EtOH)6] (ClO4)10(OH)17·14DMSO·13H2O |
37.9 |
1.8 |
7 |
376.27 |
2.689 |
41.86 |
31 |
| [Gd(mes)(H2O)6]n (1) |
36.0 |
1.9 |
9 |
472.46 |
2.484 |
33.28 |
This work |
| [Gd12Mo4O16(Hdhpimp)6(OH)4(OAc)12]·12MeOH·8H2O |
35.3 |
3 |
7 |
415.93 |
2.181 |
37.27 |
36 |
| [Gd8(O3PtBu)6(OH)2(H2O)2(HOiBu)(O2CtBu)12](NH3iPr)2 |
32.3 |
3 |
7 |
443.67 |
1.394 |
35.44 |
37 |
| [Gd10(3-TCA)22(μ3-OH)8(H2O)4] |
31.2 |
3 |
7 |
457.77 |
2.205 |
34.35 |
38 |
| [GdNa(C5O5)2(H2O)7]n |
31.0 |
3 |
7 |
586.44 |
2.359 |
27.28 |
39 |
| [Gd2(N-BDC)3(dmf)4]n |
29.0 |
1.8 |
7 |
452.14 |
1.421 |
27.48 |
12 |
| [Gd4(μ3-OH)2(bbam)2(abam)(tttt)(HOCH3)2]·11H2O |
27.2 |
3 |
7 |
632.19 |
1.506 |
24.87 |
40 |
| [Gd7(OH)6(thmeH2)5(thmeH)(tpa)6(MeCN)2](NO3)2 |
23.0 |
3 |
7 |
549.10 |
1.797 |
28.64 |
7 |
| [Gd2(fum)3(H2O)4]n·3nH2O |
20.7 |
1.2 |
5 |
391.39 |
2.515 |
40.17 |
41 |
Magnetocaloric effect in Gd(III) compounds
In general, it is well-known that magnetocaloric properties of the paramagnetic coordination compounds are dependent on the content of the central metal atoms, however, there exists no quantitative relationship which could be used to correlate ΔSM with the content of Gd. Only recently, it was proposed that ΔSM could correlate with the ratio of Mr/N(Gd) for Gd(III) complexes based on organic carboxylates, however, no quantitative relationship was given.32 Therefore, we collected the information about Gd(III) compounds containing inorganic/organic acids for which the magnetocaloric effect was studied (Table 1). Evidently, −ΔSM values are increasing with increasing ratio of Mr/N(Gd) and dependence is not linear. Therefore, we proposed the following quantitative relationship for ΔSM as| | |
−ΔSM = 8914(Mr/N(Gd))−0.913
| (10) |
However, this relationship does not take into account the density of the materials. Thus, we also suggested another correlation, in which the mass concentration of Gd atoms is utilized. The mass concentration cm(Gd) is proportional to the mass fraction of Gd (wGd) and density of crystals (ρ), therefore it holds cm(Gd) = wGdρ. Then, the following correlations was found
| | |
−ΔSM = 39.5cm(Gd)0.364
| (11) |
The correlations outlined in the eqn (10) and (11) are depicted in Fig. 5. We presume that the observed scattering of the experimental data around the proposed correlation functions is due to the small variation of the magnetic exchange and/or magnetic anisotropy of the Gd(III) ions in these compounds. Nevertheless, these correlations can be used to simply estimate magnetocaloric effect for newly prepared Gd(III) compounds.
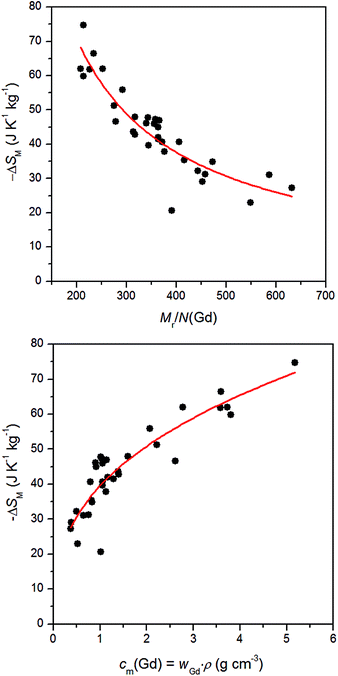 |
| | Fig. 5 The correlation of the isothermal magnetic entropy change ΔSM of the Gd(III) compounds based either on Mr/N(Gd) ratios (top) or on the mass concentration cm(Gd) (bottom). The full points are experimental data listed in Table 1 and full lines are calculated with the eqn (10) and (11), respectively. | |
Conclusions
To conclude, the magnetic and magnetocaloric properties of [Gd(mes)(H2O)6]n (1) were investigated and revealed a very weak antiferromagnetic interactions (zJ = −0.39 cm−1), with −ΔSM equals 36.0 J K−1 kg−1 at T = 2 K and B = 9 T. This value is higher than that of 29.0 J K−1 kg−1 found for [Gd2(N-BDC)3(dmf)4]n (N-BDC = 2-amino-1,4-benzenedicarboxylic acid), the next one only compound containing solely aromatic polycarboxylic acids as bridging ligands. This comparison is in agreement with our suggested correlation based on the mass concentration, because cm(Gd) = 0.83 for 1 is larger than cm(Gd) = 0.39 for [Gd2(N-BDC)3(dmf)4]n. Thus, this work revealed a large magnetocaloric effect for 1 and proposed two general quantitative correlations for the evaluation of the magnetocaloric effect of Gd(III) coordination compounds comprising organic and/or inorganic acids as ligands.
Experimental section
Synthesis
All the reagents and solvents were purchased from commercial sources and used as received. The polymeric compound [Gd(mes)(H2O)6]n (1) was prepared according to the previously reported literature procedure.13 The purity and composition of the compound (1) was analysed by elemental analysis, FTIR and powder X-ray diffraction (PXRD).
Anal. calcd for Gd1C9H15O12 (Mr = 472.5) (%), C, 22.88, H, 3.20, found: C, 22.88, H, 2.88. FTIR (cm−1): ν(O–H) = 3478 (s), 3403 (s), 3336 (s), 3253 (s), ν(C–H)arom = 3092 (m), ν(C–O) and ν(C–C)arom = 1608 (s), 1549 (s), 1432 (s), 1367 (s).
Physical methods. Elemental analysis (C, H) was performed on a Flash 2000 CHNO-S Analyser (Thermo Scientific). Infrared (IR) spectra of the complexes were recorded on a Thermo Nicolet NEXUS 670 FT-IR spectrometer (Thermo Nicolet) employing the ATR technique on a diamond plate in the range of 400–4000 cm−1. Temperature dependence of the magnetization at B = 0.1 T from 1.9 to 300 K and the isothermal magnetizations at T = 2, 5 and 10 K up to B = 9 T were measured using PPMS Dynacool VSM magnetometer (Quantum Design). Further magnetic data were collected in the temperature range from 1.9 to 10.1 K with step equal 0.2 K for magnetic fields from 0 to 9 T with step 0.25 T and subsequently used for the calculation of the magnetic entropy change. The heat capacity was measured on a PPMS Dynacool using a relaxation method in the temperature interval of 1.9–100 K and magnetic field up to 9 T. The X-ray powder diffraction pattern was recorded on an MiniFlex600 (Rigaku) instrument equipped with the Bragg–Brentano geometry, and with nickel-filtered Cu Kα1,2 radiation.
Theoretical methods. The DFT calculations were performed using the ORCA 3.0.3 computational package.42 The relativistic effects were included in all the calculations using the scalar relativistic contracted version of the def2-TZVPP basis functions43 and with the zero-order regular approximation (ZORA).44 The single point energy calculations were based on the molecular geometry derived from experimental X-ray data (Cambridge Structural Database (CSD),45 code RAVJUV) utilizing the B3LYP functional.46–48 The isotropic exchange constant J were calculated by comparing the energies of high-spin (HS) and broken-symmetry (BS) spin states utilizing both Ruiz's approach49 and Yamaguchi's approach.50 The figure showing structural motif was done with Diamond software51 and spin density plot with VESTA 3 software.52
Acknowledgements
We acknowledge the financial support from the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic, and from Palacký University in Olomouc (PrF_2016_007 and PrF_2017_018). We also thank prof. Martin Orendáč from Pavel Jozef Šafárik University in Košice for helpful discussions concerning the magnetocaloric effect.
Notes and references
- Luminescence of lanthanide ions in coordination compounds and nanomaterials, ed. A. de Bettencourt-Dias, Wiley, 2014 Search PubMed.
- R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley, 2015 Search PubMed.
- Z. Zhou and Z.-R. Lu, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5, 1 CrossRef CAS PubMed.
- K. W.-Y. Chan and W.-T. Wong, Coord. Chem. Rev., 2007, 251, 2428 CrossRef CAS.
- I. S. Yu, A. K. Zvezdin, S. P. Gubin, A. S. Mischenko and A. M. Tishin, J. Phys. D: Appl. Phys., 2001, 34, 1162 CrossRef.
- J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91 CrossRef CAS.
- J. W. Sharples, Y.-Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650 RSC.
- F. S. Guo, J. D. Leng, J. L. Liu, Z. S. Meng and M. L. Tong, Inorg. Chem., 2012, 51, 405 CrossRef CAS PubMed.
- J. W. Sharples, D. Collison, E. J. L. McInnes, J. Schnack, E. Palacios and M. Evangelisti, Nat. Commun., 2014, 5, 5321 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen, F.-S. Guo and M.-L. Tong, Coord. Chem. Rev., 2014, 281, 26 CrossRef CAS.
- R. Sibille, T. Mazet, B. Malaman and M. François, Chem.–Eur. J., 2012, 18, 12970 CrossRef CAS PubMed.
- G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592 RSC.
- K. Davies, S. A. Bourne and C. L. Oliver, Cryst. Growth Des., 2012, 12, 1999 CAS.
- M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575 CrossRef CAS PubMed.
- R. Boča, Theoretical Foundations of Molecular Magnetism, Elsevier, 1999 Search PubMed.
- A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, IOP Publishing Ltd, 2003 Search PubMed.
- Y. Meng, Y.-C. Chen, Z.-M. Zhang, Z.-J. Lin and M.-L. Tong, Inorg. Chem., 2014, 53, 9052 CrossRef CAS PubMed.
- J.-Z. Qiu, L.-F. Wang, Y.-C. Chen, Z.-M. Zhang, Q.-W. Li and M.-L. Tong, Chem.–Eur. J., 2016, 22, 802 CrossRef CAS PubMed.
- Y.-C. Chen, J. Prokleska, W.-J. Xu, J.-L. Liu, J. Liu, W.-X. Zhang, J.-H. Jia, V. Sechovsky and M.-L. Tong, J. Mater. Chem. C, 2015, 3, 12206 RSC.
- Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendac, J. Prokleska, V. Sechovsky and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851 CAS.
- E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423 CrossRef.
- Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317 RSC.
- Y. Wang, L. Qin, G.-J. Zhou, X. Ye, J. He and Y.-Z. Zheng, J. Mater. Chem. C, 2016, 4, 6473 RSC.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653 CrossRef CAS PubMed.
- S.-D. Han, X.-H. Miao, S.-J. Liu and X.-H. Bu, Inorg. Chem. Front., 2014, 1, 549 RSC.
- Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem.–Eur. J., 2013, 19, 13504 CrossRef CAS PubMed.
- F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405 CrossRef CAS PubMed.
- S. Biswas, A. Adhikary, S. Goswami and S. Konar, Dalton Trans., 2013, 42, 13331 RSC.
- Y.-L. Hou, G. Xiong, P.-F. Shi, R.-R. Cheng, J.-Z. Cui and B. Zhao, Chem. Commun., 2013, 49, 6066 RSC.
- L.-X. Chang, G. Xiong, L. Wang, P. Cheng and B. Zhao, Chem. Commun., 2013, 49, 1055 RSC.
- F.-S. Guo, Y.-C. Chen, L.-L. Mao, W.-Q. Lin, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem.–Eur. J., 2013, 19, 14876 CrossRef CAS PubMed.
- S.-J. Liu, C. Cao, C.-C. Xie, T.-F. Zheng, X.-L. Tong, J.-S. Liao, J.-L. Chen, H.-R. Wen, Z. Chang and X.-H. Bu, Dalton Trans., 2016, 45, 9209 RSC.
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed.
- J.-M. Jia, S.-J. Liu, Y. Cui, S.-D. Han, T.-L. Hu and X.-H. Bu, Cryst. Growth Des., 2013, 13, 4631 CAS.
- M. Wu, F. Jiang, X. Kong, D. Yuan, L. Long, S. A. Al-Thabaiti and M. Hong, Chem. Sci., 2013, 4, 3104 RSC.
- Y. Zheng, Q.-C. Zhang, L.-S. Long, R.-B. Huang, A. Muller, J. Schnack, L.-S. Zheng and Z. Zheng, Chem. Commun., 2013, 49, 36 RSC.
- K. H. Zangana, E. M. Pineda, J. Schnack and R. E. P. Winpenny, Dalton Trans., 2013, 42, 14045 RSC.
- S.-J. Liu, J.-P. Zhao, J. Tao, J.-M. Jia, S.-D. Han, Y. Li, Y.-C. Chen and X.-H. Bu, Inorg. Chem., 2013, 52, 9163 CrossRef CAS PubMed.
- S. Goswami, A. Adhikary, H. S. Jena and S. Konar, Dalton Trans., 2013, 42, 9813 RSC.
- J. A. Sheikh, A. Adhikary and S. Konar, New J. Chem., 2014, 38, 3006 RSC.
- L. Sedláková, J. Hanko, A. Orendáčová, M. Orendáč, C. L. Zhou, W. H. Zhu, B. W. Wang, Z. M. Wang and S. Gao, J. Alloys Compd., 2009, 487, 425 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908 CrossRef CAS PubMed.
- E. Vanlenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223 CrossRef CAS.
- H. Putz and K. Brandenburg, Diamond – Crystal and Molecular Structure Visualization, version 4.3, Crystal Impact GbR: Bonn, Germany, 2016 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Kamil Kotrle and
Zdeněk Trávníček
,
Kamil Kotrle and
Zdeněk Trávníček *
*