Open Access Article
Open Access ArticleA comparative study of inter- and intramolecular C–H aminations: mechanism and site selectivity†
Juping Wang *a,
Kangcheng Zhengb,
Binbin Lina and
Yuping Wenga
*a,
Kangcheng Zhengb,
Binbin Lina and
Yuping Wenga
aSchool of Pharmacy, Guangdong Pharmaceutical University, Guangzhou, 510006, P. R. China. E-mail: jupingwang@gdpu.edu.cn
bSchool of Chemistry and Chemical Engineering, Sun Yat-sen University, Guangzhou, 510275, P. R. China
First published on 11th July 2017
Abstract
The mechanism and site selectivity of inter-and intramolecular C–H bond aminations have been studied using the M06L method. The similarities and differences between inter- and intramolecular aminations are discussed in detail, with an emphasis on the correlation between reaction pathway and site selectivity. Our calculations show that, for both inter- and intramolecular aminations, the triplet stepwise pathway is of H-atom transfer character, while the singlet concerted pathway is of hydride-transfer character. More importantly, for intermolecular C–H bond amination, the triplet stepwise pathway is favored over the singlet one. Conversely, in the intramolecular case, the singlet concerted pathway is dominant. This inverse preference for the singlet–triplet pathway for inter- and intramolecular aminations is an important contributing factor to their inverse site selectivity. The calculated benzylic-to-tertiary (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) C–H amination ratios for the inter- and intramolecular aminations are 13
T) C–H amination ratios for the inter- and intramolecular aminations are 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, respectively, which are in agreement with experimental results of 7
17, respectively, which are in agreement with experimental results of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
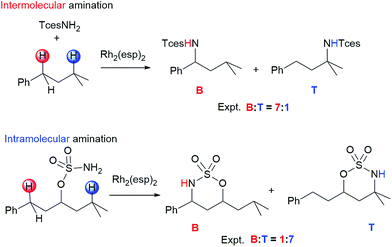
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7. Specifically, intermolecular amination favors oxidation of the secondary benzylic C–H bond over the tertiary C–H bond, whereas the intramolecular case shows a preference for tertiary C–H amination. This inverse site selectivity can be mainly attributed to the fact that inter- and intramolecular aminations proceed according to the different state pathways mentioned previously, where the enthalpic and entropic contribution to free energy differ. In addition, there is a higher energy barrier for the cleavage of the C–H bond in the intermolecular amination than in the intramolecular case, due to a much larger negative entropy of activation for the former. These results provide some valuable information for the design and deconstruction of highly selective and highly efficient C–H amination systems.
7. Specifically, intermolecular amination favors oxidation of the secondary benzylic C–H bond over the tertiary C–H bond, whereas the intramolecular case shows a preference for tertiary C–H amination. This inverse site selectivity can be mainly attributed to the fact that inter- and intramolecular aminations proceed according to the different state pathways mentioned previously, where the enthalpic and entropic contribution to free energy differ. In addition, there is a higher energy barrier for the cleavage of the C–H bond in the intermolecular amination than in the intramolecular case, due to a much larger negative entropy of activation for the former. These results provide some valuable information for the design and deconstruction of highly selective and highly efficient C–H amination systems.
1. Introduction
Selective functionalization of aliphatic C–H bonds to obtain a desired product is an exceptional challenge in organic and organometallic chemistry due to their abundance yet lack of reactivity.1–5 In one of the most important C–H functionalization methods, catalytic C–H amination reactions can lead to novel C–N bond formation,6–10 and this approach is widely applied to the synthesis of natural products, bioactive compounds, and materials.11–14 Atom-, time-, and cost-efficient opportunities have made the field of C–H amination an active area of research.15–20 In general, C–H amination is principally divided into two types:7 intra-21–23 and intermolecular24–26 aminations. Relative to the large number of catalysts available for intramolecular amination, only a few transition-metal complexes can be employed effectively to catalyze the corresponding intermolecular reaction.27–29 One of the top catalysts for performing both intra- and intermolecular C–H amination is RhII,II2(esp)2 (esp = α,α,α′,α′-tetramethyl-1,3-benzenedipropanoate), which was developed and first synthesized by Du Bois and coworkers30,31 and shows good selectivity in the presence of multiple reactive sites. It is interesting to note that competition experiments reported by Du Bois and coworkers show that RhII,II2(esp)2-catalyzed intra- and intermolecular C–H aminations exhibit an opposite site selectivity in some cases.32,33 As seen in Scheme 1, in the benzylic-to-tertiary competitive reaction of intramolecular amination, tertiary alkyl C–H bond insertion is favored over secondary benzylic oxidation. However, contrary to expectations, an analogous intermolecular competition reaction shows a preference for benzylic C–H amination. Such an exactly inverse benzylic-to-tertiary site selectivity attracts a great deal of attention, and various approaches have been made experimentally to tune or switch benzylic-to-tertiary selectivity by changing the metal core (such as Ag, Ru, Fe, etc.) or ligand of catalyst, modifying the substrate, and altering the nitrogen source.32,34 Even so, the controlling factor for this site selectivity remains unresolved, and some newly designed amination systems fail to achieve the anticipation of high selectivity. We infer that the difference in site selectivity may be attributed to disparities in their complicated mechanisms. Therefore, efforts to improve catalyst and protocols for selective C–H amination are tied intimately to a thorough understanding of the mechanistic details of these reactions. Theoretical analyses based on density functional theory (DFT) calculations have become an essential tool to shed light on these mechanisms.4a,13,35–37 To the best of our knowledge, to date, the site selectivity of dimetal-catalyzed C–H amination has been explored experimentally only, with no relative theoretical investigations. Over the past few years, we have performed some theoretical investigations on mechanisms of C–N/C–C bond formation by means of C–H functionalization,38,39 and on the electronic structures and spectra of analogous transition-metal complexes.40 Herein, in order to understand site-selective differences in nature between inter- and intramolecular C–H aminations and to further seek the defining factors of site selectivity, a DFT computational study was performed. Such an insight can also provide valuable information for designing and deconstructing catalytic inter- and intramolecular C–H amination systems of high selectivity and efficiency.2. Computational details
DFT calculations were performed with the Gaussian 09 package,41 using the M06L pure functional mode,42 which has been found to be accurate for the energies and geometries of related C–H functionalization systems including multiple pathways.37,38,43,44 In terms of the mechanism and selectivity of amination reactions, the steric effect is an important influencing factor, and sometimes even a governing factor.3b,37,45 The catalyst RhII,II2(esp)2, involving two bulk esp ligands, would give rise to a considerable steric effect.1,15,30 In order to obtain reliable computation results, we did not perform any simplification of the geometrical structures of any species in the reaction pathways. The geometries of all species were optimized in the gas phase at the basis set level below (denoted as BS1): the Stuttgart RSC 1997 Electron Core Potential (ECP) basis set with effective core potential and one additional f-type polarization function [ζf(Rh) = 1.350] was used for the Rh atom;46 the 6-31G basis set47 was used for the H, C, and O atoms in the RhII,II2(esp)2 unit of species; and a larger basis set 6-31G(d)48 was used for the H, C, N, O, S, and Cl atoms in the nitrogen source and substrate moieties of species due to a more direct relevance to reactivity. For the optimized structures, the frequency calculations were also performed at the M06L/BS1 level in order to verify the energy minima (no imaginary frequencies) and transition states (one imaginary frequency). Intrinsic reaction coordinate (IRC)49 calculations were carried out to determine the interconnection of the transition structures with the related reactants and products. Energies of the reported structures were improved by performing single-point energy calculations at the M06L level of theory with a larger basis set (denoted as BS2). The compositions of BS2 can be described as follows: the basis sets for the Rh atom and for the C, H, and O atoms in the RhII,II2(esp)2 unit were the same as those in BS1 but a higher-level basis set, 6-31G(d,p),50 was used for C, H, O, S, and Cl atoms in the nitrogen source and substrate moieties of species. In order to estimate the effect of the solvent (toluene), a single-point energy calculation was performed at the M06L/BS2 level of theory, using Truhlar and coworkers' solvation model density (SMD) solvation model51 on the gas-phase optimized geometries. All thermodynamic data discussed in the text are calculated at 298 K and 1 bar. Meanwhile, natural bond orbital (NBO) 6.0 analyses were performed at the M06L/BS2 level of theory.523. Results and discussion
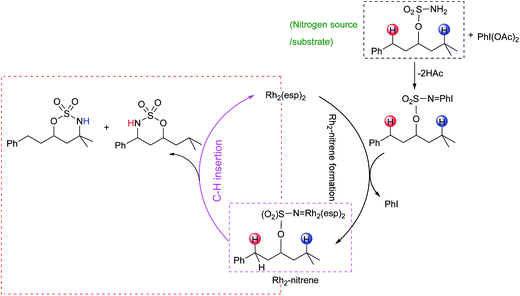
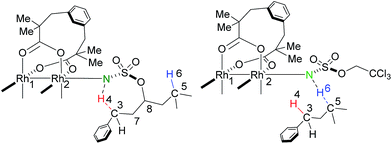
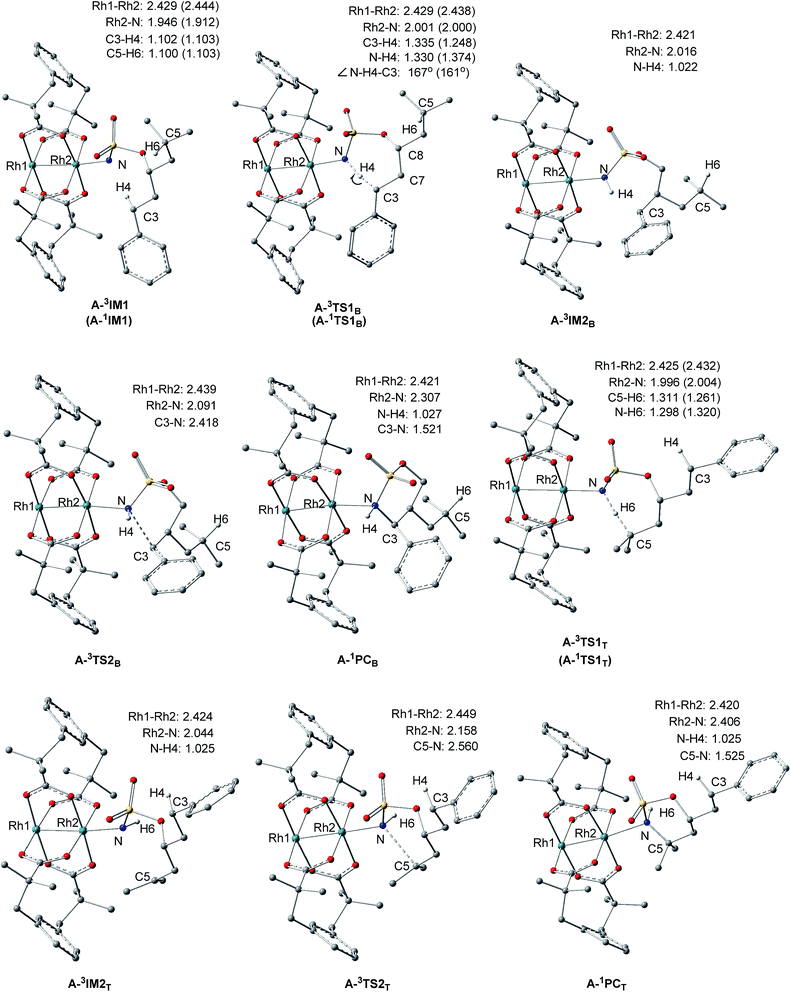
Proposed catalytic cycles for intra- and intermolecular C–H aminations are shown in Fig. 1 and S1.† Clearly, the whole amination process can be divided into two parts: the formation of an RhII,II2-nitrene intermediate and the insertion of an NR-group into the C–H bond. RhII,II2-nitrene is considered a key catalytic intermediate and is directly responsible for the NR-group insertion into the C–H bond. It is worth pointing out that the competition of benzylic-to-tertiary C–H bond amination, as the focus in this context, begins with the same RhII,II2-nitrene. For example, the intramolecular competitive amination starts from the nitrene of RhII,II2(esp)2-NO2SOC13H19 and the intermolecular case begins in the nitrene of RhII,II2(esp)2-NTces. In other words, the site selectivity, whether for inter- or intramolecular C–H amination, depends solely on those reaction steps which follow the formed RhII,II2-nitrene (vide the red box in Fig. 1 and S1†). Thus, our investigations on mechanism and site selectivity start from the RhII,II2-nitrene.In this work, the species involved in the reactions are listed as the RhII,II2(esp)2-nitrene intermediates (X-nIM1), H-transfer transition states (X-nTS1Y), the radical intermediates (X-3IM2Y), C–N bond formation transition states (X-3TS2Y), and products (X-1PCY), where X = A for intramolecular and R for intermolecular C–H aminations; n = 1 for singlet and 3 for triplet multiplicities; and Y = B for benzylic and T for tertiary C–H aminations. For the convenience of discussion, Scheme 2 presents labels of important atoms of species involved in the inter- and intramolecular C–H amination pathways.
3.1. Similarity of intra- and intermolecular aminations
As shown in Fig. 1 and S1,† for the intramolecular amination reaction, the RhII,II2-nitrene A-nIM1 (RhII,II2(esp)2-NO2SOC13H19) is composed of nitrenoid (NO2SOC13H19) and RhII,II2(esp)2. In the subsequent C–H insertion process, the nitrenoid N-atom and reactive C–H bond come from the same nitrene intermediate. For the intermolecular amination reaction, the RhII,II2-nitrene R-nIM1 (RhII,II2(esp)2-NTces) consists of nitrenoid (NTces) and RhII,II2(esp)2. In this case, the nitrenoid N-atom and reactive C–H bond come from the nitrene and substrate, respectively. and
and 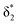 orbitals are close in energy. Similar energies allow the redistribution of one electron from the δ* to the π*, leading to differing population of the δ* and π* level in A-1IM1 and A-3IM1. Thus, the configurations of the singlet A-1IM1 and triplet A-3IM1 are
orbitals are close in energy. Similar energies allow the redistribution of one electron from the δ* to the π*, leading to differing population of the δ* and π* level in A-1IM1 and A-3IM1. Thus, the configurations of the singlet A-1IM1 and triplet A-3IM1 are 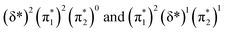 , respectively.
, respectively.
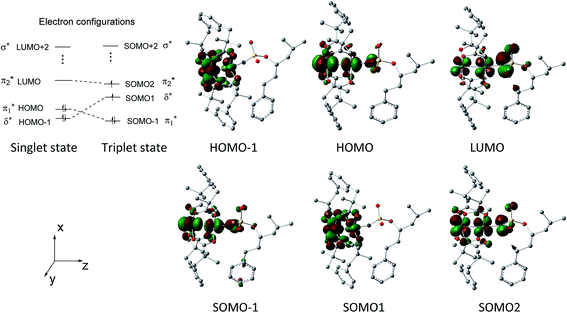
Fig. 2 shows that the HOMO-1, HOMO, LUMO of singlet A-1IM1 mainly consist of δ* (dxy)-Rh(dxy), 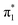 Rh(dyz)-Rh(dyz)-N(sp2′′) and
Rh(dyz)-Rh(dyz)-N(sp2′′) and 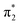 Rh(dxz)-Rh(dxz)-N(px) antibonding orbitals, respectively. It is worth noting that the three-center (Rh–Rh–N) LUMO orbital has a significant N p contribution, which indicates that the LUMO of A-1IM1 can not only readily accept two electrons from the heterolytic cleavage of the σC–H bond through the N px orbital moiety but can also delocalize these electrons to the Rh2 core via the Rh(dxz)–Rh(dxz) moiety to increase the stability of the singlet transition state for hydride transfer. Thus, singlet A-1IM1 has a strongly electrophilic reactivity.
Rh(dxz)-Rh(dxz)-N(px) antibonding orbitals, respectively. It is worth noting that the three-center (Rh–Rh–N) LUMO orbital has a significant N p contribution, which indicates that the LUMO of A-1IM1 can not only readily accept two electrons from the heterolytic cleavage of the σC–H bond through the N px orbital moiety but can also delocalize these electrons to the Rh2 core via the Rh(dxz)–Rh(dxz) moiety to increase the stability of the singlet transition state for hydride transfer. Thus, singlet A-1IM1 has a strongly electrophilic reactivity.
For triplet A-3IM1, its singly occupied molecular orbital (SOMO)-1, SOMO1, SOMO2 orbitals are composed of  Rh(dyz)-Rh(dyz)-N(spy), δ* (dxy)-Rh(dxy), and
Rh(dyz)-Rh(dyz)-N(spy), δ* (dxy)-Rh(dxy), and  Rh(dxz)-Rh(dxz)-N(px) antibonding orbitals, respectively. The three-center (Rh–Rh–N) SOMO2 orbital, in particular, has an obvious N p-character; moreover, its calculated unpaired spin densities are mainly located on the N-atom (0.984 e) and Rh2 core (0.838 e) (see Fig. 5). This obvious N p-orbital character and almost a single electron on the N-atom indicates that the SOMO2 is readily accessible to accept one electron from the hemolytic cleavage of the σC–H bond. On the other hand, the Rh2 core moiety of SOMO2 may bear considerable spins to avoid unpaired spins overly concentrating on the N-atom, facilitating crossing the triplet transition-state barrier for hydrogen-atom transfer. Therefore, triplet A-3IM1 has a high radical reactivity.
Rh(dxz)-Rh(dxz)-N(px) antibonding orbitals, respectively. The three-center (Rh–Rh–N) SOMO2 orbital, in particular, has an obvious N p-character; moreover, its calculated unpaired spin densities are mainly located on the N-atom (0.984 e) and Rh2 core (0.838 e) (see Fig. 5). This obvious N p-orbital character and almost a single electron on the N-atom indicates that the SOMO2 is readily accessible to accept one electron from the hemolytic cleavage of the σC–H bond. On the other hand, the Rh2 core moiety of SOMO2 may bear considerable spins to avoid unpaired spins overly concentrating on the N-atom, facilitating crossing the triplet transition-state barrier for hydrogen-atom transfer. Therefore, triplet A-3IM1 has a high radical reactivity.
As shown in Fig. S2(b),† the orbital characters for intermolecular R-1IM1 and R-3IM1 are similar to intramolecular A-1IM1 and A-3IM1, respectively, which indicates that, likewise, R-1IM1 also has strongly electrophilic reactivity and R-3IM1 has high radical reactivity.
Based on the above analysis, it can be concluded that both the singlet and triplet nitrenes can directly trigger NR insertion into the inert C–H bond. It should be noted that since the reactivity of nitrenes for intra- and intermolecular aminations is analogous, nitrene is not a defining factor contributing to inverse benzylic-to-tertiary site selectivity for intra- and intermolecular amination.
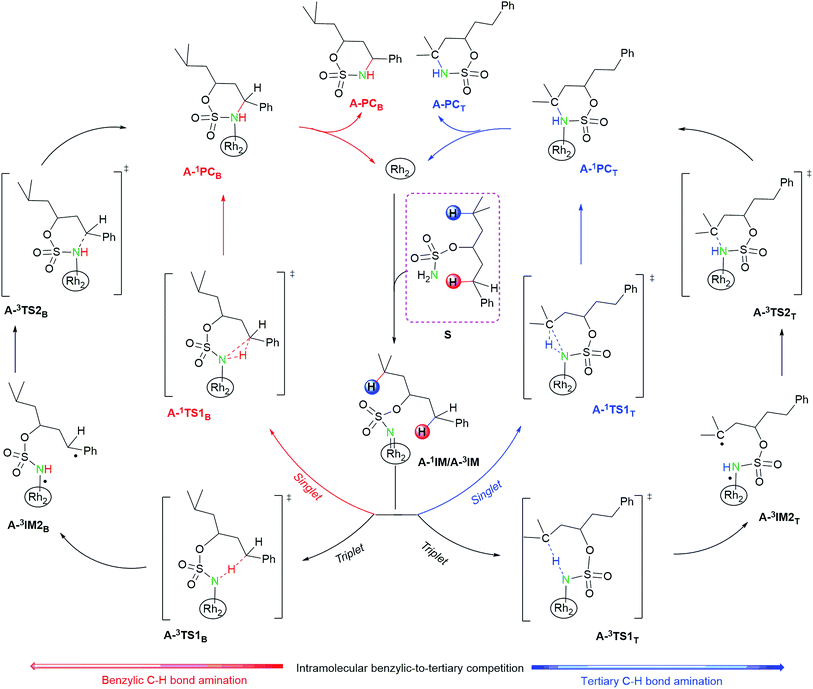 | ||
| Fig. 3 Mechanisms of benzylic-to-tertiary C–H competition for intramolecular aminations. Herein, Rh2 = Rh2(esp)2. | ||
As depicted in Fig. 3 and S3,† for both intra- and intermolecular reactions, benzylic C–H amination mechanisms are analogous to tertiary ones. Herein, the benzylic C–H amination is given as an example to elaborate the characters of singlet and triplet pathways.
3.1.2.1. Character of singlet pathway. As mentioned above, LUMOs of singlet A-1IM1/R-1IM1 accept two electrons from the heterolytic cleavage of σC3–H4 to promote the singlet pathway. In the singlet pathway, A-1IM1/R-1IM1 proceeds to the product A-1PCB/R-1PCB via the transition state A-1TS1B/R-1TS1B. The distances of C3⋯H4, N⋯H4, and C⋯N in A-1TS1B/R-1TS1B are 1.248/1.217 Å, 1.374/1.452 Å, and 2.586/2.661 Å, respectively, suggestive of a breaking C3⋯H4 bond and forming N⋯H4 and C⋯N bonds (see Fig. 3 and S3; and Fig. 4 and S4†). Moreover, in the subsequent ring-product A-1PCB/chain-product R-1PCB, the bond lengths of N–H4 and C3–N are 1.027/1.027 Å and 1.521/1.517 Å, respectively, indicating that both N–H4 and C3–N bonds are completely formed. All the above bond distances show that the formations of the N–H4 and C3–N bonds, as well as the cleavage of the C–H bond, proceed in a concerted manner. On the other hand, in the singlet pathway, there is a clear charge flow among reactive center N⋯H⋯C atoms: from A-1IM1/R-1IM1+S to A-1TS1B/R-1TS1B, the total NBO negative charges for the PhC moiety (i.e. Ph + C3) decrease greatly from −0.486/−0.494 to −0.268/−0.234 and negative charges for N-atom increase correspondingly from −0.690/−0.686 to −0.838/−0.870 (see Table 1). These change characteristics of NBO charges show that the H4 transferring process is accompanied by the partly negative charge of C3 flowing to the N-atom. Therefore, the singlet mechanisms of both intra- and intermolecular aminations are described as a concerted hydride-transfer pathway.
| Intramolecular amination | Intermolecular amination | ||||
|---|---|---|---|---|---|
| C3 + Ph | N | C3 + Ph | N | ||
| A-1IM1 | −0.486 | −0.690 | R-1IM1+S | −0.494 | −0.686 |
| A-1TS1B | −0.268 | −0.838 | R-1TS1B | −0.234 | −0.870 |
| A-1PCB | −0.065 | −0.929 | R-1PCB | −0.062 | −0.924 |
3.1.2.2. Character of triplet pathway. Unlike the singlet pathway, the triplet pathway begins in the triplet A-3IM1/R-3IM. The SOMO2 orbital of A-3IM1/R-3IM accepts one electron from the hemolytic cleavage of the σC3–H4 bond to trigger triplet radical mechanism. Triplet pathway consists of two steps: H-abstract and radical rebound processes.
In the process of H-abstract, the H4 atom of the C3–H4 bond in A-3IM1/R-3IM1 transfers to the metal-bound N-atom passing through the transition state A-3TS1B/R-3TS1B. As seen in Fig. 4 and S4,† the calculated A-3TS1B/R-3TS1B structure indicates an incipient N⋯H4 bond (1.330/1.368 Å) and an elongated C3⋯H4 bond (from 1.102/1.099 Å in A-3IM1+S/R-3IM1 to 1.305/1.284 Å in A-3TS1B/R-3TS1B, respectively). Then, the C3–H4 bond breaks completely and an N–H4 bond forms completely to generate intermediate A-3IM2B/R-3IM2B. The surface plots and values of the spin density distribution of the triplet species for intra- and intermolecular benzylic C–H aminations are shown in Fig. 5 and S5,† respectively. The calculated spins show that A-3IM2B/R-3IM2B is a triplet radical species in which one unpaired electron is located on the Rh2 core (0.676 e/0.734 e) and the other is located on C3 (0.800 e/0.768 e). In other words, the radical A-3IM2B/R-3IM2B formation is a result of the H-atom of C3 transferring to the N-atom through the hemolytic cleavage of the σC3–H4 bond.
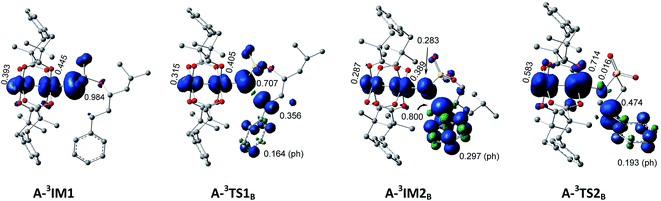 | ||
| Fig. 5 Surface plots and values of spin density distribution of the triplet species for intramolecular benzylic C–H amination. | ||
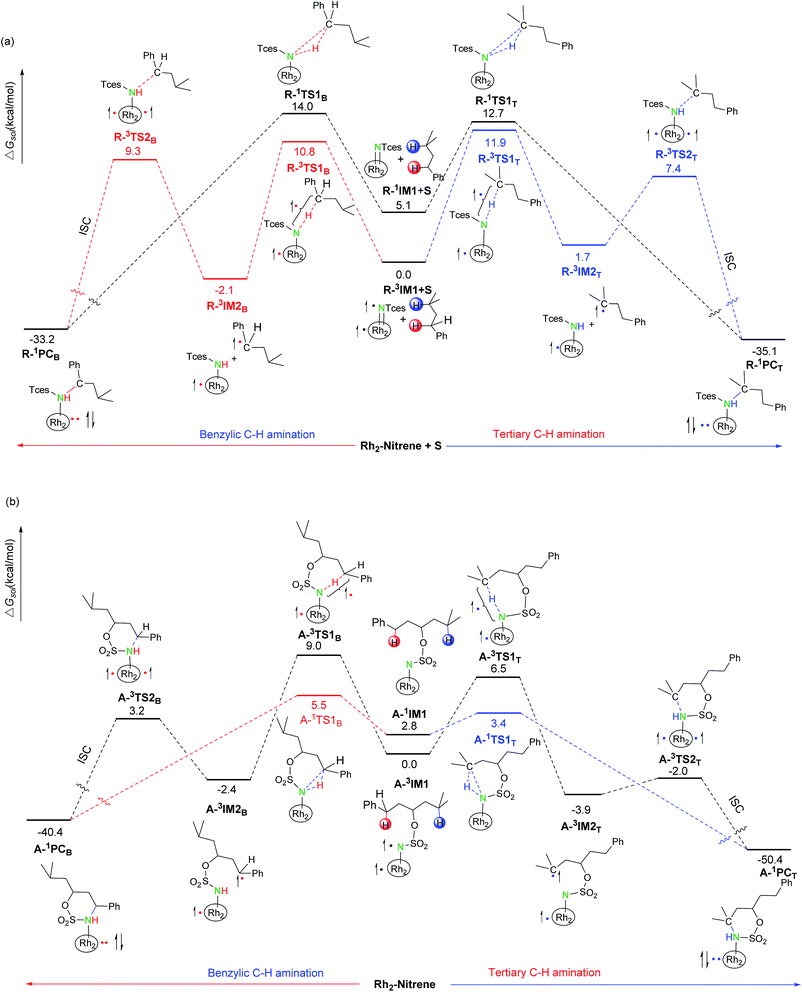
In the subsequent C–N bond formation step, via the σ* orbital, the spin-transfer and inter-system crossing trigger the C3–N bond formation via the transition state A-3TS2B/R-3TS2B with an energy barrier of 5.6/11.4 kcal mol−1 (−2.4 → 3.2/−2.1 → 9.3 kcal mol−1) (see Scheme 3). The whole processes for inter- and intramolecular benzylic C–H aminations are largely exergonic (−40.4 and −33.2 kcal mol−1, respectively).
Based on the above discussions on the H-abstract and radical rebound processes, it can be concluded that the triplet mechanisms of both intra- and intermolecular aminations are characterized as a stepwise H-atom transfer pathway.
It should be noted that since the singlet and triplet pathways of intramolecular aminations are analogous to those of the respective intermolecular aminations, it may be difficult to cause inverse site selectivity if the intra- and intermolecular aminations simultaneously proceed as the singlet or triplet pathway. Their inverse site selectivity probably originated in different spin-state pathways (vide Section 3.2.).
3.2. Difference of inter- and intramolecular C–H aminations
Most interestingly, RhII,II2(esp)2, a robust tethered dicarboxylate-derived complex, shows good catalytic activity for both inter- and intramolecular C–H aminations, but with an inverse site selectivity. In this section, we will compare their mechanistic disparities in detail to gain a deeper understanding of this inverse selectivity. The enthalpy, entropy, and free energy of activation of all pathways for inter- and intramolecular aminations are listed in Table 2.| Intermolecular aminations | Intramolecular aminations | ||||||
|---|---|---|---|---|---|---|---|
| ΔH≠R,sol | ΔS≠R | ΔG≠R,sol | ΔH≠A,sol | ΔS≠A | ΔG≠A,sol | ||
| R-3IM1+S | 0.0 | 0.0 | 0.0 | A-3IM1 | 0.0 | 0.0 | 0.0 |
| R-1TS1B | −4.2 | −61.3 | 14.0 | A-1TS1B | 3.3 | −7.3 | 5.5 |
| R-3TS1B | −4.4 | −50.9 | 10.8 | A-3TS1B | 6.6 | −8.1 | 9.0 |
| R-1TS1T | −3.1 | −53.1 | 12.7 | A-1TS1T | 1.5 | −6.1 | 3.4 |
| R-3TS1T | −3.8 | −52.7 | 11.9 | A-3TS1T | 5.9 | −1.9 | 6.5 |
| ΔG≠ = ΔH≠ − TΔS≠ | (1) |
In terms of enthalpy aspects, all intermolecular ΔH≠R,sol values are negative (−4.2, −4.4, −3.1, and −3.8 kcal mol−1) whereas all intramolecular ΔH≠A,sol values are positive (3.3, 6.6, 1.5, and 5.9 kcal mol−1). Intermolecular ΔH≠R,sol is beneficial to obtain a lower free energy of activation according to eqn (1), compared with ΔH≠A,sol. However, a larger difference comes from the entropy of activation; intermolecular ΔS≠R values are −61.3, −50.9, −53.1, and −52.7 cal mol−1 K (ΔS≠R ≪ 0) and intramolecular ΔS≠A values are −7.3, −8.1, −6.1, and −1.9 cal mol−1 K−1 (ΔS≠A is slightly less than zero). Obviously, all intermolecular ΔS≠R values are much more negative, compared with intramolecular ΔS≠R values. Indeed, the more negative intermolecular ΔS≠R not only compensates for the influence of the enthalpy of activation previously described, but also further leads to a higher ΔG≠R,sol vs. ΔG≠A,sol. The reason for a much more negative ΔS≠R vs. ΔS≠A is that two reactant species come together to form one species as intermolecular R-nIM1+S proceeds to R-nTS1Y (see Fig. S3†). Entropy is a measure of the molecular disorder of a system, and the decrease in the number of molecules indicates that the disorder of the system is significantly reduced, thus the entropy is decreased remarkably. In contrast, an acyclic single molecule converts into a cyclic single molecule without any change in the number of molecules as intramolecular A-nIM1 proceeds to A-nTS1Y (see Fig. 3). This is also an entropy-decrease process, but the degree of entropy-decrease is much less compared with the intermolecular case. It is worth noting that the negative entropic contribution to R-nTS1Y is so significant that it has become the major thermodynamic factor controlling the free energy of activation. Hence, the intermolecular hydrogen-transferring process is predominantly entropy-driven, whereas the intramolecular process is both enthalpy- and entropy-driven combined. This difference will heavily impact the selectivities of the reaction pathway and the reaction site of inter- and intramolecular aminations (vide Sections 3.2.2. and 3.2.3.).
| Intermolecular aminations | Intramolecular aminations | ||||||
|---|---|---|---|---|---|---|---|
| R-1TS1Ya | R-3TS1Ya | Pref.b | A-1TS1Ya | A-3TS1Ya | Pref.b | ||
| a Subscript Y stands for B or T.b Pref. represents a preferable pathway for the corresponding amination reaction. | |||||||
| B | 14.0 | 10.8 | Triplet | B | 5.5 | 9.0 | Singlet |
| T | 12.7 | 11.9 | Triplet | T | 3.4 | 6.5 | Singlet |
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T T |
— | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1Calcd 1Calcd |
— | B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T T |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17Calcd 17Calcd |
— | — |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1Expt. 1Expt. |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7Expt. 7Expt. |
||||||
As shown in Table 3 and Scheme 3, for intermolecular aminations, the calculated energy barrier of singlet R-1TS1B/R-1TS1T is higher than that of the corresponding triplet R-3TS1B/R-3TS1T (R-1TS1B vs. R-3TS1B = 14.0 vs. 10.8 kcal mol−1; and R-1TS1T vs. R-3TS1T = 12.7 vs. 11.9 kcal mol−1). Conversely, in the intermolecular case, the energy barrier of singlet A-1TS1B/A-1TS1T is significantly lower than that of the corresponding triplet A-3TS1B/A-3TS1T (A-1TS1B vs. A-3TS1B = 5.5 vs. 9.0 kcal mol−1; and A-1TS1T vs. A-3TS1T = 3.4 vs. 6.5 kcal mol−1). In other words, the triplet stepwise pathway is dominant for intermolecular benzylic and tertiary C–H aminations. In contrast, the singlet concerted pathway is favored over the triplet stepwise pathway for intramolecular benzylic and tertiary C–H aminations. The differences of preference in the singlet–triplet pathway between the inter- and intramolecular hydrogen-transferring processes can be explained by the drive mechanism mentioned previously. Herein, benzylic sites are given as an example to illustrate the reason for the preference of the singlet–triplet pathway.
In the intermolecular case, free energies of activation for singlet and triplet pathways are both entropy-driven, which is mainly related to the disorder of the system. However, the N, H, and C atoms of the reactive center have a trigonal arrangement (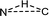 ) in singlet R-1TS1B and are almost linear (N⋯H⋯C) in triplet R-3TS1B (see Scheme. 3(a)). Clearly, the former has less disorder, and a larger negative entropy of activation (−61.3 vs. −50.9 cal mol−1 K−1), which leads to a larger free energy of activation (14.0 vs. 10.8 kcal mol−1). Therefore, the triplet stepwise pathway is preferable to the singlet concerted pathway in the intermolecular amination reaction.
) in singlet R-1TS1B and are almost linear (N⋯H⋯C) in triplet R-3TS1B (see Scheme. 3(a)). Clearly, the former has less disorder, and a larger negative entropy of activation (−61.3 vs. −50.9 cal mol−1 K−1), which leads to a larger free energy of activation (14.0 vs. 10.8 kcal mol−1). Therefore, the triplet stepwise pathway is preferable to the singlet concerted pathway in the intermolecular amination reaction.
In the intramolecular case, the difference of activation free energy of the singlet and triplet pathways predominantly arises from their activation enthalpies, which are closely related to bond cleavage and formation. In singlet A-1TS1B, the cleavage of a C–H bond is accompanied by the formation of two new bonds (N–H and C–N), while in triplet A-3TS1B, the cleavage of a C–H bond is only accompanied by the formation of one new bond (N–H). Bond formation and cleavage are exothermic and endothermic, respectively. Therefore, singlet ΔH≠A,sol (A-1TS1B) is smaller than triplet ΔH≠A,sol (A-3TS1B) (3.3 vs. 6.6 kcal mol−1), which results in a lower ΔG≠A,sol (A-1TS1B) compared with ΔG≠A,sol (A-3TS1B) (5.5 vs. 9.0 kcal mol−1). In other words, the singlet pathway is more favorable than the triplet pathway for the intramolecular hydrogen-transferring processes, which is precisely contrary to the intermolecular case.
It is worth noting that the inverse preferences of the singlet–triplet pathway for inter- and intramolecular C–H amination are an important contributing factor to their inverse site selectivity (vide Section 3.2.3.).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) only depends on the activation free energies of intermolecular triplet R-3TS1Y and intramolecular singlet A-1TS1Y, since the benzylic site contains two equally reactive C–H bonds whereas the tertiary site contains only a single 3° C–H bond. Thus, the ratio of B
T) only depends on the activation free energies of intermolecular triplet R-3TS1Y and intramolecular singlet A-1TS1Y, since the benzylic site contains two equally reactive C–H bonds whereas the tertiary site contains only a single 3° C–H bond. Thus, the ratio of B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T can be calculated using eqn (2), where B and T represent the benzylic and tertiary products, respectively; and ΔG≠B and ΔG≠T represent the activation free energies of the benzylic and tertiary hydrogen-migrating step, respectively.
T can be calculated using eqn (2), where B and T represent the benzylic and tertiary products, respectively; and ΔG≠B and ΔG≠T represent the activation free energies of the benzylic and tertiary hydrogen-migrating step, respectively.
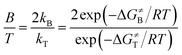 | (2) |
It can be seen from Table 3 that the energy barrier of R-3TS1B for the benzylic hydrogen-transfer is favored by 1.1 kcal mol−1 over R-3TS1T for the tertiary (11.9–10.8 = 1.1 kcal mol−1), while the energy barrier of A-1TS1B for benzylic C–H amination is 2.1 kcal mol−1 higher than that of A-1TS1T for tertiary C–H amination (5.5–3.4 = 2.1 kcal mol−1). Based on eqn (2), the calculated ratios of benzylic-to-tertiary (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) for inter- and intramolecular C–H aminations are 13
T) for inter- and intramolecular C–H aminations are 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, respectively, which is in accordance with the experimental results (7
17, respectively, which is in accordance with the experimental results (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, respectively). In other words, intermolecular amination favors oxidation of benzylic C–H bonds over tertiary sites, while the intramolecular case exhibits a preference for tertiary C–H amination.
7, respectively). In other words, intermolecular amination favors oxidation of benzylic C–H bonds over tertiary sites, while the intramolecular case exhibits a preference for tertiary C–H amination.
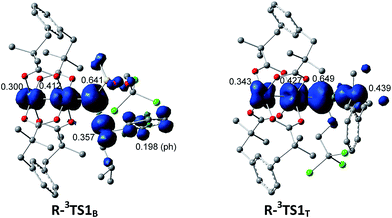
The selective amination of the secondary benzylic C–H bond over the tertiary alkyl C–H bond in the intermolecular case is closely related to their triplet stepwise pathways, in which the transition states R-3TS1B and R-3TST are clearly of radical character. For R-3TS1B, two unpaired electrons are populated on the Ph group (0.198 e), and the C3 (0.357 e), N (0.641 e), and Rh2 (0.712 e) atoms (see Fig. 6). For R-3TS1T, the unpaired spins mainly reside on the C5 (0.439 e), N (0.649 e), and Rh2 (0.770 e) atoms. Quite remarkably, the unpaired electron has been greatly delocalized to the Ph group adjacent to the C3 atom by a p–π conjugation in R-3TS1B, which is absent in R-3TS1T. It is important to note that this wider delocalization of spins can increase the stability and reduce the enthalpy of R-3TS1B. Therefore, the activation enthalpy ΔH≠R,sol (R-3TS1B) is lower than ΔH≠R,sol (R-3TS1T) (−4.4 vs. −3.8 kcal mol−1). On the other hand, the bulky Ph group and esp unit are far away from each other in R-3TS1B but close to each other in R-3TS1T (see Fig. 7), resulting in less steric hindrance, and a smaller negative entropy of activation for R-3TS1B vs. R-3TS1T (−50.9 vs. −52.7 kcal mol−1). A lower enthalpy of activation and a smaller negative entropy of activation for R-3TS1B lead to the fact that the activation free energy of R-3TS1B is lower than that of R-1TS1B, thus a preference for the benzylic site in the intermolecular amination.
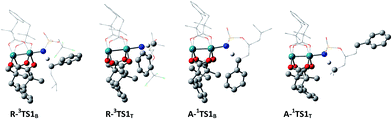 | ||
| Fig. 7 Steric hindrance between phenyl (Ph) group and esp ligand. The other H atoms except reactive H are omitted for clarity. | ||
In contrast, the site selectivity toward tertiary C–H bond amination in the intramolecular case can be explained as follows. Intramolecular C–H amination is corroborated as a singlet concerted pathway in which the transition states A-1TS1T and A-1TS1B clearly show signs of the breaking of a C–H bond along with the forming of an N–H bond and a C–N bond. The N⋯H distance of 1.320 Å and C⋯N distance of 2.572 Å in A-1TS1T is shorter than that of 1.374 and 2.586 Å in A-1TS1B, respectively, which suggests that the formations of both N⋯H and C⋯N bonds are more complete in A-1TS1T than in A-1TS1B. Because bond formation is exothermic, the activation enthalpy for A-1TS1T is less than that for A-1TS1B (1.5 vs. 3.3 kcal mol−1). Furthermore, the bulky Ph group and esp unit are far away from each other in A-1TS1T but close to each other in A-1TS1B (see Fig. 7), resulting in less steric hindrance, and a smaller negative entropy of activation for A-1TS1T vs. A-1TS1B (−6.1 vs. −7.3 kcal mol−1). A lower enthalpy of activation and a smaller negative entropy of activation of R-3TS1B leads to the fact that the activation free energy ΔG≠A,sol (A-1TS1T) is lower than ΔG≠A,sol (A-1TS1B) (3.4 vs. 5.5), thus tertiary site C–H amination is more favorable than the benzylic site in the intramolecular case.
4. Conclusion
This paper presents a theoretical investigation of the mechanism and site selectivity of inter- and intramolecular aminations. The similarities and differences of inter- and intramolecular aminations are discussed in detail. Most importantly, we report that inter- and intramolecular C–H bond aminations proceed as different spin-state pathways, and this difference is an important factor contributing to their inverse benzylic-to-tertiary site selectivity. According to the computational results, the following main conclusions can be drawn:(1) The reactivity of inter- and intramolecular RhII,II2-nitrene intermediates are analogous. Singlet A-1IM1/R-1IM1 has strongly electrophilic reactivity and triplet A-3IM1/R-3IM1 has highly radical reactivity.
(2) For both inter- and intramolecular aminations, the singlet mechanism is described as a concerted hydride-transfer pathway, while the triplet mechanism is of stepwise H-atom transfer character.
(3) All of the free energies of activation in the intermolecular hydrogen-transferring process (ΔG≠R,sol) are clearly higher than those in the intramolecular process (ΔG≠A,sol). The intermolecular hydrogen-transferring process is mainly entropy-driven, whereas the intramolecular case is both enthalpy- and entropy-driven combined.
(4) For the intermolecular C–H amination, the triplet stepwise pathway is favored over the singlet process. Conversely, for the intramolecular C–H amination, the singlet concerted pathway is dominant. The inverse preferences of the singlet–triplet pathway for inter- and intramolecular C–H amination are an important factor contributing to their inverse site selectivity.
(5) Inter- and intramolecular C–H aminations display an inverse site selectivity with calculated B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T ratios of 13
T ratios of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, respectively, which is in agreement with experimental results (7
17, respectively, which is in agreement with experimental results (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, respectively). The intermolecular insertion reaction shows a preference for the benzylic site as a result of a preferential triplet pathway, in which a lower enthalpy of activation and a smaller negative entropy of activation of R-3TS1B mean that the activation free energy of R-3TS1B is lower than that of R-3TS1T. That intramolecular tertiary C–H bond insertion is more favorable than the benzylic case can be attributed to a preferential singlet concerted pathway, in which a lower enthalpy of activation and a smaller negative entropy of activation of A-1TS1T mean that the activation free energy of A-1TS1T is lower than that of A-1TS1B.
7, respectively). The intermolecular insertion reaction shows a preference for the benzylic site as a result of a preferential triplet pathway, in which a lower enthalpy of activation and a smaller negative entropy of activation of R-3TS1B mean that the activation free energy of R-3TS1B is lower than that of R-3TS1T. That intramolecular tertiary C–H bond insertion is more favorable than the benzylic case can be attributed to a preferential singlet concerted pathway, in which a lower enthalpy of activation and a smaller negative entropy of activation of A-1TS1T mean that the activation free energy of A-1TS1T is lower than that of A-1TS1B.
This computational study has provided valuable information about inter- and intramolecular aminations, with an emphasis on addressing the correlation between reaction pathways and site selectivity. These conclusions can be applied to deconstruct the elegant and highly selective catalytic amination systems, especially the more challenging intermolecular C–H amination systems.
Acknowledgements
This work was financially supported by the Medical Scientific Research Foundation of Guangdong Province, China (no. A2015556), Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase), Natural Science Foundation of Guangdong Province, China (No. 2015A030310176), Natural Science Foundation for Young Scholars of College of Pharmacy of Guangdong Pharmaceutical University (2014), and Science and Technology Planning Project of Guangdong Province, China (no. 2013J4100071).Notes and references
- (a) J. L. Roizen, M. E. Harvey and J. Du Bois, Acc. Chem. Res., 2012, 45, 911–922 CrossRef CAS PubMed; (b) H. M. L. Davies, J. Du Bois and J.-Q. Yu, Chem. Soc. Rev., 2011, 40, 1926–1936 RSC; (c) J. Du Bois, Org. Process Res. Dev., 2011, 15, 758–762 CrossRef CAS PubMed.
- (a) S. R. Chemler, Science, 2013, 341, 624–626 CrossRef CAS PubMed; (b) M. C. White, Science, 2012, 335, 807–809 CrossRef CAS PubMed.
- (a) H. M. L. Davies and D. Morton, J. Org. Chem., 2016, 81, 343–350 CrossRef CAS PubMed; (b) H. M. L. Davies and J. R. Manning, Nature, 2008, 451, 417–424 CrossRef CAS PubMed.
- (a) M. Goswami, V. Lyaskovskyy, S. R. Domingos, W. J. Buma, S. Woutersen, O. Troeppner, I. Ivanović-Burmazović, H. Lu, X. Cui, X. P. Zhang, E. J. Reijerse, S. DeBeer, M. M. van Schooneveld, F. F. Pfaff, K. Ray and B. de Bruin, J. Am. Chem. Soc., 2015, 137, 5468–5479 CrossRef CAS PubMed; (b) H. Lu, C. Li, H. Jiang, C. L. Lizardi and X. P. Zhang, Angew. Chem., 2014, 126, 7148–7152 CrossRef.
- J. Yamaguchi, A. D. Yamaguchi and K. Itami, Angew. Chem., Int. Ed., 2012, 51, 8960–9009 CrossRef CAS PubMed.
- E. T. Hennessy and T. A. Betley, Science, 2013, 340, 591–595 CrossRef CAS PubMed.
- Y. Park, Y. Kim and S. Chang, Chem. Rev., 2017 DOI:10.1021/acs.chemrev.6b00644.
- (a) H. Kim and S. Chang, ACS Catal., 2016, 6, 2341–2351 CrossRef CAS; (b) R. Singh, K. Nagesh and M. Parameshwar, ACS Catal., 2016, 6, 6520–6524 CrossRef CAS; (c) G. Manca, E. Gallo, D. Intrieri and C. Mealli, ACS Catal., 2014, 4, 823–832 CrossRef CAS.
- D. A. Iovan and T. A. Betley, J. Am. Chem. Soc., 2016, 138, 1983–1993 CrossRef CAS PubMed.
- F. Collet, R. H. Dodd and P. Dauban, Chem. Commun., 2009, 34, 5061–5074 RSC.
- O. Robles and D. Romo, Nat. Prod. Rep., 2014, 31, 318–334 RSC.
- J. Li, J. S. Cisar, C.-Y. Zhou, B. Vera, H. Williams, A. D. Rodriguez, B. F. Cravatt and D. Romo, Nat. Chem., 2013, 5, 510–517 CrossRef CAS PubMed.
- (a) D. Intrieri, P. Zardi, A. Caselli and E. Gallo, Chem. Commun., 2014, 50, 11440–11453 RSC; (b) P. Zardi, A. Caselli, P. Macchi, F. Ferretti and E. Gallo, Organometallics, 2014, 33, 2210–2218 CrossRef CAS.
- K. Okano, H. Tokuyama and T. Fukuyama, Chem. Commun., 2014, 50, 13650–13663 RSC.
- K. P. Kornecki and J. F. Berry, Eur. J. Inorg. Chem., 2012,(3), 562–568 CrossRef CAS.
- I. S. Akhrem, J. Org. Chem., 2015, 793, 54–77 CrossRef CAS.
- J. A. McIntosh, P. S. Coelho, C. C. Farwell, Z. J. Wang, J. C. Lewis, T. R. Brown and F. H. Arnold, Angew. Chem., Int. Ed., 2013, 52, 9309–9312 CrossRef CAS PubMed.
- D. G. Musaev and S. B. Blakey, Organometallics, 2012, 31, 4950–4961 CrossRef CAS.
- R. Singh, J. N. Kolev, P. A. Sutera and R. Fasan, ACS Catal., 2015, 5, 1685–1691 CrossRef CAS PubMed.
- R. T. Gephart and T. H. Warren, Organometallics, 2012, 31, 7728–7752 CrossRef CAS.
- S. M. Paradine, J. R. Griffin, J. Zhao, A. L. Petronico, S. M. Miller and M. C. White, Nat. Chem., 2015, 7, 987–994 CrossRef CAS PubMed.
- Q. Zhang, C. Wu, L. Zhou and J. Li, Organometallics, 2013, 32, 415–426 CrossRef CAS.
- Q. Nguyen, T. Nguyen and T. G. Driver, J. Am. Chem. Soc., 2013, 135, 620–623 CrossRef CAS PubMed.
- H. Wang, Y. Li, Z. Wang, J. Lou, Y. Xiao, G. Qiu, X. Hu, H. J. Altenbach and P. Liu, RSC Adv., 2014, 4, 25287–25290 RSC.
- G. Manca, C. Mealli, D. M. Carminati, D. Intrieri and E. Gallo, Eur. J. Inorg. Chem., 2015, 29, 4885–4893 CrossRef.
- E. T. Hennessy, R. Y. Liu, D. A. Iovan, R. A. Duncan and T. A. Betley, Chem. Sci., 2014, 5, 1526–1532 RSC.
- (a) T. L. Lam, K. C.-H. Tso, B. Cao, C. Yang, D. Chen, X.-Y. Chang, J.-S. Huang and C.-M. Che, Inorg. Chem., 2017, 56, 4253–4257 CrossRef CAS PubMed; (b) F. Collet, C. Lescot, C. Liang and P. Dauban, Dalton Trans., 2010, 39, 10401–10413 RSC.
- A. Nörder, S. A. Warren, E. Herdtweck, S. M. Huber and T. Bach, J. Am. Chem. Soc., 2012, 134, 13524–13531 CrossRef PubMed.
- J. W. W. Chang, T. M. U. Ton and P. W. H. Chan, Chem. Rec., 2011, 11, 331–357 CrossRef CAS PubMed.
- C. G. Espino, K. W. Fiori, M. Kim and J. Du Bois, J. Am. Chem. Soc., 2004, 126, 15378–15379 CrossRef CAS PubMed.
- J. L. Roizen, D. N. Zalatan and J. Du Bois, Angew. Chem., Int. Ed., 2013, 52, 11343–11346 CrossRef CAS PubMed.
- E. N. Bess, R. J. DeLuca, D. J. Tindall, M. S. Oderinde, J. L. Roizen, J. Du Bois and M. S. Sigman, J. Am. Chem. Soc., 2014, 136, 5783–5789 CrossRef CAS PubMed.
- K. W. Fiori and J. Du Bois, J. Am. Chem. Soc., 2007, 129, 562–568 CrossRef CAS PubMed.
- (a) R. J. Scamp, J. G. Jirak, N. S. Dolan, I. A. Guzei and J. M. Schomaker, Org. Lett., 2016, 18, 3014–3017 CrossRef CAS PubMed; (b) M. E. Harvey, D. G. Musaev and J. Du Bois, J. Am. Chem. Soc., 2011, 133, 17207–17216 CrossRef CAS PubMed; (c) J. M. Alderson, A. M. Phelps, R. J. Scamp, N. S. Dolan and J. M. Schomaker, J. Am. Chem. Soc., 2014, 136, 16720–16723 CrossRef CAS PubMed; (d) K. W. Fiori, C. G. Espino, B. H. Brodsky and J. Du Bois, Tetrahedron, 2009, 65, 3042–3051 CrossRef CAS.
- X. H. Zhao, L. W. Chung and Y. D. Wu, Acc. Chem. Res., 2016, 49, 1302–1310 CrossRef PubMed.
- (a) V. Lyaskovskyy, A. I. O. Suarez, H. Lu, H. Jiang, X. P. Zhang and B. de Bruin, J. Am. Chem. Soc., 2011, 133, 12264–12273 CrossRef CAS PubMed; (b) Q. Ren, X. Shen, J. Wan and J. Fang, Organometallics, 2015, 34, 1129–1136 CrossRef CAS.
- (a) A. Varela-Álvarez, T. Yang, H. Jennings, K. P. Kornecki, S. N. Macmillan, K. M. Lancaster, J. B. C. Mack, J. Du Bois, J. F. Berry and D. G. Musaev, J. Am. Chem. Soc., 2016, 138, 2327–2341 CrossRef PubMed; (b) J. F. Berry, Dalton Trans., 2012, 41, 700–713 RSC; (c) X. Zhang, H. Xu and C. Zhao, J. Org. Chem., 2014, 79, 9799–9811 CrossRef CAS PubMed; (d) H. Xu, X. Zhang, Z.-F. Ke, Z.-F. Li, X.-Y. Xu, C.-Y. Su, D. L. Phillips and C. Zhao, RSC Adv., 2013, 3, 17131–17142 RSC; (e) H. Xu, K. Muto, J. Yamaguchi, C. Zhao, K. Itami and D. G. Musaev, J. Am. Chem. Soc., 2014, 136, 14834–14844 CrossRef CAS PubMed.
- (a) J. Wang, C. Zhao, Y. Weng and H. Xu, Catal. Sci. Technol., 2016, 6, 5292–5303 RSC; (b) J. Wang, Theore-tical Studies on the Mechanisms of C-N/C Formation and Cleavage Promoted by Transition Metal Complexes, Ph.D. thesis, Sun Yat-sen University, 2010.
- J. Wang, H. Xu, H. Gao, C.-Y. Su, C. Zhao and D. L. Phillips, Organometallics, 2010, 29, 42–51 CrossRef CAS.
- (a) J. Wang, K. Zheng, T.-F. Miao and E. Zhang, Sci. Adv. Mater., 2017, 9, 1197–1208 CrossRef; (b) K. Zheng, J. Wang, Y. Shen, W. Peng and F. Yun, J. Comput. Chem., 2002, 23, 436–443 CrossRef CAS PubMed; (c) K. Zheng, J. Wang, Y. Shen, W. Peng and F. Yun, Dalton Trans., 2002,(1), 111–116 RSC; (d) K. Zheng, J. Wang, Y. Shen, D. Kuang and F. Yun, J. Phys. Chem. A, 2001, 105, 7248–7253 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- S. J. Gustafson, J. T. Fuller III, D. Devarajan, J. Snyder, R. A. Periana, B. G. Hashiguchi, M. M. Konnick and D. H. Ess, Organometallics, 2015, 34, 5485–5495 CrossRef CAS.
- T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed.
- T. G. Driver, Nat. Chem., 2013, 5, 736–738 CrossRef CAS PubMed.
- (a) U. Steinbrenner, A. Bergner, M. Dolg and H. Stoll, Mol. Phys., 1994, 82, 3–11 CrossRef CAS; (b) A. Henglein, J. Phys. Chem., 1993, 97, 5457–5471 CrossRef CAS; (c) M. Kaupp, P. V. R. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366 CrossRef CAS; (d) W. H. Lam, K. C. Lam, Z. Lin, S. Shimada, R. N. Perutz and T. B. Marder, Dalton Trans., 2004,(10), 1556–1562 RSC.
- (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS; (b) J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214 CrossRef CAS.
- (a) K. J. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS; (b) R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter and J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- C. Kong, N. Jana, C. Jones and T. G. Driver, J. Am. Chem. Soc., 2016, 138, 13271–13280 CrossRef CAS PubMed.
- N. Dolan, R. J. Scamp, T. Yang, J. F. Berry and J. M. Schomaker, J. Am. Chem. Soc., 2016, 138, 14658–14667 CrossRef CAS PubMed.
- J. G. Harrison, O. Gutierrez, N. Jana, T. G. Driver and D. J. Tantillo, J. Am. Chem. Soc., 2016, 138, 487–490 CrossRef CAS PubMed.
- B. Bagh, D. L. J. Broere, V. Sinha, P. F. Kuijpers, N. P. V. Leest, B. D. Bruin, S. Demeshko, M. A. Siegler and J. I. V. D. Vlugt, J. Am. Chem. Soc., 2017, 139, 5117–5124 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Intramolecular C–H amination process (Fig. S1), important frontier orbital diagrams of Rh2-nitrene (Fig. S2), mechanisms of intramolecular C–H aminations (Fig. S3), optimized structures for intermolecular aminations (Fig. S4), surface plots of the spin density distribution (Fig. S5), NBO charges for inter- and intramolecular aminations (Table S1), and the Cartesian coordinates for the calculated structures (Table S2). See DOI: 10.1039/c7ra05032a |
| This journal is © The Royal Society of Chemistry 2017 |