Open Access Article
Open Access ArticleFirst principles DFT study of interstitial hydrogen and oxygen atoms in the MAX phase Ti2AlN
Francesco Colonna ab and
Christian Elsässerba
ab and
Christian Elsässerba
aUniversity of Freiburg, Freiburg Materials Research Center (FMF), Stefan-Meier-Straße 21, 79108 Freiburg, Germany. E-mail: francesco.colonna@fmf.uni-freiburg.de
bFraunhofer Institute for Mechanics of Materials IWM, Wöhlerstraße 11, 79108 Freiburg, Germany. E-mail: christian.elsaesser@iwm.fraunhofer.de
First published on 1st August 2017
Abstract
MAX phases are ternary metal carbides and nitrides with multi-layered crystal structures and mixed metallic-covalent bonding. They have very good thermal, chemical, and mechanical properties which make them potentially suitable as corrosion protection coatings for high-temperature energy-conversion devices such as solid oxide fuel cells. To assess the capability of MAX phases as diffusion barriers for hydrogen and oxygen, we investigate absorption and migration of interstitial H and O atoms in the MAX phase Ti2AlN by means of first-principles calculations based on density functional theory. The resulting calculated formation and migration energies indicate that a Ti2AlN coating can act as a protective diffusion barrier for both oxygen and hydrogen, but according to two different mechanisms.
1 Introduction
MAX phases are a class of ternary nano-multi-layered crystalline compounds which exhibit an outstanding combination of high mechanical stiffness, electrical and thermal conductivity, corrosion resistance, and tolerance to thermomechanical shocks.1,2 All these properties make MAX phases an interesting class of materials for a wide spectrum of technological applications.Recently, the proposed applicability of MAX as protective surface coatings of irradiated bulk metallic materials in nuclear fission or fusion reactors has stimulated several simulation studies of properties of atomic defects in MAX phases.3–5 The investigation of atomic defects, namely their formation and migration properties, is of great interest also for corrosion-protection applications in other thermo-chemo-mechanically aggressive environments. Solid Oxide Fuel Cells (SOFCs) operated at intermediate temperatures are an interesting case for the potential use of MAX phases as protective coatings. The SOFC technology offers an environment-friendly and cost-effective way of efficient energy conversion. However, the success of SOFC stack devices is impeded by the fast corrosive degradation of the stainless-steel interconnect plates between the individual oxydic cells and the concomitant cathode poisoning of the cells.6,7 Indeed, to prevent the degradation in oxidizing and reducing environments at the operating temperatures of 600–800 °C, interconnect plates made of chromium-alloyed steel6–8 are used. This material, in turn, is prone to the formation of chromium hydroxides at the surface of the interconnect plate, their subsequent evaporation, and their deposition on the surface of the oxydic cell cathode.
This chromium-poisoning mechanism is often responsible for a rapid decrease in the efficiency of energy conversion in SOFCs.7–10 Since MAX phases are known to be electrically conducting and stable in both hot and corrosive environments, they offer a good potential to be deployed as a protective surface coating for the steel interconnect plates in SOFCs stacks, and they may also enable the use of steels containing a lower concentration of chromium and thus leading to chromium poisoning at a reduced rate. In order to achieve the goal of long-term stable and efficient SOFC stack devices, it is essential to evaluate the capability of MAX phases as a protective barrier against the diffusion of both hydrogen and oxygen atoms.
Important pre-requisites for MAX phases to be usable in SOFC applications are a good thermal stability at the operation temperature and a coefficient of thermal expansion (CTE) close to those of the ceramic oxide cathodes and electrolytes, which typically range between 10.5 and 12.5 × 10−6 K−1.7,8
In this work, employing a computational first-principles method based on density functional theory (DFT), we investigate the solution of interstitial hydrogen and oxygen atoms and the pathways and barriers for their migration in the crystal structure of the prominent MAX phase Ti2AlN. The elucidation of the migration mechanisms for interstitial atoms in Ti2AlN allows to assess the potential of such a MAX phase as a protective coating material. In Section 2 we describe the computational DFT method and the atomistic structure models used for the investigation. In Section 3.1 we report our results on the solution of interstitial H and O atoms in Ti2AlN. In Section 3.2 we illustrate the migration paths, report the calculated energy barriers, and describe the distinct migration mechanisms for H and O. In Section 4 we discuss the results. Finally in Section 5 we make a summary and give some conclusions.
2 Structural models and computational method
2.1 Composition and structure of the MAX phase Ti2AlN
MAX phases are defined by the composition formula Mn+1A1Xn (n = 1, 2 or 3), where M is a transition-metal element, A is a main-group element, and X is either carbon or nitrogen. Atoms are arranged in a hexagonal crystal structure, space group P63/mmc (193), with Mn+1Xn layers interleaved by an A monolayer.2.2 Methodological details of the DFT calculations
To model formation energies and migration barriers of interstitial atoms, a hexagonal 2 × 2 × 1 supercell of the Ti2AlN crystal was used. The supercell was structurally relaxed by first-principles DFT calculations of total energies, forces, and stresses, using the GGA-PBE functional for exchange–correlation.11 All DFT calculations were done with the PWscf code of the Quantum Espresso software package12 and run with an ASE interface.13 The wave-functions of the valence electrons are represented by a plane-waves basis set with a cutoff energy of 544 eV, and the electron density and effective Kohn–Sham potential by discrete Fourier series with a cutoff energy of 2721 eV. The interactions of valence electrons with the atomic nuclei and core electrons are described by Vanderbilt's ultrasoft pseudopotentials as provided in the open-source pseudopotential library ‘GRBV’.14 Brillouin-zone integrals are evaluated on a Monkhorst–Pack mesh of 6 × 6 × 4 k-points with a Gaussian smearing of 0.02 eV. The convergence criteria was set to 1.36 × 10−6 eV for the total energy and to 2.57 × 10−4 eV Å−1 for the forces on atoms.All thermodynamic quantities were calculated following the ab initio thermodynamics formalism15 at zero pressure and temperature. The solution energy Ef[X, i] of an atom X (X = H or O) at an interstitial site i in the supercell of the Ti2AlN crystal is calculated as
| Ef[X, i] = Etot[X, i] − Etot[bulk] + μX | (1) |
To validate the computational methodology, the lattice parameters of Ti2AlN and formation energies of the three intrinsic point defects, namely the monovacancies vTi, vAl and vN were calculated and compared to literature benchmarks. Both the resulting lattice-parameter values (a = 2.995 and c = 13.65) and the formation energies for vTi, vAl and vN (3.48 eV, 3.03 eV, and 4.58 eV respectively) are in agreement with data from previous experimental measurements18 and DFT simulations.4 In Fig. 1 we compare our results for the vacancy formation energies (top) and the chemical potentials (bottom) to literature data.
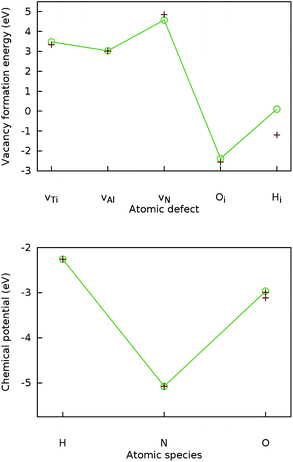 | ||
| Fig. 1 Validation of the computational DFT setup. Top: Calculated formation energies (connected by lines) for the Ti, Al, and N vacancies in Ti2AlN and for the H and O interstitials in the octahedral position Ti3Al3 compared to literature benchmarks4 (crosses). Bottom: Calculated chemical potentials (connected by lines) for H, N, and O compared to literature benchmarks16 (crosses). | ||
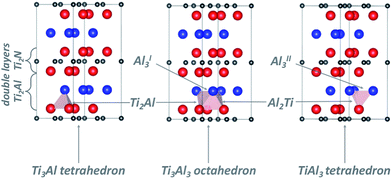
2.3 Interstitial sites for H and O atoms in the MAX phase Ti2AlN
Following the work of Baben et al.19 on Ti2AlC, Duan et al.4 investigated the solution of oxygen and hydrogen atoms at substitutional positions as well as at octahedral (Ti3Al3) and triangular (Al3) interstitial sites of the Ti2AlN crystal. Cui et al.20 reported that the dynamics of oxidation of Ti2AlN differs from that of Ti2AlC. Therefore we extended the previous studies by considering the whole set of interstitial locations in the Ti2Al (Ti–Al–Ti) double layer which are relevant for the solution and migration of H and O atoms (see Fig. 2): the Ti3Al3 octahedron, the Ti3Al and TiAl3 tetrahedrons, and the two non-equivalent triangular barrier locations AlI3 and AlII3 in the Al-plane. Moreover, Ti4 tetrahedral sites in the Ti2N (Ti–N–Ti) double layer are also considered.The migration barriers were assumed to be located either at the interface of face-sharing polyhedrons (see Fig. 2), or at the centre of N–N bonds of the Ti2Al (Ti–Al–Ti) double layer for symmetry considerations. Migration barriers were obtained via a structural relaxation in which hydrogen atoms were constrained either on the planes spanned by triangles on the polyhedron's faces, or at the N–N bond centres.
3 Results
3.1 Solution of interstitial H and O atoms
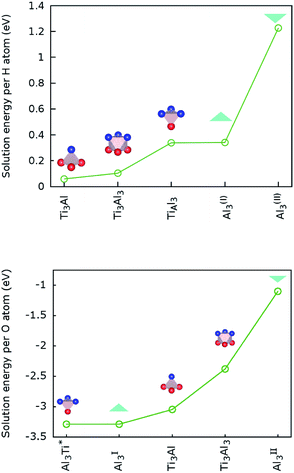
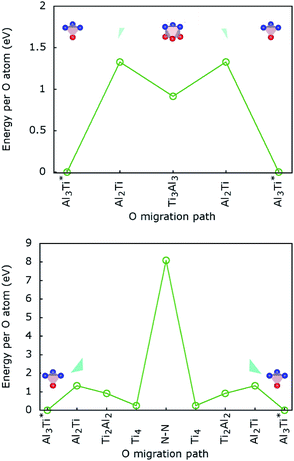
Baben et al. reported that interstitial sites are the most stable sites for atomic species dissolved in Ti2AlC and other MAX-phase carbides.19Our results for H atoms in Ti2AlN, which are displayed in Fig. 3 (top), are that hydrogen has a positive (endothermal) solution energy for all the interstitial sites introduced in Section 2.3. This means that H does not dissolve spontaneously in crystalline Ti2AlN. Its most (meta-)stable interstitial site is the tetrahedral site Ti3Al with an endothermal but close to zero solution energy of 0.06 eV. The octahedral site Ti3Al3 is the next (meta-)stable site with an endothermal solution energy of 0.1 eV. Zero point energy (ZPE) correction slightly lowers the computed solution energy for H. However, we do not expect ZPE correction to change any of the conclusions.
In contrast, oxygen exhibits a negative (exothermal) solution energy of several eV for all the interstitial sites. The results are displayed in Fig. 3 (bottom). The most stable positions for an O atom are the tetrahedral site Al3Ti and the triangular barrier location Al3. Their very small energy difference is within the computational accuracy limit. Since the Al3 triangle is the interface separating two mirror-imaged Al3Ti tetrahedra, these two geometrical locations are effectively within one single site surrounded by a triangular bipyramidal Al3Ti2 cage. The solution energy for this site is −5.51 eV. The solution energies of the tetrahedral Ti3Al and octahedral Ti3Al3 sites are higher by 0.24 and 0.91 eV, respectively. For the interstitial oxygen atom at the Ti3Al3 site our calculated solution-energy value −2.38 eV is 0.18 eV higher than the value reported by Duan et al.4
3.2 Migration of interstitial H and O atoms
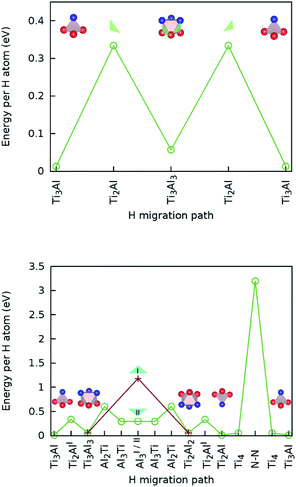
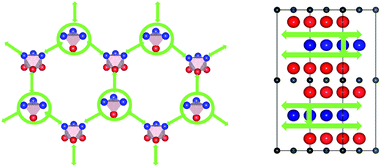
The calculated lowest migration-barrier value for interstitial hydrogen resulted to be 0.32 eV for the path TiAl3 → Ti3Al3. The inverse path has a slightly lower barrier of 0.28 eV. The barrier for the path Ti3Al3 → Ti3Al is about twice as high. These results indicate the presence of two parallel, mirror-imaged, diffusion networks in between neighbouring Ti and Al layers, as illustrated in Fig. 5 (right). Indeed, a hydrogen atom can get to the mirror-imaged Ti–Al layer via the path Ti3Al → Ti3Al3 → TiAl3 → Ti3Al3 → Ti3Almirror3 → Ti3Almirror. This migration path has a barrier of 1.2 eV, which is associated with the Ti3Al3 → TiAl3 step and located in the AlI3 triangle. A schematic representation of these diffusion channels is shown in Fig. 5 (left). An interstitial H atom migrating in the c-axis direction of the MAX crystal, with a transition state assumed in a N–N bond as motivated above, has to overcome a high barrier of more than 3 eV, which is one order of magnitude higher than the barriers in the ab-plane directions.
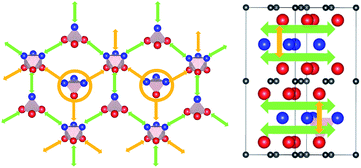
Hence, the network of migration pathways for long-range diffusion of interstitial H atoms in Ti2AlN can be described as follows: there are two mirror-imaged honey-comb networks between two neighbouring planes of Ti and Al atom with a migration barrier of 0.32 eV. These networks enable the long-range diffusion in the “lateral” directions, i.e. in the ab-plane spanned by the lattice vectors ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) and
and ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) of the hexagonal cell. The networks are further connected by a shifted hexagonal network with a barrier of 1.2 eV, which allows for a migration in the c-axis (transversal) direction at least between the adjacent Ti2Al double layer. The migration to a more remote Ti2Al double layer is hindered by the presence of the Ti2N double layer in between, with a barrier that is one order of magnitude higher. This network of pathways is illustrated by the schematic sketches in Fig. 5.
of the hexagonal cell. The networks are further connected by a shifted hexagonal network with a barrier of 1.2 eV, which allows for a migration in the c-axis (transversal) direction at least between the adjacent Ti2Al double layer. The migration to a more remote Ti2Al double layer is hindered by the presence of the Ti2N double layer in between, with a barrier that is one order of magnitude higher. This network of pathways is illustrated by the schematic sketches in Fig. 5.
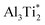 . Therefore in the case of oxygen the channels for long-range diffusion in the two mirror-imaged planes of the Ti2Al double layer are separated by virtually no barrier. As a result, there is one single effective honey-comb network for the ab-plane diffusion that connects directly two stable interstitial sites along the migration path
. Therefore in the case of oxygen the channels for long-range diffusion in the two mirror-imaged planes of the Ti2Al double layer are separated by virtually no barrier. As a result, there is one single effective honey-comb network for the ab-plane diffusion that connects directly two stable interstitial sites along the migration path 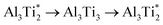 .
.The migration barrier for the path 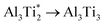 is 1.37 eV and located at the triangular Al2Ti face as shown in Fig. 6. The barrier for the inverse path
is 1.37 eV and located at the triangular Al2Ti face as shown in Fig. 6. The barrier for the inverse path 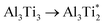 is 0.42 eV. The interstitial diffusion through the Ti2N double layers is hindered by a large barrier of over 8 eV (Fig. 6). The resulting diffusion network is depicted schematically in Fig. 7. As in the case of hydrogen the ab-plane migration for oxygen has a much lower barrier than the c-axis migration. In contrast to hydrogen, the ab-plane migration of oxygen has a simpler mechanism, namely Al3Ti* → Al3Ti3 → Al3Ti*, on a honey-comb network. But for oxygen there is a more than four times higher barrier as compared to that of hydrogen.
is 0.42 eV. The interstitial diffusion through the Ti2N double layers is hindered by a large barrier of over 8 eV (Fig. 6). The resulting diffusion network is depicted schematically in Fig. 7. As in the case of hydrogen the ab-plane migration for oxygen has a much lower barrier than the c-axis migration. In contrast to hydrogen, the ab-plane migration of oxygen has a simpler mechanism, namely Al3Ti* → Al3Ti3 → Al3Ti*, on a honey-comb network. But for oxygen there is a more than four times higher barrier as compared to that of hydrogen.
4 Discussion
There is only few discussion in literature about the absorption and diffusion of hydrogen in MAX phases. A MAX phases coating can protect a substrate from diffusing hydrogen in two ways: (1) by a high migration barrier, and (2) by a high solution energy, which hinders the absorption of the diffusing species in a first place. In the literature hydrogen absorption on interstitial sites is reported to be favoured by a slightly negative (exothermal) energy of solution, however depending on its chemical potential as function of the thermodynamic conditions.4 In the hydrogen-rich limit, instead, we get a close-to-zero but positive (endothermal) solution energy of 0.06 eV for a H atom at a Al3Ti site. This value is lower than the solution energy of hydrogen in α-iron (DFT-GGA values: 0.19 eV,21 0.16;22 experimental values: 0.296 eV,23 0.28 eV 24), which indicates that Ti2AlN cannot act as a diffusion barrier for iron-based interconnects by hindering absorption.The calculated migration barriers for both interstitial H and O atoms indicate strongly anisotropic diffusion in the MAX phase. Even in the absence of other atomic or microstructural defects, hydrogen is expected to be relatively mobile along the Ti–Al ab-planes because of its modest activation barrier of 0.32 eV for migration. This value can be compared to the ab-plane diffusion in the MAX phase Ti3AlC2, which was recently calculated by Yang et al.25 Here two non-equivalent barriers of 0.21 eV and 0.67 eV along the [−1, 0, 0] and [0, 1, 0] directions were found, indicating as well a fast ab-plane diffusion of interstitial hydrogen. Hence, the potential of Ti2AlN as a diffusion barrier for hydrogen is apparently linked to the capability of depositing dense Ti2AlN films with the ab-plane atomic layers of Ti, Al, and N growing parallel to the surface of the substrate. In this case the high migration barrier of the Ti2N double layer in the c-axis direction can effectively impede the diffusion of hydrogen.
The situation is more complicated for the case of oxygen. Recently Cui et al.20 investigated spark plasma sintered Ti2AlN and its oxydic surface scales formed after high-temperature oxidation for 1 hour. Below 900 °C (i.e. at operation temperatures of SOFCs) a double-layer scale is formed: the first layer is composed of porous TiO2 scale in contact with the bulk Ti2AlN phase, the second layer is a dense mixture of TiO2 and α-Al2O3 with a nominal composition Al2TiO5. At higher temperatures (1000–1400 °C), a complex interplay of mixing and demixing of α-Al2O3 and Al2TiO5 phases is observed. Above 1100 °C the growth rate of the scale increases steeply and void-containing layers are formed, probably due to the formation of gaseous NOx. These temperatures are above the stability limit of the MAX phase, as reported by Scabarozi et al.26 The emerged scenario is consistent with our finding that oxygen tends to be absorbed interstitially in Ti2Al double layers and to diffuse along these. Only at very high temperatures there may be some incorporation of oxygen atoms into the Ti2N double layers, which may be also facilitated by dislocations or cracks induced by the mismatch in the thermal expansions of the oxydic constituents of the scale and the bulk MAX phase. It is not clear whether complicated mixing and demixing of TiO2, α-Al2O3, and Al2TiO5 should be expected for longer operation times of SOFCs also at temperatures below 900 °C. Zhang et al.27 showed that thin films of Ti2AlN oxidized at 900 °C for 20 hours have an α-Al2O3 scale with a low content of TiO2 second phase growing parabolically in time. This indicates a diffusion-limited growth mechanism, which can be associated to slow diffusion of oxygen through the surface scale and into the Ti2AlN. Moreover, they find a low oxygen content in the interior of the Ti2AlN layer, which also indicates a diffusion rate which is significantly lower than that of H atoms, in line with our results. The analysis of results of simulations and experiments, therefore, indicates that for the case of oxygen a two-fold protection mechanism is apparently present. First, due to the formation of an oxydic scale, solution of oxygen inside the MAX phase is hindered, except for an adsorption on the surface. Second, due to a high migration barrier for interstitial oxygen in all crystal directions of the MAX phase, the oxydic scale remains confined to the surface. In contrast to the case of hydrogen, the migration barrier for oxygen is therefore expected to be significantly high even for the diffusion in the ab-plane of the MAX-phase crystal.
5 Summary and conclusions
Solution and migration of interstitial hydrogen and oxygen atoms in the MAX-phase crystal Ti2AlN were investigated in order to assess the potential capability of a MAX phase to act as a protective diffusion-barrier coating of steel components in SOFC stacks. There are further mechanisms for the solution and migration of hydrogen and oxygen relevant in practice, namely substitutional solution and vacancy-mediated diffusion of foreign atomic species inside the crystal structure or at extended microstructural defects, namely dislocations and grain boundaries. The present study, however, focused on the evaluation of the protection potential of Ti2AlN by assessing the case of the ideal crystalline limit, where no other defects than the interstitial H or O atoms are present. We obtained solution energies and migration barriers by means of first-principles DFT calculations. The results indicate that a Ti2AlN coating layer can act as a barrier against diffusion of interstitial H atoms in the c-axis direction of the MAX phase but offers no significant protection against diffusion along ab-plane directions. For interstitial O atoms, in contrast, the migration barriers in all directions are of the order of several eV. Moreover, absorption calculations and experimental results reported in the literature suggest that, when the surface of a MAX phase is in contact with oxygen, alumina and titania scales are formed. Hence, we speculate that a Ti2AlN coating on a steel interconnect plate has the potential to act as a protective diffusion barrier for hydrogen and oxygen in a SOFC stack, provided that the formation of a compact, coarse-grained, well c-axis oriented, and well ab-plane textured Ti2AlN coating can be achieved on steel by a robust and efficient deposition process.Acknowledgements
This research is supported by the Baden-Württemberg Stiftung GmbH through the research programme “CleanTech” (project CT-6 “LamiMat”). We thank Dr D. Di Stefano, Mr L. Gröner, and Dr F. Burmeister for valuable discussions, and Dr B. Ziebarth for his interface of the PWScf code to the ASE software.References
- M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281 CrossRef CAS
.
- P. Eklund, M. Beckers, U. Jansson, H. Högberg and L. Hultman, Thin Solid Films, 2010, 518, 1851–1878 CrossRef CAS
.
- S. C. Middleburgh, G. R. Lumpkin and D. Riley, J. Am. Ceram. Soc., 2013, 96, 3196–3201 CrossRef CAS
.
- J. Z. Duan, J. R. Zhang, C. L. Wang, Y. Qiu, W. S. Duan and L. Yang, RSC Adv., 2014, 4, 42014–42021 RSC
.
- Z. Zhang, H. Jin, J. Pan, J. Chai, L. M. Wong, M. B. Sullivan and S. J. Wang, J. Phys. Chem. C, 2015, 119, 16606–16613 CAS
.
- J. Wu and X. Liu, J. Mater. Sci. Technol., 2010, 26, 293–305 CAS
.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS
.
- G. Jia and L. Yang, Phys. B, 2010, 405, 4561–4564 CrossRef CAS
.
- J. Fergus, Int. J. Hydrogen Energy, 2007, 32, 3664–3671 CrossRef CAS
.
- N. Shaigan, W. Qu, D. G. Ivey and W. Chen, J. Power Sources, 2010, 195, 1529–1542 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS
.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS
.
- C. G. V. de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef
.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef
.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 5419–5423 Search PubMed
.
- M. W. Barsoum, M. Ali and T. El-Raghy, Metall. Mater. Trans. A, 2000, 31, 1857–1865 CrossRef
.
- M. Baben, L. Shang, J. Emmerlich and J. M. Schneider, Acta Mater., 2012, 60, 4810–4818 CrossRef CAS
.
- B. Cui, D. D. Jayaseelan and W. E. Lee, Acta Mater., 2011, 59, 4116–4125 CrossRef CAS
.
- D. E. Jiang and E. A. Carter, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064102 CrossRef
.
- D. Di Stefano, R. Nazarov, T. Hickel, J. Neugebauer, M. Mrovec and C. Elsässer, Phys. Rev. B, 2016, 93, 184108 CrossRef
.
- J. P. Hirth, Metall. Trans. A, 1980, 11, 861–890 CrossRef
.
- H. Wipf, Phys. Scr., T, 2001, 94, 43–51 CrossRef
.
- S. Yang, N. Hu, X. Gou, C. Wang, X. Zhu, X. Duan, W. Duan and L. Yang, RSC Adv., 2016, 6, 59875–59881 RSC
.
- T. H. Scabarozi, S. Amini, O. Leaffer, A. Ganguly, S. Gupta, W. Tambussi, S. Clipper, J. E. Spanier, M. W. Barsoum, J. D. Hettinger and S. E. Lofland, J. Appl. Phys., 2009, 105, 13543 CrossRef
.
- T. Zhang, H.-B. Myoung, D.-W. Shin and K. H. Kim, J. Ceram. Process. Res., 2012, 13, S149–S153 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2017 |